Introduction

Cotton is widely used to make fabrics such as garments, bedding, curtains, and carpets (Wang et al. 2018). Hence, it is an important fiber in the textile industry. About 25 million tons of cotton are produced annually around the world and most of them (~ 50%) are used to make the clothes (Ahmad et al. 2021). Cotton fabric is popular because it has advantages including softness, biodegradability, comfort, hypoallergenic, breathability, and environmentally friendly (being a natural fiber) (Xie et al. 2013). However, similar to other natural fibers, cotton fiber contains natural pigments that cause it to appear in yellowish-brown in natural (Oliveira et al. 2018). It must be noted that environmental factors such as soil, dust, smoke, dirt, and insects could also possibly affect the color of cotton fiber. In general, the yellowish-brown of cotton is visually associated with soiling or the lack of cleanliness and it is an attribute that must be removed.

Industrially, cotton fabric bleaching is a chemical oxidation process used to remove the yellowish-brown coloration from cotton by damaging the colorant (Oliveira et al. 2018). In other words, the bleaching process is responsible for eliminating the coloring materials from the cotton fiber to have a pure white appearance. A white fabric is highly desirable as it gives the impression of clean and pure (Jung and Sato 2013). Hence, the whiteness degree of cotton fabric is the main requirement of bleaching. Besides, the bleaching process that uses strong reducing or oxidizing agents is able to get rid of potentially hazardous contaminants such as bacteria, molds, and fungi (Gültekin 2016).

Hydrogen peroxide (H2O2) is one of the commonly used bleaching agents and is highly effective to oxidize the coloring matters (Oliveira et al. 2018). It is more preferable compared to chlorine bleach because it is gentler and less toxic (Bajpai 2007). Additionally, optical brighteners can be added to the bleaching process to increase whiteness levels (Oliveira et al. 2018). After the bleaching process, the whiteness index (WI) that indicates the whiteness degree of the cotton is measured. Whiteness is defined in colorimetric terms as a color with the highest luminosity, no hue, and no saturation. The WI is calculated from the data computed by colorimetric instruments such as colorimeter and spectrophotometer. The higher the WI, the greater the whiteness degree of the measured cotton and vice versa (Topalovic et al. 2007). If the preferred white fabric has a high reflectance, then the ideal reflectance for textile materials should approach 100 (Ferdush et al. 2019).

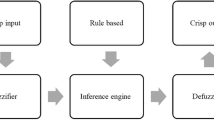
The WI of the bleached cotton fabric is perpendicular to the time duration of the bleaching process and the amount of H2O2 (Haque and Islam 2015). Contrastingly, the bursting strength of the cotton fabric decreases at prolonged duration of the bleaching process and the increase in the H2O2 concentration. On the other hand, the higher temperature can improve the rate of bleaching and shorten the processing time (Abdul and Narendra 2013). Therefore, a colorimetric analysis is usually conducted to assess and investigate the bleaching procedure on the cotton samples. Artificial neural networks and adaptive neuro-inference systems have been used as prediction models in the textile domain. However, these models require large amount of data for model parameters optimisation and are quite time consuming. To address this issue, a fuzzy predictive model had been developed by Haque et al. (2018) using a fuzzy logic designer app in MATLAB to predict the WI of cotton using the bleaching process parameters that are nonlinear. Nevertheless, this fuzzy model is unable to predict the WI for the bleaching process parameters that are not within the ranges of the input data. It does not have the capability of machine learning models such as least square support vector regression (LSSVR).

Machine learning models including LSSVR models can learn information directly from data and understand their performance across a wide range of inputs (Wexler et al. 2019). LSSVR model exhibits good predictability to forecast the desired output variable, especially for nonlinear data. Hence, it received more attention and interest from researchers in many different areas over the years (Moosavi et al. 2021; Xu et al. 2013; Zhang and Wang 2021). But it was found that minimal research is conducted using the LSSVR model on color relevant studies including WI prediction.

Thus, in this study, an effective LSSVR model, namely multi-output LSSVR (MLSSVR) is developed using the bleaching process variables and results obtained from two different case studies to estimate the WI of bleached cotton. Then, the accuracy of LSSVR is evaluated by calculating the coefficient of determination (R2), root mean square error (RMSE), and absolute mean error (MAE). Additionally, the obtained results are compared with partial least square regression (PLSR), predictive fuzzy model, locally weighted partial least square regression (LW-PLSR), and locally weighted kernel partial least square regression (LW-KPLSR) models.

Materials and methods

This section explains the bleaching process, post-treatment of cotton fabric, and WI measurement. It is followed by the MLSSVR model development, regression models parameters setting, and accuracy of the predictive performance measurement. Lastly, computer hardware and software configuration specifications are illustrated.

Bleaching process of cotton fabric and whiteness index

Case study 1

In this case study, the experimental data was taken from Haque et al. (2018). A single jersey cotton knitted fabric of 130 g/cm2 was used as the fabric samples and a 12.5 g of fabric sample with a 1:10 material liquor ratio was treated in each bleaching time. The chemicals used in the bleaching process are H2O2 as bleaching agent (with its concentration set at 1.8 g/L, 2 g/L, and 2.2 g/L), 2 g/L of sodium hydroxide as caustic soda, and 1 g/L of kappazon H53 peroxide stabilizer. For each H2O2 concentration, the bleaching process was operated at six individual temperatures (T) (i.e., 78, 83, 88, 93, 98, 103 and 108 °C) and four different times (t) (i.e., 20, 30, 40, and 50 min).

Case study 2

Similar study was also conducted by Haque and Islam (2015) using a single jersey cotton fabric but with lower weight (110 g/cm2). H2O2 was also used as the bleaching agent with three different concentrations (1.8 g/L, 2 g/L, and 2.2 g/L). However, the bleaching solution was formulated differently. It contained 1 g/L of sodium hydroxide and 1 g/L of sodium silicate stabilizer (instead of kappazon H53 peroxide stabilizer). In terms of operation, the authors studied the effects of temperature (78, 88, 98, and 108 °C) and time (20, 30, 40 and 50 min) at four different intervals.

After bleaching process, both case studies subjected the bleached fabric samples to hot washing at 70 °C followed by cold washing at 27 °C. It was then squeezed by hand and dried at 70 °C for 30 min. Lastly, the WI for each bleached fabric sample was measured using a reflectance spectrophotometer (Data color 650). For case study 2, all the bleached fabric samples were further analysed using a bursting strength testing instrument (Autoburst, SDL Atlas) and by the ISO 13038–1 method. Figure 1 is the process flow involving bleaching operations, post-treatment of fabric samples, color, and bursting strength measurements.

Fig. 1
figure 1

Flowchart explaining the bleaching operations, post-treatment of fabric samples, color, and bursting strength measurements

Full size image

Commission on Illumination (CIE) WI is one of the widely used color measurement methods for computing a WI to measure the degree of whiteness of bleached cotton fabric (Xu et al. 2015). This CIE WI generally refers to measurements made under D65 illumination, which is a standard representation of outdoor daylight. The CIE WI under CIE 1964 10° standard observer can be represented by Eq. 1 (Haque et al. 2018; Jafari and Amirshahi 2008).

$$WI = Y_{L} + 800(x_{n} - x_{c} ) + 1700(y_{n} - y_{c} )$$
(1)

where \(Y_{L}\) is the lightness, \(x_{c}\) and \(y_{c}\) are chromaticity coordinates of the bleached cotton fabric samples, and \(x_{n}\) and \(y_{n}\) are chromaticity coordinates of the illuminant. However, the CIE WI has a constraint as shown in Eq. 2 (Jafari and Amirshahi 2008).

$$40 < WI < (5Y_{L} - 280)$$
(2)

Multi-output least square support vector regression model development

In this study, LSSVR model is developed from the bleaching process parameters to predict the WI of cotton fabrics. LSSVR model is a nonlinear prediction model that derives the support vector machine (SVM) theory (Liu and Yoo 2016). Different from the SVM, LSSVR gives a better solution for the reduction of the computational burden where a set of linear equations in a dual space is utilized. In this study, a MLSSVR model was adopted. Due to the multi-output setting in this MLSSVR, it becomes a more efficient training model. The examples of the results of the MLSSVR can be found in the work Xu et al. (2013) in which the MLSSVR were tested using synthetic, corn, polymer, and broomcorn data sets. However, this MLSSVR model has yet been used to examine cotton fabric data set.

The idea of MLSSVR comes from the multi-output case done by An et al. (2009). It is letting \(Y = [y_{i,j} ] \in \Re^{l \times m}\) where \(y_{i,j}\) is the (i,j)-th of an output, \(\Re\) is the set of real numbers, and \(l \times m\) is the order of a matrix. With a given total number of data sets, NT, i.e., \(\left\{ {(x_{i} ,y^{i} )} \right\}_{i = 1}^{l}\) where \(x_{i} \in \Re^{d}\) and \(y^{i} \in \Re^{m}\) are the input vector and output vector, respectively. And the multi-output regression has an objective to estimate an output vector \(y \in \Re^{m}\) from a given input vector \(x \in \Re^{d}\) where this regression problem can be built as learning a mapping from \(\Re^{d}\) to \(\Re^{m}\). Multi-output regression solves the problem by searching the weighed value vector, \(W = (w_{1} ,w_{2} ,...,w_{m} ) \in \Re^{{n_{h} \times m}}\) and a threshold value, \(b = (b_{1} ,b_{2} ,...,b_{m} )^{T} \in \Re^{m}\) that minimises the following objective function with constraints (Eqs. 3 and 4). According to the structural risk minimization principle, the actual risk bound by the empirical risk is minimized by the objective function (Eq. 3) with its constraint (Eq. 4). The real signification on these equations is to minimize the frequency of error in the training data set used to develop the MLSSVR model. Hence, the probability of error on the testing data set is expected to be small. For more details about the structural risk minimization principle, one is referred to the work of Vapnik (1992).

$$\begin{array}{*{20}c} {\min } \\ {W \in \Re^{{m \times n_{h} }} ,b \in \Re^{m} } \\ \end{array} \Im (W,\Xi ) = \frac{1}{2}trace(W^{T} W) + \gamma \frac{1}{2}trace(\Xi^{T} \Xi ),$$
(3)
$$s.t.{\text{ Y}} = {\text{Z}}^{{\text{T}}} {\text{W}} + {\text{repmat(b}}^{{\text{T}}} {\text{,l,1)}} + \Xi ,$$
(4)

where \(\gamma\) is a positive real regularised parameter, \(\xi = (\xi_{1} ,\xi_{2} ,...,\xi_{l} )^{T} \in \Re^{l}\) is a vector containing slack variables, \(Z = (\phi (x_{1} ),\phi (x_{2} ),...,\phi (x_{l} )) \in \Re^{{n_{h} \times l}} ,\phi :\Re^{d} \to \Re^{{n_{h} }}\) is a mapping to some high or even unlimited/ infinite dimensional Hilbert space or feature space via the nonlinear mapping function \(\phi\) with \(n_{h}\) dimensions, and \(\Xi = (\xi_{1} ,\xi_{2} ,...,\xi_{m} ) \in \Re_{ + }^{l \times m}\) is a \(l \times m\) matrix consisting of slack variables with \(\Re_{ + }\) the subset of positive ones. The slack variables are used to improve not only the generalization model performance but also to yield more compact and lower complexity model (Tang et al. 2015). These slack variables are non-negative and can tolerate misclassification in the training data that is used to develop the MLSSVR model.

It can be said that the solution to the regression problem shown in Eqs. 3 and 4 disconnects between the different output variables and only need to use Cholesky decomposition, conjugate gradient, or single value decomposition, etc. to compute a single inverse matrix once that is shared by all the vectors \(w_{i} (\forall_{i} \in {\rm N}_{m} )\). Unlike the single-output case, its solution to the regression problem needs to be solved multiple times. Hence, the multi-output regression is much more efficient than the single-output regression.

According to Xu et al. (2013), to formulate the intuition of Hierarchical Bayes, all \(w_{i} \in \Re^{{n_{h} }} (i \in {\rm N}_{m} )\) is assumed to be written as \(w_{i} = w_{0} + v_{i}\), where the vectors \(v_{i} \in \Re^{{n_{h} }} (i \in {\rm N}_{m} )\) are small when the different outputs are same to each other, otherwise the mean vector \(w_{0} \in \Re^{{n_{h} }}\) are small. It can be said that \(w_{0}\) takes the information of the commonality and \(v_{i} (i \in {\rm N}_{m} )\) brings the information of the specialty. \(w_{0} \in \Re^{{n_{h} }}\), \(V = (v_{1} ,v_{2} ,...,v_{m} ) \in \Re^{{n_{h} \times m}}\), and \(b = (b_{1} ,b_{2} ,...,b_{m} )^{T} \in \Re^{m}\) are solved spontaneously to minimise the following objective function with constraints (Eqs. 5 and 6):

$$\begin{array}{*{20}c} {\min } \\ {w_{0} \in \Re^{{n_{h} }} ,V \in \Re^{{n_{h} }} ,b \in \Re^{m} } \\ \end{array} \Im (w_{0} ,V,\Xi ) = \frac{1}{2}w_{0}^{T} w_{0} + \frac{1}{2}\frac{\lambda }{m}trace(V^{T} V) + \gamma \frac{1}{2}trace(\Xi^{T} \Xi ),$$
(5)
$$s.t. \, Y = Z^{T} W + repmat(b^{T} ,l,1) + \Xi ,$$
(6)

where \(\Xi = (\xi_{1} ,\xi_{2} ,...,\xi_{m} ) \in \Re^{l \times m}\), \(W = (w_{0} + v_{1} ,w_{0} + v_{2} ,...,w_{0} + v_{m} ) \in \Re^{{n_{h} \times m}}\), \(\lambda ,\gamma \in \Re_{ + }\) are two positive real regularised parameters, and \(Z = (\phi (x_{1} ),\phi (x_{2} ),...,\phi (x_{l} )) \in \Re^{{n_{h} \times l}}\).

The Lagrangian function for the problem shown in Eqs. 5 and 6 is defined as (Eq. 7):

$$\ell (w_{0} ,V,b,\Xi ,A) = \Im (w_{0} ,V,\Xi ) - trace(A^{T} (Z^{T} W + repmat(b^{T} ,l,1) + \Xi - Y)),$$
(7)

where \(A = (\alpha_{1} ,\alpha_{2} ,...,\alpha_{m} ) \in \Re^{l \times m}\) is a matrix containing of Lagrange multipliers. The Karush-Kuhn-Tucker conditions for optimality result in the linear equations as follows (Eq. 8):

$$\left\{ \begin{aligned} \frac{\partial \ell }{{\partial w_{0} }} = & 0 \Rightarrow w_{0} = \sum\limits_{i = 1}^{m} {Z\alpha_{i} ,} \\ \frac{\partial \ell }{{\partial V}} = & 0 \Rightarrow V = \frac{m}{\lambda }ZA, \\ \frac{\partial \ell }{{\partial {\text{b}}}} = & 0 \Rightarrow A^{T} 1_{l} = 0_{l} , \\ \frac{\partial \ell }{{\partial \Xi }} = & 0 \Rightarrow A = \gamma \Xi , \\ \frac{\partial \ell }{{\partial {\text{A}}}} = & 0 \Rightarrow Z^{T} W + {\text{repmat}}(b^{T} ,l,1) + \Xi - Y = 0_{l \times m} \\ \end{aligned} \right.$$
(8)

From Eq. 8, the mean vector, \(w_{0}\) is a linear combination of \(v_{1} ,v_{2} ,...,v_{m}\). As mentioned earlier since \(\forall_{i} \in {\rm N}_{m}\), so \(w_{i}\) is assumed to be \(w_{i} = w_{0} + v_{i}\) in which \(w_{i}\) is also a linear combination of \(v_{1} ,v_{2} ,...,v_{m}\). Hence, the following objective function (Eqs. 9 and 10) can obtain an equivalent optimisation problem with constraints including only the \(V\) and \(b\).

$$\begin{array}{*{20}c} {\min } \\ {V \in \Re^{{n_{h} }} ,b \in \Re^{m} } \\ \end{array} \Im (V,\Xi ) = \frac{1}{2}\frac{{\lambda^{2} }}{{m^{2} }}V1_{m} 1_{m}^{T} V^{T} + \frac{1}{2}\frac{\lambda }{m}trace(V^{T} V) + \gamma \frac{1}{2}trace(\Xi^{T} \Xi ),$$
(9)
$$s.t.{\text{ Y}} = {\text{Z}}^{{\text{T}}} {\text{V}} + {\text{repmat(}}\frac{\lambda }{m}{\text{Z}}^{{\text{T}}} {\text{V1}}_{{\text{m}}} {\text{,1,m)}} + {\text{repmat(b}}^{{\text{T}}} {\text{,l,1)}} + \Xi$$
(10)

From Eq. 9, MLSSVR figures out a trade-off between small size vectors for every output,\(trace(V^{T} V)\) and nearness of all vectors to the mean vector, \(V1_{m} 1_{m}^{T} V^{T}\). Like the standard LSSVR, \(W\) and \(\Xi\) are discharged to get the linear system as expressed in Eq. 11.

$$\left[ {\begin{array}{*{20}c} {0_{ml \times m} } & {P^{T} } \\ P & H \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} b \\ \alpha \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {0_{m} } \\ y \\ \end{array} } \right]$$
(11)

where \(P = blockdiag\overbrace {{(1_{l} ,1_{l} ,...,1_{l} )}}^{m} \in \Re^{ml \times m}\), \(H = \Omega + \gamma^{ - 1} I_{ml} + \left( {\frac{m}{\lambda }} \right)Q \in \Re^{ml \times ml}\),\(\Omega = repmat(K,m,m) \in \Re^{ml \times ml}\),\(Q = blockdiag\overbrace {(K,K,...K)}^{m} \in \Re^{ml \times ml}\), and \(K = Z^{T} Z \in \Re^{l \times l}\) are definite matrices while \(\alpha = (\alpha_{1}^{T} ,\alpha_{2}^{T} ,...,\alpha_{m}^{T} )^{T} \in \Re^{ml}\) and \(y = (y_{1}^{T} ,y_{2}^{T} ,...,y_{m}^{T} ) \in \Re^{ml}\) are vectors. Hence, the linear system shown in the Eq. 11 has \((l + 1) \times m\) equations.

Then, the solution of Eq. 11 can be written in term of \(\alpha^{*} = (\alpha_{1}^{*T} ,\alpha_{2}^{*T} ,...,\alpha_{m}^{*T} )^{T}\) and \(b^{*}\). Hence, the respective decision function for the multiple output is expressed as Eq. 12.

$$\begin{aligned} f(x) = & \phi (x)^{T} W^{*} + b^{{*T}} = \phi (x)^{T} repmat(w_{0}^{*} ,1,m) + \phi (x)^{T} V^{*} + b^{{*T}} \\ = & \phi (x)^{T} repmat(\sum\limits_{{il}}^{m} Z \alpha _{{il}}^{*} ,1,m) + \frac{m}{\lambda }\phi (x)^{T} ZA^{*} + b^{{*T}} \\ = & repmat(\sum\limits_{{il = 1}}^{m} {\sum\limits_{{j = 1}}^{l} {\alpha _{{il,j}}^{*} {\rm K}(x,x_{j} )} } ,1,m) + \frac{m}{\lambda }\sum\limits_{{j = 1}}^{l} {\alpha ^{{j*}} {\rm K}(x,x_{j} )} + b^{{*T}} \\ \end{aligned}$$
(12)

Same as the conventional LSSVR, the linear system of MLSSVR as displayed in Eq. 11 is not positive define, hence solving Eq. 11 instantly is hard. But it can be reconstructed into the following linear system (Eq. 13):

$$\left[ {\begin{array}{*{20}c} S & {0_{ml \times ml} } \\ {0_{m \times m} } & H \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} b \\ {H^{ - 1} Pb + \alpha } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {P^{T} H^{ - 1} y} \\ y \\ \end{array} } \right],$$
(13)

with \(S = P^{T} H^{ - 1} P \in \Re^{m \times m}\). Notice that it is easy to display \(S\) that is a positive definite matrix. Then, this new linear system as shown in Eq. 13 can be solved using the following three steps:

Step 1 Solve \(\eta\), and \(\nu\) from \(H\eta = P\) and \(H\nu = y\),

Step 2 Compute \(S = P^{T} \eta\),

Step 3 Obtain the solution:\(b = S^{ - 1} \eta^{T} y,\alpha = \nu - \eta b\).

Thus, in MLSSVR, the solution of the training procedure can be obtained by solving two sets of linear equations with the same positive definite coefficient matrix \(H \in \Re^{ml \times ml}\) and the inverse matrix of \(S \in \Re_{ + }^{m \times m}\) can be computed easily (Xu et al. 2013). Figure 2 illustrates the training procedure of MLSSVR involving the mathematical equations.

Fig. 2
figure 2

Flowchart explaining the training procedure of MLSSVR involving the mathematical equations

Full size image

In this study, the radial basis function (RBF) kernel function adopted from Keerthi and Lin (2003) as shown in Eq. 14 is used in the MLSSVR.

$$k(x,z) = \exp ( - p\left\| {x - z} \right\|^{2} ),p > 0$$
(14)

where p is the positive hyperparameter of RBF kernel function. Moreover, all the tuning parameters in MLSSVP including \(\gamma\), \(\lambda\), and \(p\) are tuned and optimised using leave-one-out (LOO) procedure to obtain the average relative error, \(\delta\) as shown in Eq. 15 (Xu et al. 2013).

$$\delta = \frac{1}{l}\sum\nolimits_{i = 1}^{l} {\frac{{\left| {Y_{i} - \hat{Y}_{i} } \right|}}{{Y_{i} }}}$$
(15)

whereby \(Y_{i}\) shows the actual output and \(\hat{Y}_{i}\) shows the predicted output.

Regression models parameters setting

For case study 1, a total of 56 bleaching data sets which consists of H2O2 concentration, T, t, and the WI of the cotton fabric were adopted from Haque et al. (2018). In this study, H2O2 concentration, T and t are served as the input variables for the regression models including MLSSVR, PLSR, LW-PLSR, and LW-KPLSR models while the WI of the bleached cotton fabric is denoted as the output variable. Meanwhile, for case study 2, 48 bleaching data sets including H2O2 concentration, T, t, bursting strength (psi) and the WI of the cotton fabric were taken from Haque and Islam (2015). Different from case study 1, an additional input variable—bursting strength of bleached cotton fabric is included in the regression models. For both case studies, their datasets were exported into MATLAB software and divided into two sets, i.e., 75% for training data and 25% for testing data. Hence, they were split into 40 data sets for case study 1 and 36 data sets for case study 2 (see Table 1) to serve as training data utilized to develop the regression models and fuzzy method. Then, 16 and 12 data sets for case study 1 and 2, respectively were used as testing data for validation purposes. Moreover, training data were also employed to evaluate the performance of the MLSSVR, PLSR, LW-PLSR, and LW-KPLSR models as well as the fuzzy method. Then, RMSE, MAE, and R2 for all regression models and fuzzy method were determined and compared. Figure 3 shows a flow chart explaining the framework of the regression models and fuzzy method for the bleaching process.

Table 1 Values used for the regression models in two different case studies
Full size table
Fig. 3
figure 3

Framework of regression models and fuzzy method for the bleaching process

Full size image

NT, N1, N2, and latent variable (LV) represent the total numbers of data sets, numbers of training data sets, numbers of testing data sets, and number of LV, respectively. In this study, LV is set as 1 while the kernel parameter (bk) for LW-KPLSR with log kernel function is set as 1. The value of phi in the LW-PLSR and LW-KPLSR is fixed at 0.1 (Yeo et al. 2017). Besides, some parameters for MLSSVR model which are, \(\gamma\), \(\lambda\), and p were tuned using LOO technique to get the optimal results. The summarised parameters setting for MLSSVR, PLSR, LW-PLSR, and LW-KPLSR models are displayed in Table 1.

Accuracy of the predictive performance measurement

In this study, the performance of the prediction models is evaluated using RMSE, MAE, R2 and prediction error (PE). Both RMSE and MAE are goodness‐of‐fit indicators that describe differences in observed and predicted values (Harmel et al. 2010). RMSE as shown in Eq. 16 is the square root of the total of the squared differences between the actual and expected output. Thus, a lower RMSE implies better accuracy and predictive performance (Hocaoğlu et al. 2008).

$$RMSE = \sqrt {\frac{{\sum\nolimits_{i} {\left( {Y_{i} - \hat{Y}_{i} } \right)}^{2} }}{n}}$$
(16)

whereby n shows the number of samples.

MAE calculates the average absolute difference between the actual and predicted output value. The formula to calculate MAE is displayed in Eq. 17:

$$MAE = \frac{1}{n}\sum\limits_{1}^{n} {\left| {Y_{i} - \hat{Y}_{i} } \right|}$$
(17)

As can be seen from Eq. 18, R2 is obtained by comparing the total of the squared errors to the total of the squared deviations about its mean. R2 is used to measure the goodness of fit between real and predicted variables with value ranging between 0 and 1 (Jaeger et al. 2017).

$$R^{2} = 1 - \frac{{\sum\nolimits_{i} {\left( {Y_{i} - \hat{Y}_{i} } \right)}^{2} }}{{\sum\nolimits_{i} {\left( {Y_{i} - \overline{Y}} \right)^{2} } }}$$
(18)

whereby \(\overline{Y}\) represents the mean value of the actual output.

Additionally, PE (%) can be calculated using Eq. 19 (Guang et al. 1995).

$${\text{P}}E = \left| {\frac{{\hat{Y}_{i} - Y_{i} }}{{Y_{i} }}} \right| \times 100$$
(19)

Computer hardware and software configuration specifications

In this study, all simulation works were performed on the same computer and software system to ensure the consistency of the results from all regression models. The hardware and software configuration specifications of the used Asus ZenBook UX305 laptop are Window 10 (64 bit), MATLAB (version R2021a), 2.20 GHz Intel core M3-6Y30, 4.0 GB random-access memory and 128 GB solid state drive storage.

Results and discussion

As mentioned earlier, for case study 1, an LSSVR model that is called MLSSVR was developed using several key parameters of bleaching process, and these parameters including H2O2 concentrations, T, t, and WI of cotton fabric samples are nonlinear. Case study 2 is very similar to case study 1 except one additional parameter, i.e., bursting strength of cotton fabric samples was included to build MLSSVR model. The higher value of WI indicates the greater degree of whiteness of the cotton fabric. Whiter cotton fabric is desired before it is dyed, printed or other wet-treatments (Ferreira et al. 2019; Kabir et al. 2014). Many studies reported that WI of cotton fabric can be increased by increasing H2O2 concentrations and T (Abdul and Narendra 2013; Ferdush et al. 2019). Nevertheless, high concentrations of H2O2 could break up the unsaturated bonds (e.g., C=C) and decreases the bursting strength of cotton fabric (Ferdush et al. 2019; Haque and Islam 2015; Tang et al. 2016). Hence, optimum bleaching process parameters are required to determine the effectiveness of the bleaching process to produce a targeted cotton fabric whiteness.

The predictive modelling techniques including the MLSSVR model can be used to estimate the outcome or the results of the bleached cotton fabric such as its WI using the bleaching process parameters. Initially, a fuzzy predictive model was constructed by Haque et al. (2018) for a bleaching process using a MATLAB app that is called a fuzzy logic designer. However, this method is unable to predict beyond the range of the input data. Hence, in this study, an MLSVVR was developed using the bleaching process parameters reported in two different case studies to overcome the limitations of this fuzzy method. Moreover, other regression models including PLSR, LW-PLSR, and LW-KPLSR models were also built using the same process parameters from case study 1 and 2.

All results from these regression models and fuzzy method for case study 1 are summarized in Table 2 for comparison purpose and the results for fuzzy method were adopted from Haque et al. (2018). Moreover, the results from the regression models and fuzzy method for case study 2 are presented in Table 3 where the results for fuzzy method were generated from the fuzzy logic designer app in the MATLAB. In Tables 2 and 3, RMSE1, MAE1, and R21 are the RMSE, MAE, and R2 for training data, respectively whereas RMSE2, MAE2, and R22 are the RMSE, MAE, and R2 for testing data, respectively. From both tables, among these regression models and fuzzy method, MLSSVR with RBF kernel function provided the best predictive performance. However, the results of MLSSVR for case study 2 (Table 3), especially the results for training data (RMSE1, MAE1, and R21) are much better compared to the case study 1 (Table 2).

Table 2 Comparison of the results obtained from different models for case study 1
Full size table
Table 3 Comparison of the results obtained from different models for case study 2
Full size table

Based on Tables 2 and 3, PLSR did not work well for both case studies as its RMSE and MAE values for case studies 1 and 2 are significantly higher than MLSSVR. Furthermore, its R2 values for both case studies are lower than 0.84. PLSR which is a linear model gave the worse results as it is unable to cope with the nonlinear process data from bleaching process (Wang et al. 2021). Additionally, compared to fuzzy method, MLSSVR showed 60–445% (for case study 1) and 2080–8107% (for case study 2) lower RMSE and MAE values, and 3–112% higher R2 values. The fuzzy method involves membership function, fuzzy logic operators, and if-then rules. There are three conceptual components such as a rule case that include a selection of fuzzy rules, a database which explains the membership functions used in the fuzzy rules, and a reasoning mechanism that shows the inference way upon the rules to derive an output (Kovac et al. 2013). From Table 2, for testing data set, fuzzy method performed better than PLSR, LW-PLSR, and LW-KPLSR in which the RMSE2 and MAE2 for fuzzy method are lower and its R22 values are higher. However, in Table 3, fuzzy method performed poorer than PLSR, LW-PLSR, and LW-KPLSR.

In addition, the overall results show that the fuzzy method worked badly compared to MLSSVR. This may be due to the helps of LOO in the MLSSVR to determine the optimal tuning parameters and the RBF kernel function that helps to map the original data into a high dimensional space for better prediction of the nonlinear data. For both LW-PLSR and LW-KPLSR, it is found that MLSSVR demonstrated 101–263% for case study 1 and 175–1108% for case study 2 lower RMSE and MAE values and 1–7% for case study 1 and 0.30–15% for case study 2 higher R2 values. On the other hand, LW-PLSR and LW-KPLSR gave better results than fuzzy method for the training data set of case study 1 where their RMSE1 and MAE1 are lower and R21 are higher. Moreover, for case study 2, LW-PLSR and LW-KPLSR also performed better than fuzzy method and PLSR. This may be due to the presence of locally weighted algorithm in both LW-PLSR and LW-KPLSR which improves their predictive performance for the training data. These locally weighted based models (LW-PLSR and LW-KPLSR) are using a PLSR model that is constructed by weighting data with Euclidian distances similarity measurement (Kaneko and Funatsu 2016).

From Figs. 4 and 5, it is obvious that the predicted outputs for training data and testing data of case stud1 1 and 2 from MLSSVR are closer to the actual data compared to other regression models and fuzzy method. From Fig. 4b for testing data, except for MLSSVR, other regression models and fuzzy method performed poorer compared to training data in Fig. 4a in which their predicted outputs are far from the actual output. Similarly, besides MLSSVR in Fig. 5a, b for training and testing data, the predicted outputs from the rest of the regression model and fuzzy model are far apart from the actual data. Moreover, Fig. 6a, b illustrate the correlation between the actual and predicted values of output from MLSSVR for testing data of case study 1 and 2, respectively. From these figures, notice that all data points are close to the line which indicate that the predicted outputs from MLSSVR are near to the actual data for testing data of both case studies. In general, all the results show that MLSSVR copes much better than the rest of the methods. Hence, it can conclude that MLSSVR is an effective method to predict the WI using the bleaching process parameters.

Fig. 4
figure 4

Comparison of the predicted output values from regression models a for training data and b for testing data of case study 1

Full size image
Fig. 5
figure 5

Comparison of the predicted output values from regression models a for training data and b for testing data of case study 2

Full size image
Fig. 6
figure 6

Correlation between the actual and predicted values of output from MLSSVR for testing data of a Case study 1 and b Case study 2

Full size image

Conclusions

In the current study, LSSVR model, namely MLSSVR was developed using the experimental results of bleaching process from two different case studies to predict the WI of the cotton fabric. The input variables for case study 1 are H2O2 concentrations, T, and t while case study 2 contains 1 additional input variable, i.e., bursting strength. It is important to determine the optimal bleaching process parameters in order to achieve the highest WI of the cotton fabrics. Hence, the predictive modelling including MLSSVR plays an essential role to meet the targeted quality of cotton fabrics in the textile manufacturing processes. For both case studies, the developed MLSSVR could outperform other methods including fuzzy method, PLSR, LW-PLSR, and LW-KPLSR as it improved RMSE and MAE values by 60–8107%. Besides, its R2 values in both case studies are also very high, reaching up to 0.9999. These results denote that MLSSVR model is a potential predictive model for the bleaching process in the textile domain. In future studies, integrating a locally weighted algorithm in the MLSSVR model could be expected to enhance its predictive outcomes. Furthermore, more attention should be paid to the new aspects of the textile fiber bleaching process and the cost of the process optimization.