1 Introduction

The reinforced concrete (RC) beam can be retrofitted or strengthened using external bonding of fiber-reinforced polymer (FRP) plates. The flexural strength of a concrete beam can be increased by bonding the FRP plates to the tension face (soffit) of the reinforced concrete (RC) beam [20]. This technique has been widely used in bridges, buildings and tunnel lining due to a variety of advantages such as good corrosion resistance, ease of site handling and minimum increase in weight and structural size [28, 45, 55].

In the FRP-to-concrete bonding system, the debonding of the FRP plate from the member is usually caused by the concrete fracture close to the FRP-to- concrete interfaces. The occurrence of the debonding failure will reduce the strain of the bonded FRP plate to 20–50% of the rupture strain of the FRP plate. Therefore, FRP plates are not fully utilized when the debonding failure occurs [17, 26]. Moreover, the deformability of the strengthened member will be reduced with the premature failure [5]. A variety of factors need to be considered when explaining the bond mechanism, such as FRP material properties, adhesive, and RC properties [10]. Many experiments have been conducted to evaluate the bond strength. The two widely applied experiments are modified beam tests [56, 68], and single shear tests [3, 11, 12] as they can be easily implemented in laboratory. However, as there exist a large number of influencing variables, it is impossible to evaluate the bond strength accurately using the time and money consuming laboratory experiments.

To address this issue, statistical models were proposed to predict the bond strength [14, 34, 48]. These models evaluate the bond strength of FRP-to-concrete joints by combining the fracture energy, the axial rigidity of the FRP system and the bond width. Generally, empirical relationships are established in these models by using small test data, and there are not enough factors considered in these models. Therefore, the generalization ability of these models is not high enough.

To address this problem, machine learning (ML) algorithms are used to predict the bond strength of FRP-to-concrete joints as ML algorithms do not rely on explicit equations. Among many ML methods, support vector regression (SVR) has been extensively applied in civil engineering such as prediction of unconfined compressive strength (UCS) [19, 63], elastic modulus [50, 59], tensile strength [60] and fresh-state properties [47]. As one of the best ML algorithms, SVR is able to solve regression problems by estimating the implicit functions accurately using kernel tricks and risk minimization principles [31]. The SVR algorithm has a number of advantages over other ML models, including excellent performance on small datasets [13], and non-convergence of local solution [39]. In spite of the benefits, SVR is computationally demanding. The computational efficiency can be achieved by introducing equality constraints to achieve closed form least-square-type solutions. This form of SVR is called least-squares support vector regression (LSSVR) [52]. The prediction accuracy and generalization ability of LSSVR rely on its hyperparameters. In order to tune and find optimal hyperparameters, a new metaheuristic algorithm called beetle antennae search (BAS) is used for hyperparameter tuning. It is easy to implement and converges very fast because only one beetle is used to search rather than a beetle swarm. Thus, in the present study, the BAS is employed to tune the LSSVR model. However, the BAS can be easily trapped into a local optima [25, 64]. To solve this problem, this study modifies the BAS by incorporating the Levy flight to improve its searching efficiency. Based on this modification, a Levy-BAS based LSSVR (LBAS-LSSVR) method is proposed for predicting bond strength of FRP-to-concrete joints. This study makes several contributions to the literature as follows:

  1. (i)

    It firstly proposes a metaheuristic-based regression model to predict the bond strength of FRP-to-concrete joints. The prediction accuracy of the proposed model is higher than the other ML approaches.

  2. (ii)

    The recently developed BAS algorithm is firstly utilized to tune the hyperparameters of LSSVR, which outperforms other metaheuristic algorithms in terms of simple implementation, rapid convergence, and global optima.

  3. (iii)

    The Levy flight is incorporated into the BAS algorithm to avoid being trapped into local optima, which improves the searching efficiency of BAS obviously.

  4. (iv)

    The importance of each influencing variable on the bond strength of FRP-to-concrete joints is computed using the random forest algorithm.

The remainder of this paper will describe the applied ML methods in Sect. 2, construction of the proposed regression model in Sect. 3, and evaluation of the performance of the proposed model in Sect. 4.

2 Overview of the used algorithms

2.1 Least-squares support vector regression

Least-squares support vector regression (LSSVR) is the least-squares version of support vector regression (SVR). SVR can convert a nonlinear problem into a linear one by mapping the data from the sample space into a higher dimensional characteristic space using a kernel trick to learn the complicated relationship between predictors and outputs. SVR is extensively used due to its advantages such as excellent generalization ability, rapid learning speed and good noise-tolerating ability [9, 46].

Suppose a training dataset of n points is given as follows:

$$\left\{ {\left( {{\mathbf{x}}_1,y_1} \right),\left( {{\mathbf{x}}_2,y_2} \right), \ldots ,\left( {{\mathbf{x}}_n,y_n} \right)\} } \right.$$
(1)

where each xi is an l-dimensional real director and yi is the scalar regression value. The regression function can be derived using this dataset in the following form:

$$f\left( {\mathbf{x}} \right) = {\mathbf{w}} \cdot \varphi \left( {\mathbf{x}} \right) + b$$
(2)

where \(\varphi \left( {\mathbf{x}} \right)\) is a nonlinear mapping function; w represents the weight vector; b is the bias. f(x) is required to be as flat as possible. Flatness in (2) means the Euclidean norm of w, i.e., ||w||2 needs to be minimized [46]. If for each instance xi, the deviation between f(xi) and yi is less than \(\varepsilon\) (the largest tolerance error), the function f(xi) is said to be found. A loss function using the \(\varepsilon\)-insensitive factor is employed to measure the deviation degree:

$${\mathcal{L}}\left( {{\mathbf{x}},\mathbf{y},f} \right) = \left| {{\mathbf{y}}_{i} - f\left( {{\mathbf{x}}_{i} } \right)} \right|_{{\mathcal{E}}} = \left\{ {\begin{array}{l} {0,\quad \left| {{\mathbf{y}}_{i} - f\left( {{\mathbf{x}}_{i} } \right)} \right| < \varepsilon } \\ {\left| {{\mathbf{y}}_{i} - f\left( {{\mathbf{x}}_{i} } \right)} \right| - \varepsilon ,\quad\left| {{\mathbf{y}}_{i} - f\left( {{\mathbf{x}}_{i} } \right)} \right| \ge \varepsilon } \\ \end{array} } \right.$$
(3)

This function indicates that the training points within the \(\varepsilon\)-tube are not penalized and only the data situated on or outside the \(\varepsilon\)-tube will be used as support vectors to build f(x). According to the structural risk minimization [2], the problem can be written as follows:

$${\mathcal{R}}\left( {\mathbf{w}} \right) = \frac{1}{2}{\mathbf{w}}^{2} + \mathop \sum \limits_{i = 1}^{n} {\mathcal{L}}\left( {{\mathbf{x}},y,f} \right)$$
(4)

Some errors are allowed sometimes, and therefore slack variables \(\xi_{i}\) and \(\xi_{i}^{*}\) are introduced to cope with infeasible constraints. The above problem can then be converted into the following convex optimization form:

$$\begin{aligned} & \min_{{{\mathbf{w}},b, \xi ,\xi^{*} }} {\mathcal{R}}\left( {\mathbf{w}} \right) = \frac{1}{2}{\mathbf{w}}^{2} + C\mathop \sum \limits_{i = 1}^{n} \left( {\xi_{i} + \xi_{i}^{*} } \right) \\ & {\text{s}} . {\text{t}} .\left\{ {\begin{array}{l} {{\text{y}}_{i} - {\mathbf{w}} \cdot \varphi \left( {\mathbf{x}} \right) - b \le \varepsilon + \xi_{i} } \\ {{\mathbf{w}} \cdot \varphi \left( {\mathbf{x}} \right) + b - {\text{y}}_{i} \le \varepsilon + \xi_{i}^{*} } \\ {\xi_{i} \ge 0} \\ {\xi_{i}^{*} \ge 0} \\ \end{array} } \right. \\ \end{aligned}$$
(5)

where C is a penalty parameter to determine the trade-off between the flatness of f(x) and the penalizing extent of the sample outside the tube. An example of nonlinear SVR with an ε-tube is shown in Fig. 1.

Fig. 1
figure 1

Example of nonlinear SVR with ε-tube

Full size image

To address problems with constraints, Lagrange multipliers can be used as follows:

$$\begin{aligned} L\left( {{\mathbf{w}},b,\xi ,\alpha ,\mu } \right) & = \frac{1}{2}{\mathbf{w}}^{2} + C\mathop \sum \limits_{i = 1}^{n} \left( {\xi_{i} + \xi_{i}^{*} } \right) \\ & - \mathop \sum \limits_{i = 1}^{n} \alpha_{i} \left( {\varepsilon + \xi_{i} - {\text{y}}_{i} + {\mathbf{w}} \cdot \varphi \left( {{\mathbf{x}}_{\varvec{i}} } \right) + b} \right) \\ & - \mathop \sum \limits_{i = 1}^{n} \alpha_{i}^{*} \left( {\varepsilon + \xi_{i}^{*} + {\text{y}}_{i} - {\mathbf{w}} \cdot \varphi \left( {{\mathbf{x}}_{\varvec{i}} } \right) - b} \right) \\ & - \mathop \sum \limits_{i = 1}^{n} \left( {\mu_{i} \xi_{i} + \mu_{i}^{*} \xi_{i}^{*} } \right) \\ \end{aligned}$$
(6)

where \(\alpha_{i} \ge 0\), \(\alpha_{i}^{*} \ge 0\), \(\mu_{i} \ge 0\) and \(\mu_{i}^{*} \ge 0\) are Lagrange multipliers. When the constraint functions have strong duality and the objective function is differentiable, KKT conditions must be satisfied for each pair of the primal and dual optimal points [6] as follows:

$$\left\{ {\begin{array}{l} {\frac{\partial L}{{\partial {\mathbf{w}}}} = {\mathbf{w}} - \mathop \sum \limits_{i = 1}^{n} \left( {\alpha_{i} - \alpha_{i}^{*} } \right)\varphi \left( {{\mathbf{x}}_{\varvec{i}} } \right) = 0} \\ {\frac{\partial L}{{\partial {\text{b}}}} = \mathop \sum \limits_{i = 1}^{n} \left( {\alpha_{i} - \alpha_{i}^{*} } \right) = 0 } \\ {C - \alpha_{i} - \mu_{i} = 0 } \\ {C - \alpha_{i}^{*} - \mu_{i}^{*} = 0 } \\ \end{array} } \right.$$
(7)

In addition, the product between the constraints and the dual variables ought to be 0 based on the KKT condition at the optimal solution:

$$\left\{ {\begin{array}{*{20}c} {\alpha_{i} \left( {\varepsilon + \xi_{i} - {\text{y}}_{i} + {\mathbf{w}} \cdot \varphi \left( {{\mathbf{x}}_{\varvec{i}} } \right) + b} \right) = 0} \\ {\alpha_{i}^{*} \left( {\varepsilon + \xi_{i}^{*} + {\text{y}}_{i} - {\mathbf{w}} \cdot \varphi \left( {{\mathbf{x}}_{\varvec{i}} } \right) - b} \right) = 0} \\ {\left( {C - \alpha_{i} } \right)\xi_{i} = 0 } \\ {\left( {C - \alpha_{i}^{*} } \right)\xi_{i}^{*} = 0 } \\ \end{array} } \right.$$
(8)

By solving the above equations, the Lagrange dual problem can be derived as follows:

$$\begin{aligned} & \mathop {\hbox{max} }\limits_{i} \left( { - \frac{1}{2}\mathop \sum \limits_{i = 1}^{n} \mathop \sum \limits_{j = 1}^{n} \left( {\alpha_{i} - \alpha_{i}^{*} } \right)\left( {\alpha_{j} - \alpha_{j}^{*} } \right){\mathbf{x}}_{i}^{T} {\mathbf{x}}_{j} - \varepsilon \mathop \sum \limits_{i = 1}^{n} \left( {\alpha_{i} + \alpha_{i}^{*} } \right) + \mathop \sum \limits_{i = 1}^{n} y_{i} \left( {\alpha_{i} - \alpha_{i}^{*} } \right)} \right) \\ & {\text{s}} . {\text{t}} .\left\{ {\begin{array}{*{20}c} {\mathop \sum \limits_{i = 1}^{n} \left( {\alpha_{i} - \alpha_{i}^{*} } \right) = 0} \\ {\alpha_{i} ,\alpha_{i}^{*} \in \left[ {0,C} \right]} \\ \end{array} } \right. \\ \end{aligned}$$
(9)

From Eq. 8, the weight vector can be obtained as \({\mathbf{w}} = \sum_{i = 1}^{n} \left( {\alpha_{i} - \alpha_{i}^{*} } \right)\varphi \left( {{\mathbf{x}}_{\varvec{i}} } \right)\), and therefore the regression function can be derived as:

$$f\left( {\mathbf{x}} \right) = \mathop \sum \limits_{i = 1}^{n} \left( {\alpha_{i} - \alpha_{i}^{*} } \right)\varphi \left( {{\mathbf{x}}_{\varvec{i}} } \right){\mathbf{x}} + b$$
(10)

For LSSVR, the total error in SVR is replaced by the sum of the squared error variable \(\xi_{i}\). Therefore, the primal optimization problem in Eq. 5 can be reorganized for the LSSVR model as follows:

$$\begin{aligned} &\min_{{{\mathbf{w}},b, \xi }} {\mathcal{R}}\left( {\mathbf{w}} \right) = \frac{1}{2}\left\| {\mathbf{w}} \right\|^{2} + \frac{1}{2}C\mathop \sum \limits_{i = 1}^{n} \left( {\xi_{i}^{2} } \right) \hfill \\ &{\text{s.t.}}\; y_{i} = {\mathbf{w}} \cdot \varphi \left( {\mathbf{x}} \right) + b + \xi_{i} ,\quad \xi_{i} \in {\mathbb{R}},\text{ }i = 1, \ldots ,n \hfill \\ \end{aligned}$$
(11)

In a way similar to solving the SVR problem, the Lagrangian function should be applied to obtain the dual optimization problem of LSSVR as follows:

$$L\left( {{\mathbf{w}},b,\xi ,\lambda } \right) = \frac{1}{2}\left\| {\mathbf{w}} \right\|^{2} + \frac{1}{2}C\mathop \sum \limits_{i = 1}^{n} \left( {\xi_{i}^{2} } \right) - \mathop \sum \limits_{i = 1}^{n} \lambda_{i} \left( {{\mathbf{w}} \cdot \varphi \left( {{\mathbf{x}}_{\varvec{i}} } \right) + b + \xi_{i} - y_{i} } \right)$$
(12)

where \(\lambda_{i}\) are the Lagrangian multipliers. The following conditions should be satisfied to achieve the optimal solutions:

$$\left\{ {\begin{array}{l} {\frac{\partial L}{{\partial {\mathbf{w}}}} = {\mathbf{w}} - \mathop \sum \limits_{i = 1}^{n} \lambda_{i} \varphi \left( {{\mathbf{x}}_{i} } \right) = 0} \\ {\frac{\partial L}{{\partial \xi_{i} }} = C\xi_{i} - \lambda_{i} = 0 } \\ {\frac{\partial L}{\partial b} = \mathop \sum \limits_{i = 1}^{n} \lambda_{i} = 0 } \\ {\frac{\partial L}{{\partial \lambda_{i} }} = w \cdot \varphi \left( {{\mathbf{x}}_{\varvec{i}} } \right) + b + \xi_{i} - y_{i} = 0} \\ \end{array} } \right.$$
(13)

After the w and \(\xi\) terms are eliminated, the solutions can be obtained as follows:

$$\left[ {\begin{array}{*{20}c} 0 & {{\mathbf{e}}_{n \times 1}^{T} } \\ {{\mathbf{e}}_{n \times 1} } & {{\varvec{\Omega}} + {\mathbf{I}}_{n} /C} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} b \\ \lambda \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} 0 \\ Y \\ \end{array} } \right]$$
(14)

where \({\mathbf{e}}_{n \times 1}\) = [1,1,…,1]; \(\varvec{\lambda}= [\lambda_{1} ,\lambda_{2} , \ldots ,\lambda_{n} ]\); \(\varvec{Y} = [y_{1} ,y_{2} , \ldots ,y_{n} ]\); \({\mathbf{I}}_{n}\) is the identity matrix; \({\varvec{\Omega}}_{{\varvec{i},\varvec{j}}} = \varphi^{T} \left( {{\mathbf{x}}_{i} } \right)\cdot\varphi \left( {{\mathbf{x}}_{i} } \right) = {\mathcal{X}} ({{\mathbf{x}}_{i} ,{\mathbf{x}}_{j}})\); and \({\mathcal{X}}\) denotes the kernel function. After obtaining \(\varvec{\lambda}\) and b from Eq. (13), the regression model for LSSVR can be expressed as:

$$f\left( {\mathbf{x}} \right) = \mathop \sum \limits_{i = 1}^{n} \left( {\lambda_{i} } \right) {\mathcal{X}} \left( {{\mathbf{x}}_{i} ,{\mathbf{x}}} \right) + b$$
(15)

2.2 Beetle antennae search algorithm

Beetle antennae search (BAS) is a recently proposed metaheuristic algorithm to solve optimization problems inspired by the searching behavior of beetles [25, 62]. A beetle searches neighboring areas using two antennae and moves to a location of higher concentration of odour. Assume that the position of the beetle is represented by a vector \({\mathbf{x}}^{\varvec{i}}\) at the ith time instant (i = 1, 2,…). We define the fitness function as f(x) representing the concentration of odour at position x with its maximum value denoting the source point of the odour. It can search for the global optimum in a multi-dimensional space by a general function:

$$\frac{{\text{Minimize}}}{{\text{Maximize}}}f\left( {\mathbf{x}} \right), {\mathbf{x}} = \left[ {x_{1} ,x_{2} , \ldots ,x_{N} } \right]^{{\text{T}}}$$
(16)

The searching behavior of the beetle can be defined as follows:

$${\mathbf{b}} = \frac{{rnd\left( {k,1} \right)}}{{\left\| {rnd\left( {k,1} \right)} \right\|}}$$
(17)
$${\mathbf{x}}_{r} = {\mathbf{x}}^{i} + d^{i} {\mathbf{b}}$$
(18)
$${\mathbf{x}}_{l} = {\mathbf{x}}^{i} - d^{i} {\mathbf{b}}$$
(19)

where b is a normalized random unit vector;\(rnd(\cdot)\) is a random function; k is the dimensionality of the position; xl and xr denote left-hand side and right-hand side areas, respectively; d represents the antennae length.

The detecting behavior of the beetle is described by:

$${\mathbf{x}}^{i + 1} = {\mathbf{x}}^{i} + \delta^{i} {\mathbf{b}}\cdot{\text{sign}}\left( {f\left( {{\mathbf{x}}_{r} } \right) - f\left( {{\mathbf{x}}_{l} } \right)} \right)$$
(20)

where \(\delta^{i}\) represents the step size at the ith iteration, \({\text{sign}}\left( \cdot \right)\) is the sign function. The step size updating formula is written as:

$$\delta^{i + 1} = \eta \delta^{i}$$
(21)

where \(\eta\) is the attenuation coefficient of the step size.

3 Methodology

3.1 Dataset description

The dataset including 150 instances is collected from internationally published literature [11, 36, 41, 43, 53, 54, 58, 61, 67]. The input variables are width of the prism (WP), width of FRP (WF), modulus of elasticity of FRP (EF), thickness of FRP (TF), uniaxial compressive strength of concrete cylinder (UCS), and bond length (BL). The output variable is the bond strength of FRP-to-concrete joints (BS). The statistics of the parameters are summarized in Table 1. The relationships between input variables are visualized using a correlation matrix (Fig. 2). It can be seen that the correlations between any two input variables are pretty low, indicating that these variables will not cause multicollinearity issues [16].

Table 1 Statistics of the variables used in the dataset
Full size table
Fig. 2
figure 2

Correlation matrix of the input variables

Full size image

3.2 Levy flight BAS algorithm

In the traditional BAS algorithm, the step size of a beetle is fixed or decreases with each iteration. The BAS algorithm can be easily trapped in a local optimum. To solve the issue, this study has introduced Levy flight to adjust the step size of BAS and proposes a new Levy flight BAS (LBAS) algorithm for hyperparameter tuning. The pseudocode of LBAS is shown in Algorithm 1. Levy flight has been used in many optimization algorithms and the results are promising [40, 44, 57].

In the implementation, the step size in LBAS is updated as follows

$${\text{Step}}^{\left( t \right)} = \eta\beta\oplus Step^{{\left( {t - 1} \right)}},$$
(22)

where \(\eta\) is the same as that in Eq. (21); The product ⊕ means entrywise multiplications; β is defined as follows:

$$\beta=\left\{\begin{array}{ll}\alpha|Levy|, & \left| {f^{\left( t \right)} - f^{{\left( {t - 1} \right)}} } \right| < \mu \left( {f_{\text{w}} - f_{\text{b}} } \right)\\1, & otherwise\end{array}\right.,$$
(23)

where α ∼ U (0, 1); fw and fb are the historical worst and best fitness values; μ is a coefficient. In this study, μ=10−5; Levy is defined as follows:

$$Levy\sim\;u = t^{ - \lambda } ,\quad (1 < \lambda \le 3).$$
(24)
figure a

3.3 Evaluation and validation methods

3.3.1 Performance evaluation methods

The following performance measures are applied to assess the predictive performance of the proposed model.

  • Root-mean-square error (RMSE)

RMSE measures the difference between predicted and observed values using the following function [24]:

$${\text{RMSE}} = \sqrt {\frac{1}{n}\mathop \sum \limits_{i = 1}^{n} \left( {y_{i}^{*} - y_{i} } \right)^{2} }$$
(25)

where \(y_{i}^{*}\) is the predicted value; yi is the actual value; n is the number of data samples.

  • Correlation coefficient (R).

R measures the strength of correlation between predicted and observed values, which is described as follows: [4]

$$R = \frac{{\mathop \sum \nolimits_{i = 1}^{n} \left( {y_{i}^{*} - \overline{{y^{*} }} } \right)\left( {y_{i} - \overline{y} } \right)}}{{\sqrt {\mathop \sum \nolimits_{i = 1}^{n} \left( {y_{i}^{*} - \overline{{y^{*} }} } \right)^{2} } \sqrt {\mathop \sum \nolimits_{i = 1}^{n} \left( {y_{i} - \overline{y} } \right)^{2} } }}$$
(26)

where \(\overline{{y^{*} }}\) and \(\overline{y}\) are the mean value of predicted and observed values, respectively.

3.3.2 k-fold cross-validation

Several methods for validating the regression model have been used such as simple substitution method [8], bootstrap method [15], holdout method [29], and bolstered method [7]. Among these methods, the k-fold cross-validation (CV) is probably the most widely applied validation method for training data [49]. In this study, k was assigned to be 10 according to recommendations and the number of datasets [30]. During hyperparameter tuning, the training set is split into 10 folds. The algorithms are trained in nine folds and validated in the remaining one. This procedure is repeated for 10 times with a different fold being employed as the validating fold at each time. The 10 results from the folds can then be averaged to give a single estimation.

3.4 Hyperparameter tuning

This study applied the radial basis function (RBF) as the kernel function for LSSVR. The reasons for choosing this function are as follows: (1) more parameters need to be tuned in the polynomial kernel function, leading to a more difficult model selection process. Numerical difficulties such as underflow or overflow may be inevitable; (2) the sigmoid kernel function is conditionally positive definite for parameters in certain ranges and there exist similarities between the RBF and the sigmoid kernel function [33]; and (3) the linear kernel function is a particular case of RBF [27].

Two hyperparameters need to be tuned on the training dataset when the RBF kernel is used: the kernel parameter γ and the slack penalty coefficient C. The hyperparameters are tuned on the training set including 70% of the instances as per the recommendations of previous literature [23]. The training dataset is split into 10 subsets in which the beetle searches for the optimal hyperparameters on 9 subsets and calculate the RMSE on the remaining subset. After convergence, the optimal hyperparameters in this fold is selected out. This process repeats for 10 times based on ten-fold CV. After ten folds, the hyperparameters corresponding to the smallest RMSE is selected as the optimal hyperparameters used in this study. Finally, the predictive performance of the model is tested on the test dataset (containing 30% of the whole data points). Independent of the training dataset, this dataset is applied only for assessing the performance of the model. If a model fits well on both the training and test datasets, minimal overfitting has taken place [42].

figure b

3.5 Construction of the metaheuristic-optimized regression system

In the training set, the hyperparameters of the proposed model are tuned by 10-fold CV and LBAS. The predictive performance of the model with optimal hyperparameters are then evaluated on the test dataset. The whole procedure of the implementation of the proposed LBAS-LSSVR system is shown in Fig. 3.

Fig. 3
figure 3

Flow diagram of the LBAS based LSSVR

Full size image

4 Results and discussion

4.1 Performance of the LBAS algorithm

To assess the performance of the proposed LBAS-LSSVR model, eleven benchmark functions are used, including 6 unimodal ones and 5 multimodal ones [37]. The test results are summarized in Table 2. Here, we take f7 as an example to show the searching trajectories and convergence curves of the LBAS algorithm (see Fig. 4). From the expression of f7, it is known that when x is \(- \infty\), y is \(- \infty\). Therefore, the smaller the obtained y is, the better performance an optimization algorithm achieves. It can be seen that the beetle gradually moves “deeper and deeper”. For the BAS algorithm, the y stops decreasing at the 23rd iteration (Fig. 4e), while for the LBAS, y reaches a much smaller value (about seven times smaller) after convergence (after 550 iterations) (Fig. 4f). It can be observed from Table 2 that the solution obtained by LBAS algorithm is much closer to the global optimum, indicating the high searching efficiency of LBAS algorithm.

Table 2 Benchmark functions
Full size table
Fig. 4
figure 4

Searching trajectories of the BAS (a) and LBAS (c) algorithms in 2-D input space; top views of the searching trajectories of BAS (b) and LBAS (d); Convergence curves of the BAS (e) and LBAS (f)

Full size image

4.2 Results of hyperparameter tuning

As stated before, we have tuned the hyperparameters (C and γ) of LSSVR using LBAS and ten-fold CV. At each fold, the LBAS algorithm searches for the hyperparameters on the training set and then after convergence, the set of hyperparameters are selected out. To validate the performance of the LSSVR model with this set of hyperparameters, the RMSE value on the validation set is calculated by this model. After ten folds, ten sets of hyperparameters (C and γ) are obtained, as shown in Table 3. The hyperparameters corresponding to the smallest RMSE value on the validation set (typeset in bold) are selected as the optimal hyperparameters for further study (the hyperparameters at tenth fold). We have also plotted the RMSE versus iteration curve for the best fold, as shown in Fig. 5. It can be seen that the RMSE curve converges within 20 iterations. This indicates that LBAS is very efficient in tuning hyperparameters. In addition, the significant decrease in RMSE shows that LBAS can find optimal hyperparameters for LSSVR.

Table 3 Hyperparameter tuning of the LSSVR model
Full size table
Fig. 5
figure 5

RMSE values on the validation set at each fold (a); RMSE versus iteration on the validation set at fold 10

Full size image

4.3 Performance of the LBAS-LSSVR algorithm

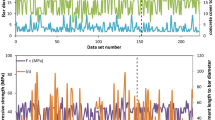
Figure 6 shows the predicted and actual BS values on the training and test sets. The bars on the horizontal line represent the difference between the actual and predicted values. It can be seen that most of the difference values are pretty small (except several noises), indicating that the LBAS-LSSVR model has high prediction accuracy. Figure 7 shows the correlation between the predicted and actual BS values on the training and test sets. It can be seen that the data points lie closely to the ideal fit, with correlation coefficients of 0.9842 and 0.9828, respectively, indicating excellent prediction performance of the LBAS-LSSVR model. In addition, the similar and low RMSE values on the training and test sets suggest that there are no under-fitting and over-fitting issues.

Fig. 6
figure 6

Scatter plot of the predicted and actual values on the training set (a) and test set (b)

Full size image
Fig. 7
figure 7

Predicted BS versus actual BS values on the training set (a) and test set (b)

Full size image

4.4 Comparison of the LBAS-LSSVR model with other models

The predictive performance of the proposed model is compared with several widely used ML models, including back propagation neural network (BPNN) [21, 51], decision tree (DT) [32, 65, 66], k nearest neighbors (kNN) [1], logistic regression (LR) [22], and multiple linear regression (MLR) [38]. The prediction performances of different models in terms of RMSE and R on training and test sets are summarized in Table 4. It can be observed that the LBAS-LSSVR model achieves the highest prediction accuracy, as indicated by the highest R value (0.983) and the lowest RMSE value (1.99 MPa) on the test set, followed by the kNN with R value of 0.947 and the RMSE of 3.52 MPa. DT performs the worst on the test set (RMSE = 5.42 MPa, R = 0.880).

Table 4 Prediction performance of the models on training and test sets
Full size table

Figure 8 displays the distribution of the residual between the actual and predicted BS value using a box plot. The box plot is constructed using five metrics: the minimum value (the lower whisker), the first quartile (the lower edge of the box), the median (the red line in the box), the third quartile (the upper edge of the box), and the maximum value (the upper whisker). It can be seen that the LBAS-LSSVR achieves the smallest residual values for all the five metrics, followed by kNN, while LR performs worst in terms of the larger distribution of the residual values. However, it should be noted that although the kNN model has achieved comparatively higher prediction accuracy, slight overfitting occurs, as the RMSE on the test set is 4.5 times larger than that on the training set (see Table 4).

Fig. 8
figure 8

Box plot of the residual between the predicted and actual BS values for different models on the test set

Full size image

A Taylor diagram is employed to quantify the degree of correspondence between the actual and predicted BS values in terms of the standard deviation, RMSE and the correlation coefficient. A model will lie nearest the “Actual” point if its predicted BS value agrees well with the actual ones, indicating this model achieves comparatively low RMSE and high correlation. It can be observed that the LBAS-LSSVR model is situated closest to the “Actual point”, suggesting this model has the highest prediction accuracy. LR has relatively large variations than the actual value, while DT has a lower correlation coefficient, in both cases, leading to a comparatively large RMSE (Fig. 9).

Fig. 9
figure 9

Performance comparison of the six models using Taylor diagram on the test set

Full size image

4.5 Variable importance

In this study, the random forest (RF) algorithm is used to calculate the variable importance [18]. The procedure is as follows: The out-of-bag sample for a tree t is defined as OOBt and the misclassification rate is denoted by errOOBt. The influencing variables are permuted randomly in OOBt to obtain a permuted sample \(O\tilde{O}B_{t}\) and the error of predictor t \(errO\tilde{O}B_{t}\) is then calculated. The variable importance of X can be written as

$$VI \left( X \right)\frac{1}{ntree}\mathop \sum \limits_{t} \left( {errO\tilde{O}B_{t} - errOOBt} \right)$$
(27)

where \(ntree\) is the number of tress in the forest.

The results show that WF is the most sensitive to the bond strength of FRP-to-concrete joints with the highest influence score (3.4776), followed by the BL (1.1419), while UCS is the least sensitive to the bond strength (0.1195). TF, WP and EF fall in between (0.7917, 0.7360 and 0.6745, respectively) (see Fig. 10). It is not unexpected that the variables related with the rigidity of the FRP have comparatively high influence on the bond strength of the FRP-to-concrete joints. When the principle tensile strength reaches the concrete tensile strength (half of the concrete uniaxial compressive strength), debonding cracks start to develop. Therefore, the UCS is not sensitive to the bond strength [35].

Fig. 10
figure 10

Importance of the influencing variables on the bond strength of FRP-to-concrete joints

Full size image

5 Conclusions

This study predicts the bond strength of FRP-to-concrete joints using an intelligent regression model. This model has high prediction accuracy and can be used to solve structural engineering problems. The recently proposed BAS algorithm is introduced to search for optimal hyperparameters for the LSSVR model. In addition, Levy flight is employed to improve the searching efficiency of BAS. The results show that incorporating Levy flight into the BAS algorithm can avoid the premature convergence to local optima. The LBAS is very efficient in tuning hyperparameters of LSSVR. The prediction accuracy of the proposed LBAS-LSSVR is pretty high, indicated by high correlation coefficient (0.9828) and low RMSE (1.99 MPa) on the test set. The variable importance result indicates the width of the FRP has the most significant influence on the bond strength, while the concrete UCS is the least sensitive variable.

It should be noted, however, that the data samples used in this study come from laboratory experiments. Thus, in the future work, the following work should be conducted: (1) to include a wider range of influencing variables (e.g., tensile strength of FRP, cement type, water-to-cement ratio of concrete, and elastic modulus of concrete) to increase the generalization ability of the proposed model, and (2) to increase the volume of data used for training and testing the proposed model. This will ensure more refined tuning of hyperparameters and further improve the ability of the model to obtain meaningful patterns form data with noise. Since it is not convenient for engineers to use algorithms in practice, a GUI that incorporates the proposed model can be implemented in the future work to facilitate the design of FRP-to-concrete composite joints for construction of infrastructure and buildings.