1 Introduction

Poincaré believed that periodic orbits are important in understanding the restricted or the general N-body problem (Poincaré 1892). The study of periodic orbits in Celestial Mechanics not only benefits the development of mathematics, but also provides the intermediate orbits for space missions and ephemerides (Hénon 1997). In Celestial Mechanics, one of the most well-known model is the circular restricted three-body problem (CRTBP), in which many families of periodic orbits are shown to exist via the continuation method or the variational approach. For more aspects about the continuation method, one can refer to Meyer et al. (2009), Cors et al. (2005), Xu and Fu (2009), and for more knowledge on the variational method, one can refer to Gordon (1977), Chenciner and Montgomery (2000), Chen (2010), and so on. One main difference between these two methods is that the continuation method includes a small parameter while the variational method does not.

The continuation method is usually adopted in order to find new families of periodic solutions in a dynamical system with a small parameter \(\varepsilon \). Consider two differential systems \({\dot{z}}=F_{0}(z)\) and \({\dot{z}}=F(z,\varepsilon )=F_{0}(z)+\varepsilon F_{p}\), which are called the approximated system and the full system, respectively. The method of finding solutions of the full system near the solutions of an approximated system is called the continuation method. If the new solutions of the case \(\varepsilon >0\) are continued from the case \(\varepsilon =0\) by the implicit function theorem, such a method is called the classical continuation method.

The classical continuation method is firstly used by Poincaré to classify symmetrical periodic orbits in the CRTBP by sorts and types with a small mass ratio of the two primaries as the small parameter (Poincaré 1892). Using the same parameter, Jefferys (1965) showed that there exists a class of doubly symmetric periodic solutions for the CRTBP in a rotating frame. Here doubly symmetric means that the periodic orbits are symmetric with respect to the line containing both primaries and a plane perpendicular to this line. By this continuation method, the mass ratio cannot be analytically very large. Without the restriction of the mass ratio, taking the small distance to one primary or the inverse of the large distance to the center of mass of both primaries as the small parameter, Howison and Meyer (2000) proved the existence of doubly symmetric periodic orbits by applying the symplectic scaling method and Arenstorf’s fixed-point theorem. For more knowledge on the symplectic scaling, one can refer to Meyer et al. (2009), and for Arenstorf’s fixed-point theorem and its corollary, one can refer to Arenstorf and Bozeman (1977), Cors et al. (2005) and related references.

It is more realistic and interesting though complicated to consider both the oblate and the third-body perturbation when studying the Lunar-type orbits in the CRTBP. In such a problem, the infinitesimal body moves around the oblate spheroid, and the other primary moves as a mass point on the equatorial plane of the oblate primary. The aim of this paper is to show the existence of the doubly symmetric periodic orbits of Lunar type around the oblate primary.

In Sect. 2, the Hamiltonian is derived from the motion of the infinitesimal body in the uniform rotating frame of both primaries, with their center of mass located at the origin. The origin is then moved to the center of the oblate primary and the resulting Hamiltonian derived. The Hamiltonian is then expanded with Legendre polynomials \(\{{\mathcal {P}}_{k}\}_{k=1}^{+\infty }\). In Sect. 3, a small parameter representing the closeness of the infinitesimal body to the oblate primary is introduced to the Hamiltonian by the symplectic scaling, and then the perturbation functions are expanded using this small parameter. In Sect. 4, orbital elements and canonical elements are introduced, and then the approximated system is expressed by the canonical elements. In Sect. 5, double symmetry is described in rectangular coordinates, orbital elements, the Delaunay elements, and the Poincaré–Delaunay elements. In Sect. 6, the approximated solutions with double symmetries are proved to be circular orbits. In Sect. 7, the von-Zeipel transformations are adopted to eliminate the short periodic effects in the first-order perturbation term, and the averaged Hamiltonian keeps the same double symmetry. The first-order system becomes integrable, and it is convenient to do error estimates in the next section. In Sect. 8, the doubly symmetric periodic solutions of the approximated system are continued to those of the full system via applying a corollary of Arenstorf’s fixed point theorem to the boundary-value equations expressed in Poincaré–Delaunay elements. In the last section, the final conclusion is summarized, and some further problems are discussed.

2 Hamiltonian system

Consider the CRTBP with only one oblate primary in the rotating frame with the center of mass located at the origin. Denote the mass of the oblate primary as \(m_{1}\), the other \(m_{2}\). The units of measure can be chosen such that the constant distance between the primaries, the total mass, and the gravitational constant are all equal to one in the new units. Let the direction of x-axis point from \(m_{1}\) to \(m_{2}\), and the z-axis be perpendicular to the motion plane of the primaries. Thus the Cartesian coordinate frame is fixed.

Introduce the position coordinate of the infinitesimal body and the conjugate momentum as \({\mathbf {x}}=(x_{1},x_{2},x_{3})^{T}\), \({\mathbf {y}}=({\dot{x}}_{1}-x_{2},{\dot{x}}_{2}+x_{1},{\dot{x}}_{3})^{T}=(y_{1},y_{2},y_{3})^{T}\). Denote \(\mu =\frac{m_{2}}{m_{1}+m_{2}}\). The position coordinates of \(m_{1}\) and \(m_{2}\) are \(\zeta _{1}=(-\mu ,0,0)^{T}\), \(\zeta _{2}=(1-\mu ,0,0)^{T}\), respectively, where the upper T represents transposition.

Under these units, the Hamiltonian function for the motion of the infinitesimal body can be written as

$$\begin{aligned} {\mathcal {H}}^{c}=\frac{1}{2}\Vert {\mathbf {y}}\Vert ^{2}-(x_{1}y_{2}-x_{2}y_{1})-\iiint \frac{ \mathrm{{d}}m}{\Vert {\mathbf {x}}-\zeta _{1}-{\mathbf {u}}\Vert } -\frac{\mu }{\Vert {\mathbf {x}}-\zeta _{2}\Vert }, \end{aligned}$$
(1)

where \({\mathbf {u}}\) is an arbitrary vector inside the oblate primary, \(\mathrm{{d}}m\) represents the uniform density of the oblate spheroid multiplied by the unit volume \(\mathrm{{d}}u_{1} \mathrm{{d}}u_{2} \mathrm{{d}}u_{3}\).

Fig. 1
figure 1

A sketch for the motion of the infinitesimal body around one oblate primary in the circular restricted three-body problem

Full size image

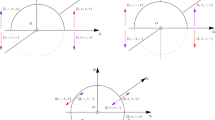
Moving the origin to the center of the oblate primary \(m_{1}\), one has \(\xi ={\mathbf {x}}+(\mu ,0,0)^{T}\), and the conjugate momentum of \(\xi \) is \(\eta =({\dot{\xi }}_{1}-\xi _{2},{\dot{\xi }}_{2}+\xi _{1},{\dot{\xi }}_{3})^{T}\). A sketch describing the motion of the infinitesimal body is shown in Fig. 1. The Hamiltonian can be written as follows:

$$\begin{aligned} {\mathcal {H}}^{\mu }=\frac{1}{2}\Vert \eta \Vert ^{2}+(\xi _{2}\eta _{1}-\xi _{1}\eta _{2})+ \mu \xi _{1}-\iiint \frac{ d m}{\Vert \xi -{\mathbf {u}}\Vert }-\frac{\mu }{\Vert \xi -(1,0,0)^{T} \Vert }-\frac{\mu ^{2}}{2} . \end{aligned}$$
(2)

Let the equatorial radius of the oblate primary be \(a_{e}\), which is small and \(a_{e}\ll |\xi |\). From Kyner (1965), the potential function of the oblate primary is:

$$\begin{aligned} \iiint \frac{ d m}{\Vert \xi -{\mathbf {u}}\Vert }=\frac{1-\mu }{\Vert \xi \Vert }\left[ 1- \sum _{k=2}^{\infty }J_{k}\left( \frac{a_{e}}{\Vert \xi \Vert }\right) ^{k}{\mathcal {P}}_{k}\left( \frac{\xi _{3}}{\Vert \xi \Vert }\right) \right] , \end{aligned}$$
(3)

where \(J_{1}=0\), \(\{J_{k}\}_{k=2}^{\infty }\) are zonal harmonic coefficients. These terms only have relationship with the latitude of the central body, and \({\mathcal {P}}_{k}\) (\(k\in {\mathbb {N}}\)) are Legendre polynomials.

The third-body perturbation function can be expanded as

$$\begin{aligned} \frac{\mu }{\Vert \xi -(1,0,0)^{T}\Vert }=\frac{\mu }{\sqrt{\Vert \xi \Vert ^{2}+1-2\xi _{1}}}=\mu +\mu \xi _{1} +\mu \sum _{n=2}^{\infty }{\mathcal {P}}_{n}\left( \frac{\xi _{1}}{\Vert \xi \Vert }\right) \Vert \xi \Vert ^{n} . \end{aligned}$$
(4)

Neglecting the constant terms, the Hamiltonian can be expanded as

$$\begin{aligned} {\mathcal {H}}_{exp}(\xi ,\eta )=&\frac{1}{2}\Vert \eta \Vert ^{2}-\frac{1-\mu }{\Vert \xi \Vert }+(\xi _{2}\eta _{1}-\xi _{1}\eta _{2}) -\mu \sum _{n=2}^{\infty }{\mathcal {P}}_{n}\left( \frac{\xi _{1}}{\Vert \xi \Vert }\right) \Vert \xi \Vert ^{n} \nonumber \\&+\frac{1-\mu }{\Vert \xi \Vert }\sum _{n=2}^{\infty }J_{n}\left( \frac{a_{e}}{\Vert \xi \Vert }\right) ^{n} {\mathcal {P}}_{n}\left( \frac{\xi _{3}}{\Vert \xi \Vert }\right) . \end{aligned}$$
(5)

The Hamiltonian (5) is well written in a perturbed form, but there is not an apparent small parameter, which is necessary for the continuation method and will be introduced in the next section.

3 Symplectic scaling

In this section, a small parameter for the Hamiltonian system (5) is introduced, following the way given by Howison and Meyer (2000). Suppose the infinitesimal body is sufficiently close to the oblate primary with a mass \(1-\mu \). This primary can be approximately considered as a mass point, as its radius is even smaller than the distance between the infinitesimal body and the oblate primary.

Let \(\varepsilon \) represents the closeness of the infinitesimal body to the oblate primary and \(\varepsilon >0\). Using the following symplectic scaling,

$$\begin{aligned} \xi \rightarrow \varepsilon ^{2}(1-\mu )^{\frac{1}{3}}\xi , \quad \eta \rightarrow \varepsilon ^{-1}(1-\mu )^{\frac{1}{3}}\eta , \end{aligned}$$
(6)

the new Hamiltonian is equal to the old Hamiltonian multiplied with \(\varepsilon ^{-1}(1-\mu )^{-\frac{2}{3}}\).

The infinitesimal body is subjected to both the oblate perturbation and the third-body perturbation. Suppose the orders of the magnitudes of the two perturbations are the same. One has

$$\begin{aligned} J_{2} a_{e}^{2}=\varepsilon ^{10}{\tilde{J}}_{2}{\tilde{a}}_{e}^{2}. \end{aligned}$$
(7)

The scaled Hamiltonian can be written as

$$\begin{aligned} {\mathcal {H}}^{\epsilon }(\xi ,\eta ,\varepsilon )&= \varepsilon ^{-1}(1-\mu )^{-\frac{2}{3}}{\mathcal {H}}_{exp}(\varepsilon ^{2}(1-\mu )^{\frac{1}{3}}\xi , \varepsilon ^{-1}(1-\mu )^{\frac{1}{3}}\eta ) \nonumber \\&= \varepsilon ^{-3}{\mathcal {H}}_{01} +{\mathcal {H}}_{02}-\varepsilon ^{3}(1-\mu )^{2/3}{\mathcal {H}}_{1}+\varepsilon ^{5}H_{R} , \end{aligned}$$
(8)

where

$$\begin{aligned} {\mathcal {H}}_{01}&=\frac{\Vert \eta \Vert ^{2}}{2}-\frac{1}{\Vert \xi \Vert } ,\end{aligned}$$
(9)
$$\begin{aligned} {\mathcal {H}}_{02}&=\xi _{2}\eta _{1}-\xi _{1}\eta _{2} , \end{aligned}$$
(10)
$$\begin{aligned} {\mathcal {H}}_{1}&=\mu {\mathcal {P}}_{2}\left( \frac{\xi _{1}}{\Vert \xi \Vert }\right) \Vert \xi \Vert ^{2} +\frac{{\tilde{J}}_{2}{\tilde{a}}_{e}^{2}}{\Vert \xi \Vert ^{3}} {\mathcal {P}}_{2}\left( \frac{\xi _{3}}{\Vert \xi \Vert }\right) . \end{aligned}$$
(11)

This section introduced a small parameter into the full Hamiltonian \({\mathcal {H}}^{\epsilon }\) by symplectic scaling. The unperturbed system \(\varepsilon ^{-3}{\mathcal {H}}_{01}\) in (9) is a Keplerian system with zero angular momentum in the rotating frame, and is like the Keplerian system in an inertial coordinate frame. This makes it suitable to use scaled osculating orbital elements to describe the perturbed orbit in the Hamiltonian (8).

4 Canonical elements

In this section, three kinds of elements are introduced, which are the osculating orbital elements, the Delaunay elements and the Poincaré–Delaunay elements. The first two are suitable for describing elliptic motions, while the latter one is suitable for circular or nearly circular orbits. The latter two are canonical elements, which are useful in canonical transformations.

Let \(r=\Vert \xi \Vert \), the instantaneous orbital elements are \(a,e,i,\varOmega ,\omega ,M\), which are semi-major axis, eccentricity, inclination, longitude of ascending node, argument of pericenter and mean anomaly, respectively. Denote \(f=f(e,M)\) as the true anomaly. The central body has the mass 1, and the gravitational constant equals one. According to the fundamental orbital theory, one has

$$\begin{aligned} \xi&=r\left( \begin{array}{c} \cos (f+\omega )\cos \varOmega -\cos (i)\sin (f+\omega )\sin (\varOmega ) \\ \cos (f+\omega )\sin \varOmega +\cos (i)\sin (f+\omega )\cos (\varOmega ) \\ \sin (f+\omega )\sin (i) \end{array}\right) , \nonumber \\ \eta&={\dot{\xi }} =\frac{C_{k}}{a(1-e^{2})} \left[ -\left( \begin{array}{c} \cos \omega \cos \varOmega -\cos (i)\sin \omega \sin \varOmega \\ \cos \omega \sin \varOmega +\cos (i)\sin (\omega )\cos \varOmega \\ \sin (i)\sin \omega \end{array}\right) \sin (f)\right. \nonumber \\&\quad \left. +\,\left( \begin{array}{c} -\sin \omega \cos \varOmega -\cos (i)\cos \omega \sin \varOmega \\ -\sin \omega \sin \varOmega +\cos (i)\cos \omega \cos \varOmega \\ \sin (i)\cos \omega \end{array}\right) (e+\cos f)\right] , \end{aligned}$$
(12)

where \(C_{k}\) is the angular momentum with the value \(\sqrt{a(1-e^{2})}\) in this Keplerian problem. Substitute the formula above into (9–11), and one gets the instantaneous Hamiltonian with osculating orbital elements,

$$\begin{aligned} {\mathcal {H}}_{01}=-\frac{1}{2a}, \quad {\mathcal {H}}_{02}=C_{k}\cos i . \end{aligned}$$
(13)

The Legendre polynomial \({\mathcal {P}}_{2}(\cdot )\) is expanded following the procedure of Tisserand expansion, see Laskar and Boue (2010). The Tisserand expansion expands each \({\mathcal {P}}_{m}(\cdot )\) (\(m\in {\mathbb {N}}\)) into triangular series, so it has the advantage of averaging \(r^{n}{\mathcal {P}}_{m}(\cdot )\) (\(n\in {\mathbb {Z}}\)). The Legendre polynomial \({\mathcal {P}}_{2}(\frac{\xi _{1}}{r})\) then becomes:

$$\begin{aligned} {\mathcal {P}}_{2}\left( \frac{\xi _{1}}{r}\right)&= \frac{3}{2}[\cos (f+\omega )\cos \varOmega -\cos (i)\sin (f+\omega )\sin \varOmega ]^{2}-\frac{1}{2} \nonumber \\&= I_{1}+I_{2}\cos 2(f+\omega -\varOmega )+ I_{3}\cos 2(f+\omega +\varOmega ) \nonumber \\&\quad +\,I_{4}[\cos 2(f+\omega )+\cos 2\varOmega ] , \end{aligned}$$
(14)

where

$$\begin{aligned}&I_{1}=\frac{3}{8}\cos ^{2}i-\frac{1}{8}, I_{2}=\frac{3}{16}(1-\cos i)^{2}, \nonumber \\&I_{3}=\frac{3}{16}(1+\cos i)^{2}, I_{4}=\frac{3}{8}(1-\cos ^{2}i) . \end{aligned}$$
(15)

One can also get

$$\begin{aligned} {\mathcal {P}}_{2}\left( \frac{\xi _{3}}{r}\right)&=\frac{3}{2}\sin ^{2}(f+\omega )\sin ^{2}i-\frac{1}{2} = -\frac{3}{4}\cos 2(f+\omega )+I_{5}, \end{aligned}$$
(16)

where

$$\begin{aligned} I_{5}=\frac{1}{4}-\frac{3}{4}\cos ^{2}i . \end{aligned}$$
(17)

Using (13–17), the Hamiltonian \({\mathcal {H}}^{\epsilon }\) in (8) can be expressed by orbital elements.

As orbital elements are not canonical, one needs to use the Delaunay elements, which are introduced as below:

$$\begin{aligned} \begin{array}{ccccccccc} L &{}=&{} \sqrt{ a}, &{} G &{}=&{} L\sqrt{1-e^{2}}, &{} H &{}=&{} G\cos i, \\ \ell &{}=&{} M, &{} g &{}=&{} \omega , &{} h &{}=&{} \varOmega , \end{array} \end{aligned}$$

and the Poincaré–Delaunay elements are expressed by Delaunay elements:

$$\begin{aligned} \begin{array}{ccccccccc} Q_{1} &{}=&{} \ell +g+h, &{} Q_{2} &{}=&{} -\sqrt{2(L-G)}\sin (g+h), &{} Q_{3} &{}=&{} \ell +g, \\ P_{1} &{}=&{} L-G+H, &{} P_{2} &{}=&{} \sqrt{2(L-G)}\cos (g+h), &{} P_{3} &{}=&{} G-H. \end{array} \end{aligned}$$

Both the Delaunay elements and the Poincaré–Delaunay elements are canonical.

The Hamiltonian \({\mathcal {H}}^{\epsilon }\) is rewritten in the following way:

$$\begin{aligned} {\mathcal {H}}^{\epsilon }&=-\frac{\varepsilon ^{-3}}{2L^{2}}-H -\varepsilon ^{3}(1-\mu )^{\frac{2}{3}}{\mathcal {H}}_{1}+\varepsilon ^{5}{\mathcal {H}}_{R} \nonumber \\&=-\frac{\varepsilon ^{-3}}{2(P_{1}+P_{3})^{2}}+\left( \frac{P_{2}^{2}+Q_{2}^{2}}{2}-P_{1}\right) -\varepsilon ^{3}(1-\mu )^{\frac{2}{3}}{\mathcal {H}}_{1}+\varepsilon ^{5}{\mathcal {H}}_{R} , \end{aligned}$$
(18)

where \({\mathcal {H}}_{1}\) can be expanded with Hansen coefficients as

$$\begin{aligned} {\mathcal {H}}_{1}&= \mu \cdot r^{2}{\mathcal {P}}_{2}\left( \frac{\xi _{1}}{r}\right) +{\tilde{J}}_{2}{\tilde{a}}_{e}^{2} \cdot r^{-3}{\mathcal {P}}_{2}\left( \frac{\xi _{3}}{r}\right) \nonumber \\&=\mu \left\{ I_{1}\sum _{k=-\infty }^{\infty }X_{k}^{2,0}(e)\cos (k Q_{1}-k(g+h)) \right. \nonumber \\&\quad \left. + \, I_{2}\sum _{k=-\infty }^{\infty }X_{k}^{2,2}(e)\cos ((k-4)Q_{1}+4Q_{3}+(2-k)(g+h))\right. \nonumber \\&\quad \left. +\,I_{3}\sum _{k=-\infty }^{\infty }X_{k}^{2,2}(e)\cos (kQ_{1}+(2-k)(g+h)) \right. \nonumber \\&\quad \left. +\,I_{4}\sum _{k=-\infty }^{\infty }X_{k}^{2,2}(e)\cos ((k-2)Q_{1}+2Q_{3}+(2-k)(g+h))\right. \nonumber \\&\quad \left. +\,I_{4}\sum _{k=-\infty }^{\infty }X_{k}^{2,0}(e)\cos (kQ_{1}-k(g+h))\cos 2(Q_{1}-Q_{3}) \right\} \nonumber \\&\quad +\,{\tilde{J}}_{2}{\tilde{a}}_{e}^{2}\left\{ -\frac{3}{4}\sum _{k=-\infty }^{\infty }X_{k}^{-3,2}(e) \cos ((k-2)Q_{1}+2Q_{3}+(2-k)(g+h)) \right. \nonumber \\&\quad \left. +\,I_{5}\sum _{k=-\infty }^{\infty }X_{k}^{-3,0}(e)\cos (kQ_{1}-k(g+h))\right\} , \end{aligned}$$
(19)

where

$$\begin{aligned} e^{2} =1-\left( 1-\frac{P_{2}^{2}+Q_{2}^{2}}{2(P_{1}+P_{3})}\right) ^{2}, \quad \cos i =1-\frac{P_{3}}{P_{1}+P_{3}-\frac{P_{2}^{2}+Q_{2}^{2}}{2}} . \end{aligned}$$
(20)

For more aspects about Hansen coefficients, one can refer to Laskar and Boue (2010). In fact, the perturbed terms \({\mathcal {H}}_{1}\) and \({\mathcal {H}}_{R}\) can be expressed by infinity series of the Delaunay elements or the Poincaré–Delaunay elements if the eccentricity e is not big. The integrable truncated system \(-\frac{\varepsilon ^{-3}}{2L^{2}}-H\) is considered as the approximated system, and \(-\varepsilon ^{3}(1-\mu )^{\frac{2}{3}}{\mathcal {H}}_{1}\) is considered as the first-order perturbation term.

In order to describe the properties of the doubly symmetric periodic orbits of the full system, the double symmetry and the solutions of the approximated system are introduced sequentially in the following two sections.

5 Double symmetry

In this section, the double symmetry is expressed by the rectangular coordinates and the canonical elements. Similar to the two-point-mass case, this Hamiltonian system with one oblate mass is invariant under these two time reversal transformations:

$$\begin{aligned} {\mathscr {R}}_{1}&: (\xi _{1},\xi _{2},\xi _{3},\eta _{1},\eta _{2},\eta _{3},t)\rightarrow (\xi _{1},-\xi _{2},-\xi _{3},-\eta _{1},\eta _{2},\eta _{3},-t), \nonumber \\ {\mathscr {R}}_{2}&: (\xi _{1},\xi _{2},\xi _{3},\eta _{1},\eta _{2},\eta _{3},t)\rightarrow (\xi _{1},-\xi _{2},\xi _{3},-\eta _{1},\eta _{2},-\eta _{3},-t) . \end{aligned}$$
(21)

According to Howison and Meyer (2000), one has the following lemma about the doubly symmetric periodic solutions of the Hamiltonian system (2):

Lemma 1

If one orbit of the Hamiltonian (2) starts from \({\mathscr {L}}_{1}^{(0)}\), and intersects \({\mathscr {L}}_{2}^{(0)}\) after time \(T>0\), then the orbit is periodic with period 4T and doubly symmetric, where

$$\begin{aligned} {\mathscr {L}}_{1}^{(0)}&=\{(\xi ,\eta )|\xi =(\xi _{1},0,0),\eta =(0,\eta _{2},\eta _{3})\}, \nonumber \\ {\mathscr {L}}_{2}^{(0)}&=\{(\xi ,\eta )|\xi =(\xi _{1},0,\xi _{3}),\eta =(0,\eta _{2},0)\} . \end{aligned}$$
(22)

This lemma tells us that if one orbit hits the \(\xi _{1}\) axis in the \(\xi _{1}\xi _{2}\) plane and the \(\xi _{1}\xi _{3}\) plane perpendicularly at two different times, then this orbit is doubly symmetric periodic. That is to say, one orbit is doubly symmetric periodic if the initial values \(\xi _{1}(0),\eta _{2}(0),\eta _{3}(0)\) are well chosen such that \(\xi _{2}(T)=\eta _{1}(T)=\eta _{3}(T)=0\).

The sets of boundary values for the double symmetry in (22) can be expressed by the orbital elements, the Delaunay elements and the Poincaré–Delaunay elements, respectively:

$$\begin{aligned}&{\mathscr {L}}_{1}^{(1)} =\{f=0 \mod \pi , \ \ \omega =0 \mod \pi , \ \ \varOmega =0 \mod \pi \}, \nonumber \\&{\mathscr {L}}_{2}^{(1)} =\{f=0 \mod \pi , \ \ \omega =\frac{\pi }{2}\mod \pi , \ \ \varOmega =\frac{\pi }{2} \mod \pi \}, \end{aligned}$$
(23)
$$\begin{aligned}&{\mathscr {L}}_{1}^{(2)} =\{\ell =0 \mod \pi , \ \ g=0 \mod \pi , \ \ h=0 \mod \pi \}, \nonumber \\&{\mathscr {L}}_{2}^{(2)} =\{\ell =0 \mod \pi , \ \ g=\frac{\pi }{2}\mod \pi , \ \ h=\frac{\pi }{2} \mod \pi \}, \end{aligned}$$
(24)
$$\begin{aligned}&{\mathscr {L}}_{1}^{(3)} =\{ Q_{1}=0 \mod \pi , \ \ Q_{2}\equiv 0, \ \ Q_{3}=0 \mod \pi \}, \nonumber \\&{\mathscr {L}}_{2}^{(3)} =\{ Q_{1}=0 \mod \pi , \ \ Q_{2}\equiv 0, \ \ Q_{3}=\frac{\pi }{2} \mod \pi \}, \end{aligned}$$
(25)

In the next section, the doubly symmetric periodic orbits of the approximated system is characterized by the two sets of boundary values \({\mathscr {L}}_{1}^{(3)}\) and \({\mathscr {L}}_{2}^{(3)}\).

6 Approximated solution

In this section, the doubly symmetric periodic orbits of the approximated system \({\mathcal {H}}_{0}=-\varepsilon ^{-3}{\mathcal {H}}_{01}+{\mathcal {H}}_{02}\) is introduced. The Hamiltonian \({\mathcal {H}}_{0}\) can be rewritten in Poincaré–Delaunay elements:

$$\begin{aligned} {\mathcal {H}}_{0}= -\frac{\varepsilon ^{-3}}{2(P_{1}+P_{3})^{2}}+\left( \frac{P_{2}^{2}+Q_{2}^{2}}{2}-P_{1}\right) , \end{aligned}$$
(26)

Denote the initial conditions of the approximated system as \(Z_{0}^{*}=(Q_{1}^{*},\ldots ,P_{3}^{*})^{T}\), and the general solution of the approximated system \(Z^{(0)}(Z_{0}^{*},t)\). The differential equations with respect to time t can be written as

$$\begin{aligned} {\dot{Z}}^{(0)}=F_{0}(Z^{(0)}) , \end{aligned}$$
(27)

and the general solution \(Z^{(0)}\) of the approximated system (26) is

$$\begin{aligned} \begin{array}{ll} Q_{1}(t)&{}= \left[ \frac{\varepsilon ^{-3}}{ (P_{1}^{*}+P_{3}^{*})^{3}}-1\right] t+Q_{1}^{*}, \\ Q_{2}(t)&{}= P_{2}^{*}\sin (t)+Q_{2}^{*}\cos (t) \\ Q_{3}(t)&{}= \frac{\varepsilon ^{-3}t}{(P_{1}^{*}+P_{3}^{*})^{3}}+Q_{3}^{*}, \\ P_{1}(t)&{}= P_{1}^{*}, \quad P_{3}(t)=P_{3}^{*}, \\ P_{2}(t)&{}= -Q_{2}^{*}\sin (t)+P_{2}^{*}\cos (t) . \end{array} \end{aligned}$$
(28)

According to Lemma 1 and the sets of boundary values in (25), \(Z^{(0)}\) is doubly symmetric and periodic if

$$\begin{aligned} \left\{ \begin{array}{ll} &{} Q_{1}^{*} = i \pi , \quad Q_{2}^{*} =0 , \quad Q_{3}^{*} = j\pi , \\ &{} Q_{1}(T) = \left( \frac{\varepsilon ^{-3}}{\left( P_{1}^{*}+P_{3}^{*}\right) ^{3}}-1\right) T+ i\pi = k\pi +i\pi , \\ &{} Q_{2}(T) = P_{2}^{*}\sin (T)=0, \\ &{} Q_{3}(T) = \frac{\varepsilon ^{-3}}{\left( P_{1}^{*}+P_{3}^{*}\right) ^{3}}T+j\pi =\left( m+\frac{1}{2}\right) \pi +j\pi , \end{array}\right. \end{aligned}$$
(29)

where i, j, k, m are positive integers, and \(k\le m\). From Eq. (29), one gets

$$\begin{aligned} T&=\frac{\varepsilon ^{-3}}{\left( P_{1}^{*}+P_{3}^{*}\right) ^{3}}T-k\pi =\left( m+\frac{1}{2}-k\right) \pi , \nonumber \\ \varepsilon ^{3}&= \frac{m+\frac{1}{2}-k}{\left( P_{1}^{*}+P_{3}^{*}\right) ^{3}\left( m+\frac{1}{2}\right) } , \quad P_{2}^{*}=0, \end{aligned}$$
(30)

so the doubly symmetric periodic orbits of the approximated system can be written as

$$\begin{aligned} \left\{ \begin{array}{lll} Q_{1}(t)=\left[ \frac{\varepsilon ^{-3}}{\left( P_{1}^{*}+P_{3}^{*}\right) ^{3}}-1\right] t+i\pi , &{} Q_{2}(t)\equiv 0, &{} Q_{3}(t)=\frac{\varepsilon ^{-3}t}{\left( P_{1}^{*}+P_{3}^{*}\right) ^{3}}+j\pi , \\ P_{1}(t) \equiv P_{1}^{*}, &{} P_{2}(t) \equiv 0, &{} P_{3}(t)=P_{3}^{*}. \end{array}\right. \end{aligned}$$
(31)
Fig. 2
figure 2

An example of the doubly symmetric periodic orbit of the approximated system with \(\varepsilon ^{3}=\frac{1}{3}\), \(L=G=1\), \(H=G\cos \frac{\pi }{4}\), and \(g=h=0\)

Full size image

One simple example for the doubly symmetric periodic solution of system (26) is the case of \(\varepsilon ^{3}=\frac{1}{3}\), \(k=m=1\), \(L=G=1\), \(H=G\cos \frac{\pi }{4}\), and \(g=h=0\). A sketch of this doubly symmetric periodic solution is given in the Fig. 2.

It is shown that doubly symmetric periodic solutions exist in the approximated system for the CRTBP. These solutions are described by Eqs. (30) and (31). The following section will eliminate the short periodic effects of the first-order perturbation term by averaging so as to give better error estimates which are useful according to the fixed-point theorem used in the procedure of the continuation.

7 Averaging

In this section, the perturbation term \({\mathcal {H}}_{1}\) is averaged such that this averaged term does not contain the short period effects about the Poincaré–Delaunay elements \(Q_{1}=\ell +g+h\) and \(Q_{3}=\ell +g\), and the conjugate momenta, the Poincaré–Delaunay elements, \(P_{1}=L-G+H\) and \(P_{3}=G-H\) are constants for the first order.

The doubly symmetric periodic orbits of the full system are continued from the circular orbits of the approximated system, and the continued orbits are elliptic with small eccentricities.

Two angular variables \(Q_{1}\) and \(Q_{2}\) in \({\mathcal {H}}_{1}\) are eliminated separately. The averaged \({\mathcal {H}}_{1}\) can be obtained from (19). One has

$$\begin{aligned} \bar{{\mathcal {H}}}_{1}&=\frac{1}{2\pi }\int _{0}^{2\pi }{\mathcal {H}}_{1} \mathrm{{d}}Q_{1} \nonumber \\&= \mu \biggl [ I_{1}X_{0}^{2,0}+I_{2}X_{4}^{2,2}\cos (4Q_{3}-2(g+h))+I_{3}X_{0}^{2,2}\cos (2g+2h) \nonumber \\&\quad +\,I_{4}X_{2}^{2,2}\cos 2Q_{3}+\frac{1}{2}I_{4}(X_{-2}^{2,0}+X_{2}^{2,0})\cos (2Q_{3}-2g-2h) \biggr ] \nonumber \\&\quad +\,{\tilde{J}}_{2}{\tilde{a}}_{e}^{2}\biggl [-\frac{3}{4}X_{2}^{-3,2}\cos 2Q_{3} +I_{5}X_{0}^{-3,0} \biggr ], \end{aligned}$$
(32)

and

$$\begin{aligned} \bar{\bar{{\mathcal {H}}}}_{1}&=\frac{1}{2\pi }\int _{0}^{2\pi }\bar{{\mathcal {H}}}_{1} \mathrm{{d}}Q_{3} \nonumber \\&=\mu \left[ \left( 1+\frac{3}{2}e^{2}\right) I_{1}+\frac{5}{2} I_{3} e^{2}\cos (2g+2h)\right] +{\tilde{J}}_{2}{\tilde{a}}_{e}^{2}(1-e^{2})^{-3/2}I_{5} , \end{aligned}$$
(33)

where \(\cos 2(g+h)\) and \(\sin 2(g+h)\) can be derived from the Poincaré–Delaunay elements \(Q_{2}\) and \(P_{2}\). If one substitutes (20) into (32), the \(\bar{\bar{{\mathcal {H}}}}_{1}\) can be explicitly expressed in Poincaré–Delaunay elements.

The generating function of the first averaging procedure can be written as

$$\begin{aligned} {\mathcal {S}}^{(1)}={\mathcal {S}}^{(1)}(Q_{1},Q_{2},Q_{3},P_{1}',P_{2}',P_{3}'), \end{aligned}$$

where the primed variables are the new variables. The relationship between old and new variables is

$$\begin{aligned} \begin{array}{ccc} Q_{1}' = Q_{1} + \frac{\partial {\mathcal {S}}^{(1)}}{\partial P_{1}'}, &{}\quad Q_{2}' = Q_{2} + \frac{\partial {\mathcal {S}}^{(1)}}{\partial P_{2}'}, &{}\quad Q_{3}' = Q_{3} + \frac{\partial {\mathcal {S}}^{(1)}}{\partial P_{3}'}, \\ P_{1}' = P_{1} - \frac{\partial {\mathcal {S}}^{(1)}}{\partial Q_{1}}, &{}\quad P_{2}' = P_{2} - \frac{\partial {\mathcal {S}}^{(1)}}{\partial Q_{2}}, &{}\quad P_{3}' = P_{3} - \frac{\partial {\mathcal {S}}^{(1)}}{\partial Q_{3}} . \end{array} \end{aligned}$$

Substitute the old variables by the new variables to do Taylor expansions, one has

$$\begin{aligned} \frac{\varepsilon ^{-3}}{(P_{1}'+P_{3}')^{3}}\frac{\partial {\mathcal {S}}^{(1)}}{\partial Q_{1}} =\varepsilon ^{3}(1-\mu )^{\frac{2}{3}} \left( {\mathcal {H}}_{1}(Q_{1,2,3},P_{1,2,3}')-\bar{{\mathcal {H}}}_{1}(Q_{2,3},P_{1,2,3}')\right) , \end{aligned}$$
(34)

so the \({\mathcal {S}}^{(1)}\) can be solved. In a similar way, the second generating function \({\mathcal {S}}^{(2)}(Q_{1,2,3}'\), \(P_{1,2,3}'')\) can be solved by

$$\begin{aligned} \frac{\varepsilon ^{-3}}{(P_{1}''+P_{3}'')^{3}}\frac{\partial {\mathcal {S}}^{(2)}}{\partial Q_{3}'} =\varepsilon ^{3}(1-\mu )^{\frac{2}{3}} \left( \bar{{\mathcal {H}}}_{1}(Q_{2,3}',P_{1,2,3}'')-\bar{\bar{{\mathcal {H}}}}_{1}(Q_{2}',P_{1,2,3}'')\right) , \end{aligned}$$
(35)

where the double primed variables are the newer variables. The formulas of both \({\mathcal {S}}^{(1)}\) and \({\mathcal {S}}^{(2)}\) are not given here because they are long and not difficult to calculate.

The new Hamiltonian without the primes can be written as:

$$\begin{aligned} \bar{{\mathcal {H}}}^{\epsilon }&=-\frac{\varepsilon ^{-3}}{2(P_{1}+P_{3})^{2}} +\left( \frac{P_{2}^{2}+Q_{2}^{2}}{2}-P_{1}\right) \nonumber \\&\quad -\varepsilon ^{3}(1-\mu )^{\frac{2}{3}}\bar{\bar{{\mathcal {H}}}}_{1}(Q_{2},P_{1},P_{2},P_{3}) +{\mathcal {O}}(\varepsilon ^{5}) . \end{aligned}$$
(36)

This section gives the averaged first-order system by the Zeipel method. In the generating functions \( {\mathcal {S}}^{(1)}\) and \( {\mathcal {S}}^{(2)}\), the angular variables are the old variables, and the conjugate momenta are the new variables. The implicit transformations can be solved by iterations. In the following section, the doubly symmetric periodic solutions of the approximated system are continued.

8 Continuation

This section gives the proof of the existence of the doubly symmetric periodic orbits of the full system. The proof is based on a proposition derived from Arenstorf’s fixed-point theorem. This proposition is given by Cors et al. (2005) and is stated as follows.

Proposition 1

(Cors, Pinyol and Soler) Let U be an open domain in \({\mathbb {R}}^{n}\), \(I\subset {\mathbb {R}}\) an open neighborhood of the origin and \(f: U\times I \rightarrow {\mathbb {R}}^{n}\) with \(f(0,0)=0\), differentiable with respect to \(x\in U\), and \(f_{x}(0,0)\) non-singular. Assume that there exist \(c>0, k>0\) such that for \(x\in U\), \(\varepsilon \in I\),

  1. 1.

    \(\Vert f_{x}(x,\varepsilon )-f_{x}(0,0)\Vert \le c(\Vert x\Vert +\varepsilon )\),

  2. 2.

    \(\Vert f(0,\varepsilon )\Vert \le k\varepsilon \) .

Then there exists a function \(x(\varepsilon ) \in U\), defined for \(\varepsilon \in I' \subset I\), such that \(f(x,\varepsilon )=0\) and \(x(0)=0\).

The norms used here are defined as \(\Vert X\Vert =\max _{1\le i\le n}|X_{i}|\) for \(X \in {\mathbb {R}}^{n}\) and \(\Vert A\Vert =\sup _{ \Vert X\Vert =1 } \Vert A X\Vert \) for \( A \in {\mathbb {R}}^{n\times n}\). Let \({\mathbf {D}}F\) denote the matrix in which the elements are the partial derivatives of the vector function F with respect to the vector X.

The \(f(x,\varepsilon )\) described in Proposition 1 is in fact composed of three equations, which are about the boundary values of three angular variables. It is difficult to check whether \(\Vert f_{x}(x,\varepsilon )-f_{x}(0,0)\Vert \) and \(\Vert f(0,\varepsilon )\Vert \) are bounded as described in this proposition. Before giving the explicit \(f(x,\varepsilon )\) and the proof of the final conclusion, one needs to make the error estimates.

Consider the differential equation system of the Hamiltonian (36)

$$\begin{aligned} {\dot{Z}}=F(Z,\varepsilon )=F_{0}(Z_{2,4,5,6},\varepsilon )+\varepsilon ^{3}F_{1}(Z_{2,4,5,6})+\varepsilon ^{5}F_{R}(Z,\varepsilon ), \end{aligned}$$
(37)

where \(Z=(Q_{1},Q_{2},\ldots ,P_{3}) \in {\mathbb {R}}^{6}\), \(F=(F^{(1)},F^{(2)},\ldots ,F^{(6)})\in {\mathbb {R}}^{6}\), \(F^{(i)}=\frac{\partial \bar{{\mathcal {H}}}^{\epsilon }}{\partial P_{i}}\), and \(F^{(i+3)}=-\frac{\partial \bar{{\mathcal {H}}}^{\epsilon }}{\partial Q_{i}}\), \((i=1,2,3)\).

As \(\varepsilon \) is small enough, \(Z(Z_{0},t,\varepsilon )-Z^{(0)}(Z_{0},t)\) is bounded when time is finite. The vector functions \(F_{0}\), \(F_{1}\) and \(F_{R}\) are continuous, and their derivatives with respect to Z are bounded in a compact region near \(Z^{(0)}\). In order to give the error estimates according to Proposition 1, a lemma on the differential equations of the Hamiltonian system (36) is mentioned.

Lemma 2

Let \(Z^{(1)}(Z_{0},t)\) be a solution of

$$\begin{aligned} {\dot{Z}}^{(1)}(Z_{0},t)={\mathbf {D}}_{Z^{(0)}} F_{0}Z^{(1)}+F_{1}|_{Z^{(0)}} \end{aligned}$$
(38)

with an initial condition \(Z^{(1)}(Z_{0},0)={\mathbf {0}}\). In a finite time interval \(t\in [0,t_{0}]\), the solution of the full system (37) can be expressed as

$$\begin{aligned} Z(Z_{0},t,\varepsilon )=Z^{(0)}(Z_{0},t)+\varepsilon ^{3}Z^{(1)}(Z_{0},t)+Z_{R}(Z_{0},t,\varepsilon ), \end{aligned}$$
(39)

where \([Z-Z^{(0)}]|_{Z_{0}}\) is of order \(\varepsilon ^{3}\) and \(Z_{R}(Z_{0},t,\varepsilon )\) is of order \(\varepsilon ^{5}\). In addition, \({\mathbf {D}}_{Z_{0}}Z^{(1)}\) is bounded, and \({\mathbf {D}}_{Z_{0}}Z_{R}\) is of the order \(\varepsilon ^{5}\).

Proof

The proof can be referred to Howison and Meyer (2000), Cors et al. (2005).

Let \(Z^{(0)}(Z_{0}^{*},t)\) be a doubly symmetric periodic solution of the differential equation (27). Denote a set of initial values of the full system as \(Z_{0}\), which is very near \(Z_{0}^{*}\),

$$\begin{aligned} Z_{0}&=Z_{0}^{*}+(0, 0, 0, \delta P_{1}, \delta P_{2}, \delta P_{3})^{T} \nonumber \\&=(i\pi , 0, j\pi , P_{1}^{*}+\delta P_{1}, \delta P_{2}, P_{3}^{*}+\delta P_{3})^{T}. \end{aligned}$$
(40)

Specially, \(P_{1}(0)=P_{1}^{*}+\delta P_{1}\) and \(P_{3}(0)=P_{3}^{*}+\delta P_{3}\). Suppose \(Z_{0}\) is well chosen, such that \((Q_{1},Q_{2},Q_{3})=(i\pi +k\pi ,0,(j+m+\frac{1}{2})\pi )\) after time \(T=(m+\frac{1}{2}-k)\pi +\delta T\), and \(Z(Z_{0},t)\) is a doubly symmetric periodic solution of the full system.

The errors between \(Z(Z_{0},t)\) and \(Z^{(0)}(Z_{0},t)\) can be preliminarily estimated by

$$\begin{aligned} \Vert Z(Z_{0},t,\varepsilon )-Z^{(0)}(Z_{0},t)\Vert&\le \int _{0}^{t}\Vert {\dot{Z}}-{\dot{Z}}^{(0)}\Vert \mathrm{{d}} s \nonumber \\&\le \int _{0}^{t}\Vert {\mathbf {D}}_{Z^{(0)}}F_{0} \cdot (Z-Z^{(0)})\Vert \mathrm{{d}}s + C_{1}\varepsilon ^{3}t, \end{aligned}$$
(41)

where \(C_{1}>0\) is a constant, \(\max \{\Vert F_{1}\Vert , \Vert F_{R}\Vert \}<C_{1}\), and

$$\begin{aligned} {\mathbf {D}}_{Z^{(0)}}F_{0}=\left( \begin{array}{cccccc} 0 &{}\quad 0 &{}\quad 0 &{}\quad -\frac{3\varepsilon ^{-3}}{(P_{1}(0)+P_{3}(0))^{4}} &{}\quad 0 &{}\quad -\frac{3\varepsilon ^{-3}}{(P_{1}(0)+P_{3}(0))^{4}} \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 1 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad -\frac{3\varepsilon ^{-3}}{(P_{1}(0)+P_{3}(0))^{4}} &{}\quad 0 &{}\quad -\frac{3\varepsilon ^{-3}}{(P_{1}(0)+P_{3}(0))^{4}} \\ 0 &{}\quad 0 &{}\quad 0 &{} \quad 0 &{} \quad 0 &{}\quad 0 \\ 0 &{}\quad -\,1 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \end{array}\right) . \end{aligned}$$

In a finite time, \(P_{1}(t)-P_{1}(0)\) and \(P_{3}(t)-P_{3}(0)\) are of order \(\varepsilon ^{5}\), and thus \(Q_{1}(t)-Q_{1}^{(0)}(t)\) and \(Q_{3}(t)-Q_{3}^{(0)}(t)\) can be estimated roughly to be of the order \(\varepsilon ^{2}\). Denote \(C_{0}>0\) as a constant, such that

$$\begin{aligned} \Vert Q_{1}(t)-Q_{1}^{(0)}(t)\Vert&\le \int _{0}^{t}\frac{3\varepsilon ^{-3}}{(P_{1}(0)+P_{3}(0))^{4}}{\mathcal {O}}(\varepsilon ^{5})\mathrm{{d}}s +C_{1}\varepsilon ^{3} t \\&\le \int _{0}^{t} C_{0} \Vert Q_{1}(s)-Q_{1}^{(0)}(s)\Vert \mathrm{{d}}s+C_{1}\varepsilon ^{3}t, \end{aligned}$$

and

$$\begin{aligned} \Vert P_{1}(t)-P_{1}^{(0)}(t)\Vert \le \int _{0}^{t}\Vert \varepsilon ^{5}F_{R}+C_{1}\varepsilon ^{6}\Vert \mathrm{{d}}s\le C_{1}\varepsilon ^{5}t . \end{aligned}$$

Similarly, \(Q_{3}\) and \(P_{3}\) have the same property. One has

$$\begin{aligned} \left( \begin{array}{c} {\dot{Q}}_{2} \\ {\dot{P}}_{2} \end{array}\right) =\left( \begin{array}{cc} 0 &{}\quad 1 \\ -\,1 &{} \quad 0 \end{array}\right) \left( \begin{array}{c} Q_{2} \\ P_{2} \end{array}\right) +\left( \begin{array}{c} \varepsilon ^{3}F_{1}^{(2)}+{\mathcal {O}}(\varepsilon ^{5}) \\ \varepsilon ^{3}F_{1}^{(5)}+{\mathcal {O}}(\varepsilon ^{5}) \end{array}\right) , \end{aligned}$$

and thus both \(Q_{2}\) and \(P_{2}\) are of order \(\varepsilon ^{3}\).

In all, one has

$$\begin{aligned} \Vert Z(Z_{0},t,\varepsilon )-Z^{(0)}(Z_{0},t)\Vert \le \int _{0}^{t}C_{0}\Vert Z-Z^{(0)}\Vert \mathrm{{d}}s + C_{1}\varepsilon ^{3}t. \end{aligned}$$

According to Gronwall’s inequality, one has

$$\begin{aligned} \Vert Z-Z^{(0)}\Vert \le \frac{C_{1}}{C_{0}}\varepsilon ^{3}(e^{C_{0}t}-1). \end{aligned}$$
(42)

Using an expansion of Taylor series, one can show that (38) and (39) are correct. In fact, (38) and (39) are also valid for the Hamiltonian (18) before averaging, because the Zeipel transformation is nearly identity with the order \(\varepsilon ^{6}\).

The eigenvalues of matrix \({\mathbf {D}}_{Z^{(0)}}F_{0}\) are four zeros and \(\pm i\). One has \( \Vert {\mathbf {D}}F_{0} \cdot Z_{R}\Vert \le C_{0} \Vert Z_{R}\Vert \), and

$$\begin{aligned} \Vert Z_{R}\Vert&\le \int _{0}^{t}\Vert {\dot{Z}}-{\dot{Z}}^{(0)}-\varepsilon ^{3}{\dot{Z}}^{(1)}\Vert \mathrm{{d}}s \le \int _{0}^{t}\Vert {\mathbf {D}}_{Z}F_{0} \cdot Z_{R}\Vert \mathrm{{d}}s+C_{2}\varepsilon ^{5}t \nonumber \\&\le \int _{0}^{t}C_{0}\Vert Z_{R}\Vert \mathrm{{d}}s+C_{2}\varepsilon ^{5}t, \end{aligned}$$
(43)

where \(C_{2}>0\) is a constant. According to Gronwall’s inequality, one has

$$\begin{aligned} \Vert Z_{R}\Vert \le \frac{C_{2}}{C_{0}}\varepsilon ^{5}(e^{C_{0}t}-1). \end{aligned}$$

One has the fundamental solution matrix for (38),

$$\begin{aligned} {\varvec{\Phi }}(t)=\exp {({\mathbf {D}}F_{0} \cdot t)}=\left( \begin{array}{cccccc} 1 &{} 0 &{} 0 &{} -\frac{3\varepsilon ^{-3}t}{(P_{1}+P_{3})^{4}} &{} 0 &{} -\frac{3\varepsilon ^{-3}t}{(P_{1}+P_{3})^{4}} \\ 0 &{}\quad \cos t &{}\quad 0 &{}\quad 0 &{}\quad \sin t &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 1 &{}\quad -\frac{3\varepsilon ^{-3}t}{(P_{1}+P_{3})^{4}} &{}\quad 0 &{}\quad -\frac{3\varepsilon ^{-3}t}{(P_{1}+P_{3})^{4}} \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 1 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad -\sin t &{}\quad 0 &{}\quad 0 &{}\quad \cos t &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 1 \end{array}\right) , \end{aligned}$$

where \({\varvec{\Phi }}^{-1}(t)={\varvec{\Phi }}(-t)\), \(P_{1,3}=P_{1,3}(0)\).

\(Z^{(1)}\) can be solved by the following way,

$$\begin{aligned} Z^{(1)}&={\varvec{\Phi }}(t)\int _{0}^{t}{\varvec{\Phi }}(-s)F_{1}(Z^{(0)})\mathrm{{d}}s \nonumber \\&=-(1-\mu )^{\frac{2}{3}} \left( \int _{0}^{t}F_{1}^{(1)}\mathrm{{d}}s,{\mathcal {O}}(\delta P_{2}),\int _{0}^{t}F_{1}^{(3)}\mathrm{{d}}s,0,{\mathcal {O}}(\delta P_{2}),0\right) ^{T}, \end{aligned}$$
(44)

where

$$\begin{aligned}&\int _{0}^{t} F_{1}^{(1)}\mathrm{{d}}s=\left( \frac{3}{4}\mu -\frac{3}{2}{\tilde{J}}_{2}{\tilde{a}}_{e}^{2}\right) \frac{P_{1}P_{3}}{(P_{1}+P_{3})^{3}}t+{\mathcal {O}}(\delta P_{2}^{2}), \nonumber \\&\int _{0}^{t} F_{1}^{(3)}\mathrm{{d}}s=\frac{3}{2}{\tilde{J}}_{2}{\tilde{a}}_{e}^{2}\frac{P_{1}^{2}}{(P_{1}+P_{3})^{3}}t+ {\mathcal {O}}(\delta P_{2}^{2}). \end{aligned}$$
(45)

As \(P_{1}+P_{3}\) is bounded away from zero, the derivative of \(Z^{(1)}\) with respect to \(Z_{0}\) is bounded. Following the way of Cors et al. (2005), the derivative of \(Z_{R}\) with respect to \(Z_{0}\) is also bounded at the order of \(\varepsilon ^{5}\). \(\square \)

Using Proposition 1 and Lemma 2, Theorem 1 can now be proved as follows.

Theorem 1

In the circular restricted three-body problem with one oblate primary, there exists a family of Lunar-type doubly symmetric periodic orbits around the oblate primary, where the other primary moves on the equatorial plane of the oblate primary.

Proof

For the full system, one has

$$\begin{aligned}&Q_{1}(T)=\left[ \frac{\varepsilon ^{-3}}{(P_{1}^{*}+P_{3}^{*}+\delta P_{1} +\delta P_{3})^{3}}-1 \right] T +i\pi +\varepsilon ^{3}Q_{1}^{(1)}+\varepsilon ^{5}Q_{1}^{(R)}=k\pi +i\pi , \nonumber \\&Q_{2}(T)=\delta P_{2}\sin T +\varepsilon ^{3} Q_{2}^{(1)}+\varepsilon ^{5}Q_{2}^{(R)}=0, \nonumber \\&Q_{3}(T)=\frac{\varepsilon ^{-3}}{(P_{1}^{*}+P_{3}^{*}+\delta P_{1}+\delta P_{3})^{3}}T+j\pi +\varepsilon ^{3} Q_{3}^{(1)}+\varepsilon ^{5}Q_{3}^{(R)}=j\pi +\left( m+\frac{1}{2}\right) \pi , \end{aligned}$$
(46)

Fix \(T_{0}=(m+\frac{1}{2}-k)\pi \) finite, let m and k be sufficiently large as the order of \(\varepsilon ^{-3}\), one gets \({\varvec{\Psi }}(\delta T,\delta P_{2}, \delta P_{1}+\delta P_{3})\). \({\varvec{\Psi }}_{1}\) is derived from \(Q_{3}(T)-Q_{1}(T)=T+j\pi -i\pi \), \({\varvec{\Psi }}_{2}\) is derived from \(Q_{2}(T)\). As \(P_{1}+P_{3}=L\), denote \(\delta L=\delta P_{1}+\delta P_{3}\). Substitute (30) into \(Q_{3}(T)\), divide by \((m+\frac{1}{2})\pi \), and one can derive \({\varvec{\Psi }}_{3}\):

$$\begin{aligned}&{\varvec{\Psi }}_{1}= \delta T +\varepsilon ^{3} (Q_{3}^{(1)}-Q_{1}^{(1)})+{\mathcal {O}}(\varepsilon ^{5})=0, \nonumber \\&{\varvec{\Psi }}_{2}= \pm \delta P_{2} \cos \delta T +\varepsilon ^{3} Q_{2}^{(1)}+{\mathcal {O}}(\varepsilon ^{5})=0, \nonumber \\&{\varvec{\Psi }}_{3}=\frac{1+\frac{\delta T}{T_{0}}}{\left( 1+\frac{\delta L}{L^{*}}\right) ^{3}}-1 +\frac{1}{(m+\frac{1}{2})\pi }[ \varepsilon ^{3} Q_{3}^{(1)}+{\mathcal {O}}(\varepsilon ^{5})]=0 . \end{aligned}$$
(47)

Let \(X=(\delta T, \delta P_{2}, \delta L)\), one has

$$\begin{aligned} \frac{\partial {\varvec{\Psi }}({\mathbf {0}},0)}{\partial X}= \left( \begin{array}{ccc} 1 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad \pm \, 1 &{}\quad 0 \\ \frac{1}{T_{0}} &{}\quad 0 &{}\quad -\frac{3}{L^{*}} \end{array}\right) , \end{aligned}$$
(48)

so \({\varvec{\Psi }}_{X}({\mathbf {0}},0)\ne 0\). One has \( \Vert {\varvec{\Psi }}_{X}({\mathbf {0}},\varepsilon )\Vert \le C_{1}\varepsilon \), and

$$\begin{aligned}&\Vert {\varvec{\Psi }}_{X}(X,\varepsilon )-{\varvec{\Psi }}_{X}(0,0)\Vert \nonumber \\&\le \Vert {\varvec{\Psi }}_{X}(X,\varepsilon )-{\varvec{\Psi }}_{X}(X,0)\Vert + \Vert {\varvec{\Psi }}_{X}(X,0)-{\varvec{\Psi }}_{X}(0,0)\Vert \nonumber \\&\le C_{1}\varepsilon ^{3}+ \max (\Vert \delta T\Vert ,\Vert \delta P_{2}\Vert ,\Vert \delta L\Vert ) \le C_{3}(\Vert X\Vert +\varepsilon ), \end{aligned}$$
(49)

where \(C_{3}\) is a positive constant.

The sets of the boundary values \(Q_{1,2,3}\) are also satisfied by the inverse procedure of the Zeipel transformations. According to Proposition 1, there exists a function Z of \(Z_{0}\) and \(\varepsilon \) such that \(Z(Z_{0},t,\varepsilon )\) is a doubly symmetric periodic solution of the full system. \(\square \)

The conclusion of this section is that there exist doubly symmetric periodic orbits of Lunar type around one oblate primary in the CRTBP, where the mass point primary moves on the equatorial plane of the oblate primary. In addition, the infinitesimal body is supposed not to be close to the motion plane of the primaries, as the octupole perturbation cannot be neglected for nearly coplanar motions.

9 Discussion

This paper considers the perturbation of the oblateness of the central primary, and gives a similar result to Howison and Meyer (2000). The approach followed in this study can be applied almost identically for the classical CRTBP, so it can give the result of Howison and Meyer (2000) in a somewhat different way.

The direct theorem used in this paper for the continuation is different from that one applied in the paper of Howison and Meyer (2000). This paper takes use of the averaging, which makes the first-order system integrable. The error estimates for the continuation are given in a different way that is easier to understand. It is sensible to calculate the solutions of the first-order system, as this helps people to study the characteristics and visualize the double-symmetric periodic orbits, and to find the bounds for the small parameter. It is also interesting to consider the problem about the Lunar-type symmetric periodic orbits around one symmetric ellipsoid in a rotating frame.