Global search for low-thrust transfers to the Moon in the planar circular restricted three-body problem

Abstract

This paper globally searches for low-thrust transfers to the Moon in the planar, circular, restricted, three-body problem. Propellant-mass optimal trajectories are computed with an indirect method, which implements the necessary conditions of optimality based on the Pontryagin principle. We present techniques to reduce the dimension of the set over which the required initial costates are searched. We obtain a wide range of Pareto solutions in terms of time of flight and mass consumption. Using the Tisserand–Poincaré graph, a number of solutions are shown to exploit high-altitude lunar flybys to reduce fuel consumption.

1 Introduction

Electric propulsion is a key technology for space exploration, as has been demonstrated by the Deep Space 1 (Rayman et al. 2000), DAWN (Russell et al. 2007), SMART-1 (Racca et al. 2002), and HAYABUSA (Kawaguchi et al. 2008) missions. The high fuel efficiency of ion engines enables microsatellite missions, such as PROCYON (Funase et al. 2014) and Lunar IceCube (Folta et al. 2016). However, the design of low-thrust trajectories remains a challenging task, especially in the Earth–Moon system, where multi-body dynamics is important and solutions include multiple revolutions.

Several studies have presented optimal low-thrust transfers in the Earth–Moon system, starting from Earth orbits and targeting libration point orbits, distant retrograde orbits, and orbits around the Moon (Kluever and Pierson 1995; Betts and Erb 2003; Topputo 2007; Mingotti et al. 2009; Ozimek and Howell 2010; Caillau et al. 2012; Zhang et al. 2015). Although global searches were sometimes performed (Russell 2007; Ohndorf et al. 2009; Abraham et al. 2013), solutions with longer transfer times have not yet been fully explored. Such solutions cannot be easily designed because they require hundreds of revolutions around the Earth, which is computationally costly, and high-altitude lunar flybys (Ross and Lo 2003; Ross and Scheeres 2007; Topputo et al. 2008; Belbruno et al. 2008; Jerg et al. 2009; Grover and Ross 2009; Campagnola and Russell 2010; Lantoine et al. 2011; Campagnola et al. 2014), which require the use of chaotic dynamics in multi-body regimes.

In the present paper, we compute mass-optimal transfers to the Moon in the planar, circular, restricted, three-body problem for a wide range of transfer times and for two representative thrust levels. The optimal control is computed with an indirect method; however, the transversality conditions are not fully enforced, because of the well-known numerical instabilities of bang-bang solutions (Russell 2007). Instead, we perform an extensive search over the set of initial costates and extract the Pareto-front of suboptimal solutions. In the present study, we apply two techniques to reduce the dimension of the search set: assuming an initial tangential thrust and using the similarity to two-body dynamics on the initial orbit around the Earth. Finally, Pareto-front solutions are analyzed using the Tisserand–Poincaré graph, where low-propellant-mass solutions are found to exploit the 2:5 resonance, as reported by Pernicka et al. (1995) and Topputo et al. (2005) for trajectories using impulsive maneuvers.

The remainder of the present paper is organized as follows. Section 2 summarizes the dynamical model, the Tisserand–Poincaré graph, the optimal control problem, and the method in Russell (2007). Section 3 presents methods by which to reduce the dimension of the search set. Finally, Sect. 4 presents the computational results of low-thrust transfers to the Moon.

2 Background

2.1 Dynamics

The planar, circular, restricted, three-body problem (PCR3BP) describes the motion of a massless particle m (a spacecraft) under the gravitational influence of two massive celestial bodies $m_1$ (Earth) and $m_2$ (Moon), which are revolving on circular orbits around their barycenter. This simplified model captures the essential dynamics of a spacecraft in the Earth–Moon system assuming the negligible inclination of the spacecraft trajectory.

In the present study, we consider the dynamics of the PCR3BP in the barycentric rotating frame, where $m_1$ and $m_2$ are fixed on the x-axis (Szebehely 1967). The equations of motion include thrust and a mass equation, the dimensionless form of which is given as (Russell 2007)

$$\begin{aligned} \dot{\varvec{X}}= & {} \varvec{f}(\varvec{X}, \varvec{u}, t), \end{aligned}$$

(1)

$$\begin{aligned} \varvec{X}&{:=}&\begin{bmatrix} \varvec{r} \\ \varvec{v} \\ m \end{bmatrix}, \end{aligned}$$

(2)

$$\begin{aligned} \varvec{f}(\varvec{X}, \varvec{u}, t)&{:=}&\begin{bmatrix} \varvec{v}, \\ \varvec{g}(\varvec{r})+\varvec{h}(\varvec{v})+\varvec{u}T/m, \\ -T/V_e \end{bmatrix}, \end{aligned}$$

(3)

where t is time, $\varvec{r} {:=}[x ~ y]^T$, $\varvec{v} {:=}[v_x ~ v_y]^T$, and m are the position, velocity, and mass of a spacecraft, $\varvec{u}$ is the thrust direction ($|\varvec{u}|=1$), T is the thrust magnitude, $V_e$ is the exhaust velocity of an engine, and

$$\begin{aligned}&\displaystyle \varvec{g}(\varvec{r}) {:=}\begin{bmatrix} x-\frac{\mu (x-1+\mu )}{\{(x-1+\mu )^2+y^2\}^{3/2}}-\frac{(1-\mu )(x+\mu )}{\{(x+\mu )^2+y^2\}^{3/2}} \\ y-\frac{\mu y}{\{(x-1+\mu )^2+y^2\}^{3/2}}-\frac{(1-\mu )y}{\{(x+\mu )^2+y^2\}^{3/2}} \end{bmatrix}, \end{aligned}$$

(4)

$$\begin{aligned}&\displaystyle \varvec{h}(\varvec{v}) {:=}\begin{bmatrix} 2 v_y \\ -2 v_x \end{bmatrix}. \end{aligned}$$

(5)

The equations are non-dimensionalized with a length scale factor of $m_1$–$m_2$ distance, a time scale factor of (orbital period of $m_1$ and $m_2$)/$2\pi$, and a unit mass scale factor of $m_1+m_2$. Table 1 summarizes the physical constants used for the PCR3BP.

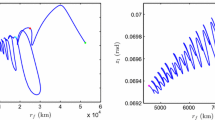
Figure 1a shows an example of a low-thrust transfer in the Earth–Moon PCR3BP. During coast arcs, the system given by Eq. (1) preserves the Jacobi constant

$$\begin{aligned} C = - ({v_x}^2 + {v_y}^2) + (x^2 + y^2) + \frac{2(1-\mu )}{\sqrt{{(x+\mu )}^2+y^2}} + \frac{2\mu }{\sqrt{{(x-1+\mu )}^2+y^2}} + \mu (1-\mu ). \end{aligned}$$

(6)

Figure 1b shows the change in the Jacobi constant in the final part of the transfer. The final value of the Jacobi constant becomes slightly higher than that of $L_1$, i.e., $C_{L_1}$, as shown in the magnified inset figure, which indicates that the spacecraft is energetically captured around the Moon (Koon et al. 2011).

Table 1 Physical constants

Fig. 1

a Example of a low-thrust transfer in the Earth–Moon PCR3BP. The thick arcs represent the thrust arcs. b Change in the Jacobi constant C in the final part of the transfer in a. The horizontal line represents the Jacobi constant of $L_1$. The inset figure magnifies the ending part of the change in the Jacobi constant

2.2 Tisserand–Poincaré graph

The Tisserand–Poincaré (T–P) graph is a powerful tool for analyzing the global space of solutions. The T–P graph is a Poincaré section of the system given by Eq. (1); the section is placed far from $m_2$, so that the states of a spacecraft are well represented by its osculating orbital elements around $m_1$. The graph includes level sets of the Tisserand parameter, which approximates the Jacobi constant and is a measure of the spacecraft velocity relative to $m_2$ ($v_\infty$).

Fig. 2

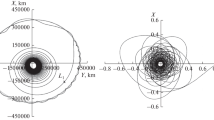
Osculating perigees and apogees of the trajectory in Fig. 1a (triangles) and those of ESA’s SMART-1 (circles) in the T–P graph

Figure 2 shows an example T–P graph with level sets of the Tisserand parameter. (Here, $T_{L_1}$ is the Tisserand parameter associated with $L_1$, and $T_{L_3}$ is the Tisserand parameter associated with $L_3$.) The graph includes lines of slope −1, which are constant-period level sets. The period is determined by the resonant ratio N:M, where N is the number of revolutions of the Moon, and M is the number of spacecraft revolutions in the inertial frame.

Figure 2 also shows the boundaries (solid curves) of the trajectories reachable from the resonances (Campagnola et al. 2012) via a lunar flyby. The region bounded by $T_{L_1}$ and $T_{L_3}$ corresponds to the low-energy regime. There are also the level sets of $v_{\infty }$ in the patched-conics domain. See Campagnola and Russell (2010) and Campagnola et al. (2012, 2014) for details of the T–P graph.

Figure 2 shows the osculating perigees and apogees of the trajectory in Fig. 1a (triangles) and those of the trajectory of ESA’s SMART-1 (circles, for every T–P graph in the present paper). In order to analyze the trajectories, we plot osculating perigees and apogees on Poincaré sections at perigees only when the distance from the center of the Moon is greater than 70,000 km.

The plot reveals that the trajectory in Fig. 1a exploits the 2:5 resonance before reaching the Moon realm. In the present paper, we demonstrate that this is a common feature of a number of long-time-of-flight solutions. The plot also shows that SMART-1 eventually used the 1:2 resonance. Note that these trajectories move in the low-energy regime, which cannot be handled by the patched-conics model.

2.3 Mass-optimal problem in the PCR3BP

In the present study, we consider mass optimal problems with performance index

$$\begin{aligned} J=-m_{ f}, \end{aligned}$$

(7)

and boundary conditions

$$\begin{aligned} \varvec{\psi }(t_0, t_f, \varvec{X}_0, \varvec{X}_{ f}, \tau )=0, \end{aligned}$$

(8)

where the subscripts 0 and f represent initial and final values, respectively, $\varvec{X}_0$ and $\varvec{X}_{ f}$ are the boundary states of the dynamical system given by Eq. (1), and $\tau$ is a parameter, which will be explained more in detail later.

The optimal control Hamiltonian is defined through the costates $\varvec{\lambda }$ as

$$\begin{aligned} H(\varvec{X}, \varvec{\lambda }, \varvec{u}, t)=\varvec{\lambda }^{T}_{r}\varvec{v}+\varvec{\lambda }^{T}_{v}(\varvec{g}(\varvec{r})+\varvec{h}(\varvec{v})+\varvec{u}T/m)-\lambda _m\frac{T}{V_e}, \end{aligned}$$

(9)

where the subscripts of $\varvec{\lambda }$ denote the components of $\varvec{\lambda }$.

The Pontryagin principle (Pontryagin 1987) states that the optimal control ($\varvec{u}_{opt}$, $T_{opt}$) is the one that globally minimizes the Hamiltonian, and is provided by the following equations [see for example Lawden (1963) and Russell (2007)]:

$$\begin{aligned} \varvec{u}=-\frac{\varvec{\lambda }_v}{|\varvec{\lambda }_v|}, \end{aligned}$$

(10)

and

$$\begin{aligned} \begin{aligned} T=&0 \;\;\, (S<0),\\ T=&T_{max} \,\;\; (S>0), \\ 0\le&\,T \le T_{max}\, \;\;(S=0), \end{aligned} \end{aligned}$$

(11)

where

$$\begin{aligned} S=\frac{|\varvec{\lambda }_v|}{m}+\frac{\lambda _m}{V_e} \end{aligned}$$

(12)

is the switching function.

The Pontryagin principle also provides the equations of motion for the costates

$$\begin{aligned}&\displaystyle \dot{{\varvec{\lambda }}}_{\varvec{r}}=- {\left( \frac{\partial \varvec{g}}{\partial \varvec{r}}\right) }^T {\varvec{\lambda }}_{\varvec{v}}, \end{aligned}$$

(13)

$$\begin{aligned}&\displaystyle \dot{{\varvec{\lambda }}}_{\varvec{v}}=-{\varvec{\lambda }}_{\varvec{r}}-{\left( \frac{\partial \varvec{h}}{\partial \varvec{v}}\right) }^T {\varvec{\lambda }}_{\varvec{v}}, \end{aligned}$$

(14)

$$\begin{aligned}&\displaystyle {\dot{\lambda }_m}=-|\varvec{\lambda }_{\varvec{v}}|\frac{T}{m^2}, \end{aligned}$$

(15)

and the full set of boundary conditions (transversality conditions):

$$\begin{aligned} H_0= & {} \frac{d \varPhi }{d t_0}, \end{aligned}$$

(16)

$$\begin{aligned} H_f= & {} -\frac{d \varPhi }{d t_f}, \end{aligned}$$

(17)

$$\begin{aligned} \varvec{\lambda }_0= & {} -\frac{d \varPhi }{d \varvec{X}_0}, \end{aligned}$$

(18)

$$\begin{aligned} \varvec{\lambda }_f= & {} \frac{d \varPhi }{d \varvec{X}_{ f}}, \end{aligned}$$

(19)

$$\begin{aligned} 0= & {} \frac{d \varPhi }{d \tau }, \end{aligned}$$

(20)

where

$$\begin{aligned} \varPhi (t_0, t_f, \varvec{X}_0, \varvec{X}_{ f}, \varvec{\nu })=J+{\varvec{\nu }}^T \varvec{\psi }(t_0, t_f, \varvec{X}_0, \varvec{X}_{ f}, \tau ), \end{aligned}$$

(21)

and $\varvec{\nu }$ are Lagrange multipliers associated with the boundary constraints given by Eq. (8).

2.4 Brief summary of Russell (2007)

Typical indirect methods try to solve the transversality conditions given by Eqs. (16) through (20), with iterative techniques that rely on first-order derivatives and converge to local minima. They are numerically unstable because of the discontinuous control, which is provided in a feedback form by Eqs. (10) and (11).

For these reasons, Russell (2007) proposed a method of searching through the set of admissible initial states and costates, defined by the initial conditions and by Eqs. (18) and (20), and disregarding the transversality conditions on the final costates. Although not all of the trajectories are optimal, the computation of a single solution is very quick because no iterative procedure is implemented. Thus, the method enabled global searches for low-thrust transfers, and trade-off studies by globally filtering the optimal solutions for a wide range of time of flights. An example was shown for transfers from a near circular 125,000 km orbit at the Earth to a 50,000 km distant retrograde orbit at the Moon in the PCR3BP [for another example, see Russell (2007)].

3 Global search approach

This paper implements a global search method that is similar to that of Russell (2007), but computes low-thrust trajectory solutions from a lower Earth orbit of approximately 35827   km altitude, which requires more revolutions around the Earth, to the vicinity of the Moon with a Jacobi constant greater than that of $L_1$ (thus ensuring permanent capture). Moreover, we focus on longer-time-of-flight solutions. Thus, we develop techniques to reduce the search space to a computationally manageable set. The details of the method and techniques are described in the reminder of this section.

3.1 Problem formulation

In the present study, the initial conditions are those for an approximately one-day initial periodic orbit (IPO) in the PCR3BP around the Earth with a radius similar to that of GEO. The IPO is parameterized by the time-like parameter $\tau$ (Russell 2007) ($0 \le \tau \le 0.238716$ in non-dimensional units), with the maximum value of $\tau$ corresponding to approximately one day, which is the period of the IPO. Therefore, $\tau$ uniquely defines the position on the IPO where the spacecraft ignites the thruster for the first time.

For every trajectory presented in the present paper, the final condition is a capture around the Moon, defined by a state close to the Moon ($x_{L_1} \le x \le 1.15$ and $-0.15 \le y \le 0.15$) and a Jacobi constant higher than that of $L_1$ ($C_{ f} \ge C_{L_1}$) to ensure permanent capture near the Moon. The present study investigates low-thrust transfers of two thrust levels between these boundary states. Table 2 shows the spacecraft parameters, and Table 3 summarizes the initial conditions of the IPO. The spacecraft mass m and the thrust magnitude T are non-dimensionalized by using the initial spacecraft mass $m_0$. Since the present paper seeks the Pareto-front of optimal solutions, we search mass-optimal solutions for different final times of up to 695.7 days.

In summary, the initial conditions are

$$\begin{aligned} \varvec{\psi } {:=}\begin{bmatrix} \varvec{r}_0-\varvec{r}^{*}_0(\tau ) \\ \varvec{v}_0-\varvec{v}^{*}_0(\tau ) \\ m_0-m^{*}_0 \\ t_0 \\ \end{bmatrix}=\varvec{0}, \end{aligned}$$

(22)

where $*$ denotes the user-defined value. The final conditions are not included in $\varvec{\psi }$, because we are going to disregard the associated transversality conditions. The final time is found implicitly, as the earliest time when the final conditions are met.

Table 2 Spacecraft parameters

Table 3 Initial conditions of the initial periodic orbit

3.2 Set of admissible initial conditions

The admissible initial states can be easily searched, because they belong to a one-dimensional closed set parametrized by $\tau$. The admissible initial costates are computed using the transversality conditions. We first rewrite Eq. (7) (Russell 2007; Ozimek and Howell 2010) as

$$\begin{aligned} J=-km_f\quad (k>0). \end{aligned}$$

(23)

Then the transversality condition given by Eq. (19) associated with the mass:

$$\begin{aligned} \lambda _{m_f}=-k, \end{aligned}$$

(24)

is automatically satisfied by choosing

$$\begin{aligned} \lambda _{m_0}=-1, \end{aligned}$$

(25)

because k is a free parameter and $\lambda _m$ decreases with time. Equation (18) generates free multipliers for the initial costates, which are combined with Eq. (20) (Russell 2007)

$$\begin{aligned} \varvec{\lambda }_{r_0} \frac{d \varvec{r}^{*}_0(\tau )}{d \tau }+\varvec{\lambda }_{v_0} \frac{d \varvec{v}^{*}_0(\tau )}{d \tau }=0. \end{aligned}$$

(26)

The set of admissible costates is open and three dimensional, being defined by the two scalar Eqs. (25) and (26) in the five-dimensional space of $\varvec{\lambda }_0$. In summary, the total set of admissible initial conditions is open and four-dimensional including $\tau$. Though Russell (2007) globally explored the four-dimensional search set, an extensive search over this set with longer transfer times and from a lower initial orbit is computationally very costly. Therefore, we use the following techniques to reduce the search space to a manageable set.

3.3 Reduction of the search set

3.3.1 Initial thrust direction

We assume that the initial thrust direction is tangential to the IPO. Since the tangential thrust changes the Jacobi energy maximally, it could be a good option for the initial thrust direction to compute suboptimal solutions, with the advantage of reducing the search set. Thus, $\lambda _{v_{x_0}}$ and $\lambda _{v_{y_0}}$ can be related to the initial velocity $v_{x_0}$ and $v_{y_0}$ through Eq. (10) as

$$\begin{aligned} \begin{aligned} -\frac{\lambda _{v_{x_0}}}{|\varvec{\lambda _{v_0}}|}=&\frac{v_{x_0}}{|\varvec{v}_0|}, \\ -\frac{\lambda _{v_{y_0}}}{|\varvec{\lambda _{v_0}}|}=&\frac{v_{y_0}}{|\varvec{v}_0|}. \end{aligned} \end{aligned}$$

(27)

Fig. 3

Polar coordinates for the velocity, acceleration, and costates on the initial periodic orbit

3.3.2 Similarity to two-body dynamics

We express Eq. (26) using $\frac{d \varvec{r}_0(\tau )}{d \tau }=\varvec{v}_{0}$, $\frac{d \varvec{v}_0(\tau )}{d \tau }=\varvec{a}_{0}$ (asterisks are omitted for brevity), and the polar coordinates shown in Fig. 3 for the velocity, acceleration, and costates on the IPO as

$$\begin{aligned} |\varvec{\lambda }_{r_0}| |\varvec{v}_{0}| \cos {(\theta _{\lambda _{r_0}} - {\theta _{v_0}})}+|\varvec{\lambda }_{v_0}| |\varvec{a}_{0}| \cos {(\theta _{\lambda _{v_0}} - {\theta _{a_0}})}=0. \end{aligned}$$

(28)

Equation (27) can be rewritten as

$$\begin{aligned} \theta _{\lambda _{v_0}}=\theta _{v_0}+\pi . \end{aligned}$$

(29)

Substituting Eq. (29) into Eq. (28) yields

$$\begin{aligned} |\varvec{\lambda }_{v_0}|=\frac{|\varvec{v}_{0}|}{|\varvec{a}_{0}|}|\varvec{\lambda }_{r_0}| \frac{\cos {(\theta _{\lambda _{r_0}} - {\theta _{v_0}})}}{\cos {(\theta _{v_0} - {\theta _{a_0}})}}, \end{aligned}$$

(30)

which is used to determine $|\varvec{\lambda }_{v_0}|$ as a function of $|\varvec{\lambda }_{r_0}|$ and $\theta _{\lambda _{r_0}}$.

Table 4 Parameters for a grid search (coarse/fine)

Table 5 Admissible region of trajectories

Fig. 4

a Pareto (dark) and non-Pareto (light) solutions in terms of time of flight (TOF) and mass consumption ($\varDelta m$) for the case in which $T_{max}$ = 0.3 N. b Pareto solutions extracted from a

Fig. 5

Trajectories of the selected Pareto solutions shown in Fig. 4b. The nearly circular thick orbit represents the initial periodic orbit around the Earth. The two black points indicate the Earth (left) and the Moon (right), and the numbers indicate the TOF and $\varDelta m$, respectively

The dynamics on the IPO resembles the circular orbit in the two-body problem, and the velocity and the acceleration on the IPO are nearly perpendicular to each other:

$$\begin{aligned} \cos {(\theta _{v_0}-\theta _{a_0})}\approx 0. \end{aligned}$$

(31)

Thus, from Eqs. (30) and (31), we have

$$\begin{aligned} \cos {({\theta }_{\lambda _{r_0}}-\theta _{v_0})}\approx 0, \end{aligned}$$

(32)

or equivalently,

$$\begin{aligned} \begin{aligned} \theta _{\lambda _{r_0}}-\theta _{v_0}=&\frac{\pi }{2}+\epsilon , \\ \theta _{\lambda _{r_0}}-\theta _{v_0}=&-\frac{\pi }{2}+\epsilon , \end{aligned} \end{aligned}$$

(33)

where $|\epsilon |\ll 1$.

From Eq. (33), we use $\epsilon$ as a parameter to compute $\theta _{\lambda _{r_0}}$. Since the signs of both sides of Eq. (30) must be the same, we need only investigate $\epsilon$, which satisfies

$$\begin{aligned} \frac{\cos {({\theta }_{\lambda _{r_0}}-\theta _{v_0})}}{\cos {(\theta _{v_0}-\theta _{a_0})}}\ge 0. \end{aligned}$$

(34)

Fig. 6

Osculating perigees and apogees of the Pareto solutions of odd numbers in Fig. 5 in the T–P graph

Fig. 7

Magnification of the final part of transfers in Fig. 6

In summary, our method requires a search over the three-dimensional $\tau -|\varvec{\lambda }_{r_0}|-\epsilon$ set, but with $|\epsilon |\ll 1$. Since the dimension of the search set directly affects computational cost, the presented techniques ease the global search for low-thrust transfers.

Fig. 8

Osculating perigees and apogees of the Pareto solutions of even numbers in Fig. 5 in the T–P graph

Fig. 9

Magnification of the final part of transfers in Fig. 8

It could be possible to apply the presented techniques to other problems such as targeting a specific orbit around the Moon, where initial guesses could be provided for subsequent local optimization, and a global search from a specific near-circular, inclined initial orbit in the spatial problem, where one extra dimension would be added to the search set.

4 Global search for low-thrust transfers to the Moon

Based on the procedure in the previous sections, we perform two grid searches (coarse and fine) in the $\tau -|\varvec{\lambda }_{r_0}|-\epsilon$ set using the Runge–Kutta–Fehlberg method of orders 4 and 5 with a tolerance of $10^{-10}$. Table 4 summarizes the search set and corresponding numbers of grid points using a coarse/fine notation if needed, and Table 5 shows the admissible region of trajectories during the integration. We use all of the solutions obtained from both grid searches to show the following results.

Table 6 Final resonances of all 14 Pareto solutions with TOFs longer than 265 days for the case in which $T_{max}$ = 0.3 N

Fig. 10

a Pareto (dark) and non-Pareto (light) solutions in terms of TOF and $\varDelta m$ for the case in which $T_{max}$ = 0.15 N. b Pareto solutions extracted from a

Fig. 11

Trajectories of the selected Pareto solutions from Fig. 10b. The nearly circular thick orbit represents the initial periodic orbit around the Earth. The two black points indicate the Earth (left) and the Moon (right). The numbers indicate the TOF and and $\varDelta m$, respectively

Fig. 12

Osculating perigees and apogees of the Pareto solutions of odd numbers in Fig. 11 in the T–P graph

Fig. 13

Magnification of the final part of transfers in Fig. 12

Fig. 14

Osculating perigees and apogees of the Pareto solutions of even numbers in Fig. 11 in the T–P graph

Fig. 15

Magnification of the final part of transfers in Fig. 14

4.1 Low-thrust transfers to the Moon for $T_{max}$ = 0.3 N

This section summarizes the computational results for $T_{max}$ = 0.3 N and the initial mass $m_0$ = 1500 kg, which correspond to an initial acceleration that is slightly higher than that of SMART-1. Figure 4a shows the solutions in terms of time of flight (TOF) and mass consumption ($\varDelta m$), where the dark points represent the Pareto solutions and the light points represent the non-Pareto solutions. For clarity, Fig. 4b shows the extracted Pareto solutions. Unfortunately, it is difficult to make a direct comparison with the results in previous works because boundary conditions are different.

Figure 5 shows the trajectories of the twelve representative Pareto solutions shown in Fig. 4b, numbered #1 to #12. The thrust arcs tend to appear near the Earth and the Moon, and the coast arcs typically appear in the “three-body” region where the lunar perturbation becomes significant.

Figures 6 and 8 show the twelve Pareto solutions on the T–P graph. For clarity, Fig. 6 shows the odd-numbered solutions and Fig. 7 shows its magnification, whereas Fig. 8 shows the even-numbered solutions and Fig. 9 shows its magnification. The T–P graph indicates that trajectories with lower perigees can exploit larger effects of resonant lunar flybys (see the boundaries of the trajectories reachable from the resonances). This is why the solutions having smaller $\varDelta m$ exhibit less inclined paths.

Solutions #7, #9, and #12 exploit 2:5 resonance in the final phase before reaching the Moon realm. This is in contrast to SMART-1, which used 1:2 resonance as in solutions #8 and #11. Previous studies indicated that the invariant manifolds emanating from $L_1$ were close to 2:5 resonance in the Earth–Moon system (Pernicka et al. 1995; Topputo et al. 2005). Thus, future missions to the Moon may be able to further reduce $\varDelta m$ by exploiting 2:5 resonance to pass through low-energy manifold tubes (Koon et al. 2011) around $L_1$ while accepting some transfer time and radiation dose penalties. Table 6 summarizes the final resonances of the Pareto solutions with TOFs longer than 265 days.

4.2 Low-thrust transfers to the Moon for $T_{max}$ = 0.15 N

This section summarizes the computational results for $T_{max}$ = 0.15 N and the same initial mass, $m_0$ = 1500 kg, which correspond to an initial acceleration similar to that of the JAXA proposed DESTINY mission (Kawakatsu et al. 2014).

Figure 10a shows the solutions in terms of TOF and $\varDelta m$. For clarity, Fig. 10b shows the extracted Pareto solutions. Since the acceleration is smaller than that in Sect. 4.1, the solutions have longer TOFs.

Figure 11 shows the trajectories of the twelve representative Pareto solutions in Fig. 10b, numbered from #1 to #12. Trajectories for which $T_{max}=0.15$ N include longer intervals of thrust arcs, as compared to those for which $T_{max}=0.3$ N, but exploit lunar flybys to reduce fuel consumption.

Table 7 Final resonances of all 24 Pareto solutions with TOFs longer than 365 days for the case in which $T_{max}$ = 0.15 N

Fig. 16

Distribution of Pareto solutions for a $T_{max}$ = 0.3 N and b $T_{max}$ = 0.15 N in terms of TOF and the parameter $\tau$, shaded in accordance with the value of $\varDelta m$

Fig. 17

Distribution of Pareto solutions for a $T_{max}$ = 0.3 N and b $T_{max}$ = 0.15 N in terms of TOF and the parameter $\epsilon$, shaded in accordance with the value of $\varDelta m$

Fig. 18

Distribution of Pareto solutions for a $T_{max}$ = 0.3 N and b $T_{max}$ = 0.15 N in terms of TOF and the parameter $|\lambda _{r_0}|$, shaded in accordance with the value of $\varDelta m$

Figures 12 and 14 show the twelve Pareto solutions on the T–P graph. For clarity, Fig. 12 shows the odd-numbered solutions and Fig. 13 shows its magnification, whereas Fig. 14 shows the even-numbered solutions and Fig. 15 shows its magnification. As summarized in Table 7, many Pareto solutions with small $\varDelta m$ and long TOF exploit the 2:5 resonance before reaching the Moon realm.

4.3 Distribution of solutions

Figure 16 shows the distribution of the Pareto solutions for (a) $T_{max}$ = 0.3 N and (b) $T_{max}$ = 0.15 N in terms of the TOF and the parameter $\tau$, shaded in accordance with the value of $\varDelta m$. Figures 17 and 18 show the distributions of the Pareto solutions for (a) $T_{max}$ = 0.3 N and (b) $T_{max}$ = 0.15 N in terms of the TOF and the parameters $\epsilon$ and $|\varvec{\lambda }_{r_0}|$ respectively. The value of $\epsilon$ corresponds to the first equation of Eq. (33) because the second equation of Eq. (33) always violates the constraints for the minimum distance from the Earth in Table 5.

The Pareto solutions for both values for $T_{max}$ exhibit no tendencies for $\tau$ or $\epsilon$, but show the characteristic distributions for $|\varvec{\lambda }_{r_0}|$, i.e., solutions with smaller $|\varvec{\lambda }_{r_0}|$ tend to result in smaller $\varDelta m$ but longer TOF. Therefore, these results indicate that $|\varvec{\lambda }_{r_0}|$ characterizes the families of low-thrust transfers to the Moon. Note that Fig. 18 indicates the existence of even faster or cheaper solutions beyond the bounds on $|\varvec{\lambda }_{r0}|$. However, we already computed a wide range of Pareto solutions, the fastest solution of which is a nearly continuous-thrust transfer and the cheapest solution of which is a multiple-gravity-assisted transfer, and searching even faster or cheaper solutions is beyond the scope of this paper.

Fig. 19

Distribution of Pareto (dark dots) and non-Pareto (light dots) solutions for a $T_{max}$ = 0.3 N and b $T_{max}$ = 0.15 N in terms of the parameters $\tau$ and $\epsilon$. The curve represents $\epsilon '$ in Eq. (35)

4.4 Further refinement for $\epsilon$

Figure 19 shows the distribution of the Pareto (dark dots) and non-Pareto (light dots) solutions for (a) $T_{max}$ = 0.3 N and (b) $T_{max}$ = 0.15 N in terms of the parameters $\tau$ and $\epsilon$. The curve represents

$$\begin{aligned} \epsilon '=-\frac{\pi }{2}+\theta _{a_0}-\theta _{v_0}, \end{aligned}$$

(35)

which heuristically replaces $\theta _{\lambda _{r_0}}$ with $\theta _{a_0}$ in the first equation of Eq. (33).

Since the obtained solutions shadow the curve of $\epsilon '$, Fig. 19 indicates a heuristic that we can target $\epsilon$ in the vicinity of $\epsilon '$ in order to further reduce the search set of $\epsilon$ in future studies.

5 Conclusions

In the present paper, we presented global searches of low-thrust transfers to the Moon in the planar, circular, restricted, three-body problem. The method used herein implements the necessary conditions of optimality from the Pontryagin principle to define an initial search space that is four dimensional and open. We assumed an initial tangential thrust and used an analogy with two-body dynamics to reduce the size of the search space. For two representative thrust levels, we computed a wide range of Pareto solutions in terms of time of flight and mass consumption, including many long-time-of-flight solutions that had not been fully explored in previous studies. Analysis via a Tisserand–Poincaré graph showed that numerous solutions exploit high-altitude lunar flybys, and 2:5 resonance is useful for reducing fuel consumption. A new heuristic indicated the possibility of further reducing the search set in future studies.