Fuel optimization for low-thrust Earth–Moon transfer via indirect optimal control

Abstract

The problem of designing low-energy transfers between the Earth and the Moon has attracted recently a major interest from the scientific community. In this paper, an indirect optimal control approach is used to determine minimum-fuel low-thrust transfers between a low Earth orbit and a Lunar orbit in the Sun–Earth–Moon Bicircular Restricted Four-Body Problem. First, the optimal control problem is formulated and its necessary optimality conditions are derived from Pontryagin’s Maximum Principle. Then, two different solution methods are proposed to overcome the numerical difficulties arising from the huge sensitivity of the problem’s state and costate equations. The first one consists in the use of continuation techniques. The second one is based on a massive exploration of the set of unknown variables appearing in the optimality conditions. The dimension of the search space is reduced by considering adapted variables leading to a reduction of the computational time. The trajectories found are classified in several families according to their shape, transfer duration and fuel expenditure. Finally, an analysis based on the dynamical structure provided by the invariant manifolds of the two underlying Circular Restricted Three-Body Problems, Earth–Moon and Sun–Earth is presented leading to a physical interpretation of the different families of trajectories.

1 Introduction

For some years now, Moon exploration is experiencing renewed interest as an intermediate step to explore and colonize our Solar system. Several missions like SMART-1 (Racca et al. 2002), GRAIL (Roncoli and Fujii 2010) or SELENE (Kato et al. 2008) have been launched to the Moon.

If a manned base were to be established on the lunar surface, a low-cost transfer between the Earth and the Moon should be considered. Two main types of low-energy transfers have been envisioned up to now. On one side, low-energy impulsive transfers have been designed (see Koon et al. 2001; Moore et al. 2012). On the other side, electric propulsion has emerged as a capital technology to reduce the fuel budget of space trajectories due to its high specific impulse. Several interplanetary missions such as Deep Space 1 (Rayman et al. 2000), DAWN (Russell et al. 2007) and HAYABUSA (Kawaguchi et al. 2008) or the lunar mission SMART-1 have demonstrated the interest of this technology.

Both impulsive and low-thrust low-energy Earth–Moon transfers are characterized by their long duration compared to that of the Hohmann transfer or any more energetic transfer. This makes them inappropriate for manned missions. However, their lower cost makes them good candidates for cargo and instrumental transport missions.

The dynamics of a spacecraft in the Earth–Moon system can be modeled in several ways. The simplest formulations are based on the patched conics approximation (see Bate et al. 1971) or on the Circular Restricted Three-Body Problem (CR3BP), see Szebehely (1967), which takes into account the gravitational influences of the Earth and the Moon. In Russell (2007) the author combines optimal control theory and adjoint-control transformations to determine low-thrust Earth–Moon transfers in the CR3BP. In Zhang et al. (2014) and Chen (2016) the authors apply Pontryagin’s Maximum Principle (PMP), see Bryson and Ho (1975) for a detailed description of the maximum principle, to compute low-thrust transfers in the CR3BP. In Taheri and Abdelkhalik (2015) feasible Earth–Moon transfers are designed by using shape-based methods in the Planar CR3BP (PCR3BP).

Although the gravitational influence of the Sun is not significant in the vicinity of the Earth and the Moon, it has been revealed (see Koon et al. 2001) that the Sun’s perturbation gives rise to new kind of low-energy transfers. Trajectories taking benefit from the Sun’s perturbation partially follow the invariant manifolds of the two underlying CR3BPs. More precisely, the invariant manifolds of Lyapunov orbits around Lagrange points of the two CR3BPs can be matched at intermediate points leading to low-energy transfers. Thus, initial attempts to find a low-energy Earth–Moon transfer consist in looking for cheap connections between the two manifolds by means of impulsive maneuvers (see Koon et al. 2001; Ren and Shan 2014; Sousa-Silva and Terra 2016).

Other authors take into account the Sun’s perturbation by considering the Bicircular Restricted Four-Body Problem (BR4BP) (see Simó et al. 1995). For example, an exhaustive list of impulsive transfers in the BR4BP and its classification in several families is given in Topputo (2013). In Qi and Xu (2016) three-impulse low-energy Earth to Moon transfers are computed in the bicircular model. The Sun’s influence on impulsive transfers is also studied in Filho and da Silva Fernandes (2017). Mingotti et al. (2012) compute low-thrust Earth–Moon transfers using the invariant manifolds of the two coupled PCR3BPs to obtain an initial guess. Then, this first guess is transposed into the BR4BP and optimized using direct optimal control methods. Direct methods discretize state and control variables leading to the solution of a huge mathematical programming problem (see Betts 1998). Due to the high sensitivity of the dynamics with respect to the initial conditions, it may not always be possible to convert this discrete solution into a continuous trajectory.

An alternative approach is to use indirect optimal control methods. For example, in Shen and Casalino (2014) impulsive transfers are optimized in the Earth–Moon system using an indirect approach. In Oshima et al. (2017) low-thrust transfers are computed in the PCR3BP by using the PMP. However, all the necessary conditions are not satisfied in this paper.

In the present paper, the PMP is used to compute minimum-fuel trajectories in the BR4BP. Two solution methods are proposed to satisfy all the necessary conditions arising from the PMP, i.e., to find the zero of the associated shooting function. The first one consists in using continuation or homotopy techniques. The other one is based on a massive exploration of the search domain containing the unknowns of the shooting function. The output of this second method has revealed several families of trajectories with different shapes, fuel consumptions and times of flight fulfilling all the PMP conditions.

The spacecraft is assumed to depart from a circular Low Earth Orbit (LEO) at an altitude $H_0$. In addition, an initial velocity increment $\Delta v_0$ is provided to the spacecraft by the launcher. From that point on, the spacecraft only relies on its low-thrust engine to complete the transfer. The final orbit is a circular Lunar Orbit (LO) with an altitude equal to $H_f$.

The paper is organized as follows. In Sect. 2 the problem is formulated and the dynamics equations of the Planar BR4BP (PBR4BP) are given. Then, the optimal control problem is stated and the necessary optimality conditions are derived from the PMP. The two solution methods used to solve the problem are subsequently described. In Sect. 3, the results of the massive exploration approach are presented. Several families of transfer trajectories are shown and classified according to physical considerations. Finally, Sect. 4 provides conclusions and future prospects.

2 Problem formulation

The transfer optimization problem is tackled considering a model that takes into account the gravitational influences of the Earth, the Moon and the Sun. The PBR4BP (Earth–Moon–Sun) is considered. The objective is to study the motion a spacecraft equipped with a low-thrust propulsion system and submitted to the gravitational attraction of the three major bodies.

2.1 The Planar Circular Restricted Three-Body Problem

The problem is first modeled as a PCR3BP (see Szebehely 1967). The motions of the Earth and the Moon are assumed planar and circular around the Earth–Moon barycenter. For homogenization purposes, the units involved have been adimensionalized. Therefore, the Earth–Moon distance is set to 1 DU (Distance Unit). The Time Unit (TU) is set in such a way that the Moon completes a full revolution in $2\pi ~TU$. Finally, let $m_E$ (resp. $m_M$) denotes the mass of the Earth (resp. of the Moon), the sum $m_E+m_M$ is set to 1 MU (Mass Unit). Then, the dynamics only depends on one parameter, the mass ratio $\mu$ defined as

$$\begin{aligned} \mu =\frac{m_M}{m_E+m_M}. \end{aligned}$$

(1)

Finally, a rotating frame (O, x, y) is considered in which the Earth (whose mass is equal to $1-\mu$) and the Moon (whose mass is equal to $\mu$) are fixed at coordinates $(-\,\mu ,0)$ and $(1-\mu ,0)$, respectively.

Under these assumptions, the potential function of the PCR3BP is defined as

$$\begin{aligned} \varOmega = \frac{x^2 + y^2}{2} + \frac{ 1-\mu }{r_1} + \frac{\mu }{r_2} + \frac{\mu (1-\mu )}{2}, \end{aligned}$$

(2)

where $r_1^2=(x+\mu )^2 + y^2$ and $r_2^2= (x+\mu -1)^2 + y^2$. The Jacobi constant $J_C$ is a first integral for the motion and is defined as

$$\begin{aligned} J_C(x,y,v_x,v_y)= 2\varOmega - (v_x^2+v_y^2 ), \end{aligned}$$

(3)

where $v_x$ and $v_y$ denote the velocities of the spacecraft in the rotating frame.

A value equivalent to the Jacobi constant is the energy of the PCR3BP defined as $E(x,y,v_x,v_y)=-\,J_C(x,y,v_x,v_y)/2$. Thus, reducing the value of the Jacobi constant is equivalent to increasing the energy of the spacecraft.

For a given value c of the Jacobi constant, it is possible to define the set of points in the phase space associated with this value

$$\begin{aligned}\tilde{{\mathcal {H}}}_{c}=\{ (x,y,v_x,v_y) | J_C(x,y,v_x,v_y)=c\}.\end{aligned}$$

The projection of $\tilde{{\mathcal {H}}}_{c}$ into the configuration space ($x-y$ space) gives the Hill’s region ${\mathcal {H}}_{c}$, i.e., the set of positions $(x,y)\in {\mathbb {R}}^2$ for which a velocity exists such that the Jacobi constant is equal to c. The boundary of the Hill’s region is known as the zero-velocity curve (see Szebehely 1967).

The PCR3BP presents a rich dynamic structure. The potential function defined in Eq. (2) shows five fixed points called Lagrange points ($L_i,~i=1,\dots ,5$). Three of them ($L_i, ~i=1,2,3$) are collinear on the x axis and exhibit a saddle$\times$center linear stability. The other two ($L_i,~i=4,5$) form two equilateral triangles with the Earth and the Moon. Their linear stability is of type center$\times$center for typical values of the mass parameter $\mu$ given in Eq. (1).

Hill’s region ${\mathcal {H}}_{c}$ may exhibit three, two or one connected components depending on the value of the Jacobi constant. Three sub-regions characterize Hill’s region. The first two sub-regions are located around each of the primaries, Earth and Moon. The third one is the exterior region. When $J_C$ decreases, the two sub-regions associated with the primaries become connected through the so-called $L_1$ neck. When $J_C$ continues to decrease, the sub-region associated with the Moon becomes connected to the exterior sub-region through the so-called $L_2$ neck.

Once these connections are established, from each of the collinear Lagrange points periodic orbits appear which are called Lyapunov orbits. Thanks to the saddle part of the linear stability, from these periodic orbits emanate stable and unstable manifolds. A complete description of the dynamic structure of the PCR3BP and missions analysis associated with that structure can be found in Koon et al. (2011).

2.2 The controlled Planar Bicircular Restricted Four-Body Problem

The Sun is added as a perturbation to the PCR3BP model. It is considered as a mass in the Earth–Moon plane rotating around the Earth–Moon barycenter in a circular orbit. Therefore, its position is given by $(x_s,y_s)=(\rho _s\cos \omega ,\rho _s\sin \omega )$, where $\rho _s$ is the Sun’s distance to the Earth–Moon barycenter and $\omega =\omega _s t + \omega _0$ is the phase of the Sun given by the angular velocity of the Sun in the reference frame $\omega _s$ and the initial phase $\omega _0$. Introducing Sun’s perturbation, the potential function becomes

$$\begin{aligned} \varOmega _s = \varOmega + \frac{m_s}{r_s}- \frac{m_s}{\rho _s^2}(x\cos \omega + y \sin \omega ), \end{aligned}$$

(4)

where $\varOmega$ is given in Eq. (2), $r_s^2 = (x-\rho _s\cos \omega )^2 + (y-\rho _s\sin \omega )^2$ and $m_s$ is the adimensional mass of the Sun. This leads to the so-called PBR4BP.

Finally, the spacecraft can be controlled by means of a low-thrust engine inducing an acceleration that can be written as

$$\begin{aligned} \mathbf {a}_t= \mathbf {u} \frac{F_{\max }}{m}, \end{aligned}$$

(5)

where $F_{\max }$ is the maximum thrust modulus of the engine, $\mathbf {u}=(u_1,u_2)^{\top }$ is the normalized thrust vector satisfying $\Vert \mathbf {u}\Vert \le 1$ and m is the mass of the spacecraft. This mass decreases over time according to $\dot{m}=-\,\Vert \mathbf {u}\Vert F_{\max }/I_{sp}g_0$, where $I_{sp}$ denotes the specific impulse of the engine and $g_0$ is the acceleration of gravity at sea level. Let us notice that, after normalization of Eq. (5), the initial mass of the spacecraft is equal to 1 SMU (Spacecraft’s Mass Unit).

Remark 1

Two different mass units have been introduced, the first one (MU) for the massive bodies related to the gravitational field and the other one (SMU) for the spacecraft related to the thrust equation.

Therefore, the dynamics equations of the spacecraft are given by

$$\begin{aligned} \left\{ \begin{array}{l} \dot{x} = v_{x},\\ \dot{y} = v_{y},\\ \dot{v}_{x} = 2v_{y} + \varOmega _{s,x} + \frac{u_1 F_{\max }}{m},\\ \dot{v}_{y} = -2v_{x} + \varOmega _{s,y} + \frac{u_2 F_{\max }}{m},\\ \dot{m}= -\,\Vert \mathbf {u}\Vert \frac{F_{\max }}{I_{sp}g_0}, \end{array} \right. \end{aligned}$$

(6)

where $\varOmega _{s,x}$ and $\varOmega _{s,y}$ are the derivatives of $\varOmega _s$ with respect to x and y, respectively. In the following, Eq. (6) will be written as $\dot{\mathbf {\xi }}= \varphi (t,\mathbf {\xi },\mathbf {u})$, with $\mathbf {\xi }=(x,y,v_x,v_y,m)^{\top }$. Let us notice here that $\varphi$ depends explicitly on time t due to the time dependency of the Sun’s phase $\omega$.

2.3 Problem statement

The aim of this paper is to determine transfer trajectories departing from an initial circular Low Earth Orbit (LEO) and arriving to a circular Lunar Orbit (LO) with the minimum fuel consumption. Thus, the goal is to maximize the mass of the spacecraft when arriving to the Moon, or equivalently to minimize $-\,K \cdot m(t_{f})$ with $K>0$. Therefore, the problem can be written under the form of an optimal control problem with free terminal time as follows

$$\begin{aligned} ({\mathbf {P}}) \left\{ \begin{array}{l} \min -K m({ t}_{ f})\\ \begin{array}{rl} s.t. \dot{\mathbf {\xi }}= \varphi (t,\mathbf {\xi }, \mathbf {u}),\\ \Vert \mathbf {u}\Vert \le 1,\\ h_0(\mathbf {\xi }(t_0))=0,\\ h_f(\mathbf {\xi }(t_{f}))=0,\\ { t}_{ f} \text{ free } , \\ \end{array} \end{array} \right. \end{aligned}$$

(7)

where $h_0(\mathbf {\xi }(t_0))$ (resp. ${ h}_{ f}(\mathbf {\xi }(t_{f}))$) denotes the initial (resp. final) conditions. The initial time $t_0$ can be fixed to 0 with no loss of generality. Indeed, considering ${\tilde{t}}_0 \ne 0$ associated with an initial Sun’s phase ${\tilde{\omega }}_0$ is equivalent to considering $t_0=0$ associated with a new initial phase $\omega _0 = {\tilde{\omega }}_0 + {\tilde{t}}_0\omega _s$.

The initial conditions in problem Eq. (7) can be written as follows

$$\begin{aligned} h_0(\mathbf {\xi }(t_0))= \left( \begin{array}{c} h_{0,1}(\mathbf {\xi }(t_0))\\ h_{0,2}(\mathbf {\xi }(t_0))\\ h_{0,3}(\mathbf {\xi }(t_0))\\ h_{0,4}(\mathbf {\xi }(t_0)) \end{array} \right) =0, \end{aligned}$$

(8)

where

$$\begin{aligned} h_{0,1}(\mathbf {\xi }(t_0))= & {} (x(t_0)+\mu )^2 + y(t_0)^2 - r_0^2, \nonumber \\ h_{0,2}(\mathbf {\xi }(t_0))= & {} (x(t_0)+\mu )(v_{x}(t_0) - y(t_0)) + y(t_0)(v_{y}(t_0)+x(t_0) +\mu ),\nonumber \\ h_{0,3}(\mathbf {\xi }(t_0))= & {} (v_{x}(t_0) - y(t_0))^2 + (v_{y}(t_0) + x(t_0) + \mu )^2 - (v_0 + \Delta v_0)^2,\nonumber \\ h_{0,4}(\mathbf {\xi }(t_0))= & {} m(t_0)-1, \end{aligned}$$

(9)

$r_0=R_e+H_0$ is the initial radius of the LEO, $R_e$ the Earth’s radius, $H_0$ is the initial altitude and $v_0$ the velocity modulus given by $v_0=\sqrt{\frac{1-\mu }{r_0}}$. Let us recall here that an initial velocity increment $\Delta v_0\le \Delta v_{\max }$ is delivered by the launcher where $\Delta v_{\max }$ is fixed and depends on the launch vehicle capabilities. Let us notice that $\Delta v_0$ is fixed for each instance of the problem. See also Remark 2.

The final circular LO is determined by the following relation

$$\begin{aligned} h_f(\mathbf {\xi }(t_{f}))= \left( \begin{array}{c} h_{f,1}(\mathbf {\xi }(t_{f}))\\ h_{f,2}(\mathbf {\xi }(t_{f}))\\ h_{f,3}(\mathbf {\xi }(t_{f}))\\ \end{array} \right) =0, \end{aligned}$$

(10)

where

$$\begin{aligned} h_{f,1}(\mathbf {\xi }(t_{f}))= & {} (x(t_{f})+\mu -1)^2 + y(t_{f})^2 - r_f^2, \nonumber \\ h_{f,2}(\mathbf {\xi }(t_{f}))= & {} (x(t_{f})+\mu -1)(v_{x}(t_{f}) - y(t_{f})) + y(t_{f})(v_{y}(t_{f})+x(t_{f})+\mu -1),\nonumber \\ h_{f,3}(\mathbf {\xi }(t_{f}))= & {} (v_{x}(t_{f}) - y(t_{f}))^2 + (v_{y}(t_{f}) + x(t_{f}) + \mu -1)^2 - v_f^2 , \end{aligned}$$

(11)

$r_f=R_m+H_f$ is the radius of the LO, $R_m$ is the Moon’s radius and $v_f$ is the modulus of the velocity given by $v_f=\sqrt{\frac{\mu }{r_f}}$.

Remark 2

In Eq. (7), $\omega _0$ and $\Delta v_0$ are considered as fixed parameters. That said, optimal trajectories associated with different values of $\omega _0$ and $\Delta v_0$ will be presented in Sect. 3. Each trajectory is a solution of a particular instance of problem Eq. (7).

The optimal control $\mathbf {u}$ must satisfy the first-order necessary optimality conditions given by Pontryagin’s Maximum Principle (PMP) (Bryson and Ho 1975). Let the Hamiltonian of problem Eq. (7) be defined as follows

$$\begin{aligned} H(t,\mathbf {\xi },\mathbf {p},\mathbf {u})=\mathbf {p}^\top \varphi (t,\mathbf {\xi },\mathbf {u}), \end{aligned}$$

where $\mathbf {p}=(p_x,p_y,p_{v_x},p_{v_y},p_m)^{\top }$ is the costate vector and $\mathbf {u}$ the control vector.

Therefore, the developed form of the Hamiltonian is

$$\begin{aligned} H(t,\mathbf {\xi },\mathbf {p},\mathbf {u})= & {} p_x v_x + p_y v_y + p_{v_x}\left( 2v_y+\varOmega _{sx} + \frac{u_1 F_{\max }}{m}\right) \nonumber \\&+\ p_{v_y} \left( -2v_x+\varOmega _{sy}+\frac{u_2F_{\max }}{m}\right) + p_m \left( -\,\Vert \mathbf {u}\Vert \frac{F_{\max }}{I_{sp}g_0}\right) . \end{aligned}$$

(12)

The optimal control $\mathbf {u}$ must minimize the Hamiltonian H over all possible controls satisfying $\Vert \mathbf {u}\Vert \le 1$. Neglecting all the terms which do not contain the control and applying the Cauchy–Schwartz inequality we get

$$\begin{aligned} \mathbf {u} = -\,\eta \frac{\mathbf {p}_v}{\Vert \mathbf {p}_v\Vert }, \end{aligned}$$

(13)

where $\mathbf {p}_v=(p_{v_x},p_{v_y})^{\top }$ and $\eta$ determines the normalized thrust modulus and depends on the switching function,

$$\begin{aligned} {\mathcal {S}}(m,\mathbf {p})=-\,p_m -I_{sp}g_0\frac{\Vert \mathbf {p}_v\Vert }{m}, \end{aligned}$$

(14)

as follows

$$\begin{aligned} \eta =\left\{ \begin{array}{ll} 0 &{}~~~ {\mathcal {S}}(m,\mathbf {p}) > 0\\ {\overline{\eta }} \in [0,1] &{}~~~{\mathcal {S}}(m,\mathbf {p}) =0\\ 1 &{}~~~ {\mathcal {S}}(m,\mathbf {p})<0 \end{array} \right. . \end{aligned}$$

(15)

In addition, the PMP gives expressions for the dynamics of the costates as $\dot{\mathbf {p}}=-\,\nabla _\xi H$, leading to

$$\begin{aligned} \left\{ \begin{array}{l} \dot{p}_x= \frac{-\,\partial H}{\partial x}= -\,p_{v_x}\varOmega _{s,xx}- p_{v_y} \varOmega _{s,yx},\\ \dot{p}_y= \frac{-\,\partial H}{\partial y}= -\,p_{v_x}\varOmega _{s,xy}- p_{v_y} \varOmega _{s,yy},\\ \dot{p}_{v_x}= \frac{-\,\partial H}{\partial v_x}= -\,p_x +2p_{v_y},\\ \dot{p}_{v_y}= \frac{-\,\partial H}{\partial v_y}= -\,p_y-2p_{v_x},\\ \dot{p}_m= \frac{-\,\partial H}{\partial m}= \frac{F_{\max }}{m^2} ( p_{v_x} u_1 + p_{v_y} u_2 ), \end{array} \right. \end{aligned}$$

(16)

where

$$\begin{aligned} \varOmega _{s,xx}=\frac{\partial ^2 \varOmega }{\partial x^2},\quad \varOmega _{s,xy}=\varOmega _{s,yx}=\frac{\partial ^2 \varOmega }{\partial x \partial y},\quad \varOmega _{s,yy}=\frac{\partial ^2 \varOmega }{\partial y^2}. \end{aligned}$$

(17)

Finally, the transversality conditions can be obtained from the PMP. By defining $\phi (\mathbf {\xi }(t_0), \mathbf {\xi }(t_{f}), \mathbf {\nu }_0,\mathbf {\nu } _f)=-\,Km(t_{f}) + \mathbf {\nu _0}^\top h_0(\mathbf {\xi }(t_0)) + \mathbf {\nu _f}^\top h_f(\mathbf {\xi }(t_{f}))$, where $h_0$ and $h_f$ are the initial and final conditions defined in Eqs. (8–11) and $\mathbf {\nu }_0$ and $\mathbf {\nu }_f$ are auxiliary parameters. Then, the transversality conditions can be written as

$$\begin{aligned} \mathbf {p}(t_0)=\frac{-\,\partial \phi }{\partial \mathbf {\xi }_0}(\mathbf {\xi }(t_0), \mathbf {\xi }({ t}_{ f}), \mathbf {\nu }_0,\mathbf {\nu } _f), \quad \mathbf {p}({ t}_{ f})=\frac{\partial \phi }{\partial \mathbf {\xi }_f}(\mathbf {\xi }(t_0), \mathbf {\xi }({ t}_{ f}), \mathbf {\nu }_0,\mathbf {\nu }_{ f}). \end{aligned}$$

(18)

Eliminating the auxiliary variables $\mathbf {\nu }_0$ and $\mathbf {\nu }_f$ from the ten conditions Eq. (18) leads to the following three equivalent ones

$$\begin{aligned} \left\{ \begin{array}{l} p_{x}(t_0) y(t_0) - p_{y}(t_0) (x(t_0)+\mu ) + p_{v_x}(t_0) v_{y}(t_0) - p_{v_y}(t_0) v_{x}(t_0)=0,\\ p_{x}(t_{f}) y(t_{f}) - p_{y}({ t}_{ f}) (x({ t}_{ f}) + \mu -1) + p_{v_x}({ t}_{ f}) v_{y}({ t}_{ f}) - p_{v_y}({ t}_{ f}) v_{x}({ t}_{ f})=0,\\ p_{m}({ t}_{ f})=-\,K. \end{array} \right. \end{aligned}$$

(19)

One can notice that there is no condition on $p_m(t_0)$. Thus, $p_m(t_0)$ is an unknown that has to be determined by the solution method.

Since the final time is free, a last equation has to be satisfied according to the PMP

$$\begin{aligned} H({ t}_{ f},\mathbf {\xi }({ t}_{ f}),\mathbf {p}({ t}_{ f}),\mathbf {u}({ t}_{ f}))+ \frac{\partial \phi }{\partial { t}_{ f}}(\mathbf {\xi }(t_0),\mathbf {\xi }({ t}_{ f}),\mathbf {\nu }_0,\mathbf {\nu }_{ f})=0. \end{aligned}$$

(20)

The second term in Eq. (20) is null since $t_{f}$ does not appear in the expression of $\phi$. Therefore, the condition that must be satisfied is

$$\begin{aligned} H(t_{f},\mathbf {\xi }({ t}_{ f}),\mathbf {p}({ t}_{ f}),\mathbf {u}({ t}_{ f}))=0. \end{aligned}$$

(21)

Now, solving Eq. (7) through the PMP reduces in determining eleven variables (the states $\mathbf {\xi }(t_0)$ and costates $\mathbf {p}(t_0)$ at the initial time plus the final time $t_{f}$) such that eleven equations are satisfied: the four boundary conditions at the initial time Eq. (8), the three boundary conditions at the final time Eq. (10), three transversality conditions given in Eq. (19) and condition Eq. (21).

In order to reduce the number of equations and the complexity of their resolution, a new set of variables is introduced. First, since the initial and final orbits are circular, they can be described by only two angles $\alpha$ and $\beta$ and two integer parameters $s_0$ and $s_f$.

As a matter of fact, the initial and final conditions Eqs. (8–11) can be rewritten as follows

$$\begin{aligned} x(t_0)= & {} -\,\mu -r_0\sin \alpha ,\quad x({ t}_{ f})=1-\mu -{ r}_{ f}\sin \beta ,\nonumber \\ y(t_0)= & {} r_0\cos \alpha ,\quad y({ t}_{ f})={ r}_{ f}\cos \beta ,\nonumber \\ v_{x}(t_0)= & {} (s_0 (v_0 + \Delta v_0) + r_0)\cos \alpha ,\quad v_{x}({ t}_{ f})=(s_fv_f+ r_{ f})\cos \beta ,\nonumber \\ v_{y}(t_0)= & {} (s_0 (v_0 + \Delta v_0) + r_0)\sin \alpha ,\quad v_{y}({ t}_{ f})=(s_fv_f+ r_{ f})\sin \beta , \end{aligned}$$

(22)

where $s_0$ (resp. $s_{ f}$) is the direction of rotation on the initial (resp. final) circular orbit and can take values $+\,1$ or $-\,1$.

Then, the first two transversality conditions in Eq. (19) can be written under the following form

$$\begin{aligned} \mathbf {p}(t_0)^\top \mathbf {w}_0=0\quad \text{ and }\quad \mathbf {p}({ t}_{ f})^\top \mathbf {w}_{ f}=0. \end{aligned}$$

(23)

This means that the initial (resp. final) costate vector must be orthogonal to the vector $\mathbf {w}_0$ (resp. $\mathbf {w}_f$) defined as follows

$$\begin{aligned} \mathbf {w}_0= \left( \begin{array}{c} r_0\cos \alpha \\ r_0\sin \alpha \\ (s_0(v_0+\Delta _0)+ r_0)\sin \alpha \\ -\, (s_0(v_0+\Delta _0)+ r_0)\cos \alpha \end{array}\right) ,\quad \mathbf {w}_f= \left( \begin{array}{c} r_{ f}\cos \beta \\ r_{ f}\sin \beta \\ (s_f v_f+ { r}_{ f})\sin \beta \\ -\, (s_f v_f+ { r}_{ f})\cos \beta \end{array}\right) . \end{aligned}$$

(24)

Now, the orthogonal space to $\mathbf {w}_0$ can be generated by the three following independent unit vectors

$$\begin{aligned} \mathbf {w}_1^0=\left( \begin{array}{c} -\,\sin \alpha \\ \cos \alpha \\ 0\\ 0 \end{array}\right) ,~~~~ \mathbf {w}_2^0=\left( \begin{array}{c} 0\\ 0\\ \cos \alpha \\ \sin \alpha \end{array}\right) ,~~~~ \mathbf {w}_3^0=\left( \begin{array}{c} a^0\cos \alpha \\ a^0 \sin \alpha \\ b^0\sin \alpha \\ -\,b^0\cos \alpha \end{array}\right) , \end{aligned}$$

(25)

where $a^0=\frac{s_0(v_0+\Delta v_0)+r_0}{\sqrt{(s_0(v_0+\Delta v_0)+r_0)^2+r_0^2}}$ and $b^0=\frac{-\,r_0}{\sqrt{(s_0(v_0+\Delta v_0)+r_0)^2+r_0^2}}$. Then, $\mathbf {p}(t_0)$ can be written as a linear combination of the three above vectors

$$\begin{aligned} \mathbf {p}(t_0) = \gamma _1 \mathbf {w}_1^0+ \gamma _2 \mathbf {w}_2^0+ \gamma _3 \mathbf {w}_3^0, \end{aligned}$$

(26)

for any $(\gamma _1, \gamma _2, \gamma _3)\in {\mathbb {R}}^3$.

Analogously, the value of $\mathbf {p}(t_{f})$ is determined by a triplet $(\zeta _1,\zeta _2,\zeta _3)\in {\mathbb {R}}^3$ and three independent vectors ($\mathbf {w}_1^f,\mathbf {w}_2^f,\mathbf {w}_3^f$)

$$\begin{aligned} \mathbf {p}(t_{f}) = \zeta _1 \mathbf {w}_1^f+ \zeta _2 \mathbf {w}_2^f+ \zeta _3 \mathbf {w}_3^f, \end{aligned}$$

(27)

where

$$\begin{aligned} \mathbf {w}_1^f=\left( \begin{array}{c} -\,\sin \beta \\ \cos \beta \\ 0\\ 0 \end{array}\right) ,~~~~ \mathbf {w}_2^f=\left( \begin{array}{c} 0\\ 0\\ \cos \beta \\ \sin \beta \end{array}\right) ,~~~~ \mathbf {w}_3^f=\left( \begin{array}{c} a^f\cos \beta \\ a^f \sin \beta \\ b^f\sin \beta \\ -\,b^f\cos \beta \end{array}\right) , \end{aligned}$$

(28)

and $a^f=\frac{s_f v_f+r_f}{\sqrt{(s_f v_f+rf)^2+r_f^2}}$ , $b^f=\frac{-\,r_f}{\sqrt{(s_f v_f+rf)^2+r_f^2}}$.

The triplet $(\zeta _1,\zeta _2,\zeta _3)\in {\mathbb {R}}^3$ can be represented in spherical coordinates as follows

$$\begin{aligned} \zeta _1= & {} \kappa \cos \theta _2 \cos \theta _1,\nonumber \\ \zeta _2= & {} \kappa \cos \theta _2 \sin \theta _1,\nonumber \\ \zeta _3= & {} \kappa \sin \theta _2, \end{aligned}$$

(29)

with $\kappa >0$.

2.4 First solution: continuation methods

In order to determine variable $\mathbf {z}=(\alpha , s_0, \gamma _1, \gamma _2,\gamma _3,p_m(t_0),t_{f})$ that satisfies all the necessary optimality conditions given in the previous section, a shooting function F is built. A common technique consists in using root-finding methods to find the zeros of function F leading to the so-called shooting methods.

2.4.1 Principles of the continuation approach

Before defining the shooting function some additional considerations must be taken into account. On one side, it is known (Bertrand and Epenoy 2002) that function F may be non-differentiable and that its Jacobian may be singular on a large domain due to the bang-bang structure of the optimal control given in Eqs. (13) and (15). Thus, Newton-like methods may fail to converge. More information on that topic can be found in Bertrand and Epenoy (2002). The authors propose to smooth the control by adding a logarithmic term in the cost function of Eq. (7), leading to the following problem

$$\begin{aligned} ({\mathbf {P}}_\varepsilon ) \left\{ \begin{array}{l} \min -K m(t_{f})- \varepsilon \frac{F_{\max }}{I_{sp}g_0}\displaystyle \int _{t_0}^{t_{f}} \left[ \log \Vert \mathbf {u}(t)\Vert +\log (1-\Vert \mathbf {u}(t)\Vert )\right] dt\\ \begin{array}{ll} s.t. \dot{\mathbf {\xi }}=&{} \varphi (t,\mathbf {\xi }, \mathbf {u}),\\ &{}\Vert \mathbf {u}\Vert \le 1,\\ &{}h_0(\mathbf {\xi }(t_0))=0,\\ &{}h_f(\mathbf {\xi }(t_{f}))=0,\\ &{}t_{f} \text{ free }, \\ \end{array} \end{array} \right. \end{aligned}$$

(30)

whose Hamiltonian function is given by

$$\begin{aligned} H_\varepsilon (t,\mathbf {\xi }(t), \mathbf {p}(t), \mathbf {u}(t))= & {} H(t,\mathbf {\xi }(t), \mathbf {p}(t), \mathbf {u}(t))\nonumber \\&-\,\varepsilon \frac{F_{\max }}{I_{sp}g_0}\left( \log \Vert \mathbf {u}(t)\Vert +\log (1-\Vert \mathbf {u}(t)\Vert )\right) . \end{aligned}$$

(31)

Note that the original problem can be recovered by setting $\varepsilon =0$. From the Hamiltonian Eq. (31) any positive value of $\varepsilon$ will determine a smooth control given by

$$\begin{aligned} \mathbf {u}_\varepsilon (t)= -\,\eta _\varepsilon \frac{\mathbf {p}_v(t)}{\Vert \mathbf {p}_v(t)\Vert }, \end{aligned}$$

(32)

where the normalized thrust modulus is given by

$$\begin{aligned} \eta _\varepsilon = \frac{2\varepsilon }{{\mathcal {S}}(m(t),\mathbf {p}(t))+2\varepsilon +\sqrt{{\mathcal {S}}(m(t),\mathbf {p}(t))^2+4\varepsilon ^2}},\end{aligned}$$

(33)

and the switching function ${\mathcal {S}}$ is defined in Eq. (14).

The dynamics equations of both the states and the costates as well as the initial, the final and the transversality conditions do not depend on $\varepsilon$ and remain the same as for the original problem ($\varepsilon =0$). However, Eq. (21) becomes

$$\begin{aligned} H_\varepsilon (t_{f},\mathbf {\xi }(t_{f}), \mathbf {p}(t_{f}), \mathbf {u}_\varepsilon (t_{f}))=0. \end{aligned}$$

(34)

Moreover, in order to reduce the sensitivity of the dynamics equations at close distance to the Moon, the final radius $r_f$ has been fixed to a large value, typically $r_f=50000$ km corresponding to the final altitude $H_f=48303$ km. For this value of $r_f$, the convergence radius of Powell’s hybrid method (Powell 1970) is large enough to allow an arbitrary choice of the initial guess. Once a first solution is found, the radius $r_f$ is reduced by means of a continuation method.

Taking into account the previous considerations, the shooting function becomes

(35)

where

$$\begin{aligned} TC(\mathbf {\xi }(t_{f}),\mathbf {p}(t_{f}))= & {} p_{x}(t_{f}) y(t_{f}) - p_{y}(t_{f}) (x(t_{f}) + \mu -1)\nonumber \\&+\, p_{v_x}(t_{f}) v_{y}(t_{f}) - p_{v_y}(t_{f}) v_{x}(t_{f}), \end{aligned}$$

(36)

and the value of $\Delta v_0$ has to be set here so as the value of $\omega _0$ and the value of K that can be set to $K=1$.

Table 1 Physical parameters

Table 2 Spacecraft parameters

More precisely, two different shooting functions $F_{s_0}$ are defined, the first one for $s_0=1$ and the other one for $s_0=-\,1$. In order to search for the optimal solution the zero of both shooting functions Eq. (35) is computed. Notice here that the value of parameter $s_f$ disappears thanks to the squared term in the third condition of Eq. (35).

In order to compute $\mathbf {\xi }(t_{f}), \mathbf {p}(t_{f})$ and $\mathbf {u}_\varepsilon (t_{f})$ the states and costates at time $t_0$ are first determined from $\alpha$, $\gamma _1$, $\gamma _2$, $\gamma _3$ and $p_{m}(t_0)$ following Eqs. (22) and (26). Then these initial conditions are propagated forward in time according to Eqs. (6) and (16) up to time $t_{f}$ using Eqs. (32) and (33) for the control.

The propagation is carried out using a method of order 8 (more information on the propagation method can be found in Dormand and Prince 1980). Finally, the zeros of the shooting functions defined in Eq. (35) are computed using Powell’s hybrid method (Powell 1970).

Once the zero $\mathbf {z}^{(0)}$ of Eq. (35) has been found (for a given value of $s_0$), the radius $r_f$ is decreased by using a continuation method introducing $r_f$ as an additional variable in the shooting function Eq. (35) (see Allgower and Georg 1990). Then, at each step i, a zero of the shooting function $\mathbf {z}^{(i)}$ is computed and at the same time $r_f$ is decreased by a small step $\delta r_f$. Theoretically, if $\delta r_f$ is small enough, $\mathbf {z}^{(i-1)}$ is sufficiently close to $\mathbf {z}^{(i)}$ and is a good initial guess that enables the convergence of Powell’s hybrid method at the current step i.

It turns out that the shooting function associated with $s_0=1$ (that corresponds to the optimal trajectory here) exhibits turning points, i.e., values of $r_f$ at which the gradient of the shooting function has a null $r_f$-component. This implies that whatever the value of $\delta r_f$ the shooting function has no neighboring zero. This problem has been circumvented by using predictor-corrector methods (also known as pseudo arc-length methods), for further information see Allgower and Georg (1990). In this case, at each step, instead of reducing the value of $r_f$ by $\delta r_f$, the next value is computed using the gradient of function F. Thus, the turning points are no longer an issue.

2.4.2 Numerical results

The numerical values for the physical constants and the spacecraft constants used in the continuation experiments can be found in Tables 1 and 2. The parameters related to the spacecraft have been selected according to Mingotti et al. (2012) for the sake of comparison.

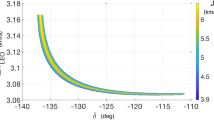
Figure 1 shows the projection of the solution path of Eq. (35) for $s_0=+\,1$ on the ($r_f,\alpha$) plane. Each point on the blue curve corresponds to a zero of the shooting function. It seems from the plot that there exist singular points. However, these points only appear on the projection of the solution path on the plane $(r_f,\alpha )$ that has been selected. When all the components of $\mathbf {z}$ are analyzed at the same time those singular points do not exist.

In Fig. 1 one can notice that the shooting function presents several turning points. The existence of turning points indicates that the same final circular orbit can be obtained from different values of $\alpha$. However, the final mass associated with these different transfers is not the same. On the same figure it can be seen that as the spacecraft approaches the Moon, the number of turning points increases. This is due to the sensitivity of the problem to the initial conditions.

Since the maximum thrust modulus $F_{\max }$ is small, as $r_f$ decreases, the number of revolutions around the Moon increases. Each time an additional revolution appears a turning point is generated as can be seen on the plot on the right that shows a zoom on the last part of the continuation.

The continuation procedure stops at a radius equal to $r_f=4580$ km. Note that, at the last step, the norm of the Jacobian matrix of the shooting function $\Vert DF_{s_0=1}\Vert$ is of the order of $10^4$ and the condition number of that matrix is of the order of $10^8$. It can also be observed that the shooting function on the last steps suffers from numerical cancellations that cause the loss of some digits of precision. The combined effect of these three numerical problems leads to the divergence of Powell’s hybrid method.

Fig. 1

Continuation path $z_1=\alpha$ plotted as a function of the final radius $r_f$ for $\varepsilon =0.5$. The green, red, cyan and blue dots correspond to the trajectories shown in Fig. 2. The color used for each trajectory is related to the color of the corresponding dot

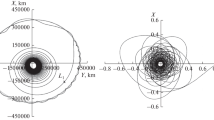
Figure 2 shows four examples of trajectories obtained at different steps of the continuation procedure corresponding to $r_f= 50000$ km, $r_f=25000$ km, $r_f=18000$ km and $r_f=4580$ km (respectively, in green, red, cyan and magenta). The right plot of the figure is a zoom view centered at the Moon.

Fig. 2

Sample trajectories obtained during the continuation method. Each trajectory corresponds to a different final radius $r_{ f}$ according to the legend. The Earth and the Moon are plotted as black circles

As a conclusion, the continuation approach on parameter $r_f$ suffers from numerical difficulties when $r_f$ approaches its target value, typically $r_f=5000$ km, although $\varepsilon$ has been set to a large value here ($\varepsilon =0.5$). One may think that the continuation procedure on parameter $\varepsilon$ will be even more difficult for this fixed value of $r_f$. In addition, this approach does not easily allow to generate different locally optimal trajectories. As a matter of fact, $\Delta v_0$ and $\omega _0$ must be set due to the forward propagation required for computing the shooting function.

2.5 Second solution: massive exploration

The second solution consists in implementing a massive exploration of the unknown variables of the shooting function in order to solve problem Eq. (7). In this approach, there is no need to smooth the control as the differentiability of the shooting function is not required. As a matter of fact, the direct exploration of the set of unknown variables avoids the use of Powell’s hybrid method as will be seen below.

Notice that some of the tricks that are used here are similar to those used in Dixon and Biggs (1972).

2.5.1 General description of the method

To reduce the number of cases to explore, some choices have been made and additional tricks have been introduced.

The goal is to start at $t=t_{f}$ satisfying the terminal conditions Eq. (10), the transversality conditions Eqs. (19) (those that apply at time $t_{f}$) and (21) and to integrate backwards in time Eqs. (6) and (16) until the initial conditions Eq. (8) and the first transversality condition in Eq. (19) are satisfied. In practice, the numerical integration is stopped when one of the following four cases is met:

• 1. Equation (8) and the first condition in Eq. (19) are satisfied at a given time $t_0$.

• 2. There is a collision with the Moon (the distance between the spacecraft and the Moon’s surface becomes too small).

• 3. The spacecraft exits the Earth–Moon region toward the outer planets or the Sun.

• 4. A given maximum time of flight is achieved before any of the previous three cases occur.

The important point is that the backward propagation ensures the fulfillment of the terminal conditions at $t=t_{f}$ that are difficult to achieve via forward propagation due to the strong sensitivity of the dynamics in the vicinity of the Moon (see Sect. 2.4).

At the opposite, thanks to the initial $\Delta v_0$ provided by the launcher, satisfying the initial conditions at the end of a backward propagation is less difficult. As a matter of fact, the initial velocity can be modified as follows:

Assuming that at some time $t_0$ of the backward propagation the spacecraft is located at $(x(t_0),y(t_0),v_{x}(t_0),v_{y}(t_0))$ such that the first condition in Eq. (8) is satisfied:

$$\begin{aligned} (x(t_0)+\mu )^2+y(t_0)^2=r_0^2. \end{aligned}$$

(37)

Then, the $\Delta v$ required to satisfy condition $h_{0,3}(\mathbf {\xi }(t_0))=0$ given in Eq. (8) can be easily computed. Let alpha be the angle on the departure orbit defined by $\alpha =\arctan _2(-\,x(t_0)-\mu ,y(t_0))$¹ [see Eq. (22)], and consider the following velocity vector

$$\begin{aligned} \mathbf {v}_{c,s_0}=( (s_0 v_0+r_0) \cos \alpha ,(s_0 v_0+r_0) \sin \alpha ), \end{aligned}$$

(38)

where $s_0=+\,1$ or $s_0=-\,1$ denotes the direction of the rotation on the circular orbit. It is possible to compute the instantaneous velocity change as follows

$$\begin{aligned} {\varvec{\Delta }} \mathbf {v} = \left( \begin{array}{c}\Delta v_{x}\\ \Delta v_{x}\end{array}\right) = \left( \begin{array}{c} v_{x}(t_0)\\ v_{y}(t_0) \end{array}\right) - \mathbf {v}_{c,s_0}. \end{aligned}$$

(39)

Finally, condition $h_{0,3}(\mathbf {\xi }(t_0))=0$ is satisfied by choosing the value of $s_0$ that leads to the lowest value of $\Delta v_0=\Vert {\varvec{\Delta }} \mathbf {v}\Vert$.

Notice that using backward propagation the final time $t_{f}$ is fixed and the initial time $t_0$ is determined by the fulfillment of the conditions defined in case 1 above. This is equivalent to set the initial time and let the final time free. The initial phase of the Sun $\omega _0$ is one of the parameters that are explored in the massive exploration.

Now, assuming that $\Vert \mathbf {u}(t_{f})\Vert \ne 0$, the value of $p_m(t_{f})$ can be determined from Eq. (21) as

$$\begin{aligned} p_m(t_{f})= & {} \frac{I_{sp}g_0}{\Vert \mathbf {u}(t_{f})\Vert F_{\max }}\Big ( p_x(t_{f})v_x(t_{f}) + p_y(t_{f}) v_y(t_{f})\nonumber \\&\left. +\, p_{v_x}(t_{f}) \left( 2v_y(t_{f})+\varOmega _{s,x}(t_{f}) +\frac{u_1(t_{f}) F_{\max }}{m(t_{f})} \right) \right. \nonumber \\&+\, p_{v_y}(t_{f}) \left( -\,2v_x(t_{f})+\varOmega _{s,y}(t_{f}) +\frac{u_2(t_{f})F_{\max }}{m(t_{f})}\right) \Big ), \end{aligned}$$

(40)

where $\mathbf {u}(t_{f})$ is given by Eqs. (13) and (15). On the other side, from the last condition in Eq. (19), $p_{m}(t_{f})=-\,K$ where K is a positive number. Therefore, as long as Eq. (40) returns a negative value, a value of K that fulfills the PMP statement can be selected.

2.5.2 Tricks to reduce the exploration set

When approaching the Moon, the spacecraft must reduce its velocity in order to reach the final circular orbit. In order to maximize the rate of decrease of the velocity, the angle between the thrust vector $\mathbf {u}$ and the velocity $\mathbf {v}=(v_x,v_y)^{\top }$ must be close to $\pi$ at $t=t_{f}$. Using Eqs. (13), (22) and (27), satisfying this condition is equivalent to set $\zeta _3=0$ and to choose $\zeta _2$ with the same sign as that of $s_f v_f+r_f$.

In addition, assume that the derivative of this angle is close to zero at the final time $t_{f}$, or equivalently that

$$\begin{aligned} \frac{d}{dt} \Big (v_x(t) p_{v_y}(t)-v_y(t) p_{v_x}(t)\Big )_{t=t_{f}}\approx 0. \end{aligned}$$

(41)

This ensures that the thrust will reduce the spacecraft’s velocity during a time interval before $t_{f}$. A second benefit of satisfying these conditions is to reduce the possibility of collisions with the Moon close to $t=t_{f}$ (case number 2 of the above stopping conditions). Enforcing Eq. (41) as an equality together with the conditions above for $\zeta _2$ and $\zeta _3$ and using Eqs. (27), (6) and (16), the triplet $(\zeta _1,\zeta _2,\zeta _3)$ is obtained as

$$\begin{aligned} {\overline{\zeta }}_1= & {} \kappa (\sin \beta \varOmega _{s,x}(t_{f})-\cos \beta \varOmega _{s,y}(t_{f}) ),\nonumber \\ {\overline{\zeta }}_2= & {} \kappa (s_f v_f + r_f),\nonumber \\ {\overline{\zeta }}_3= & {} 0, \end{aligned}$$

(42)

where $\kappa >0$ is a free scale variable. Therefore, the massive exploration will be carried out considering only values of $\zeta _1$, $\zeta _2$ and $\zeta _3$ close to those given in Eq. (42). Since the final result is independent from the modulus of the costate vector, due to the fact that in the PMP all the costates can be multiplied by the same factor without modifying the solution, the value of $\kappa$ can be arbitrarily set to 1.

The values obtained in Eq. (42) can be converted in the ($\theta _1,\theta _2$) spherical coordinates given in Eq. (29)

$$\begin{aligned} {\overline{\theta }}_1(\beta )= \arctan _2( (s_f v_f + r_f),\varOmega _{s,x}(t_{f}) \sin \beta -\varOmega _{s,y}(t_{f}) \cos \beta ) ,~~~~~ {\overline{\theta }}_2=0. \end{aligned}$$

(43)

In summary, the variables that are considered in the massive exploration are $\beta$, $s_f$, $\omega _0$, $m(t_{f})$, $\theta _1$ and $\theta _2$.

Small changes in those variables may have a strong impact on the final conditions obtained at $t=t_0$ due to the sensitivity of the problem. For that reason, the following trick is used to select values that satisfy Eq. (37) at a given time $t_0$.

Variables $\beta$, $\omega _0$, $m(t_{f})$, $\theta _1$ and $\theta _2$ are sampled leading to a grid, $G_{\{i\}}\ (i=1,\dots , N)$, and the integer parameter $s_f$ is fixed to $+\,1$ or $-\,1$ (a complete exploration requires that both values be explored).

The chances to satisfy Eq. (37) by backward propagation are low. In order to increase the number of final trajectories that arrive to the desired radius $r_0$ the following strategy is used. Let $G_i$ and $G_{i-1}$ be two points of the grid $G_{\{i\}}$ corresponding to trajectories that miss the Earth [Eq. (37) is not satisfied] from above and from below, respectively, with respect to the y axis leading to opposite directions of rotation with respect to the Earth. By continuity, there exists an intermediate point between $G_i$ and $G_{i-1}$ for which there is collision with the Earth. Therefore, there exists a point for which Eq. (37) is satisfied.

The direction of rotation is given via the sign of the angular velocity $V_a$ of the spacecraft computed in the inertial frame centered at the Earth that can be written as

$$\begin{aligned} V_a = \frac{(v_y(t)+x(t)+\mu )(x(t) +\mu )-(v_x(t)-y(t))y(t)}{\sqrt{(x(t) +\mu )^2+y(t)^2}}. \end{aligned}$$

(44)

If the angular velocities with respect to the Earth of two neighboring grid points $G_i$ and $G_{i-1}$ are of opposite signs, then the bisection method is used to find a trajectory satisfying Eq. (37).

Notice that in the setting of the problem the initial $\Delta v_0$ is performed parallel to the velocity on the initial circular orbit [second condition in Eq. (8)]. However, the ${\varvec{\Delta }} \mathbf {v}$ computed in Eq. (39) does not satisfy this condition in general. Now, using the last two points $G_i$ and $G_{i-1}$, it is possible by bisection to find two trajectories with a tangential departure from the initial LEO. Each one corresponds to a rotation in opposite direction around the Earth ($V_a<0$ corresponding to $s_0=1$ and $V_a>0$ corresponding to $s_0=-\,1$).

The procedure described above ensures that the first three conditions in Eq. (8) are satisfied. Now, the only conditions that remain to be satisfied in step 1 of the massive exploration algorithm described above are $h_{0,4}(\mathbf {\xi } (t_0))=0$ and the first transversality condition in Eq. (19).

3 Results

In this section the results obtained through the massive exploration are presented. Several families of transfer trajectories have been detected. The altitude of the final Lunar Orbit is set to $H_f=5000$ km.

The parameters used for the massive exploration together with their respective search intervals are given by

• $\beta \in [ 0,2\pi ]$,

• $s_f=\pm \, 1$,

• $\omega _0\in [0,2\pi ]$,

• $m(t_{f})\in [0.93, 0.99]$,

• $\theta _1\in [{\overline{\theta }}_1(\beta )-\delta \theta _1,{\overline{\theta }}_1(\beta )+ \delta \theta _1]$ and

• $\theta _2\in [\overline{\theta }_2-\delta \theta _2, \overline{\theta }_2+\delta \theta _2]$,

where $\delta \theta _1=2\pi /1000$ and $\delta \theta _2=10^{-3}$. The physical and spacecraft parameters are given in Tables 1 and 2, respectively, except for $\Delta v_0$ and $\omega _0$ that are not fixed here.

The massive exploration that has been performed led to six different families of transfer trajectories from the initial LEO to the final LO: A, B, C, D, E and F. Each trajectory in a given family is a local minimum of problem Eq. (7) for given values of $\Delta v_0$, $\omega _0$ and $\Delta t=t_{f}-t_0$. Table 3 shows the best representative of each family in terms of the total fuel consumption $\Delta m=m_0-m(t_{f})$. The third column shows the transfer duration in days. The fourth column gives the initial Sun’s phase and the last one the initial $\Delta v_0$ provided by the launcher.

In addition, the three low-thrust trajectories obtained from Mingotti et al. (2012) are given at the end of the table for the sake of comparison. Note that the target circular LO in that reference is an orbit at an altitude of 100 km. In order to compare both results, the additional mass consumption $\Delta m_{res}$ and the additional transfer duration $\Delta t_{res}$ required to lower the orbit down from $H_f=5000$ to 100 km are estimated using Edelbaum’s formula (Edelbaum 1961). The additional velocity increment is given by

$$\begin{aligned} \Delta v_{res}=\sqrt{v_{f}^2+v_{{ f},100}^2 -2v_{ f}v_{{ f},100}}\ , \end{aligned}$$

(45)

where $v_{f,100}$ is the velocity modulus of the circular orbit at an altitude of 100 km. Therefore, Eq. (45) reduces to $\Delta v_{res}=v_{f,100}-v_{f}$. Now, using the rocket equation (Tooley et al. 2009)

$$\begin{aligned} \Delta v_{res}=I_{sp}g_0\ln \frac{m({ t}_{ f})}{{ m}_{{ f},100}}, \end{aligned}$$

(46)

where $m_{{ f},100}$ is the mass obtained at the altitude of 100 km.

Assuming a continuous maximum thrust for the final reduction of the radius, the following approximations are obtained $\Delta m_{res}=25.5$ kg and $\Delta t_{res}= 17.32$ days. These values are added to the results in Table 3 given in parenthesis next to the transfer duration and fuel consumption for comparison with Mingotti et al. (2012). Observe that the solutions found improve those of Mingotti et al. in either the fuel consumption ($\Delta m$), the time duration ($\Delta t$) or the initial impulse ($\Delta v_0$). In addition, the method introduced is able to find other solutions that do not follow the Sun–Earth and Earth–Moon manifolds.

Remark 3

At this altitude the gravitational influences of the Earth and the Sun are small compared to that of the Moon. Therefore, a two-body approximation is accurate enough to compute the additional time and fuel that are required to decrease the orbit down to a lower altitude.

Table 3 Summary of the results obtained during the massive exploration classified according to the transfer duration and the way the spacecraft approaches the Moon

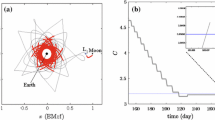
Figure 3 shows all the transfers obtained through the massive exploration in terms of the fuel consumption $\Delta m$ plotted as a function of the time of flight $\Delta t$ (top) and the initial $\Delta v_0$ (bottom). Each dot in the plot represents a local minimum of a specific instance of problem Eq. (7) associated with a given $\Delta v_0$ and initial Sun’s phase $\omega _0$. As expected, the longer the time of flight the smaller the total fuel consumption. It can be observed that the trajectories are grouped in different families, each one being characterized by a particular shape of the transfers. In what follows some of these families for which the fuel consumption and the time of flight are more favorable, i.e. a low fuel consumption or a small time of flight, are highlighted.

Fig. 3

Gray: fuel consumption of the optimal transfer $\Delta m$ as a function of the time of flight $\Delta t=t_{f}-t_0$ (top) and the initial $\Delta v_0$ (bottom). The different colors identify each of the families obtained. Table 3 gives additional information for the best representative of each family in terms of fuel consumption $\Delta m$

The classification is carried out in terms of the dynamical structure of the trajectories analyzed in one of the two underlying PCR3BP (Earth–Moon and Sun–Earth). The main structures that determine the shape of the transfers are the dynamical counterparts in the PBRFBP of the invariant manifold of Lyapunov periodic orbits around the Lagrange points $L_i~~ (i=1,2)$. In all the plots that follow the thrust arcs are colored in orange while the coast arcs are colored in blue.

The first classification criterion is the transfer duration. One can distinguish between short/medium duration transfers lasting at most 120 days and long duration transfers lasting more than 120 days.

The second characteristic that drives the classification is the neck of the Hill’s region that allows the entry of the spacecraft to the Moon’s vicinity, either $L_1^{EM}$ or $L_2^{EM}$. Notice that, during a coast arc, the main force acting on the spacecraft when approaching the final LO is the gravitational attraction of the Moon followed by that of the Earth.

All the transfers that have been found contain a last phase that consists in the approach to the final orbit, when the radius with respect to the Moon is reduced down to $r_f$. Figure 4 shows a zoom in the Moon’s region for a sample trajectory in family B. The left plot shows the trajectory in the synodic coordinate frame while the right one presents the same trajectory in the inertial Moon frame. It can be observed that this decrease is based on a succession of thrust arcs and coast arcs that lead to an increase of $J_C^{EM}$ up to the value of the final LO. As can be seen from the bottom left plots in Figs. 5, 6, 7 and 8 and the middle plots in Figs. 9 and 10, the increase of the Jacobi constant occurs during the thrust arcs. Therefore, transfers with longer thrust arcs correspond to a faster decrease of the radius. The fuel consumption is similar in all cases. This comes from the fact that the total duration of the thrust arcs is almost the same in all cases.

Fig. 4

Last phase of a trajectory in family B in the rotating frame and the Moon inertial frame

3.1 Short/medium duration transfers through $L_1^{ EM}$

The transfers of these different families are characterized by an approach to the Moon’s neighborhood through the $L_1^{EM}$ neck and by a short to medium time of flight.

3.1.1 Family A

Transfers in family A are characterized by two thrust arcs performed close to the Earth that inject the spacecraft close to the stable manifold of a Lyapunov orbit around $L_1^{EM}$. Then, the trajectory follows the unstable manifold of the same orbit and arrives to the Moon’s neighborhood. Both manifolds, stable and unstable, are shown in Fig. 5 (top) together with the trajectory in the Earth–Moon rotating frame.

The fuel consumption for this family varies between 34.5 and 40.5 kg and the time of flight is around 90 days. The initial $\Delta v_0$ required is around 3120 m/s.

Fig. 5

Top: transfers of family A in the Earth–Moon rotating reference frame. Bottom left: Jacobi constant in the Earth–Moon PCR3BP. The thrust arcs (orange) and coast arcs (blue) are highlighted. Bottom-right: Thrust profile of a sample transfer

3.1.2 Family B

Family B is split in three subfamilies $\hbox {B}_1$, $\hbox {B}_2$ and $\hbox {B}_3$. These families are characterized by the same Moon’s approach path. The spacecraft arrives to the Moon following the stable manifold of a Lyapunov orbit around $L_1^{EM}$. The injection to that manifold is done by means of a thrust arc performed when the spacecraft is close to the $L_3^{EM}$ region. Now, each subfamily differs in the way this region is reached by the spacecraft. Figure 6 shows the trajectories of the three subfamilies in the Earth–Moon and the Sun–Earth rotating frames.

Fig. 6

Top: trajectories of subfamily $\hbox {B}_1$ (solid), $\hbox {B}_2$ (dashed) and $\hbox {B}_3$ (dot-dashed) in the Earth–Moon (left) and the Sun–Earth (right) rotating reference frames. Bottom: Jacobi constant in the Earth–Moon PCR3BP (left), the thrust arcs (orange) and coast arcs (blue) are highlighted, and thrust profile of a sample transfer of subfamily $\hbox {B}_1$ (right)

Subfamily $\hbox {B}_1$ corresponds to trajectories arriving to the $L_3^{EM}$ region following the inner stable manifold of a Lyapunov orbit. More precisely, the spacecraft departs from the Earth with a high energy value for which all the space is accessible, i.e., Hill’s region coincides with the (x, y)-space. Two thrust arcs are performed to reduce the energy down to the energy of the desired Lyapunov orbit. It can be seen that during the second coast arc (corresponding to the passage through the $L_3^{EM}$ region), the value of $J_C^{EM}$ is nearly constant. This pattern repeats at the third thrust arc when the spacecraft enters the Moon’s region. This can be seen in the bottom left plot in Fig. 6, where the Jacobi constant in the Earth–Moon system is plotted. It can be appreciated that the Jacobi constant remains almost fixed in the two coast arcs.

The fuel consumption associated with this subfamily varies from 33 to 37.5 kg. The transfer time is between 47.7 and 65.7 days and the initial $\Delta v_0$ takes values between 3126 and 3156 m/s.

Transfers in subfamily $\hbox {B}_2$ are based on a long thrust arc at the Earth departure in the opposite direction of the Moon, directly to the $L_3^{EM}$ region. This makes the transfer fast and expensive.

With a time of flight between 35.7 and 55.7 days this subfamily exhibits the fastest transfers. As it is expected for a fast transfer, the fuel consumption (between 44.4 and 51 kg) is also in the high range. The initial $\Delta v_0$ required takes values between 3116 and 3123 m/s.

Finally, subfamily $\hbox {B}_3$ consists in intermediate transfers between subfamily $\hbox {B}_1$ and subfamily $\hbox {B}_2$. The spacecraft arrives to the $L_3^{EM}$ region through the exterior stable manifold of a Lyapunov orbit around $L_3^{EM}$.

These different thrust profiles lead to fuel consumptions between 26.5 and 35.5 kg. The initial $\Delta v_0$ takes values between 3125 and 3185 m/s.

3.2 Short/medium duration transfers through $L_2^{ EM}$

The transfers of these different families correspond to an arrival to the Moon’s neighborhood through the $L_2^{EM}$ neck with a short to medium time of flight.

3.2.1 Family C

Family C is split in two subfamilies $\hbox {C}_1$ and $\hbox {C}_2$. These families are characterized by a direct arrival to the Moon’s region through the $L_2^{EM}$ neck. The spacecraft departs from the Earth with a high energy in the Earth–Moon system and the thrust is used to reduce this energy down to the energy of $L_2^{SE}$. Small differences are noticeable between subfamily $\hbox {C}_1$ and subfamily $\hbox {C}_2$.

The transfers in subfamily $\hbox {C}_1$ have a longer time of flight because once the spacecraft enters the Moon’s region it first visits the $L_1^{EM}$ vicinity using the stable and unstable invariant manifolds of a periodic orbit around that point to improve the fuel consumption. On the other hand, in subfamily $\hbox {C}_2$ the spacecraft starts the decreasing phase after arriving to the Moon’s region.

The fuel consumption for subfamily $\hbox {C}_1$ varies from 34.5 to 38.5 kg and the time of flight is slightly longer than 90 days. The initial $\Delta v_0$ varies between 3146 and 3161 m/s.

Subfamily $\hbox {C}_2$ contains trajectories with the second shortest times of flight ranging between 43 and 71.3 days. The fuel consumption is also reduced with respect to that of subfamily $\hbox {B}_2$ and varies between 32.1 and 40.9 kg. The initial $\Delta v_0$ takes values between 3158 and 3170 m/s.

In both subfamilies, the energy in the Sun–Earth system is not large enough to allow the aperture of the $L_1^{SE}$ neck. Therefore, the manifolds of the Sun–Earth system do not play any role here. However, as in the case of subfamilies $\hbox {B}_1$, $\hbox {B}_2$ and $\hbox {B}_3$, it can be observed in the Sun–Earth rotating frame (Fig. 7 top right) that the first thrust arc is performed when the spacecraft is approaching the zero-velocity curve. Intuitively, one may think that the control takes profit of the low velocity of the spacecraft to change the direction of the trajectory in an efficient way.

3.2.2 Family D

Family D is made of a set of transfers for which the access to the Moon’s region is made through $L_1^{EM}$. These transfers are based in a long thrust arc at the Earth departure that puts the spacecraft on a stable invariant manifold of a large amplitude Lyapunov orbit around $L_1^{EM}$. Then, the spacecraft departs from the periodic orbit around $L_1^{EM}$ through the unstable manifold.

The trajectories of this family are not optimal in terms of fuel consumption. Indeed, it is possible to find transfers with the same duration and a lower fuel consumption. However, the initial $\Delta v_0$ required for this family is the smallest that has been found.

Figure 8 shows the transfers of family D in the Earth–Moon rotating frame (top) as well as the evolution of the Jacobi constant $J_C^{EM}$ (bottom left) and the thrust profile (bottom-right). The fuel consumption for this family varies between 34.5 and 38.5 kg and the time of flight is around 75 days. The initial $\Delta v_0$ takes values between 3100 and 3110 m/s.

Fig. 7

Top: transfers of subfamily $\hbox {C}_1$ (solid) and subfamily $\hbox {C}_2$ (dashed) in the Earth–Moon (left) and Sun–Earth (right) rotating reference frames. Bottom left: Jacobi constant in the Earth–Moon PCR3BP. The thrust arcs (orange) and coast arcs (blue) are highlighted. Bottom-right: thrust profile of a sample trajectory

Fig. 8

Top: trajectories of family D in the Earth–Moon rotating reference frame. Bottom: Jacobi constant in the Earth–Moon PCR3BP (left). The thrust arcs (orange) and coast arcs (blue) are highlighted. Thrust profile (right)

3.3 Long duration transfers

The transfers of these families are characterized by a long duration time of flight.

3.3.1 Family E

Family E corresponds to the longest time of flight and lowest fuel consumption transfers that have been obtained. After Earth departure and a small thrust arc, the spacecraft follows the stable manifold of a Lyapunov orbit around $L_1^{SE}$. Then, it departs from the neighborhood of $L_1^{SE}$ through the unstable manifold of another less energetic orbit in the Sun–Earth system. This change of energy is due to the gravitational effect of the Moon. As can be seen in Fig. 9 (middle-right) $J_C^{SE}$ is not constant during the first coast arc. The smaller the distance between the Moon and the spacecraft the higher are these variations of the energy. Both the stable and unstable manifolds are plotted in Fig. 9 (top right). Finally, the unstable manifold of the $L_1^{SE}$ periodic orbit brings the spacecraft toward the Moon. The trajectory seen in the Earth–Moon system is close to the stable manifold of a Lyapunov orbit around $L_2^{EM}$. This allows the spacecraft to access to the Moon’s region. These kind of transfers has been identified in Mingotti et al. (2012).

Fig. 9

Top: transfers of family E in the Earth–Moon (left) and the Sun–Earth (right) rotating reference frames. Middle: Jacobi constant in the Earth–Moon PCR3BP (left) and Sun–Earth PCR3BP (right), the thrust arcs (orange) and coast arcs (blue) are highlighted. Bottom: thrust profile (left) and trajectory in the Earth inertial reference frame (right) of a sample transfer in the family

The main characteristic of family E is that it includes transfers with the lowest fuel consumption ranging from 10.5 to 31.5 kg. However, the transfer durations are important, typically between 126.7 and 155.7 days. The initial $\Delta v_0$ is also in the high range since it is required to put the spacecraft close to the $L_1^{SE}$ region. The value of $\Delta v_0$ varies between 3144 and 3227 m/s.

3.3.2 Family F

Family F is made of transfers that use the practical stability regions around $L_4^{EM}$ and $L_5^{EM}$ observed in McKenzie and Szebehely (1981), Gómez et al. (2001) and Simó et al. (2013); Pérez-Palau et al. (2015). Those regions are regions of the space where a spacecraft may remain for a long-time interval. One can notice that after some time in this region, a small thrust arc is performed by the spacecraft to leave this region and arrive to the Moon through the $L_1^{EM}$ or $L_2^{EM}$ necks (see Fig. 10).

The family is divided in two subfamilies, $F_4$ and $F_5$. Subfamily $F_4$ consists in those trajectories that arrive to the $L_4^{EM}$ practical stability region. In this case, the spacecraft enters the Moon’s region through the neck opened at $L_2^{EM}$. On the other side, the $F_5$ subfamily is made of trajectories that arrive to the $L_5^{EM}$ practical stability region. In this case, the spacecraft enters the Moon’s region through the $L_1^{EM}$ neck.

A characteristic of this family of transfers is that, although the fuel consumption is not optimal with respect to the long transfer duration, the value of $\Delta v_0$ is the smallest that has been found for these transfer times.

Figure 10 shows the transfers of family F in the Earth–Moon rotating frame (top) as well as the value of the Jacobi constant (middle) and the thrust profile (bottom). The left plots correspond to the $F_4$ subfamily and the right ones to the $F_5$ subfamily. The fuel consumption of family F varies between 34.5 and 39.5 kg and the time of flight is around 160 days. The initial $\Delta v_0$ required takes values between 3110 and 3120 m/s.

Fig. 10

Trajectories (top) of the $F_4$ (left) and the $F_5$ (right) subfamilies in the Earth–Moon rotating reference frame. Jacobi constant in the Earth–Moon PCR3BP (middle). The thrust arcs (orange) and coast arcs (blue) are highlighted. Thrust profile of a sample transfer of each family (bottom)

3.4 Comparison of the families obtained

Although the transfers obtained in Topputo (2013) are based on two impulsive maneuvers, some of the transfer trajectories obtained in the present paper can be considered as an equivalent low-thrust version of them. Concretely, transfers in families C are direct transfers from the Earth to the Moon corresponding to family a in the cited paper. Family D is also close to family a in Topputo. However, due to the long thrust arc between the Earth and the Moon the spacecraft performs a bigger spiral out to reach the Moon. Families A, $\hbox {B}_2$ and $\hbox {B}_3$ are the corresponding equivalent to family b in Topputo. However, family $\hbox {B}_1$ corresponds to families c,  d in Topputo’s paper. Family E in the present paper corresponds to families o and p in Topputo’s paper as well as to the families obtained in several papers exploiting the invariant manifolds of the Sun–Earth system. Finally, family F is completely new and does not appear in Topputo’s paper. That happens because in the cited paper the author only considers two maneuvers and family F requires at least three impulses: one to reach the $L_4$ or $L_5$ region, a second one to leave the region and the last one to get captured by the Moon.

The effect of the Sun has also been studied for the different trajectories. The same sampling experiments have been performed without the Sun’s influence. The results show that families A, B, C and F still exist when the Sun’s perturbation is neglected. Families D and E have not been found.

4 Conclusions

In this paper, the problem of designing low-energy transfers between a LEO and a LO using low-thrust propulsion has been considered in a bicircular model using indirect optimal control. More precisely, the problem has been formulated as an optimal control problem and the PMP has been applied. It has been shown that classical continuation techniques are not effective to solve the problem. The strong sensitivity of the dynamics with respect to the initial conditions prevents Powell’s hybrid method to converge and to find a zero of the shooting function. For that reason, a massive exploration based on a wise choice of the variables to explore has been implemented.

As a result of the massive exploration, a large number of local minima have been found. These minima have been analyzed by means of dynamical system tools. The well-known invariant manifold theory has been used to understand the different transfers and to classify them in different families according to their shapes. Among those families, some trajectories similar to impulsive trajectories already identified in the literature have been found. These trajectories exploit the invariant manifold structure of both the Sun–Earth and the Earth–Moon PCR3BPs. In that family, it has been shown that the fuel consumption can be reduced through an increase of the transfer duration.

In addition to the transfer strategies already identified, new kind of transfers have been found that exploit the invariant manifold structure of the Earth–Moon system perturbed by the Sun. Those families allow faster but more expensive transfers in terms of fuel. Finally, transfers exploiting the practical stability regions of the Earth–Moon PRC3BP have been identified.

The thrust profile associated with the trajectories that have been found exhibit several thrust arcs instead of a unique thrust arc at the end of the transfer as suggested by Mingotti et al. (2012).

The following step of the study will be to compute minimum-fuel Earth–Moon transfers in the three-dimensional BR4BP by taking into account the inclination of Moon’s orbit.

Then, it will be necessary to study how to transpose the trajectories obtained in a full ephemeris problem.