Introduction

For patients with focal epilepsy resistant to medical therapy, epilepsy surgery can lead to a life free of seizures. In planning for resection, one must correctly identify the brain region(s) where seizures arise (Rosenow and Lüders 2001). To this end, a presurgical evaluation routine is applied, initially consisting of noninvasive studies (structural MRI, scalp EEG, and functional neuroimaging studies). In complex surgical cases, these noninvasive studies inform where electrodes are placed on the cortex or inside the brain parenchyma to record intracranial EEG (iEEG). Despite the use of visual iEEG analysis, the current gold standard for mapping the seizure onset, only 33–68 % of the patients undergoing resective surgery become seizure-free (Bulacio et al. 2012; Carrette et al. 2010). For the rest, approximately half of the poor seizure outcomes are thought to be due to incorrect preoperative seizure-onset localization (Bulacio et al. 2012).

A growing body of research has applied quantitative methods studying connectivity among brain regions in order to complement the standard iEEG analysis of epileptic activity (Andrzejak et al. 2015; van Mierlo et al. 2014). These efforts have contributed to a better understanding of epilepsy as a network-based disorder (Wilke et al. 2011; Yaffe et al. 2015), and have driven new research fields such as virtual epilepsy surgery (Sinha et al. 2014). Methods based on functional connectivity model the statistical dependencies among time-series in the time or frequency domain into spatially resolved connectivity matrices. If analyzed over time to characterize seizures, these matrices reflect the dynamic interactions among the iEEG time-series during the course of the seizure, and are used to derive network graphs mapping the seizure onset and propagation. Among an extensive array of functional connectivity measures, multivariate, linear, frequency-domain measures based on the concept of Granger causality (Granger 1969) have shown promising results in localizing the regions of seizure onset (Korzeniewska et al. 2014; van Mierlo et al. 2011, 2013; Varotto et al. 2010, 2012; Wilke et al. 2008, 2010, 2011). Briefly, it is said that one time-series Granger-causes a second if its past values help predict the second better than the past values of the second alone. Accordingly, Granger-causality measures use autoregressive (AR) models to denoise and parametrize the iEEG ‘seizure signal’ with a set of AR coefficients encoding the linear contribution of its recent past (Schlögl 2000).

To address signal nonstationarities in the time domain typical of seizures, two basic AR modeling approaches have been used. In the segmentation approach, the iEEG data is divided in short windows of relative signal stationarity shifting in time, and the AR coefficients are estimated for each segment (Ding et al. 2000; Korzeniewska et al. 2014; Wilke et al. 2010, 2011). In an alternative approach, AR coefficients are allowed to vary in time and can be estimated adaptively (Wilke et al. 2008, 2009). Among several adaptive AR algorithms tested, linear random-walk models based on Kalman filter (Kalman 1960; Kalman and Bucy 1961) have performed well when analyzed with model error and adaptation speed criteria (Arnold et al. 1998; Schlögl 2000), and have been used successfully to map the regions of seizure activity (van Mierlo et al. 2011, 2013; Wilke et al. 2008).

The application of the Kalman-filter AR models to high-dimensional data requires a significant computational effort (Arnold et al. 1998; Blinowska 2011). As a result, these models have been applied thus far to a limited number of iEEG channels/time-series (up to 60, Toppi et al. 2012), often handpicked based on preferential involvement in the process under study (‘signal-enriched’ channels) or other data reduction criteria (Milde et al. 2010). This approach suffers from a hidden-source problem since multivariate connectivity methods assume that all relevant signals are analyzed (Schlögl and Supp 2006). Moreover, data reduction amplifies the inherent limitation of iEEG recordings in sampling cerebral activity when used for mapping certain neurophysiological events. For example, seizure-onset localization by iEEG requires at times an extensive implantation of hundreds of intracranial electrode contacts due to the narrow, near-field view of intracranial recordings.

The aim of this study is to evaluate a well-published multivariate adaptive AR model based on Kalman filter (Arnold et al. 1998), and a computationally efficient AR model derived from it, for their potential application to high-dimensional (up to 192) time-series. The two AR models differ in how they account for the measurement or observational noise that may contaminate the recordings. This paper is organized as follows: (1) The theoretical framework of the two models is exposed. (2) The AR coefficients resulting from the application of each model to simulated seizures are used to estimate the underlying connectivity structures in the presences of various degrees of correlated noise. Thereby, the relative performance of the two models in characterizing the ground-truth seizure networks is evaluated. (3) The onset of iEEG seizures recorded in three surgical patients is identified by mapping the time-variant connections based on the two AR models. The resulting seizure-onset estimates are compared based on colocalization with the resection volume, and the correlation of the dynamic connectivity maps based on the two models is determined. Next, the effect of AR modeling of lower- and higher-density seizure datasets is analyzed. (4) The computational cost of the two models is evaluated. (5) Finally, the results and significance of the Kalman filter approach herein are discussed.

Materials and Methods

Autoregressive Modeling

In its scalar form, an AR model of order p is given by.

$$y(n) = \mathop \sum \limits_{k = 1}^{p} a_{k} y(n - k) + e(n),$$
(1)

where y(n) is the nth observation of a signal or time-series, \(a_{1} \ldots a_{p}\) are AR coefficients specifying the linear contribution of the previous p signal observations, and e(n) is assumed a series of independent, normally distributed variables uncorrelated over time (zero autocorrelation at lag \(i, i > 0\)), with zero mean and variance \(\sigma^{2}\)(i.d. \(\sim N(0,\sigma^{2} )\). In effect, e(n) is a white-noise process reflecting the uncertainty in predicting the signal of interest recursively (prediction error).

For a multivariate time-series, the vector representation of a time-variant AR process is.

$${\mathbf{y}}(n) = \mathop \sum \limits_{k = 1}^{p} {\mathbf{A}}_{k} (n){\mathbf{y}}(n - k) + {\mathbf{e}}(n),$$
(2)

where \({\mathbf{y}}(n) = \left( {y_{1} (n), y_{2} (n) \ldots y_{s} (n)} \right)^{T}\) for s signals/channels, A k is the s × s coefficient matrix at delay k, and \({\mathbf{e}}\left( n \right) = \left( {e_{1} \left( n \right), e_{2} \left( n \right) \ldots e_{s} \left( n \right)} \right)^{T}\).

The application of the Kalman algorithm to estimate the AR coefficients makes use of the state-space model of the AR process, which consists of a system or state equation,

$${\mathbf{x}}(n + 1) = {\mathbf{F}}(n + 1,n){\mathbf{x}}(n) + {\mathbf{v}}_{1} (n),$$
(3)

and an observation or measurement equation,

$${\mathbf{y}}(n) = {\mathbf{H}}(n){\mathbf{x}}(n) + {\mathbf{v}}_{2} (n)$$
(4)

Equation (3) relates the state vector x(n) of AR coefficients,

$${\mathbf{x}}(n) = \left( {a_{111} (n), \ldots ,a_{1s1} (n),a_{112} (n), \ldots ,a_{1s2} (n), \ldots ,a_{1sp} (n),a_{211} (n), \ldots ,a_{ssp} (n)} \right)^{T} ,$$
(5)

to the state at time n + 1 by defining the state transition matrix, F(n + 1, n), and the system white-noise process v 1(n) = N(0, Q 1(n)). In Eq. (4), H(n) is called the measurement matrix, and relates the current system state to the current observation of the system. H(n) contains the past system observations Y(n) = (y T(n − 1), y T(n − 2)…y T(n − p)):

$${\mathbf{H}}\left( n \right) = {\mathbf{I}}_{s} \otimes {\mathbf{Y}}\left( n \right) = \left( {\begin{array}{*{20}c} {{\mathbf{Y}}\left( n \right)} & {} & 0 \\ {} & \ddots & {} \\ 0 & {} & {{\mathbf{Y}}\left( n \right)} \\ \end{array} } \right) ,$$
(6)

where \(\otimes\) denotes the Kronecker product of matrices. v 2(n) represents the measurement noise, v 2(n) = N(0, Q 2(n)).

The state vector x(n) can be estimated using the Kalman recursion. Modeling state transitions as a white-noise process (random walk) with a diagonal system noise covariance matrix Q 1(n) leads to a simplified representation of the Kalman filter equations:

$$\begin{aligned} {\mathbf{e}}(n) = {\mathbf{y}}(n) - {\mathbf{H}}(n){\hat{\mathbf{x}}}(n|n - 1) \hfill \\ {\mathbf{R}}(n) = {\mathbf{H}}(n){\mathbf{K}}(n,n - 1){\mathbf{H}}^{T} (n) + {\mathbf{Q}}_{2} (n) \hfill \\ {\mathbf{G}}(n) = {\mathbf{K}}(n,n - 1){\mathbf{H}}^{\text{T}} (n){\mathbf{R}}^{ - 1} (n) \hfill \\ {\hat{\mathbf{x}}}(n + 1|n) = {\hat{\mathbf{x}}}(n|n - 1) + {\mathbf{G}}(n){\mathbf{e}}(n) \hfill \\ {\mathbf{K}}(n,n) = {\mathbf{K}}(n,n - 1) - {\mathbf{G}}(n){\mathbf{H}}(n){\mathbf{K}}(n,n - 1) \hfill \\ {\mathbf{K}}(n + 1,n) = {\mathbf{K}}(n,n) + {\mathbf{Q}}_{1} (n) \hfill \\ \end{aligned}$$
(7)

Here, \({\hat{\text{x}}}\) denotes the estimate of the true system state x, R(n) = E[e(n)e T(n)] is the one-step prediction error covariance matrix, K(n, n) is the a posteriori (filtered) state error covariance matrix, and G(n) is the Kalman gain matrix, which in effect weighs the information in the measurements against the a priori knowledge of the system state.

When applying the Kalman algorithm to real data, the structure and update processes of the Q 1 and Q 2 covariance matrices are not known. Previous work has evaluated various Q 1 and Q 2 estimates under different noise statistics assumptions (Kasess 2002; Schlögl 2000). Here, we define the AR model m1 by the following two noise covariance equations:

$${\mathbf{Q}}_{1} (n) = {\mathbf{I}}_{L} UC ,$$
(8)

where L = s 2 × p, and.

$${\mathbf{Q}}_{2} (n) = (1 - UC){\mathbf{Q}}_{2} (n - 1) + UC{\mathbf{e}}(n){\mathbf{e}}^{T} (n)$$
(9)

UC is the update coefficient (0 < UC < 1) encoding the speed of adaptation of the AR model. The m1 model (Arnold et al. 1998) was shown to generate reliable estimates for various time-series data types and suggested to perform better than several adaptive and segmentation-based AR models. m1 performance was robust when compared with several Kalman-filter implementations using alternative Q 1 and Q 2 formulations (Kasess 2002). In addition, several successful applications of m1 in modeling seizure propagation have been reported (van Mierlo et al. 2011, 2013; Wilke et al. 2008).

In the multivariate case, a more stringent assumption is that the measurement noise is instantaneously uncorrelated across time-series (Kasess 2002). That is, for i, j time-series, the zero-lag measurement-noise cross-correlation corr i,j (n, 0) = E(v 2i (n)v 2j (n)) and its normalization with the zero-lag auto-correlation values for i, j (Z i,j (n, 0)) are negligible:

$$Z_{i,j} (n,0) = corr_{i,j} (n,0)/\sqrt { corr_{i,i} (n,0) corr_{j,j} (n,0)} \cong 0$$
(10)

In this case, off-diagonal elements of Q 2(n) can be ignored, and the measurement noise update equation becomes.

$${\mathbf{Q}}_{2} (n) = (1 - UC){\mathbf{Q}}_{2} (n - 1) + \left( {{\text{diag(}}{\mathbf{e}} ( {\text{n)}}{\mathbf{e}}^{T} (n))} \right)$$
(11)

Here, Eqs. (8), (11) define the AR model m2. Since Q 2(n) is diagonal,

$${\mathbf{Q}}_{2} (n) = \left( {\begin{array}{*{20}c} {q_{21} (n)} & {} & 0 \\ {} & \ddots & {} \\ 0 & {} & {q_{2s} (n)} \\ \end{array} } \right) ,$$
(12)

and the initial values of the state error covariance matrix K are assumed to be diagonal or block diagonal,

$${\mathbf{K}}(1,0) = \left( {\begin{array}{*{20}c} {{\mathbf{K}}_{1} (1)} & {} & 0 \\ {} & \ddots & {} \\ 0 & {} & {{\mathbf{K}}_{s} (1)} \\ \end{array} } \right) ,$$
(13)

Kalman equations can be separated into i = 1…s distinct Kalman filters:

$$\begin{aligned} e_{i} (n) = y_{i} (n) - {\mathbf{Y}}(n){\hat{\mathbf{x}}}_{i} (n|n - 1) \hfill \\ r_{i} (n) = {\mathbf{Y}}\left( n \right){\mathbf{K}}_{i} (n,n - 1){\mathbf{Y}}^{T} (n) + q_{2i} (n) \hfill \\ {\mathbf{g}}_{i} (n) = {\mathbf{K}}_{i} (n,n - 1){\mathbf{Y}}^{T} (n)r_{i}^{ - 1} (n) \hfill \\ {\hat{\mathbf{x}}}_{i} (n + 1|n) = {\hat{\mathbf{x}}}_{i} (n|n - 1) + {\mathbf{g}}_{i} (n)e_{i} (n) \hfill \\ {\mathbf{K}}_{i} (n,n) = {\mathbf{K}}_{i} (n,n - 1) - {\mathbf{g}}_{i} (n){\mathbf{Y}}(n){\mathbf{K}}_{i} (n,n - 1) \hfill \\ {\mathbf{K}}_{i} (n + 1,n) = {\mathbf{K}}_{i} (n,n) + {\mathbf{Q}}_{1i} (n) \hfill \\ \end{aligned}$$
(14)

As such, model m2 offers significant computational advantages, in part due to matrix size operations reduced by the order of s. At the same time, it is expected that m1 models highly correlated time-series more accurately.

Time-Variant Functional Connectivity

In order to evaluate the causal information flow between time-series, the signal represented by the AR coefficients can be used to derive Granger-causality measures of connectivity. To estimate functional connections in the frequency-domain, the Fourier transform of AR coefficients is first applied, as follows:

$${\mathbf{e}}_{f} (f) = {\mathbf{A}}_{f} (f){\mathbf{y}}_{f} (f) ,$$
(15)

where

$${\mathbf{A}}_{f} (f,n) = - \mathop \sum \limits_{k = 0}^{p} {\mathbf{A}}_{k} (n) e^{ - i2\pi fk}$$
(16)

e f , y f and A f are spectral transforms of the residuals, measured signal and AR coefficient matrices, respectively, and A 0(n) is the s × s identity matrix.

Within the class of frequency-based connectivity measures, the partial directed coherence (PDC, Baccala and Sameshima 2001) has been extensively used to model causal information flow in multivariate time-series. Both time-invariant and adaptive PDC representations have been applied to EEG-recorded seizures in order to characterize the seizures-onset regions and map the epileptic networks (Moeller et al. 2013; Omidvarnia et al. 2011; Varotto et al. 2010, 2012). PDC estimates the direct connections between time-series and their generators from indirect, or cascade, flows, within a functional network (Astolfi et al. 2008; Baccala and Sameshima 2001; Blinowska 2011). These connections are also directed, expressing the information flow between channels in source-sink terms. The adaptive PDC formulation used here estimates the spectral information from channel j to channel \(i,\) as follows:

$$iAWPDC_{j \to i} (n) = \frac{1}{{f_{2} - f_{1} }} \mathop \sum \limits_{{f = f_{1} }}^{{f_{2} }} \left( {\frac{{\left| {A_{ij} (f,n)} \right|^{2} }}{{\mathop \sum \nolimits_{k = 1 }^{s} \left| {A_{ik} (f,n)} \right|^{2} }} S_{j} (f,n)^{2} } \right) ,$$
(17)

where S j denotes the power-spectral density of channel j (Plomp et al. 2014). iAWPDC represents the spectrally-weighted squared PDC, which emphasizes the information flow at spectral peaks within a frequency band of interest (f 1:f 2). iAWPDC has been applied recently to EEG data from surgical epilepsy patients and generated robust connectivity estimates when compared with other PDC formulations (Plomp et al. 2014, 2015). Here, iAWPDC is used to evaluate the ability of m1 and m2 to model simulated iEEG seizures in the presence of noise with various cross-correlation structures.

Simulations

30-sec, 10-channel seizure epochs were generated at a sampling frequency of 250 Hz. Each epoch consisted of baseline or background activity modeled as 1/f multivariate random noise, and a seizure signal modeled as a sinusoid with a frequency evolving from 12 Hz at the seizure onset to 8 Hz at the seizure end (van Mierlo et al. 2011). The seizure began after a 10-sec preseizure baseline, and propagated successively from one channel to a maximum of three other channels chosen randomly for a total of 6 ‘ictal’ channels, after a delay between channels varying from 4 to 16 ms and a sample or phase delay of 4–12 ms. The sinusoid signal was added to the background noise at a signal-to-noise ratio (SNR) of −5, 0, or 5 dB. SNR was defined as.

$$SNR = 10\log_{10} P_{signal} /P_{noise}$$
(18)

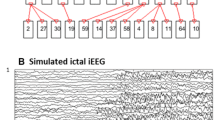
An example of a simulated seizure and its corresponding network graph is shown in Fig. 1.

Fig. 1
figure 1

Simulated seizure. a iEEG seizure epoch consisting of a 10-sec baseline prior to the seizure onset (vertical red line) in channel 1 (red) and spread to ictal channels 2–6 (blue), b connectivity graph depicting the direct connections between ictal channels during the seizure (Color figure online)

Full size image

Several measurement-noise correlation structures were used to generate random, fully correlated, and focally correlated noise types. To this end, the noise covariance matrix entries for the (i, j) channel pairs were controlled using the normalized cross-correlation index Z i,j . Random noise allowed only momentary instantaneous (zero-lag) correlations among times-series, thereby it was decorrelated over time (expected \(\mathop \sum \limits_{{n_{1} }}^{{n_{t} }} Z_{ij} (n,0) = 0\) for all i, j pairs and t observations). Fully correlated noise, i.e. identical noise time-series, was obtained by setting Z i,j (n, 0) to 1 for all (i, j) at each time point. Focally correlated noise was generated by setting Z i,j (n, 0) to 1 for three and five channel pairs (i, j) at all t time points, corresponding to instances when up to half of all channels/time-series are fully cross-correlated over time. These limit noise structures allow a ‘stress test’ of the ability of the m1 and m2 models to estimate the seizure signal connections encoded by the AR coefficients and iAWPDC, and by extension, the direct connections characterizing the seizure network.

Combining various SNR values and noise types resulted in 12 seizure epoch groups, each consisting of 50 individual seizure epochs. Within a group, each epoch was characterized by a unique noise time-series created with a random number generator. In addition, seizure epochs grouped based on focally correlated noise contained distinct channel-pair combinations with identical noise time-series chosen randomly from the range of possible spatial configurations of such combinations within the seizure connectivity matrix.

AR Model Evaluation Based on Simulations

The functional connectivity profiles of the seizures in each of the 12 seizure groups were estimated with the m1 and m2 AR models in combination with iAWPDC. Each iEEG time-series was z-scored by subtracting its mean and dividing by standard deviation. m1 and m2 were applied using a model order p of 5, and an update coefficient UC of 10−4 selected by minimizing a model error index (REV, Schlögl 2000). iAWPDC values were calculated for a frequency window ranging from 2 to 50 Hz with a frequency resolution of 0.3 Hz. The analysis resulted in 24 connectivity data groups containing m1- and m2-derived connectivity matrices.

Next, these matrices were thresholded in order to separate significant connections from noise and recover the functional networks of interest. Selecting the optimal threshold is problematic when analyzing real data of unknown structure (Wang et al. 2014). With simulated data, the designed signal connections (Fig. 1b) constitute the ground truth against which various connectivity estimates can be evaluated and compared. Here, for each seizure, the network imposed by the propagated seizure signal served as the ground truth. In turn, this was used to calculate the number of true/false-positive and true/false-negative direct connections present in the m1- and m2-based connectivity matrices as a function of threshold. A receiver operating characteristic (ROC) curve was built for each connectivity matrix by varying the applied threshold from 0 to 1 in 0.01 steps, and the corresponding area under the curve (AUC) was calculated. The larger the AUC, the better an AR model was considered in identifying the underlying connectivity structure of the simulated seizure. Here, AUC values were adjusted so that AUC = 1 in case a threshold existed for which a model fully identified the ground-truth network of a simulated seizure (Wang et al. 2014). To assess the relative performance of the m1 and m2 AR models, the mean AUC values were first compared among connectivity data groups with repeated-measures analysis of variance (rANOVA). Between-group comparisons were then performed by applying the Tukey–Kramer correction for multiple testing at a significance level of 0.05.

Real Data

Individual iEEG seizures were analyzed from three patients who had undergone intracranial monitoring followed by curative epilepsy surgery (tailored resections) at the University of Texas Health Science Center at San Antonio (Table 1).

Table 1 Clinical patient characteristics and seizure connectivity analysis parameters
Full size table

iEEG was recorded with subdural grids and strips (±  depth electrodes) at a 500-Hz sampling frequency. The implantation scheme (patient 1) is depicted for illustration in Fig. 2.

Fig. 2
figure 2

Intracranial electrode configuration. a grid and strip electrodes overlying the lateral right hemisphere cortex, b IFG contacts in relation to the reconstructed resection volume; G ground, IF inferior frontal strip, IFG inferior frontal grid, MF middle frontal strip, O occipital strip, P parietal strip, SF superior frontal strip, SFG superior frontal grid

Full size image

For analysis, seizure epochs consisted of 10-sec preseizure and 30-sec seizure segments identified by visual inspection of a clinical electroencephalographer. For each seizure, two iEEG datasets were generated to examine whether using a large number of unselected channels in multivariate connectivity analyses of the seizure networks is feasible. First, a dataset comprised the 50 channels with the most prominent involvement in the electrographic seizure discharge based on visual analysis of the tracings. This reduced dataset was presumed to contain the seizure signal at a relatively high SNR. Second, a dataset consisting of all recorded time-series was selected. Next, the m1 and m2 AR models were applied to the z-scored 50-channel dataset. The full channel set was analyzed with the m2 model exclusively, because the memory cost associated with m1 application would be prohibitive (see Computational cost section below). The AR parameters (\(p, UC\)) used to calculate iAWPDC estimates were selected for each dataset to minimize the model error (Schlögl 2000). iAWPDC values calculated for the reduced and full seizure datasets were then thresholded at the 95 % percentile of a range of iAWPDC values modeling the corresponding channel subsets of carefully chosen baseline iEEG segments of 55-70-sec duration (van Mierlo et al. 2011, 2013). This study was approved by the local institutional ethics research board.

AR Model Evaluation Based on Real Data

While there is no ground-truth network graph for real datasets, in the case of seizures, the ability of a functional connectivity method to identify the channels driving the seizure, i.e. map the seizure onset, can inform of the method’s ability to estimate correctly the causal information flow among time-series. As such, localizing the onset of a seizure to the resection volume in a patient free of seizures after surgery is supportive of a method’s mapping accuracy.

In this study, the number of outgoing direct connections weighted based on the matrix of thresholded iAWPDC values from a channel or node to all other nodes was calculated at each time point, in order to estimate the prominence of that node within the seizure network. This number represents the outdegree, a time-dependent graph theoretical measure expressed as.

$$\emptyset_{j} (n) = \mathop \sum \limits_{k = 1}^{s} C_{kj} (n) iAPDC_{kj} (n) ,$$
(19)

where \(C_{kj} (n) = 1\) if iAPDC kj (n) is at or above the threshold applied, and C kj (n) = 0 otherwise (van Mierlo et al. 2013). Next, the resection volume was reconstructed as in Lie et al. (2015), and the electrode channels colocalizing with the resection were determined.

The ability to identify the seizure onsets by connectivity analysis was probed by superimposing maps of the outdegree values calculated over time and the contacts within the resection volume. In addition, the dynamic correlation between the outdegree-over-time maps resulting from the application of the m1 and m2 models (50-channel dataset), and between the restricted and full datasets processed with m2, were estimated with the Pearson correlation coefficient. Briefly, a sliding time-window approach was used, with step/window lengths of 0.002 s/0.002 s (one time sample) and 0.25 s/0.5 s (Leonardi and Van De Ville 2015). For each time window, mean channel-specific outdegree values were ranked, transformed to normal scores and compared between datasets with the Pearson correlation coefficient (Bishara and Hittner 2012).

Computational Cost

The memory and time costs of modeling times-series with m1 and m2 using graphics processing unit (GPU)-optimized code in MATLAB were estimated on 1-sec iEEG epochs of progressively larger datasets (16–192 channels) on a workstation PC with an 8-core Intel Xeon Processor E5-2667 v3 and a NVIDIA Quadro K6000 GPU with 12 GB memory.

Results

Simulated Data

The relative performance of the m1 and m2 AR models when estimating direct connectedness in simulated networks with known structures was assessed using a workflow exemplified in Fig. 3.

Fig. 3
figure 3

Functional connectivity analysis steps using the m1 and m2 AR models. a The designed signal connectivity matrix of a seizure sinusoid encoding direct connections (red) formed during seizure propagation, b Examples of measurement-noise structures, including random noise with a diagonal noise covariance matrix (left) with small-value off-diagonal elements (white) reflecting negligible cross-correlation between channels, focally correlated noise (blue) for five channel pairs (middle), and fully correlated noise (right), c–e Time-averaged iAWPDC connectivity matrices derived with m1 or m2 for individual seizures designed using signal and noise structures depicted in a and b, respectively (left, middle). Here, added noise was random noise (c) focally correlated noise in five channel pairs (d) and fully correlated noise (e) at SNR = 0 dB. The corresponding ROC plots are shown on the right (c, d, e) (Color figure online)

Full size image

In addition to the SNR used, seizure simulations differed based on their noise structure. The mean (standard deviation, stdev) values of the correlation index \(Z\) were 0.002 (0.01) for the pooled random noise structures, 0.06 (0.01) and 0.22 (0.02) for the focally correlated noise (three and five channel pairs, respectively), and 1(0) for the fully correlated noise. rANOVA of the AUC values resulting from ROC analyses used the AR model type as within-subject factor (Fig. 4). Statistically significant differences between the m1 and m2 model performance were obtained for the noise type used, \(F(3,588) = 184.62, p_{value} < 0.001\), and for a combined SNR-noise variable, \(F(11,588) = 54.55, p_{value} < 0.001\). In the latter case, between-group comparisons disclosed small, yet statistically significant differences between m1- and m2-derived mean AUC values for seizure groups containing fully correlated noise (Fig. 4).

Fig. 4
figure 4

Comparison of mean AUC values among seizure groups analyzed with m1 and m2. Corr_3c, Corr_5c and Corr_full label three-channel pair, five-channel pair, and fully correlated noise structures, respectively. Error bars represent AUC stdev for the respective groups. * p value  < 0.001 (Tukey–Kramer post hoc test)

Full size image

Real Data

The seizure onsets were mapped by estimating the dynamic changes in the strength of direct functional connections encoded by the outdegree, for channel datasets processed with m1 (50-channel set only) and m2 in conjunction with iAWPDC. The channels driving the functional connectivity outflow during the course of the seizures colocalized with the reconstructed resection volume for both m1 and m2 model analyses and the reduced and full datasets for all seizures analyzed. Patient 1, 2 and 3 data are displayed in Fig. 5, Online Resource 1 and 3, respectively.

Fig. 5
figure 5

Colocalization of the seizure-onset estimates based on outdegree and the resection volume (patient 1). a preictal baseline and EEG seizure onset (arrow) in the 50-channel dataset (upper), and the corresponding outdegree-over-time maps derived from connectivity analyses using m1/iAWPDC (middle) and m2/iAWPDC (lower). Boxed channels fall within the resection volume, b EEG recording of the same seizure in the full (n = 113) channel dataset (upper), and the corresponding outdegree-over-time map using m2/iAWPDC (lower)

Full size image

Next, the correlation over time between outdegree estimates based on the two AR models (50-channel data) and for the restricted and full channel datasets (m2) was calculated. Outdegree value ranks were highly, if variably, correlated over time, whether results from the two AR model analyses (50 channels) or m2-processed reduced and full channel data were compared (Fig. 6, and Online Resource 2 and 4).

Fig. 6
figure 6

Dynamic correlation of the outdegree maps estimated based on m1 and m2 (patient 1). Time-matched Pearson correlation of the outdegree values resulting from m1 or m2 application. c channel, rho mean Pearson correlation coefficient

Full size image

Computational Cost

The Kalman filter-based analysis is computationally expensive due to a rather large number of iterations, matrix operations, and matrix sizes. The current GPU code implementation of the m1 AR model is inspired by functions from the BioSig library (Vidaurre et al. 2011) and aims to reduce the run time of such analysis. m2 code replaces large 2D matrices with 3D arrays that shift the inputs of the s Kalman filters Eq. (14) to the 3rd dimension, thereby reducing the size of filter-specific matrix operations (multiplication and inversion).

The memory cost of GPU-based operations is often limiting given the relatively small GPU memory sizes (≤  24 GB) of currently available units. In the case of m1, the memory cost per iteration is O(s 4 × p 2), representing the size of the state error covariance matrix K (linear fit f(x) = 1.01s 4 p 2 + 17.97, root-mean-square error 3.37), whereas for m2 it is O(s 3 × p 2) (f(x) = 1.01s 3 p 2 + 14.93, root-mean-square error 0.61). Table 2 lists the empirical memory and time costs attained when processing 1-sec iEEG segments with the m1 and m2 models using two model order values spanning a range commonly used in the literature:

Table 2 Computational cost of AR analysis based on 1-sec iEEG epochs.—out of memory
Full size table

At this time, up to 100-channel time-series can be modeled with m1 (at low model order values). m2 accommodates high-density recordings of up to 192 channels, and is comparatively more time efficient (> 100 fold faster at high channel numbers). The connectivity analysis of a 30-sec seizure simulated in 192 electrodes at 250 Hz and processed with m2 (p = 5) over a frequency band of 2:50 Hz took 30 min to complete and was able to reconstitute the true network structure represented by designed signal matrix (Online Resource 5).

Discussion

This study demonstrates that adaptive, multivariate functional-connectivity analyses can be conducted on high-dimensional time-series using Kalman filter-based AR models. These models are advantageous when applied to iEEG data, in that they allow the estimation of observational or measurement noise in the recordings and can accommodate signal nonstationarities (Sommerlade et al. 2012) without requiring data partition into epochs of quasi-stationarity. Unlike segmentation-based approaches (Wilke et al. 2010, 2011) however, Kalman-filter based models have been applied until now to a small number of iEEG channels/time-series (up to 60, Toppi et al. 2012), due to their significant computational effort (Arnold et al. 1998; Blinowska 2011). Here, GPU-accelerated implementations of m1, a well-studied random-walk vector AR model introduced by Arnold et al. (1998), and m2, a computationally efficient sequential derivation of m1, were developed and used to process up to 100 and 192 time-series, respectively. Since this range applies to electrode numbers used in many complex iEEG evaluations in epilepsy surgery candidates, results support the possibility of routine large-scale, fully data-driven and quasi-automated multivariate functional-connectivity analyses of seizure dynamics. The current approach ameliorates the hidden-source problem of iEEG recordings, obviating the hitherto need for time-series preselection before high-dimensional adaptive connectivity calculations are conducted (Milde et al. 2010). A more granular iEEG connectivity estimation may also facilitate cross-modality comparisons, especially when large-scale global connectivity studies using dense-array (scalp) EEG, magnetoencephalography, resting-state functional MRI, or diffusion-weighted imaging are planned. In addition, high-dimensional Kalman-based modeling has general applicability to data acquired with imaging techniques other than iEEG (Molenaar et al. 2016). These are all avenues to advance the view on how epileptic networks operate (Stufflebeam et al. 2011; van Dellen et al. 2009).

Whether including all available iEEG data for seizure-onset localization is beneficial in all cases needs further exploration. In practice, the number and location of electrode implants is determined based on more or less accurate localization hypotheses drawn noninvasively, and eloquent (i.e. functionally relevant) cortex mapping needs. In addition, long-range functional changes at the scale of the fully sampled space have been noted during the seizures in both iEEG (Jiménez-Jiménez et al. 2015) and functional MRI (Englot et al. 2009) recordings. These changes may not reflect the seizure discharge proper or affect the seizure outcome after resective surgery (Jiménez-Jiménez et al. 2015) but may contribute significant connections in an analysis including a larger number of sampling contacts.

While such analysis may, in some cases, add ‘noise’ to localization estimates, it is independent of an often biased and laborious visual iEEG interpretation, in contrast to data preselection approaches. High-dimensional connectivity estimations may also change the relative connection weights for ‘signal-enriched’ time-series that would usually be preselected. As Fig. 6, Online Resource 2 and 4 show, the time-variant ranking of the outdegree values for several channels common to the reduced (50) and full channel sets changed as a result of the number of channels analyzed, leading to a variable, if overall high, degree of correlation between the analyses of the two datasets. Future studies including patients rendered seizure-free by surgery and those with continued seizures despite undergoing resection will expand our understanding of the relative localization accuracy of high-density connectivity analysis.

Here, a computationally efficient method based on thresholds determined on a preseizure baseline was used (van Mierlo et al. 2011, 2013). Of the more computationally demanding surrogate statistics alternatives (Florin et al. 2011; He et al. 2011), thresholding based on random permutations uses a large number of AR model repetitions or runs to generate the distribution of a connectivity measure (e.g. iAWPDC) under the null hypothesis. Since an individual run is processed efficiently on the GPU of a workstation PC with the present AR model coding strategy, the significant workload imposed by random permutations can be handled by the parallel distribution of runs to individual GPUs on a GPU supercomputer with fairly straightforward code adaptations. These thresholding techniques, and analytical approaches when available, merit further evaluation in simulation and real seizure studies.

Previously unreported, the analysis of simulated data suggests that the m1 AR model performs best in the presence of decorrelated noise. The m1 and m2 model accuracy decreases as the degree of noise correlation increases, with further modest reductions in m2 performance when the simulated noise is highly and globally cross-correlated (Fig. 4). Checking and correcting for correlated noise in real EEG recordings is problematic, because the artefactual and biological noise sources are difficult to separate, the boundaries between the seizure proper and seizure-related ictal electrographic changes are uncertain, and the presence of epileptiform patterns during baseline and volume conduction is confounding. One gross approximation of the ictal noise cross-correlation is to calculate the mean Z index on a baseline recording as done herein, assuming that the seizure epoch consists of a ‘seizure signal’ linearly added to noise with a correlation structure similar to that of the baseline used. A low Z value may increase the confidence in the estimated connectivity maps. Another approach is to compare the connectivity estimates for serial seizures in the same patient, among which the measurement noise correlation may vary. Since repeated seizures in individual patients often produce rather similar iEEG signals, they may be seen as realizations of the same stochastic process (Jouny et al. 2007; Korzeniewska et al. 2014). Finding conserved spatial motifs for the direct connections characterizing each of these seizures may improve seizure-onset mapping accuracy of the methods analyzed in this study. In addition, noise reduction techniques can be used to account for highly correlated noise. These include processing the raw recordings with methods such as independent-component analysis prior to the AR modeling step (Mullen et al. 2011), and excluding the frequency bands (main and harmonics) corresponding to the peak power of the line noise when conducting broadband frequency-domain connectivity estimations (Korzeniewska et al. 2014).

Future Directions

Several lines of research may be pursued to evaluate high-dimensional connectivity methods based on Kalman filtering in the context of epilepsy surgery. First, future simulation studies are needed to compare the performance of the linear AR models herein (m1, m2) with extended Kalman-filter methods (Omidvarnia et al. 2011; Sommerlade et al. 2012) in conjunction with a broader range of direct (Baccalá et al. 2013; Korzeniewska et al. 2003) and indirect (van Mierlo et al. 2011, 2013) adaptive multivariate connectivity measures. Such tests can be conducted within a systematic framework using generative linear and nonlinear models, and various system and measurement noise types and frequency bands of interest (Wang et al. 2014). Second, comparative real-data studies of the degree of overlap between the estimated seizure networks, interictal epileptic and resting-state networks, and those revealed by controlled interventions such as cortico-cortical evoked potentials (Enatsu et al. 2012) may help better understand the process of ictal propagation in epilepsy. Third, any localization estimates based on dynamic functional connectivity need validation against seizure-altering treatments targeting network nodes focally. Colocalization of the seizure connectivity maps (here; van Mierlo et al. 2013) or virtual resections derived from connectivity data (Sinha et al. 2014) with the actual resection volume reconstructions or electrode contacts used for electrical stimulation therapy (Morrell et al. 2011), can help validate a particular connectivity approach when considering the postoperative (or post-stimulation) seizure control in individual patients (Brodbeck et al. 2011).

Steps such as these will help assess the potential for integration of high-density connectivity analysis methods based on Kalman filtering into the formal presurgical evaluation of epilepsy surgery candidates.