Drag Coefficient and Turbulence Mixing Length of Local Climate Zone-Based Urban Morphologies Derived Using Obstacle-Resolving Modelling

Abstract

Large-eddy microscale simulations of eleven local climate zone-based (LCZ) urban morphologies with various building plane and frontal area density are used to investigate the flow characteristics and provide vertical profiles of velocity, sectional drag coefficient, and turbulence mixing length. The urban morphologies are procedurally generated to mimick real urban districts. The simulations are performed with the MesoNH-IBM meteorological research model, which allows to represent explicitly the obstacles and to account for the impact of the large scale turbulence structures on the urban canopy layer (UCL). The results show that, in heterogeneous building height UCLs, the streamwise velocity profile is not exponential, the mixing length is not constant and the equivalent sectional drag coefficient formula based on bulk morphology parameters is not valid. Comparatively to an non-urban mixing length increasing linearly with the distance from the ground, the UCL mixing length is higher for $z/h_\textrm{mean} \in [0 - \approx 0.75]$, because of the turbulent structures generated by the buildings and lower above, because of the shear generated at the building roofs. These differences extend up to several times the mean building height. The vertical profile of the dispersive momentum flux (DMF) in the UCL is in agreement with the literature; positive DMF is found upstream of the buildings whereas negative DMF is localized downstream. Although the DMF is lower than the turbulent momentum flux for most of the LCZs, it is not negligible for midrise and highrise LCZs. The large-scale atmospheric boundary-layer turbulence has a negligible influence on most of the investigated horizontally-averaged quantities. This suggests that considering a neutral stratification and a wind flow aligned with the buildings, most of the turbulence within the UCL is generated by the buildings themselves.

1 Introduction

Cities are heterogeneous areas which modify the dynamical and the thermodynamical structure of the atmospheric boundary-layer (ABL). At the microscale (1–10 m), solving the flow within the urban canopy layer (UCL) is an unsteady and three-dimensional problem requiring obstacle-resolving models. At larger scales, where numerical weather prediction (NWP) models operate, the microscale flow characteristics such as subgrid turbulence, building drag, vegetation drag, and surface energy exchanges have to be parametrized. Their parametrization is a key point for the accuracy of NWP wind speed and temperature predictions in urban areas. The urban canopy parametrizations can be classified into two categories: single-layer urban-canopy models (UCMs) and multi-layer UCMs.

For single-layer UCMs (Masson 2000; Kusaka et al. 2001), the first atmospheric model level is placed at the top of the UCL, i.e., all the UCL is below the surface of the atmospheric model. The UCM and the atmospheric model are exchanging bulk-averaged quantities. With this approach, the urban surface fluxes’ direct influence on the ABL is restricted to the lowest level of the atmospheric model. Single-layer UCMs can be considered as surface-layer scheme for NWP models.

Multi-layer UCMs (Martilli et al. 2002; Schoetter et al. 2020) discretize the UCL in several layers. Each of these layers interacts and exchanges horizontally-averaged quantities with the atmospheric model. Multi-layer UCMs act as boudary-layer scheme for NWP models and they are able to represent the vertical heterogeneity of the UCL. Contrary to single-layer UCMs, the buildings are immersed in the atmospheric model and their effects have to be taken into account in the atmospheric model at all levels which intersect the buildings.

The single-layer UCMs are limited to low- and midrise cities, like European ones, and to model resolutions down to 1 km (Trusilova et al. 2016). This corresponds to the resolution of operational limited-area NWP models. However, future NWP models are expected to operate down to 100 m horizontal resolution (Barlow et al. 2017), and for all types of urban morphologies existing worldwide, including Asian and North American highrise megacities. Multi-layer UCMs are therefore the most suitable tool to represent urban areas in future NWP models.

In multi-layer UCMs, the building’s effects on the flow can be parametrized by means of a drag force, which reduces the wind speed, and by changes in the turbulent mixing via the imposition of an urban-specific turbulence mixing length (Schoetter et al. 2020). However, avalaible parametrizations are most often too simple. Considering the mixing length for instance, a constant turbulence length scale is generally used along the entire height of the UCL (Santiago and Martilli 2010; Schoetter et al. 2020). This is called into question by Castro (2017) and Blunn et al. (2022), who, based on numerical reproduction of numerous laboratory-scale experimental datasets from the literature, show that the mixing length in the UCL is not constant.

The other bottleneck of multi-layer UCMs’ parametrizations is the urban morphologies upon which they are built. Most of them are homogeneous-height staggered or aligned cubes which form a very idealized urban canopy [see Castro (2017) or Blunn et al. (2022) for references]. The few datasets (like Xie et al. (2008)) that include a heterogeneity in the obstacle height show that sectional drag coefficient or mixing length vertical profiles are significantly different from those obtained for homogeneous urban canopies (Castro 2017; Blunn et al. 2022).

Improved parametrizations for multi-layer UCMs should therefore be derived for more realistic urban morphologies, which should cover the range of typical morphologies existing globally. A brute force approach would be to conduct obstacle-resolving simulations for real city samples (e.g., Millward-Hopkins et al. 2013; Kanda et al. 2013) to derive UCMs parameters. However, simulating at the microscale resolution all cities existing worldwide or even in a large country is computationally too expensive. An alternative is to derive the UCM parameters for urban morphologies based on the local climate-zones (LCZs) classification from Stewart and Oke (2012). The LCZs have been originally created to classify the worldwide urban forms in order to distinguish their impact on the local thermal climate, but they can be adapted to focus on the urban forms aerodynamical properties. Given the widespread use of LCZ, previous initiatives like the World Urban Database and Access Portal Tools (WUDAPT, Ching et al. (2018)) project have developed methods to create LCZ maps based on satellite data (e.g., Bechtel et al. 2015; Demuzere et al. 2022). The UCM parameters can therefore be determined using numerically expensive microscale simulations for urban districts mimicking the LCZs, and these results can be combined with an LCZ map to obtain the spatial distribution of UCM parameters like the building drag coefficient.

The purpose of the present paper is to provide new insights into the flow characteristics such as velocity, sectional drag coefficient, turbulence mixing length and turbulence kinetic energy (TKE) for LCZ-based urban morphologies using an obstacle-resolving version of the non-hydrostatic research atmospheric model Meso-NH (Lac et al. 2018). The paper is organized as follows: the model is presented in Sect. 2, the quantification of the buildings influence upon the ABL is detailed in Sect. 3, the LCZ-based urban morphologies are presented in Sect. 4, and the numerical configurations are given in Sect. 5. The results are described and analysed in Sect. 6. Finally, a summary and conclusion is proposed in Sect. 7.

2 Mesoscale Atmospheric Model Meso-NH for Obstacle-Resolving Simulations

The Meso-NH model (Lac et al. 2018) is a non-hydrostatic research atmospheric model which can simulate atmospheric flows from the mesoscale (tens of kilometres and day-long phenomena) to the microscale. The grid-nesting approach (Stein et al. 2000) is used to perform dynamical downscaling. The conservation laws for mass, momentum, energy, and the ideal gas law are the base of the Meso-NH governing equations. To filter the elastic effects generated by acoustic waves, Meso-NH uses the anelastic approximation of the pseudo-incompressible system of Durran (1989).

The C-grid of Mesinger and Arakawa (1976) spatially discretizes the numerical domain. The present work is restricted to cartesian grids and flat terrains. For the horizontal directions, a regular grid size with ${\Delta }_x={\Delta }_y={\Delta }$ is used.

The Reynolds-stress term in the momentum equation is estimated within a large eddy simulation (LES) framework. Similarly to most NWP models, Meso-NH uses an 1.5 higher-order turbulence scheme (TKE-L). Its description can be found in Cuxart et al. (2000). In the present version, it requires the calculation of the subgrid turbulence kinetic energy ($e_{sb}=1/2(\overline{u'^2}+\overline{v'^2}+\overline{w'^2})$, where $u'$, $v'$, and $w'$ are the x-, y-, and z-turbulence velocity components) through a prognostic equation and a diagnostic adaptative mixing length given in Honnert et al. (2021).

The wind advection is discretized using, either CEN4TH, a fourth-order centred scheme, or WENO5, a fifth-order weighted essentially non-oscillatory scheme. Explicit numerical diffusion is not appropriate with WENO5, whereas CEN4TH requires numerical diffusion, which is characterized by the e-folding time $t_c$ of 2${\Delta }_x$ waves. Explicit Runge–Kutta schemes are used for time integration (Lunet et al. 2017).

Performing obstacle-resolving simulations with meteorological models requires the use of the immersed boundary method (IBM). The IBM developement within the Meso-NH framework is described in Auguste et al. (2019). The UCL is separated into two distinct regions: a fluid region in which the classical fluid conservation laws are applied and a solid region having a volume similar to the embedded obstacles. The interface between the two regions is defined by a continuous LevelSet Function (LSF, Sussman et al. (1994)), $\phi$. The LSF absolute value, $\mid \phi (x,y,z) \mid$, gives the minimal distance between a grid point and the interface whereas its sign allows to distinguish between the solid ($\phi >0$) and the fluid ($\phi <0$) region.

The IBM implementation in Meso-NH has been validated by Auguste et al. (2019) against wind tunnel observations and for the Mock Urban Setting Test experiment (MUST, Biltoft (2001); Yee and Biltoft (2004)) idealized urban-like environment. Nagel et al. (2022) extended the validation for the MUST experiment to pollutant transport and realistic incoming turbulence.

In Auguste et al. (2019) and Nagel et al. (2022), the LSF was generated for geometric objects whose surfaces were analytically known. In the present work, a new LSF calculation method has been implemented in MesoNH-IBM. For each urban morphology, the buildings’ spatial arrangement is first done with an in-house procedural city generator, from which the output result is a three-dimensional geometrical file in wavefront (.obj) format. The geometrical file contains the triangulated interface between the buildings and the atmosphere. For a given facet $F_i$, its coordinates are written such that its normal ${{\textbf{n}_{\textbf{F}_{\textbf{i}}}}}$ points outside of the building.

An iterative procedure is undertaken to build the LSF from the geometrical file. For each point ($P_i$) of the domain, the distance $d_{P_i{F_i}}$ between $P_i$ and each triangular facet $F_i$ is calculated following the three-dimensional method given in Jones (1995). The vector ${\textbf{v}_{{\textbf{F}}_{\textbf{i}}}}$, defined between the center of the facet and $P_i$, is also calculated. The LSF, which is the minimal value of $d_{P_iF_i}$ at each point is then given by:

$$\begin{aligned} \phi (x,y,z) = \text {min}(d_{P_i{F_i}}(x,y,z))(-\text {sgn}({\textbf{v}_{{\textbf{F}}_{\textbf{i}}}}.{\textbf{n}_{\textbf{F}_{\textbf{i}}}})). \end{aligned}$$

(1)

The second term on the r.h.s. of Eq. 1 gives the sign of the LSF, i.e., negative if $P_i$ is outside of the building and positive if Pi is inside.

Fig. 1

LSF determination in the case of two sharp angle facets sharing an edge

As explained in Jones (1995), $P_i$ can be closest to the face of the facet, one of its side, or one of its vortices. For the last two cases, Eq. 1 can lead to inconsistencies in the LSF. It typically happens for buildings with sharp angles, as illustrated in the example shown in Fig. 1. The facets $F_1$ and $F_2$ are sharing an edge, the minimal distance $d_{P_iP_{F_i}}$ between $P_i$ and those two facets is identical. Because the point is outside of the building, the LSF at $P_i$ should be negative. However, following Eq. 1, the resulting LSF is negative if ${P_{F_i}}$ belongs to $F_1$ and positive if $P_{F_i} \in F_2$. This is why, when $P_i$ is closest to a side or a vertex of a facet, $d_{P_iP_{F_i}'}$, the distance between $P_i$ and its projection on the $F_i$ plan is calculated. At the end of the iterative procedure, $P_{F_i}$ is attributed to the facets for which $d_{P_iP_{F_i}'}$ is the highest. In the example shown in Fig. 1, $P_{F_i}$ belongs to $F_1$ and is negative, as expected.

3 Quantification of Buildings Influence Upon the Atmospheric Boundary-Layer

3.1 Urban Morphology Parameters

The simplest way to describe the various urban morphologies is through morphometrics non-dimensional ratios. In the present work, the building plane area and frontal area density ($\lambda _p$, $\lambda _f,$ Grimmond and Oke 1999) are considered as functions of height, which makes them suitable for the description of urban environments with non-uniform building height or shape; they are denoted with $\lambda _{pz}$ and $\lambda _{fz}$.

Fig. 2

Sketch illustrating the building plane area density $\lambda _{pz}(z)$ (a) and the building frontal area density $\lambda _{fz}(z)$ (b)

As illustrated in Fig. 2a, the building plane area density $\lambda _{pz}(z)$ reads:

$$\begin{aligned} \lambda _{pz}(z)=\sum dA_p(z)/A_t, \end{aligned}$$

(2)

where $A_p(z)=\sum dA_p(z)$ is the total plane area of the buildings at height z and $A_t$ is the total horizontal area. The commonly used plane area building density ($\lambda _p$) corresponds to $\lambda _{pz}(z=0)$.

The building frontal area density $\lambda _f(z)$ is defined for the thin horizontal slab between z and $z+dz$ (Fig. 2b):

$$\begin{aligned} \lambda _{fz}(z)=\sum dA_f(z)/A_t, \end{aligned}$$

(3)

where $A_f(z)=\sum dA_f(z)$ is the part of the total frontal area of the buildings ($A_f$) between z and $z+dz$. Using $\lambda _{fz}(z)$ allows to account for the building height heterogeneity. The building frontal area density is linked to the building frontal area index, $\lambda _f$ following:

$$\begin{aligned} \lambda _f=\int _{0}^{h_\textrm{max}} \lambda _{fz}(z) \ dz. \end{aligned}$$

(4)

3.2 Intrinsic and Comprehensive Double Averaging of Turbulent Quantities

Multi-layer UCMs are vertically discretized in thin horizontally-averaged slabs. As a consequence, multi-layer UCMs assume that the flow and the canopy geometry are homogeneous in the horizontal directions within each grid-cell of the model. Quantities extracted from building-resolved models should therefore be horizontally double averaged in order to be used in multi-layer UCMs. In urban canopies, the volume fraction occupied by the obstacles could be significant and the question of performing an intrinsic (over the fluid volume only) or comprehensive (over the total volume) double average arises.

Considering a prognostic variable $\varphi (t,x,y,z)$, defined within the fluid region only. The $\langle \cdot \rangle$, $\overline{\cdot }$, $\cdot ^{\prime }$ and $\widetilde{\cdot }$ operators can be applied to $\varphi$, resulting in its spatial average, time average, turbulent ($\varphi ^{\prime }=\varphi -\overline{\varphi }$) and dispersive fluctuations ($\widetilde{\varphi }=\overline{\varphi }-\langle \overline{\varphi } \rangle$), respectively. Here, we assume that the averaging region is an $x-y$ plane. The intrinsic and comprehensive (subscript “c”) horizontal spatial average of $\varphi$ can be written:

$$\begin{aligned} \langle \varphi \rangle (t,z)=\frac{1}{A_a(z)}\int _{x,y \in A_a (z)} \varphi (t,x,y,z) \ dx dy , \end{aligned}$$

(5)

and

$$\begin{aligned} \langle \varphi \rangle _c (t,z)=\frac{1}{A}\int _{x,y \in A_a(z)} \varphi (t,x,y,z) \ dx dy , \end{aligned}$$

(6)

where $A_a(z)$ is the fluid area of the thin horizontal slab at height z and $A=A_a(z)+A_p(z)$, the total area of the slab, i.e., including the solid volume. The total area A is constant all along the vertical. There is a simple relationship between the comprehensive and intrinsic average:

$$\begin{aligned} \langle \varphi \rangle _c (t,z) = \epsilon (z) \ \langle \varphi \rangle (t,z), \end{aligned}$$

(7)

where $\epsilon (z)=1-\lambda _p(z)$ is the fluid fraction.

The relation between averages of spatial derivatives and spatial derivatives of averages is more complex as the averaging does not commute with spatial differentiation. It is given by the spatial averaging theorem (Whitaker 1999), rewritten here for horizontal spatial averaging. For the intrinsic average it reads:

$$\begin{aligned} \left\langle \frac{\partial \varphi }{\partial x_i}\right\rangle =\frac{\partial \langle \varphi \rangle }{\partial x_i}+\frac{\langle \varphi \rangle \ \partial \epsilon }{\epsilon \partial x_i}+\frac{1}{A_a}\oint _{\partial \Omega } \varphi \ n_i \ dl , \end{aligned}$$

(8)

and for the comprehensive average:

$$\begin{aligned} \left\langle \frac{\partial \varphi }{\partial x_i}\right\rangle _c =\frac{\partial \langle \varphi \rangle _c }{\partial x_i} + \frac{1}{A}\oint _{\partial \Omega } \varphi \ n_i \ dl , \end{aligned}$$

(9)

where $x_i$ is the spatial direction ($x_1 = x, x_2 = y$, $x_3 = z$), $\partial \Omega$ is the line integral along which the building contour is defined (solid/fluid interface), and $n_i$ is the surface normal $x_i$-component. The surface normal is directed from fluid to solid.

The first term on the right-hand side (r.h.s.) of Eqs. 8 and 9 is the spatial derivative of the corresponding average of $\varphi$. The second term on the r.h.s. of Eq. 8 accounts for the changes in the averaging region. This term is not present in Eq. 9, because the comprehensive-averaged region remains unchanged with height in the UCL. The last term in both equations accounts for discontinuities in flow properties over the surface of the embedded obstacles.

Depending on the prognostic variable or the direction considered, Eqs. 8 and 9 can be simplified. The UCL can be assumed as horizontally homogeneous within the averaging region, i.e., $\epsilon$ depends only on z. As a consequence, the second term on the r.h.s. of Eq. 8 is zero for the horizontal derivative (i = 1,2). Still for horizontal derivatives, if $\varphi$ is constant at the fluid-solid interface, the last term on the r.h.s. of Eqs. 8 and 9 becomes zero. It is the case for the velocity if no-slip boundary conditions are applied. For the vertical derivative (i = 3), the third term on the r.h.s. of Eqs. 8 and 9 is zero for variables having $\varphi$ = 0 at the vertical facing interfaces. Again, this is the case for the velocity if no-slip boundary conditions are used.

When it comes to urban flows, performing intrinsic or comprehensive averaging is a recent and still open question (Castro 2017; Xie and Fuka 2018; Schmid et al. 2019; Sützl et al. 2021; Blunn et al. 2022). All the authors agree on the fact that the double-averaged momentum equations derived using intrinsic or comprehensive averaging are equally valid. However, if the double averaged quantities shall be used to derive a parametrization for mesoscale models, the global momentum has to be conserved. In other words, the parametrizations have to be coherent with the averaging technique chosen. For one-dimensional column NWP models, the building solid volume is generally not considered and using a parametrization obtained with comprehensive averaging is therefore recommended (Castro 2017; Xie and Fuka 2018; Schmid et al. 2019).

In the present work, the intrinsic averaged quantities are presented because their physical meaning is clearer since they are directly representative of the fluid (Sützl et al. 2021; Blunn et al. 2022).

3.3 Double-Averaged Momentum Equation

The double-averaged momentum equation is derived in Schmid et al. (2019). Starting from the instantaneous momentum equation, the time-averaging and the spatial-averaging operators are successively applied to obtain the double-averaged momentum equation for a statistically stationary and horizontally homogeneous flow. As in Schmid et al. (2019) or Blunn et al. (2022), further simplifications are made to obtain the intrinsic and comprehensive double-averaged momentum equation given in Eqs. 10 and 11: the atmosphere is considered as neutral, the viscous drag and the mean viscous force are neglected for the highly turbulent flow prevailing in the UCL.

$$\begin{aligned}{} & {} \langle \overline{F_m} \rangle -\frac{\partial \langle \overline{u_i^{\prime }w^{\prime }}\rangle }{\partial z}-\frac{\partial \langle {\widetilde{u_i}\widetilde{w}}\rangle }{\partial z}-\frac{(\langle \overline{u_i^{\prime }w^{\prime }}\rangle +\langle {\widetilde{u_i}\widetilde{w}}\rangle )}{\epsilon }\frac{\partial \epsilon }{\partial z}-\frac{1}{\rho } \left\langle \frac{\partial \overline{p}}{\partial x_i}\right\rangle = 0, \end{aligned}$$

(10)

$$\begin{aligned}{} & {} \langle \overline{F_m} \rangle _c -\frac{\partial \langle \overline{u_i^{\prime }w^{\prime }}\rangle _c}{\partial z}-\frac{\partial \langle {\widetilde{u_i}\widetilde{w}}\rangle _c}{\partial z}-\frac{1}{\rho } \left\langle \frac{\partial \overline{p}}{\partial x_i}\right\rangle _c= 0, \end{aligned}$$

(11)

where $u_i$ is the spatial direction ($u_1 = x$, $u_2 = y$), p is the pressure and $\rho$ is the air density. In the following, only the streamwise component of the flow will be considered so that $u_i=u$.

The first term on the l.h.s of Eqs. 10 and 11 is the specific body force that drives the flow. In most computational fluid dynamics (CFD) simulations, a mean streamwise pressure gradient is prescribed to compensate the friction due to building walls, roofs, and the ground. In the present Meso-NH simulations, instead, a geostrophic wind is prescribed which results from the balance between the large scale pressure gradient and the Coriolis force.

The second and third terms on the l.h.s. of Eqs. 10 and 11 are the gradients of turbulent (TMF) and dispersive momentum flux (DMF), respectively. The DMF is also denoted as dispersive stress in the literature (Raupach and Shaw 1982; Martilli and Santiago 2007) and represents the transport by time-averaged structures smaller than the size of the averaging volume like recirculation cells behind buildings for instance.

The fourth term on the l.h.s. of Eq. 10 results from the application of the spatial averaging theorem to the time-averaged momentum equation. It accounts for the changes in the averaging volume with height. The last term on the l.h.s. of Eqs. 10 and 11 is the pressure (or form) drag due to the roughness elements.

3.4 Parametrization of the Building Drag and the Momentum Fluxes

Equations 10 and 11 show that the non-linear momentum fluxes and the drag force have to be parametrized in UCMs. Concerning Meso-NH, the drag is parametrized by the mean of a drag force term (Schoetter et al. 2020). This is a very common approach, for which details can be found in Macdonald (2000) or Coceal and Belcher (2004).

An array of obstacles with a total frontal area $A_f$ and a sectional drag coefficient $c_d(z)$ distributed over the total area $A_t$ (Fig. 2) is considered. The force acting at height z can be written:

$$\begin{aligned} dF_d(z) = \rho \ c_d(z)\ \langle \overline{u^2}(z)\rangle A_f(z). \end{aligned}$$

(12)

Contrary to Coceal and Belcher (2004), the meteorological convention is preferred to the engineering convention: the drag coefficient is not defined including a factor of half. Following Coceal and Belcher (2004), the volume of the averaging slab at height z is $A_p(z)dz$. The total force per unit volume acting on the air at height z reads then:

$$\begin{aligned} F_{dv}(z) =\rho \ c_d(z)\ \langle \overline{u^2}(z)\rangle \frac{A_f(z)}{A_p(z)dz}, \end{aligned}$$

(13)

where $F_{dv}$ corresponds to the last term on the l.h.s. of Eqs. 10 and 11 multiplied by the air density, i.e., the horizontally-averaged mean pressure gradient across the obstacles. The sectional drag coefficient reads now:

$$\begin{aligned} c_d(z) = \frac{{\Delta } \langle \overline{p}(z)\rangle A_p(z)dz}{\rho \langle \overline{u^2}(z)\rangle \langle L \rangle A_f(z)}\ , \end{aligned}$$

(14)

where ${\Delta }\langle \overline{p}\rangle$ is the horizontally-averaged mean pressure deficit between the buildings back and front faces and $\langle L \rangle$ is the mean building length in the streamwise direction.

The TMF is often parametrized using the K-theory approach. For the intrinsic average, the TMF can be written:

$$\begin{aligned} \langle \overline{u'w'} \rangle = - \langle K_{m} \rangle \left\langle \frac{\partial \overline{u}}{\partial z}\right\rangle , \end{aligned}$$

(15)

where $K_{m}$ is the momentum eddy-diffusivity. It can be expressed with a first-order momentum mixing-length-closure approach. For models based on a Prandtl mixing length closure, $K_{m}$ reads:

$$\begin{aligned} \langle K_{m} \rangle = \langle l_{m} \rangle ^2 \bigg |\left\langle \frac{\partial \overline{u}}{\partial z}\right\rangle \bigg | , \end{aligned}$$

(16)

where $l_{m}$ is the mixing length. For intrinsic (Eq. 17) and comprehensive (Eq. 18) average, using the spatial averaging theorem, the mixing length can be calculated following Schmid et al. (2019) and Blunn et al. (2022):

$$\begin{aligned} \langle l_{m} \rangle= & {} -\dfrac{\sqrt{\langle \overline{u'w'} \rangle }}{\sqrt{\bigg | \dfrac{\partial \langle \overline{u}\rangle }{\partial z}+\dfrac{\langle \overline{u}\rangle }{\epsilon }\dfrac{\partial \epsilon }{\partial z}\bigg | \bigg ( \dfrac{\partial \langle \overline{u}\rangle }{\partial z}+\dfrac{\langle \overline{u}\rangle }{\epsilon }\dfrac{\partial \epsilon }{\partial z} \bigg )}}, \end{aligned}$$

(17)

$$\begin{aligned} \langle l_{m} \rangle _c= & {} -\dfrac{\sqrt{\epsilon ^3\langle \overline{u'w'} \rangle _c}}{\sqrt{\bigg | \dfrac{\partial \langle \overline{u}\rangle _c}{\partial z}\bigg | \bigg ( \dfrac{\partial \langle \overline{u}\rangle _c}{\partial z}\bigg )}}. \end{aligned}$$

(18)

For the higher-order scheme used in Meso-NH, the momentum eddy-diffusivity reads:

$$\begin{aligned} \langle K_{m} \rangle = \langle l_{m} \rangle \sqrt{\langle e \rangle } , \end{aligned}$$

(19)

where e is the total TKE. Equation 19 is written here under its general form, i.e without any constant, because they are specific to each numerical model. Using the spatial averaging theorem, the corresponding mixing length for intrinsic (Eq. 20) and comprehensive (Eq. 21) average is written:

$$\begin{aligned} \langle l_{m} \rangle= & {} -\dfrac{{\langle \overline{u'w'} \rangle }}{{\sqrt{e} \bigg ( \dfrac{\partial \langle \overline{u}\rangle }{\partial z}+\dfrac{\langle \overline{u}\rangle }{\epsilon }\dfrac{\partial \epsilon }{\partial z} \bigg )}}, \end{aligned}$$

(20)

$$\begin{aligned} \langle l_{m} \rangle _c= & {} -\dfrac{{\epsilon ^{3/2}\langle \overline{u'w'} \rangle _c}}{\sqrt{\langle e \rangle _c}{\bigg ( \dfrac{\partial \langle \overline{u}\rangle _c}{\partial z}\bigg )}}. \end{aligned}$$

(21)

The DMF parametrization can be done by calculating a new turbulent length scale using the total momentum fluxes (turbulent and dispersive) as described in Nazarian et al. (2020), for instance. Here, it would require to include the DMF terms in Eq. 17. Most of the UCMs use a mixing length formulation based on the TMF only. Because the main purpose of the present work is to use the obstacle-resolving simulations to derive parameters for the UCMs, the DMF is not included in the mixing length formulation but investigated separately. The same solution was adopted in Blunn et al. (2022).

Table 1 Description, 3D view, and main characteristics of the LCZ-based urban morphologies. $\sigma _H$ is the standard deviation of individual building heights

4 Local Climate Zone-like Urban Morphologies

The investigated urban morphologies are based on the combination of two classifications: the LCZs of Stewart and Oke (2012) and the GENIUS classification of Tornay et al. (2017), which is based on a survey with urban planners on which urban morphologies typically occur in French cities. The 10 urban LCZs aim to classify urban form and function in terms of their impact on the thermal climate. The urban LCZs are characterized by the surface structure, surface cover, building materials, and anthropogenic heat flux. In the present study, only the direct effect of the urban morphology on the near-surface flow is investigated. Potential feedbacks between thermal processes and the flow are not taken into account since the present study focuses on near-neutral atmospheric conditions. With this assumption, for the wind environment, the surface cover and structure are much more important than the building materials or the anthropogenic heat flux. For this reason, the lightweight lowrise LCZ7 is excluded, since it only differs from LCZ3 by the use of light materials. The GENIUS classification reveals that for two LCZs (Compact Midrise LCZ2 and Open Lowrise LCZ6), there exist two types of morphologies which might have different aerodynamical properties: buildings aligned with the roads of a building block which might have an internal courtyard, and buildings which rather have the form of rows. Therefore, for LCZ2 the compact midrise blocks (LCZ2a) and compact midrise rows (LCZ2b) are considered. Similarly, for LCZ6, the open lowrise blocks (LCZ6a) and the open lowrise rows (LCZ6b) are defined. The resulting 11 urban morphologies are presented in Table 1.

The urban morphologies have been procedurally generated in a way to mimick real urban districts. Their horizontal extent is a square of 800 m length, except for LCZ4 (1200 m). The square axes are parallel to the x- and y-axis of the Meso-NH domain. This means that the streamwise wind (from west to east, thus from $-x$ to $+x$ direction) is perpendicular to the building front. Furthermore, the building orientation is not random, but most buildings are oriented in the same way as the entire district, i.e. their walls are parallel to the x- or y-axis. Different results might be obtained for different angles of the incoming wind. This is the case for the drag coefficient (Santiago et al. 2013) and the DMF (Castro 2017; Blunn et al. 2022). Each urban district is also characterised by a central square and two main roads which transect the district with a 45$^{\circ }$ degree angle to the x- and y-axes (diagonally) (Fig. 3).

Fig. 3

Building spatial arrangement for LCZ2a (a) and LCZ3 (b)

Figure 4 shows the vertical profile in the UCL of $\lambda _{pz}(z)$ (Fig. 4a) and $\lambda _{fz}(z)$ (Fig. 4b). Both parameters strongly vary from the ground to the top of the UCL. The LCZ10 morphology, for instance, has one of the smallest $\lambda _{pz}(z)$ near the ground but one of the highest above $z/h_\textrm{max}$ = 0.6. Trying to describe realistic urban flows behaviour with ground-based (such as $\lambda _p$) or depth-integrated (such as $\lambda _f$) morphological parameters does not allow to account for the height heterogeneity inherent to these urban morphologies. To this end, Sützl et al. (2021) defined a generalized frontal area index, ${\Lambda }_f$, that characterizes the vertical distribution of the frontal area in the UCL:

$$\begin{aligned} {\Lambda }_f(z)=\int _{z}^{h_\textrm{max}} \lambda _{fz}(z) \ dz. \end{aligned}$$

(22)

Using this generalized frontal area index, Sützl et al. (2021) propose an alternative height representation of the buildings, the scaled frontal area:

$$\begin{aligned} \xi (z)\frac{\Lambda _f(z)}{\lambda _f}. \end{aligned}$$

(23)

Figure 4c shows the vertical profile of the scaled frontal area. As for the non-uniform building height cases of Sützl et al. (2021), $\xi$ is composed of piecewise linear functions $\xi (z)$.

5 Numerical Configurations

5.1 Multiscale Configuration

In order to simulate a realistic inflow, the large scale atmospheric turbulence prevailing in the ABL is accounted for by using four nested domains with increasing horizontal resolution (Fig. 5). This dynamical downscaling has successfully been performed by Nagel et al. (2022) for the regular array of containers of the MUST experiment.

Fig. 4

Vertical profiles within the UCL of building plane area density (a), building frontal area density (b), and scaled frontal area (c)

A one-way grid-nesting approach is used: the father domain variables influence the son domain variables but not vice-versa. The mesh is cartesian in all the domains. The coarsest domain is called D1. It is a 76.8 km side square domain and has a horizontal resolution of 96 m. Cyclic boundary conditions are employed for D1, therefore, its horizontal extent is infinite from a physical point of view. Due to its coarse resolution, only the largest eddies of the neutral ABL are resolved in D1. The flow results from a balance between the Coriolis force, a geostrophic wind which represents the large scale pressure gradient, and the surface friction. The grid nesting method is used for the lateral boundaries of the three finer domains. D2 and D3 are 19.2 km and 4.8 km side squares with a horizontal resolution of 24 m and 4 m, respectively. The finest resolution domain D4 (${\Delta }_x = {\Delta }_y =1$ m) extends 1.5 km and 1.2 km in x- and y-direction, respectively. The urban districts have a horizontal extent of 800 m by 800 m and are placed at 200 m distance from the north, east, and south boundaries to avoid wind channeling between the buildings and the model boundary, and 500 m distance from the west boundary to allow for the turbulence cascade in the inertial subrange to adapt to the higher resolution. For LCZ1, the D4 resolution is 1.5 m to better resolve the narrow streets and for LCZ4 the urban district has a 1200 m by 1200 m horizontal extent. The D4 domain extends 2.4 km in both directions, for LCZ1 and 2.8 km and 2 km in x- and $y-$direction for LCZ4.

The vertical mesh is common to all the domains. Except for LCZ1 and LCZ4, the vertical grid size is constant ($\varDelta _z= 1$ m) to about 5 m above $h_\textrm{max}$. Above that height, it increases with a constant geometric ratio of 1.095 until ${\Delta }_z$ reaches 50 m. For LCZ1, $\varDelta _z= 1.5$ m. For LCZ4, $\varDelta _z= 2$ m and the constant geometric ratio is equal to 1.08 until ${\Delta }_z$ reaches 75 m. The ABL is near neutral and extends up to 1500 m a.g.l., an inversion layer with a lapse rate of 3.10$^{-3}$ K m$^{-1}$ is prescribed above. A Rayleigh relaxation layer is located above z = 2000 m to damp gravity waves. The ceiling of the domain is rigid which corresponds to a free-slip condition.

The predominant wind being known, the D3 and D4 domains are placed in the right part (with respect to the cartesian system represented in Fig. 5) of their parent domain. This is a common method to optimise the transition fetch between two nested domains (e.g. Wiersema et al. 2020; Nagel et al. 2022).

In all the domains, the ground friction is characterized by an aerodynamic roughness length $z_0=$ 0.045 m and modeled with SURFEX (Masson et al. 2013). The turbulent fluxes of sensible and latent heat at the surface are prescribed as 0 W m$^{-2}$.

The turbulence recycling method introduced by Nagel et al. (2022) is used to enhance the turbulence scale transition between two nested subdomains. In D2 and D3, as shown in Fig. 5, the velocity fluctuations are added to the large-scale velocity fields coming from the father domain at the western boundary. As in Nagel et al. (2022), it has been found that between D3 and D4, the turbulence scale transition naturally happens within a very reduced fetch. The turbulence recycling is therefore not used in D4.

Fig. 5

The multiscale configuration. The recycling method is applied to the western boundaries of domains D2 and D3. The dashed lines indicate the positions of the recycling vertical planes. The LCZ3 urban morphology is represented in D4 as an example

Following Lac et al. (2018), CEN4TH/RKC4 is used for D1, D2, and D3 since it is the most appropriate to perform LES of the ABL due its very low intrinsic diffusivity. For D4, the WENO5 and RK53 schemes are used for the wind advection and the time marching respectively. The WENO5 scheme has been selected because it is the most appropriate to sharp gradient areas (Lunet et al. 2017). A summary of the numerical configurations is given for each domain in Table 2.

Table 2 Numerical configurations

5.2 Computational Fluid Dynamics-Like Configuration

Similar to Nagel et al. (2022), the CFD-like configuration consists of a single domain having the resolution, the vertical grid and most of its properties identical to the corresponding D4 domain of the multiscale configuration. The turbulence is generated with the turbulence recycling method. The major difference is that the CFD-like configuration is forced with a velocity profile extracted from the multiscale configuration. The CFD-like configuration has also different horizontal dimensions. For low- and midrise they are of 1.9 km and 1.2 km in x- and $y-$directions, respectively. The additional 400 m are placed upstream of the urban district, allowing for the turbulence to develop. For the highrise LCZ4, the domain is 3.6 km and 2.0 km in x- and $y-$directions, respectively.

6 Results and Discussion

6.1 Instantaneous Flow Fields

Figure 6 shows vertical and horizontal cross sections of the instantaneous wind speed $U(x,y,z,t)=\sqrt{u(x,y,z,t)^2+v(x,y,z,t)^2}$ for a part of LCZ3 (Fig. 6a, d), LCZ5 (Fig. 6b, e), and LCZ6a (Fig. 6c, f). The vertical cross sections show that the buildings influence the ABL well above their maximum height. A wind sheltering effect can also be observed in the wakes of the tallest buildings. This phenomenon is common for non-uniform UCL and is found in small-scale laboratory models (Xie et al. 2008; Millward-Hopkins et al. 2011) and real urban morphologies (Hertwig et al. 2019).

Figure 6d, e and f show the horizontal cross sections of the wind speed and velocity at z = 2 m. The three LCZs exhibit very different building arrangement and wind patterns. LCZ3 has a compact UCL, buildings are close one to the other. The streets are very similar to urban canyons. The wind is channeled in these narrow canyon streets, mostly along the x-direction, where the highest wind speeds are found. LCZ5 presents buildings with a similar horizontal extension than LCZ3 but their arrangement is less dense ($\lambda _p=0.31$ vs $\lambda _p=0.40$), allowing for more space between buildings. As a consequence, the streets are larger and their pattern is less obvious. The wind speed organization is more complex and includes recirculation cells in the sheltered areas downstream of tall buildings. Buildings in LCZ6a might have an internal courtyard. The area chosen presents a combination of very narrow streets and large building-free areas. This allows for recirculation but also strong acceleration areas.

Fig. 6

Vertical and horizontal cross section of the instantaneous wind-speed field for LCZ3 (a,d), LCZ5 (b,e), and LCZ6a (c,f)

6.2 Vertical Velocity Profiles

Figure 7 shows spatially-averaged, axial mean streamwise velocity and TKE profiles. In Fig. 7a, height and velocity are normalized by $h_\textrm{mean}$, and the mean wind velocity at z = $h_\textrm{mean}$, respectively.

The different urban morphologies present a strong variety of velocity profiles. Most of the velocity profiles exhibit an inflection point which is generated by the drag due to the buildings. For the highrise morphologies (LCZ1 and LCZ4), the inflection point is rather pronounced and located between $h_\textrm{mean}$ and 1.5$h_\textrm{mean}$. As described in Sützl et al. (2021), this transition indicates a separation between within- and above-UCL flow. Within the UCL, the flow is obstructed by the buildings, the velocity is importantly reduced and the velocity profile presents a concave shape. Above the UCL, the velocity profile becomes convex, showing that a boundary-layer profile develops. This inflection point is more important for the highrise morphologies but, even for these cases, the transition remains less sharp than what is reported in Sützl et al. (2021) for homogeneous UCLs. For the midrise (LCZ2a, LCZ2b, LCZ5, LCZ10), the blocks of open lowrise (LCZ6a), and the large lowrise (LCZ8) morphologies, the separation between within- and above-UCL flow is less evident since the profiles present a more gradual transition between a slightly concave or approximatively linear shape in the UCL to a convex one above it. For the rows of open lowrise (LCZ6b) and the sparsely-built lowrise (LCZ9), no inflection point can be clearly identified. This is because these morphologies are very sparsely built. The flow, almost not obstructed by the buildings presence, is similar to a rough boundary layer (Ghisalberti 2009).

The inflection point presence in most of the LCZs is coherent with the heterogeneous UCLs literature, where it is found for idealized (Xie et al. 2008; Sützl et al. 2021) and several real (Giometto et al. 2016, 2017; Auvinen et al. 2020; Cheng and Yang 2022) morphologies. More generally, the inflection point is a characteristic of obstructed shear flow (Ghisalberti 2009). It should be emphasized here that the shear layer generated at the top of the UCL presents local variations due to the canopy elements. This is not the case for other obstructed shear flows like vegetation canopy (Raupach et al. 1996) or permeable medium (see Fig. 3 of (Ghisalberti 2009)) where a mixing-layer analogy is assumed. As a consequence, local velocity profiles, and, more precisely, local values of the velocity vertical gradient at the inflection point are varying in the UCL (not shown here but already observed in Coceal et al. (2007a) for homogeneous-height UCLs). The inflection point recovered in Fig. 7a is therefore the expression of the spatial double averaging operation.

Fig. 7

Vertical profiles of normalized (a), non-normalized (b) streamwise velocity, and TKE (c) profiles for the LCZ1-LCZ10 urban morphologies within and above the UCL. The dots in the velocity profile (Exp) correspond to the exponential profile given by Eq. 24 with $a = 1.5$

The LCZ2a profile presents small negative streamwise velocity near the surface. It is also observed for LCZ1 up to $z/h_\textrm{mean}$ $\approx$ 0.3. The reversed flow regions behind the obstacles are large enough such that the spatially-averaged streamwise velocity close to the surface becomes negative for LCZ2. This phenomenon has already been observed by Castro (2017) for urban morphologies with uniform building height. For the highrise and compact LCZ1, the phenomenon extends higher in the UCL.

Previous studies assumed that the velocity profile in the UCL follows an exponential function (Macdonald 2000) and can be described as follows:

$$\begin{aligned} u/u_\textrm{hmean} = \textrm{exp}[a({z}/{h_\textrm{mean}}-1)]\ , \end{aligned}$$

(24)

where a is a constant. However, Castro (2017) shows that this assumption is generally not true for uniform-height urban morphologies. He also shows that for Xie et al. (2008)’s heterogeneous-height morphology, an exponential function with a = 1.5 seems to provide a reasonable fit in the range 0.25 $<z/h_\textrm{mean}<$ 1.

It is clear from Fig. 7a that the velocity profiles for most of the urban morphologies investigated here are not exponential (LCZ6b-LCZ10, for instance). Equation 24, with a = 1.5, is plotted on Fig. 7a. It fits reasonably well the LCZ5 velocity profile only, and this is restricted to the range 0.25 $<z/h_\textrm{mean}<$ 1.25. Modifying the value of a does not extend that range or provide a better fit for other LCZs. These results confirm and extend Castro (2017)’s conclusion: the streamwise velocity profile in the UCL of urban morphologies with homogeneous and heterogeneous building height does not follow an exponential function.

Figure 7b shows the non-normalized velocity profiles. The highrise urban morphologies (LCZ1 and LCZ4) present very distinguished velocity profiles. As already mentioned, the inflection point is much more pronounced and the streamwise velocity is strongly reduced within the UCL, more than for the other urban morphologies. It is particularly clear for LCZ1, where the velocity is negative (because of reversed flow) or below 0.25 m s$^{-1}$ ($\approx$ 0.025 % of the free-stream velocity) up to $h_\textrm{mean}$. A velocity overshoot is observed above 2 $h_\textrm{max}$. This overshoot, much more important for LCZ1 than LCZ4, is most probably a numerical artefact as it can be reduced, but not removed, by increasing the urban morphologies horizontal extension. Results above 1.5 $h_\textrm{max}$ for LCZ1 should therefore be treated with caution.

Figure 7c shows that the TKE profiles are similar for the different LCZs. The spatially-averaged TKE peaks around the height of the tallest buildings, a result in agreement with Xie et al. (2008) for non-uniform height obstacles. For the highrise LCZs, the peak is above $h_\textrm{max}$. This is particularly true for LCZ1 with a peak around 1.25 $h_\textrm{max}$.

Identification of key parameters upon which the velocity profiles scale is not an easy task. For an urban canopy with uniform building height, $\lambda _p$ is often considered as a key parameter (e.g., Santiago et al. 2008; Castro 2017). However, two urban morphologies can have an almost identical streamwise velocity profile within and above the UCL, like LCZ6b and LCZ9, but different $\lambda _p$ (0.23 and 0.11). Urban morphologies can also have an identical $\lambda _p$, like LCZ6b and LCZ10 but very different streamwise velocity profiles. Similar results are found for the frontal area density, $\lambda _f$. It confirms that $\lambda _p$ and $\lambda _f$ are not sufficient for the description of more realistic geometries with non-uniform building height. This is in agreement with Sützl et al. (2021) who found that nine idealized urban-morphologies with identical $\lambda _p$ and $\lambda _f$ present very different velocity profiles.

Fig. 8

Vertical profiles of sectional drag coefficient (a) and normalized cumulative drag function (b) within the UCL

6.3 Vertical Profiles of Sectional Drag Coefficient and Cumulative Drag Function

Figure 8a shows the vertical profiles of sectional drag coefficient within the UCL (up to $z=h_\textrm{max}$). The sectional drag profiles present similarities between most of the urban morphologies, only the highrise LCZ1 and LCZ4 present relevant differences. For all urban morphologies, the sectional drag values are zero at the top of the UCL. For low- and midrise LCZs, moving to the bottom of the UCL, the sectional drag values are first slowly increasing. Then, for the lower heights, they increase strongly because the velocities become very small there (Fig. 7). It is occuring below $z/h_\textrm{max}$ = 0.2 for most of the urban morphologies and below $z/h_\textrm{max}$ = 0.4 for LCZ2a. These large sectional drag values close to the ground are inherent to the sectional drag definition given in Eq. 14. For some authors, this will result in a parametrization issue such that they have proposed alternatives as the modified ($c_\textrm{dmod}$, Martilli and Santiago 2007) or the equivalent sectional drag coefficient ($c_\textrm{deq}$, Santiago and Martilli 2010).

In the region above $z/h_\textrm{max}$ = 0.8, some sectional drag profiles present inconsistencies such as negative values. At these levels, the number of buildings can be very low, as shown in Fig. 4a. The pressure deficit is then estimated based on very few buildings and the drag results are strongly influenced by their geometry. Sectional drag results above $z/h_\textrm{max}$ = 0.8 might therefore not be representative.

Between these upper and lower limits, differences are noticeable between the different low- and midrise urban morphologies. The geometries presenting a higher $\lambda _f$ (LCZ2a and LCZ5) have a higher sectional drag coefficient. They are also the urban morphologies having the most pronounced velocity deficit in the UCL (Fig. 7b).

The highrise LCZ1 and LCZ4 sectional drag coefficient profiles are different. Both have higher sectional drag values, which is consistent with the important velocity deficit displayed in Fig. 7b. The LCZ1 case presents spikes above 0.5 $h_\textrm{max}$. This is a consequence of the important building height heterogeneity and is in agreement with the $\lambda _{pz}$ and $\lambda _{fz}$ profiles (Figs. 4a, b). This kind of profile is similar to the one obtained by Castro (2017) for the random building height case of Xie et al. (2008).

For several urban morphologies (LCZ2b, LCZ3, LCZ6a, LCZ6b, LCZ8, and LCZ9), the mean sectional drag value between the upper and lower limits is around 0.4. However, considering the sectional drag coefficient as a constant, as done by Coceal and Belcher (2004), is an oversimplification (Castro 2017). The most rigourous way to parametrize the drag coefficient as a constant is to use the equivalent sectional drag coefficient of Santiago and Martilli (2010):

$$\begin{aligned} c_\textrm{deq} = \frac{\int _{0}^\textrm{hmax}{\Delta } \langle \overline{p}(z)\rangle dz}{\rho \int _{0}^\textrm{hmax} \langle \overline{u}(z)\rangle \langle \overline{u}(z)\rangle dz}\ . \end{aligned}$$

(25)

Based on homogeneous-height staggered cubes morphologies, Santiago and Martilli (2010) proposed to define $c_\textrm{deq}$ as an function of $\lambda _p$:

$$\begin{aligned} c_\textrm{deq}(\lambda _p) = \left\{ \begin{array}{ll} 3.32\lambda _p^{0.47} &{} \text{ for } \lambda _p \le 0.29 \\ 1.85 &{} \text{ otherwise. } \end{array} \right. \end{aligned}$$

(26)

The $c_\textrm{deq}$ value given by MesoNH-IBM for the homogeneous-height configuration described in Cheng and Castro (2002) (see Appendix) is 1.97, which is close to the value of 1.73 given by Eq. 26.

The $c_\textrm{deq}$ and the $c_\textrm{deq}(\lambda _p)$ values, calculated with Eqs. 25 and 26 are given in Table 3 for the eleven LCZ-based urban morphologies. The $c_\textrm{deq}$ values are much lower than those obtained from Eq. 26, indicating that the latter is not valid for more realistic morphologies with heterogeneous building height, a limit already mentioned in Santiago and Martilli (2010). For the LCZ-based urban morphologies, no simple relationship between $c_\textrm{deq}$ and morphological parameters such as $\lambda _p$ or $\lambda _f$ has been found.

Table 3 Values of $c_\textrm{deq}$ and $c_\textrm{deq}(\lambda _p)$ for the eleven LCZ-based urban morphologies. SA10 refers to Santiago and Martilli (2010) formula (Eq. 26)

It is worth mentioning that the highest $c_\textrm{deq}$ values are found for urban morphologies having a pronounced UCL velocity deficit and a higher sectional drag coefficient like LCZ1, LCZ4, LCZ5 or LCZ10. On the contrary, urban morphologies presenting a slight UCL velocity deficit, like LCZ6a or LCZ9, have the lowest $c_\textrm{deq}$ values. This result is not found with the SA10 formula, which gives the same equivalent sectional drag coefficient value for LCZ1 and LCZ6a for instance. Moreover, the $c_\textrm{deq}$ values obtained in the present work are close to those given for a constant drag coefficient in the literature. Values ranging from 0.1 (Uno et al. 1989) to 1 (Coceal and Belcher 2004) are found and 0.4 is often used (Martilli et al. 2002; Hamdi and Masson 2008; Schoetter et al. 2020). The latter, considering the meteorological convention, turns into 0.2 which is very close to the $c_\textrm{deq}$ values found for most of the LCZs. This suggests that the 0.4 constant value commonly used for the drag coefficient is appropriate for most of the LCZs, although it might underestimate the drag for highrise urban morphologies.

Figure 8b displays the normalized cumulative drag function ($\tau _D/\tau _0$) vertical profiles within the UCL. This cumulative drag function, introduced in Sützl et al. (2021), describes the accumulation of building drag in the UCL towards the ground. In the present work, only the form drag is considered:

$$\begin{aligned} \tau _D(z)=\int _{z}^{h_\textrm{max}} \frac{{\Delta } \langle \overline{p}(z)\rangle }{\langle L \rangle } \ dz. \end{aligned}$$

(27)

As in Sützl et al. (2021), the cumulative drag function is normalized by the kinematic surface stress $\tau _0=\tau _D(0)$ and plotted as a function of $1-\xi (z)$. Similarly to Sützl et al. (2021), there is a strong relationship between the cumulative drag and the vertical building structure. As for the sectional drag coefficient, some profiles present inconsistencies in their upper part (LCZ6a, LCZ6b, LCZ9) with negative cumulative drag function. Again, this is due to the very few buildings generating non representative results at these heights.

The cumulative drag function simulated for LCZ2b, LCZ3, LCZ5, LCZ10 agrees well with the $s(\xi )$ third-order polynomial fit proposed by Sützl et al. (2021). Others, like LCZ1, LCZ2a, and LCZ4 deviate in the upper part but the overall agreement remains reasonable. One reason for the differences observed could be that, contrary to Sützl et al. (2021), there is no constant $\lambda _p$ or $\lambda _f$ between the various urban morphologies. No clear relationship between the deviation of these morphological variables from their values in Sützl et al. (2021) and the deviation from the proposed fit is found. Another reason could be that a specific building type is predominant per LCZ urban morphology, like elongated buildings for LCZ6b, buildings with an internal courtyard for LCZ2a, and highrise buildings for LCZ1 and LCZ4. In Sützl et al. (2021) almost all building types (except the highrise ones and those with an internal courtyard) are represented in the non-uniform building heights morphologies. The present results suggest that a distributed-drag parametrization based on the third-order polynomial proposed by Sützl et al. (2021) is a reasonable choice for most of the LCZs but might need further refinement to be applicable to highrise cities.

6.4 Vertical Profiles of Turbulence Mixing Length and Turbulence Momentum Flux

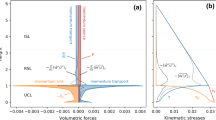
Figure 9a–c shows the vertical profiles of the turbulence mixing length (normalized by $h_\textrm{mean}$), the wind velocity vertical gradient, and the TMF of the LCZ1-LCZ10 urban morphologies within and above the UCL.

Fig. 9

Vertical profiles of normalized turbulence mixing length (a), vertical gradient of streamwise wind velocity (b), and TMF (c) of the LCZ1-LCZ10 urban morphologies within and above the UCL

Except for LCZ1, the evolution of the mixing length along the vertical is similar for all urban morphologies. The mixing length is low near the ground because the size of turbulent eddies is limited by the distance to the ground. Above, it increases linearly up to $z/h_\textrm{mean}\in [0.4-0.75]$ where the mixing-length maximum within the UCL, $\langle l_m \rangle ^\textrm{max}$, is reached. The largest values of $\langle l_m \rangle ^\textrm{max}/h_\textrm{mean}$ are obtained for the LCZs having the highest buildings (LCZ4, and LCZ5). A result probably due to the turbulent structures generated by the tallest buildings of these urban morphologies.

Above that maximum location, the vertical velocity gradient is increasing much faster than the TMF, resulting in a decrease of the mixing-length values for all the urban morphologies. The minimum, $\langle l_m \rangle ^\textrm{min}/h_\textrm{mean}$, is reached for $z/h_\textrm{mean}\in [0.9{-}1.25]$, i.e., at the lowest end of the shear layer at the UCL top. For most of the LCZs, the mixing length remains small up to the top of the UCL, i.e for $z/h_\textrm{mean}\in [1.5-1.75]$. This is expected because the eddies generated at roof level are small in scale (Ghisalberti 2009; Blunn et al. 2022) but also because the strong shear at roof level restricts, in a time-averaged sense, the penetration of large eddies from above the UCL (Coceal et al. 2006; Kono et al. 2010). The important part of the UCL over which this phenomenon occurs ($z/h_\textrm{mean}\in [0.9-1.75]$) is due to the building height heterogeneity. For $z/h_\textrm{mean}\in [1{-}1.75]$, spikes can be observed in the mixing length and vertical velocity gradient profiles for some LCZs. This is the result of the shear generated at the top of the buildings and appears mostly for urban morphologies where $\lambda _{pz}(z)$ presents steps (i.e where $\sigma _H$ is important), like LCZ2a, LCZ2b, LCZ4, LCZ5 and LCZ10.

Above the UCL, for $z/h_\textrm{mean}\in [2.5-4]$, the vertical velocity gradient is decreasing faster than the TMF such that the mixing length is increasing strongly up to $z/h_\textrm{mean}\approx$ 4. As in Blunn et al. (2022), this region is assumed to be the inertial sublayer. For most of the urban morphologies (except LCZ1 and LCZ4), the mixing length below $z/h_\textrm{mean}\approx$ 2.5 is non-linear and strongly influenced by the UCL. Above $z/h_\textrm{mean}\approx$ 4, the mixing length values are non-linearly increasing, which is due to the influence of the ABL large-scale structures.

The characteristic vertical profile of turbulence mixing length described in Blunn et al. (2022) is also found in the present work. In the UCL, the mixing-length profile is varying between three extrema. Above it, there is a transition zone before reaching the linear mixing-length profile of the inertial layer that is no longer influenced by the buildings.

The LCZ1 mixing length profile differs from the others within the UCL. In several parts of the UCL, the TMF is positive, the flow is counter-gradient and the mixing length can therefore not be computed. This result is also reported in Blunn et al. (2022) for dense and staggered homogeneous-height UCL. Here, the result is found in a more realistic urban morphology, where the horizontal position of the buildings is more random. This might indicate that the mixing length is not an appropriate variable to describe the flow characteristics in very dense and highrise UCLs. In the other parts of the UCL, the velocity is very low, the vertical velocity gradient and the TMF are close to zero, such that the mixing length is spiky. In Fig. 9a, the LCZ1 mixing length profile is the result of a 5 grid points moving average up to $z/h_\textrm{mean}$=1.5 to smooth it.

The LCZ1 and LCZ4 vertical velocity gradient tends to zero above the UCL. This is a consequence of the presumed artificial velocity overshoot observed in Fig. 7b. This makes it impossible to calculate a mixing length above that height for these two urban morphologies, but does not call into question the results within the UCL.

Fig. 10

Horizontal and vertical cross sections of turbulent shear stress for LCZ2a (a,d), LCZ4 (b,e), and LCZ9 (c,f). The black dashed lines in the horizontal cross section show where the corresponding LCZ vertical cross section is taken. Because the vertical extension of the chosen cross sections is much smaller than the horizontal one, the vertical axis is made dimensionless by $h_\textrm{mean}$ in subplots a, b, and c. The velocity vectors are also displayed in subfigures d, e, and f

6.5 Turbulent Shear Stress

Horizontal and vertical cross sections of turbulent shear stress ($\overline{u'w'}$) for different LCZs are shown in Fig. 10. The horizontal cross sections are shown at $z/h_\textrm{mean}$=0.25, i.e near the bottom of the canopy.

Focusing on the vertical cross sections, it is observed that shear layers are shed from the tops of the taller buildings, causing large negative values of $\overline{u'w'}$ in that region. Overall, the patterns of turbulent shear stress are found to be very different for the various LCZs. For the area of LCZ4 presented in Fig 10b, the buildings have a similar height and are close one to another. A strong shear layer is formed at the top of the UCL and it does not penetrate much into the canopy. A very different pattern can be observed for the sparse LCZ9. The shear stress generated at the roof is less intense but penetrates deep into the canopy. Because it is a very open canopy, there is also significant value of shear stress produced by the wind flowing directly over the ground. Sheltering effects can be observed for LCZ2a. There is no shear shed from the rightmost building in Fig. 10a because it is sheltered by the taller building in front of it.

As already observed in Coceal et al. (2007a), the shear generated at the top of urban canopies is more related to the individual elements than to the global canopy itself. In addition, Blunn et al. (2022) show that for homogeneous-height urban canopies, the turbulence is not dominated by mixing-layer eddies, except for very dense configurations. As a consequence, urban canopies distinguish from other obstructed shear flows, a result already observed in Ghisalberti (2009).

Fig. 11

Vertical profiles of DMF (a) and ratio of DMF to TMF (b) of the LCZ1-LCZ10 urban morphologies within and above the UCL

6.6 Dispersive Momentum-Flux Characteristics

Figure 11a shows the vertical profiles of DMF for the LCZ1-LCZ10 urban morphologies within and above the UCL. Overall, the DMF magnitude increases with height in the UCL up to $z/h_\textrm{mean}$ = 0.5–1.0. Similar to what is reported in Blunn et al. (2022), for most of the LCZs, the DMF is negative in the middle and near the UCL top but is positive near the ground. Three cases do not follow that general pattern. As in Yoshida and Takemi (2018), DMF is always negative in the UCL for the highrise LCZ1 and LCZ4. On the contrary, it is always positive for the sparsely-built LCZ9. For LCZ6b, the general positive and negative pattern is found but the DMF values are almost zero. The DMF values are higher for urban morphologies with higher buildings. This confirms Yoshida and Takemi (2018) findings that high buildings have an important contribution to the DMF in the UCL. Horizontal and vertical cross sections of different LCZs are shown in Fig. 12. The horizontal cross sections are shown at $z/h_\textrm{mean}$=0.25, i.e near the bottom of the canopy. Three cases are represented here: LCZ2a, which follows the general pattern, LCZ4, which is representative of the highrise morphologies, and LCZ9. Overall, the DMF is negative downstream of the buildings and positive on their windward face, a result in agreement with previous work (Coceal et al. 2007b; Yoshida and Takemi 2018; Blunn et al. 2022) on both homogeneous and heterogeneous-height morphologies.

In details, the buildings organization strongly influences the DMF. For LCZ2a, an urban morphology with an important building density ($\lambda _p=0.53$), the recirculations in the building wakes are limited by the presence of the downstream obstacle. Close to the ground, the downstream negative fluxes have a less important horizontal extent than the positive ones, resulting in a positive spatial average DMF. In Fig. 12d, the negative and positive fluxes have similar horizontal extent resulting in a spatial average DMF close to zero at $z/h_\textrm{mean}=0.25$. A result in agreement with Fig. 11a. In the middle and the top of the UCL, the downstream negative fluxes have a larger horizontal extent than the positive ones and dominate the spatial average DMF (not shown). The negative and positive DMF are also found within the courtyards of LCZ2a, indicating that permanent turbulent structures exist there. For LCZ4, the negative fluxes prevail, even close to the ground. The positive and negative DMF areas on the front and back faces of highrise buildings correspond to what is reported for the V10 case of Yoshida and Takemi (2018), including the small negative DMF structure at the edge of the front face. For LCZ9, the positive and negative DMF areas are overall found upstream and dowstream of the buildings. Their spatial extent is however limited, especially for isolated buildings. When buildings are close enough for the flow around one being impacted by the presence of others, the DMF intensities are higher and positive DMF areas are slightly more important than negatives ones.

Fig. 12

Horizontal and vertical cross sections of DMF for LCZ2a (a,d), LCZ4 (b,e), and LCZ9 (c,f). The black dashed lines in the horizontal cross section show where the corresponding LCZ vertical cross section is taken. Because the vertical extent of the chosen cross sections is much smaller than the horizontal one, the vertical axis is made dimensionless by $h_\textrm{mean}$ in subplots a, b, and c. The velocity vectors are also displayed in subfigures d, e, and f

The ratios of DMF to TMF are shown in Fig. 11b. For most of the LCZs (except LCZ1 and LCZ4), the DMF to TMF ratio is between 0.– 0.4 for $z/h_\textrm{mean}\ \in$ [0.4–1], a value in agreement with Xie et al. (2008)’s random height morphologies. Concerning the highrise morphologies, the LCZ1 case is not relevant since the TMF is close to zero in the UCL. For LCZ4, the ratio of DMF to TMF is above unity in the UCL, reaching the value of 2. It is considerably larger than what is reported in Yoshida and Takemi (2018) and Akinlabi et al. (2022) for idealized and realistic cases, respectively, but in the range of what can be observed for oblique flow on an homogeneous urban canopy (Castro 2017). This is most probably because the study of Yoshida and Takemi (2018) and Akinlabi et al. (2022) considered only a limited number of highrise buildings whereas an entire highrise district is investigated here.

The present results show that TMF and DMF are evolving differently along the UCL height and that their ratio is not constant for most of the investigated urban morphologies. This is in agreement with Blunn et al. (2022) and suggests that TMF and DMF are not governed by the same processes. The DMF can be associated with the time-averaged building-scale spatial fluctuations of the flow whereas the TMF is mainly generated by the strong shear at the building roofs.

Overall, although the DMF is lower than the TMF for most of the LCZs, it is not negligible for mid and highrise LCZs. This supports the conclusion of several previous studies (Castro 2017; Blunn et al. 2022; Akinlabi et al. 2022) arguing that DMF should probably be taken into consideration in multi-layer UCMs. The manner of how it should be accounted for is an open question. On the one hand, Castro (2017) recommends to include the DMF in the mixing length following the approach proposed by Coceal and Belcher (2004). On the other hand, Blunn et al. (2022) argue that DMF should be treated separately because it is not directly related to the vertical velocity gradient upon which the mixing length approach is built. Advocating for either choice is beyond the scope of the present paper but this question should be remembered for future parametrization.

All the previous assessments for the DMF are valid for an $0^{\circ }$ incoming flow only. According to the literature (Giometto et al. 2016; Castro 2017; Blunn et al. 2022) the DMF might be more important for oblique flow configurations.

Fig. 13

Vertical profiles of normalized mean velocity (a), TKE (b), sectional drag coefficient (c) and mixing length (d) of the LCZ4, LCZ5, LCZ6b, and LCZ9 urban morphologies with and without the large scale ABL turbulence in the incoming wind

6.7 Influence of the Atmospheric Boudary-Layer Larger Scale Turbulence

Most of the numerical studies investigating the flow properties in an idealized urban environment are performed with CFD codes which are unable to account for ABL turbulence. In the present work, using a meteorological research model and performing a dynamical downscaling allows to account for the ABL turbulence impact on the flow characteristics of the LCZ-based urban morphologies. Numerical simulations have been performed on the CFD-like configuration presented in Sect. 5.2 in order to discuss the influence of the large-scale ABL turbulence on the present results.

Figure 13 shows the space and time averaged vertical profiles of velocity (13a), TKE (13b), sectional drag coefficient (13c) and turbulence mixing length (13d) for LCZ4, LCZ5, LCZ6b, and LCZ9 in the multiscale and the CFD-like configurations. For the sake of clarity, not all LCZs are displayed in Fig. 13. For the low- and midrise LCZs, except for the TKE, the profiles are almost identical within the UCL. Above it, the velocity becomes larger and the mixing length smaller for the CFD-like configurations. This is coherent with the fact that CFD-like configurations do not represent the large-scale ABL turbulence. The same observations apply for the highrise LCZs. For these morphologies, the velocity in the bottom part of the UCL is slightly lower for the CFD-like configuration, which is in agreement with the slightly larger sectional drag coefficient displayed in Fig. 13c. The profiles are, however, relatively similar.

Overall, the present results suggest that, considering a neutral stratification, most of the turbulence within the UCL is generated by the buildings themselves. This is in agreement with Fig. 9a, where the mixing length in the middle of the UCL is more important for higher buildings.

Recent literature shows that accounting for the ABL turbulence improves the wind speed and the pollutant dispersion prediction in idealized (Nagel et al. 2022) and realistic (Wiersema et al. 2020) urban environments. Here, even for the highrise LCZs, the influence of the ABL turbulence is rather low, most probably because the focus is on horizontally-averaged quantities. Parametrization of UCM can therefore be built upon results obtained from CFD models as in Blunn et al. (2022) and Sützl et al. (2021), keeping in mind that with this method, the drag coefficient might be overestimated near the ground for highrise LCZs.

Fig. 14

Vertical profiles of normalized mixing length of the LCZ1-LCZ10 urban morphologies obtained with the intrinsic average (solid line), comprehensive average (dashed line), a Prandtl-type closure (dark) or a TKE-L closure formulation (grey). The dotted lines are obtained from a configuration without buildings

6.8 Influence of the Horizontal Double-averaging Procedure Choice on the Mixing Length Profiles

The mixing length vertical profiles presented in Figs. 9 and 13 are obtained with an intrinsic average and a Prandtl-type mixing length closure (Eq. 17). Figure 14 compares these results with the vertical profiles obtained with a comprehensive average or a TKE-L closure formulation.

Focusing first on the closure choice, it appears that the shape of the vertical profiles is almost identical for both formulations but that the TKE-L closure provides a smaller mixing length at each vertical level. This result reminds that, when deriving a mixing length parametrization for mesoscale models based upon microscale model results, one should obviously take care to the turbulence formulation closure consistency.

The local extrema of the mixing length have a smaller magnitude when using the comprehensive averaging procedure. This is observed for both turbulence closure formulations and is in agreement with Fig. 11 of Blunn et al. (2022). Similar to previous work (Xie and Fuka 2018; Schmid et al. 2019; Blunn et al. 2022), the present results show that the averaging technique provides different mixing length vertical profiles in the UCL.

The dotted lines in Fig. 14 are obtained from a configuration without buildings. The associated mixing length can therefore be seen as a non-urban one, increasing linearly with the distance from the ground. Comparison between the non-urban and the LCZs mixing length informs about the influence of the UCL. The deviation between the urban and the non-urban mixing length is similar for both averaging methods. In the lower part of the UCL, up to $z/h_\textrm{mean} \approx$ 0.75, the urban mixing length is higher than the non-urban one. This is verified for all configurations but is more pronounced for highrise (LCZ4) and midrise LCZs (like LCZ5). It is probably due to the turbulent structures generated by tall buildings.

Above $z/h_\textrm{mean} \approx$ 0.75, the urban mixing is lower than the non-urban one. This is probably the result of the small-size coherent structures generated at the top of the roofs. The city presence generates perturbutations resulting in higher shear stress, TMF, and TKE up to several times the mean building height (not shown here). For the highrise LCZ4, the perturbutations can be found up to $z/h_\textrm{mean} \approx$ 4, where the urban and non-urban mixing length evolve similarly with height. For the midrise (LCZ2a, LCZ2b, LCZ5, LCZ10) and the lowrise (LCZ3, LCZ6a, LCZ6b LCZ8, LCZ9) morphologies, the perturbutations extend up to $z/h_\textrm{mean} \approx$ 7 and $z/h_\textrm{mean} \approx$ 14, respectively.

The mixing length is not calculated everywhere in the UCL for LCZ1. This is a consequence of the positive TMF observed in Sect. 6.4 for this urban morphology. The present results show that a mixing length parametrization based on the TMF only cannot be derived for LCZ1. Including the DMF in the mixing length formulation, as proposed by Nazarian et al. (2020) for instance, allows to calculate a mixing length in the UCL for LCZ1 (not shown here). Accounting or not for the DMF in the mixing length is however a matter of debate in the literature (Blunn et al. 2022) and is beyond the scope of the present study.

7 Summary and Conclusion

We conducted large-eddy microscale simulations with the MesoNH-IBM meteorological research model of eleven LCZ-based urban morphologies. The aim is to investigate the flow characteristics such as velocity, TKE, drag, mixing length, TMF, and DMF, but also to provide velocity, sectional drag coefficient, and mixing length reference vertical profiles for the urban environment. The urban morphologies are procedurally generated in a way to mimick real urban districts.

For none of the investigated urban morphologies, a streamwise velocity profile following an exponential function in the UCL is found. This confirms Castro (2017)’s conclusion and extends it to urban morphologies with heterogeneous building height. In addition, the spatially-averaged TKE peaks at the height of the tallest buildings, which is in agreement with Xie et al. (2008)’s findings for non-uniform height obstacles.

The present results show that ground-based (such as $\lambda _p$) or depth-integrated (such as $\lambda _f$) morphological parameters are not suited to describe the flow characteristics for geometries with non-uniform building height because they do not account for the height heterogeneity inherent to these urban morphologies. As a consequence, the equivalent sectional drag coefficient $c_\textrm{deq}$ formula proposed by Santiago and Martilli (2010) is not valid for the LCZ-based urban morphologies studied here. New values of $c_\textrm{deq}$ are proposed for each urban morphology, but no simple relationship between $c_\textrm{deq}$ and the usual morphological parameters has been found. An alternative to the usual morphological parameters is the generalized frontal area index ${\Lambda }_f$ defined by Sützl et al. (2021). It characterizes the vertical distribution of the frontal area in the UCL. Most of the vertically-distributed stress profiles agree well when plotting them against ${\Lambda }_f$. Some, like LCZ6, LCZ10, and the highrise LCZ1 and LCZ4 present however a clear deviation. A distributed-drag parametrization based on the third-order polynomial proposed by Sützl et al. (2021) seems therefore a reasonable choice for most of the LCZs but might need further refinement to be applicable to all urban morphologies, especially for highrise cities.

Concerning the mixing length, the results show that it is not constant in the UCL, which is in agreement with Castro (2017) and Blunn et al. (2022). The vertical profile of turbulence mixing length, resulting from a competition between wind shear and TMF, is in accordance with Blunn et al. (2022). The mixing length profile in the UCL is varying between three extrema: it increases linearly from a zero value at the ground up to a local maximum around $z/h_\textrm{mean}\in [0.4{-}0.75]$, then it decreases and remains small near the UCL top. Above, it continuously increases up to several times the mean building height. At that height, the building influence vanishes and the mixing length profile evolves similarly to an non-urban mixing length. Comparatively to an non-urban mixing length increasing linearly with the distance from the ground, the UCL mixing length is higher for or $z/h_\textrm{mean} \in [0 - \approx 0.75]$, because of the turbulent structures generated by the buildings and lower above, because of the shear generated at the building roofs.

The horizontal averaging procedure (intrinsic or comprehensive) impacts the mixing length vertical profiles in the UCL, which is in agreement with the literature (Xie and Fuka 2018; Schmid et al. 2019; Blunn et al. 2022). The local extrema of the mixing length have a smaller magnitude when using the comprehensive averaging procedure. As a consequence, when building or using a parametrization, consistency should be verified between the double-averaged momentum equation solved in the UCM and the averaging procedure chosen to derive the parameters. Because the parametrization itself is beyond the scope of the present paper, no recommendation for one of the averaging procedures can be given here.

The DMF repartition in the UCL is in agreement with the literature, positive DMF is found upstream of the buildings whereas negative DMF is localized downstream. Its spatial extent depends on the buildings arrangement and for most LCZs it results in negative DMF in the middle and near the UCL top but positive DMF near the ground. For the highrise cases, the DMF is always negative because the dominating recirculation cells at the back side of the buildings extend from the top of the UCL to the ground. Although the DMF is lower than the TMF for most of the LCZs, it is not negligible for a given number of them, especially for highrise cases. This supports the conclusion of Castro (2017), Akinlabi et al. (2022) and Blunn et al. (2022) who argue that DMF should be taken into consideration by upscaling parametrizations.

For low- and midrise LCZs, the large-scale ABL turbulence has a negligible influence on most of the horizontally-averaged quantities. Only the TKE profiles present noticeable differences. For highrise LCZs, small differences can also be found for velocity and sectional drag coefficient profiles, but the overall profiles remain similar. This suggests that considering a neutral stratification, most of the turbulence within the UCL is generated by the buildings themselves. As a consequence, an improved UCM parametrization based on mixing length or drag can also be built upon results obtained from CFD models as in Sützl et al. (2021) and Blunn et al. (2022).

The sectional drag and mixing length reference profiles obtained for the eleven LCZ-based urban morphologies are expected to serve as a starting point towards the improvement of multi-layer UCMs dynamical parametrization. These profiles are currently being implemented in the multi-layer version of SURFEX (Schoetter et al. 2020) to force mesoscale simulations, with the aim to improve them over cities. These mesoscale simulations will be performed using Meso-NH, the numerical model currently used to determine the reference profiles. Using the same numerical model between the two configurations may also help to clarify what is the most appropriate horizontal averaging procedure.

Another perspective could be to identify how the flow characteristics differ for oblique inflow wind. From the literature it could be expected that TMF production would increase and DMF would be more important (Blunn et al. 2022), which could significantly modify the mixing length profiles.

It is also possible that the LCZs defined here are not sufficiently discriminating. New LCZs may have to be added to be representative of all the worldwide city types, like almost-uniform height highrise LCZs for living districts of Asian megacities, for instance. It could also be of interest to provide reference profiles for combined LCZs, which is more likely to occur in real cities.

Appendix: Validation of the Sectional Drag Coefficient Calculation in MesoNH-IBM

The ability of MNH-IBM to accurately simulate the sectional drag coefficient is validated for a staggered cubes arrangement. The results are compared with the experimental wind-tunnel measurements from Cheng and Castro (2002). This dataset has already been used as reference for Direct Numerical Simulations (DNS, Coceal et al. 2006) and Reynolds-Averaged Navier–Stokes (RANS, Santiago et al. 2008) simulations.

The arrangement, made of 140 staggered cubes, is shown in Fig. 15. All cubes are identical with 0.1 m aside. The distance between each cube in a row and the distance between two consecutive rows is 0.1 m. As a consequence, $\lambda _p=\lambda _f= \$0.25. The domain dimensions are 4.5, 3.75, and $\approx$ 0.6 m, in the x-, y- and z-direction, respectively. It follows the guideline given by Franke et al. (2011) for the size of a CFD urban computational domain. The mesh is cartesian, with a horizontal resolution of ${\Delta }_x={\Delta }_y=0.005$ m. In the vertical direction, for $z<$0.2 m, the vertical grid size is constant and ${\Delta }_z = 0.005$ m. Above 0.2 m, it increases with a constant geometric ratio of 1.07. 20 grid points are used to discretize the cubes in each direction. According to Auguste et al. (2019), this resolution allows to solve with a good accuracy the flow around an isolated cube in MNH-IBM.

A steady logarithmic velocity profile with $u_{*} = 0.45$ m s$^{-1}$ and $z_0$ = 0.001 m is imposed at the left boundary. The obstacles are represented with the IBM and the ground friction, characterized by an aerodynamic roughness length of $z_0$ = 0.001 m, is modeled with SURFEX. The turbulent surface fluxes of sensible and latent heat are prescribed as 0 W m$^{-2}$.

No pressure gradient can be imposed in Meso-NH to maintain the flow. As a consequence, periodic boundary conditions cannot be imposed for a domain containing obstacles. In the previous studies (Coceal et al. 2006; Santiago et al. 2008) periodic boundary conditions were imposed laterally and streamwise to simulate an infinite number of cubes. Here, the drag calculation is only performed on cubes number 1–4 (Fig. 15a) and 136 cubes are added to mimick an infinite array. A sensitivity study has shown that, for the present 140 cubes array, adding cubes in any direction does not change the sectional drag coefficient results in a relevant manner (not shown).

Fig. 15

Time-averaged wind speed at z=h/2 (a) and vertical profile of sectional drag coefficient ($c_d(z)$) (b). For the $c_d(z)$ profile, the results are spatially-averaged over the cubes number 1 to 4

Figure 15 shows the time-averaged wind speed at $z\,{=}\,h$/2 on the left panel and the vertical profile of the sectional drag coefficient ($c_d(z)$) on the right panel. For the $c_d(z)$ profile, the results are averaged over 6 s of dynamics and over the cubes 1 to 4. Averaging over a longer time does not change the results. The sectional drag coefficient follows the tendency given in the literature: it remains around a constant value in the upper half of the UCL and increases rapidly in the lower UCL because of the small velocity close to the ground. Above $z/h \ = \$0.4, the present LES results overestimate by approximatively a factor of 2 the experimental reference of Cheng and Castro (2002). Overall, the results are in good agreement with the literature. In terms of accuracy, they lie between the DNS of Coceal et al. (2006) and the RANS of Santiago et al. (2008), as expected. This proves that MNH-IBM is a suitable tool to calculate the sectional drag coefficient for an array of obstacles.