A New Aerodynamic Parametrization for Real Urban Surfaces

Abstract

This study conducted large-eddy simulations (LES) of fully developed turbulent flow within and above explicitly resolved buildings in Tokyo and Nagoya, Japan. The more than 100 LES results, each covering a 1,000 $\times$ 1,000 m$^{2}$ area with 2-m resolution, provide a database of the horizontally-averaged turbulent statistics and surface drag corresponding to various urban morphologies. The vertical profiles of horizontally-averaged wind velocity mostly follow a logarithmic law even for districts with high-rise buildings, allowing estimates of aerodynamic parameters such as displacement height and roughness length using the von Karman constant $=$ 0.4. As an alternative derivation of the aerodynamic parameters, a regression of roughness length and variable Karman constant was also attempted, using a displacement height physically determined as the central height of drag action. Although both the regression methods worked, the former gives larger (smaller) values of displacement height (roughness length) by 20–25 % than the latter. The LES database clearly illustrates the essential difference in bulk flow properties between real urban surfaces and simplified arrays. The vertical profiles of horizontally-averaged momentum flux were influenced by the maximum building height and the standard deviation of building height, as well as conventional geometric parameters such as the average building height, frontal area index, and plane area index. On the basis of these investigations, a new aerodynamic parametrization of roughness length and displacement height in terms of the five geometric parameters described above was empirically proposed. The new parametrizations work well for both real urban morphologies and simplified model geometries.

1 Introduction

Aerodynamic parametrization of urban surfaces is important, especially in mesoscale meteorological analyses in which it is difficult to explicitly resolve individual roughness elements. Recently developed simple urban canopy models have helped to improve predictions of the urban surface energy balance (Grimmond et al. 2010, 2011) because these models can account for the larger heat storage of cities compared to flat surfaces. However, the aerodynamic parametrizations used in urban canopy models are commonly poor in terms of fluid dynamics, and the precise estimation of drag due to urban surfaces and the improvement of corresponding aerodynamic parametrizations still remain unsolved. The conventional aerodynamic parametrizations for urban surfaces have been derived mostly from experiments assuming relatively simple arrays of buildings of uniform height (e.g., see the review by Grimmond and Oke 1999). The relevant geometric parameters used (such as plane area index, frontal area index, and average building height) have been minimal. However, real urban surfaces are far from such simple configurations, and even simple arrays of buildings with variable heights can provide much larger drag than those with a homogeneous height, as shown by wind-tunnel experiments (Macdonald et al. 1998a; Cheng and Castro 2002; Hagishima et al. 2009; Zaki et al. 2011), outdoor experiments (Kanda and Moriizumi 2009), and numerical simulations (Kanda 2006; Jiang et al. 2008; Xie et al. 2008; Nakayama et al. 2011). In particular, the experiments by Hagishima et al. (2009) and by Zaki et al. (2011) demonstrated that the displacement height of urban-like surfaces with variable height can be larger than the average building height. This strongly suggests that the simple extension of conventional models is difficult and that other relevant geometric parameters should be included in the parametrizations.

Computational fluid dynamical approaches using direct numerical simulation (DNS) or large-eddy simulation (LES) are promising, in that the precise estimation of drag and related aerodynamic parameters is possible. These approaches provide rich temporal and spatial information, resulting in reliable horizontally-averaged statistics. Although there have been many applications of DNS and LES to simple building arrays, models of real urban districts are still rare. Most previous applications of LES to real cities were focused on detailed spatial and temporal analyses of the wind environment and pollutant dispersion at the sites of interest (Letzel et al. 2008; Nozu et al. 2008; Tamura 2008; Bou-Zeid et al. 2009; Xie and Castro 2009; Letzel et al. 2012). However, feedbacks to improve bulk aerodynamic parametrizations are still lacking.

This paper has two aims: the first is the precise estimation of drag over real urban surfaces in Tokyo and Nagoya, Japan, using a LES model with three-dimensional digital building maps. The more than 100 LES runs conducted in this study provide a large database of bulk flow properties, including roughness parameters, horizontally-averaged turbulent statistics, the floor drag/total drag ratio, and representative geometric parameters for the districts. The second aim is the development of new aerodynamic parametrizations on the basis of the LES database that are applicable for both complex real urban surfaces and conventional simple building arrays. Two methods were used to estimate the aerodynamic parameters: the first was a conventional regression of roughness length $(z_0)$ and displacement height $(d)$ with the von Karman constant $(\kappa = 0.{4})$. The other method was that of Leonardi and Castro (2010), i.e., the regression of $z_0$ and the variable von Karman constant $\kappa$ using $d$, which was separately and physically determined as the central height of drag action.

2 Experimental Design for Large-Eddy Simulation

2.1 LES Model

The parallelized large-eddy simulation model (PALM) was used in our study (Letzel et al. 2008, 2012; Castillo et al. 2011; Inagaki et al. 2012; Park et al. 2012). The numerical schemes used were the second-order Piacsek–Williams form C3 scheme for advection and the third-order Runge–Kutta scheme for time integration. The fractional step method ensures incompressibility, and the Temperton algorithm for the fast Fourier transform (FFT) was used to solve for the resulting Poisson equation for the perturbation pressure (Raasch and Schröter 2001). An implicit filtering of the governing equations followed the Schumann volume-balance approach, while turbulence closure for the LES was based on the modified Smagorinsky model, with the flux–gradient relationships of the 1.5-order Deardorff scheme.

The mask method used in PALM to explicitly resolve solid obstacles on a rectangular grid, which was based on the method of Kanda et al. (2004), proceeded as follows: numerical computation was executed at each grid point as if there were no obstacles, and forcing induced by physical boundary conditions was introduced to grid points corresponding to obstacle surfaces, wherein zero wall-normal velocities define the wall positions (Letzel et al. 2008). The simplified and optimized mask method used in PALM reduced a three-dimensional obstacle into two-dimensional topography, improving the performance and minimizing the computational load. The wall function was based on Monin–Obukhov similarity theory and prescribed a Prandtl layer for each wall surface (Letzel 2007).

2.2 Computational Set-Up

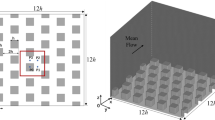
The streamwise $(x)$, spanwise $(y)$, and vertical $(z)$ sizes of the computational domain were 1,000 m $(L_x )$, 1,000 m $(L_y)$, and 600 m $(L_z)$, respectively, with a uniform spatial resolution of 2 m. The total grid number was 500 by 500 by 300 along the $x, \,y$, and $z$ axes, respectively. The bottom surface consisted of a realistic building geometry or idealized simple arrays of buildings (see Sect. 3), with the local topographic relief ignored in order to purely focus on the urban geometrical effect. The streamwise direction was set from west to east for all runs. Because of the large number of districts used and the inherent diversity and weak regulation of building construction in Tokyo, the surface structures, such as the major street angles relative to the given wind direction, were variable.

The neutrally-stratified atmospheric boundary layer was simulated by initially setting a uniform streamwise velocity $(u)$ of 3 m s$^{-1}$ with zero surface heat flux. All surfaces were non-slip, whereas the top boundary was slip. Cyclic conditions were set for both horizontal directions, and the volume flux of flow was conserved by adjusting the streamwise static pressure gradient. The simulation was continued until the flow reached a fully-developed quasi-steady turbulent state. The integration time for each LES run was variable (around 5 h; results from the last two hours were used for all investigations).

Conventional aerodynamic parametrizations are based on the logarithmic velocity law and are thus derived from surface-layer scaling with neutral stratification. Real urban boundary layers are often composed of two layers: a surface layer in which mechanical turbulence is dominant and a mixed layer in which thermal turbulence is dominant. Therefore, a fully developed urban atmospheric boundary layer with neutral stratification up to 600 m should rarely exist in practice. The current extreme numerical set-up without thermal effects can vertically extend the surface layer, thereby ensuring the existence of a logarithmic wind profile region or inertial sublayer. This set-up is used simply for the derivation of aerodynamic parameters for urban surfaces, which is indispensable under the framework of fluid dynamics. Whether a real urban boundary layer permits the existence of an inertial sublayer (Rotach 1999) depends on the synoptic conditions, which we do not address here.

The outer-layer fluctuation, whose horizontal scale is much larger than that of surface-layer eddies, has little influence on the momentum transport and logarithmic wind profile in the surface layer, as observed in wind-tunnel experiments (Hattori et al. 2010), outdoor experiments (Inagaki and Kanda 2008, 2010), and numerical simulations (Castillo et al. 2011). Therefore, the aerodynamic parameters will be valid even under outer-layer fluctuations.

Very large-scale longitudinal motion of low momentum regions have been observed in neutrally-stratified wall-bounded flows (e.g. Tomkins and Adrian 2003; Hutchins and Marusic 2007; Inagaki and Kanda 2010; Araya et al. 2011). If the horizontal extension of the domain size relative to the height is too small to resolve these longitudinal structures, some artificial influence on the turbulent statistics is a concern. This is examined by comparing two preparatory simulations; one has the standard domain size with a surface geometry, the other has the double domain size in the streamwise direction with the duplicated surface geometry. Both use the periodic boundary conditions. As one of the most extreme situations, a commercial area with densely built-up high rise buildings (ID98) is selected for the geometry of the bottom surface. The results can be found at the following site (http://www.ide.titech.ac.jp/~kandalab/download/LES_URBAN/Vp_Lx_2LX.pdf). The horizontally-averaged Reynolds stress and velocity distributions are almost the same, whereas the velocity variances are slightly different.

3 Building Data

3.1 Original Building Data: MAPCUBE

The original building data, MAPCUBE, were commercially provided from the CAD Centre Corporation in Japan. The original building data format was a two-dimensional array of building heights with a horizontal resolution of 1 m. One file covered 4,000 m in the west–east direction $(x)$ and 3,000 m in the south–north direction $(y)$. This file was divided into 12 areas of 1,000 $\times$ 1,000 m$^{2}$ with downsizing into 2-m resolution for use in PALM, which reads this data format and automatically converts the values to either 0 (= air) or 1 (= solid buildings) integer values of a three-dimensional field for the masking method. Among all Tokyo (622 $\text{ km }^2$) and Nagoya (322 $\text{ km }^2$) files, 107 representative districts (97 in Tokyo and 10 in Nagoya) were selected for the present LES runs. Similar three-dimensional building digital maps are now becoming available commercially, but they are still very expensive. Ratti et al. (2002) estimated the geometric parameters of London (UK), Toulouse (France), Berlin (Germany), Salt Lake City (USA), and Los Angeles (USA) using similar digital elevation maps, but the areas covered were limited (around a few $\text{ km }^2$ at most). As an example, Fig. 1 shows maps of building height for three distinctive surface geometries: (a) a cluster of skyscrapers, (b) business or commercial districts with mostly mid-height buildings and a few isolated towers, and (c) a low residential area. Only buildings were considered and objects such as vegetation and automobiles were ignored.

Fig. 1

Maps of building height for three different urban surfaces. a Skyscrapers (ID97 in Table 1), b business district (ID 96 in Table 1), and c residential area (ID76 in Table 1)

3.2 Bulk Geometric Parameters

The bulk geometric parameters used were the spatially-averaged statistics over the whole 1,000 $\times$ 1,000 $\times$ 600 m$^{3}$ dimensions of the file. Although various geometric parameters were examined, the following five parameters were found to be most relevant for the new parametrizations: the average building height $H_\mathrm{ave}$, the maximum building height $H_\mathrm{max}$, the standard deviation of building height $\sigma _\mathrm{H}$, the plane area index $\lambda _\mathrm{p}$ (the ratio of the plane area occupied by buildings to the total floor area), and the frontal area index $\lambda _\mathrm{f}$ (the ratio of the frontal area of buildings to the total floor area). The values of $\lambda _\mathrm{f}$ were calculated in the dominant wind direction (east–west), but even the average values for all 360$^{\circ }$ directions showed almost no difference (the correlation coefficient was 0.998).

Although these parameters are theoretically independent, significant correlations were found among them. Figure 2a shows the correlation between $\lambda _\mathrm{f}$ and $\lambda _\mathrm{p}$ for the selected 1,000 $\times$ 1,000 m$^2$ districts (filled circles) together with all 1,000 $\times$ 1,000 m$^2$ districts in Tokyo (open circles) and five non-Japanese cities (triangles) from Ratti et al. (2002). The selected areas for the present LES were representative of all domains (622 $\text{ km }^2$) in Tokyo. The areas in which the value of $\lambda _\mathrm{p} < 0.2$ were all classified as “non-urban” land use in the conventional mesoscale simulations, which is why all the selected areas had values of $\lambda _\mathrm{p} > 0.2$. Four non-Japanese cities (Toulouse, Berlin, Salt Lake City, and Los Angeles; filled circles) followed this relationship, although London (filled triangle) did not. The values of $\lambda _\mathrm{f}$ can be approximated empirically by a quadratic function of $\lambda _\mathrm{p}$ up to $\lambda _\mathrm{p} = 0.45$ as

$$\begin{aligned} \lambda _\mathrm{f} =1.42\lambda _\mathrm{p} ^{2}+0.4\lambda _\mathrm{p} \quad \left( {0.45>\lambda _\mathrm{p} >0.05} \right) \!. \end{aligned}$$

(1)

Note that $\lambda _\mathrm{f}$ is always ${<}2\lambda _\mathrm{p}$. The upper limit of $\lambda _\mathrm{p}$ (around 0.45) is probably a result of building regulations. Figure 2b shows the close correlation of $\sigma _\mathrm{H}$ with $H_\mathrm{ave}$ in Tokyo, Nagoya, and the five non-Japanese cities as

$$\begin{aligned} \sigma _\mathrm{H} =1.05H_\mathrm{ave} -3.7. \end{aligned}$$

(2)

The zero limit of $\sigma _\mathrm{H}$ gives about 3.5 for $H_\mathrm{ave}$, which is around the height of a one-storey house. Although $H_\mathrm{max}$ could be correlated with $\sigma _\mathrm{H}$ as

$$\begin{aligned} H_\mathrm{max} =12.51\sigma _\mathrm{H} ^{0.77}, \end{aligned}$$

(3)

as shown in Fig. 2c, the scatter was large, especially for non-Japanese cities. This scatter is expected because large cities generally have a high-rise building or tower as a landmark at their centres. The precise height of such landmarks should be obtained from other data sources. If necessary, the height of the highest building in a district can be measured directly using a low-cost laser range finder.

The relationships expressed in Eqs. 1–3 are empirical relations applicable to Tokyo, Nagoya, and hopefully other Japanese cities with similar building regulations and planning. Of the five geometric variables for other non-Japanese cities, only $\lambda _\mathrm{p}$ can be easily generated from general town maps. The other four variables are more difficult to acquire owing to the requirement of height information. When the complete set of five variables is unavailable for a city, empirical formulations can be used as a first attempt.

Fig. 2

Relations among bulk geometric parameters. a $\lambda _\mathrm{f}$ versus $\lambda _\mathrm{p}$, b $\sigma _\mathrm{H}$ versus $H_\mathrm{ave}$, and c $H_\mathrm{max}$ versus $\sigma _\mathrm{H}$. Filled circles selected 1,000 $\times$ 1,000 m$^2$ districts, open circles all 1,000 $\times$ 1,000 m$^2$ districts in Tokyo (622 $\text{ km }^2$), filled triangles Toulouse (France), Berlin (Germany), Salt Lake City (USA), Los Angeles (USA), and open triangle London (England). The five non-Japanese datasets are from Ratti et al. (2002)

3.3 Addition of Simple Arrays of Buildings

To ensure robust parametrization, 23 simple arrays of buildings were added to the LES database. The arrays used were only square or staggered. Among 23 cases, 16 were arrays of homogeneous cubes or cuboids, and 7 were arrays of cuboids of variable height. The additional LES results for these simple arrays of buildings could be used for comparison with experimental data for the same geometries from the literature. Moreover, the results are useful for clarifying the differences in statistics among real urban geometries and simple artificial building arrays.

4 LES Database

4.1 Database

The LES results for 107 different urban surfaces, together with 23 simple arrays of buildings, provide a database of urban surface properties and turbulent flow statistics. Hereafter we call this database LES-Urban, which is composed of three different files for each urban surface: the colour map of building height (Fig. 2), the header file containing the bulk aerodynamic and geometric variables (Table 1), and the profile file containing the horizontally-averaged turbulent statistics and corresponding layered geometric parameters (not shown here). The horizontally-averaged turbulence statistics include wind velocity $(u)$, the standard deviations of $u, v,$ and $w,$ normalized by the friction velocity $u_{*}$, turbulent kinetic energy normalized by $u_{*}$, and total vertical momentum flux (Reynolds stress $+$ dispersive stress). LES-Urban is available open access at the following website; http://www.ide.titech.ac.jp/~kandalab/download/LES_URBAN/index.html.

Table 1 Example for the list of the header files of LES-Urban, containing the bulk geometric and aerodynamic variables

Because direct validation of LES-Urban was difficult, its results were compared with other data sources from the literature. The data used included two aerodynamic parameters of interest, the roughness length $z_0$ and the displacement height $d$, for idealized simple building arrays. The estimation of total drag or friction velocity is critical in the precise regression of the aerodynamic parameters (Cheng and Castro 2002; Cheng et al. 2007). Therefore, the experiments in which the total drag was numerically estimated from the balance of momentum in the domain (see Sect. 4.3) or directly measured using large floating elements were selected for the comparison. The data used for the comparison were from wind-tunnel experiments for aligned and staggered arrays of cubes (Cheng et al. 2007), wind-tunnel experiments for square and staggered arrays of buildings both with homogeneous height and variable height (Hagishima et al. 2009), wind-tunnel experiments for staggered arrays of buildings with variable height (Zaki et al. 2011), and DNS for staggered cube arrays (Leonardi and Castro 2010).

4.2 Momentum-Flux Profiles in Relation to Geometric Parameters

The height of the momentum-flux peak $H_\mathrm{uw}$ was observed above the mean building height in real cities (Kastener-Klein and Rotach 2004), but it was close to the maximum building height in the simple arrays of buildings with variable height (Kanda 2006). Here we examined $H_\mathrm{uw}$ in relation to geometric parameters for our aerodynamic parametrization. Figure 3 shows the profiles of the total vertical momentum flux (Reynolds stress $+$ dispersive stress) for the selected three specific urban surfaces, i.e., skyscrapers ID97, business district ID96, and residential area ID76, each of which corresponds to the area in Fig. 1. The cluster of skyscrapers with large $H_\mathrm{max}$ and $\sigma _\mathrm{H}$ produced a large momentum flux, and $H_\mathrm{uw}$ was close to $H_\mathrm{max}$. Although the business district has several scattered high rise buildings and thus a large $H_\mathrm{max}$, the major buildings of the area were of medium height with relatively smaller $\sigma _\mathrm{H}$. Consequently, in the business district, the momentum flux peak was smaller than that of the skyscrapers, and $H_\mathrm{uw}$ existed around the middle of $H_\mathrm{max}$ and $H_\mathrm{ave} +\sigma _\mathrm{H}$. The smallest $H_\mathrm{max} , \,\sigma _\mathrm{H}$, and $H_\mathrm{ave}$ values of the low-storey residential area minimized the momentum flux, and the range between $H_\mathrm{max}$ and $H_\mathrm{ave} +\sigma _\mathrm{H}$ was narrowest. $H_\mathrm{uw}$ still existed in this range.

Fig. 3

Profile of horizontally-averaged momentum flux for three different urban surfaces. a Skyscrapers ID97, b business district ID96, and c residential area ID76. The densely shaded area is the local plane area density for each 2-m layer, the lightly shaded area is the standard deviation of building height $\sigma _\mathrm{H}$ around the average building height $H_\mathrm{ave}$ (horizontal line), and the maximum building height $H_\mathrm{max}$ is shown by the dotted line

We confirmed that all values of $H_\mathrm{uw}$ existed between $H_\mathrm{max}$ and $H_\mathrm{ave} +\sigma _\mathrm{H}$ (not shown here). This was a good suggestion for the parametrization of $d$.

4.3 Estimation of Total Drag and Drag Partition

Provided that a quasi-steady turbulent state is achieved throughout a given region and the boundaries are cyclic in the $x$ and $y$ directions, the total drag can be easily and precisely derived from the balance of momentum in the $x$ direction using the imposed pressure gradient to maintain the flow rate (Leonardi and Castro 2010). The Navier–Stokes equation in the $x$-direction is

$$\begin{aligned} \frac{Du}{Dt}=-\frac{1}{\rho }\frac{\partial P}{\partial x}+\left( {\frac{\partial \tau _{xx} }{\partial x}+\frac{\partial \tau _{xy} }{\partial y}+\frac{\partial \tau _{xz} }{\partial z}} \right) , \end{aligned}$$

(4)

where $D/Dt$ is the substantial derivative, $u$ is the velocity component in the $x$ direction, $P$ is pressure, and $\tau _{xx} , \,\tau _{xy}$, and $\tau _{xz}$ are viscous stress components in the $x$ direction. The pressure gradient term can be decomposed into a constant part, which forces a given flow rate against the total drag, and a perturbation part, as $\partial P/\partial x=\partial p/\partial x+\partial p_*/\partial x$. The temporal and spatial average of Eq. 4 over the 1,000 $\times$ 1,000 m$^2$ horizontal plane leads to

$$\begin{aligned} \frac{D\left\langle {\bar{{u}}} \right\rangle }{Dt}=-\frac{1}{\rho }\left\langle {\frac{\overline{\partial p} }{\partial x}} \right\rangle +\frac{\partial \left\langle {-\overline{uw} } \right\rangle }{\partial z}-\left\langle {\overline{D_\mathrm{build} } } \right\rangle . \end{aligned}$$

(5)

The horizontal and temporal averages are represented by brackets and overbars, respectively. In the horizontal averaging process, both the perturbation pressure term and viscous stress terms integrated along the fluid and building boundaries remain. They result in a drag term owing to buildings, expressed by the final term $\left\langle {\overline{D_\mathrm{build} } } \right\rangle$. Note here that the advective component of momentum flux $-\left\langle {\overline{uw} } \right\rangle$ is composed of turbulent and dispersive contributions. Further integration of Eq. 5 from the floor $(z=0)$ to the domain top $(z=L_z)$ shows that the total drag per unit floor area $\tau _*$ (right hand side of Eq. 6) is easily derived from the constant pressure gradient (left hand side of Eq. 6). Numerically, partitioning of the total drag into drag at the floor and drag caused by the buildings is also possible as

$$\begin{aligned} \underbrace{-L_z \frac{1}{\rho }\left\langle {\overline{\frac{\partial p}{\partial x}} } \right\rangle }_\mathrm{forcing}=\underbrace{\bar{{\tau }}_{z=0} /\rho }_\mathrm{drag\, of\, floor}+\underbrace{\mathop \int \limits _0^{H_\mathrm{max} } \left\langle {\overline{D_\mathrm{build} } } \right\rangle \text{ d }z}_\mathrm{drag\, of\, buildings}=\underbrace{\tau _*/\rho \;.}_\mathrm{total\, surface\, drag} \end{aligned}$$

(6)

The dependence of the total drag on the geometric parameters will be discussed in detail later along with the parametrization of the roughness length. Here we briefly overview the behaviour of the drag partition. The ratios of drag at the floor $(D_\mathrm{s} =\bar{{\tau }}_{z=0} /\rho )$ to the total drag $(D_\mathrm{f} =\tau _*/\rho )$ are plotted in terms of $\lambda _\mathrm{p}$ (Fig. 4a). The values of $D_\mathrm{s} /D_\mathrm{f}$ for real urban surfaces (filled circles) decreased reasonably with increasing $\lambda _\mathrm{p}$ because the denser canopies had smaller portions of floor area and thus the ventilation near the floor decreased. The values of $D_\mathrm{s} /D_\mathrm{f}$ for the uniform building arrays (open circles) are systematically larger and more scattered than those for real urban surfaces. These large values of $D_\mathrm{s} /D_\mathrm{f}$ are probably owing to the enhancement of the flow near the floor by the simple street network. Inagaki et al. (2012) demonstrated in a LES simulation of a regular cube array that strong sweeps in the canopy mostly occur in the street axis parallel to the mean wind, which enhances the friction drag on the floor. The large scatter of $D_\mathrm{s} /D_\mathrm{f}$ is mainly due to the array types of square or staggered even with the same geometrical parameters; the former gives much larger values than the latter. This can also be explained by the enhancement of the flow near the floor by the simpler street network of square arrays.

Fig. 4

a The ratio of drag at the floor $(D_\mathrm{s} )$ to the total drag $(D_\mathrm{f} )$ versus $\lambda _\mathrm{p}$, b $D_\mathrm{s} /D_\mathrm{f}$ versus $\lambda _\mathrm{f} /\lambda _\mathrm{p}$. Filled circles real urban surfaces from LES-Urban, grey circles simple arrays with variable building height from LES-Urban, open circles uniform building arrays from LES-Urban, and open triangles staggered array of cubes from DNS by Leonardi and Castro (2010)

These tendencies are more clearly observed in the plot of $D_\mathrm{s} /D_\mathrm{f}$ versus $\lambda _\mathrm{f} /\lambda _\mathrm{p}$ (Fig. 4b). Because of the close correlation of $\lambda _\mathrm{f}$ and $\lambda _\mathrm{p}$ (Fig. 2a), larger values of $\lambda _\mathrm{f} /\lambda _\mathrm{p}$ imply denser and taller canopies. Thus it is reasonable that $D_\mathrm{s} /D_\mathrm{f}$ decreases with increasing $\lambda _\mathrm{f} /\lambda _\mathrm{p}$. Again, the uniform building arrays (open circles) give much larger values of $D_\mathrm{s} /D_\mathrm{f}$ than real urban surfaces (filled circles). The simple arrays of buildings with variable height (grey circles) give values of $D_\mathrm{s} /D_\mathrm{f}$ much closer to, but still slightly larger than, those of real urban surfaces. These results indicate that height variability is a key factor for modelling the real world, but even with variable heights of buildings the simple arrays are not perfect.

Note that $D_\mathrm{s} /D_\mathrm{f}$ from DNS (open triangle) is smaller than that from LES even for the same staggered cube arrays. This is due to the difference in the numerical treatment of the floor boundary condition. The DNS resolves the viscous sublayer and thus the skin friction is directly estimated, whereas LES uses wall functions depending on the parameter of the local roughness $z_{\mathrm{l}0}$ length at the floor and walls (0.1 m in this case).

4.4 Estimation of Aerodynamic Surface Parameters

Two major aerodynamic parameters, the aerodynamic roughness length $z_0$ and displacement height $d$, can be derived from the logarithmic law over urban-like surfaces as

$$\begin{aligned} \bar{{u}}=\frac{u_*}{\kappa }\ln \left( {\frac{z-d}{z_0 }} \right) , \end{aligned}$$

(7)

where $u_*=\sqrt{\frac{\tau _*}{\rho }}.$ The estimated aerodynamic parameters often show large scatter even for the same idealized urban-like surfaces. This can be attributed mainly to the differences in the method of estimating total drag $\tau _*$ and thus $u_*$, and differences in the regression procedure for two major parameters (Cheng and Castro 2002; Cheng et al. 2007). The direct estimation of total drag described in Sect. 4.3 can avoid the uncertainty in $u_*$. Among the available regression procedures, here we examine two major methods: one is the conventional two-parameter regression of $z_0$ and $d$ using the least-squares method with the von Karman constant of 0.4, hereafter called Method 1. The other is that by Leonardi and Castro (2010), in which two parameters $z_0$ and $\kappa$ are regressed using the least-squares method, and $d$ is directly estimated as the central height of the total drag or momentum absorption (Jackson 1981), hereafter called Method 2. This implies that $\kappa$ is variable (i.e., no longer constant) in Method 2.

Although the logarithmic fitting region varies according to the surface geometry, all regressions were performed consistently for the level between $H_\mathrm{max} +0.2H_\mathrm{ave}$ and $H_\mathrm{max} +H_\mathrm{ave}$. This criterion makes the fitting region for cube arrays $1.2H$ to $2H$, which is considered to be within the roughness sublayer (e.g. Cheng and Castro 2002). Some cases have extended logarithmic fitting regions to higher altitudes, whereas some other cases have limited logarithmic fitting regions at closer to the top of the highest building. Homogeneous cube arrays are the typical case of the former and the real building arrays with skyscrapers of variable height are the typical case of the latter. The higher the fitting region, the slightly lower (higher) the regressed roughness length (displacement height), for the cases with an extended logarithmic fitting region. The above criterion for the logarithmic fitting is just a common region where all the mean wind profiles follow the logarithmic law. Probably owing to the extended urban boundary layer with neutral stratification and the horizontally-averaged velocity profiles, the regressions worked fairly well for all LES runs even with highly inhomogeneous districts (Fig. 5), so long as the above logarithmic fitting criterion is used.

Fig. 5

Logarithmic law fitting of horizontally-averaged velocity for all LES runs. a Method 1 and b Method 2

Figure 6 shows a comparison of the aerodynamic parameters between the two methods described above. The displacement heights using Method 2 were lower than those using Method 1 by 25 % on average (Fig. 6a), meaning that the central height of momentum absorption is generally lower than the displacement height obtained from simple logarithmic law fitting. This result is consistent with the findings of Kanda (2006) and Leonardi and Castro (2010). In contrast, the roughness lengths using Method 2 were larger than those using Method 1 by 20 % on average (Fig. 6b). The new aerodynamic parametrizations proposed later (Sect. 5) were found to be valid for both methods, although the best-fit constant parameters used in the equations were slightly different. In the following section, we mainly discuss the results from Method 1, which is conventional, familiar, and easy to access. Method 2 requires momentum flux profiles, and it is unclear how to handle a variable von Karman constant in the parametrization.

Fig. 6

Comparison of regressed aerodynamic parameters between two methods: a displacement height $d/H_\mathrm{max}$ and b roughness length $z_0 /H_\mathrm{ave}$. Solid lines are the best-fitted linear lines, and the dotted lines indicate 1:1. Filled circles real urban surfaces from LES-Urban, and open circles simple building arrays from LES-Urban. All LES runs are plotted

Figure 7 shows the relationships between the regressed von Karman constant, and (a) the roughness Reynolds number $Re_*=u_*z_0 /\nu$ ($\nu$ is the viscosity of air), or (b) the plane area density. The calculated von Karman constants in this study are mostly ${<}0.4$ as obtained in flat terrain. Although Andreas et al. (2006) suggested from their observations over Antarctic sea ice that the von Karman constant may depend on the roughness Reynolds number, the present regressed values of $\kappa$ from Method 2 appear to be largely scattered and the dependency on $Re_*$ is weak. The values of $\kappa$ for simple building arrays appear to decrease in proportion with increasing $\lambda _\mathrm{p}$, but those for real urban surfaces have a weak relationship with $\lambda _\mathrm{p}$.

Fig. 7

Regressed von Karman constant $(\kappa )$ using Method 2 versus a roughness Reynolds number and b plane area density. Filled circles real urban surfaces from LES-Urban, grey circles simple arrays with variable building height from LES-Urban, open circles simple array of cubes from LES-Urban, and open triangles simple array of cubes from DNS by Leonardi and Castro (2010)

5 New Aerodynamic Parametrization for Real Urban Surfaces

5.1 Aerodynamic Surface Parameters Plotted by the Conventional Macdonald Equation

First we tested the performance of the Macdonald equation in the current real urban database and examined whether a simple extension of this classic formulation was possible. According to Macdonald et al. (1998b), $z_0$ and $d$ are described as

$$\begin{aligned}&\displaystyle \frac{d}{H_\mathrm{ave} }=1+A^{-\lambda _\mathrm{p} }\left( {\lambda _\mathrm{p} -1} \right) ,\end{aligned}$$

(8)

$$\begin{aligned}&\displaystyle \frac{z_0 (\text{ mac })}{H_\mathrm{ave} }=\left( {1-\frac{d}{H_\mathrm{ave} }} \right) \exp \left[ {-\left\{ {0.5\beta \frac{C_\mathrm{lb} }{\kappa ^{2}}\left( {1-\frac{d}{H_\mathrm{ave} }} \right) \lambda _\mathrm{f} } \right\} ^{-0.5}} \right] , \end{aligned}$$

(9)

where $A$ and $\beta$ are parameters with values of 4.43 and 1.0, respectively, $C_\mathrm{lb} = 1.2$ is the drag coefficient of an obstacle, and $\kappa = 0.4$ is the von Karman constant, for simple staggered building arrays with uniform height. The parameters $A$ and $\beta$ were originally optimized for different arrays, but are used as constants for this simplification.

Most $d/H_\mathrm{ave}$ values of real urban surfaces (filled circle) are far above the prediction of Macdonald and also larger than 1.0 (Fig. 8a), implying that the displacement height is greater than the average building height. Next, we examined the simple replacement of $H_\mathrm{ave}$ with $H_\mathrm{max}$ in Eq. 8 (Fig. 8b). The results show that most of the $d/H_\mathrm{max}$ values of real urban surfaces were far below the predictions of Macdonald and also different from simple arrays with variable building height (grey circle and triangle). Such large departures of the $d/H_\mathrm{ave}$ values of real urban surfaces from Macdonald’s prediction suggest the difficulty of simple extensions of this conventional method.

Fig. 8

a $d/H_\mathrm{ave}$ versus $\lambda _\mathrm{p}$ with Macdonald equation (Eq. 8), and b same as Fig. 8a but replacing $H_\mathrm{ave}$ with $H_\mathrm{max}$, i.e., $d/H_\mathrm{max}$ versus $\lambda _\mathrm{p}$. Filled circles real urban surfaces from LES-Urban, grey circles simple arrays with variable building height from LES-Urban, open circles uniform building arrays from LES-Urban, and triangles simple arrays with variable building height from the experiments by Hagishima et al. (2009). The solid line shows the Macdonald Eq. 8. The corresponding results from Method 2 is open access in the following website. http://www.ide.titech.ac.jp/~kandalab/download/LES_URBAN/FIG_METHOD2.pdf

Considering the actual range of $\lambda _\mathrm{f} \le 2\lambda _\mathrm{p}$ (see Fig. 2a), we compared the Macdonald predictions of $z_0 /H_\mathrm{ave}$ for $\lambda _\mathrm{f} =\lambda _\mathrm{p}$ (solid line) and $\lambda _\mathrm{f} =2\lambda _\mathrm{p}$ (dotted line) with those from the LES database (Fig. 9a). Although some of the $z_0 /H_\mathrm{ave}$ values for real urban surfaces were again far beyond Macdonald’s prediction, some were still within range; also, all values of $z_0 /H_\mathrm{ave} < 1.0$. The replacement of $H_\mathrm{ave}$ with $H_\mathrm{max}$ in Eq. 9 did not work well, as most $z_0 /H_\mathrm{ave}$ values of real urban surfaces were less than the prediction of Macdonald (Fig. 9b). These results suggest that $H_\mathrm{ave}$ is still an appropriate length scale for $z_0$ and that the Macdonald equation might be still be valid with some modifications.

Fig. 9

a $z_0 /H_\mathrm{ave}$ versus $\lambda _\mathrm{p}$, with the Macdonald Eq. 9, and b same as (a) but replacing $H_\mathrm{ave}$ with $H_\mathrm{max}$, i.e., $z_0 /H_\mathrm{max}$ versus $\lambda _\mathrm{p}$. Filled circles real urban surfaces from LES-Urban, grey circles simple arrays with variable building height from LES-Urban, open circles uniform building arrays of from LES-Urban, and triangles simple arrays of buildings with variable height from the experiments by Hagishima et al. (2009). The solid line shows Macdonald Eq. 9 for $\lambda _\mathrm{f} =\lambda _\mathrm{p}$. The dotted line shows the Macdonald Eq. 9 for $\lambda _\mathrm{f} =2\lambda _\mathrm{p}$. The corresponding results from Method 2 is open access in the following website. http://www.ide.titech.ac.jp/~kandalab/download/LES_URBAN/FIG_METHOD2.pdf

5.2 New Aerodynamic Surface Parametrization of Displacement Height

We propose a new parametrization of displacement height for real urban surfaces

$$\begin{aligned}&\frac{d}{H_\mathrm{max} }=c_0 X^{2}+\left( {a_0 \lambda _\mathrm{p} ^{b_0 }-c_0 } \right) X,\end{aligned}$$

(10a)

where

$$\begin{aligned}&X=\frac{\sigma _\mathrm{H} +H_\mathrm{ave} }{H_\mathrm{max} },\quad 0\le X\le 1.0, \end{aligned}$$

(10b)

where $a_0 , \,b_0$, and $c_0$ are the regressed constant parameters, i.e., 1.29, 0.36, and $-0.17$, respectively, for Method 1. Method 2 provides different constant parameters $a_0 , \,b_0$, and $c_0$ as 0.86, 0.28, and $-0.18$, respectively. Considering that $d$ can be interpreted physically as the central height of momentum absorption (Jackson 1981), the momentum flux profile should be most influential on $d$. $H_\mathrm{max}$ seems to be the appropriate length scale for the normalization of $d$ because $H_\mathrm{max}$ is the upper limit of $d$. Then, the key parameter of $X$ was found both physically and empirically. As demonstrated in the momentum flux profiles (see Fig. 3), a peak in momentum flux exists between $\sigma _\mathrm{H} +H_\mathrm{ave}$ and $H_\mathrm{max}$, and thus these two heights are likely to be important. Among various non-dimensional parameters composed of three geometric variables, $X$ was found to perform best. The physical meaning of $X$ is clear: it is the representative building height above the average building height $(\sigma _\mathrm{H} +H_\mathrm{ave} )$ relative to the maximum building height $H_\mathrm{max}$. The upper limit of $X = 1$ means an array of buildings of homogeneous height, and the lower limit of $X = 0$ means a district in which the highest building is an isolated tower that is exceptionally higher than the major buildings around it and has a negligibly small cross section. The equation above at the upper limit of $X = 1$ can provide the displacement height for simple arrayed cubes as follows:

$$\begin{aligned} \frac{d}{H_\mathrm{max} }=\frac{d}{H_\mathrm{ave} }=a_0 \lambda _\mathrm{p} ^{b_0 }. \end{aligned}$$

(11)

The performance of Eq. 11 at $X = 1$, i.e., $\sigma _\mathrm{H} = 0$ and $H_\mathrm{max} =H_\mathrm{ave}$, appears to be fairly good for the current LES database and experimental dataset (Fig. 10a).

Fig. 10

Applicability of new aerodynamic parametrizations in the case of $\sigma _\mathrm{H} = 0$ (homogeneous buildings) by Method 1. a $d/H_\mathrm{max}$ versus $\lambda _\mathrm{p}$, with the new parametrization Eq. 11 as the lower limit of $X = 1$ in Eq. 10. The solid line shows Eq. 11. The “staggered” (open circles) and “square” (open squares) points are from LES-Urban, “DNS” (open triangles) is from Leonardi and Castro (2010), “EXP(Hagishima)” is from Hagishima et al. (2009), and “EXP(Cheng)” is from Cheng et al. (2007). b $z_0 /H_\mathrm{ave}$ versus $\lambda _\mathrm{p}$ with the new parametrization 13 as the lower limit of $Y = 0$ in Eq. 12. The solid line shows Eq. 13. The symbols are all the same as in (a). The corresponding results from Method 2 is found in the following website. http://www.ide.titech.ac.jp/~kandalab/download/LES_URBAN/FIG_METHOD2.pdf

Practically, the construction of Eq. 10 started from Eq. 11 to ensure applicability to conventional idealized cube arrays at the extreme limit. Consequently, $d/H_\mathrm{max}$ can be successfully regressed in terms of $X$ and $\lambda _\mathrm{p}$ (Fig. 11). Although the scatter is still large, Eq. 11 can roughly predict the normalized displacement height for real urban surfaces in Tokyo and Nagoya (white symbols except $X = 1$), in laboratory experiments both with inhomogeneous building height (grey symbols) and homogeneous building height ($X = 1$), as shown in Fig. 11.

Fig. 11

$d/H_\mathrm{max}$ versus $(\sigma _\mathrm{H} +H_\mathrm{ave} )/H_\mathrm{max}$ with the new parametrization by Method 1. The lines show Eq. 10, while open symbols are from LES-Urban, shaded symbols are from Hagishima et al. (2009), and filled symbols are from Zaki et al. (2011). The plots at $X = 1$ are consistent with Fig. 10a. The corresponding results from Method 2 is found in the following website. http://www.ide.titech.ac.jp/~kandalab/download/LES_URBAN/FIG_METHOD2.pdf

5.3 New Aerodynamic Surface Parametrization of Roughness Length

We propose a new parametrization of roughness length for real urban surfaces in the form of a modified Macdonald equation:

$$\begin{aligned}&\frac{z_0 }{z_0 (\text{ mac })}=b_1 Y^{2}+c_1 Y+a_1 , \end{aligned}$$

(12a)

where

$$\begin{aligned}&Y=\frac{\lambda _\mathrm{p} \sigma _\mathrm{H} }{H_\mathrm{ave} },\quad 0\le Y, \end{aligned}$$

(12b)

where $a_1 , \,b_1$, and $c_1$ are the regressed constant parameters, i.e., 0.71, 20.21, and $-0.77$, respectively. $z_0 (\text{ mac })$ is the roughness length obtained from two Macdonald equations, (8) and (9). Method 2 provides constant parameters $a_1 , \,b_1$, and $c_1$ as 0.93, 8.93, and 4.68, respectively. $z_0$ is always smaller than $H_\mathrm{ave}$ (Fig. 9a), and thus $H_\mathrm{ave}$ still appears to be the appropriate scale length for roughness. Unlike the parametrization of $d$, which is determined only from the momentum flux profile, the parametrization of $z_0$ should also reflect the integrated aspect of momentum absorption within the canopy. We have several reasons to believe that the modified Macdonald equation works well. First, the Macdonald formulation of $z_0$ has a physical background. Second, the departure of the prediction of the Macdonald equation from the LES results is not as large as that of the displacement height. Third, previous laboratory and numerical experiments reported that $\sigma _\mathrm{H}$ significantly increases $z_0$ in accordance with increasing $\lambda _\mathrm{p}$ (Macdonald et al. 1998a; Kanda 2006; Hagishima et al. 2009; Zaki et al. 2011). Then the finding of the key parameter $Y$ was rather straightforward, considering the potential importance of $\sigma _\mathrm{H}$ and $\lambda _\mathrm{p}$ on $z_0$ as mentioned above. Although the highest building is known to influence the drag (Kanda 2006; Xie et al. 2008), $H_\mathrm{max}$ does not appear explicitly in Eq. 12. In addition, the close correlation of $H_\mathrm{max}$ with $\sigma _\mathrm{H}$, as in Fig. 2c, suggests that the influence of $H_\mathrm{max}$ is implicitly included in $Y$ through $\sigma _\mathrm{H}$.

The above equation at the lower limit of $Y = 0$ can provide roughness lengths for simple arrays of cubes as follows:

$$\begin{aligned} \frac{z_0 }{z_0 (\text{ mac })}=a_1 . \end{aligned}$$

(13)

The performance of Eq. 13 at $Y=0$, i.e., $\sigma _\mathrm{H} =0$, was good for the current LES database and experimental dataset, although some scatter remained, mainly owing to the fixed parameters $A$ and $\beta$ in Eqs. 9 and 10 irrespective of the array type (staggered or square), as shown in Fig. 10b. For practicality, the construction of Eq. 12 started first from Eq. 13 to ensure applicability for conventional idealized cube arrays at the extreme limit. The best fit value of $a_1\, (= \, 0.71) < 1.0$ means that the original Macdonald equation systematically overestimates the roughness length of simple cube arrays. Figure 12 demonstrates that the new parametrization in Eq. 12 could roughly predict the normalized roughness length for real urban surfaces in Tokyo and Nagoya together with those for simple building arrays. Densely built up areas with highly inhomogeneous skylines, i.e., areas with large $Y$, can have roughness lengths five times greater than those of the original Macdonald equations.

Note here that the new parametrization of the roughness length Eq. 12 is independent of the displacement height in Eq. 10a. This inconsistency in the formulation is attributed to their empirical derivation. The original Macdonald’s equation, Eq. 9, has a theoretical background and includes the displacement height Eq. 8.

Fig. 12

$z_0 /z_0 (\text{ mac })$ versus $\lambda _\mathrm{p} \sigma _\mathrm{H} /H_\mathrm{ave}$ with the new parametrization by Method 1. Solid line Eq. 12, filled circles realistic geometry of LES-Urban, grey circles variable height of LES-Urban, open circles uniform building arrays of LES-Urban, open triangles Hagishima et al. (2009), and grey triangles Zaki et al. (2011). The plots at $Y=0$ are consistent with Fig. 10b. The corresponding results from Method 2 is open access in the following website. http://www.ide.titech.ac.jp/~kandalab/download/LES_URBAN/FIG_METHOD2.pdf

5.4 Performance of the New Parametrizations

Figure 13 shows the correlation between the roughness parameters predicted only from geometric information using the proposed new aerodynamic parametrization and those from LES-Urban. The performance of the new parametrizations was acceptable; the correlation coefficients between LES-Urban and the predictions for $d/H_\mathrm{max}$ and $z_0 /H_\mathrm{ave}$ were 0.78 and 0.55, respectively.

Fig. 13

Performance of new aerodynamic parametrizations by Method 1. Filled circles realistic geometry of LES-Urban, and open circles simple building arrays of LES-Urban and experiments used in Figs. 11 and 12. a Displacement height normalized by maximum building height $(d/H_\mathrm{max})$ from LES-Urban and experiments ($x$-axis: observation) versus that from new parametrization ($y$-axis: prediction by Eq. 10). b Roughness length normalized by average building height $(z_0 /H_\mathrm{ave})$ from LES-Urban and experiments ($x$-axis: observation) versus that from new parametrization ($y$-axis: prediction by Eq. 12). The map of building height for the districts with the ID number is in Fig. 14. The corresponding results from Method 2 is open access in the following website. http://www.ide.titech.ac.jp/~kandalab/download/LES_URBAN/FIG_METHOD2.pdf

However, there were poor predictions in some districts (ID numbers in Fig. 13). The districts with poor roughness parameter predictability commonly had poorly represented area-averaged geometric parameters contributing to the momentum exchange process, as illustrated below. The area of $d/H_\mathrm{max}$ overestimation (ID87 in Fig. 13a) included a cluster of high-rise buildings of similar heights $(H_\mathrm{max} \approx H_\mathrm{ave})$ concentrated only in the centre of the domain (Fig. 14a). In such cases, the value of $(\sigma _\mathrm{H} +H_\mathrm{ave} )/H_\mathrm{max}$ became large, similar to the case of homogeneous buildings (see Fig. 11), and caused a large estimation of $d/H_\mathrm{max}$. One difference from the homogeneous building array is the clustering of the buildings, which creates broad vacancies where high wind speed can occur at the lowest layer. The displacement height then becomes small.

The area of large overestimation of $z_0 /H_\mathrm{ave}$ (ID60 in Fig. 13b) had isolated high buildings aligned in the current wind direction (Fig. 14b). The current wind direction maximizes the interference of wakes among individual isolated taller buildings. The area-averaged geometric parameters cannot account for such wind-direction dependencies, leading to an overestimation of $z_0 /H_\mathrm{ave}$ in this case. As was seen, the large departures between the observed and predicted roughness parameters can be attributed to the representativeness of the area-averaged geometric parameters. For example, even districts with the same values of $\lambda _\mathrm{f}$ can differ in terms of how frontal areas overlap in the dominant wind direction, such as for square and staggered arrays. The addition of wind direction-dependent geometric parameters to the aerodynamic parametrization should improve the predictability of $d/H_\mathrm{max}$ and $z_0 /H_\mathrm{ave}$, although derivation and parametrization can be difficult.

Fig. 14

Map of building height for districts where the new parametrization performed poorly, a ID87, b ID60 or a very high and slender tower exists, c ID10, d ID63. See also Fig. 13, which shows the plot corresponding to the ID numbers

The appropriateness of the normalization of $d$ using “$H_\mathrm{max}$” even to the areas with an extremely high, slender, and isolated tower, should be examined. Figure 14c (ID 10) and Fig. 14d (ID 63) are such areas. The tallest cylindrical tower in ID10 is very slender, i.e., 216 m tall and 8 m in diameter. However, the predictability of $d/H_\mathrm{max}$ in ID10 is fairly good (Figs. 11, 13). As expected, exceptionally tall towers make the values of $X$ and $d/H_\mathrm{max}$ small due to the nature of Eq. 10. The value of $d/H_\mathrm{max}$ in ID63 is, however, underestimated (Figs. 11, 13). The tallest tower in ID63 is a quadrangular pyramid 333 m tall and with an 80 m length at the basement. One possible reason for the underestimation is the influence of three or four middle class towers (100–150 m high). A few middle class towers can significantly contribute to the drag formation but only slightly increase $X$ by increasing $H_\mathrm{ave}$ and $\sigma _\mathrm{H}$. Another possibility is the poor regression of Method 1 for the coexistence of an extreme high tower and a few scattered middle class towers. The value of $d/H_\mathrm{max}$ from Method 2, whereby the displacement height is physically determined from LES, is much smaller than that from Method 1 (Table 1) and closer to the predicted value of Eq. 10. However, the regressed von Karman constant of Method 2 is 0.27 (Table 1) and thus another serious problem arises, i.e., how to model the variable Karman constant.

6 Concluding Remarks

The LES database (LES-Urban) of 107 districts in Tokyo and Nagoya, together with 23 conventional simplified arrays of buildings, clearly illustrated the essential difference in bulk flow properties over real urban surfaces and over simplified arrays. The bulk indices such as the aerodynamic roughness parameters, floor drag/total drag ratio, and variable von Karman constants (only Method 2) were all systematically different between the real cities and simplified models. Simplified street networks significantly enhanced the streams near the floor and minimized the interferences of wakes among individual buildings. However, height variation of buildings, even in simple arrays, produced results that were closer to those for real urban surfaces, meaning that the variability of the building heights is more relevant than the complexity of the streets.

Even though the bulk flow properties of simple arrays of buildings and of real cities are very different, the proposed new aerodynamic parametrizations of $z_0$ and $d$ using combinations of just five geometric parameters, $H_\mathrm{ave} , \,H_\mathrm{max} , \,\sigma _\mathrm{H} , \,\lambda _\mathrm{f}$, and $\lambda _\mathrm{p}$, worked fairly well for real urban morphologies, as well as for conventional simplified model geometries. Although the relations proposed were basically empirical, the processes of deriving the parametrization form and of introducing each explanatory variable $X=\left( {\sigma _\mathrm{H} +H_\mathrm{ave} } \right) /H_\mathrm{max}$ and $Y=\lambda _\mathrm{p} \sigma _\mathrm{H} /H_\mathrm{ave}$ were based on physical insights obtained from LES-Urban and the literature. The roughness parameters $z_0$ and $d$ normalized by the average building height for real urban surfaces can be several times larger than those predicted by the conventional Macdonald equations, and the new parametrizations were largely improved to reproduce these large roughness parameters.

The unexpected by-products of this research are interesting and worth noting for further applications. First, the empirical relationship between $\sigma _\mathrm{H}$ and $H_\mathrm{ave}$ appears to be applicable not only for Japanese cities but also for major world cities. Further investigation for various major cities is necessary to compile a fuller aerodynamic parameter database (e.g., Ratti et al. 2002). Second, LES-Urban contains a huge dataset of vertical profiles of turbulent flow statistics. This database will be useful for improving multilayer urban canopy modelling (e.g., Santiago et al. 2008) because real urban canopies are complex, and thus the resulting dispersive fluxes are larger and wind profiles are more difficult to model than for simple building arrays. Third, if the von Karman constant is not constant but variable (Andreas et al. 2006; Leonardi and Castro 2010), further investigations are necessary. Although detailed discussion of the mechanism of variable von Karman constants is beyond the scope of the present paper, the bulk parameters derived from Method 2 can be helpful for future examinations.

Finally several suggestions or cautions regrading the implementation of the new parametrizations into general numerical mesoscale models are given. First, the displacement height should not be treated in the framework of Monin–Obukhov similarity but should be directly added to the topography, because the value can be several dozens of metres and also higher than the thickness of the lowest grid of the mesoscale models. This treatment was confirmed to work fairly well (Varquez et al. 2012). Second, the most appropriate grid size for the application of new parametrizations is around 1 km. The dependency of grid resolution on the simulation result is currently unknown.