A Wind-Tunnel Simulation of the Wake of a Large Wind Turbine in a Weakly Unstable Boundary Layer

Abstract

Measurements have been made in the wake of a model wind turbine in both a weakly unstable and a baseline neutral atmospheric boundary layer, in the EnFlo stratified-flow wind tunnel, between 0.5 and 10 rotor diameters from the turbine, as part of an investigation of wakes in offshore winds. In the unstable case the velocity deficit decreases more rapidly than in the neutral case, largely because the boundary-layer turbulence levels are higher with consequent increased mixing. The height and width increase more rapidly in the unstable case, though still in a linear manner. The vertical heat flux decreases rapidly through the turbine, recovering to the undisturbed level first in the lower part of the wake, and later in the upper part, through the growth of an internal layer. At 10 rotor diameters from the turbine, the wake has strong features associated with the surrounding atmospheric boundary layer. A distinction is drawn between direct effects of stratification, as necessarily arising from buoyant production, and indirect effects, which arise only because the mean shear and turbulence levels are altered. Some aspects of the wake follow a similarity-like behaviour. Sufficiently far downstream, the decay of the velocity deficit follows a power law in the unstable case as well as the neutral case, but does so after a shorter distance from the turbine. Tentatively, this distance is also shorter for a higher loading on the turbine, while the power law itself is unaffected by turbine loading.

1 Introduction

Wind turbines operate in the atmospheric boundary layer (ABL) where the mean flow and turbulence are driven by mechanical production and, in convective conditions, by buoyant production, while for inversion conditions the turbulence is suppressed through buoyancy forces inhibiting vertical motions, except in neutral or near-neutral conditions where neither effect is significant. The distributions of mean velocity and turbulence quantities with height are very different in each of these categories of airflow, depending upon the degree to which the flow is stable or unstable. It is to be anticipated, therefore, that there should be at least a significant effect of airflow category on the performance of a wind turbine and on the behaviour of its wake. Indeed, several studies have shown this to be so. Overland, inversion conditions exist predominantly in the nocturnal boundary layer, while convective conditions predominate during daytime. Light wind conditions are arguably of particular interest in the optimization of wind-farm output, where one turbine extracting too much power can starve one or more downwind turbines because of a wake deficit that is too large (Hancock 2013).

In terms of the effects on power output, the studies include those of Motta and Barthelmie (2005), Sathe and Bierbooms (2007), van den Berg (2008), Wagner et al. (2009), Wharton and Lundquist (2010), Barthelmie et al. (2011) and Peña et al. (2014). It is not necessary here to review these in detail, but a few points are worth raising. Wharton and Lundquist (2010) observed, for a given hub-height mean wind speed, a higher power output when the airflow was stable compared to the neutral case, and a lower output when the airflow was convective. They attributed this to the differences in shear in the mean wind-speed profile, with high shear corresponding to stable flow, with an attendant ‘low’ level of vertical mixing, and low shear arising because of a ‘high’ level of vertical mixing in the unstable case. The behaviour in the stable case can be made more complex by the presence of a nocturnal low-level jet, as noted by Wharton and Lundquist (2010). Field studies of turbine wake measurements include those of Baker and Walker (1984), Högström et al. (1988), Magnusson and Smedman (1994, (1996, (1999), Trujillo et al. (2011) and Iungo and Porté-Agel (2014), while the effect of wakes as inferred from the power output from downwind turbines is given by, for example, Barthelmie et al. (2010) and Hansen et al. (2012). A number of the above-cited papers classify the observations in terms of the prevailing flow stability, and it is clear that the effects of stability, while largest at low wind speeds and being site-dependent, are certainly large or significant over the lower half of the typical operating speed range, for most of the time. Hansen et al. (2014) demonstrate significant effects of atmospheric stability on fatigue loads from measurements on an instrumented 2 MW turbine. Abkar and Porté-Agel (2014), by means of large-eddy simulation, show the effect of stable and convective flow on wake development of a single turbine, against that in a baseline neutral flow. The data analysis by Argyle and Watson (2012) for two UK offshore sites, for example, indicates that the flow is non-neutral for over 70 % of the time. Comparable findings were obtained in the UpWind project (Hansen et al. 2012). However, assessments of wind resource for wind farms assume neutral-flow conditions (see e.g. Sanderse et al. 2011). In the context of wind turbines, relatively little is known about the influence of non-neutral conditions.

The ABL is characterized by several parameters. For a neutral ABL this is the boundary-layer height, $h$, the friction velocity, $u_{*}$, and the aerodynamic roughness length, $z_{0}$, while for a non-neutral ABL additional parameters are relevant. In the surface layer, with a depth of about $0.1h$, the scaling parameters are the surface temperature, $\Theta _{0}$, the surface heat flux, denoted here by $(\overline{w\theta })_{0}$, and the thermal roughness length, $z_{0\theta }$. The (surface) Obukhov length, $L_{0}$, is defined by $L_{0}=-\Theta u_{*}^{3}/(\kappa g (\overline{w\theta })_{0})$, where $\Theta$ is the absolute temperature, $\kappa$ is the von Karman constant, and $g$ is the acceleration due to gravity. The height of the ABL, whether convective or neutral, is usually defined in terms of an overlying inversion layer, and in which the turbulence is weak compared to that in the ABL.

In contrast to a neutral ABL, where the height $h$ is (say) ${\approx }1~\hbox {km}$, the height of a stable boundary layer may be ${<}200\hbox { m}$, while the height of a convective boundary layer is typically ${>}2\hbox { km}$.¹ Given the size of current large wind turbines—for a 5 MW turbine the hub height and blade length would typically be 90 and 60 m, respectively—the rotor will be subjected to a wide range of energy-containing length scales in the oncoming flow, with the tip-top height possibly exceeding the height of a stable ABL, while for a convective layer it may be immersed within the surface layer. Therefore, for a stable ABL flow, the strength of the inversion above the ABL, the ‘imposed’ condition, is clearly an important condition, while for a convective ABL the strength of the inversion is likely to be of minor importance.

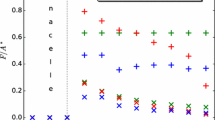
In addition to the change of length scale, $h$, with the influence of stabilizing or convective forces, there is also a very marked change in the levels of turbulence to which a wind turbine and its wake are subject. Now, an increase in ABL turbulence level can be expected to subject the turbine blades to increased levels of fluctuating velocity and incidence and, therefore, to increased levels of fluctuating lift and drag, and to influence the growth and deficit decay of the blade wakes. But, in this interaction, the length scale of energy containing motions of the ABL will be orders of magnitude larger than that of the blade boundary layers and blade wakes, and of the blade chord.² Thus, since the effects of stability or instability are primarily large-scale effects, it can be anticipated that there will be no ‘direct’ effects of stability or instability on the turbine blades; the effects will be merely ‘indirect’ because of stability or instability in the ABL determining the level of turbulence and also mean shear. However, the wake of the turbine, once it has developed sufficiently, will have a length scale that is of order the rotor diameter, $D$, which is two orders of magnitude larger than that of the blade chord for a typical turbine. Therefore, for large turbines, it is to be anticipated that two effects will be present in the wake; indirect effects associated simply with the level of turbulence and mean shear in the ABL; direct effects arising from the presence of buoyancy forces. In an earlier study, Hancock and Pascheke (2014b) inferred indirect and direct effects in their case of a stable boundary layer. Figure 1 shows an increase of wake width when compared with neutral flow, and a marked reduction in the wake half-height, both inferred as predominantly direct effects in that case.

Fig. 1

Variation of wake half-height, $H$, and wake width, $W$, with distance $x/D$, for the measurements of Hancock and Pascheke (2014b)

Wind-tunnel studies of wind-turbine wakes in non-neutral flow have also been made by Chamorro and Porté-Agel (2010) for a stable ABL, and by Zhang et al. (2013) for a convective flow. In terms of bulk Richardson number, $Ri_{b}$, the study of Zhang et al. (2013) had $Ri_{b} = -0.13$, whereas in the present study $Ri_{b}= -0.34$, with $Ri_{b}=g h \Delta \Theta /(\Theta U_{0}^{2})$. Note, $\Delta \Theta$ is the difference in temperature between height $h$ and the surface, and $U_{0}$ is the wind speed at height $h$. Zhang et al. (2013) observed a more rapid reduction in the maximum velocity deficit and higher wake turbulence, although the differences were not as large as in the present investigation, owing to the difference in Richardson number. They only give measurements in a vertical plane (aligned with the turbine hub axis), so there is no information on the width of the wake, for example. Results of related studies are given in Hancock et al. (2012, (2014) and Hancock and Farr (2014).

2 Wind Tunnel, Wind Turbine, Instrumentation and Reference Boundary Layers

Details are mostly as given in Hancock et al. (2013) and, for the model turbine, in Hancock and Pascheke (2014b), but are repeated here for completeness. In terms of simulating flow in a boundary-layer tunnel, two obvious similarity parameters are the ratio of the turbine rotor diameter to the Obukhov length, $D/L_{0}$, and the ratio $h/L_{0}$. The hub height is also a relevant parameter, of course; here we assume it is in fixed proportion to the diameter. Hancock et al. (2013) have shown that the temperature gradient in the mixed layer (and also the overlying inversion) for similarity, full-to-model scale, is governed by,

$$\begin{aligned} \left( {\frac{D}{U_\mathrm{R}}}\right) ^{2}\frac{\partial \Theta }{\partial z}=\hbox {constant}, \end{aligned}$$

(1)

where $U_\mathrm{R}$ is a reference velocity at some geometrically equivalent height. Thus, for similarity, as $D/U_\mathrm{R}$ is decreased, the temperature gradient must be increased according to Eq. 1.

2.1 Wind Tunnel and Instrumentation

Measurements were made in the EnFlo wind tunnel that has a working section 20 m long, 3.5 m wide and 1.5 m high. It is an open-return suck-down type with 15 heaters at the working section inlet (each covering 100 mm in height) and a heat exchanger between the end of the working section and the fans, supplied by a chilled water system. As only a 3 m width of the floor is heated (or cooled for stable flow), Perspex side panels were employed in all cases, from the working section inlet to $X = 18\hbox { m}$, where $X$ is the distance from the working-section inlet. Irwin-type flow-generator spires (Irwin 1981) were placed at the working section inlet, and were formed from slightly truncated triangles, 1490 mm high, 150 mm wide at the bottom, 10 mm wide at the top, spaced laterally 660 mm. (No fence was employed.) The surface roughness elements were sharp-edged brick-like blocks 50 mm wide, 16 mm high, 5 mm thick, standing on the 50 mm $\times$ 5 mm face. They were placed in a staggered arrangement with streamwise and lateral pitches of 360 and 510 mm, respectively, with alternate rows displaced laterally to give the staggered pattern.

The laser Doppler anemometer (LDA) probe, fast-response cold-wire temperature probe and a mean-temperature thermocouple probe were supported on the main wind-tunnel probe traversing system, and freely moveable vertically between $z = 40$ and 1050 mm, where $z$ is the distance from the wind-tunnel floor. Measurements at a lower height would have been influenced more by the local flow generated by the individual roughness elements, rather than the smoothed-out effect seen at larger $z$. The cold wire was set at about 3 mm behind the LDA measuring volume, and the thermocouple set to the side separated by about 15 mm from the measuring volume. The frequency response of the cold-wire system was high enough to include the first decade of the inertial subrange. The measuring volume of the Dantec 27 mm FibreFlow probe was about 3 mm in length, and so an offset of the cold wire by this distance was deemed satisfactory. The cold-wire probe was calibrated against the mean temperature of the thermocouple. Only the streamwise and vertical velocity components were measured. Errors associated with using the LDA in a non-isothermal flow are considered in Hancock and Pascheke (2014a) and can be shown to be negligible. A reference ultrasonic anemometer was placed at $X = 5\hbox { m}$, $z = 1\hbox { m}$, $Y = -0.78\hbox { m}$, where $Y$ is the lateral position from the centreline. The reference speed, $U_{\mathrm{REF}}$, for all measurements was $1.5\hbox { m s}^{-1}$.

Sample periods for each point were 3 min. The main source of error in first-order and second-order moments was in the statistical sampling interval, for which the error bands are about $\pm 1~\%$ for mean velocity and about $\pm 10~\%$ for Reynolds stresses and turbulent heat flux. (Profiles of non-dimensional parameters such as the correlation coefficients are smoother than the constituent turbulence quantities.) The absolute uncertainty in $z$ was about $\pm 2\hbox { mm}$ owing to a slight undulation in the floor and variation in the probe traverse rails system, and is small enough to be ignored. The error in the intervals in $z$ was negligible. Data acquisition was by means of the standard LabView-based software system of the laboratory.

2.2 Baseline Boundary Layers

The baseline boundary layers include a neutral boundary layer and a weakly convective boundary layer, details of which are given in Hancock et al. (2013). In summary, the neutral boundary layer is based on ESDU (2001, (2002) guidelines, adjusted to a reference speed of $10\hbox { m s}^{-1}$ at a height of 10 m, for a typical offshore sea-surface roughness, and a full-to-model scale ratio of 300:1. In the first instance, the aerodynamic roughness length for a sea surface at full scale was taken to be typically 0.0005 m (see also Stull 1988). Magnusson and Smedman (1996), for example, took $z_{0} = 0.0005\hbox { m}$ in their offshore field study. However, at the scale ratio of 300:1, the roughness length would be less than 0.002 mm, and would have been far too small for the surface to be aerodynamically rough. This is a well-known problem for wind-tunnel simulations of low surface roughness, and it is necessary to use substantially larger roughness. Even so, the roughness Reynolds number, $z_{0}u_{*}/\nu$, where $u_{*}$ is the friction velocity and $\nu$ is the kinematic viscosity, was less than the lower limit of 1 suggested by Heist and Castro (1998). But, as far as could be ascertained over the range of wind speed available in the wind tunnel (Hancock and Pascheke 2014a), there is no Reynolds number dependence.

The unstable boundary layer was formed by heating the wind-tunnel floor to a uniform temperature, and using the inlet heaters to provide a prescribed inlet temperature profile. This profile was determined in an iterative manner as described in Hancock et al. (2013), based on vertical profiles measured in the downstream flow. That used here is case U5, which has an inversion imposed at the top. Details are given in Table 1.

Table 1 Scale parameter values for the neutral and convective cases

As just mentioned, previous measurements had shown the neutral case to be Reynolds-number independent, and no further checks were made in this regard, since it was expected that roughness effects as such would not be influenced by the unstable (or stable) stratification. Varying the Reynolds number in a non-neutral flow is not straightforward, as the temperature profile would also have to be changed as the flow speed was changed, in order to maintain the same ratio of buoyancy to inertial forces, and was not attempted. As anticipated, the aerodynamic roughness length was found to be close to that for the neutral case, the discrepancy between the two in Table 1 being regarded as insignificant. The effect of roughness is local to the surface and at a very much smaller scale by orders of magnitude than that of the largest scales in the flow, which are the ones that are principally affected by buoyancy. See also, for example, Stull (1988).

2.3 Model Turbine

Aerodynamic and constructional details of the turbine rotor are given in Hancock and Pascheke (2014b), so only summary details are given here. The rotor diameter, $D ({=}2R)$, was 416 mm. The rotor was designed for and operated at a tip-speed ratio $(\hbox {TSR}) = \Omega R/U_{\mathrm{HUB}}$ of 6, where $\Omega$ is the rotor angular velocity and $U_{\mathrm{HUB}}$ is the mean velocity at hub height in the absence of the turbine. Rotation was clockwise, i.e. positive $\Omega$, about the $X$-axis. The blade pitch setting, controlled by means of a grub screw in the rotor hub, was in fact set slightly differently from that employed in Hancock and Pascheke (2014b). Here, the thrust coefficient, $C_{\mathrm{T}}$, was lower and is estimated to have been about 0.42. The measurements for both the neutral and unstable flows were made at the same Reynolds number, based on $U_{\mathrm{REF}}$. Earlier measurements (Hancock and Pascheke 2014b) had shown that the turbine wake exhibited no more than a weak Reynolds number dependence.

The turbine rotor with a profiled 13 mm diameter hub was mounted on the shaft of a motor-plus-gearbox, of diameter 13 mm and length 60 mm, to represent a typical nacelle. Hub height was 300 mm. The tower, a circular cross-section tube, was also 13 mm in diameter, connected at its lower end to a small but heavy rectangular base. The motor, acting as a generator, was a Maxon motor (RE-13-118617; 6V; 3W) controlled by a four-quadrant controller (4-Q-DC-Servoamplifier LSC; 0-30W). The gearbox (4:1 step up) was needed in order to maintain speed control in turbulent flow. In the measurements here, the turbine was at $X = 12\hbox { m}$.

3 Results

The measurements of the baseline undisturbed flows presented here have already been compared with surface-layer and mixed-layer scaling in Hancock et al. (2013). Only those details immediately relevant to the wake measurements are given here, therefore. One particular point to note, though, is that the turbulence levels are substantially higher than is given by the ‘standard forms’ available in the general literature, arising from the weak level of instability of the present case, and supported by the measurements of Ohya and Uchida (2004).

3.1 Profiles of Mean Velocity and Reynolds Stresses

Figure 2 shows profiles of mean velocity and Reynolds stresses in a vertical plane coincident with the turbine hub axis, for both the neutral and unstable cases, where $Z$ is the vertical distance from the turbine rotor axis. Profiles of the same quantities, but on a horizontal plane coincident with the turbine rotor axis are shown in Fig. 3. In each of these, the respective profiles in the absence of the wind turbine are also given, where the positions of these profiles are provided in terms of distance from the turbine, at $x/D = 0, 4.8$ and 9.6 in Fig. 2, for example (rather than in terms of $X$). Clearly, from Fig. 2, each of the Reynolds stresses in the upper part of the undisturbed unstable flow are still developing with streamwise distance, rather than exhibiting the degree of horizontally homogeneous flow seen in the neutral case. Nevertheless, the variation is small enough to draw useful conclusions.

Fig. 2

Vertical profiles of mean velocity and Reynolds stresses in the turbine wake, and in the undisturbed flow. Neutral, left; unstable, right, with symbols as in a and e. Full and broken lines show profiles for undisturbed flow. Lines joining symbols are added to aid visualization. Legends in this and all other figures show stations from the turbine in terms of diameter, $D$. Surface is at $Z/D = -0.72$

From Figs. 2a, e and 3a, e two features are immediately obvious. One is that the magnitude of the mean velocity deficit with respect to the undisturbed flow is less in the unstable case, and that the wake is growing more rapidly in the vertical direction. It can also be seen from the profiles at $X/D = 3$ that the double minima in $U$ disappear more quickly. That is, because of the higher level of turbulence external to the wake, the wake is developing more rapidly. A third feature is the distinctly different shape of the profile at $x/D = 10$, in Fig. 2e. Discussion about this particular aspect is deferred to Sect. 3.4.

Fig. 3

Horizontal profiles of mean velocity and Reynolds stresses in the turbine wake at hub height. Neutral, left; unstable, right, with symbols as in a and e. Full and broken lines show profiles for the undisturbed flow. Lines joining symbols are added to aid visualization

For $\overline{u^{2}}$, the overall levels in the unstable case, as seen in Fig. 2f, are higher than in the neutral case, Fig. 2b, but the development of the wake is such that there is, at least at hub height, a less noticeable difference between the profiles of Fig. 3b and f. As has been observed previously, for instance by Hassan (1993), the idea of ‘added turbulence’, of the wake-generated turbulence ‘added’ to the background turbulence, is of little quantitative use, as in parts of the wake $\overline{u^{2}}$ falls below the undisturbed level. Hancock and Pascheke (2014b), where the same behaviour was observed for the neutral case but not for the stable case, suggested this might be due to a blocking effect of the turbine on the turbulence upstream of the rotor, suppressing $\overline{u^{2}}$, and also seen in the early part of the wake. Why this mechanism should not have been seen in the stable case is not clear. Here, suppression of $\overline{u^{2}}$ to below the undisturbed level is more marked in the unstable case, where it is also seen for $\overline{w^{2}}$, in Fig. 2g. The idea of added turbulence assumes in effect that the two fields of turbulence, those of the wake and in the atmospheric boundary layer, do not interact and are therefore uncorrelated, so that the two fields add in the mean-square of velocity fluctuation. Such an assumption is more likely to be valid when the length scales are widely separated. That is, for small wind turbines, but less likely to be so for large turbines.

The effect on the Reynolds shear stress $-\overline{uw}$ is somewhat more dramatic in the comparisons provided by Figs. 2d, h, and 3d, h. In the undisturbed unstable flow, the level, like $\overline{w^{2}}$, is substantially higher than in the neutral layer, and in Fig. 2h the negative excursions in the lower part of the wake with respect to this level are also substantially greater, and more negative than the negative peak for the neutral case, Fig. 2d. Behaviour related to that seen in Fig. 2h is also seen in Fig. 3h. Asymmetry is seen in Fig. 3d, and in Fig. 3h, though the forms are different. The profiles at $X/D = 3$ both show two minima, for example, but differ in shape and magnitude. An asymmetry is assumed to arise from the inherent asymmetry in the wake associated with the non-uniformity in the upstream flow and the rotor rotation and the consequential (opposite-sense) rotation in the wake.

3.2 Profiles of Temperature and Heat Flux

Profiles of mean temperature, $\Theta$, root-mean-square of the temperature fluctuation, ${\theta }^{'}$, and vertical and streamwise kinematic heat fluxes, $\overline{w\theta }$ and $\overline{u\theta }$, respectively, are given in Fig. 4, for the measurements on the vertical plane. The heat fluxes are given both as correlation coefficients, $\overline{w\theta }/{w}^{'}{\theta }^{'}$ and $\overline{u\theta }/{u}^{'}{\theta }^{'}$, where ${u}^{'}=\overline{u^{2}}^{1/2}$ and ${w}^{'}=\overline{w^{2}}^{1/2}$, and normalized by the surface heat flux of the undisturbed flow, denoted by $(\overline{w\theta })_{0}$. The same quantities for the measurements on the horizontal plane are given in Fig. 5.

Fig. 4

Vertical profiles of mean temperature, r.m.s. temperature fluctuations, and heat fluxes in the turbine wake and undisturbed flow. Symbols as in a. Full and broken lines show profiles for undisturbed flow. Lines joining symbols are added to aid visualization

Fig. 5

Horizontal profiles of mean temperature, r.m.s. temperature fluctuations, and heat fluxes in the turbine wake, at hub height. Symbols as in a. Broken line shows averaged profiles for the undisturbed flow. Lines joining symbols are added to aid visualization

There is little clear effect on the mean temperature, as seen in the vertical profiles in Fig. 4a, though from Fig. 5a there would seem to be a slight temperature increase in the wake. In the stable case (Hancock and Pascheke 2014b) a distinct change was seen in the vertical profile. The vertical profiles of ${\theta }^{'}$, Fig. 4b, clearly show an effect, a reduction, only at the first two stations, $x/D = 0.5$ and 1. A slight reduction can also be seen in the early part of the wake in the lateral profiles, in Fig 5b. There is, nevertheless, a very clear effect on the heat fluxes.

The vertical profile of the vertical heat flux, $\overline{w\theta }$, in Fig. 4f, shows a rapid reduction in the first part of the wake, seen at both $x/D = 0.5$ and 1. As well as being striking, it is not obvious why this should occur. The double minima seen at these two stations resemble features in the profiles of mean velocity and Reynolds stresses in the near wake, in Fig. 2. The presence of these turbine-wake-like features in the heat flux suggests that buoyancy effects have been heavily disrupted. The fact that the mean temperature gradient remains non-zero, implies that $\overline{w\theta }$ could not be zero; fluctuating vertical motions would carry a fluid element to a region where the surrounding temperature is different. Nevertheless, buoyant production, though reduced, remains substantial.

At $x/D = 3$, the heat flux has reverted to about that of the undisturbed level in the lower part of the wake (i.e. below $Z/D = 0$), while at the same station there is no noticeable change from the suppressed level in the upper part. It is some distance further downstream before the heat flux in the upper part has increased to the undisturbed level (which is to be expected, sufficiently far downstream). The fact that the recovery of heat flux occurs first in the lower part of the flow, nearer the surface, where the dominant length scales are smaller, suggests the rate of recovery is dependent on length scale.

In the lateral profile, Fig. 5f, a clear but smaller reduction is seen, but not in fact when compared with that in Fig. 4f at $Z/D = 0$, where the variation is less than at other heights. It is supposed, therefore, that lateral profiles at different heights would show more marked effects.

The behaviour seen here is in very marked contrast to that seen in the stable case (Hancock and Pascheke 2014b), where there was no sudden change in $\overline{w\theta }$ in the first part of the wake $(x/D \le 1)$, except for a small region near the tip, where there was an increase. Then, by $x/D = 3$, a substantial increase occurred in the upper half of the wake, but with no clear change in the lower part. Further downstream $(x/D \ge 7)$ a still higher level was seen over the whole of the wake to a peak level comparable in magnitude with that in Fig. 4f for the unstable case.

The correlation coefficient, $\overline{w\theta }/{w}^{'}{\theta }^{'}$, in Fig. 4e, shows that the efficiency of the turbulence to transfer heat is reduced. The horizontal heat flux, Figs. 4d and 5d, is reduced, except at the top of the wake, where it is increased. Below the top, the correlation coefficient, $\overline{u\theta }/{u}^{'}{\theta }^{'}$, is also reduced in magnitude compared with the undisturbed level. Hancock and Pascheke (2014b) observed a dramatic increase in the magnitude of $\overline{w\theta }/{w}^{'}{\theta }^{'}$, while the behaviour of $\overline{u\theta }/{u}^{'}{\theta }^{'}$ is comparable with that here, but with opposite sign.

3.3 Wake Growth

The measures of wake half-height, $H$, and wake width, $W$, are defined in terms of the velocity deficit from the profiles in the vertical and horizontal planes, respectively, as the point at which the velocity has decreased by $0.1\Delta U$ below its undisturbed level,³ where $\Delta U$ is the corresponding maximum in the deficit, $U(Z,\;Y=0)-U(Z,\;Y=0)_{0}$ or $U(Z=0,\;Y)-U(Z=0,\;Y)_{0}$ and suffix zero denotes the undisturbed profile. In the early part of the wake, where there is a double minimum, $\Delta U$ has been based on the average of the two minima. Note that the height, $H$, is taken from the hub axis $(Z = 0)$, to the point where the deficit is $0.1\Delta U$, while the width is taken as the distance either side of the hub axis $(Y = 0)$ to the point where the deficit is $0.1\Delta U$. In a precisely axi-symmetric wake $W = 2H$. The results are shown in Fig. 6a, and for both the neutral and unstable cases it can be seen that growth in height and width is reasonably close to a linear one. As already noted, the height and width are larger in the unstable case, except near the turbine where there is only a slight difference. Figure 6b shows the ratio $2H/W$: for the neutral case this is slightly less than 1 for most of the measured wake, reaching about 1 at the last two stations, while for the unstable case, though more scattered, this ratio is larger than 1, but also with an increasing trend. On this basis, the height is increasing more rapidly than the width, although it may be the case that the height at which the width is a maximum is itself changing differently in the two cases; measurements on the plane $Z = 0$ might not provide the best measure of width. Linear growth of wake width and height is widely assumed. See for, example, Bastankhan and Porté-Agel (2014) for a recent discussion and comparison with large-eddy simulations for a range of turbulence levels in a neutral flow.

Fig. 6

Variation of wake half-height and wake width with distance $x/D$: a $H$ and $W$; b the ratio $2H/W$

Figure 6a poses an interesting question. The wake is growing more rapidly and its deficit decreasing more rapidly in the unstable case. What then if the width or half-height is compared with the respective measure of the velocity deficit, $\Delta U$? The results are shown in Fig. 7. ($\Delta U$ based on $U(Z=0,\;Y)-U(Z=0,\;Y)_{0}$ is different from that based on $U(Z,\;Y=0)-U(Z,\;Y=0)_{0}$.) In the early part of the wake, the deficit increases, as is to be expected from actuator disk theory, before turbulent mixing proceeds to reduce it, while at the same time the wake continues to grow. This explains the shape of the variation in the early part of the wake, where the deficit first increases then decreases. Further downstream, the width as a function of $\Delta U$ in the unstable case becomes indistinguishable from that in the neutral case, while the half-height is perhaps slightly greater.

Fig. 7

Variation of wake half-height and wake width with velocity deficit strength, $\Delta U$. Broken lines are $H/D=0.47 \Delta U^{-1/2}$ and $W/D=0.90 \Delta U^{-1/2}$. Full lines—see text

Figure 8 shows selected mean velocity profiles superimposed that, by chance, happen to be at about the right distances, $x/D$, to illustrate the point below. Figure 8a, c each show two pairs of profiles from the horizontal plane (which can be read self evidently as profiles of velocity deficit); Fig. 8a shows the profile at $x/D = 4$ in the neutral wake and that at $x/D = 2$ in the unstable wake, and Fig. 8c shows profiles at $x/D = 8$ and 5. The features in each pair are almost identical, to the extent of the detail of the asymmetric double minimum in Fig. 8a. Profiles at the same stations but from the vertical plane are shown in Fig. 8b and d, where these are the velocity deficits $U(Z,\;Y=0)-U(Z,\;Y=0)_{0}$. As with the comparison in the horizontal plane, the profiles in Fig. 8b are close to the extent that the feature near the maximum deficit, the residual of what was once a double maximum, is very nearly the same in the two cases.

Fig. 8

Example mean velocity profiles in neutral and unstable flow: a, c horizontal profiles; b, d vertical profiles. Legends give state and distance from turbine, for each profile

For a wake in which the upstream flow velocity and the far-field pressure are uniform it is possible to measure the drag of a body by means of measurements in the wake alone, from the momentum flux integral

$$\begin{aligned} \int \int {U(U_{0}-U)\;\hbox {d}Y\hbox {d}Z}. \end{aligned}$$

(2)

However, this approach cannot be used when the upstream velocity field is non-uniform without in essence each streamline in the wake being traced to its upstream condition. But, it is reasonable to infer, from the very close similarity of the profile pairs in Fig. 8, that the axial force on the turbine in the two cases is very nearly the same. That is, that the thrust coefficient, $C_{\mathrm{T}}$, is the same in the two cases, as was supposed (but see below), at least as a first approximation. Also, it is worth commenting in passing that, although the profile pairs exhibit ‘similarity’, similarity in a wake requires the velocity deficit, $\Delta U$, to be small compared with the upstream velocity, $U_{\mathrm{HUB}}$, say. See, for example, Townsend (1976), where it is shown that sufficiently far downstream in an axi-symmetric wake, that is where $\Delta U$ is sufficiently small, the velocity deficit, $\Delta U$, varies as $X^{-2/3}$, while the length scale, $\Lambda$ say, varies as $X^{1/3}$. That is, $\Lambda =k \Delta U^{-1/2}$, where $k$ is a constant. Figure 7 shows this variation, with $k = 0.47$ for the half-height, and $k = 0.90$ for the width, with remarkably close concurrence in the later part of the wake. Figure 7 also shows curves inferred from results presented in Fig. 9, which are discussed below.

Fig. 9

Variation of velocity deficit strength, $\Delta U$, with $x/D$: a $\Delta U/U_{HUB}$; b $(\Delta U/U_{HUB})/K$. Figure includes data from Hancock and Pascheke (2014b), denoted by (HP)

Now, even though it appears that $C_{\mathrm{T}}$ is about the same in the two cases, field measurements of power output have shown a dependency on ABL stability, as noted in the Introduction. An effect on $C_{\mathrm{T}}$ would therefore be expected. However, the present measurements are not sufficient to clarify this point further.

As observed by Magnusson and Smedman (1994), Zhang et al. (2013) and Hancock and Pascheke (2014b) the wake deficit sufficiently far from the turbine can be represented by a power law, of the form

$$\begin{aligned} \Delta U/U_{\mathrm{HUB}} =K\;(x/D)^{n}, \end{aligned}$$

(3)

where $n$ is about –0.8, independent of stability, and $K$ increases with increasing stability as a result of the slower reduction of the deficit. The present results for the variation of $\Delta U$ with $x/D$ are given in Fig. 9a, with $\Delta U$ from the profiles of $U(Y)$. (As before, where these profiles have a double minimum, $\Delta U$ is based on the mean of the two minima.) As expected, Fig. 9a shows that $\Delta U$ is smaller in the unstable case than it is in the neutral case, but in the near wake ($x/D < 3$, say) the difference is clearly less than it is further downstream. This is consistent with the more rapid growth of the wake as already discussed (Fig. 6).

Figure 9a also contains the data of Hancock and Pascheke (2014b) for a stable boundary layer where, as expected, the deficit is larger for the stable case than it is for the neutral case. (For their two cases there is perhaps a slight decrease in the difference in $\Delta U$ with increasing distance.) As can also be seen from this figure, the two neutral cases are not the same, and this is because of a slightly different setting of the pitch of the turbine blades. The same data are given in Fig. 9b, but normalized by $K$, with $K = 1.36$ and 0.91 for the neutral and unstable cases, respectively, and 1.37 and 1.53 for the neutral and stable cases of Hancock and Pascheke (2014b). The unstable case, presumably as a result of its more rapid development, follows this decay law from a smaller $x/D$ than do the other cases. In contrast, the present neutral case does not follow this form until $x/D$ is larger than those values pertaining to the other cases. The results given in Hancock and Pascheke (2014b) indicate that Eq. 3 can be generalized to $(\Delta U/U_{\mathrm{HUB}})/K=f(x/D)$. But, from Fig. 9b, this is clearly not so.

Magnusson and Smedman (1994) proposed that $K$ varies as $K\approx 1.25+5 Ri_{D}$, where $Ri_{D}$ is a gradient Richardson number based on temperature and velocity differences across the height of the rotor disk, $D$, in the undisturbed flow. The present measurements indicate a substantially smaller sensitivity to $Ri_{D}$, with $K\approx 1.36+0.4Ri_{D}$, while those of Hancock and Pascheke (2014b) also indicate comparably smaller sensitivity with $K\approx 1.37+0.5Ri_{D}$. Nevertheless, the present value for the neutral case is not that different from theirs. The measurements of Zhang et al. (2013), though, led to markedly smaller values of $K$ for their neutral and unstable cases. $K$ was about 0.85 in the neutral case, and they suggest this is associated with loading conditions of the turbine. A different, albeit tentative, conclusion is drawn here.

The value for $K = 1.36$ for the neutral case is in essence identical to that of Hancock and Pascheke (2014b) (at 1.37) even though the turbine in their case was more highly loaded than it is here. Given that $\Delta U/U_{\mathrm{HUB}}$ in the early part of the wake at least must also depend on $C_{\mathrm{T}}$, this is an interesting result, and needs more detailed investigation than is perhaps possible from these two sets of measurements. A tentative conclusion is that the larger velocity deficit in the early part of the wake gives rise to stronger wake turbulence and a more rapid reduction in velocity deficit (see Fig. 9a), such that, sufficiently far downstream, the initial conditions of the wake are lost. Indeed, loss of initial conditions is a central aspect of Townsend’s (1976) similarity analysis. Comparison of the Reynolds stresses of Fig. 2 with those of Fig. 4 in Hancock and Pascheke (2014b) does show slightly lower levels in the present case. The lower level would also explain the slower development to follow the form of Eq. 3, seen in Fig. 9b.

Although the neutral and unstable wakes of the present study follow that of a self-preserving form, namely $\Lambda =k \Delta U^{-1/2}$, the wake deficit, $\Delta U$, does not vary as $X^{-2/3}$. Of course, in the early part of the wake the mean velocity profiles, which have a double minimum, are not self-preserving and the deficit is not small. Nevertheless, the conformity to $\Lambda =k \Delta U^{-1/2}$ may be of practical utility. The full lines shown in Fig. 7 are based upon curve fits to the neutral and unstable data of $\Delta U/U_{HUB}$ against $x/D$, and the linear fits for $H$ and $W$ shown in Fig. 6, where the respective $\Delta U$ has been taken. The effect is simply to provide a smoothed curve through the measurements presented in Fig. 7, of $H$ and $W$ as functions of $\Delta U$.

The data of Fig. 9 are given again in Fig. 10, but with $\Delta U$ normalized by the respective maximum value, $\Delta U_{\mathrm{MAX}}$, where these maxima (of 0.36, 0.39, 0.45, 0.51) have been inferred from the trends in the curves near each maximum (rather than the largest single value). Evidently, there is little difference between one case and another, for $x/D < 2$. On this basis, there appears to be a universal behaviour in the near wake. Although both stability and turbulence level are different in each of the three types of (neutral, stable and unstable) flow, the inference drawn here is that in the near wake the effect of stability is predominantly an indirect one.

Fig. 10

Variation of normalized velocity deficit strength, $\Delta U/\Delta U_{MAX}$, with $x/D$. Figure includes data from Hancock and Pascheke (2014b), denoted by (HP)

3.4 Direct Effects of Stability

On the basis of the vertical heat flux profiles in Fig. 4f, there is no part of the wake (as assessed from $x/D = 0.5$ onwards) that is uninfluenced by stability; buoyant production is present, but is reduced markedly in magnitude immediately downstream of the turbine. Though not pursued further here, as can be seen from the mean velocity and shear stress profiles, the shear production is much larger in the near wake, and so buoyant production would be relatively smaller.

As noted earlier, the profile of mean velocity at $x/D = 10$ in Fig. 2e (and also in Fig. 3e) is distinctly different in shape from those further upstream in this figure (and also Fig. 3e). Moreover, the shape of this profile in Fig. 2e below $Z/D = 0.5$ is more like that of the undisturbed profile, but at a reduced magnitude. This, together with the fact that the vertical heat flux profile at this station, seen in Fig. 4f, is close to that of the undisturbed flow, is a clear example of the wake attaining characteristics of the surrounding boundary layer as the distance from the turbine increases. Nearer the turbine, the progressive development of the vertical heat flux profile with increasing streamwise distance indicates that the development of this characteristic is through the growth of an internal layer, a feature of the wake, with a corresponding diminution (with increasing distance) of the vertical extent of reduced heat flux and buoyant production in the upper part.

The growth of the vertical heat flux in the stable case investigated by Hancock and Pascheke (2014b) also has features of an internal layer, though one starting high in the wake. (It is presumed that this increased level would eventually fall to that of the undisturbed flow sufficiently far downstream.)

4 Concluding Comments

Wind-tunnel measurements have been made of first- and second-order moments of velocity and temperature, in vertical and horizontal planes aligned with the hub axis, in the wake of a model wind turbine in the interval $x/D = 0.5$ to 10, for an unstable ABL flow and a baseline neutral flow. The unstable flow had a mild capping inversion above $z \approx 1200\hbox { mm}$. The degree of horizontal homogeneity was less for the unstable case than for the neutral case, which was closely horizontally homogeneous, but sufficient for the effects on the wake to be assessed. On the basis of the surface Obukhov length, $L_{0}$, the unstable case was weakly convective, but more convective than that of Zhang et al. (2013). Here, the bulk Richardson number, $Ri_{b}$, was $-0.34$, compared with $-0.13$ in their case.

Wake width and half-height grow linearly, and more rapidly in the unstable case, in contrast to the stable case investigated by Hancock and Pascheke (2014b) where the half-height grew less rapidly but the width more rapidly than in the neutral case. The velocity deficit decreases more rapidly for the convective flow, primarily because of the higher turbulence level in the ABL. Mean velocity profiles in the two cases have very similar shapes, but at substantially different distances from the turbine. Downstream of the first part of the wake, that is from about $x/D = 3$, the width and half-height grow in accord with the similarity relationship $\Lambda =k \Delta U^{-1/2}$ between length and velocity-deficit scales. This close comparability adds support to the inference that indirect effects are present over most of the measured length. Overall, though, the wakes do not conform to self-similarity.

Measurements of the vertical heat flux show a substantial reduction as the flow passes through the turbine, increasing first in the lower part of the wake, and then in the upper part, through the growth of an internal layer, before recovering to the undisturbed level by $x/D = 10$. The efficiency of the turbulence in transferring heat in the vertical direction remains reduced, however, which is an effect of the smaller-scale turbulence generated in the wake. The effect on the vertical heat flux is in marked contrast to that in a stable boundary layer (Hancock and Pascheke 2014b), where initially there is only a small effect as the flow passed through the turbine, increasing first in the upper part before reaching a level well above that of the undisturbed profile, to a level comparable to that seen here in the undisturbed flow. The growth has features of an internal layer, though one starting high in the wake. Further work is needed in order to understand the physics associated with both the rapid reduction of heat transfer through the turbine (but not in the stable case) and the growth of the internal layer.

A decay law for the velocity deficit strength $\Delta U/U_{\mathrm{HUB}} =K\;(x/D)^{-0.8}$ is followed for $x/D \ge 4$ in the unstable case, and for $x/D \ge 6$ in the neutral case, with $K = 0.91$ and 1.36 for the two cases, respectively. It is perhaps surprising that this form still works for both unstable and stable flows, especially when direct effects are present. Tentatively (as inferred from two neutral cases), for a given ABL state, the distance along the wake at which this form is followed depends upon the initial conditions of the wake, that is, the loading on the turbine, a higher loading leading to a shorter distance because of the stronger shear-generated turbulence.