Wind-Tunnel Simulation of the Wake of a Large Wind Turbine in a Stable Boundary Layer: Part 2, the Wake Flow

Abstract

Measurements have been made in the wake of a model wind turbine in both a neutral and a stable atmospheric boundary layer, in the EnFlo stratified-flow wind tunnel, between 0.5 and 10 rotor diameters from the turbine, as part of an investigation of wakes in offshore winds. In the stable case the velocity deficit decreased more slowly than in the neutral case, partly because the boundary-layer turbulence levels are lower and the consequentially reduced level of mixing, an ‘indirect’ effect of stratification. A correlation for velocity deficit showed the effect of stratification to be the same over the whole of the measured extent, following a polynomial form from about five diameters. After about this distance (for the present stratification) the vertical growth of the wake became almost completely suppressed, though with an increased lateral growth; the wake in effect became ‘squashed’, with peaks of quantities occurring at a lower height, a ‘direct’ effect of stratification. Generally, the Reynolds stresses were lower in magnitude, though the effect of stratification was larger in the streamwise fluctuation than on the vertical fluctuations. The vertical heat flux did not change much from the undisturbed level in the first part of the wake, but became much larger in the later part, from about five diameters onwards, and exceeded the surface level at a point above hub height.

1 Introduction

Part 1 (Hancock and Pascheke 2013) presented the results for a case of a stable atmospheric boundary-layer (ABL) simulation in the absence of a turbine, and a reference neutral case. In summary, the outcome of that work is that neutral and the stable atmospheric boundary layers were set up that were very nearly invariant with streamwise distance in the second half of the wind-tunnel working section, and exhibited Reynolds-number independence to the extent that this could be tested. Invariance with distance is useful when it comes to observing the wake development of one or more machines in series in that the external influence is constant. As set out there, two conditions are relevant in categorizing stable conditions, the surface Obukhov length, $L_{0}$, and the temperature gradient (or Brunt-Väisäla frequency, $N$) imposed from above. The imposed condition, relative to the surface condition can be expressed in terms of the non-dimensional group $L_0 N/u_*$, where $u_*$ is the friction velocity. The surface layer generally conformed to Monin-Obikhov similarity.

Defining a bulk Richardson number as $R_\mathrm{b} =Hg(\Theta _{\mathrm{HUB}} -\Theta _0 )/\overline{T} U_{\mathrm{HUB}}^{2}$, where $H$ is the height of the wind-turbine hub and the other terms are also as defined in Part 1, then in the present experiments $R_\mathrm{b} \approx 0.034$ and in those of Chamorro and Porté-Agel (2010) it is about 0.039. Their measurements were made in a growing boundary layer over a smooth wall. As will be discussed further in Sect. 4, their results exhibit fundamental differences to those given here, which are much more consistent with the field measurements of Magnusson and Smedman (1994) at the Alsvik wind farm. Lu and Porté-Agel (2011) set out the results of a large-eddy simulation of an infinite array of flow-aligned wind turbines, achieved by virtue of periodic boundary conditions, with an overlying inversion of 0.01 K m$^{-1}$, comparable with that here. They do not include a neutral case for comparison.

The results show, as anticipated, that there are both ‘direct’ and ‘indirect’ effects of stratification. The latter is, for example, associated with a reduced rate of deficit reduction in the earlier part of the wake, caused by the lower level of turbulence intensity in a stable ABL (compared with the neutral case) and reduced turbulent mixing. The former is, for example, associated with the reduced vertical growth and increased lateral growth in the later part of the wake, and, it is supposed, would require stability effects to be adequately represented in any computational modelling of the wake.

2 Model Wind Turbine

A major consideration that had to be taken into account in designing the model turbine was that the Reynolds number was smaller by a factor of more than 300 than that of the full-size machine. Another major aspect was, or rather might have been, the difficulty of constructing aerofoil-shaped blades of typical section at this scale, and at low cost. However, Sunada et al. (1997) have shown that at blade-chord Reynolds numbers applicable here (roughly $10^{4}$) standard aerofoil profiles do not behave as they do at high Reynolds numbers. Indeed, they also showed that ‘thin plate’ aerofoils behave more like standard aerofoils at high Reynolds number, except that they stall at a lower lift coefficient, $C_\mathrm{L}$. On the basis of their results it was supposed for the design of the turbine blades that the lift curve slope, $\hbox {d}C_\mathrm{L}/\hbox {d}\alpha$, was 0.1 per degree, that the maximum in $C_\mathrm{L}, C_\mathrm{L max}$, was 0.8, and that $C_\mathrm{L}$ for the design case, $C_\mathrm{L(design)}$, was 0.6, where $\alpha$ is the blade incidence angle. It was further supposed that the drag coefficient, $C_\mathrm{D}$, was given by $C_\mathrm{D} =\varepsilon \;C_\mathrm{L(design)}$, where $\varepsilon$ is a parameter that was allowed to vary in order to observe the effect of drag on other parameters. The $C_\mathrm{D}$ assumed is comparable with values given by Laitone (1997).

Now $C_\mathrm{L} = 0.6$ is about half that of a typical wind-turbine blade in low to medium wind speeds (see, for example, Fuglsang and Bak (2004). But, rather conveniently, in blade-element theory both $C_\mathrm{L}$ and also $C_\mathrm{D}$ are in product with the blade chord, $c$. Therefore, in the design of these model turbines the blade chord was enlarged by a factor of 2 from that initially supposed. This increase in chord has the drawback of increasing the drag, but the drag will in any case be incorrect. The design tip-speed ratio $({\textit{TSR}}) = \Omega R/U_{\mathrm{HUB}}$, was chosen to be 6, where $\Omega$ is the angular velocity, $U_{\mathrm{HUB}}$ is the upstream mean velocity at hub-height, and $R (= D/2)$ is the tip radius. The pitch axis of the uncambered blade was radial and at 1/4-chord; with the symmetrical section there should therefore have been no moment about the (aerodynamic centre) pitch axis. Figure 1 shows the blade chord and twist, $\psi$. From $r = 0.25R$ outwards the chord varied as 1/$r$, and is a constant-circulation blade. Inwards of $0.25 R$, the chord length was arbitrarily reduced linearly. An advantage of the increasing chord is that the chord Reynolds number does not decrease with decreasing radius as it would for a more conventional shape, but stays very nearly constant. Figure 2 shows the turbine mounted in the working section and the Irwin-type spires (see Part 1) can also be seen.

Fig. 1

Blade chord and twist

Fig. 2

View looking upstream of the model turbine and part of the working section. The five Irwin-type spires at the working section inlet, surface-roughness elements and reference anemometer can also be seen

The blades themselves were made from a lay-up of three layers of thin fibreglass matting in a resin on a former made to the blade’s chord and twist profile. The blade thickness was about 0.9 mm and the tip chord was 10 mm. The tip radius, $R$, was 208 mm, and the blades could be pitched manually. The reproducibility of the model turbine characteristics was found to be very good, with negligible difference in the wake of one turbine compared with another. At the wind speeds used in these experiments no force balance was available that could be used in the wind tunnel that would give accurate measurement of axial force (typically 0.13 to 0.26 N). Neither was it possible to measure the power coefficient. The blade element calculation ignoring tip loss gave a thrust coefficient, $C_\mathrm{T}$, of 0.53, while wake measurements in a uniform flow gave an indication of the effect of tip loss, reducing $C_\mathrm{T}$ to about 0.48. This was calculated from the blade-element method by adjusting the blade incidence near the tip to give a wake profile close to that measured. Blade drag has only a very weak affect on $C_\mathrm{T}$, so the assumption for drag is not significant.

The turbine rotor with a profiled 13-mm diameter hub was mounted on the shaft of a motor-plus-gearbox, of diameter 13 mm and length 60 mm, to represent a typical nacelle. The tower, a circular cross-section tube, was also 13 mm in diameter, connected at its lower end to a small but heavy rectangular base. The motor, acting as a generator, was a Maxon motor (RE-13-118617; 6V; 3W) controlled by a four-quadrant controller (4-Q-DC-Servoamplifier LSC; 0-30W). The gearbox was needed in order to maintain speed control in turbulent flow.

Ideally, the present measurements would be fully independent of Reynolds number. From the blade-element analysis, the power coefficient can be expected to be dependent on Reynolds number in that it is dependent on blade drag, while the thrust coefficient is no more than weakly dependent on blade drag, being primarily dependent on lift. Figure 3 shows the mean velocity, $U$, and the Reynolds stresses $\overline{u^{2}}$ and $-\overline{uw}$, normalized by $U_\mathrm{HUB}$, from horizontal and vertical traverses through the hub axis, at $x = 3D$, for two reference speeds; $x$ is the streamwise distance from the turbine-rotor reference plane, located at the pitch axes of the blades. While some slight differences can be seen they are nevertheless small. Although the neutral-flow measurements had been made at a reference speed of $2.5 \text {m} \;\text {s}^{-1}$, the stable flow measurements were made at a reference speed of $1.5 \text { m} \text { s}^{-1}$ in order to maintain the heating and cooling requirements within preferred limits. As noted in Part 1, the heat transfer requirements for a given stability condition vary as $U^{3}$ (where $U$ is the streamwise velocity). From Fig. 3 it was inferred that the neutral flow measurements did not need to be repeated at the lower reference speed, and it is our view that any slight difference in wake structure in the neutral flow at these two speeds would have been small or negligible compared with differences as a result of the stable stratification. Nevertheless, the reader may wish to exercise some caution on this point.

Fig. 3

Effect of Reynolds number on a model turbine for neutral flow, $\textit{TSR} = 6, x/D = 3$

In all the measurements presented here, the turbine was placed on the working-section centreline at $X = 10$ m (where $X$ is the distance from the working-section inlet) for the neutral case, and at $X = 11$ m for the stable case so as to allow a slightly larger flow-development distance. Unfortunately, this meant that the further most downstream station for the stable case was $x = 9.5D$ rather than $x = 10D$, as in the neutral case, because of a limitation imposed by the length of the probe’s fibre-optic cable, but this is of relatively small consequence in interpreting the results. Instrumentation techniques were as given in Part 1.

3 Wake Measurements

Before discussing the measurements it should perhaps be emphasized that the boundary-layer height, $h$, in the stable case is about half that of the neutral case, so there is a change of scale of the energy-containing motions as well as the effect of stability itself. We did not attempt to maintain the same boundary-layer height (it is likely this would have been difficult to achieve), and so, some points of interpretation will therefore need to be carefully made. Moreover, had we maintained $h$ equal in both cases, it is only one of a number of ‘integral’ length scales that we could have used as a basis to match the two cases.

3.1 Momentum and Reynolds Stresses

Figure 4 shows profiles of $U, \overline{u^{2}}, \overline{w^{2}}$ and $- \overline{uw}$ along vertical traverse lines, where $Z$ is the height with respect to the hub (i.e. $Z=z-H$), while Fig. 5 shows the same quantities, but along horizontal traverse lines at hub height, where $Y$ is the lateral distance from the centreline. In these and subsequent figures, the surface is at $Z/D = -0.72$. In both figures, those sets on the left show profiles in the neutral atmosphere, while those on the right show profiles in the stable atmosphere. In each case the rotational speed, $\Omega$, was fixed by the design tip-speed ratio. The actual TSR was in the range 5.9–6.0 in the neutral case and 5.8–5.9 in the stable case; the slight variation is negligible. In Fig. 4, each set of profiles show the respective profiles for the undisturbed flow,¹ and profiles for the undisturbed flow are also given in Fig. 5.

Fig. 4

Vertical profiles of mean velocity and Reynolds stress in the turbine wake. Neutral, left; stable, right, with symbols as in (a) and (e). Legends in this and all other figures show stations from the turbine in terms of diameter $D$ or, for the undisturbed flow, from the working section inlet in units of mm. Surface is at $Z/D = - 0.72$

Fig. 5

Horizontal profiles of mean velocity and Reynolds stress in the turbine wake. Neutral, left; stable, right, with symbols as in (a) and (e). Lines with symbol show profiles for the undisturbed flow

From the profiles of $U(Z/D)$ and $U(Y/D)$—in Figs. 4a, e and 5a,e, respectively—one feature is immediately obvious. This is that the velocity deficit is larger for the stable case, as is to be expected as a result of the lower level of ABL turbulence in the latter, and the reduction in mixing that can be expected to follow. Another feature that is evident in Fig. 5a, e is that in the neutral case there is an asymmetry in the near-wake profiles as far as $x \approx 3D$, possibly further, but not in the stable case. There is, of course, an inherent asymmetry associated with a rotor in a non-uniform flow and it is assumed this may be the cause, but a similar behaviour would also be expected in the stable case. The asymmetry was consistently observed in the neutral case (in other experiments not included here), though it is not understood why the stable case is different. A weaker asymmetry would be anticipated because of a lower level of non-uniformity (in the upstream flow) as inferred from $\partial U/\partial z$ over the disk height; a bulk measure of $\partial U/\partial z$ is roughly 1/3 smaller for the stable flow. The background level, $U(Y/D)$, as can be seen from Fig. 5a, e, is sufficiently uniform to discount the asymmetry as arising in the upstream flow.

The slight peak in $U$ above the undisturbed level at the wake edge seen at $x = 0.5D$ in Fig. 5a, e arises from the flow external to the streamtube passing through the rotor disk. The blockage imposed by the turbine causes this external flow to accelerate around the disk edge. Further downstream the peak diminishes as the flow decelerates, and is ‘lost’ as a result of the wake’s growth.

There is a less obvious feature, observed by comparing respective pairs of neutral- and stable-case velocity profiles near to the edge of the wake. A detailed comparison of $U(Z/D)$ (near the top edge, not shown separately) in fact shows that there is negligible difference between the pairs at $x = 0.5D, 1D$ and $3D$. In contrast, at $x = 5D, 7D$ and $9.5D\; (10D)$, comparison shows that there is much less growth in the vertical direction for the stable case. Comparison of $U(Y/D)$ near the wake (lateral) edge shows that there is also negligible difference between the pairs at $x = 0.5D, 1D$ and $3D$, while those at $x = 5D, 7D$ and $9.5D \; (10D)$ show the wake is slightly wider in the stable case. The lower level of turbulence external to the wake in the stable case would be expected to cause a lower growth rate, both vertically and laterally, though here, a different behaviour is exhibited, as just outlined. Therefore, it is inferred that an inhibited vertical growth of the latter part of the wake, and an increased lateral growth, is due to the inhibiting influence of stability from above, showing that a not untypical stable mean temperature gradient is large enough to very nearly or perhaps completely suppress vertical growth.

Thus, it appears that the early part of the wake—to about as far as $x/D = 3$ in the instance here—develops independently of stratification as such. The lower level of turbulence in the ABL in the stable case leads to a slower reduction in the momentum deficit, but there is not otherwise a direct effect of stability on this zone of the wake. Further downstream, the wake becomes clearly and directly influenced by stabilizing effects. At least part of the explanation could lie with the change in wake length scale from one being determined in the very near-wake by the blade chord, which is at least an order of magnitude smaller than the scale of the rotor diameter. Further downstream, this small-scale detail must be largely or completely lost, and the dominant length scale becomes that of the wake diameter, and more likely to interact with the turbulence of the ABL. However, the Reynolds stresses give a more complex picture.

From the profiles of $\overline{u^{2}}$ in Fig. 4b, f it can be seen that the magnitudes are lower in the stable case, partly to be expected as a result of the lower level of turbulence in the upstream flow. And, when the various profiles are compared with respect to the upstream flow profile, there is also a clear difference in ‘added’ turbulence ($\overline{u^{2}}$ minus its undisturbed level). Also, whereas in the neutral case there are regions where $\overline{u^{2}}$ falls distinctly below the upstream profile, it falls no more than marginally below in the stable case. It is assumed this reduction below the upstream level, though seen clearly only in the neutral case, is a consequence of the turbine blocking streamwise fluctuations (much as a porous screen,² perpendicular to the flow, reduces normal velocity fluctuations). Some further evidence is given in Sect. 3.3, from spectral measurements. A reduction below the upstream level can also be seen in Fig. 5b, though it is not understood why, if blocking is in fact the mechanism, a reduction is not seen in the stable case (Fig. 5f). Lu and Porté-Agel (2011) observed a reduction in both $\overline{u^{2}}$ and the turbulent kinetic energy in the flow below the turbine disk, and a reduction was also seen by Hassan (1993), but attributed to a reduction in mean velocity gradient. At $x/D = 0.5$ and 1, the most noticeable difference in $\overline{u^{2}}$ (Fig. 4b, f) is near the top of the wake, where the peaks are substantially smaller in the stratified case, but the profiles are not so altered lower down in the wake. These smaller peaks near the top of the wake are in contrast to slightly larger mean velocity gradients, $\partial U/\partial z$. At $x/D = 3$ and 5, the greatest difference is again in the peak near the tip, but further downstream the differences are not so marked.

The picture for $\overline{u^{2}}$ provided by Fig. 5b, f is notably different, compared with that from Fig. 4b, f. Even at $x/D = 3$, the peaks at about $Y/D=\pm 0.5$ are larger in the stable case both absolutely and (more so) with respect to the upstream levels, and this persists for the whole of the wake further downstream. It appears this may be connected with the larger gradients seen in the mean velocity profiles, but see below.

When it comes to $\overline{w^{2}}$ in Fig. 4c, g the change in $\overline{w^{2}}$, compared with the respective upstream profiles, is not so marked as it is for $\overline{u^{2}}$ (in Fig. 4b, f). This is intriguing in that it indicates that the effect of stabilizing stratification, which is expected to suppress vertical motion, is in fact larger for $\overline{u^{2}}$, continuing to beyond $x/D = 5$. The effect in the ‘far’ wake (say, beyond $x/D = 5$) of reduced vertical growth rate, seen in the mean velocity profiles, is also seen in the top edges of the profiles of $\overline{w^{2}} , \overline{u^{2}}$ and $- \overline{uw}$. The picture for $\overline{w^{2}}$ provided by Fig. 5c, g shows a higher level of ‘added’ turbulence at and beyond $x/D = 7$, perhaps (but probably not) connected with the larger mean velocity deficit in the stable case.

The profiles of $- \overline{uw}$ in Fig. 4d, h and in Fig. 5d, h, show reduced peaks near the turbine for the stable case. The lateral profiles at $x/D = 7$ and 9.5 of the stable case in Fig. 5 clearly show higher levels than in the neutral case, more so when compared with the undisturbed profiles. However, there is an exaggerated effect here; from Fig. 4 it can be seen that the predominant peaks at the later stations occur at a significantly lower $Z$ in the stable case, consistent with the reduced growth rate in the vertical direction. This may also account for the observations above, from Fig. 5, regarding $\overline{u^{2}}$ and $\overline{w^{2}}$ in these later stations (but not obviously so at $x/D = 3$ and 5), the higher levels measured at hub height in the stable case arising from a downward displacement or ‘squashing’ of the wake. The asymmetry seen in the lateral distribution of $- \overline{uw}$, in Fig. 5d, is still seen in the stable case, in Fig. 5h, but not so distinctly. Quite why it should be less distinct is not immediately obvious but it may be a consequence of reduced mean flow non-uniformity across the rotor disk (as inferred earlier from a reduced $\partial U/\partial z)$.

In summary, the effects of stable stratification are present directly or indirectly in the whole of the wake (at least from $x/D = 0.5$ onwards), with ‘selective’ rather than wholesale uniform changes in Reynolds stresses, an unchanged growth rate to about $x/D = 3$, and a clearly reduced vertical growth and slightly increased lateral growth rate from about $x/D = 5$, in a ‘squashed’ wake. This almost complete cessation in vertical growth will undoubtedly have been brought about by the level of imposed stability in the flow above hub height. Counter to expectation, the effect of stable stratification on $\overline{u^{2}}$ is larger than it is on $\overline{w^{2}}$.

3.2 Temperature and Heat Flux

Profiles of mean temperature, $\Theta$, r.m.s. of temperature fluctuations, ${\theta }'$, and heat fluxes, $\overline{u\theta }$ and $\overline{w\theta }$, are given in Figs. 6 and 7. Here, of course, the profiles are for the stable case alone. Both $\overline{u\theta }$ and $\overline{w\theta }$ are shown as correlation coefficients, and normalized by the undisturbed surface heat flux, $(\overline{w\theta })_0$. Likewise, $\theta _*$ is the temperature scale of the undisturbed flow. Profiles for the undisturbed flow are also given.

Fig. 6

Vertical profiles of mean temperature, r.m.s. temperature fluctuations, and heat fluxes in the turbine wake. Symbols as in (a). Full and broken lines show profiles for undisturbed flow. Lines joining symbols in (c), (e) and (f) are added to aid visualization

Fig. 7

Horizontal profiles of mean temperature, r.m.s. temperature fluctuations, and heat fluxes in the turbine wake. Symbols as in (b). Lines with symbol show profiles for the undisturbed flow

One of the striking features is seen in the vertical profiles of mean temperature, in Fig. 6a. Overall, at each of the six stations the temperature profile of the upstream flow is broadly maintained. But, in the centre of the near wake, most noticeable at $x/D = 3$, there is a marked flat section, which for part falls below the upstream profile. It is supposed that mixing leads to this flat profile and to the slight fall. The other main feature is that below hub height, and partly above, the temperature profiles show warmer fluid than in the undisturbed profile. It is curious that there is a larger effect on the temperature profiles near $Z/D = -0.5$, than there is near $Z/D = +0.5$, where, for the latter, the turbulence levels are substantially higher than for the former, as can be seen from Fig. 4. The higher temperature must be a result of increased mixing caused by the turbine wake, and may or may not lead to increased heat flux with the surface (discussed below). The fluctuation intensity, ${\theta }^{\prime }$, in Fig. 6b does not follow a similar development to that for the mean temperature. The lateral variations of $\theta$ and also of ${\theta }^{\prime }$ in Fig. 7a, b are comparable in magnitude with the departure from the upstream seen in the vertical profiles.

Of the heat fluxes, it is easier to discuss the vertical profiles of $\overline{w\theta }$ first, both in terms of its correlation coefficient and as a normalized heat flux—Fig. 6e, f. In the early part of the wake ($x/D = 0.5$ and 1), these show no more than relatively small departures from the undisturbed profiles. At $x/D = 3$, marked increases exist above hub height, but below hub height there is still no substantial change. However, the profiles at $x/D = 5$ and onwards show much increased levels over the whole of the wake and, what is more, not only are the profiles very comparable with each other, the heat-flux peak exceeds the surface value by a factor of about 1.6 at a level above hub height. Near the surface, curiously, $\overline{w\theta }$ is close to the unperturbed level. Between these two vertical positions $\overline{w\theta }/{w}^{\prime }{\theta }^{\prime }$ is about constant, ${\approx }-0.45$; in the wake, the steep gradients in $\overline{w\theta }$ and $\overline{w\theta }/{w}^{\prime }{\theta }^{\prime }$, which were near the surface in the upstream flow, are now at the top edge of the wake. The computations of Lu and Porté-Agel (2011) also show a large increase in vertical heat flux near the top of the wake, rather like that here, though not exceeding the undisturbed level at the surface, and a reduction nearer and at the surface. If there was a reduction in surface heat flux in the present experiment it is much less obvious than the reduction seen in their computations.

The horizontal heat flux, $\overline{u\theta }$, Fig. 6c, d, is increased in the upper part of the wake and decreased in the lower part, to the extent of a change in sign. The lateral profiles of $\overline{u\theta }$ in Fig. 7c, d have a clear asymmetry in much the same way as seen in the Reynolds shear stress, $-\overline{uw}$, and is assumed to be connected with the correlation between $w$ and $\theta$. The profiles of $\overline{w\theta }$ show, in Fig. 7e, f, a comparable development with $x/D$ to that seen in the vertical profiles above hub height, with the development of steep gradients at the edge.

As noted earlier, Fig. 7 also shows the undisturbed level of the respective quantities. The variation in each is small compared with the variations in the wake, though in Fig. 7a, b the levels appear at first sight to be respectively below and above the overall trend in the wake. However, in Fig. 7b, the levels at the edge of the wake at $x/D = 1$ and 3 fairly closely match that in the undisturbed flow, with the interesting suggestion that ${\theta }^{\prime }$ is reduced below this level at the edge of the wake further downstream. This aspect was not appreciated at the time of the experiments, and measurements to larger $Y/D$ would have been helpful in this regard.

Thus, from the information just presented, the effect of the wake is large enough to have a marked effect on the mean temperature profile of the atmospheric boundary layer, with an implied high level of mixing in the first part of the wake, tending to smear out the temperature gradient. Further downstream this relaxes, as is to be expected. There is also a large effect on the heat flux in the wake, though the surface heat flux might be only slightly affected.

3.3 Spectra

Spectra of the streamwise velocity fluctuation, $F_{11}(k)$, normalized by $D$ and $\overline{u^{2}}$, are given in Fig. 8, for $x/D = 1$ and 5, in the range $-0.5 \le Z/D \le +0.5$, where the wavenumber $k$ has been calculated assuming Taylor’s hypothesis, with the convection velocity taken as the local mean velocity in the wake. $F_{11} (k)$ is as defined in Part 1. There are a number of points to make.

In the normalized terms of these figures there is not much variation in each set, except in two instances in the neutral flow in Fig. 8a. Leaving these two aside for the moment, there is, though, a distinct change in shape between $x/D = 1$ and $x/D = 5$. At the first station there is a mild but distinct ‘bulge’ above $kD \approx 7$, which does not appear at the second station $(x/D = 5)$, and is attributed to significant energy at smaller scales in the early stage of the wake development. At $x/D = 5$, there is a more distinct ‘knee’ in the spectra, and the density in the low wavenumber range is flatter. It is assumed that the energy in the bulge for $x/D = 1$ has moved to larger length scales and therefore lower wavenumbers, giving rise to this more distinct knee shape for $x/D = 5$.

Fig. 8

Velocity spectra, $F_{11}(k)$ in neutral and stable cases. Neutral, left; stable, right. Top $x/D = 1$; bottom $x/D =5$. Data in (a) and (c) give $Z/D$ (additional profile in (a)) at $Z/D = 0.19$). Straight line in each indicates slope of $-5/3$

The shape at low wavenumbers seen in Fig. 8a is rather like that in the undisturbed flow, Fig. 10a of Part 1, except for the two cases noted above, which show a notably different shape. The vertical positions of these two correspond to minima in the profile for $\overline{u^{2}}$ in Fig. 4b. It is believed that this is evidence for the turbine having a ‘blocking effect on’ the streamwise fluctuations of the upstream flow (rather as the surface blocks vertical fluctuation, though without forcing the fluctuations to zero at the turbine). Such an effect would be expected to occur at wavenumbers such that $kD=O(1)$, which is indeed seen to be the case in Fig. 8a. No comparable response was seen in the stable case (Fig. 8c), though it is perhaps significant that all the spectra are flatter at low wavenumbers than the spectra in the undisturbed stable flow of Fig. 10a of Part 1.

For the stable and neutral flows the rotor frequency is in the range kD $=$ 16 to 21, and the blade-passing frequency three times this. No peaks are seen near either of these wavenumbers for the neutral flow, but a small peak is seen in the stable case for $x/D = 1$. These are present at $Z/D = +0.25$ and $-0.25$, but not in the other spectra. Oddly, they are at the rotor frequency rather than the blade-passing frequency, and it is not clear why this is so, but it is perhaps because there was a slight deficiency in one of the blades. It is assumed that features associated with the blade flow disappeared more slowly owing to the lower turbulence level in the stable ABL. In neither the neutral nor the stable case is there clear evidence of distinct tip-vortex structures having persisted as far as $x/D = 1$.

There is another point to draw from the spectra for the stable case. From Fig. 9c of Part 1, near the rotor tip-top height, $ND/U\; (= kD)$ is $\approx$0.25. From Fig. 8, although at the bottom end of the measurement range, there is no indication of additional energy of waves at frequency $N$. If $L$ is the wavelength of frequency $N$, and $D$ the length scale of the disturbance caused by the presence of the turbine, then $L/D=2\pi /(ND/U)$ is $\approx$25, which is in excess of an order of magnitude larger than unity. That is, the absence of wave motion at frequency $N$ is assumed to be because the respective wavelengths are sufficiently separated. For a discussion of waves in stratified flow see, for example, Scorer (1967).

Fig. 9

Maximum velocity deficit as a function of distance from the turbine. a in ‘log-log’ form; b $\Delta U$ normalized by $K$, in linear form

4 Further Discussion

In contrast to the measurements here, Chamorro and Porté-Agel (2010) observed a more rapid reduction in the wake momentum deficit for the stable case, as far as $x/D \approx 10$, beyond which there was little difference in the velocity deficit between the stable and neutral cases. This more rapid reduction is certainly a counter-intuitive result, and one they found rather surprising (F. Porté-Agel, private communication, 2010). They found $\overline{u^{2}}$ to be larger at and around the tip-top height, for several diameters downstream but, as here, $- \overline{uw}$ was smaller in magnitude. At the tip-bottom height, they found a more negative $-\overline{uw}$ in the stable case, whereas here it is less negative. We have no explanation as to why the two studies give such contrasting results. Moreover, it seems unlikely that increasing stability should first cause a more rapid reduction in velocity deficit before causing a less rapid reduction.

The field measurements of Magnusson and Smedman (1994) more closely resemble the measurements here. They observed a slower reduction of the momentum deficit, though not a reduced vertical growth rate for the stable boundary layer. The lateral growth rate was comparable in the two cases, except perhaps in the nearest station $(4.2D)$ where it was a little less. The ‘added’ streamwise turbulence ($\overline{u^{2}}$ minus its undisturbed level) was larger in the stable case, qualitatively not as observed here. They also observed a power-law behaviour for the maximum deficit, $\Delta U$, of the form

$$\begin{aligned} \Delta U/U_{\mathrm{HUB}} =K\left( {x/D} \right) ^{n}, \end{aligned}$$

(1)

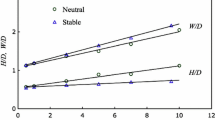
where $n$ was $-0.8$, independent of stability, and $K$ was 1.25 and 1.5 for cases of unstable and stable stratification. The deficit for the present measurements, taken from the horizontal traverses (Fig. 5), is shown in Fig. 9a in terms of Eq. 1 and as

$$\begin{aligned} \left( {\Delta U/U_{\mathrm{HUB}} } \right) /K=\left( {x/D} \right) ^{n}, \end{aligned}$$

(2)

in Fig. 9b, with $n = -0.8$ and $K = 1.37$ and 1.53 for the neutral and stable cases, respectively. Where the profiles $U(Y)$ exhibit a double minimum, the $\Delta U$ given in these figures is based on the mean of the two minima. These figures also indicate a more general result than the power law of the above, namely that $\left( {\Delta U/U_{\mathrm{HUB}} } \right) /K=f\left( {x/D} \right)$, for $x/D \gtrsim 0.5$, where only $K$ is dependent on the level of stratification, the power-law form applying for $x/D\gtrsim 5$. The rate of reduction of the deficit is larger than that given by the classical analysis of Townsend (1976) in which $n =-2/3$. This is to expected as a result of the turbulence external to the wake which is not represented in that analysis, though there is no obvious difference in the index for the two cases investigated here, neutral and stable, for which the levels of external turbulence are different. That a change is seen at $x/D = 0.5$ means of course that the effect occurs in the early part of the near-wake development. Lower levels of ABL turbulence would reduce bodily ‘transverse’ convection of the blade wakes and thereby, it is inferred, give a reduced rate of blade wakes merging and mixing.

Magnusson and Smedman (1994) suggest the change in $K$ with Richardson number, $\partial K/\partial \;Ri \approx$ 5, where $Ri$ is defined as an average gradient Richardson number, with gradients based on (upstream) velocity and temperature differences across the height of the rotor disk, each divided by the rotor diameter. The present results indicate a much smaller value of $\partial K/\partial Ri$. In the advective-time analysis of Magnusson and Smedman (1999), the near-wake time scale $(t_0)$ was adjusted to fit a far-wake relation to the measurements for the stable and unstable cases, implying of course, influence starting in the near wake. Their near-wake time scale for the present case is equivalent to $x/D \approx 0.53$. While their far-wake form can be fitted to the present measurements, the fit can only be achieved with changes to the constants.

5 Concluding Comments

Results have been presented firstly in Part 1 for a case of a stable offshore ABL and a reference neutral offshore ABL, followed herein by results for the wake of a single turbine for each type of boundary layer. The wake measurements show a complex behaviour, more so in terms of the behaviour of the Reynolds stresses. The mean velocity profiles show very little influence in the first part of the wake other than a slower reduction of the momentum deficit in the stable case. In both cases, the deficit $\Delta U$ followed the form $\left( {\Delta U/U_{\mathrm{HUB}} } \right) /K=f\left( {x/D} \right)$ from $x/D \approx 0.5$ onwards, and a power-law form from $x/D \approx 5$, where $K$ increases with increasing stability. A slower reduction is to be expected from the lower level of turbulence in the stable ABL, an effect described herein as indirect. But the effect is seen here to have started as close as $0.5D$ from the turbine, suggesting the thrust coefficient $(C_\mathrm{T})$ may have been higher. $\Delta U/U_{\mathrm{HUB}}$ must also depend upon $C_\mathrm{T}$, of course, as the latter in effect implies an initial condition for the wake. Here it is significant to note the field measurements of Magnusson (1999). He observed a larger mean velocity deficit in a stable atmosphere compared with that in an unstable atmosphere at $1D$ from the turbine operating at nominally the same $C_\mathrm{T}$, qualitatively consistent with the present measurements.

After about three diameters, the wake growth changes notably, showing very little vertical growth, and a slightly larger lateral growth, as compared with the neutral case. This inhibited vertical growth rate is most likely a direct consequence of the level of stratification above the ABL. Generally, the Reynolds stresses over and above the ‘background’ levels of the ABL turbulence are diminished, and peaks occur at a lower height. Unexpectedly, there is a larger effect on the streamwise fluctuations than there is on the vertical fluctuations, at least as inferred from $\overline{u^{2}}$ and $\overline{w^{2}}$, the primary effect of stability being to inhibit the latter. The wake alters the mean temperature profiles, causing an increase below hub height, but also a slight decrease above hub height in the earlier part of the wake. The vertical heat flux is also increased, above that in the undisturbed boundary layer, but not at the surface where it appears to be unchanged or slightly reduced, the steep gradient in heat flux moving from near the surface to the edge of the wake.