Wind-Tunnel Simulation of the Wake of a Large Wind Turbine in a Stable Boundary Layer. Part 1: The Boundary-Layer Simulation

Abstract

Measurements have been made in both a neutral and a stable boundary layer as part of an investigation of the wakes of wind turbines in an offshore environment, in the EnFlo stratified flow wind tunnel. The working section is long enough for the flow to have become very nearly invariant with streamwise distance. In order to be systematic, the flow profile generators of Irwin-type spires and surface roughness were the same for both neutral and stable conditions. Achieving the required profiles by adjusting the flow generators, even for neutral flow, is a highly iterative art, and the present results indicate that it will be no less iterative for a stable flow (as well as there being more conditions to meet), so this was not attempted in the present investigation. The stable-case flow conformed in most respects to Monin–Obukhov similarity in the surface layer. A linear temperature profile was applied at the working section inlet, resulting in a near-linear profile in the developed flow above the boundary layer and ‘strong’ imposed stability, while the condition at the surface was ‘weak’. Aerodynamic roughness length (mean velocity) was not affected by stability even though the roughness Reynolds number ${<}1$, while the thermal roughness length was much smaller, as is to be expected. The neutral case was Reynolds-number independent, and by inference, the stable case was also Reynolds-number independent.

1 Introduction

A fundamental feature of any wind turbine is that there is necessarily a reduction of the momentum of the flow that passes through its ‘disk’ as a result of the forces on the blades. The wake that develops is of major significance for any other wind turbine on which it impinges and, in the context of multiple turbines in a wind farm array, there are interactions of one wake with another, as well as of wake impingement. The full or partial impingement of the wake of one or more turbines on another turbine leads to high levels of fluctuating load on the blades as well as a reduced environmental mean wind speed and therefore reduced power output. This reduction in power output from turbines in a row that happens to be aligned with the prevailing wind direction is more acute at low wind speeds (relating to how wind turbines are operated in order to maximize power output); at a high wind speed, a given power output leads to only a small reduction in mean wind speed, but at low speed the reduction is relatively larger, meaning that the downwind turbines are ‘starved’ of flow momentum. It has long been recognized (see e.g. Ainslie 1988) that an increased level of turbulence in the upstream flow leads to a more rapid mixing and a more rapid reduction in the velocity deficit, which can have the bonus of allowing wind turbines to be placed closer together than they should otherwise be.

The effect of flow non-uniformity and turbulence in an approaching flow on a wind turbine depends upon the characteristics of the turbulence, such as mean shear, intensity and length scale, and the same must be true of the effect on the wake of the turbine. The turbulence, mean shear and the turbulent length scales are affected by the degree of stable or unstable stratification, in addition to surface roughness. Stable boundary layers are much less deep than neutral or convective boundary layers, such that the height may be less than turbine blade-tip top height of large horizontal-axis machines (${\approx } 150 \hbox { m}$ for a 5 MW turbine), compared with typically 1–2 km for a neutral or unstable boundary layer.

It is not intended here to review the general literature on wake development, very nearly all of which refers to the neutral boundary layer in the case of wind-tunnel simulations. For reviews, refer to Vermeer et al. (2003) and, for example, Sanderse (2009), Chamorro and Porté-Agel (2010), Lu and Porté-Agel (2011), Adaramola and Krogstad (2011) and Sanderse et al. (2011). For field data, data have to be filtered for the naturally arising levels of stability. A recent extensive collection of field data, as well as assessment of wake prediction methods, are to be found in the UpWind project (Barthelmie et al. 2011). That study shows, for example, that the airflow at the Horns Rev wind farm during the one year of the data collection was in neutral or near-neutral conditions for only 30 % of the time, 25 % in stable and 45 % in unstable or very unstable conditions. The data show a clear and substantial dependence on stability of both the power output from successive turbines in a row, and of the wind speed along the row.

The present work is part of a programme of work on wind-turbine wakes within a consortium programme of research with particular regard to large offshore wind farms, funded under the SUPERGEN programme of the UK Engineering and Physical Sciences Research Council. The purpose of the work on wakes is to gain a better understanding of wake development: the interaction of one wake with another, the effect of single or multiple wake impingement on a turbine, and the way that a turbine wake develops as a result of impingement. In the first phase of our work on wake simulation the principal concerns were to establish a modelling scale commensurate with the facilities of the EnFlo wind tunnel, to design and manufacture suitable model turbines, and to develop associated instrumentation and data acquisition. In this phase, three atmospheric boundary-layer simulations were set-up: offshore neutral, rural onshore neutral, and offshore stable. This paper, Part 1, is concerned with the last of these, with the first as a baseline. Only the wakes of one and two turbines were studied in the initial phase, with multiple turbines in offshore, neutral, stable and unstable cases being a focus for the second phase. Two model turbine types were built that have different wake momentum deficit profiles. One of these was used in the work reported in Part 2 (Hancock and Pascheke 2014) in the first-phase study of the effects of stable stratification.

The atmospheric boundary layer (ABL) is not easy to characterize parametrically. Here, we suppose a general framework of three depths (or heights) within an Ekman layer: a layer in which Reynolds stresses are significant, of height $h$, and heights associated with the mean velocity and potential temperature profiles. Following, for instance, Mironov and Fedorovich (2010) we take the friction velocity, $u_*$, the surface Obukhov length, $L_{0}$, and the Coriolis parameter, $f$, as scales for the surface layer, and $u_*,\,f$ and the Brunt–Väisälä frequency, $N$, as scales for the turbulent flow above the surface layer, with $N$ ‘imposed’ at height $h$ representing the potential temperature gradient at this height and for some distance above. From dimensional analysis we have¹

$$\begin{aligned} \frac{hf}{u_*}=F_1 \left( {\frac{L_0 N}{u_*},\;\frac{N}{f}} \right) , \end{aligned}$$

(1)

or, equally,

$$\begin{aligned} \frac{h}{L_0 }=F_2 \left( {\frac{L_0 N}{u_*},\;\frac{N}{f}} \right) . \end{aligned}$$

(2)

Mironov and Fedorovich (2010) give an equation for this functional form. The two sets of scales lead to classifying a stable boundary layer in terms of surface-flux conditions and ‘imposed’ or ‘external’ conditions, and to sub-classifications of surface-flux dominated and external-stability dominated. In the context of wind-tunnel experiments, necessarily $f = 0$, reducing the second of the above equations to $h{/}L_0 =F_3 ({L_0 N{/}u_*})$. Here, we consider the case of a weak surface-flux condition and a strong external condition, and the flow is compared with that for neutral conditions. Such a combination of stability arises in a nocturnal jet, for instance.

If, as a very rough guide, we take $h$ as typically 1,000 m for the neutral ABL and 200 m for a stable boundary layer of the type studied here, and suppose in each case that surface scaling applies over 20 % of these heights then, at the wind-tunnel scale of 1:300, the surface scaling would apply within roughly 0.7 and 0.13 m, respectively. A turbine of 5 MW size has a hub height of typically 90 m and a blade radius of 60 m (see Sect. 2). At 1:300 scale the rotor disk lies between 0.1 and 0.5 m in height. So, with the above suppositions, the rotor is either within the surface layer or almost entirely above it. A related and important model-scale consideration is that of surface roughness, for the sea surface typically has a low roughness length (see e.g. Stull 1988), which if simply scaled down by the above scale factor would not be aerodynamically fully rough (at the wind-tunnel flow speed)—a well-known problem for wind-tunnel simulation. Therefore, the roughness has to be disproportionately larger in size in order to achieve Reynolds-number independence, but not larger than is necessary in order to achieve this. This does lead to a limitation on the accuracy of simulation for the near-surface flow.

Our work is presented in two parts (see also Hancock and Pascheke 2014). So as to be systematic, the case of stable stratification was generated from the baseline provided by the offshore neutral case. As will be described in more detail in the next section, the offshore neutral ABL was simulated by a system of Irwin-type spires and surface roughness, selected by adjustment over many iterations (of ‘science plus art’) to give a logarithmic mean velocity profile and profiles of turbulence intensity that were deemed typical of offshore neutral conditions as guided by the ESDU (2001); ESDU (2002) framework. The stable cases investigated were then generated by providing a temperature gradient at the working section inlet, and by cooling the floor, but without change to the flow generators. As will be seen, the lower part of the layer follows Monin–Obukhov similarity. The structure of the boundary layer under the influence of stabilizing forces is different from that of a neutral boundary layer and it seemed unlikely that the same flow generators could, together with the heating and cooling, provide the correct structure over the whole depth. Nevertheless, the flow generated is a stable boundary layer and is expected to provide insight into the effects of stable stratification as well as a database of measurements for assessment and development of prediction methods.

For particularly relevant work, see Magnusson and Smedman (1994), Ohya and Uchida (2003), and Chamorro and Porté-Agel (2010). The second of these investigated a boundary layer that was stratified in a way that is comparable to that here. The third found the wake to develop not only in a contrary way to that in Part 2, but in a way that would not be expected, given that the effect of stabilization is to reduce turbulence levels. The present results are qualitatively consistent with the field measurements of Magnusson and Smedman (1994). These papers will be discussed in due course. As regards prediction of wakes, the effects of stratification have yet to be included. See, for example, the recent review of Sanderse et al. (2011), and other papers from the Euromech (2012) meeting.

The simulated ABL in the present work was set up to be as close to equilibrium as could be achieved, where equilibrium here is in the sense that the flow is invariant with streamwise distance. This has the advantage that the mean flow and turbulence external to the wake are constant along its length, and is a feature that is of advantage for the experiments on the wakes of turbines one behind another. The wind-tunnel experiments of Ohya and Uchida (2003) and Chamorro and Porté-Agel (2010) were in spatially growing boundary layers.

2 Wind Tunnel and Instrumentation

The EnFlo wind tunnel is specially designed to simulate the ABL under neutral, stable or unstable conditions, where the stratification is achieved by means of heating elements across the working-section inlet, working-section panels that can be either heated or cooled, and a heat-removal heat exchanger at the end of the working section. In order that the flow can be stratified to levels of practical interest, while at the same time maintaining reasonable power requirements for heating and cooling, the working-section flow speed is restricted to about $3\hbox { m s}^{-1}$. The heater elements are able to provide 800 kW, and the chilling plant necessarily has similar capacity. As will be seen, doubling the flow speed, for example, would require eight times the heat transfer capability to maintain the same stratification conditions. The wind tunnel is of suck-down open-return configuration, with a working section that is 20 m in length, 3.5 m in width and 1.5 m in height. The wind tunnel has a bell-mouth type entry with heaters and flow-smoothing screens and honeycomb at inlet, but it does not have a settling chamber and contraction upstream of the working section, primarily because of space constraints.

Wind-flow profiles were generated by means of Irwin-like spires (Irwin 1981) mounted at the working-section inlet, together with sharp-edged roughness elements mounted on the floor. A photograph showing the spires is given in Fig. 2, Part 2. No barrier or fence as is sometimes employed was used. The shape of the spires and the roughness elements were developed in an iterative trial-and-error manner so as to match offshore airflow characteristics as given by ESDU (2001); ESDU (2002). In establishing the final configuration over 60 combinations of generator shape and roughness element spacing were tested, including a rural-roughness onshore case. In each of these combinations measurements were made at a number of stations in the second half of the working section, the first half being taken up with flow development. The five spires used in the experiments reported here were slightly truncated triangles with a base width of 150 mm and a tip width of 10 mm at a height of 1,490 mm, spaced laterally at intervals of 660 mm. The roughness elements were sparsely-spaced sharp-edged blocks 50 mm wide, 16 mm high and 5 mm thick, standing on the $50\hbox { mm} \times 5\hbox { mm}$ face. They were placed in a staggered arrangement with streamwise and lateral pitches of $360\hbox { mm} \times 510\hbox { mm}$, respectively, alternate rows being displaced laterally by 255 mm to give the staggered pattern.

Measurements of mean velocity and Reynolds stresses were made using a Dantec, FibreFlow, two-component frequency-shifted laser Doppler anemometry (LDA) system. The probe head was held by a traversing system that hung from rails mounted on the wind-tunnel roof; these rails allowed a streamwise traverse from $X = 5\hbox { m}$ to $X = 19\hbox { m}$, where $X$ is the distance from the working-section inlet. One of two orientations of the probe allowed measurement of $U(t)$ and $W(t)$, the other of $U(t)$ and $V(t)$, where $U(t),\,V(t)$ and $W(t)$ are respectively the streamwise, transverse and vertical instantaneous velocity components. Later, we use $U$ to denote the streamwise mean velocity, and $u,\,v$ and $w$ to denote the streamwise, transverse and vertical fluctuations, respectively. In the spectral analysis of the LDA measurements, the sample-and-hold method was used, and found to give good agreement at the high frequency end with hot-wire measurements (in neutral flow), while interpolation onto a uniform time base confirmed the attenuation effect of low-pass filtering at these frequencies.

Mean flow temperatures were measured with thermocouples and the fluctuating temperature by means of a cold-wire probe held at 3 mm behind the LDA measurement volume in order to measure the turbulent kinematic heat fluxes. Heist and Castro (1998) give a brief review of this technique for measuring turbulent heat flux. They used an essentially identical system in the same wind tunnel in comparable conditions and showed that the frequency response of the cold wire was sufficient to include the first decade of the inertial subrange, to about 300 Hz. The separation of 3 mm is equivalent to about the same frequency at typical mean convection speeds. As here, they also observed no significant degradation of frequency response as a result of the flow seeding. Compared with an isothermal flow, LDA measurements in principle will be affected by spatial and temporal temperature variations along the length of the beams and the back-scatter light paths. A necessarily simplified analysis is given in the Appendix, where it is demonstrated that the effects are negligible in the present application.

The wind-tunnel reference velocity, $U_\mathrm{REF}$, was measured using an ultrasonic anemometer permanently mounted in an upstream position, at $X = 5\hbox { m}$, to one side of the wind-tunnel centreline. Control of the wind tunnel, of probe position, of the model turbines, of the LDA and temperature probe measurements and other data acquisition was provided by National Instruments LabView-based software.

At the outset of the work, the physical size of the flow generators and the roughness elements, and their spatial distribution, were variables. Another variable was the physical size of the model wind turbines. Ideally, the turbines would be as large as possible, but constrained by the requirement to be able to have a number of wind turbines in the working section separated both in the streamwise and lateral directions. A scale factor of 1:300 was chosen. The model turbines themselves represented a 5 MW turbine, with a hub height of 90 m and a rotor diameter of 120 m. This inevitably led to a roughness length that is physically disproportionately large, but is a compromise that has to be made in wind-tunnel simulation for low surface roughness.

3 Scaling Considerations

The basis here of the scaling between full scale and wind-tunnel scale is to require the Obukhov length, $L$, to be constant in proportion to the rotor diameter, $D$. Although the turbine and its wake are not considered until Part 2, we present the scaling considerations here. The Obukhov length is defined as

$$\begin{aligned} \frac{L}{D}=-\frac{1}{\kappa }\frac{\overline{T} }{g}\frac{(-\overline{uw} )^{3/2}}{\overline{w\theta } }\frac{1}{D} \end{aligned}$$

(3)

where $\overline{T}$ is the mean absolute temperature, $\overline{w\theta }$ is the kinematic vertical heat flux, $g$ is the acceleration due to gravity, and $\kappa$ and $-\overline{uw}$ are the von Karman constant and the kinematic Reynolds shear stress, respectively. At $z = 0$, where $z$ is the height from the surface, $L=L_{0}$, say, so that

$$\begin{aligned} \frac{L_0 }{D}=-\frac{1}{\kappa }\frac{\overline{T} }{g}\frac{u_*^3 }{(\overline{w\theta })_0 }\frac{1}{D}, \end{aligned}$$

(4)

where $u_*$ is the friction velocity and $(\overline{w\theta } )_0$ denotes the surface kinematic heat flux. Now, the temperature fluctuations are driven by the mean temperature gradient, $\partial \Theta {/}\partial z$, where $\Theta$ is the mean potential temperature, and so in scale terms we can expect the r.m.s. of the temperature fluctuations, ${\theta }'$, to be given by

$$\begin{aligned} {\theta }'\;\sim \frac{\partial \Theta }{\partial z}D. \end{aligned}$$

(5)

Thus, $\frac{L_0}{D}$ can be represented by $\frac{1}{\kappa }\frac{\overline{T}}{g}\frac{u_{*}^3 }{\left( {{w}'\frac{\partial \Theta }{\partial z}D} \right) }\frac{1}{D}$ where ${w}'=\overline{w^{2}} ^{1/2}$, requiring for similarity,

$$\begin{aligned} \frac{\partial \Theta }{\partial z}\frac{D^{2}}{u_*^2 }\;=\;\hbox {constant}, \end{aligned}$$

(6)

where it has also been assumed that ${w}'\propto u_{*}$ For similarity, and since $u_{*} \propto U_\mathrm{{REF}}$, it follows that $(\partial \Theta {/}\partial z)(D{/}U_\mathrm{{REF}})^{2}= \hbox { constant}$. This last relation shows, for instance, that if $U_\mathrm{{REF}}$ is doubled then $\partial \Theta {/}\partial z$ must by increased by a factor 4 to maintain similarity, requiring the power to the heaters to be increased by a factor 8. This last point can be seen by supposing the working-section inlet temperature profile is a function $q(z)$, that is $\Theta -\Theta _{-\infty } \propto q(z)$, where $\Theta _{-\infty }$ is the temperature upstream of the heater. The above similarity condition implies that $\Theta -\Theta _{-\infty } \propto U^{2}q(z)$. (This can be seen by supposing two self-similar temperature profiles corresponding to two self-similar velocity profiles.) The heat transfer per unit span, $Q$, at the wind-tunnel inlet is

$$\begin{aligned} Q= C_\mathrm{P} \int \rho {U(\Theta -\Theta _{-\infty })\hbox { d}z} , \end{aligned}$$

(7)

where $C_\mathrm{P}$ is the coefficient of specific heat at constant pressure, $\rho$ is the density and the integral is over the working-section depth. From the foregoing we see that the integrand varies as $U^{3}$.

For similarity we also require $L_0 N{/}u_*= \hbox { constant}$, where the Brunt–Väisälä frequency, $N$, is defined by $N^{2}=(g{/}\overline{T})(\partial \Theta {/}\partial z)$, and is taken to be that imposed on the simulated ABL from above. Constancy of $L_0 N{/}u_*$ here implies constancy of $ND{/}u_*$, or constancy of $ND{/}U_\mathrm{{REF}}$. The same can be said via the gradient Richardson number, $Ri=g(\partial \Theta /\partial z)/{\overline{T}} (\partial U/\partial z)^{2}$, whence it follows that

$$\begin{aligned} \left( {\frac{D}{U_\mathrm{{REF}}}} \right) ^{2}\frac{\partial \Theta }{\partial z} = \hbox { constant}, \end{aligned}$$

(8)

as before, implying larger gradients of mean temperature in laboratory experiments to that of full scale, by the ratio of

$$\begin{aligned} \sim \left( {D/U_\mathrm{{REF}}}\right) _{\hbox {Full}}^2/\left( {D/U_\mathrm{{REF}}}\right) _{\hbox {Model}}^2. \end{aligned}$$

(9)

Note, in the laboratory, the mean potential temperature, $\Theta$, and static temperature, $T$, are essentially the same; with $\partial \Theta /\partial z=\partial T/\partial z+g/C_\mathrm{P}$, in the laboratory, the temperature gradient is typically $10\hbox { K m}^{-1}$, while the gravity term is $\approx 0.01\hbox { K m}^{-1}$.

4 Measurements in the Simulated ABL

Before presenting the measurements it is useful to present some of the main points of the Obuhov similarity analysis, as set out for instance by Kaimal and Finnigan (1994). In the surface layer, $L_{0}$ is the length scale in addition to the roughness length scale, $z_{0},\,u_*$ is the velocity scale and $\theta _{*}$ is the temperature scale, where

$$\begin{aligned} \theta _{*} =\frac{-(\overline{w\theta })_0 }{u_{*}}. \end{aligned}$$

(10)

Defining the function $\phi _m$ as

$$\begin{aligned} \phi _m \equiv \frac{\kappa z}{u_{*}}\frac{\partial U}{\partial z}, \end{aligned}$$

(11)

and using the expression for $\phi _m$ cited by Dyer (1974) and others for a stable boundary layer, namely

$$\begin{aligned} \phi _m =1+5\frac{z}{L_0 }, \end{aligned}$$

(12)

for $0\le z/L_0$, leads to

$$\begin{aligned} U=\frac{u_{*}}{\kappa }\left[ {\ln \left( {\frac{z}{z_0}} \right) +5\frac{z-z_0}{L_0}}\right] . \end{aligned}$$

(13)

Similarly, defining $\phi _h$ as

$$\begin{aligned} \phi _h \equiv \frac{\kappa z}{\theta _{*}}\frac{\partial \Theta }{\partial z}, \end{aligned}$$

(14)

and following Högström (1988); Högström (1996) for $\phi _h$, we have supposed

$$\begin{aligned} \phi _h =0.95+8\frac{z}{L_0}, \end{aligned}$$

(15)

which leads to

$$\begin{aligned} \Theta -\Theta _0 =\frac{\theta _{*}}{\kappa }\left[ {0.95 \ln \left( {\frac{z}{z_{0h}}}\right) +8\frac{z-z_{0h}}{L_0}} \right] , \end{aligned}$$

(16)

where $\Theta _0$ is the surface temperature and $z_{0h}$ is the thermal roughness length. Högström (1988); Högström (1996) and earlier workers conclude that the linear relationships for $\phi _m$ and $\phi _h$ are valid for $z/L_0 \le 0.5$, the slopes becoming less steep for $z/L_0 > 0.5$ and then levelling off (there being relatively few data around and above $z/L_0 = 1$). Since the Monin–Obukhov similarity only applies in the surface layer, the extent of validity is also constrained by the extent of the surface layer; for weak stable stratification $z/L_0 = 1$ is well above the surface layer.

Unless otherwise stated, all measurements are presented at laboratory scale; height, $z$, and distance, $X$, are in units of mm and m, respectively, and temperature in units of degrees Celsius.

4.1 Neutral Boundary Layer

Profiles of mean velocity, $U$, turbulence intensity (defined as ${u}'/U,\,{v}'/U,\,{w}'/U$ for each of the velocity components, where the prime denotes the root-mean square, r.m.s., of the respective fluctuation) and Reynolds shear stress are shown in Fig. 1, over a range of $X$ and normalized by $U_\mathrm{{REF}}$. Figure 1b shows profiles according to the logarithmic law, $U/u_{*} =(1/\kappa )\ln (z/z_0)$, where $u_{*}$ has been obtained from the trend of the Reynolds shear-stress profiles near $z = 0$, and the roughness length, $z_{0}$, obtained by fitting the logarithmic law to the measured neutral velocity profiles; $u_{*}$ and $z_{0}$ are given in Table 1. A value of 0.40 has been taken for $\kappa$ throughout, in agreement with Högström (1996). Strictly, the logarithmic profile only applies in the surface layer, although it is shown over the full height of the measurements in Fig. 1a. Table 1 also gives the roughness Reynolds numbers. We have used as a guide the results of Snyder and Castro (2002), which demonstrated that a sharp-edged roughness element is aerodynamically rough if the Reynolds number $u_{*} z_0/\nu > 1$.

Fig. 1

Mean velocity, Reynolds shear-stress and turbulence intensity profiles in the neutral boundary layer. Symbols as in a. Symbol key: distance from working section inlet, in mm, in this and following figures. In a the continuous line is Eq. 13 with $L_0^{-1} = 0$. In d, e, f the full and broken lines are for roughness lengths of 0.005 and 0.0005 m at full scale (see text), respectively

Table 1 Boundary-layer parameters (wind-tunnel scale)

From the profiles of $U(z)/U_\mathrm{{REF}}$ it can be seen that the mean velocity shows no significant variation with $X$. As regards the turbulence, the profiles show no significant variation of ${u}'/U$ or $-\overline{uw}/U_\mathrm{{REF}}^2$, and a slight variation of ${v}'/U$. Clearly, ${w}'/U$ is the slowest to adjust to an equilibrium profile. The plots of intensity also show the levels for different surface roughness based on ESDU (2001); ESDU (2002), for a mean wind speed of $10\hbox { m s}^{-1}$ at a height of 10 m. These are shown in the figure for full-scale roughness of 0.005 and 0.0005 m, and from these reports $z_{0}$ has been taken as being in the range 0.0001–0.001 m as typical of a sea surface (see also Stull 1988). Magnusson and Smedman (1996) took $z_{0} = 0.0005\hbox { m}$ in their offshore field study.

The measured profiles follow fairly well the trend of the ESDU data, though the levels are slightly above the trend near the surface. This is assumed to be because the roughness has to be disproportionately large at wind-tunnel scale, more so for smaller (full-scale) roughness length, in order to maintain fully rough conditions. It may have been possible with further trials to have achieved a closer concurrence but it is likely that this would have taken many more iterations of flow-generator configuration. Figure 2 shows the r.m.s. velocity fluctuations normalized by the friction velocity. As can be seen, near the surface the levels are comparable with, though consistently lower than, those cited in Arya (1988), namely 2.4, 1.9 and 1.4, for ${u}'/u_{*},\,{v}'/u_{*}$ and ${w}'/u_{*}$, respectively.

Fig. 2

Intensities normalized by friction velocity. Neutral flow. Symbols as in b

Although, as can be seen from Table 1, the roughness Reynolds number does not quite meet the guide set by Snyder and Castro (2002), no Reynolds-number dependence was found. Figure 3 shows the mean velocity profiles and Reynolds stresses over a reference speed range of $1.6{-}2.8\hbox { m s}^{-1}$, normalized by the mean velocity at $z = 300\hbox { mm}$ (the height of the turbine hub), $U_\mathrm{{HUB}}$. While, ideally, the speed range would have been larger, none of these profile sets shows any hint of a Reynolds-number dependence, including near the surface. It is assumed that this is because the roughness elements themselves, though sparsely spread out, are ‘relatively large’ and sharp-edged. Based on the velocity at a height equal to that of the roughness element, the Reynolds number is about 1500. Given the constancy of the profiles in Fig. 3 it was decided that it was not necessary to repeat the measurements at the lower speed used for the stable boundary layer (but see also Part 2). The lower speed was used to maintain the heat transfer power requirements to an acceptable level. As will be seen, the same value of roughness length applies in the stable case.

Fig. 3

Effect of the reference speed on normalized mean velocity and Reynolds stresses. Neutral flow. Symbols as in a

4.2 Stable Boundary Layer

The flow generators and the surface roughness were exactly as for the neutral stratification; the only change with respect to the neutral case was that the flow at the working-section inlet was heated to a prescribed temperature profile, and the cooled fetch of the working-section floor from $X = 7\hbox { m}$ onward maintained at a fixed temperature.² Thus it was possible to observe the direct effect of changing just the inlet temperature profile and the surface temperature. But it does mean too that the Irwin spires were taller than they ideally would have been for the reduced height of the boundary layer. As will be seen, the flow, once settled to essentially invariant conditions, followed the Monin–Obukhov surface-layer similarity in most respects.

Figure 4 shows the mean velocity, Reynolds shear stress and the streamwise and vertical intensities, while Fig. 5 shows the mean temperature profiles. The temperature at the working-section inlet, which increased linearly to the top of the working section, is also shown in Fig. 5. The first observation to make about the measured profiles of Figs. 4 and 5 is that between $X = 11$ and 15 m there is little variation with $X$, as will be confirmed from other quantities discussed below. We expected that a stably stratified flow might take longer to settle to a closely invariant state, stemming from the reduced level of mixing. The mean velocity profiles, which are also presented semi-logarithmically (Fig. 4b), follow the expected form of Eq. 13 as far as $z \approx 200\hbox { mm}$. As with the neutral flow, $u_{*}$ has been obtained from extrapolation of the Reynolds shear-stress measurements (as indicated in Fig. 4c). The roughness length, $z_{0}$, has been assumed to be equal to that for neutral flow, as given again in Table 1 (consistent with Stull 1988). The justification for this is that the roughness was thought to be small enough for stratification effects to have no significant local effect on the flow around the roughness elements, but large enough to avoid Reynolds-number effects. No investigation of Reynolds number was made in the stratified case because changing flow speed would have required a change in inlet and surface temperatures, which would have been time consuming to obtain properly comparable conditions. Satisfyingly, the assumptions made here are supported by the good agreement between the measured and expected forms for the near-surface part of the layer. As an indication of the change in the mean velocity profile from a neutral flow, the broken line in Fig. 4a, b is that given by Eq. 13, but with the buoyancy term ignored. Zilitinkevich and others (see for example, Zilitinkevich and Calanca 2000) have proposed a form for the mean velocity profile, and also the mean temperature profile, that includes $L_0 N/u_{*}$ as a parameter, though this is inconsistent with the surface layer depending only upon surface-related scales. This is not pursued further here.

Fig. 4

Profiles of mean velocity, Reynolds shear stress and turbulence intensities. Stable flow. Symbols as in a. Full lines in a, b are Eq. 13; broken lines are Eq. 13 but ignoring the buoyancy term. Line in c is a supposed fit to the trend of the data. Broken lines in d, e are for a roughness of 0.0005 m at full scale as in Fig. 1

Fig. 5

Mean temperature profiles. Symbols as in a. Full line as given by Monin–Obukhov similarity theory. Broken line is the inlet temperature profile

For the temperature profiles, $\theta _{*}$ has been calculated from an extrapolation of the heat flux (discussed later), and $\Theta _0$ is the temperature of the cooled floor. The thermal roughness length, $z_{0h}$, which has been observed repeatedly to be $\ll z_{0 }$ (see, for instance, Beljaars and Holtslag 1991; Duynkerke 1999), has been adjusted to fit the data of Fig. 5 in this near-surface region. $\Theta _0$ and $z_{0h}$, are given in Table 1. Ideally, the whole of the floor would have been uniformly cooled to a given temperature, but as mentioned earlier this facility was not available at the time of the experiments. Fortunately, the fact that the various quantities measured show no significant streamwise variation near the surface or further out gives confidence that the consequence of an un-cooled initial section was minor. This is assumed to be because the length scales were sufficiently reduced under stable conditions for its effect to have become insignificant at the measurement stations. Defining a bulk Richardson number as $R_\mathrm{b}=Hg(\Theta _\mathrm{{HUB}} -\Theta _0 )/{\overline{T}} U_\mathrm{{HUB}}^2$ then $R_\mathrm{b}$ was about 0.034, where $H$ is taken as 300 mm (the height of the model wind-turbine hub) and where $\Theta _\mathrm{{HUB}}$ is the mean temperature at height $H$, respectively.

From Fig. 4 it can be seen that the Reynolds shear stress has fallen to zero at about $z = 500\hbox { mm}$. At this height, $h$, the temperature gradient as seen in Fig. 5a is ‘large’. This latter figure also shows a temperature profile according to Monin–Obukhov similarity, as a reference, though it is not supposed valid that far from the surface. The gradient $\partial \Theta /\partial z$ at $z = 500\hbox { mm}$ is roughly $20\hbox { K m}^{-1}$. At full scale, assuming a wind speed of, say, $10\hbox { m s}^{-1}$ rather than the $\approx 1.5\hbox { m s}^{-1}$ of these experiments, Eq. 9 gives this as equivalent to $4.9 \times 10^{-4}\times 20 \hbox { K} \hbox { m}^{-1}= 0.01 \hbox { K } \hbox {m}^{-1}$, comparable to levels given, for example, by Marht et al. (1979) and Andre and Mahrt (1982), and with more recent data given by Steeneveld et al. (2007).

Before discussing other quantities, mention needs to be made regarding the friction velocities given in Table 1, referenced to both $U_\mathrm{{REF}}$ and the velocity, $U_\mathrm{{HUB}}$, in the respective undisturbed flow. The effect of stable stratification is to reduce the level of turbulent activity and thereby reduce the level of wall shear stress and hence reduce $u_{*}$, as is seen to be the case with respect to $U_\mathrm{HUB}$, but not with respect to $U_\mathrm{{REF}}$. While it is essential to measure and cite a reference velocity, the reference velocity was measured in the developing part of the flow that was different in the two flows.

Not surprisingly, in view of the shape of the mean velocity profiles and the expected effect of stratification, there is a much more rapid decrease in $- \overline{uw}$ with $z$, than there is in the neutral case. For most of the layer the intensities ${u}'/U$ and ${w}'/U$ are also clearly lower. But, near the surface and near the top of the profiles, the levels are more comparable. Similar features are seen in Fig. 6, compared with Fig. 2, for ${u}'/u_{*}$ and ${w}'/u_{*}$. Comparability near the surface is to be expected from surface-layer similarity for small surface stratification (see, for example, Nieuwstadt 1984). The magnitude of turbulence intensity at the top end of the profiles is assumed to be due in part to the spires extending to the full height of the tunnel. In the absence of the spires ${u}'/U$ was about 2.3 %. Regarding the turbulence at this height as ‘free-stream turbulence’ the effect will have been to cause, it is assumed, an increase in surface shear stress, estimated at less than 1.5 %, an increase in boundary-layer depth, and some flattening of the mean velocity and Reynolds stress profiles in the outer part (Hancock and Bradshaw 1989).

Fig. 6

Turbulence intensities normalized by friction velocity. Stable flow. Symbols as in a

Figure 7 shows $-\overline{u\theta }$ and $\overline{w\theta }$, normalized by the surface heat flux³, $(\overline{w\theta })_0$, which has been obtained by a linear extrapolation to $z = 0$; the three sets of profiles follow closely a single consensus that has been used as the basis of the extrapolation, though arguably a lower surface value could have been inferred. $\overline{u\theta }$ is larger in magnitude than $\overline{w\theta }$ and, overall, decreases more slowly to zero with height. This figure also shows the r.m.s. of the temperature fluctuations, ${\theta }'$, normalized by $\theta _{*}$. (Other measurements, not shown here, made with a steeper gradient of inlet temperature, gave a steeper gradient in ${\theta }'$; the rise in ${\theta }'$ is associated with the gradient in mean temperature.) As mentioned in the Introduction, Ohya and Uchida (2003) conducted a similar experiment that had a near-linear temperature profile at the flow inlet giving a mean temperature profile much like those of Fig. 5 (though their layer was developing from a leading edge over a rough surface, rather than as here, from flow generators). They made measurements at only one streamwise station and did not make comparisons with Monin–Obukhov similarity. At the lowest level of stability they observed a variation in ${\theta }'$ quite like that in Fig. 7c, namely a decrease with increasing $z$ followed by a rise, which they attributed as here to the rise in the mean temperature. For further relevant discussion see also Ohya (2001) and Nieuwstadt (1984).

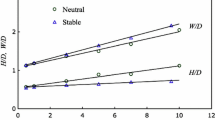
Figure 8 shows the local Obhukov length, $L$, defined by Eq. 3, and $\phi _m$ and $\phi _h$ defined by Eqs. 11 and 14, respectively, where for the latter two $z$ is normalized by $L_0$. The plots for $\phi _h$ and $\phi _m$ also give the analytic forms given be Eqs. 12 and 15. Near the surface the trend of the measured $\phi _m$ is larger than that given by Eq. 12 (with a slope of about 8 rather than 5), but the rise is then followed by a dramatic fall at $z/L_0 \approx$ 0.1. The trend of the measured $\phi _h$, on the other hand, is fairly close to Eq. 15 for $z/L_{0} \lesssim 0.15$ (roughly $z = 200\hbox { mm}$), but without a dramatically rapid change above this height.

Fig. 8

Profiles of local Obukhov length, and functions $\phi _m$ and $\phi _h$. Symbols as in a. Line in b is Eq. 12; line in c is Eq. 15

Figure 9 shows the flux Richardson number, $R_{f}$, and the ratio of flux and gradient Richardson numbers, $R_f /Ri$, where $R_f =g(-\overline{w\theta })/{\overline{T}} (-\overline{uw } \partial U/\partial z)$, and the Brunt-Väisälä frequency, $N$, normalized by $D/U$. $R_{f}$ is compared with the form given by $R_f =(K_h /K_m )\left( {z/L_0 } \right) \left( {0.95+8z/L_0} \right) /\left( {1+5z/L_0 } \right) ^{2}$, where the ratio of eddy diffusivities, $K_h /K_m \;\left( {=R_f /Ri} \right)$, has been taken as 0.85. There is comparable agreement between this form and the measurements as far as $z/L_{0}$ of about 0.12. Figure 10 gives an example of spectra, $F_{11} (k)$ and $F_{33} (k)$, for $u$ and $w$ fluctuations respectively, at $z = 300\hbox { mm}$, normalized with the respective mean square of the fluctuations, for both the neutral and stratified cases. $F_{ii} (k)$ was obtained from the respective (cyclic) frequency spectrum, $E_{ii} (f)$, by $F_{ii} (k)=(U/4\pi )\;E_{ii} (f)$, where the wavenumber, $k$, is given by $k=2\pi f/U$, assuming the mean velocity $U$ is the convection velocity. The figure also shows the neutral flow surface-layer spectra (see Kaimal and Finnigan 1994), which in terms of frequency, are

$$\begin{aligned} E_{11} (f)=\frac{102\;u_*^2 z/U}{(1+33fz/U)^{5/3}}, \end{aligned}$$

(17)

and

$$\begin{aligned} E_{33} (f)=\frac{2.1\;u_*^2 z/U}{1+5.3\;(fz/U)^{5/3}}. \end{aligned}$$

(18)

Strictly, if the surface-layer depth is ${\approx } 0.2$ of the boundary-layer height, $h$, the spectra of Fig. 10 are above the surface layer. Table 1 gives $h$ based on the height at which the shear stress has become close to zero. Nevertheless, the neutral-flow spectra compare well with these forms, $F_{11} (k)$ showing slightly more energy at the high wavenumber end and slightly less at low wavenumbers. The agreement for $F_{33} (k)$ is much closer. Comparatively, the effect of stratification is a small but noticeable reduction in $F_{33} (k)$ at low wavenumbers, which would be expected as a result of a reduced vertical length scale. From Fig. 9, ND/U is about 0.2 at this height. The spectra in Fig. 10 do not exhibit any indication of a peak at this wavenumber.

Fig. 9

Profiles of flux Richardson number, Richardson number ratio, and the Brunt–Väisälä frequency. Symbols as in a. Line in a: see text

Fig. 10

Spectra in neutral and stable flow, at $z = 300\hbox { mm}$: a $F_{11}$ (k), b $F_{33}$ (k). Full line Neutral; diamonds Stable. Broken line Spectral forms of Kiamal and Finnegan (1994, see text). Full lines Slope of –5/3

5 Concluding Comments

Results have been presented for a baseline neutral simulation of an offshore boundary layer, and for a case of stable stratification. In the neutral case the flow became invariant with streamwise distance, closely following a standard logarithmic-law profile for the mean velocity and intensity profiles closely comparable with those taken from the ESDU (2001); ESDU (2002) guidelines. Variation of flow reference speed showed no indication of Reynolds-number dependence even though the roughness Reynolds number was less than the supposed minimum of 1.

The stable case was also very nearly invariant with streamwise distance in the second half of the working section, and closely followed the Monin–Obukhov similarity to height of about $z = 200\hbox { mm}$. The boundary layer was generated using the same Irwin-spire flow generators at the working section inlet and the same surface roughness for the neutral base-line flow. No baseline profiles were used for the stable case above the surface layer, but it is clear that matching to a set is likely to be as iterative a task as it was for the neutral case. The ‘imposed’ stability was generated by providing a linear temperature profile at the working section inlet, which gave a boundary-layer temperature profile that was approximately linear in the downstream flow above the boundary layer. In the classification of Stull (1988) this is close to that of ‘linear’. At full scale, the Obukhov length, $L_{0}\,\approx 380\hbox { m}$ and the imposed stability, $N\,\approx 0.018\hbox { s}^{-1}$, and taken as being respectively, ‘weak’ and ‘strong’.

As anticipated, the surface roughness, formed from relatively large but sparsely spaced elements, behaved with the same aerodynamic roughness length for the stable case as for the neutral case. Moreover, this concurrence provides evidence that the roughness was sufficiently large to be Reynolds-number independent, even though the roughness Reynolds number was only 0.51 in the stable case. Achieving Reynolds-number independence at wind-tunnel scale is particularly challenging for typical sea surface roughness.

Appendix: Effect of Temperature on LDA Measurements

The refractive index, $n$, of air is dependent on temperature, and so the path of a constituent ray, and therefore that of a beam, may change. In a turbulent flow the path followed by a beam will vary along its length according to the variation of temperature with time along its length. As this is not known a simplified analysis is all that can be made. We follow the line of analysis set out by Resagk et al. (2003). If $s$ is the distance along the ray from its origin at the probe lens, and $\mathbf{\underline{r}}$ the position vector of a point along the ray then

$$\begin{aligned} \frac{\hbox {d}}{\hbox {d}s}\left( {n\frac{\hbox {d}\mathbf{\underline{r}}}{\hbox {d}s}} \right) = \mathrm{grad}\;n, \end{aligned}$$

(19)

(Born and Wolf 1999). The case of practical concern here is when the gradient is perpendicular to the ray direction, $\xi$. Then, if $\eta$ is the lateral displacement, this equation reduces to $\hbox {d}^{2}\eta /\hbox {d}\xi ^{2}=(1/n) \hbox {d}n/\hbox {d}\eta$, and since the departure of $n$ from unity is in any case small (see below), we obtain

$$\begin{aligned} \frac{\hbox {d}^{2}\eta }{\hbox {d}\xi ^{2}}\approx \frac{\hbox {d}n}{\hbox {d}\eta } = \beta , \end{aligned}$$

(20)

say. Making the further assumptions that a focused beam can be represented by two rays converging at an angle of $\pm \phi$ and that the gradient $\beta$ is constant across the beam leads to the lateral displacement,$\Delta \eta$, of the focus according to

$$\begin{aligned} \Delta \eta =\frac{\beta }{2}F^{2}\left( {\frac{2\delta }{F\phi }-1} \right) \end{aligned}$$

(21)

where $2 \delta$ is the beam separation at the lens and $F$ is the distance to the focus. It can also be shown that the angle of the beam, $\alpha$, at the focus is given by $\beta F$.

Now, supposing the gradients are moderate enough for both beams (at small internal angle $2 \Phi$) to be affected equally, then Eq. 21 gives the lateral deflection of the measuring volume from the probe axis, and there is no movement along the probe axis. There is also no change in the angle between the beams and therefore no change in fringe spacing. Conversely, assuming the gradient across one beam is equal and opposite in magnitude to that across the other, leads to no lateral deflection of the measuring volume but does lead to a displacement from the probe according to

$$\begin{aligned} \Delta \xi =\frac{\beta F^{2}}{2(\Phi +\alpha )}\left( {\frac{2\delta }{F\phi }-1} \right) , \end{aligned}$$

(22)

where $\xi$ now denotes the distance along the probe axis, rather than along a beam. The change in beam internal angle is $2\alpha$, and the fractional change in Doppler frequency $\delta f/f=- \alpha /(\Phi +\alpha )$.

Now, taking $\hbox {d}n/\hbox {d}T \approx 9.8 \times 10^{-7} \hbox { K}^{-1}$, and noting $dT/d\eta$ has units Km$^{-1}$, so that $\beta = 9.8 \times 10^{-7}$ d $T$ /d $\eta$ (m$^{-1}$) and the probe parameters lead to $\alpha =4.9\times 10^{-8}\;\hbox {d}T\hbox {/d}\eta ,\,\Delta \eta =1.2 \times 10^{-9}\;\hbox {d}T\hbox {/d}\eta \,(\hbox {m})$ and $\Delta \xi =1.5\times 10^{-8}\;\hbox {d}T\hbox {/d}\eta \,(\hbox {m})$. From Fig. 7 $\partial {\phi }'/\partial z$ is not larger than about $3\hbox { K m}^{-1}$, so even if instantaneously $\partial \phi (t)/\partial z$ was, say, three order of magnitude larger then, $\alpha \approx 1.5 \times 10^{-4}$, and $\Delta \eta \approx 3.7\, \upmu \hbox {m}$ and $\Delta \xi \approx 46 \,\upmu \hbox {m}$, or about 3 % of the respective measuring volume dimensions. (If only one beam is supposed affected, then this fraction is about 1.5 %.) The fractional change in Doppler frequency is about 0.18 %. In conclusion, the effects of temperature fluctuations are expected to be negligible.