Parametrization of Drag and Turbulence for Urban Neighbourhoods with Trees

Abstract

Urban canopy parametrizations designed to be coupled with mesoscale models must predict the integrated effect of urban obstacles on the flow at each height in the canopy. To assess these neighbourhood-scale effects, results of microscale simulations may be horizontally-averaged. Obstacle-resolving computational fluid dynamics (CFD) simulations of neutrally-stratified flow through canopies of blocks (buildings) with varying distributions and densities of porous media (tree foliage) are conducted, and the spatially-averaged impacts on the flow of these building-tree combinations are assessed. The accuracy with which a one-dimensional (column) model with a one-equation ($k$–$l$) turbulence scheme represents spatially-averaged CFD results is evaluated. Individual physical mechanisms by which trees and buildings affect flow in the column model are evaluated in terms of relative importance. For the treed urban configurations considered, effects of buildings and trees may be considered independently. Building drag coefficients and length scale effects need not be altered due to the presence of tree foliage; therefore, parametrization of spatially-averaged flow through urban neighbourhoods with trees is greatly simplified. The new parametrization includes only source and sink terms significant for the prediction of spatially-averaged flow profiles: momentum drag due to buildings and trees (and the associated wake production of turbulent kinetic energy), modification of length scales by buildings, and enhanced dissipation of turbulent kinetic energy due to the small scale of tree foliage elements. Coefficients for the Santiago and Martilli (Boundary-Layer Meteorol 137: 417–439, 2010) parametrization of building drag coefficients and length scales are revised. Inclusion of foliage terms from the new parametrization in addition to the Santiago and Martilli building terms reduces root-mean-square difference (RMSD) of the column model streamwise velocity component and turbulent kinetic energy relative to the CFD model by 89 % in the canopy and 71 % above the canopy on average for the highest leaf area density scenarios tested: $0.50\hbox { m}^{2}~\hbox {m}^{-3}$. RMSD values with the new parametrization are less than 20 % of mean layer magnitude for the streamwise velocity component within and above the canopy, and for above-canopy turbulent kinetic energy; RMSD values for within-canopy turbulent kinetic energy are negligible for most scenarios. The foliage-related portion of the new parametrization is required for scenarios with tree foliage of equal or greater height than the buildings, and for scenarios with foliage below roof height for building plan area densities less than approximately 0.25.

1 Introduction

Vegetation is common in urban areas worldwide, and its inclusion in models of the physical environment of cities is critical for the proper simulation of the neighbourhood-scale energy balance (Grimmond et al. 2011), street-level climate (Shashua-Bar and Hoffman 2000), and air pollutant dispersion (Gromke and Ruck 2007, 2009; Vos et al. 2013). Furthermore, it is an important design tool in urban environmental management (Oke 1989; Bowler et al. 2010). Urban vegetation may even be critical for the prevention of exacerbated urban-rural temperature differences during heat waves (Li and Bou-Zeid 2013).

Trees offer shade and shelter to pedestrians and buildings, and modify near-surface turbulent and radiative exchanges. Furthermore, they increase absorption and deposition of pollutants (Litschke and Kuttler 2008), emit biogenic volatile compounds (a temperature-dependent process; Calfapietra et al. 2013), and affect pollutant dispersion by exerting drag on the flow and reducing exchange between the canopy and the above-canopy flow (Gromke and Ruck 2009; Vos et al. 2013). Hence, a prime challenge for numerical models of the urban environment is to account for the physical and chemical effects of urban vegetation. In essence, the interactions between vegetation and the ‘built’ fabric (e.g., buildings, streets) in cities must be better understood and modelled. These interactions are more complex, and are expected to be more significant, for trees than for shorter vegetation.

Trees are expected to interact with buildings primarily in terms of flow dynamics (e.g., sheltering) and radiation exchange (e.g., shading); the former is the focus of the present contribution. Trees and buildings shelter each other and both modify their shared turbulent and thermal environments; however, the neighbourhood configurations and scales of analysis for which these effects are significant remain an open question. Trees also shade buildings and other trees, and vice versa, and exchange diffuse radiation with buildings; a neighbourhood-scale model for these interactions has recently been developed (Krayenhoff et al. 2014). To contextualize the development of a model for the impacts of trees on urban flow dynamics, existing models of flow through canopies of trees (i.e., forests) and buildings (i.e., non-treed cities) are reviewed below.

1.1 Modelling Neutral Flow Through Urban and Forest Canopies

Models of urban meteorology, climate, and pollutant dispersion must account for a broad range of scales, from individual elements at the city surface ($<$10$^{2}$ m) to transport across, into and out of the urban airshed ($\approx$10$^{4}$–10$^{6}$ m). Due to computational limitations, mesoscale model grid resolution has an upper limit on the order of $10^{2}$–$10^{3}$ m (issues of turbulence parametrization aside, e.g., see Wyngaard 2004). Because this resolution is too coarse to explicitly compute the flow around individual features such as buildings and trees, these features are then subgrid and their effects on the mean flow must be parametrized at the neighbourhood, or local, scale, e.g. by an urban canopy parametrization (UCP; Martilli 2007; Santiago and Martilli 2010).

Process-based numerical models of urban meteorology and climate (i.e., urban canopy models) have been designed in recent years to predict the time-averaged effects of canopy micrometeorology and to be coupled with mesoscale atmospheric models. Many of these models use highly parametrized and empirically-based means of calculating vertical profiles of wind speed and momentum flux, and the exchange of scalars between and above the canopy (e.g., Masson 2000; Kusaka et al. 2001), while some add additional theoretical detail such as the vertical diffusion of momentum (e.g., Coceal and Belcher 2004; Kondo et al. 2005) or theory regarding the exchange of scalars (e.g., Harman and Belcher 2006). What is referred to here as a UCP is subsumed in several multi-layer urban canopy models. A UCP typically includes a 1.5-order $k$–$l$ turbulence closure and is based on the representation of canopy-induced processes in the equations of vertical exchange of momentum and turbulent kinetic energy (TKE), such as drag and the generation and dissipation of TKE (Martilli et al. 2002; Dupont et al. 2004; Hamdi and Masson 2008; Santiago and Martilli 2010). Therefore, UCPs are multi-layer by definition, which allows for (but does not guarantee) reduced parametrization of the canopy physics, inclusion of building (and tree foliage) height distributions, and more detailed prediction of the street-level flow and dispersion.

Similar parametrizations of canopy flow exist for vegetation (forest) stands. Simple mixing-length models for vegetation canopies originated with Cionco (1965), and these ideas were later extended to urban canopies (Macdonald 2000; Coceal and Belcher 2004). While such first-order models have limitations, they are nevertheless useful for a variety of purposes (Katul and Albertson 1998). Higher-order models have fewer limitations but greater requirements for closure coefficients and hence more degrees of freedom. Pyles et al. (2000), for example, include a third-order turbulence parametrization and the thermal effects of the canopy and the surface. However, Katul et al. (2004) find that 1.5-order $k$–$l$ models performed as well as second-order closures across multiple vegetation canopy datasets, and they require fewer closure constants and associated degrees of freedom. In their words, such models are “attractive for linking the biosphere to the atmosphere in large-scale atmospheric models or multi-layer soil-vegetation-atmosphere transfer schemes within heterogeneous landscapes.”

1.2 Modelling Flow in Treed Urban Neighbourhoods

Most model representations of vegetated urban canopies ‘tile’ urban and soil-vegetation surface models, such that they interact independently with the atmospheric model in each grid square (e.g., Lemonsu et al. 2004). With this approach, built and natural surface exchanges only influence each other indirectly via the atmospheric model, and potentially important vegetation-building interactions, and tree-building interactions in particular, are not included.

Building-tree interaction in the context of urban canopy flow may be conceptualized in two ways. Trees exert a drag on the flow and hence reduce the absolute drag force exerted by buildings, and this effect does not require parametrization but simply the inclusion of drag terms for both buildings and trees in the solution of the canopy momentum balance (i.e., an integrated approach instead of a tile approach). Trees also affect the relative impact of buildings on the flow: the efficiency with which buildings remove momentum from the flow, which is proportional to the ratio between the drag force and the square of the mean wind velocity at the same height and is also referred to as the sectional building drag coefficient $(C_\mathrm{DB})$. An analogous phenomenon, albeit operating at a smaller scale, is the sheltering between plant elements identified by Thom (1971) and confirmed by Brunet et al. (1994). This latter sense of building-tree interaction is investigated here. If this effect is significant, its parametrization for any combination of building and foliage arrangement and densities is likely to be complex.

The situation for turbulence production in building and tree wakes is identical, because it depends not only on the mean velocity at each level for both tree and buildings, but also on their respective drag coefficients (i.e., TKE production by element wakes is proportional to the rate of removal of mean momentum by element drag). Turbulence length scales, however, are ‘overall’ properties of the flow, unlike drag, which may be represented as separate source terms for buildings and trees. A key question is whether trees affect length scales in addition to the substantial effects of buildings (e.g., Santiago and Martilli 2010).

Two urban canopy models have included the flow effects of both buildings and trees and their absolute effects on each other. Dupont et al. (2004) integrate the effects of tall vegetation on momentum and turbulence budgets into a multi-layer model but do not account for building-tree interaction. The single-layer urban canopy model of Lee and Park (2008) includes the effects of trees within canyons only, and in a highly parametrized fashion. Several multi-layer flow models for (urban) obstacles exist, but none includes vegetation (e.g., Martilli et al. 2002; Coceal and Belcher 2004).

The present work represents the combined effects of trees and buildings on the spatially-averaged mean flow with a relatively simple parametrization. These effects are assessed in the three-dimensional (3-D) flow and subsequently parametrized in a one-dimensional (1-D) approach. Airflow within and above vegetation and especially urban canopies is fully 3-D, but in many applications the horizontal spatial variability cannot be resolved. Hence a filter, consisting of horizontal averaging over an area much larger than the size of the obstacles, is applied in order to reduce the canopy-atmosphere exchanges to one dimension (vertical). Effects of 3-D processes must be accounted for in 1-D models in order to capture the vertical variation of the flow, hence appropriate horizontal averaging is critical (Raupach and Shaw 1982). Here we extend previous work that parametrizes 3-D flow processes in 1-D vertical diffusion models for urban canopies (e.g., Santiago and Martilli 2010). Assessment of the effects of foliage-related processes on flow, and their interaction with building-related processes, where each process is represented by a source term or modification thereof in the flow equations (Sect. 2), is a new contribution. The overall aim is to present a methodology for the development of a UCP for urban canopies with trees.

1.3 Objectives and Degrees of Freedom

Considering the complexity of flow through ‘urban’ arrays with tree foliage, theoretical approaches such as those developed for forest and building-only cases (e.g. Cionco 1965; Belcher et al. 2003) are less plausible. Here, a parametrization scheme is developed based on results from a 3-D computational fluid dynamics (CFD) model. The methodology of Santiago and Martilli (2010) forms the backbone of the current contribution (Fig. 1). The CFD model is first evaluated against wind-tunnel measurements to ensure model robustness and accuracy (Web Supplement, Simon-Moral et al. 2014). Subsequently, obstacle-resolving CFD model simulations of neutrally-stratified flow through canopies of blocks (buildings) with various distributions and densities of porous media (tree foliage) are conducted, and the spatially-averaged impacts on the flow of these building-tree combinations are assessed. Based on the CFD model results, a parametrization of the vertically-distributed impacts of trees on the mean flow and turbulence in urban canopies for neutral conditions is formulated, explicitly considering building-tree interaction. The new CFD model-derived parametrization of drag and turbulence contributes to the full inclusion of vegetation in multi-layer urban canopy models and neighbourhood-scale dispersion models.

Fig. 1

The Santiago and Martilli (2010) methodology. Higher fidelity models and measurements are used to inform or test simpler models (grey boxes/brown arrows). The objective is to determine spatial-mean flow profiles (yellow boxes) with a column model informed by fully-parameterized inputs (green box), i.e., an independent urban canopy parametrization. Thick blue arrows indicate model output, thin blue arrows indicate model input. Orange numbers indicate the section in which the model or process (i.e., testing or model input) is described or used

A large range of building-tree configurations could be considered in the design of the CFD model simulations. Relatively large simplifications are made here, viz. regular arrays of cubic blocks (buildings) with foliage layers of thickness $H/2$ (where $H$ is building height), and foliage evenly distributed in the horizontal across the non-built area at each height. Even foliage distribution is chosen for simplicity; note that discontinuous foliage distributions give somewhat different results. Moreover, wind direction is maintained perpendicular to windward building faces for all simulations; the dynamic effects of varying wind direction have been explored for non-treed configurations (Santiago et al. 2013a), and they result in additional complexities such as lift forces that are beyond the current scope. Other findings suggest that the aerodynamic effects of trees depend on wind direction as well as building configuration (Buccolieri et al. 2011). Here, only building plan area density, tree foliage layer height and leaf area density are varied, resulting in three degrees of freedom.

A methodology to formulate the one-dimensional UCP for urban canopies with trees is developed. First, the ability of the 1-D column model to reproduce spatially-averaged CFD model results is evaluated (Sect. 2.4, Appendix). Subsequently, the new parametrization for impacts of urban trees on flow is developed from, and contextualized by, the four primary objectives of this work:

• (A) to assess the relative importance of the (source/sink) terms added to the momentum and TKE budgets in the column model to represent the effects of urban tree foliage on flow profiles, as compared to the 3-D CFD model (Sect. 3);

• (B) to determine if trees and buildings can be treated independently, or if their relative impacts on the flow (e.g., their efficiencies as momentum sinks, i.e., their drag coefficients) are affected by each other’s presence (Sect. 3);

• (C) to assess the accuracy of the resulting parametrization, which is based on those terms found in Sect. 3 to be important to the correct reproduction of the spatially-averaged flow profiles in urban neighbourhoods with trees (Sect. 4);

• (D) to determine for which combinations of foliage heights, and building and foliage densities, tree foliage-related source/sink terms significantly affect spatially-averaged flow in addition to the building-related source terms (Sect. 4).

Section 2 discusses the equations of fluid flow that form the basis of the 3-D CFD model and the column model (i.e., the UCP), while Sect. 3 addresses objectives A and B, and Sect. 4 addresses objectives C and D. Section 4 also updates parameters for the Santiago and Martilli (2010) parametrization of spatially-averaged flow through non-treed urban neighbourhoods, and Sect. 5 concludes with a summary and conclusions.

2 Numerical Models

A 1-D column model with $k$–$l$ closure is developed to represented effects of buildings and trees on vertical exchange in the urban canopy. To generate it as a stand-alone model, inputs are parametrized based on results from a 3-D Reynolds-averaged Navier–Stokes (RANS) CFD model with standard $k$–$\varepsilon$ turbulence closure. Hence, a 3-D CFD model that accurately represents the primary effects of the key canopy processes on vertical profiles of flow is essential. A 3-D RANS flow model with standard $k$–$\varepsilon$ turbulence closure is chosen because there is an established history of its use for flows through building and tree canopies; it has been shown to accurately reproduce profiles of spatially-averaged flow properties from measurements and high fidelity flow models (e.g., Santiago et al. 2008, 2010; Web Supplement); and it is computationally efficient, and thus more appropriate for the investigation of multiple scenarios. Cheng et al. (2003) found that large-eddy-simulation (LES) models requires two to three orders of magnitude more computational power than RANS models with standard $k$–$\varepsilon$ closure; hence, a RANS modelling approach is considered more feasible here.

2.1 Three-Dimensional RANS $k$–$\varepsilon$ Model and Parametrization of Foliage Effects

The CFD model solves the steady-state RANS equations in three dimensions. Prognostic equations for both the TKE $(k)$ and its rate of dissipation $(\varepsilon )$ are solved, and model simulations proceed until a steady state is achieved. A description of the CFD model equations for the non-treed cases, and the source terms required to represent buildings, can be found in Santiago et al. (2007). The commercial code STAR-CCM+ is used (CD-adapco 2012).

The domain height is $4H$, where $H$ is building (cube) height, and domain length and width are each the sum of two building widths $(2H)$ and two street widths. Symmetry conditions are imposed in the spanwise direction, and periodic boundary conditions are imposed in the streamwise direction. Simulations are forced by a horizontal pressure gradient $(\tau )$, from which a scaling velocity $u_{\tau } =\sqrt{4\tau H/\rho }$ can be derived, where $\rho$ is the air density $(\hbox {kg m}^{-3})$. At the domain top, zero normal derivatives are prescribed; a Cartesian grid is used, which resolves each cube with 16 cells in each dimension. Grid independence is tested by doubling the number of cells in each dimension to 32, and 16 cells across each cube face is determined to be sufficient (not shown). Further details are available in Santiago et al. (2008) and Santiago and Martilli (2010).

Source and sink terms arise in, or are added to, the momentum, TKE, and TKE dissipation rate equations to represent the effects of tree foliage on the 3-D flow, following Santiago et al. (2013b). This particular combination of source and sink terms originates for flows through plant canopies (Green 1992; Liu et al. 1996). Its applicability to foliage in urban environments requires further testing, in particular because it has been developed in the context of a single-band turbulence model and coefficients of the source and sink terms are determined for flows without buildings, and buildings modify the turbulence spectrum. Nevertheless, there are precedents for its use in urban environments (e.g., Dupont et al. 2004; Santiago et al. 2013b), and investigation of its merit is beyond the scope of the current analysis.

Form drag due to foliage results from the spatial averaging of the Navier–Stokes equations at the scale of the numerical grid, which is not of sufficient resolution to resolve leaves and branches. Form drag is parametrized as follows (Green 1992; Liu et al. 1996),

$$\begin{aligned} S_{u_{i}} =-L_\mathrm{D}C_\mathrm{DV} U \bar{{u}}_{i}, \end{aligned}$$

(1)

where $u_{i}$ is the appropriate wind velocity component, $U$ is the wind speed $\sqrt{\sum _{i=1,3} {u_{i}^{2}}}$, both in $\hbox {m s}^{-1}$, $L_\mathrm{D}$ is the leaf area density $(\hbox {m}^{2}\hbox { m}^{-3})$, and $C_\mathrm{DV}$ is the sectional drag coefficient for the foliage (dimensionless). The drag coefficient of the forest foliage has been found to range between 0.15 and 0.30 (e.g., Li et al. 1985; Massman 1987), and the optimized value of 0.20 determined by Katul and Albertson (1998) is chosen here. $C_\mathrm{DV}$ acts as a blunt covering parameter, and its value typically includes the impacts of sheltering at several scales (typically shoot-crown), an effect related to foliage clumping. Furthermore, nuanced effects on $C_\mathrm{DV}$ such as leaf fluttering and streamlining, which depend on wind speed (e.g., Walter et al. 2012), are not explicitly included.

Equation 1 represents a sink of momentum due to foliage-atmosphere interaction that originates from averaging of the momentum equation. This sink of mean momentum implies a source of turbulence due to the extraction of mean kinetic energy from the flow (assuming total conversion of mean kinetic energy to TKE), which is a source in the TKE equation and is parametrized as,

$$\begin{aligned} S_{k}=L_\mathrm{D}C_\mathrm{DV} U^{3}. \end{aligned}$$

(2)

This term is often referred to as wake production. However, while vegetation clearly generates turbulent energy at a rate approximated by Eq. 2, it does so at the scale of the drag elements (i.e., leaves and branches). For vegetation, these ‘wake’ scales are small and hence turbulence generated in this fashion dissipates more rapidly to heat than turbulence generated by the shear of the mean flow or the building wakes (Raupach and Shaw 1982). Observations demonstrate that turbulent kinetic energy in vegetation canopies derives primarily from the downwards transport of shear-generated TKE at or above the canopy top, and the same has been observed in a dense urban canopy for $z < 0.7H$ (Christen et al. 2009). Evidence of wake-generated TKE in canopies (as predicted by Eq. 2, above) is not apparent, presumably because it dissipates rapidly (Raupach and Shaw 1982, Meyers and Baldocchi 1991). In fact, despite the rapid generation of wake turbulence, the typical effect of vegetation is to reduce overall turbulence levels (Green 1992; Green et al. 1995), as larger turbulent eddies are chopped up by the small foliar drag elements. The representation of this ‘short circuiting’ of the turbulent energy cascade is not possible with a one-band model of turbulent energy (Raupach and Shaw 1982). Nevertheless, Green (1992) proposed a parametrization of this enhanced dissipation of turbulence generated by foliage element drag (but not by building drag) with an addition to the prognostic equation for $k$. Wilson (1988) presents heuristic logic that supports addition of this term. With this addition the source term for tree foliage instead reads,

$$\begin{aligned} S_{k}= L_\mathrm{D} C_\mathrm{DV} \left( {\underbrace{\beta _\mathrm{p}U^{3}}_{I}-\underbrace{\beta _\mathrm{d} k U}_{II}}\right) , \end{aligned}$$

(3)

where $\beta _\mathrm{p} = 1.0$ (no direct conversion to heat) and $\beta _\mathrm{d} = 6.5$ based on Sanz (2003). Liu et al. (1996) found that this additional sink term (i.e., $\beta _\mathrm{d}k~U$) was critical for the correct reproduction of experimentally-measured $k$ in a forest canopy. An alternative approach would be to add a source term in the $\varepsilon$ equation (see discussion in Web Supplement), or split the turbulent spectrum into two or more wavebands (e.g., Wilson 1988). However, Eq. 3 is followed here, and the corresponding source terms in the $\varepsilon$ equation are (Sanz 2003),

$$\begin{aligned} S_{\varepsilon }=L_\mathrm{D} C_\mathrm{DV} \left( {C_{\varepsilon 4} \frac{\varepsilon }{k}U^{3}-C_{\varepsilon 5} \beta _\mathrm{d} U \varepsilon } \right) , \end{aligned}$$

(4)

where $C_{\mathrm{e}4}=C_{\mathrm{e}5} = 1.26$ based on analytical expressions from Sanz (2003) and values used by Dalpé and Masson (2009). Several authors find $C_{\varepsilon 5}< C_{\varepsilon 4}$ provides better comparisons against wind-tunnel results (e.g. Liu et al. 1996; Foudhil et al. 2005), and this as well as the merit of the parametrization as a whole is further discussed in the Web Supplement.

Results of the 3-D RANS CFD model with tree foliage implementation as described here are used to parametrize the coefficients necessary to represent the spatially-averaged profiles in the column model (Sect. 2.2).

2.2 One-Dimensional Column $k$–$l$ Model

A mesoscale model (or any model that represents urban areas at the neighbourhood-scale) requires vertical profiles of the effects of buildings and trees on the spatially-averaged mean flow. Hence, the overall objective is to accurately represent the effects of a variety of simple arrangements of buildings and trees on the spatially-averaged vertical profiles of flow properties. This requires that the interactions between buildings and trees are considered.

Two averaging processes operate on the momentum equation in a mesoscale model. First, all variables are time- or ensemble-averaged, to separate turbulent features from the mean flow, i.e. Reynolds decomposition. Second, all variables are spatially-averaged in the horizontal, typically at the local or neighbourhood scale (100–10,000 m), to filter out features smaller than the scale of the mesoscale grid. Neglecting Coriolis and buoyancy effects, and assuming the spatially-averaged time mean flow is horizontally homogenous (and hence, zero mean vertical velocity due to the assumed incompressibility), the mean advection and viscous dissipation terms are zero, and non-vertical divergences of turbulent and dispersive momentum fluxes are also zero, the (one-dimensional) equation for the evolution of the spatial mean of the time-averaged flow is,

$$\begin{aligned} \frac{\partial \left\langle {\bar{{u}}} \right\rangle }{\partial t}=-\underbrace{\frac{\partial \left\langle {\overline{u^{\prime }w^{\prime }}} \right\rangle }{\partial z}}_{I}-\underbrace{\frac{\partial \left\langle {\overline{\tilde{u} \tilde{w}}} \right\rangle }{\partial z}}_{II}-\frac{1}{\rho }\underbrace{\frac{\partial \left\langle {\bar{{p}}} \right\rangle }{\partial x_{i}}}_{III}-\frac{1}{\rho }\underbrace{\left\langle {\frac{\partial \tilde{p}}{\partial x_{i}}} \right\rangle }_{IV}+\underbrace{\nu \left\langle {\nabla ^{2}\tilde{u}} \right\rangle }_{V}, \end{aligned}$$

(5)

where the overbar denotes the time mean and angle brackets the spatial mean, $u^{\prime }$ is the departure of the instantaneous horizontal velocity at a fixed point from the time or ensemble mean (i.e. turbulent fluctuation), $\tilde{u}$ is the departure of the time-averaged velocity from the spatial mean at the same vertical level (i.e. dispersive fluctuation), $p$ is the pressure, and $\rho$ is the air density (assumed to be constant). Martilli and Santiago (2007) describe the averaging technique in more detail, and formally define the turbulent and dispersive fluctuations. Terms on the right-hand side of Eq. 5 are the divergence of the spatially-averaged turbulent flux of momentum $(I)$; the divergence of the spatially-averaged dispersive flux of momentum (II); the spatially-averaged acceleration due to the large-scale pressure gradient (III), and the spatially-averaged acceleration due to dispersive pressure variation (form drag; IV); and the spatial-average of dispersive viscous dissipation (viscous drag; $V$). The impact of neglecting the dispersive flux (term II in Eq. 5) is discussed in Sect. 2.3.

The turbulent flux of momentum in Eq. 5 is parametrized using a K-theory approach,

$$\begin{aligned} \left\langle {\overline{u^{{\prime }}w^{{\prime }}}} \right\rangle =-K_{m}\frac{\partial \left\langle {\bar{{u}}} \right\rangle }{\partial z}, \end{aligned}$$

(6)

where $K_{m}$ is the turbulent diffusion coefficient for momentum, computed with a $k$–$l$ closure,

$$\begin{aligned} K_{m}=C_{k}l_{k}\left\langle k \right\rangle ^{\frac{1}{2}}, \end{aligned}$$

(7)

where $C_{k}$ is a model constant and $l_{k}$ is a length scale. The evolution of the spatially-averaged TKE is calculated with a prognostic equation. Assuming horizontal homogeneity and hence no mean vertical wind at the averaging scale, parametrizing the turbulent flux of $k$ in the shear production and turbulent transport terms with K-theory (e.g., Eq. 6), neglecting the pressure transport term, and representing the viscous dissipation rate with $\varepsilon$, we are left with,

$$\begin{aligned} \frac{\partial \left\langle {\bar{{k}}} \right\rangle }{\partial t}= & {} \underbrace{K_{m}\left[ {\left( {\frac{\partial \left\langle {\bar{{u}}} \right\rangle }{\partial z}} \right) ^{2}+\left( {\frac{\partial \left\langle {\bar{{v}}} \right\rangle }{\partial z}} \right) ^{2}} \right] }_{I}+\underbrace{\frac{\partial }{\partial z}\left( {K_{m}\frac{\partial \left\langle {\bar{{k}}} \right\rangle }{\partial z}} \right) }_{II}-\underbrace{\frac{\partial \left\langle {\tilde{k} \tilde{w}} \right\rangle }{\partial z}}_{III}-\underbrace{\left\langle \varepsilon \right\rangle }_{IV} \nonumber \\&-\underbrace{\left\langle {{\widetilde{u_{i}^{\prime }u_{j}^{\prime }}} \frac{\partial \tilde{u}_{i}}{\partial x_{j}}} \right\rangle }_{V}+\underbrace{s_{k}}_{VI}, \end{aligned}$$

(8)

where terms on the right-hand side of Eq. 8 are shear production at the horizontal averaging scale $(I)$; divergence of the spatial mean turbulent transport of $k$ (II); divergence of the dispersive transport of $k$ (III); viscous dissipation (IV); and wake production (shear production by dispersive motions, i.e., at scales smaller than the horizontal averaging; $V$). Note that Eq. 8 implies the existence of analogous equations for mean kinetic energy and dispersive kinetic energy. An additional sink term (VI) has been added to account for the dissipative effects of tree foliage (i.e. term II in Eq. 3; term $I$ in Eq. 3 is a parametrization of term $V$ in Eq. 8). Term III (dispersive transport) is neglected by Santiago and Martilli (2010) and here too, and this is discussed in Sect. 2.3.

The dissipation rate of TKE $(\varepsilon )$ in Eq. 8 is not determined by a prognostic equation as in the 3-D CFD model (Sect. 2.1), but is modelled more simply as,

$$\begin{aligned} \left\langle \varepsilon \right\rangle =C_{\varepsilon } \frac{\left\langle k \right\rangle ^{\frac{3}{2}}}{l_{\varepsilon \mathrm{bv}}}, \end{aligned}$$

(9)

where $l_{\varepsilon \mathrm{bv}}$ is a dissipation length scale, which in the present context has been modified by the presence of buildings (“b”) and tree foliage (“v”), and $C_{\varepsilon }$ is a model constant (dimensionless). While several values of $C_{k}$ (i.e., Eq. 7) and $C_{\varepsilon }$ have been proposed in the literature, $l_{k} C_{k}$ and $l_{\varepsilon }/C_{\varepsilon }$ are parametrized instead of $l_{k}$ and $l_{\varepsilon }$ in the present work, and hence results are independent of $C_{k}$ and $C_{\varepsilon }$ (Santiago and Martilli 2010).

To solve prognostic Eqs. 5 and 8 several additional terms require parametrization and inclusion. In the momentum equation (Eq. 5), the drag due to buildings and tree foliage is parametrized as follows (Foudhil et al. 2005; Santiago and Martilli 2010),

$$\begin{aligned} \frac{1}{\rho }\underbrace{\left\langle {\frac{\partial \tilde{p}}{\partial x_{i}}} \right\rangle }_{IV}=-\left( {\overbrace{B_\mathrm{D}C_\mathrm{DBv}}^{1}+\overbrace{L_\mathrm{D}C_\mathrm{DV}}^{2}} \right) \;\left\langle {\bar{{U}}} \right\rangle \left\langle {\bar{{u}}_{i}} \right\rangle , \end{aligned}$$

(10)

where $B_\mathrm{D}$ is sectional building area density ($\hbox {m}^{2}$ of area facing the wind per $\hbox {m}^{3}$ of outdoor air volume), $L_\mathrm{D}$ is the neighbourhood-average leaf area density ($\hbox {m}^{2}$ of one-sided leaf area per $\hbox {m}^{3}$ of outdoor air volume), $U$ is the wind speed, $C_\mathrm{DV}$ is the drag coefficient for tree foliage (= 0.2, as in the CFD model). $C_\mathrm{DV}$ in the CFD model (Sect. 2.1) informs foliage drag at the grid scale ($\approx$1 m), whereas here in the column model it informs neighbourhood-average drag at a particular height. Moreover, clumping of urban tree foliage at crown-neighbourhood scales is typically substantial. This is not a concern in the emulation of the CFD model results, which are based on homogenously-distributed foliage across the domain (neighbourhood); however, clumping at these larger scales must be accounted for in application to real neighbourhoods. Marcolla et al. (2003) propose one method for doing so: use the foliage clumping coefficient as defined for radiative transfer through canopies to determine an ‘effective $L_\mathrm{D}$’.

$C_\mathrm{DBv}$ is the sectional drag coefficient for buildings when foliage is present, where

$$\begin{aligned} C_\mathrm{DBv} = {\overbrace{\upomega }^{3,4}} C_\mathrm{DB}, \end{aligned}$$

(11)

and where $C_\mathrm{DB}$ is the sectional drag coefficient for buildings without any tree foliage in the domain, and $\omega$ represents the effect of the foliage on the building drag coefficient for a particular building and foliage configuration. Hence, interaction between buildings and trees is accounted for in the building drag coefficient, because the foliage drag coefficient is fixed. This interaction between buildings and trees is a relative effect. That is, simply by including a drag term for buildings and another for tree foliage, they each impact the absolute effect the other has on the flow. However, they do not affect each other’s drag coefficient, or drag ‘efficiency’. The question investigated here is whether the presence of tree foliage affects the sectional drag coefficient of buildings, that is, the drag force that they exert relative to the inertial force in the same atmospheric layer.

As in the CFD model, the loss of momentum (and therefore mean kinetic energy) due to building and foliage drag implies a reciprocal production of TKE. Furthermore, the more rapid dissipation of the fine ‘wake’ scale turbulence produced by tree foliage that is incorporated in the CFD model (Eq. 3) must also be included here. Therefore, terms $V$ and VI in the $k$-equation (Eq. 8) become,

$$\begin{aligned} \underbrace{\left\langle {\overline{u_{i}^{\prime }u_{j}^{\prime }} \frac{\partial \tilde{u}_{i}}{\partial x_{j}}} \right\rangle }_{V}+\underbrace{s_{k}}_{VI}=\left( {\overbrace{B_\mathrm{D} C_\mathrm{DBv}}^{5}+\overbrace{L_\mathrm{D}C_\mathrm{DV}}^{6}} \right) \;\left\langle {\bar{{U}}} \right\rangle ^{3}-\overbrace{\beta _\mathrm{d}L_\mathrm{D}C_\mathrm{DV} \left\langle {\bar{{k}}} \right\rangle \left\langle {\bar{{U}}} \right\rangle }^{7}. \end{aligned}$$

(12)

Finally, the turbulent length scale ($l_{k}$, in Eq. 7) is derived from the dissipation length scale ($l_{\varepsilon \mathrm{bv}}$, in Eq. 9). Following Santiago and Martilli (2010),

$$\begin{aligned} C_{k}l_{k}=C_{\mu }\frac{l_{\varepsilon \mathrm{bv}}}{C_{\varepsilon }}, \end{aligned}$$

(13)

where $C_{\mu }$ is a model constant equal to 0.09, and $l_{\varepsilon \mathrm{bv}}/C_{\varepsilon }$ is derived from the CFD model simulation (or a parametrization) and is the dissipation length scale (divided by $C_{\varepsilon })$ in the presence of a built canopy and tree foliage,

$$\begin{aligned} \frac{l_{\varepsilon \mathrm{bv}}}{C_{\varepsilon }}= \frac{l_{\varepsilon }}{C_{\varepsilon }}{\overbrace{\upnu }^{9}}{\overbrace{\upvarpi }^{8}}, \end{aligned}$$

(14)

where $l_{\varepsilon }/C_{\varepsilon }$ is calculated by the CFD model or parametrized for the equivalent case without buildings or tree foliage, $\upnu$ is dimensionless and represents the effect of buildings on the length scale for a particular configuration, and the dimensionless factor $\upvarpi$ represents the effect of the foliage on the length scale for a particular building and foliage configuration. Note $l_{\varepsilon \mathrm{b}}=l_{\varepsilon \mathrm{bv}}$ when $\varpi = 1$.

2.3 Dispersive Processes

The 1-D column model approach in Sect. 2.2 cannot account for the effects of dispersive processes present in the 3-D CFD model without the inclusion of a parametrization. Three primary dispersive process are in operation in the CFD model: dispersive transport of mean momentum $\left\langle {\overline{\tilde{u} \tilde{w}}} \right\rangle$ (Eq. 5), dispersive transport of turbulent kinetic energy $\left\langle {\tilde{k} \tilde{w}} \right\rangle$ (Eq. 8), and dispersive shear production (wake production), which is parametrized in the column model by terms 5 and 6 in Eq. 12. Given the variability of dispersive processes with urban configuration and incident wind direction, a theoretical approach to the representation of dispersive transport terms is unlikely at present. Thus, an empirical approach is required, derived from the 3-D model presumably. However, our present objective is the inclusion of the effects of tree foliage on flow in urban neighbourhoods, and we therefore opt to proceed with our analysis as if dispersive transport processes were negligible. This is in line with previous studies (e.g. Santiago and Martilli 2010). Dispersive transport processes are in fact non-negligible for some scenarios studied here (e.g., “Intermediate Building Plan Area Density” section in Appendix) and probably for many real urban configurations. Hence, the subsequent analysis seeks to represent the effects of urban tree foliage on the spatially-averaged flow given that dispersive motions are ignored in the column model.

2.4 Assessment of the Column Model with CFD Model Results

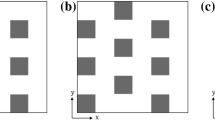
The fidelity with which the 1-D column model reproduces vertical profiles of the spatially-averaged flow from the 3-D CFD model is assessed for a range of urban block scenarios with varying heights and densities of tree foliage (Fig. 1). A staggered formation of cubic blocks, 16 m (and 16 cells) on a side, is used in the CFD model (Figs. 2, 3), as in Santiago and Martilli (2010). The staggered formation is chosen because the aligned formation with wind direction identical to the street direction results in a ‘channeling’ flow (e.g., Simon-Moral et al. 2014), which yields tree foliage impacts that are highly specific to this particular combination of building configuration and wind direction. The analysis is performed for plan area density of buildings $\uplambda _{P} = 0.25$ (Fig. 2), and the results are subsequently extended over the full range of $\uplambda _{P}$ with the aid of additional simulations for $\uplambda _{P} = 0.00$, 0.06, 0.11, and 0.44 (e.g., Fig. 3). Given that neighbourhood-scale (spatially-averaged) results are desired, tree foliage is represented in a simplified manner, and consists of 8-m thick layers, evenly distributed across (or above) the canopy air space with foliage tops at heights of 8, 12, 16, 20, and 24 m, and leaf area densities of 0.06, 0.13, 0.25, and 0.50 $\hbox {m}^{2}~\hbox {m}^{-3}$ (e.g., Fig. 2). This range of tree foliage heights permits analysis of the distinct effects of tree foliage on the flow at different heights relative to the buildings, e.g. deep in the canopy vs. the canopy-top shear layer vs. above the built canopy. Foliage is represented as a porous medium and different plant structures (e.g. leaves vs. branches) are not distinguished (Eqs. 10, 12).

Fig. 2

The five tree foliage height scenarios that are simulated, as well as the case without trees (a), for $\uplambda _{P} = 0.25$: b Tree1 (0–8 m); c Tree2 (4–12 m); d Tree3 (8–16 m); e Tree4 (12–20 m); f Tree5 (16–24 m). Building height $H$ is 16 m and foliage layer thickness is 8 m. Leaf area density varies between the following for each scenario: 0.06, 0.13, 0.25, and 0.50 $\hbox {m}^{2}~\hbox {m}^{-3}$. Airflow is from the left and perpendicular to the building faces (staggered block array)

Fig. 3

An example foliage height (Tree2) for the $\uplambda _{P} = 0.11$ (a) and $\uplambda _{P} = 0.44$ (b) building densities. All other features are the same as Fig. 2

Flow profiles from the column model are compared against spatially-averaged profiles from the CFD model for all combinations of urban plan area built densities, foliage heights, and foliage densities, including the foliage-free cases. Exact profiles of the building drag coefficient $(C_\mathrm{DBv})$ and the dissipation length scale $(l_{\varepsilon \mathrm{bv}})$ for each scenario are extracted from the CFD model and used as input to the column model. $C_\mathrm{DBv}$ at each height is based on the pressure drop between windward and leeward faces of the buildings, and the spatially-averaged wind speed, at the same height. Hence, the column model receives the best possible information from the CFD model, and differences between the models are due to differences in formulation (e.g. $k$–$l$ vs. $k$–$\varepsilon$ turbulence schemes) and to the 3-D vs. 1-D representation of the flow (i.e., dispersive motions).

The root-mean-square difference (RMSD) between spatially-averaged profiles from the CFD and column models is calculated for the profiles of the spatially-averaged streamwise velocity component $\left\langle {\bar{{u}}} \right\rangle$, turbulent kinetic energy $\left\langle {\bar{{k}}} \right\rangle$, and Reynolds stress $\left\langle {\overline{u^{\prime }w^{\prime }}} \right\rangle$. The RMSD is chosen as the comparative statistic because it more effectively includes rare but extreme differences in the overall measure of difference as compared to the mean absolute difference or ‘hit rate’ approaches (e.g., Schlünzen et al. 2004). The RMSD is calculated over two height ranges: the canopy layer ($0 < z \le H$), where vertical and horizontal transport of scalars is critical; and (approximately) the above-canopy roughness sublayer $(H < z \le 2H))$, so as to capture the largest vertical exchanges. The RMSD varies depending on the size of samples compared; however, RMSD values compared below all occur over the same number of sample points, avoiding this drawback. The RMSD is normalized by $u_{\tau }$ for $\left\langle {\bar{{u}}} \right\rangle$, and by its square for $\left\langle {\bar{{k}}} \right\rangle$ and $\left\langle {\overline{u^{{\prime }}w^{{\prime }}}} \right\rangle$, and therefore represents the difference normalized by flow forcing. Note that the Reynolds stress $\left\langle {\overline{u^{{\prime }}w^{{\prime }}}} \right\rangle$ is always well-reproduced (“Intermediate Building Plan Area Density” section in the Appendix) and is not analyzed further.

Average differences between the models are less than or equal to those reported by Santiago and Martilli (2010) for non-treed scenarios; differences are even smaller for cases with tree foliage above the buildings (see Appendix). Hence, while there is opportunity for improvement, it is concluded that the column model performs adequately in terms of reproducing spatial-mean flow profiles.

3 Impacts of Tree Foliage on Flow: Important Processes

In this section objectives A and B are addressed: source terms required to represent spatially-averaged flow through simplified urban neighbourhoods with trees are determined, and the potential to treat impacts of buildings and trees on the flow independently is studied. To address these objectives, the suite of scenarios in Sects. 2.4 and “Intermediate Building Plan Area Density” section in Appendix are re-run multiple times, and in each run select terms, as identified by numbers ‘2’ through ‘8’ in Eqs. 10, 11, 12, and 14, are individually removed from the column model equations. Each term that is removed represents a particular impact of buildings or tree foliage on the flow. These terms are named, defined and further described in Table 1. In this section, profiles of variables required to compute the Bdrag-u (term 1: building drag coefficient $C_\mathrm{DB}$) and Blength-u,k (term 9: length scale modification due to buildings $l_{\varepsilon \mathrm{b}}$) terms in Table 1 are derived from the CFD model simulation for each scenario for input to the column model. In Sect. 4, by contrast, an updated version of the Santiago and Martilli (2010) parametrization of these variables is applied (Fig. 1).

Table 1 Terms investigated and the equations in which they appear

Each term is deemed ‘significant’ if its removal from the column model equations increases the RMSD of wind speed and/or turbulent kinetic energy with the CFD model (see Appendix), normalized by $u_{\tau }$ and $u_{\tau }^{2}$, respectively, by $\approx$100 % or more. A threshold of 100 % indicates that a term is only ‘significant’ if its removal causes a model difference at least as large as differences caused by neglect of all processes in the 1-D model relative to the 3-D model, namely dispersive fluxes and processes affecting dissipation rate. The purpose of these simulations is to determine which building- and foliage-related terms are essential to reproduce in the column model the spatially-averaged flow profiles computed by the CFD model. Analysis is first performed for all scenarios with a building plan area density $(\uplambda _{P})$ of 0.25, and in Sect. 3.2 it is extended to the full range of $\uplambda _{P}$. Throughout the discussion the non-hyphenated terms include drag and associated terms (e.g. wake production terms); moreover the $-u$, $-k$, and $-u,k$ add-ons indicate the equation that the term applies to. These add-ons are dropped in later sections for brevity (e.g., Figs. 4 and 6) or to indicate combinations of terms, only where specified in the text (e.g., Fig. 5).

Fig. 4

Change in column model RMSD compared to the CFD model for the spatially-averaged streamwise velocity component (a) and spatially-averaged TKE (b) with the removal of each of seven building/tree foliage induced terms (Table 1). Median and maximum change in RMSD across the 20 treed scenarios at $\uplambda _{P} = 0.25$ are calculated for two atmospheric layers ($0 < z \le H$, $H < z\le 2H$). Horizontal lines indicate the actual RMSD with all terms included, i.e., the $\Delta {\textit{RMSD}}$ that equates to a 100 % increase in RMSD

Fig. 5

Profiles of the spatially-averaged mean streamwise velocity component (a) and TKE (b) from the CFD model, and from the column model with the cumulative introduction of several foliage-induced terms at building density $\uplambda _{P} = 0.25$. All scenarios have foliage density $L_\mathrm{D} = 0.50~\hbox {m}^{2}~\hbox {m}^{-3}$, and the Tree3, Tree4 and Tree5 scenarios are presented. The Bdrag term simulation includes no foliage-related terms, but only building-related terms 1, 5, and 9 in Table 1

Fig. 6

Change in RMSD of the column model relative to the CFD model for $0 < z \le 2H$ and for spatially-averaged streamwise velocity component (a, c, e) and TKE (b, d, f), with the removal of each of eight building/tree foliage induced terms/modifications (Table 1). Several building plan area fractions ($\uplambda _{P} = 0.00$ [Forest], 0.06, 0.11, 0.44), tree layer heights, and foliage densities, are displayed

3.1 Intermediate Building Plan Area Density

Figure 4a presents, for two height ranges, the maximum and median change in RMSD between the column and 3-D models across all 20 scenarios with $\uplambda _{P} = 0.25$ from Sect. 2.4, i.e., all combinations of the following: foliage tops at heights of 8, 12, 16, 20, and 24 m, and leaf area densities of 0.06, 0.13, 0.25, and $0.50~\hbox {m}^{2}\,\hbox {m}^{-3}$. These RMSD changes result from the removal of each term that represents an impact of the buildings or the tree foliage on the spatially-averaged streamwise velocity component. For removal of the terms Bdragv-u and Bprodv-u, $\omega$ in Eq. 11 is determined from the CFD model simulations.

The drag force due to tree foliage (term Vdrag-u) is the most important term in Fig. 4a; it significantly affects flow both above and within the canopy. Production of TKE by the buildings (term Bprod-k) is modestly important for flow above the canopy $(H < z\le 2H)$, but not significant. The RMSD increase due to removal of any other terms is much smaller than RMSD between the column model and the CFD model determined in “Intermediate Building Plan Area Density” section in the Appendix, as indicated by the colour-coded horizontal lines in Fig. 4a. Notably, modification of the building drag and the length scales due to the presence of foliage (‘interaction’ terms Bdragv-u and Blengthv-u,k) are insignificant (Fig. 4a).

The foliage drag term in the momentum equation (term Vdrag-u) is also the foliage-related term with the largest impact on spatially-averaged TKE (Fig. 4b), particularly for scenarios where foliage protrudes above the buildings (i.e., Tree4, Tree5). The corresponding production term in the TKE equation (term Vprod-k), while significant above-canopy for some cases, produces a much smaller impact. The enhanced dissipation term that represents short-circuiting of the turbulent cascade (term Vdiss-k) is of similar magnitude to the RMSD between the column and CFD models in the median (Fig. 4b), suggesting that it should be included.

Although not shown in Fig. 4, the drag force induced by buildings (term Bdrag-u) is the most important term, and, depending on the variable ($\left\langle {\bar{{u}}}\right\rangle$ or $\left\langle {\bar{{k}}} \right\rangle )$, atmospheric layer ($0 < z \le H$, or $H<z \le 2H$), and statistic (maximum or median), the increase in RMSD induced by its absence is a factor 3 to 100 times larger than the next most significant term (Vdrag-u). Likewise, modification of length scales by the buildings is also important (Santiago and Martilli 2010) and is included in all simulations.

Accounting for both the streamwise velocity component and TKE, modification of both the length scales (term Blengthv-u,k/term 8), and the building drag coefficient in both $\left\langle {\bar{{u}}} \right\rangle$ and $\left\langle {\bar{{k}}} \right\rangle$ equations (terms Bdragv-u and Bprodv-k/terms 3 and 4), due to the presence of tree foliage, are unimportant, and so these three terms can be neglected for $\uplambda _{P} = 0.25$. Hence, ‘interaction’ between buildings and trees are unimportant to the spatial mean flow, at least for the range of scenarios tested ($\uplambda _{P} = 0.25$, variable tree height and density), and effects of buildings and trees on flow may be treated independently. Similarly, terms related to production of turbulence are of lesser importance, but their existence is implied by addition of the all-important drag terms in the momentum equation.

Foliage-related terms are added one at a time, in order from most to least impactful in terms of profiles of spatially-averaged velocity and TKE, to assess the essential combination of terms required to represent building-foliage combinations. The TKE production term due to trees (Vprod-k/term 6) is appended to its corresponding momentum drag term (Vdrag-u/term 2). Together they are referred to as ‘Vdrag’. Furthermore, all building terms (i.e., Bdrag-u and Bprod-k/terms 1 and 5, and Blength/term 9) are included in all simulations, so as to focus on those terms required to represent tree foliage in urban scenarios.

Profiles of the spatially-averaged streamwise velocity component are shown in Fig. 5a for three scenarios where foliage is expected to be more significant (i.e., taller, dense foliage): Tree3, Tree4, and Tree5 with $L_\mathrm{D} = 0.50~\hbox {m}^{2}~\hbox {m}^{-3}$. The primary impact on the streamwise velocity component, particularly for foliage that protrudes above the buildings (Tree4, Tree5), is the foliage drag and turbulence production ($+$Vdrag). These same terms also reduce TKE, and therefore vertical transport, from ground level up to the top of the foliage layer, and do so to a greater extent the more foliage protrudes above the buildings (Fig. 5b). Enhanced dissipation generated by foliage ($+$Vdiss) slightly enhances the above-canopy wind (Fig. 5a) by reducing TKE within the foliage layer (Fig. 5b), thereby diminishing turbulent momentum flux down into the canopy.

The final two modifications ($+$Blengthv, $+$Bdragv) do make minor adjustments to the flow profiles, in particular for cases with tree foliage protruding above the rooftops. However, they are dwarfed by impacts on flow profiles of adding the Vdrag and Vdiss terms.

3.2 Low and High Building Plan Area Densities

Foliage drag and turbulence production (terms Vdrag-u and Vprod-k), and enhanced dissipation of TKE by foliage (term Vdiss-k), significantly influence flow for $\uplambda _{P} = 0.25$. To determine whether additional foliage-related source terms are significant at other built densities, select foliage scenarios from Sect. 3.1 are re-run for building plan area densities $\uplambda _{P} = 0.00$, 0.06, 0.11, and 0.44. The Bdrag-u term is included in the analysis, for comparison, and because it may be less important at lower $\uplambda _{P}$. The modification of length scales due to buildings (term Blength-u,k) is included in all simulations.

The highest leaf area density $(L_\mathrm{D} = 0.50~\hbox {m}^{2} \hbox {m}^{-3})$ is evaluated for most tree-layer heights at each $\uplambda _{P}$, as denser foliage is most likely to exert a significant impact on the flow. A more realistic neighbourhood average $L_\mathrm{D}$ of $0.13~\hbox {m}^{2}~\hbox {m}^{-3}$ is also evaluated for select scenarios. Particular attention is paid to scenarios where trees and buildings are approximately the same height (Tree2, Tree3, Tree4), where ‘interaction’ between the two is most likely. The following scenarios are not studied: foliage deep within dense building arrangements (Tree1 at $\uplambda _{P} = 0.44$), where it will have little effect, or foliage well above sparse building densities (Tree5 at $\uplambda _{P}= 0.06$), where it will dominate.

Drag due to buildings and foliage (terms Bdrag and Vdrag) clearly dominates in most cases for both the spatially-averaged streamwise velocity component and spatially-averaged TKE (Fig. 6). Enhanced dissipation (term Vdiss) and modification of length scales (term Blengthv) by the foliage are both of some importance, particularly at the lower building densities, and for TKE and the streamwise velocity component, respectively. Turbulence production by building and foliage wakes (terms Bprod and Vprod), as well as interaction terms Bdragv and Bprodv, are of minimal importance across the full range of scenarios.

The Blengthv term is the only one indentified here in addition to those in Sect. 3.1 as being important to the correct reproduction of CFD model flow profiles for urban canopies with trees, and even for lower, more realistic neighbourhood-average foliage densities such as $L_\mathrm{D} = 0.13~\hbox {m}^{2}~\hbox {m}^{-3}$ (Fig. 6). This effect on length scales by foliage is primarily of consequence for $\uplambda _{P} = 0.06$; it is already modest for $\uplambda _{P} = 0.11$. Furthermore, the Blengthv term, being a foliage-building interaction term, is complex in its variation with building and foliage density and distribution. In effect, its representation in the 1-D column model would require a parametrization based on relations derived from a suite of CFD model simulations. This is judged to be outside the scope of the current work, and the Blengthv term is omitted from the parametrization. The impacts of this omission are explored in Sect. 4. Hence, considering results for both the streamwise velocity component and TKE in Fig. 6, the results obtained for $\uplambda _{P} = 0.25$ hold for all $\uplambda _{P} \ge 0.11$.

3.3 Proposed Parametrization of Building and Tree Impacts on Flow: Source and Sink Terms

Based on the results in Sects. 3.1 and 3.2, only four terms in Table 1 are required to parametrize the effects of buildings and foliage on the flow (strictly, for $\uplambda _{P} \ge 0.11$),

• (A) The Bdrag-u term in the momentum equation (Eq. 10): $\overbrace{B_\mathrm{D}C_\mathrm{DBv} \left\langle {\bar{{U}}} \right\rangle \left\langle {\bar{{u}}} \right\rangle }^{1}$;

• (B) The Vdrag-u term in the momentum equation (Eq. 10): $\overbrace{\beta _\mathrm{p}L_\mathrm{D}C_\mathrm{DV} \left\langle {\bar{{U}}} \right\rangle \left\langle {\bar{{u}}} \right\rangle }^{2}$;

• (C) The Vdiss-k term in the TKE equation (Eq. 12): $\overbrace{\beta _\mathrm{d}L_\mathrm{D}C_\mathrm{DV} \left\langle {\bar{{k}}} \right\rangle \left\langle {\bar{{U}}} \right\rangle }^{7}$; and

• (D) The Blength-u,k term, with consequences for both momentum and TKE equations (Eq. 14),

  $$\begin{aligned} \frac{l_{\varepsilon \mathrm{b}}}{C_{\varepsilon }}=\overbrace{\frac{l_{\varepsilon }}{C_{\varepsilon }}\omega }^{9}. \end{aligned}$$

Additionally, two other terms are marginally important but are implied by the corresponding drag terms in the momentum equation (Raupach and Shaw 1982), and so are included in the TKE equation in order to conserve total (mean plus turbulent) kinetic energy, viz,

• (E) The Bprod-k term in the TKE equation (Eq. 12): $\overbrace{B_\mathrm{D}C_\mathrm{DBv} \left\langle {\bar{{U}}} \right\rangle ^{3}}^{5}$; and

• (F) The Vprod-k term in the TKE equation (Eq. 12): $\overbrace{\beta _\mathrm{p}L_\mathrm{D}C_\mathrm{DV} \left\langle {\bar{{U}}} \right\rangle ^{3}}^{6}$.

Modification of length scales due to the presence of foliage, i.e., the Blengthv term, is of some importance for $\uplambda _{P} < 0.11$ (approximately). However, it is neglected for reasons discussed in Sect. 3.2, and impacts of this omission are evaluated during parametrization testing (Sect. 4.2).

Overall, important effects due to buildings and tree foliage, represented in the model as source terms, are the reduction in the mean wind speed by both buildings and trees (via drag terms), enhanced dissipation of turbulence by buildings (via length scale reduction) and tree foliage (via short-circuit term), and the reduction of vertical turbulent transport in and immediately above the building canopy (via length scale reduction). Drag due to buildings and foliage generates pronounced wind gradients above the canopy, and therefore shear production, indirectly. Impacts of foliage on length scales are ignored here but are of moderate importance for select scenarios: i.e., those with higher foliage densities, and which are either unaccompanied by buildings or whose foliage tops are below or approximately coincident with building height for low building densities.

Most significantly, terms that represent the interactions between buildings and trees in the current formulation, Bdragv-u and Bprodv-k, are unimportant across all scenarios simulated here. Hence, buildings and trees may be treated independently in terms of their effects on the spatially-averaged flow (e.g., Dupont et al. 2004); for example, while the drag force due to buildings is affected by the presence of tree foliage, because the mean wind speed is reduced by foliage, the building drag coefficient need not be modified due to the presence of tree foliage. Thus, parametrization of the effects of urban neighbourhoods with trees on flow can be greatly simplified.

Finally, results presented in this section arise in the context of the simple representation in the CFD model of neighbourhood configuration and building and foliage impacts. Furthermore, they are affected by neglect in the column model of the effects of dispersive motions in the CFD model (e.g. Sect. 2.3). Hence, the relative importance of each term may be affected by these approximations.

4 Parametrization of Tree Foliage and Building Impacts on Flow

To address objectives C and D in Sect. 1.3, the parametrization of the effects of buildings and trees on the flow determined in Sect. 3 is tested against CFD model results, and the range of scenarios for which foliage-related terms 2, 6, and 7 (terms Vdrag-u, Vprod-k and Vdiss-k, respectively; Table 1) are required is determined. The column model is run with only the six source terms or modifications denoted by A-F in Sect. 3.3: Bdrag-u and Vdrag-u in the momentum equation (Eq. 10), Vdiss-k, Bprod-k, and Vprod-k in the TKE equation (Eq. 12), and Blength-u,k, i.e., modification of the length scales due to the presence of buildings (affecting both equations). The RMSD is determined for all scenarios, and profiles of spatially-averaged quantities are compared for select cases.

Building-induced length scale modifications ($\nu$ in Eq. 14) and drag coefficients $(C_\mathrm{DB})$ are parametrized in this section, in contrast to Sect. 3 and in Appendix, where building-induced length scale modifications and drag coefficients are taken directly from CFD model output (Fig. 1). Hence, we test the efficacy with which the 1-D model acts as an urban canopy parametrization for neighbourhoods with trees. In particular, its ability to reproduce spatially-averaged flow profiles with the new parametrization of urban tree foliage is evaluated. The RMSD between the column model and the CFD model arises from model differences (1-D vs. 3-D, $k$–$l$ vs. $k$–$\varepsilon$), as in Sect. 3 and in Appendix, and additionally from the neglect of foliage-building interaction and foliage impacts on length scales, and from the parametrization of building-related terms $C_\mathrm{DB}$ and $l_{\varepsilon \mathrm{b}}$ (i.e., imperfect inputs), which are derived from Santiago and Martilli (2010). However, coefficients for their parametrization require updating.

4.1 Parametrization of Building Impacts: Santiago and Martilli (2010) Parameters

$C_\mathrm{DB}$ values (Eq. 11; $C_\mathrm{deq}$ in Santiago and Martilli 2010) and $l_{\varepsilon \mathrm{b}}$ (Eq. 14) are computed using the Santiago and Martilli (2010) parametrization with updated parameters. The Santiago and Martilli (2010) simulations are re-done with the stricter convergence criteria possible due to increased computational power. Slight changes in vertical profiles of the mean wind and TKE are observed, as well as more important differences in the distribution of pressure over obstacle faces. Parameters are updated based on current CFD model results for block arrays without porous media (i.e., without trees) at the following densities: $\uplambda _{P} = 0.06$, 0.11, 0.16, 0.25, 0.33, and 0.44. The updated parameterization of building drag coefficient and length scales, for scenarios without tree foliage (i.e., block arrays), is as follows.

Drag coefficient $(C_\mathrm{deq})$:

$$\begin{aligned} C_\mathrm{deq} (\lambda )= & {} 3.67,\quad \text {for}\;\lambda >0.33 \end{aligned}$$

(15a)

$$\begin{aligned} C_\mathrm{deq} (\lambda )= & {} 7.30\lambda ^{0.62},\quad \text {for}\;\lambda \le 0.33 \end{aligned}$$

(15b)

where $\lambda$ is either $\uplambda _{P}$ or $\uplambda _\mathrm{F}$, the building frontal area density.

Length scales $(l_{\varepsilon \mathrm{b}})$:

$$\begin{aligned} \frac{l_{\varepsilon \mathrm{b}}}{C_{\varepsilon }}= & {} \alpha _{1} \left( {H-d(\lambda )}\right) ,\quad \text {for}\;z/H\le 1.0 \end{aligned}$$

(16a)

$$\begin{aligned} \frac{l_{\varepsilon \mathrm{b}}}{C_{\varepsilon }}= & {} \alpha _{1} \left( {z-d(\lambda )} \right) ,\quad \text {for} \;1.0\le z/H\le 1.5 \end{aligned}$$

(16b)

$$\begin{aligned} \frac{l_{\varepsilon \mathrm{b}}}{C_{\varepsilon }}= & {} \alpha _{2} \left( {z-d_{2}(\lambda )} \right) ,\quad \text {for}\;z/H\ge 1.5 \end{aligned}$$

(16c)

where $\alpha _{1} = 1.95$ and $\alpha _{2} = 1.07$ are the revised values. While $\alpha _{2}$ does not vary with $\lambda$, $\alpha _{1}$ is a weak function of $\lambda$. However, $\alpha _{1}$ is assumed constant here, as in Santiago and Martilli (2010) and Simon-Moral et al. (2014), and it is determined by minimizing both the median and maximum RMSD of the spatially-averaged streamwise velocity component between $H$ and $2H$ over all $\lambda$. The RMSD values of the spatially-averaged streamwise velocity component, TKE, and Reynolds stress below $H$, and TKE and Reynolds stress between $H$ and $2H$, are not sensitive to the choice of $\alpha _{1}$. Note that Simon-Moral et al. (2014) find similar values for aligned arrays of cubes: $\alpha _{1} = 2.19$ and $\alpha _{2} = 1.20$. Hence, length scales are relatively insensitive to building configuration.

The updated parametrization of displacement height $(d)$ is,

$$\begin{aligned} \frac{d(\lambda )}{H}=\lambda ^{0.15}, \end{aligned}$$

(17)

which matches the formulation obtained by Simon-Moral et al. (2014) for aligned arrays of cubes. This suggests, as they mention, that displacement height is not sensitive to the configuration for regular arrays of cubes, at least for wind direction normal to cube faces.

Finally,

$$\begin{aligned} d_{2}(\lambda )=1.5H\left( {1-\frac{\alpha _{1}}{\alpha _{2}}} \right) +d(\lambda )\frac{\alpha _{1}}{\alpha _{2}}, \end{aligned}$$

(18)

where the variable $\lambda$ in Eqs. 15a, 15b–18 is intentionally not identified as either $\uplambda _{P}$ or $\uplambda _\mathrm{F}$. Because $\uplambda _{P}=\uplambda _\mathrm{F}$ for all scenarios studied here, it is not clear which is more relevant in each equation. However, it is most likely that displacement height is a function of $\uplambda _{P}$, whereas drag coefficient depends more strongly on $\uplambda _\mathrm{F}$.

4.2 Testing the Urban Canopy Parametrization of Building and Tree Impacts on Flow

Here, we test the new parametrization of building and tree impacts on spatially-averaged flow. It also includes an assessment of the relative importance of the tree foliage-related terms across a range of scenarios; that is, when is the current parametrization required over and above the Santiago and Martilli (2010) parametrization for building-only scenarios? The column model is run for all scenarios in Sect. 3, and the RMSD compared to CFD model results is determined. Only the six source terms identified in Sect. 3.3 are included to represent the effects of buildings and tree foliage; building-tree interaction terms (terms 3 and 4 in Table 1) and the effects of trees on the length scales (term 8) are not included. These six source terms comprise the proposed parametrization (Sect. 3.3). Building impacts on drag and length scales are parametrized according to Santiago and Martilli (2010) with updated coefficients from Sect. 4.1; $\textit{RMSD} \le 0.5$ is considered acceptable, and $\textit{RMSD} > 1.0$ is considered to be a poor performance; recall that RMSD in all cases is for $\left\langle {\bar{{u}}} \right\rangle$ and $\left\langle {\bar{{k}}} \right\rangle$ normalized by $u_{\tau }$ and $u_{\tau }^{2}$, respectively.

The updated parametrization of building terms in Sect. 4.1 is first assessed (Table 2). The mean RMSD across all $\uplambda _{P}$ scenarios for the spatially-averaged streamwise velocity component is 0.21 in the canopy and 0.52 above, as compared to the mean RMSD values of 0.37 in the canopy and 0.71 above reported in Santiago and Martilli (2010). Corresponding values for the spatially-averaged TKE are 0.44 and 0.11, which are comparable to those in Santiago and Martilli (2010): 0.46 and 0.19. Hence, the new parametrization coefficients for building drag and length scales improve the ability of the column model to predict the streamwise velocity component, whereas TKE is predicted with similar accuracy.

Subsequently, scenarios from Sect. 3.1, with variable foliage height and density at $\uplambda _{P} = 0.25$, are simulated with the new parametrization implemented in the column model. For the range of scenarios considered, the spatially-averaged streamwise velocity component and TKE vary more with foliage height than with foliage density, and this is reproduced by the parametrization (Fig. 7). As noted in previous sections, foliage reduces RMSD in the canopy, in particular when the foliage is located above the buildings, and when it has greater density. The parametrization captures this phenomenon, which is particularly apparent in the upper canopy for $\left\langle {\bar{{k}}}\right\rangle$ (Fig. 7c, d). Largest errors for both $\left\langle {\bar{{u}}}\right\rangle$ and $\left\langle {\bar{{k}}} \right\rangle$ tend to appear in the building shear zone (i.e., $z \approx H$), or well above the canopy (Fig. 7).

Table 2 RMSD of $\left\langle {\bar{{u}}} \right\rangle$ and $\left\langle {\bar{{k}}} \right\rangle$ between the CFD model and the column model with updated Santiago and Martilli (2010) parameters, as a function of building density $(\uplambda _{P})$ and for scenarios without tree foliage

Simulations for the complete range of combinations of building densities, foliage heights and foliage densities sampled in Sects. 3.1 and 3.2, with the new parametrization in the column model, yield RMSD relative to the CFD model of $\le$0.43 for the spatially-averaged TKE, and $\le$0.40 for the spatially-averaged streamwise velocity component in the canopy (Table 3). The column model is not able to reproduce the above-canopy streamwise velocity component as well, and largest errors result for foliage layers within the building canopy (i.e., Tree1, Tree2, Tree3) at lower building densities ($\uplambda _{P} = 0.11$, and especially 0.06) or higher building densities $(\uplambda _{P} = 0.44)$. This phenomenon is reduced for $\uplambda _{P} = 0.25$ (Fig. 7). Notable also is that lower foliage densities can increase the RMSD (Table 3).

Fig. 7

Profiles of the spatially-averaged streamwise velocity component (a, b) and spatially-averaged TKE (c, d) from CFD model results (symbols) and the column model with the new parametrization (lines) for $\uplambda _{P} = 0.25$. Panels a, c show variation with foliage density for Tree5; panels b, d show variation with foliage height for $L_\mathrm{D} = 0.25~\hbox {m}^{2}~\hbox {m}^{-3}$

Table 3 RMSD of $\left\langle {\bar{{u}}} \right\rangle$ and $\left\langle {\bar{{k}}} \right\rangle$ with the proposed parameterization as a function of building density and tree foliage height for foliage area densities 0.50 $\hbox {m}^{2}~\hbox {m}^{-3}$ and $L_\mathrm{D} = 0.13~\hbox {m}^{2}~\hbox {m}^{-3}$

RMSD values of the spatially-averaged streamwise velocity component and TKE, further normalized by the vertical mean of spatially-averaged $\left\langle {\bar{{u}}} \right\rangle$ and $\left\langle {\bar{{k}}} \right\rangle$, respectively, and over the appropriate atmospheric layer ($0 < z \le H$, or $H < z \le 2H$), tell a different story. Because the streamwise velocity component increases with $z$, larger RMSD values above the canopy are due in part to an increased magnitude of $\left\langle {\bar{{u}}} \right\rangle$. RMSD of the streamwise velocity component normalized by its layer mean is in fact of similar magnitude ($\approx$20 %) in both atmospheric layers (not shown). The RMSD of the spatially-averaged TKE normalized by its vertical mean is low above the canopy and substantially higher within the building canopy, because $\left\langle {\bar{{k}}} \right\rangle$ is very small there due to the dampening effect of foliage. Overall, model differences are small relative to the mean magnitude of quantities in the mean and turbulent flow.

Bracketed values in Table 3 are percentage changes of RMSD that result from the inclusion of tree foliage-related terms in the proposed parametrization (terms 2, 6, and 7), in addition to the building-related terms of Santiago and Martilli (2010) and Sect. 4.1. For most scenarios they reduce RMSD of both $\left\langle {\bar{{u}}} \right\rangle$ and $\left\langle {\bar{{k}}} \right\rangle$ within and above the canopy to a fraction of the value without the foliage terms; median reductions are 89 % in the canopy and 71 % above the canopy for $L_\mathrm{D} = 0.50~\hbox {m}^{2}~\hbox {m}^{-3}$ scenarios. To summarize, the proposed parametrization has a significant impact, even when foliage density is reduced from 0.50 to 0.13 m$^{2}$ m$^{-3}$.

Foliage in the canopy for $\uplambda _{P} = 0.25$ and 0.44 is the only subset of scenarios for which foliage terms are less consequential. Therefore, foliage components of the proposed parametrization are most critical for foliage that protrudes above the building canopy, and for foliage in the canopy for $\uplambda _{P} < 0.25$ (approximately). Low density tree foliage protruding above the buildings is always important; for example, median decrease in RMSD of $\left\langle {\bar{{u}}} \right\rangle$ and $\left\langle {\bar{{k}}} \right\rangle$ over the two atmospheric layers, for Tree4 and Tree5 scenarios with $\uplambda _{P} = 0.25$ and $L_\mathrm{D} = 0.06~\hbox {m}^{2}~\hbox {m}^{-3}$, is 80 % when foliage-related terms are included in addition to building-related terms. This is akin to the disproportionate effect on drag and $\left\langle {\bar{{k}}} \right\rangle$ production of tall, isolated buildings (Xie et al. 2008): low density foliage above the mean drag element height (the buildings) exerts a disproportionate influence, and additional foliage density results in ‘diminishing returns’ in terms of the total drag of the elevated foliage.

Notably, if the Bdragv and Bprodv terms (terms 3 and 4 in Table 1, respectively) are extracted from the CFD model and applied to the parametrized drag coefficients there is a small decrease in RMSD for low $\uplambda _{P}$ with canopy foliage and a larger increase for $\uplambda _{P} = 0.44$ with canopy foliage; overall, RMSD is more often and substantially increased than decreased amongst scenarios considered in this section (not shown). As such, interaction terms Bdragv and Bprodv do not lower column model RMSD when implemented for the present suite of scenarios.

Considering these results, neglect of foliage impacts on length scales, and on building drag coefficients in particular, is deemed justified. Parsimonious parametrization of the Blengthv term is problematic given the range of potential building-foliage configurations. Moreover, its importance only approaches or exceeds the proposed parametrization of foliage impacts on the flow for very specific cases. Hence, it is simply noted here that the parametrization may perform less well when foliage exists in the building canopy and $\uplambda _{P}$ is approximately $\le$0.11; foliage in the building canopy is relatively unimportant for $\uplambda _{P} \ge 0.25$. Overall, the tree foliage-related terms included in the new parametrization (Sect. 3.3) are simple to include, they improve results in virtually all scenarios tested, often substantially, and hence they should be included in all scenarios that include tree foliage.

4.3 Extension of the Parametrization: Multiple Building Heights and Clumping

To apply the new parametrization for neighbourhoods with multiple building heights, the building drag coefficient $(C_\mathrm{DB})$ at each height is determined from Eq. 15a, 15b based on the actual building density at that height. Length scales are determined based on Eq. 16a, 16b assuming $H$ is the mean building height. This approach assumes that drag is accurately treated as a sectional phenomenon, that sectional drag coefficients determined from flow through regular arrays of cubes can be generalized, and that length scales are determined by mean building height regardless of building height distribution. While unlikely to be fully robust, these assumptions provide a first approach to modelling spatially-averaged flow for complex building geometries, and their robustness requires assessment.

Tree foliage distributions in urban areas are typically clumped at the crown-neighbourhood scale, not distributed randomly as assumed here. Use of an effective $L_\mathrm{D}$, which is much smaller than the actual $L_\mathrm{D}$, is a potential solution. Marcolla et al. (2003) suggest that effective $L_\mathrm{D}$ for use in parametrization of drag may be based on the clumping coefficient used for radiation interception by foliage (e.g., Krayenhoff et al. 2014). Moreover, buildings may be ‘clumped’ at the neighbourhood scale, an issue that has so far not been addressed in terms of urban canopy modelling.

5 Summary and Conclusions

Urban canopy parametrizations designed to be coupled with mesoscale models must predict the average effects on the neighbourhood-scale flow at each height of obstacles in and above the canopy, without resolving the obstacles. To assess these neighbourhood-scale effects on the flow for simplified geometries, the results of microscale simulations are horizontally averaged. Here, obstacle-resolving CFD model simulations of neutrally-stratified flow through canopies of blocks (buildings) that have various distributions and densities of porous media (tree foliage), are conducted, and the spatially-averaged impacts on the flow of these building-tree combinations are assessed. The CFD model, with standard $k$–$\varepsilon$ turbulence scheme and standard parametrization of foliage effects on flow, is evaluated against two sets of wind-tunnel measurements (Web Supplement). The accuracy with which a one-dimensional (column) model with $k$–$l$ turbulence scheme represents the spatially-averaged CFD model results is assessed (Sect. 2.4, Appendix). The representation of individual effects of trees and buildings in the column model are evaluated in terms of relative importance (Sect. 3), and the resulting parametrization is evaluated against the CFD model results (Sect. 4).

This work presents a methodology for determining the source and sink terms required in the momentum and TKE equations to represent the spatially-averaged impacts of tree foliage on flow in urban areas. It builds on the work of Santiago and Martilli (2010) for neighbourhoods without trees. Considering the effects of both buildings and trees on flow, terms deemed important and included in the proposed parametrization are the following (Sect. 3.3): drag terms due to buildings and tree foliage in the momentum equation (and, although much less important, corresponding production terms in the TKE equation for energy conservation), enhanced dissipation of TKE by the small tree foliage wakes in the TKE equation, and the modification of length scales due to buildings.

The most notable finding is that trees do not significantly affect the efficiency with which buildings exert drag on the flow and produce turbulence, i.e., building sectional drag coefficients do not require modification due to the presence of tree foliage to accurately predict spatially-averaged flow profiles in and above treed urban canopies. In other words, the impact of buildings on the flow relative to flow forcing is not affected by the presence of tree foliage; therefore, the impacts of trees and buildings on the spatially-averaged flow can be represented independently in the prognostic equations for momentum and TKE. Hence, sheltering between buildings and trees is not significant, using a definition of sheltering analogous to that of Thom (1971) for the plant element scale. However, the presence of trees significantly affects the absolute value of the drag force exerted by buildings, and vice versa, for a given forcing pressure gradient. Hence, tiling urban and natural surface-atmosphere exchange schemes is inadequate, and integrated treatment of flow dynamics for urban neighbourhoods with trees is essential.

Impacts of tree foliage on length scales are also neglected in the new parametrization; for most of the scenarios considered, these effects are dwarfed by the terms included in the parametrization. Neglect of foliage impacts on length scales causes significant errors for select cases, in particular for scenarios with foliage that is below or vertically coincident with sparse buildings $(\uplambda _{P} \le 0.11)$. Hence, this is a limitation of the new parametrization.

Overall, results indicate that tree foliage with spatial-average leaf area density $\ge$0.06 m$^{2}$ m$^{-3}$ (the lowest density tested here) significantly affects the spatially-averaged mean and/or turbulent flow for a range of building densities $0.06 < \uplambda _{P} \le 0.44$ if foliage protrudes above buildings. It also significantly affects the spatially-averaged flow if foliage is at or below building canopy height for $\uplambda _{P} \le 0.11$, and possibly for $0.11 < \uplambda _{P} < 0.25$. The proposed parametrization of tree foliage impacts on the flow (Sect. 3.3) should be included for these scenarios in addition to the Santiago and Martilli (2010) parametrization for building-only neighbourhoods. Because it is easy to include, it is recommended that it be included in all simulations that include tree foliage. Updated parameters for the Santiago and Martilli (2010) parametrization for non-treed urban neighbourhoods are presented in Sect. 4.1.

Conclusions presented herein are for neutrally-stratified conditions, and derive from a specific wind direction (perpendicular to cube faces), and a specific range of configurations: staggered cubic arrays with interspersed and evenly-distributed foliage layers of thickness $H/2$, where $H$ is building height. While recent work shows significantly different flow effects for different wind directions (Buccolieri et al. 2011; Santiago et al. 2013a), as well as for more realistic urban morphologies as compared to the uniform height block arrays used here (Kanda et al. 2013), the focus of the present work is an important step toward the inclusion of trees in the parametrization of neighbourhood-scale urban flow (e.g., for mesoscale modelling purposes). Moreover, tree foliage serves to reduce the specificity of dispersive motions that are introduced when modelled urban configurations are constrained to block arrays. Regardless, future studies with flow models of greater accuracy and/or thermal stratification and/or more realistic urban surface configurations and/or wind direction variation can draw on the methodology presented here. Additionally, results are valid for scenarios for which $L_\mathrm{D} C_\mathrm{DV} \le 0.1~\hbox {m}^{2}~\hbox {m}^{-3}$, since the maximum values of $L_\mathrm{D}$ and $C_\mathrm{DV}$ chosen are 0.50 m$^{2}$ m$^{-3}$ (i.e., leaf area index in the range 2.24–3.75 m$^{2}$ m$^{-2}$, depending on $\uplambda _{P}$) and 0.2, respectively. Neighbourhood-average $L_\mathrm{D}$ is unlikely to rise substantially above 0.50 m$^{2}$ m$^{-3}$ for most neighbourhoods; urban tree canopy cover rarely exceeds 50 % (e.g., Nowak et al. 1996), and $L_\mathrm{D}$ for most tree species is less than 1–2 m$^{2}$ m$^{-3}$. $C_\mathrm{DV}$ of 0.20 is perhaps the most commonly cited drag coefficient for trees, and tree foliage will exert a smaller impact on the flow for any values $<$0.20. Nevertheless, it is unlikely that modestly higher values of $L_\mathrm{D} C_\mathrm{DV}$ would produce results that depart radically from those presented here. Overall, results presented herein are specific to these conditions and also contingent on the accuracy of the CFD model and the parametrization of foliage impacts (i.e., construction of the source and sink terms) in both the CFD and the column models (Sect. 2). Nevertheless, this is the first CFD model analysis of the interaction between bluff obstacles and porous media in terms of the spatial-average mean flow and turbulence, and it provides justification for a simple approach to the representation of tree foliage impacts on flow in urban environments.

The new parametrization is a critical step in the development of a comprehensive urban canopy model for urban neighbourhoods with trees, a model that will be useful for planning purposes (scenario testing) and weather and air pollution forecasting. A model for radiative exchange and shading in urban neighbourhoods with trees has recently been developed (Krayenhoff et al. 2014). In order to solve the energy balances of tree foliage elements, the momentum forcing is required, and this is greatly simplified by the knowledge that interaction effects can be neglected, and that trees affect length scales minimally for most scenarios. Implementation of the proposed parametrization for drag and TKE in a $k$–$l$ column model is a simple way to capture the principal impacts of trees and buildings on neighbourhood-average flow and turbulence. Hence, the primary effects of buildings and trees on the flow have been accounted for at this point, and a truly flexible and robustly-parametrized multi-layer urban canopy energy balance model with trees is now possible.

Appendix: Testing the Column Model with CFD Model Results

In this section the fidelity with which a 1-D column model with $k$–$l$ turbulence closure reproduces profiles of spatially-averaged flow as simulated by a 3-D CFD model with standard $k$–$\varepsilon$ closure, is assessed for all urban block scenarios (i.e., with and without tree foliage). The suite of urban configurations and methodology are described in Sect. 2.4. Configurations with building plan density $\uplambda _{P} = 0.25$ are first evaluated, and analysis is subsequently extended to other $\uplambda _{P}$ values.

1.1 Intermediate Building Plan Area Density

RMSD values for the profiles of the spatially-averaged streamwise velocity component $\left\langle {\bar{{u}}} \right\rangle$, spatially-averaged turbulent kinetic energy $\left\langle {\bar{{k}}} \right\rangle$, and spatially-averaged Reynolds stress $\left\langle {\overline{u^{\prime }w^{\prime }}} \right\rangle$, are shown for all scenarios in Fig. 8, where the spatial average is over the outdoor atmosphere only. RMSD values are normalized by the scaling wind velocity $(u_{\tau })$ for $\left\langle {\bar{{u}}} \right\rangle$, and by its square for $\left\langle {\bar{{k}}} \right\rangle$ and $\left\langle {\overline{u^{{\prime }}w^{{\prime }}}} \right\rangle$, and therefore represent the difference between the models normalized by flow forcing.

Fig. 8

RMSD values of the spatially-averaged streamwise velocity component (a), TKE (b), and Reynolds stress (c) between the column and CFD models for all scenarios with building density $\uplambda _{P} = 0.25$. RMSD values are for two atmostpheric layers: canopy ($0 < z\le H$) and above-canopy ($H < z \le 2H$). Leaf area density, from left to right for each foliage height, is 0.06, 0.13, 0.25, and 0.50 m$^{2}$ m$^{-3}$. The $y$-axis scale is magnified for $\left\langle {\overline{u^{{\prime }}w^{{\prime }}}} \right\rangle$. $u_{\tau } = 0.45~\hbox {m s}^{-1}$

The Reynolds stress is always well-reproduced by the column model (i.e., normalized $\textit{RMSD} < 0.05$; Fig. 8c), and hence profiles of $\left\langle {\overline{u^{{\prime }}w^{{\prime }}}} \right\rangle$ are not a focus of the subsequent analysis. RMSD for both $\left\langle {\bar{{u}}} \right\rangle$ and $\left\langle {\bar{{k}}} \right\rangle$ is substantially reduced when the tree foliage layer protrudes above the building tops (i.e., Tree4 and Tree5; Fig. 8a, b). This is primarily true for $\left\langle {\bar{{u}}} \right\rangle$ above the canopy and $\left\langle {\bar{{k}}} \right\rangle$ in the canopy. The major part of this effect is not simply reduction of the magnitude of $\left\langle {\bar{{u}}} \right\rangle$ and $\left\langle {\bar{{k}}} \right\rangle$, as RMSD values normalized by local averages of $\left\langle {\bar{{u}}} \right\rangle$ and $\left\langle {\bar{{k}}} \right\rangle$, respectively, remain substantially lower for Tree4 and Tree5 relative to the other scenarios (not shown). Furthermore, this is true for all tree foliage densities, suggesting that even small leaf area densities (e.g. $0.06~\hbox {m}^{2}~\hbox {m}^{-3}$) above the roof height can substantially reduce column model error relative to the no-tree case.

These tendencies are related to the impact of tree foliage on the dispersive transport of momentum in the canopy in the CFD model (primarily downwards), which is not represented in the column model. When $L_\mathrm{D} = 0.06~\hbox {m}^{2}~\hbox {m}^{-3}$ is added in the lower half of the building canopy (Tree1), the dispersive transport is virtually unchanged, whereas it decreases by a factor of $\approx$4 when this same layer is added above the canopy (Tree5). It decreases further by a factor of $\approx$3 as leaf area density increases to $0.50~\hbox {m}^{2}~\hbox {m}^{-3}$ for Tree5, whereas it only decreases by 25 % for the same increase of $L_\mathrm{D}$ in the Tree1 case. Hence, tree foliage deep in the canopy has little effect on the dispersive (‘subgrid’) flow, regardless of its density, whereas density is more important for tree foliage above the building canopy. Clearly, the height of the tree foliage relative to the building tops is a critical variable in the determination of the effects of both elements on the flow. Note that these results are contingent on uniformly distributed foliage, and foliage clumping at crown-neighbourhood scales would presumably diminish the dampening effect of foliage on dispersive motions.

Profiles of $\left\langle {\bar{{u}}} \right\rangle$ and $\left\langle {\bar{{k}}} \right\rangle$ in Fig. 9 confirm that agreement between the models is better with foliage above the canopy (Tree5), and for dense foliage in the upper part of the canopy (Tree3, $L_\mathrm{D} = 0.50~\hbox {m}^{2}~\hbox {m}^{-3}$) than for cases without trees or foliage deeper in the canopy, particularly for TKE in the canopy. Figure 9 also confirms that even small densities above the canopy (i.e., Tree5) strongly influence the profiles of mean flow. The column model has most difficulty representing TKE in the canopy for both the non-treed scenario, as in Santiago and Martilli (2010), and scenarios with foliage in the canopy (Fig. 9b). Trees introduce several additional processes/terms in the canopy, some of which are not included in the column model formulation but which directly affect TKE (e.g., terms in the $\varepsilon$-equation, Eq. 4).

Fig. 9

Profiles of the spatially-averaged streamwise velocity component (a) and TKE (b) from the CFD (symbols) and column (lines with corresponding colours) models, for foliage height scenarios Tree1, Tree3, and Tree5 (see domain visualizations above plots), each with low and high leaf area densities as indicated in the legend. Building density is $\uplambda _{P} = 0.25$. Results from both models for the foliage-free (No Trees) case are plotted in each panel

The column model is able to reproduce the CFD model profiles of the spatially-averaged streamwise velocity component and TKE, for scenarios with tree foliage, as well or better than for the cases without trees (i.e., those of Santiago and Martilli 2010). RMSD values are less than 0.7 $u_{\tau }$, or its square $u_{\tau }^{2}$, for $\left\langle {\bar{{u}}} \right\rangle$ and $\left\langle {\bar{{k}}} \right\rangle$, respectively, both in the canopy and above it (Fig. 8a, b). RMSD values fall to about 10 % of these forcing values for scenarios with tree foliage extending higher than the rooftops; a likely explanation is that foliage renders the flow less 3-D and more amenable to prediction in a 1-D framework. In other words, dense tree foliage that extends above the buildings reduces the importance of dispersive processes to a greater degree.

Median RMSD values over all simulations (with and without tree foliage) at $\uplambda _{P} = 0.25$ are 0.13 and 0.31 for $\left\langle {\bar{{u}}} \right\rangle$ in and above the canopy, respectively, and 0.25 and 0.23 for $\left\langle {\bar{{k}}} \right\rangle$ in and above the canopy, respectively. Overall, the 1-D column model performs similar to or better than a column model with the Santiago and Martilli (2010) building-only parametrization, relative to the CFD model for all scenarios, for $\uplambda _{P} = 0.25$.

1.2 Low and High Building Plan Area Densities

The column-CFD model comparison is extended to other built densities. Building plan area densities $(\uplambda _{P})$ of 0.00, 0.06, 0.11, and 0.44 are simulated with tree foliage height and density variation as in Sect. 3.2. Column-CFD model differences for these built densities closely resemble those at $\uplambda _{P} = 0.25$ for $\left\langle {\bar{{u}}} \right\rangle$, $\left\langle {\bar{{k}}} \right\rangle$ and $\left\langle {\overline{u^{{\prime }}w^{{\prime }}}} \right\rangle$ (not shown). As for $\uplambda _{P} = 0.25$, RMSD values are larger above the canopy for $\left\langle {\bar{{u}}} \right\rangle$ and in the canopy for $\left\langle {\bar{{k}}} \right\rangle$, but overall the spatially-averaged CFD model profiles are well-reproduced by the column model (Fig. 10). Trees consistently reduce RMSD. RMSD values at these other built densities are of similar magnitude to, or smaller than, that for $\uplambda _{P} = 0.25$ (not shown). Average RMSD is less than or equal to that reported by Santiago and Martilli (2010) for the scenarios without trees. Hence, it is concluded that the column model performs sufficiently well for all $\uplambda _{P}$.

Fig. 10

Profiles of the spatially-averaged streamwise velocity component (a) and TKE (b) from the CFD (symbols) and column (lines with corresponding colours) models, for three building densities $(\uplambda _{P})$, with foliage density $L_\mathrm{D} = 0.50~\hbox {m}^{2}~\hbox {m}^{-3}$ and varying foliage height. The “Forest” scenario has foliage for $0 \le z \le H/2$, and no buildings

1.3 Sensitivity to Parameter $C_{\varepsilon 5}$ in the CFD Model

The $C_{\mathrm{e}5}$ parameter in Eq. 4 determines the sink of dissipation rate $(\varepsilon )$ in the CFD model, and spatially-averaged flow results are quite sensitive to this parameter. There is evidence that lower values of this parameter (relative to the theoretical value of 1.26 computed based on Sanz (2003), used here as the default) may be more accurate, at least relative to select wind-tunnel measurements (see Web Supplement). Hence, select scenarios in Figs. 4 and 8 are reproduced with $C_{\varepsilon 5}$ = 1.00 and $C_{\varepsilon 5} = 1.10$ in the CFD model: Tree2, $L_\mathrm{D} = 0.50~\hbox {m}^{2}~\hbox {m}^{-3}$; Tree4, $L_\mathrm{D} = 0.50~\hbox {m}^{2}~\hbox {m}^{-3}$; Tree4, $L_\mathrm{D} = 0.06~\hbox {m}^{2}~\hbox {m}^{-3}$. The column model is also re-run for each case and again with each source term in Table 1 removed, with modified sectional drag coefficients and length scales output from the CFD model. The ability of the column model to reproduce the CFD model profiles of $\left\langle {\bar{{u}}} \right\rangle$, $\left\langle {\bar{{k}}} \right\rangle$, and $\left\langle {\overline{u{\prime }w^{\prime }}} \right\rangle$ is effectively identical. RMSD values between the column and CFD models changes by less than 0.08, 0.03, and 0.02, respectively. As such, we conclude that the correspondence of the column model with the CFD model is not significantly affected by the choice of $C_{\varepsilon 5}$ in the CFD model over the range $C_{\mathrm{e}5} =$ 1.00–126. Furthermore, the same terms identified in Sect. 3.3 are significant (not shown), and hence it is concluded that terms deemed important for inclusion in the new parametrization are not affected by the choice of $C_{\varepsilon 5}$ in the CFD model over the range $C_{\mathrm{e}5} =$ 1.00–126.