A Multi-layer Radiation Model for Urban Neighbourhoods with Trees

Abstract

A neighbourhood-scale multi-layer urban canopy model of shortwave and longwave radiation exchange that explicitly includes the radiative effects of tall vegetation (trees) is presented. Tree foliage is permitted both between and above buildings, and mutual shading, emission and reflection between buildings and trees are included. The basic geometry is a two-dimensional canyon with leaf area density profiles and probabilistic variation of building height. Furthermore, the model accounts for three-dimensional path lengths through the foliage. Ray tracing determines the receipt of direct shortwave irradiance by building and foliage elements. View factors for longwave and shortwave diffuse radiation exchange are computed once at the start of the simulation using a Monte Carlo ray tracing approach; for subsequent model timesteps, matrix inversion rapidly solves infinite reflections and interception of emitted longwave between all elements. The model is designed to simulate any combination of shortwave and longwave radiation frequency bands, and to be portable to any neighbourhood-scale urban canopy geometry based on the urban canyon. Additionally, the model is sufficiently flexible to represent forest and forest-clearing scenarios. Model sensitivity tests demonstrate the model is robust and computationally feasible, and highlight the importance of vertical resolution to the performance of urban canopy radiation models. Full model evaluation is limited by the paucity of within-canyon radiation measurements in urban neighbourhoods with trees. Where appropriate model components are tested against analytic relations and results from an independent urban radiation transfer model. Furthermore, system response tests demonstrate the ability of the model to realistically distribute shortwave radiation among urban elements as a function of built form, solar angle and tree foliage height, density and clumping. Separate modelling of photosynthetically-active and near-infrared shortwave bands is shown to be important in some cases. Increased canyon height-to-width ratio and/or tree cover diminishes the net longwave radiation loss of individual canyon elements (e.g., floor, walls), but, notably, has little effect on the net longwave loss of the whole urban canopy. When combined with parametrizations for the impacts of trees on airflow and hydrological processes in the urban surface layer, the new radiation model extends the applicability of urban canopy models and permits more robust assessment of trees as tools to manage urban climate, air quality, human comfort and building energy loads.

1 Introduction

The presence of a three-dimensional urban canopy alters local weather and climate in cities and has multifaceted impacts on the urban environment. This has consequences for the prediction of weather, air pollution dispersion and building energy loads, and for neighbourhood design or modification to promote thermal comfort and energy conservation. Fortunately, urban effects on local climate and meteorology can be predicted by well-evaluated numerical models that incorporate the relevant urban elements and physical processes.

Process-based numerical models of urban meteorology and climate have primarily been limited to the buildings and streets that together form the archetypal ‘urban canyon’ (Nunez and Oke 1977). Several recent urban canopy models (UCMs) designed to be coupled with mesoscale atmospheric models have significantly enhanced our ability to predict the climatic effects of urban development at the neighbourhood scale $(10^{2}{-}10^{4}\,\hbox { m})$. These models can be broadly divided into single-layer (e.g., Masson 2000; Kusaka et al. 2001; Kanda et al. 2005b; Harman and Belcher 2006; Oleson et al. 2008) and multi-layer (e.g. Martilli et al. 2002; Dupont et al. 2004; Kondo et al. 2005) models. In simple terms, single-layer models have only one atmospheric layer in the urban canopy, i.e., between the buildings. This means that they estimate air temperature, wind speed and humidity at a single level, and these values are assumed to be representative of the whole urban canopy. Multi-layer models compute meteorological variables for several vertical layers within the canopy, which allows for (but does not guarantee) reduced parametrization of the canopy physics, inclusion of building height distributions, and more detailed prediction of the street level climate and dispersion. UCMs typically account for momentum absorption by the urban surfaces as well as the heat exchanges of horizontal (road and roof) and vertical (wall) facets via conduction, convection and radiation. Some include latent heat fluxes and basic urban hydrology (e.g., Masson 2000), but very few integrate vegetation (Lee and Park 2008; Lemonsu et al. 2012).

Vegetation is common in cities worldwide, and its inclusion in models has been shown to be critical for the proper simulation of the neighbourhood energy balance (e.g., Grimmond et al. 2011), street-level climate, and air pollutant dispersion. Furthermore, it is an important design tool in urban environmental management (Oke 1989; Bowler et al. 2010). Soil and vegetation store water and slow its release, thereby moderating climate by buffering the rate of evaporation. Trees in particular also offer shade and shelter to pedestrians and buildings, and modify near-surface turbulent and radiative exchanges. Furthermore, they increase absorption and deposition of pollutants, emit biogenic volatile compounds (a temperature-dependent process), and affect pollutant dispersion by exerting drag on the flow. Hence, the current challenge in numerical models of the urban environment is to account for the physical and chemical effects of urban vegetation. In essence, the direct interactions between vegetation and the ‘built’ fabric (e.g., buildings, streets) in cities must be better understood and modelled. These interactions are more significant, and more complex, for trees than for shorter vegetation.

Trees interact with buildings primarily in terms of flow dynamics (e.g., sheltering) and radiation exchange; the latter is the focus of the present contribution. Buildings shade trees and other buildings, and trees shade buildings and other trees. Diffuse radiation is exchanged between buildings, between and within trees, and between buildings and trees, enhancing ‘radiation trapping’. Hence, the challenge undertaken here is to represent these varied and complex interactions with an internally consistent numerical model that is relatively simple and computationally undemanding.

Most urban climate model representations of vegetated neighbourhoods have ‘tiled’ urban and soil-vegetation surface models, such that they may interact only indirectly, via an atmospheric model (e.g., Lemonsu et al. 2004). With this approach, important vegetation–building interactions, and tree–building interactions in particular, are not included (Fig. 1). To date, only two process-based UCMs have integrated explicit building–vegetation interaction. Lemonsu et al. (2012) integrate low vegetation (e.g., grass) into a multi-layer version of the Town Energy Balance model (Hamdi and Masson 2008) and demonstrate improved simulation of the canyon microclimate. An urban canyon model developed by Lee and Park (2008) and Lee (2011) also includes the effects of trees, however, it is a single-layer model that permits tree foliage only in the canyon space.

Fig. 1

Indirect interaction (via the atmospheric model) with the tile approach (a) as compared to direct built-vegetation interaction with integrated urban vegetation modelling (b). UCM urban climate model. SVAT (soil-vegetation-atmosphere transfer) scheme

Multi-layer UCMs are better equipped to represent the vertical distributions of tree foliage (e.g., Pyles et al. 2000) and built elements (e.g., Martilli et al. 2002) and their impacts on canopy-layer climate and dispersion, but no model is capable of both at present. The present contribution develops a multi-layer model for exchange of shortwave and longwave radiation in urban canopies that explicitly includes building–tree interaction and retains significant flexibility in terms of the layout of building and tree foliage elements. The new model discussed herein represents a significant improvement over ‘tile’ approaches to the inclusion of vegetation, and contributes to the full inclusion of vegetation in multi-layer urban canopy models.

Section 2 discusses radiation exchange modelling essentials, and the model formulation is presented in Sect. 3 model sensitivity and performance are evaluated in Sect. 4 and Sect. 5 summarizes the findings, and concludes with guidelines for future model development and integration of this radiation code into full UCMs. Finally, the Appendix includes tests of the accuracy and computational efficiency of the model and recommends optimal parameter values.

2 Radiation Exchange Modelling

This section provides a brief background of the methods applied in later sections to model radiation exchange: ray tracing, Monte Carlo simulation and view-factor computation.

2.1 Ray Tracing and Radiosity Approaches

Ray tracing is a common technique in complex radiative transfer modelling where the action of individual bundles of energy (i.e., rays) are assessed separately rather than solving for the overall radiation exchange concomitantly (Siegel and Howell 2002). Radiosity solutions, by contrast, assume Lambertian emission/reflection and construct a matrix of view factors (or shape or configuration factors), each of which represents the fraction of radiation emitted or reflected from one surface patch that is incident on another. However, as scenario complexity increases computational loads increase rapidly and view-factor determination often becomes unachievable. With ray tracing, relations describing the interaction of radiation bundles with the environment may be applied to geometries of arbitrary complexity, and with only modest increases of computational cost. Another advantage of ray tracing is that individual ray paths are explicit, and hence radiation interaction with optically active (e.g., translucent) media and non-Lambertian surfaces is possible. To date, UCMs do not use ray tracing, and hence they are obliged to substantially simplify the geometries of real neighbourhoods (e.g., infinite street length, constant street width) so that view factors can be determined analytically. Conversely, microscale urban models have typically used ray tracing due to their more complex surface representation, often in combination with view factors (Krayenhoff and Voogt 2007; Asawa et al. 2008).

2.2 Monte Carlo Ray Tracing for View Factor Determination

Monte Carlo ray tracing (MCRT) refers to the tracking of radiation bundles through an arrangement of objects, where the start position, direction of emission, and interaction with objects (e.g. absorption and [direction of] scattering) are subject to random sampling from probability density functions that characterize the behaviour of each component. The benefits of MCRT include its robustness, simplicity, and flexibility of implementation. Computational requirements are substantial; however, increasingly fast and cheap computer power is mitigating this drawback. Furthermore, MCRT is ideally suited to parallelization, that is, to the division of a computational task into smaller tasks that can be undertaken concurrently with different processors. MCRT has previously been used in several urban radiation modelling studies (Aida and Gotoh 1982; Kobayashi and Takamura 1994; Montavez and Jimenez 2000; Kondo et al. 2001).

MCRT has been adapted to compute view factors between objects. A large number of rays are sent in random directions (or random-weighted directions, according to the appropriate probability density function) from random positions on an object and the first object to intercept each ray is recorded. The view factor from one object to another is then simply the fraction of rays leaving the first object that is intercepted by the second. Accurate estimation of view factors demands careful selection of ray numbers, ray start locations and ray departure angles (Walker et al. 2010). Effectively, computationally-demanding MCRT is used only once to determine the view factors for a given environment. Thereafter, an efficient matrix solution makes use of these stored view factors to compute radiation exchange between elements of the environment.

3 Urban Radiation Model with Integrated Trees

The current model builds on the two-dimensional multi-layer ‘canyon’ geometry of Martilli et al. (2002). It largely reformulates the model physics and computational methods in order to incorporate several processes, most significantly the radiative interactions and effects of tree foliage. The new model also addresses the weaknesses in the Martilli et al. (2002) formulation identified by Schubert et al. (2012); it incorporates sky-derived diffuse solar radiation, permits full radiative interaction of lower roofs with canyon (and now foliage) elements, and fully accounts for the radiative effects of fractional building coverage at each height (i.e., it conserves energy).

As implied in Sect. 2, a range of computational methods are exploited in order to permit urban configurations of variable complexity while optimizing both accuracy and computation time. Ray tracing tracks direct shortwave radiation as it descends through the domain, impinging on different elements of the urban system (Sect. 3.2). A Monte Carlo ray tracing implementation (Sect. 3.3) computes view factors between building and tree foliage elements for diffuse shortwave and longwave reflection and emission (these calculations are performed only once at the beginning of a model run, and may be stored for future use). A system of linear equations is then solved to model an ‘infinite’ number of reflections between these elements using the stored view factors (Sect. 3.4); as such, reflections are not computed explicitly via ray tracing. Hence, MRCT-determined view factors determine the exchange between all tree foliage and built elements that are visible to each other, including the interception and scattering of diffuse and reflected shortwave radiation, and of emitted and scattered longwave radiation. Figure 2 outlines the different model components and their computational methods, as well as their outputs and frequency of application. Table 1 lists the inputs required to run the model; despite its flexibility the model requires relatively few input parameters.

Fig. 2

The order in which computational procedures are effected in the radiation model (numbers), their computational flow (thin grey arrows), numerical methods (red, in brackets) and outputs (yellow), and their frequency of application in simulations using a mesoscale/urban canopy model (left). *See Table 1

Table 1 Inputs for neighbourhood radiation model with tree foliage

While the radiation model operates in two dimensions, it accounts for three-dimensionality in two ways. Firstly, the actual three-dimensional path of each ray is selected by Monte Carlo simulation and subsequently mapped onto the two-dimensional model domain. Secondly, the ratio of the three-dimensional (3-D) to two-dimensional path length of each ray is accounted for during travel through layers containing foliage (e.g., see Sects. 3.2.2 and 4.1.2). The Bouguer–Lambert–Beer law is used to model radiation interception by layers of foliage (Campbell and Norman 1998; Sinoquet et al. 2001). All elements are assumed to be Lambertian and hence emit and reflect radiation diffusely.

The model is designed for both shortwave $({\approx } 0.4{-}3.0\, \upmu \hbox {m})$ and longwave $({\approx } 3.0{-}100.0\, \upmu \hbox {m})$ radiation wavelength bands. For the purposes of the present model, all wavelengths (or wavelength ranges) in the shortwave spectrum exhibit the same basic behaviour, and the same is true for longwave. An obvious example of the spectral difference between shortwave and longwave is that the former frequently has a direct beam component, but longwave does not. Furthermore, longwave radiation is emitted by all non-sky elements in the model, whereas shortwave radiation is not. Most of the subsequent discussion assumes that shortwave and longwave are “broadband,” that is, they encompass the ranges as defined above; however, provided wavelength-specific reflection and transmission coefficients the model can be applied to scenarios with narrower bands (e.g., see Sect. 4.1.4).

Detailed model geometry is presented in the next section, followed by ray tracing of direct solar radiation in Sect. 3.2, view-factor determination by Monte Carlo ray tracing in Sect. 3.3, and finally the solution of infinite reflections by matrix inversion in Sect. 3.4.

3.1 Two-Dimensional Urban Geometry

Urban areas are conceptualized in the model as very long urban canyons with equally-spaced buildings of equal width, randomly-ordered and present according to a building-height probability distribution (Fig. 3). Note that this conceptualization may underestimate overall wall area relative to real cities by ignoring walls that face along-canyon, such as exist when buildings forming one side of a canyon are of different heights. Nevertheless, the current model geometry is then derived from the conceptualization in Fig. 3, and consists of layers divided by levels in the vertical, and an infinite succession of alternating ‘building’ and ‘canyon’ columns in the horizontal (Fig. 4a). From a ray-tracing perspective, this is equivalent to the assumption of periodic boundary conditions at the lateral boundaries. Five types of ‘elements’ interact radiatively in the model: roof, wall, ground (or road, street, canyon floor), tree foliage, and ‘sky’. ‘Element’ is used to refer to a type of facet (e.g. a wall or roof), whereas a ‘patch’ describes an individual unit that interacts radiatively (i.e., a roof at one level, the street floor, one layer of a wall, or one layer of tree foliage). Walls and tree foliage are divided into layers, whereas roofs exist at one or more levels. There are nz layers, each with identical thickness $\Delta z$, where layer nz contains the highest layer of building and/or foliage. Ground and ‘sky’ are each present at one level only.

Fig. 3

Two-dimensional view of the conceptualization of the urban surface that underlies the model geometry: buildings are infinitely long (into the page), of equal width and equally-spaced, and their heights are specified by a height frequency distribution and buildings of different heights are randomly ordered in the horizontal. Foliage layers of different densities are present above and between buildings and at random horizontal locations. An example building density profile and foliage distribution in terms of a leaf area density (LAD) profile is shown

Fig. 4

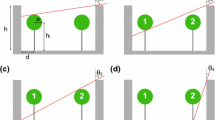
A portion of the model domain for the example urban neighbourhood with trees illustrated in Fig. 3, highlighting aspects of the two-dimensional model geometry (a). The two possible cases when a ray passes an upstream or downstream building corner in a single ray step (b), e.g. as indicated by “I” and “II” in a. Depending whether a ray’s effective zenith $\theta _\mathrm{e}$ is greater than $\varphi$ (ray 2) or less than $\varphi$ (ray 1) different patches intercept the ray

The spatially-averaged building density (probability) at each height in a neighbourhood is represented as a profile of building density (transparency) in the two-dimensional model (as illustrated in Fig. 3). For example, consider a building-height distribution in a residential area as follows: 50 % of buildings are 5.0 m tall, 25 % are 7.5 m tall, and the remaining 25 % are 10.0 m tall (i.e., Figs. 3 and 4a, with $\Delta z = 2.5\hbox { m}$). In this case the building column in the 2-D model will contain walls that intercept 25 % of incident radiation above 7.5 m, 50 % of incident radiation for 5.0–7.5 m, and 100 % of incident radiation below 5.0 m. Meanwhile, roofs at 7.5 m and at 10.0 m each intercept 25 % of incident radiation, while roofs at 5.0 m intercept 50 % of incident radiation. Finally, it is important to note that the building column may have any percentage of its ‘roofs’ at a height of $z = 0$. This permits cases without buildings to be represented, such as forest or forest-clearing scenarios.

The adjacent ‘canyon’ column layers may contain tree foliage according to an input profile of leaf area density in the canyon space, $L_{D}(iz)$, in $\hbox {m}^{2}$ of single-sided leaf area per $\hbox {m}^{3}$, which is also used to approximate the effects of woody parts (see Sect. 3.3.1). Likewise, layers in the building column with building fraction $<$1 may contain tree foliage according to a different input profile $L_{D2}(iz)$. One building column and one canyon column together define one ‘urban unit’, and their widths are $\Delta x_\mathrm{b}$ and $\Delta x_\mathrm{c}$, respectively (Fig. 4a). Effectively, the urban unit is the computational domain and the horizontal boundary conditions are cyclic.

Tree foliage is treated as a surface ‘patch’ that is divided into small pieces (e.g., leaves) of different orientation angles and dispersed throughout a layer. A spherical leaf angle distribution is chosen because it eliminates directionality and is a reasonable approximation to real plant canopies (Campbell and Norman 1998). Unlike previous urban vegetation models (e.g., Lee and Park 2008) tree foliage may be present in the building column above rooftops, or on ‘green roofs’, and in both columns above the tallest buildings, a common occurrence in many lower-density residential neighbourhoods.

During ray tracing, the urban unit is replicated in the horizontal due to the partially transparent nature of the foliage and any building layers that are present with less than 100 % probability. Depending on their direction of travel, rays may pass horizontally through many iterations of the cyclic two-column urban unit prior to complete attenuation by elements of the urban surface or ‘escape’ to the sky. Rays incident at each patch are aggregated over all iterations of the urban unit in the whole domain to obtain the total view factor, or flux, for each patch.

3.2 Incident Direct Shortwave Radiation

The instantaneous distribution of direct solar irradiance over the model geometry is solved by means of ray tracing. A user-defined number of rays (ni),¹ each representing an equivalent bundle of shortwave radiation energy, are evenly-placed over the width of one urban unit at a constant height $z_\mathrm{max} + 1.5\Delta s \cos (\theta _\mathrm{e})$, where $\Delta s$ is the actual ray increment in metres, $\theta _\mathrm{e}$ is the effective 2-D solar zenith angle, and $z_{\mathrm{max}}$ is the top of the tallest tree layer or the tallest roof level, whichever is higher. The rays proceed down through the domain with step size $\Delta s$ until they reach ground level $(z < 0)$ after nj steps, where

$$\begin{aligned} \Delta s=\Delta s_\mathrm{in} \min (\Delta z,\Delta x_\mathrm{c} ,\Delta x_\mathrm{b}), \end{aligned}$$

(1)

and $\Delta s_\mathrm{in}$ is the step size input by the user (sensitivity to $\Delta s_\mathrm{in}$ is presented in “Direct solar irradiance: number of rays and ray step size” section in the Appendix). Their path is given by the effective 2-D solar zenith angle

$$\begin{aligned} \theta _\mathrm{e} =\max \left[ {\tan ^{-1}\left( {\frac{\tan (\theta )}{\sin (\chi )}} \right) ,\theta _{\mathrm{e},\max } } \right] , \end{aligned}$$

(2)

where $\theta$ is the solar zenith angle, $\chi$ is the angle between the solar azimuth and the street direction (Martilli et al. 2002, Eq. A12), and a maximum value of $\theta$ is imposed in order to avoid infinite iterations during periods with low solar elevation,

$$\begin{aligned} \theta _{\mathrm{e},\max } =\tan ^{-1}\left( {\frac{100 \left( {\Delta x_\mathrm{b} +\Delta x_\mathrm{c} } \right) }{z_{\max } }} \right) , \end{aligned}$$

(3)

with the factor of 100 deemed sufficiently large to avoid significant influence on the results for realistic scenarios, but small enough to prevent excessive computation times.

3.2.1 Interception by Buildings

As the rays travel downwards they impinge on wall and roof patches, and travel through foliage layers. The canyon can be oriented in any direction, and hence a canyon of non-specific orientation is considered throughout. In fact, multiple canyons, each with a unique orientation and geometry, can be modelled in order to faithfully represent a particular urban canopy or neighbourhood.

An individual ray may be intercepted by the same surface patch more than once due to the semi-transparency of the building surfaces and foliage layers and the periodicity of the horizontal boundary conditions (hence the necessity of the index $j$ below). When a ray $i$ crosses from the canyon to the building column in layer iz during ray step $j$, it contributes

$$\begin{aligned} \Delta Wl_{i,j} (iz)&= \beta r_{i,j-1} \Gamma (iz+1)=-\Delta r_{i,j},\end{aligned}$$

(4a)

$$\begin{aligned} \Delta Wr_{i,j} (iz)&= \left( {1-\beta } \right) \,r_{i,j-1} \Gamma (iz+1)=-\Delta r_{i,j}, \end{aligned}$$

(4b)

to the total ray strength incident on layer iz of the left (Wl) and right (Wr) canyon walls, where $\beta = 1$ for $\chi {<}\pi$ and $\beta = 0$ for $\chi {>}\pi$ (since both walls cannot be sunlit at the same time), and $\Gamma (iz+1)$ is the probability of walls in layer iz, or the probability of having a building with height equal to or greater than level iz+1 (Martilli et al. 2002). The ray in turn loses an equal amount $(\Delta r_{i,j})$ from its previous fractional energy, or strength, $r_{i,j-1}$ (non-dimensional), leaving it with ray strength

$$\begin{aligned} r_{i,j} =r_{i,j-1} -\Delta r_{i,j}. \end{aligned}$$

(5)

When a ray $i$ does not cross from the canyon to the building column during ray step $j$, or if it does so in layer iz but $\Gamma (iz+1) = 0$, we have simply

$$\begin{aligned} \Delta Wl_{i,j} (iz)=\Delta Wr_{i,j} (iz)=\Delta r_{i,j} =0. \end{aligned}$$

(6)

When a ray $i$ crosses level iz in the building column, it loses the following ray strength to roof level iz

$$\begin{aligned} \Delta R_{i,j} (iz)=r_{i,j-1} \gamma _\mathrm{e} (iz)|_\mathrm{building\,column} =-\Delta r_{i,j}, \end{aligned}$$

(7)

where $\gamma _\mathrm{e}(iz)$ is the effective probability of a building roof at level iz

$$\begin{aligned} \gamma _\mathrm{e} (iz)=\left\{ {\begin{array}{l@{\quad }l} \frac{\gamma (iz)}{\left( {1-\Gamma (iz+1)} \right) },&{}\mathrm{for}\;\Gamma (iz+1)<1 \\ 0,&{}\mathrm{for}\;\Gamma (iz+1)=1 \\ \end{array}} \right. , \end{aligned}$$

(8)

and $\gamma (iz)$ is the actual probability of a building roof at level iz (Martilli et al. 2002), and may take any value $\le$1 here. This effective building-height probability $\gamma _\mathrm{e}(iz)$ allows the model geometry (Fig. 4a) to preserve the energy partitioning inherent in the 3-D conceptualization of the urban surface in Fig. 3. In effect, Eq. 8 accounts for the fact that a ray in the model building column at a height $z$ only exists in those columns in the 3-D conceptualization (Fig. 3) where the building height is ${<}z$, otherwise it would be inside a fully opaque building.

When a single ray step crosses both a column boundary and a vertical level with $\gamma (iz+1) > 0$ the ray has passed a building corner at the ‘downstream’ (Fig. 4, I) or ‘upstream’ (Fig. 4, II) edges. To determine whether the ray passes above or below the corner, the ‘zenith’ angle of the line segment joining the ray’s final position to the corner ($\varphi$ in Fig. 4b) is compared to the effective solar zenith angle $(\theta _\mathrm{e})$. The result determines whether the roof intercepts the ray, and if it is an upstream corner, which wall patch intercepts the ray. With these simple tests a high degree of accuracy is achieved with fewer rays.

3.2.2 Interception by Tree Foliage

Tree foliage may be present in either the canyon or the building column. In the latter case it is only present to the extent that the building is transparent in layer $iz$ (i.e., $[1 - \Gamma (iz+1)]$). Tree foliage intercepts rays at each ray step according to the Bouguer–Lambert–Beer law (i.e., the turbid medium model),

$$\begin{aligned} \Delta V\mathrm{c}_{i,j} (iz)&= r_{i,j-1} \left[ {1-\exp \left( {-K_{bs} \Omega L_{DC} (iz) \Delta s f_i } \right) } \right] =-\Delta r_{i,j} ,\end{aligned}$$

(9a)

$$\begin{aligned} \Delta V\mathrm{b}_{i,j} (iz)&= r_{i,j-1} \left[ {1-\exp \left( {-K_{bs} \Omega \,L_{DB} (iz) \Delta s f_i } \right) } \right] =-\Delta r_{i,j} , \end{aligned}$$

(9b)

where $\Delta s$ is the 2-D ray step size (m), $f_{i}$ is the ratio of 3-D (actual) to 2-D (model) distance travelled by the ray, $L_{DC}(iz)$ and $L_{DB}(iz)$ are the leaf area densities $(\hbox {m}^{2}\hbox { m}^{-3})$ at layer iz in the canyon and building columns, respectively (i.e., leaf area density is a property of the foliage at a given height in a given column, rather than a neighbourhood average), and $K_{bs}$ is the foliage extinction coefficient (dimensionless). This is a widely-used model of radiation interception by vegetation foliage (e.g., Sinoquet et al. 2001); $\Omega$ is a clumping factor that takes the value 1.0 for random foliage distributions, and smaller for more clumped distributions (Campbell and Norman 1998). It encompasses the effects of clumping at several scales, e.g. from shoots to crowns, and it is a global parameter in that it applies to all foliage in the model. It is important to note that $\Omega$ is also a property of the foliage (not of the neighbourhood geometry), and hence applies only to the building-free volume of the domain (i.e., 1 – $\Gamma$ (iz + 1) for layer iz).

Clumping is the norm rather than the exception in forests (Kucharik et al. 1999), and it is required in order for Eq. 9 to apply to non-random foliage distributions. Urban foliage distributions tend to have greater clumping at larger (e.g., crown) scales, even when considering neighbourhood averages; hence, smaller values of $\Omega$ than are typical for forests are generally required. An example that may have relevance to typical urban forests is an open savannah ecosystem with substantial clumping at the (between-)crown scale. Ryu et al. (2010) determined the clumping coefficient in such an ecosystem to be $0.49\pm 0.10$. Better estimation of urban clumping may be possible based on the work of Chen et al. (2008), who develop an analytic model of the effects on clumping of heterogeneous canopies of tree spacing, tree width, crown depth, solar zenith angle, leaf angle distribution and leaf area density.

For vegetation with a spherical leaf angle distribution the foliage extinction coefficient $K_{bs}$ for beam radiation density travelling a certain distance in the vertical and impinging on a horizontal level, depends on solar zenith angle (Campbell and Norman 1998)

$$\begin{aligned} K_{bs} (\theta )=\frac{1}{2 \cos (\theta )}. \end{aligned}$$

(10)

This is considered a good first approximation for all types of canopies (Chen et al. 1997), and includes interception by both sides of the leaves. However, Eq. 10 is directionally-independent if leaf angles are assumed to be spherically and randomly distributed, and the leaves are approximately randomly distributed in space (i.e., $\Omega \approx 1$). For these conditions, the extinction coefficient is constant at $K_{bs} = 0.5$ in the direction of radiation (ray) travel.

3.2.3 Interception by the Ground

Those rays that reach ground level $(z = 0)$ contribute to the ground, or street, as follows,

$$\begin{aligned} \Delta G_{i,j} =r_{i,j-1} =-\Delta r_{i,j}. \end{aligned}$$

(11)

This is always true in the canyon column. In the building column, however, rays only reach the ground for scenarios where some ‘rooftops’ are at ground level, i.e., $\Gamma (2) < 1.0$.

3.2.4 Total Incident Direct Shortwave Radiation

Finally, incident direct shortwave flux density to each surface patch is computed as

$$\begin{aligned} K_P^\mathrm{dir} (iz)=\frac{K^\mathrm{dir}}{ni}\frac{\sum _{i=1}^{ni} {\sum _{j=1}^{nj} {\Delta P_{i,j} (iz)} } }{A_P (iz)}, \end{aligned}$$

(12)

where$K^{dir}$ is the incoming direct shortwave irradiance on an unobstructed horizontal surface element, and $P$ is replaced by Wl, Wr, R, Vc, and Vb for patches of wall (left and right), roof, and tree foliage in the canyon and building column, respectively, and nj is the maximum number of ray steps taken by any of the ni rays. Incident direct shortwave flux density to the ground $(G)$ is calculated analogously, but only at one level (no iz index).

The $A_{P}$ terms are the area of each patch as a fraction of the total horizontal area of the urban unit,

$$\begin{aligned} A_\mathrm{Wl} (iz)&= A_\mathrm{Wr} (iz)=\frac{\Delta z\,\Gamma (iz+1)}{\Delta x_\mathrm{b} +\Delta x_\mathrm{c} },\end{aligned}$$

(13a)

$$\begin{aligned} A_\mathrm{R} (iz)&= \frac{\Delta x_\mathrm{b} \,\gamma (iz)}{\Delta x_\mathrm{b} +\Delta x_\mathrm{c} },\end{aligned}$$

(13b)

$$\begin{aligned} A_\mathrm{G}&= \frac{\Delta x_\mathrm{c} }{\Delta x_\mathrm{b} +\Delta x_\mathrm{c} },\end{aligned}$$

(13c)

$$\begin{aligned} A_{{Vc}} (iz)&= \frac{2\,L_{DC} (iz)\,\Omega \,\Delta z \Delta x_\mathrm{c} }{\Delta x_\mathrm{b} +\Delta x_\mathrm{c} },\end{aligned}$$

(13d)

$$\begin{aligned} A_{Vb} (iz)&= \frac{2\,L_{DB} (iz)\,\Omega \,\Delta z \Delta x_\mathrm{b} \left( {1-\Gamma (iz+1)} \right) }{\Delta x_\mathrm{b} +\Delta x_\mathrm{c}}, \end{aligned}$$

(13e)

where the area of tree foliage ($A_{Vc}$ or $A_{Vb})$ is taken as the ‘active’ portion of the complete two-sided leaf area, in which the effective leaf area density (e.g., $L_{DC} (iz) \Omega$) is used in place of the actual leaf area density at each level. Hence, the foliage in a given layer interacts radiatively as a single surface patch, but for radiation interception purposes one that is broken into many small pieces (i.e., leaves) of random 3-D orientation. For clumped foliage $(\Omega < 1.0)$ some of these leaves effectively do not emit radiation towards, or intercept radiation from, the surroundings, as they are situated at the interior of ‘foliage clumps’.

At this point, direct shortwave radiation receipt prior to reflections is determined. Subsequently, diffuse receipt is computed using view factors, followed by infinite reflections between all surface patches. Furthermore, the emission and reflection of longwave radiation are calculated based on these same view factors. Hence, view factors between all interacting patches must be known in order to proceed.

3.3 View Factors for Longwave and Reflected Shortwave Radiation

View factors between all surface patches are computed once with Monte Carlo ray tracing (MCRT), and are then used to calculate diffuse radiation exchange for the remainder of a mesoscale or urban canopy model simulation. As a result, the computational expense associated with ray tracing occurs only once at the start of the simulation, or, in principle, occurs only once for a given neighbourhood configuration. In other words, the calculation of view factors by MCRT is part of the pre-processing of the land-surface description only, and is not involved in the prognostic portion of the model.

3.3.1 Ray Starting Point and Direction

A user-defined number of rays nk are ‘emitted’ from each patch and view factors are determined based on the first patch to intercept each ray. Rays begin at a random point along a surface patch, or at a random location in a layer of foliage. A ray leaving a solid patch (roof, ground, wall) may take any direction into the hemisphere adjacent to the surface. The zenithal angle of its path is chosen from a weighted random distribution because all surface elements are assumed to be isotropic, or Lambertian, emitters and reflectors,

$$\begin{aligned} \theta _k^{\textit{sfc}} =\sin ^{-1}\left( {\sqrt{\zeta _k }} \right) =\cos ^{-1}\left( {\sqrt{1-\zeta _k }} \right) =\frac{\cos ^{-1}\left( {1-2 \zeta _k } \right) }{2}, \end{aligned}$$

(14)

where $\zeta _{ k}$ is a random number between 0 and 1, and its azimuthal angle is simply

$$\begin{aligned} \varphi _k^{\textit{sfc}} =2\pi \xi _k, \end{aligned}$$

(15)

where $\xi _{ k}$ is another random number between 0 and 1 (Siegel and Howell 2002). The weighted distribution of zenith angle (Eq. 14) results from the combined effects of increasing solid angle per zenithal increment $\hbox {d}\theta$ [as $\hbox {sin}(\theta )$], and decreasing intensity in W $\hbox {sr}^{-1}$ [as $\hbox {cos}(\theta ^{\textit{sfc}})$, i.e. Lambert’s cosine law], as $\theta$ increases.

Rays leaving a layer of tree foliage are assumed isotropic and therefore choose from a full sphere $(4\pi$ solid angle) with equal probability, and require 2 nk rays to preserve ray density per solid angle. Hence, scattering of shortwave and longwave radiation by leaves is assumed to have no preferred direction. In other words, forward scattering (transmission) and backward scattering (reflection) are assumed equal, a classic simplification for shortwave radiation incident on leaves (Sinoquet and Bonhomme 1992). In reality, coniferous shoots (assemblages of needles) typically exhibit some enhanced backward scattering relative to forward scattering (Smolander and Stenberg 2003), and many deciduous leaves exhibit specular reflection and reduced transmission of shortwave at high (grazing) incidence angles. However, it is challenging to account for these phenomena without explicit ray tracing of the reflection and transmission processes. In the deciduous case, there is little effect on the absorption coefficient of leaves at these grazing angles, as decreased transmission is approximately offset by enhanced reflection (Monteith and Unsworth 2008).

There are two further points regarding the assumption of isotropic scattering from foliage layers. Woody portions of trees do not transmit radiation, which is problematic in terms of the assumption of directionally-uniform scattering. However, they represent the minority of the radiative effects of trees for evergreens and deciduous leaf-on scenarios. Furthermore, tree leaves are typically positioned so as to preferentially mask (e.g., shade) the woody elements (Kucharik et al. 1998). Deciduous leaf-off scenarios may suffer from larger relative errors, but the absolute impacts of bare trees on radiation exchange tend to be smaller than for leaf-on scenarios. Similarly, while leaves transmit and reflect similar amounts of shortwave irradiance, they do not transmit longwave radiation. Hence, the assumption of isotropic scattering from foliage layers is incorrect for these wavelengths. However, the errors induced by this assumption will be minimal for two reasons: a) reflection coefficients of leaves are small in the longwave spectrum $({\approx }0.01{-}0.06$; Oke 1987); and b) foliage layers receive comparable intensities of longwave radiation from every direction, unlike shortwave radiation. Fortunately, isotropic emission of longwave radiation from trees is a reasonable assumption.

View factors from the sky to each patch (as opposed to sky view factors, which are view factors from each patch to the sky) are required to compute the receipt of incoming longwave and diffuse shortwave. A patch’s sky view factor is equal to the area-weighted view factor (i.e., Eq. 18) from the sky to the patch, assuming an isotropic sky radiance distribution. Several models take advantage of this fact (e.g. Masson 2000; Kusaka et al. 2001; Krayenhoff and Voogt 2007). However, this relation does not hold for vegetation or for anisotropic sky radiance distributions, and hence explicit computation of view factors from the sky to each patch is included.

Rays leaving the ‘sky’ begin at a random horizontal location in each of several equal intervals along the width of the urban unit, and at a user-defined height above the tallest roofs or trees $({\ge }1.1[z_\mathrm{max}+\Delta z])$; results are insensitive to both the height and interval width for isotropic sky radiance. For simplicity, each ray selects from a downward-facing hemisphere ($2\pi$ solid angle) using Eqs. 14 and 15. This approach is also known as the isotropic model of sky diffuse radiation; it is a reasonably good assumption for longwave radiation with overcast conditions but less so for clear conditions (Monteith and Unsworth 2008). It is also a significant assumption for shortwave diffuse radiation, particularly for clear conditions. More complex sky radiance distributions could easily be incorporated and are left for future work.

3.3.2 Ray-Environment Interaction

Once a starting point and direction are determined for a ray $k$ originating from a patch $P$, it remains to compute its incidence upon, and dissipation by, other surface patches. Downward travelling rays use the same set of relations as for incident direct shortwave (Sect. 3.2; replace $i$ index with $k$). The only difference is that each ray now has a unique direction of travel. Equation 9 with $K_{bs} = 0.5$ remains valid for foliage layers, due to the assumption of a spherical leaf-angle distribution.

Upward travelling rays cannot impinge on roofs or ground, and hence use a subset of these same relations, namely Eqs. 4 and 9. When an upward travelling ray $k$ takes a step $j$ such that it exceeds height $z_\mathrm{max}+\Delta s$ the remainder of its energy is ‘lost’ to the sky,

$$\begin{aligned} \Delta S_{k,j} =r_{k,j-1} =-\Delta r_{k,j} , \end{aligned}$$

(16)

and contributes to the total reflected shortwave radiation (albedo), or to the upward-directed longwave radiation.

Finally, recall that tree foliage is treated as a ‘surface patch’ that is divided into small pieces (i.e., leaves) of random orientation dispersed throughout a layer. All of the leaves in each layer are assumed to have the same properties and states: view factors, surface temperatures, and so on. This has important implications for the resolution with which a tree canopy is represented, and is explored further in the “Building wall and foliage layer resolution” section in the Appendix. A property that emerges naturally from ray tracing with this geometry is that each layer of tree foliage, in contrast to other facets in the model, has a ‘self view factor’. That is, a portion of its emitted or scattered radiation is incident on itself. In other words, a ray that starts its journey in the middle of a foliage layer has a certain likelihood of being intercepted by neighbouring leaves in the same layer.

3.3.3 Diffuse Exchange Between Patches

Diffuse exchange (i.e., reflection/scattering and emission) between patches during the simulation is computed as follows,

$$\begin{aligned} D_{\textit{PQ}} (iz,jz)=\Psi _{\textit{PQ}} (iz,jz)\,D_{P} (iz), \end{aligned}$$

(17)

where $D_{P}(iz)$ is the emitted or reflected/scattered flux density from the $iz\mathrm{th}$ level (or patch) of surface element ${P}, \Psi _{\textit{PQ}}(iz,jz)$ is the area-weighted view factor from the $iz^{th}$ level of surface $P$ to the $jz\mathrm{th}$ level of surface element $Q$, and $D_{\textit{PQ}}$ (iz, jz) is the emitted or reflected flux density incident on the $jz\mathrm{th}$ level of surface element $Q$ that originates from the $iz\mathrm{th}$ level of surface element $P$. Area weighted view factors are calculated as follows,

$$\begin{aligned} \Psi _{\textit{PQ}} (iz,jz)=\psi _{\textit{PQ}} (iz,jz) \frac{A_{P} (iz)}{A_Q (jz)}, \end{aligned}$$

(18)

where $A_{P}$ and $A_{Q}$ are given by Eqs. 13a–e, and $\psi _{\textit{PQ}}(iz,jz)$ is previously determined from MCRT as the fraction of ray energy leaving the $iz\mathrm{th}$ level of surface element $P$ that is incident on, and intercepted by, the $jz\mathrm{th}$ level of surface element $Q$,

$$\begin{aligned} \psi _{\textit{PQ}} (iz,jz)=\left. {\frac{1}{nk}\,\sum _{k=1}^{nk} {\sum _{j=1}^{nj} {\Delta Q_{k,j} (jz)} } } \right| _{\mathrm{rays}\,k\,originate\,from\,iz\mathrm{th}\,level/ layer\,of\, P}, \end{aligned}$$

(19)

where “$P$” and “$Q$” are each one of Wl or Wr, R, Vc or Vb, G, or $S$, and the $\Delta Q_{k,j}(jz)$ are computed as in Eqs.  4, 7, 9, 11, and 16, respectively. Hence, $\psi _{\textit{PQ}}$ (iz, jz) is the fraction of ray energy (i.e., emitted/reflected radiation) leaving $P(iz)$ that is incident on $Q(jz)$. It is important to note here that diffuse exchange between tree foliage layers and other urban elements, between different foliage layers, and within a foliage layer, occurs by means of view factors calculated by MCRT (Eq. 19). Hence, tree foliage emits longwave radiation (Eqs.  23-25), and intercepts (and subsequently absorbs or scatters) longwave that is scattered or emitted by other model elements (Eq. 9 and Sect. 3.3.2), in addition to intercepting, absorbing and scattering direct and diffuse shortwave radiation.

3.4 Infinite Reflections and Total Patch Absorption

There are a maximum of 2nz wall patches, nz + 1 roof levels, one ground level, and 2nz foliage layers. Hence, a system of 5nz + 2 equations and 5nz + 2 unknowns is solved by matrix inversion to determine both total incident shortwave radiation, and total incident longwave radiation, at each surface patch after infinite reflections. The following equations apply to a canyon of any orientation.

3.4.1 Total Incident and Absorbed Shortwave Radiation

The total shortwave radiation incident on the left wall after infinite reflections is given by

$$\begin{aligned} K_{\textit{Wl}} (iz)&= \underbrace{\beta \,K_{Wl}^\mathrm{dir} (iz)+\Psi _{\textit{SW}} (iz) K^\mathrm{dif}}_\mathrm{sky}+\underbrace{\sum _{jz=1,nz} {\Psi _{\textit{WW}} (jz,iz)\,\alpha _W K_{\textit{Wr}} (jz)} }_{\mathrm{right}\,\mathrm{wall}} \nonumber \\&+\underbrace{\sum _{jz=1,nz+1} {\Psi _{\textit{RW}} (jz,iz)\,\alpha _{R} K_{R} (jz)} }_{\mathrm{roof}}+\underbrace{\Psi _{\textit{GW}} (iz)\,\alpha _{G} K_{G} }_{\mathrm{floor} (\mathrm{street})} \nonumber \\&+\underbrace{\sum _{jz=1,nz} {\Psi _{\textit{VcW}} (jz,iz)\,\alpha _V K_{\textit{Vc}} (jz)} }_{\mathrm{canyon}\,\mathrm{column}\,\mathrm{vegetation}}+\underbrace{\sum _{jz=1,nz} {\Psi _{\textit{VbW}} (jz,iz)\,\alpha _\mathrm{V} K_{\textit{Vb}} (jz)}}_\mathrm{building\,column\,vegetation},\nonumber \\ \end{aligned}$$

(20)

where $K^\mathrm{dif}$ is the diffuse shortwave from the sky, and the $\alpha _{P}$ are the albedos of the different patches $P$. Total shortwave incident on the right wall after infinite reflections is given by switching “$l$” with “$r$” and “$\beta$” with “$(1 - \beta$)” in Eq. 20. The equation for total shortwave radiation incident on canyon column tree foliage layers after reflections is

$$\begin{aligned} K_{\textit{Vc}} (iz)&= \underbrace{K_{\textit{Vc}}^\mathrm{dir} (iz)+\Psi _{\textit{SVc}} (iz)\,K^\mathrm{dif}}_\mathrm{sky}+\underbrace{\sum _{jz=1,nz} {\Psi _{\textit{WVc}} (jz,iz)\,\alpha _{W} \left( {K_{\textit{Wl}} (jz)+K_{\textit{Wr}} (jz)} \right) } }_\mathrm{left\,and\,right\,walls} \nonumber \\&+\underbrace{\sum _{jz=1,nz+1} {\Psi _{\textit{RVc}} (jz,iz)\,\alpha _{R} K_{R} (jz)} }_\mathrm{roof}+\underbrace{\Psi _{\textit{GVc}} (iz)\,\alpha _{G} \,K_{G} }_{\mathrm{floor} (\mathrm{street})} \nonumber \\&+\underbrace{\sum _{jz=1,nz} {\Psi _{\textit{VcVc}} (jz,iz)\,\alpha _{V} K_{\textit{Vc}} (jz)} }_\mathrm{canyon\,column\,vegetation}+\underbrace{\sum _{jz=1,nz} {\Psi _{\textit{VbVc}} (jz,iz) \alpha _{V} K_{\textit{Vb}} (jz)} }_\mathrm{building\,column\,vegetation}.\nonumber \\ \end{aligned}$$

(21)

The equation for building column tree foliage layers is identical except all instances of “Vc” are swapped for “Vb”, and vice versa. Roofs are all assumed horizontal (flat, non-pitched roofs), and hence do not interact with other roofs or the ground,

$$\begin{aligned} K_\mathrm{R} (iz)&= \underbrace{K_{R}^\mathrm{dir} (iz)+\Psi _{\textit{SR}} (iz)\,K^\mathrm{dif}}_\mathrm{sky}+\underbrace{\sum _{jz=1,nz} {\Psi _{\textit{WR}} (jz,iz)\,\alpha _{W} \left( {K_{\textit{Wl}} (jz)+K_{\textit{Wr}} (jz)} \right) } }_\mathrm{left\,and\,right\,walls} \nonumber \\&+\underbrace{\sum _{jz=1,nz} {\Psi _{\textit{VcR}} (jz,iz)\,\alpha _{V} K_{\textit{Vc}} (jz)} }_\mathrm{canyon\,column\,vegetation}+\underbrace{\sum _{jz=1,nz} {\Psi _{\textit{VbR}} (jz,iz)\,\alpha _{V} K_{\textit{Vb}}(jz)}}_\mathrm{building\,column\,vegetation}.\nonumber \\ \end{aligned}$$

(22)

Street floor total incident shortwave is determined identically to roofs with the “$R$” subscript replaced by “$G$” (i.e., different view factors), and the elimination of the iz index as there is only one ground level. Finally, total absorbed shortwave radiation at each patch is $(1-\alpha _{P})K_{P}({ iz})$, where $\alpha _{P}$ is the albedo of surface element $P$, and $P$ is one of Wl, Wr, Vc, Vb, $R$, or $G$ (both walls have the same albedo, likewise for both sets of foliage layers).

All built (flat) surfaces reflect radiation diffusely. However, $\alpha _\mathrm{V}$ for the foliage layers represent the fraction of shortwave that is reflected and transmitted, i.e. radiation incident on leaves is assumed to scatter forward and backward equally (Sect. 3.3.1). Strictly, the photosynthetically-active (PAR) and near infrared (NIR) portions of the shortwave spectrum should be modelled separately as their vegetation scattering coefficients $\alpha _{v}$ differ greatly (Campbell and Norman 1998). This can be achieved by running the solar reflection component of the model (Eqs. 20–22) twice, once for PAR and once for NIR (see Sect. 4.1.4).

3.4.2 Total Incident and Absorbed Longwave Radiation

All view factors for longwave exchange are identical to their shortwave counterparts unless different sky radiance models are used for the two wavebands, in which case the view factors from the sky to the urban elements will differ. The total longwave radiation incident on the left wall after infinite reflections is given by

$$\begin{aligned} L_\mathrm{Wl} (iz)&= \underbrace{\Psi _{\textit{SW}} (iz)\,L^\mathrm{sky}}_\mathrm{sky}+\underbrace{\sum _{jz=1,nz} {\Psi _{\textit{WW}} (jz,iz)\,\left[ {\left( {1-\varepsilon _{W} } \right) \,L_{\textit{Wr}} (jz)+\varepsilon _{W} \sigma T_{\textit{Wr}} ^{4}(jz)} \right] } }_\mathrm{right \,wall} \nonumber \\&+\underbrace{\sum _{jz=1,nz} {\Psi _{\textit{VcW}} (jz,iz)\,\left[ {\left( {1-\varepsilon _{V} } \right) \,L_{\textit{Vc}} (jz)+\varepsilon _{V} \sigma T_{\textit{Vc}} ^{4}(jz)} \right] } }_\mathrm{canyon\,column\,vegetation} \nonumber \\&+\underbrace{\sum _{jz=1,nz} {\Psi _{\textit{VbW}} (jz,iz)\,\left[ {\left( {1-\varepsilon _{V} } \right) \,L_{\textit{Vb}} (jz)+\varepsilon _{V} \sigma T_{\textit{Vb}} ^{4}(jz)} \right] } }_\mathrm{building\,column\,vegetation} \nonumber \\&+\underbrace{\Psi _\mathrm{GW} (iz)\,\left[ {\left( {1-\varepsilon _{G} } \right) \,L_{G} +\varepsilon _{G} \sigma T_\mathrm{G} ^{4}} \right] }_\mathrm{floor (street)} \nonumber \\&+\underbrace{\sum _{jz=1,nz+1} {\Psi _{\textit{RW}} (jz,iz)\,\left[ {\left( {1-\varepsilon _{R} } \right) \,L_{R} (jz)+\varepsilon _{R} \sigma T_{R} ^{4}(jz)} \right] } }_\mathrm{roof}, \end{aligned}$$

(23)

where $L^\mathrm{sky}$ is longwave irradiance from the sky, and $\varepsilon _{P}$ is emissivity from patch $P$. Total longwave incident on the right wall after infinite reflections is given by the analogous equation (switch “$l$” and “$r$”). For tree foliage layers the equation is as follows,

$$\begin{aligned} L_{Vc} (iz)&= \underbrace{\Psi _{\textit{SVc}} (iz)\,L^\mathrm{sky}}_\mathrm{sky}+\underbrace{\sum _{jz=1,nz} {\Psi _{\textit{WVc}} (jz,iz)\,\left[ {\begin{array}{l} \left( {1-\varepsilon _{W} } \right) \,\left( {L_{\textit{Wl}} (jz)+L_{\textit{Wr}} (jz)} \right) \\ +\varepsilon _{W} \sigma \,\left( {T_{\textit{Wl}} ^{4}(jz)+T_{\textit{Wr}} ^{4}(jz)} \right) \\ \end{array}} \right] } }_\mathrm{left \,and\, right \,walls} \nonumber \\&+\underbrace{\sum _{jz=1,nz} {\Psi _{\textit{VcVc}} (jz,iz)\,\left[ {\left( {1-\varepsilon _{V} } \right) \,L_{\textit{Vc}} (jz)+\varepsilon _{V} \sigma T_{\textit{Vc}} ^{4}(jz)} \right] } }_\mathrm{canyon\,column\,vegetation} \nonumber \\&+\underbrace{\sum _{jz=1,nz} {\Psi _{VbVc} (jz,iz)\,\left[ {\left( {1-\varepsilon _{V} } \right) \,L_{\textit{Vb}} (jz)+\varepsilon _{V} \sigma T_{\textit{Vb}} ^{4}(jz)} \right] } }_\mathrm{building\,column\,vegetation} \nonumber \\&+\underbrace{\Psi _{\textit{GVc}} (iz)\,\left[ {\left( {1-\varepsilon _{G} } \right) \,L_{G} +\varepsilon _{G} \sigma T_{G} ^{4}} \right] }_\mathrm{floor (street)} \nonumber \\&+\underbrace{\sum _{jz=1,nz+1} {\Psi _{\textit{RVc}} (jz,iz)\,\left[ {\left( {1-\varepsilon _{R} } \right) \,L_{R} (jz)+\varepsilon _{R} \sigma T_{R} ^{4}(jz)} \right] } }_\mathrm{roof}. \end{aligned}$$

(24)

As for shortwave, the equation for building-column tree foliage layers is identical except all instances of “Vc” are swapped for “Vb”, and vice versa. And again, roofs do not interact with other roofs or the ground,

$$\begin{aligned} L_{R} (iz)&= \underbrace{\Psi _{SR} (iz)\,L^\mathrm{sky}}_\mathrm{sky}+\underbrace{\sum _{jz=1,nz} {\Psi _\textit{WR} (jz,iz)\,\left[ {\begin{array}{l} \left( {1-\varepsilon _{W} } \right) \,\left( {L_{\textit{W}l} (jz)+L_{\textit{W}r} (jz)} \right) \\ +\varepsilon _\mathrm{W} \sigma \,\left( {T_\mathrm{Wl} ^{4}(jz)+T_\mathrm{Wr} ^{4}(jz)} \right) \\ \end{array}} \right] } }_\mathrm{left\,and\,right\,walls} \nonumber \\&+\underbrace{\sum _{jz=1,nz} {\Psi _{\textit{VcR}} (jz,iz)\,\left[ {\left( {1-\varepsilon _{V} } \right) \,L_{\textit{Vc}} (jz)+\varepsilon _{V} \sigma T_{\textit{Vc}} ^{4}(jz)} \right] } }_\mathrm{canyon\,column\,vegetation} \nonumber \\&+\underbrace{\sum _{jz=1,nz} {\Psi _{\textit{VbR}} (jz,iz)\,\left[ {\left( {1-\varepsilon _{V} } \right) \,L_{\textit{Vb}} (jz)+\varepsilon _{V} \sigma T_{\textit{Vb}} ^{4}(jz)} \right] }}_\mathrm{building\,column\,vegetation}. \end{aligned}$$

(25)

Street floor total incident longwave has an identical equation to that for roofs with the “$R$” subscript replaced by “$G$” (i.e., different view factors), and the iz index eliminated as there is only one ground level. Total absorbed longwave radiation at each patch is $\varepsilon _{P}L_{P}(iz)$, where $P$ is one of Wl, Wr, Vc, Vb, R, or $G$ (both walls have the same emissivity, likewise for both sets of foliage layers).

4 Model Approximations and Testing

The purpose here is to assess the spatial distribution of radiation receipt and absorption given by the proposed model as a function of scenario (building geometry, vegetation distribution, solar angle). Model parameters (numbers of rays, ray step size, vertical resolution) are considered in the Appendix. The physics of the proposed model are robust given the following assumptions

• 1. All surface elements are diffuse (Lambertian) emitters and reflectors.

• 2. The Bouguer–Lambert–Beer law for radiation transmission with a spherical leaf angle distribution and clumping index is a good approximation for spatially-heterogeneous distributions of urban tree foliage.

• 3. Trees scatter both shortwave and longwave bands equally in forward and backward directions (see Sect. 3.3.1).

Importantly, there are several assumptions implicit in the two-dimensional model geometry itself, many of which are common in urban canopy modelling. The proposed model geometry is based on the following assumptions and approximations.

• 1. The combination of two or more 2-D ‘infinite’ canyon geometries of appropriate orientation permits the faithful reproduction of the neighbourhood-average radiation distribution (by height and surface element type) of real 3-D geometries.

  • a. The effects of small-scale structures or variation (e.g., building width variation, pitched roofs, chimneys, balconies, windows, cars, etc.) can be neglected.

  • b. The infinitely long canyon is a good representation of all non-built spaces in an urban canopy (backyards, courtyards, laneways, intersections, etc.).

• 2. Model resolution in the vertical is essential for the representation of urban canopy processes for most neighbourhoods, and it is more important than model resolution in the horizontal (i.e., further division of the ‘canyon’ and ‘building’ columns).

• 3. Tree foliage is approximately evenly-distributed across canyon spaces, at the crown-scale, when averaged over neighbourhoods.

The ‘validation’ of the current model over all realistic scenarios is extremely difficult. Moreover, given the highly complex nature of real urban geometries, in particular those that include trees, to the authors’ knowledge appropriate observational datasets are not currently available. Therefore, only three types of testing are performed on the model: (a) energy conservation tests on all model components (not shown here for brevity’s sake, but have been conducted and the model conserves energy within the bounds of numerical error); (b) sensitivity tests to determine model parameters that yield sufficient accuracy while minimizing computation time (Appendix); and (c) system response tests to demonstrate that modelled distributions of radiation exchange for different arrangements of built and foliage elements as a function of solar angle agree with expected neighbourhood-scale responses (Sects. 4.1 and 4.2).

4.1 System Responses—Shortwave Radiation

Several scenarios are presented to demonstrate: (a) the impacts of tree foliage of different heights and densities on these radiation distributions; and (b) that the model distributes shortwave radiation in a realistic manner for a range of geometries and solar zenith angles. Distribution of direct and diffuse shortwave irradiance over the modelled urban surface, and subsequent (infinite) reflections, are both modelled in order to allocate absorbed shortwave radiation in each scenario. Figure 5 outlines the radiative parameters and the range of urban geometries considered in these scenarios, while Table 2 details the specific solar angle, building arrangement, and density and location of tree foliage in each scenario. The simulations in this section meet or exceed the minimum recommendations detailed in the Appendix in terms of the computational parameters (number of rays, ray step size) and wall and foliage vertical resolution. The reader’s attention is drawn in particular to the assessment of the importance of sufficient wall and foliage layer resolution in “Building wall and foliage layer resolution” section in the Appendix. The results have implications for urban canopy radiation models generally, and suggest that single-layer radiation models in particular may introduce substantial errors.

Fig. 5

Model geometries and solar zenith angles for shortwave radiation system response tests. B building, V vegetation (tree) foliage, numbers refer to foliage layer, and subscripts refer to building (e.g. “${V2}_\mathrm{b}$”) or canyon (e.g. “${V2}_\mathrm{c}$”) columns. Vertical resolution is 1 m for all simulations. Roof, ground and wall albedos are 0.15, 0.15 and 0.25, respectively; foliage reflection and transmission coefficients sum to 0.50

4.1.1 Solar Zenith Angle

The impact of solar zenith angle on the vertical distribution of shortwave absorption in the canopy is examined for a canyon with moderate $H/W$ and two building heights (Fig. 6a). Three solar zenith angles are simulated, and a fourth scenario assumes all incoming shortwave is diffuse and isotropic. Most obvious is the increased absorption at 0, 6 and 12 m, corresponding to the ground and the two roofs, respectively (Fig. 6a; note that a flatter slope indicates greater absorption in a given layer). These horizontal surface elements result in a comparatively larger total (3-D) area per 1-m vertical interval, and hence greater absorption. Further, lower walls (0–6 m) absorb more than upper walls (6–12 m) because they are present with double the frequency—all buildings have walls from 0 to 6 m, whereas only the taller B2 buildings have walls from 6 to 12 m. When $\theta = 70^{\circ }$ the lower portions of the walls absorb less radiation because they are shaded by upstream buildings. Finally, roof-level interval absorption (at 6 and 12 m) is approximately the same for all scenarios because they are present with the same frequency. Note that cumulative absorption at ground level fails to reach 100 % by an amount that corresponds to the albedo for each scenario.

Table 2 Solar angle, and building and tree foliage characteristics for the shortwave scenarios

As solar zenith angle increases, the median height of shortwave absorption (${\approx } 45$th percentile) shifts higher in the canopy, from ${\approx }1\hbox { m}$ for $\theta = 20^{\circ }$ to ${{\approx }}5.5\hbox { m}$ for $\theta = 45^{\circ }$ to ${\approx }6.5\hbox { m}$ for $\theta = 70^{\circ }$, notably elevating the overall albedo (Fig. 6a). This corresponds to an increase of wall absorption at the expense of canyon floor absorption as the Sun moves lower in the sky. Notably, the diffuse-only scenario distributes energy in the vertical similarly to scenarios with low to moderate solar zenith angle, and with equivalent overall albedo; however, unlike the other scenarios, it distributes radiation evenly to both walls (not shown). Overall the model reproduces known behaviour, such as the increase of neighbourhood albedo with solar zenith angle (Aida 1982; Christen and Vogt 2004; Kanda et al. 2005a).

Fig. 6

Cumulative percent (from top of canopy) of shortwave irradiance absorbed, after infinite reflections, as a function of: a solar zenith angle; b tree foliage density and clumping; c tree foliage height; and d shortwave frequency band. Each data point corresponds to the total absorption both above and at the corresponding level $(z)$. Overall neighbourhood albedo $(\alpha )$ for each scenario appears in the legend. Specifics of the urban configuration and foliage characteristics for each scenario appear in Table 2. a The ‘diffuse’ simulation assumes all incoming shortwave radiation is diffuse and isotropic. b LAI values are neighbourhood averages; LAI $=$ 1.0 corresponds to leaf area density $L_{D} = 0.375\hbox { m}^{2}\hbox { m}^{-3}$. Solar zenith angle is $45^{\circ }$ for all but the final scenario. c Solar zenith angle is $20^{\circ }$. d Solar zenith angle is $45^{\circ }$ and diffuse is 15 % of incoming. Foliage reflection and transmission coefficients combine to be 0.50 for broadband, 0.20 for PAR, and 0.80 for NIR. $^{*}$Effective 2-D solar zenith angle is $45^{\circ }$, actual solar zenith angle is $67.1^{\circ }$, and solar azimuth is $25^{\circ }$ from the canyon orientation, i.e. $\chi = 25^{\circ }$ (as opposed to $90^{\circ }$ for the remainder of the scenarios)

4.1.2 Tree Foliage Height, Density, and Clumping

The impacts of tree foliage density on shortwave radiation absorption are explored for a canyon of $H/W = 0.5$ with a 4 m thick layer of tree foliage above the canyon space. The leaf area index (LAI) and clumping of this foliage layer are varied and the resulting scenarios are compared to a non-vegetated case, where LAI is the neighbourhood-average value. Foliage characteristics are chosen to represent cases with moderate (LAI $=$ 1.0) and high (LAI $=$ 3.0) urban tree coverages and relatively ‘patchy’ foliage distributions $(\Omega = 0.5)$. Results are shown for a solar zenith angle of $45^{\circ }$ (Fig. 6b).

Tree foliage shifts shortwave absorption from roofs, ground, and walls up to the vegetated layer, substantially increasing the average height of shortwave absorption (Fig. 6b). An increase in foliage density (LAI) and a decrease in foliage clumping (i.e., greater $\Omega$) both enhance this effect. In fact, the effective $LAI (= LAI_\Omega$; Chen et al. 1997) determines the interception efficiency of the foliage; each increase of the effective LAI, from 0.5 (Scenario 6b.2), to 1.0 $(\Omega = 1.0$; Scenario 6b.3), to 1.5 (LAI $=$ 3.0; Scenario 6b.4), results in additional shortwave absorption, but with ‘diminishing returns’. The overall albedo ($\alpha$) varies little between scenarios 6b.2 to 6b.4, but decreases more noticeably for the scenario without tree foliage (6b.1).

The final scenario (6b.5) illustrates the importance of accounting for the 3-D path lengths of rays travelling through foliage. Contrary to the other scenarios, which have the solar beam perpendicular to the canyon direction $(\chi = 90^{\circ }$), the solar zenith is increased to $\theta = 67.1^{\circ }$ and the solar azimuth relative to the canyon axis is reduced to $\chi = 25^{\circ }$, which preserves the effective (2-D) solar zenith angle at $\theta _{e} = 45^{\circ }$. The absorption by the 7–11 m tree foliage layer increases by 39 %, reducing absorption by 23 % for walls and by ${\approx }10\,\%$ for roofs and ground, relative to Scenario 6b.2. Furthermore, overall albedo increases significantly (by ${\approx }0.02$). A strictly 2-D model would not capture this important effect, which exists for all solar azimuth angles such that $\chi \ne 90^{\circ }$.

The height of the tree foliage also affects the vertical distribution of shortwave radiation absorption (Fig. 6c). A 4-m thick layer of foliage corresponding to a neighbourhood $LAI = 1.0$ is placed with its base at heights of 1 m (low), 7 m (mid) and 13 m (high) in the canyon with two building heights from Fig. 6a. The additional absorption attributable to foliage at each level is evident in Fig. 6c, as is the corresponding reduction of canyon-floor absorption relative to the vegetation-free scenario. As expected, elevation of the foliage layer increases the average height of shortwave absorption. Distributing the same neighbourhood LAI evenly in the horizontal (“$V3_\mathrm{c}, V3_\mathrm{b}$”, or Scenario 6c.5) has a small effect, e.g., a 10 % reduction in roof absorption and a similar percent increase in wall absorption. The variation of overall albedo is intriguing: the addition of foliage in the lowest part of the canyon has very little effect, whereas foliage layers at heights V2 and V3 clearly increase overall albedo.

A more straightforward and complete example of this effect is shown in Fig. 7. The same canyon of width $\Delta x_\mathrm{c} = 12\hbox { m}$ is chosen, but with buildings uniformly 6 m tall $(H/W = 0.5$), and with a 4-m foliage layer characterized by $L_\mathrm{D} = 0.375\hbox { m}^{2}\hbox { m}^{-3}$ and $\Omega = 0.5$ (neighbourhood $LAI = 1.0$) present at varying heights in and above the canyon. Interestingly, introduction of the foliage layer adjacent to the ground (“0” on the x-axis in Fig. 7) reduces the overall albedo as compared to the non-vegetated case for small solar zenith angle $(\theta = 20^{\circ })$. Overall, neighbourhood albedo increases approximately linearly as the foliage layer ascends from ground level, peaking when the middle of the foliage layer is even with the roof level and descending to an asymptote thereafter (Fig. 7). The exact character of this effect likely depends on the albedos of the foliage, walls, and ground, and also on the built structure and foliage density and distribution. The main point is that such a phenomenon can only be captured with integrated modelling of building and trees; it cannot be captured with the tile approach (Fig. 1a) or a single-layer approach to the integration of urban trees in UCMs.

Fig. 7

Neighbourhood albedo as a function of foliage layer base height for solar zenith angles $20^{\circ }$ and $45^{\circ }$. A 12 m wide canyon is simulated with 6 m tall buildings $(H/W = 0.5)$ and a 4-m thick tree foliage layer in the canyon column $(L_{D} = 0.375\hbox { m}^{2}\hbox { m}^{-3}, \Omega = 0.5)$. Horizontal lines indicate the albedo without the foliage layer for each scenario

Fig. 8

Partitioning of total incoming shortwave irradiance between different elements of the urban canopy—buildings (roofs, walls), ground, tree foliage, and reflected radiation—for select cases based on scenarios from Fig. 6a–c. Scenarios in columns A–D have 50 % B1 buildings and 50 % B2 buildings, whereas columns E and F have only B1 buildings (Fig. 5). Foliage layers are: $V1_{\mathrm{c}}$ (low), $V3_{\mathrm{c}}$ (high), $V2_{\mathrm{c}}$ (scenarios E and F). Solar zenith angle is $\theta = 45^{\circ }$ for scenarios B-F

Overall the model produces physically reasonable modifications to vertical profiles of shortwave absorption as a function of foliage layer density, height, and clumping. It is clear that the height and density of tree foliage significantly modulates the vertical distribution of solar radiation absorption in urban canopies. Tree foliage absorbs a greater fraction of shortwave irradiance at higher leaf area densities, and with reduced clumping and greater exposure to the direct beam (e.g. foliage located above buildings), and for higher solar zenith angles.

4.1.3 Partitioning Between Urban Elements

The vertical distribution of shortwave absorption (Fig. 6a–c) gives information on the heights that experience maximum radiation loading, and therefore that are most likely to exhibit either significant energy exchange with the atmosphere, or storage. However, the distribution of solar absorption between urban elements (roofs, walls, tree foliage, ground) is also likely to be critical in predicting building energy load and/or pedestrian thermal comfort. Furthermore, current UCMs, with or without the tile approach, are all incapable of capturing the effects of tree foliage height and density on partitioning of shortwave absorption between urban elements.

Figure 8 displays the partitioning between urban elements for select cases based on scenarios from Fig. 6a–c. Scenarios A and B demonstrate the shift of absorption from the ground to the building walls with increasing solar zenith angle (e.g., Fig. 6a) for a vegetation-free canyon with two building heights $(H/W = 0.5, 1.0)$, each present with equal frequency. The addition of a 4-m thick layer of $0.375\hbox { m}^{2}\hbox { m}^{-3}\,(\Omega = 0.5)$ tree foliage in the lower canyon decreases the wall and road absorption but does not affect the roofs (scenario C). The equivalent foliage layer above the canyon (scenario D) absorbs about twice as much shortwave as that in scenario C, shielding roofs and walls to a greater extent. Scenarios E and F in Fig. 8 retain the foliage layer above the canyon but include only one building height, at 6 m or $H/W = 0.5$ (i.e., as in Fig. 6b). Scenario E shows increased ground-level absorption and reduced wall absorption compared to scenario D due to the loss of the taller (12 m) buildings, and consequent loss of wall area (by 33 %). Finally, the effect of increasing foliage density above the canyon is substantial (scenario F vs. scenario E), with tree foliage now absorbing almost half of the incoming shortwave.

Overall it is wall and ground-level absorption that vary most profoundly across these scenarios, in particular with solar zenith angle, relative wall area, and leaf area density. Roof absorption varies to a lesser degree, mainly in response to elevated, dense foliage. The presence of trees shifts solar radiation absorption away from built surface elements, in general, and away from different built surfaces depending on foliage height and solar zenith angle. The interplay of these effects is impossible to capture with the tile approach or highly parametrized canyon vegetation radiation models. To the extent that the current model geometry represents the distributions of radiation exchange of real urban canopies, it is clearly capable of evaluating the effects of tree heights and foliage densities on neighbourhood-average building and ground-level (e.g., pedestrian) radiative loads for different solar angles.

4.1.4 Photosynthetically-active and Near-Infrared Bands

The simulations in Sects. 4.1.1–4.1.3 have treated shortwave radiation as a single “broad” band. However, vegetation exhibits radically different absorption and scattering behaviour over different portions of the shortwave spectrum, whereas most building materials display less wavelength-dependent variation. Vegetation absorbs the majority of incident ultraviolet radiation (UV; ${\approx }0.29{-}0.40 \,\upmu \hbox {m}$) and photosynthetically-active radiation (PAR; ${\approx }0.40{-}0.70 \,\upmu \hbox {m}$), whereas it scatters the majority of near-infrared radiation (NIR; ${\approx }0.70{-}2.80\, \upmu \hbox {m}$; Monteith and Unsworth 2008; Escobedo et al. 2011). For clear-sky conditions UV typically accounts for ${\approx }5\,\%$, PAR for ${\approx }50\,\%$, and NIR for ${\approx }45\,\%$ of solar irradiance (e.g., Escobedo et al. 2011). As PAR and UV have similar leaf reflectances, they are lumped together in the following simulations, and the relative importance of separating PAR+UV from NIR is explored (hereafter, “PAR+UV” is referred to as “PAR” only).

Scenario 6b.2 $(LAI = 1.0, \Omega = 0.5)$, with a 4-m thick vegetation layer above a 6-m tall canyon and a solar zenith of $45^{\circ }$, is re-run with scattering/reflection in PAR and NIR bands treated independently. Combined foliage reflection and transmission coefficients are assumed to be 0.50, 0.20, and 0.80, for broadband, PAR, and NIR, respectively (Monteith and Unsworth 2008). Corresponding foliage absorption coefficients are 0.50, 0.80, and 0.20, respectively. Reflection coefficients of all ‘urban’ materials are assumed invariant between the wavelength bands. PAR and NIR are each assumed to compose 50 % of the broadband shortwave flux density and the vertical distribution of absorption is computed in each case. The total broadband radiation absorption as the sum of the PAR and NIR scenarios is also calculated (“PAR+NIR” in Fig. 6d).

The most obvious feature in Fig. 6d is the enhancement of PAR absorption and decrease of NIR absorption in the 7–11 m foliage layer, relative to the broadband case. There is a small reciprocal reduction (increase) of PAR (NIR) absorption at the roof, wall and ground surface elements. Meanwhile, the cumulative profile of absorption of shortwave energy with and without the PAR/NIR split (“PAR+NIR” and “Broadband,” respectively) is similar. Individual patch absorption is also similar; median relative differences are 1 % for built surface patches and 6 % for foliage layers. The overall neighbourhood albedo differs by 0.006 between these approaches, an effect that increases for higher solar zenith angle (0.010 for $\theta = 70^{\circ }$) or higher foliage density (0.023 for LAI = 3.0), but decreases for lower solar zenith angle (0.005 for $\theta = 20^{\circ }$) or foliage layers in the canyon (0.003 for foliage layer at 1–5 m).

These results suggest that separation of PAR and NIR can be moderately important in terms of overall shortwave receipt for scenarios with denser foliage and/or elevated foliage relative to the buildings. It appears it is likely to be critical for the accurate estimation of PAR absorption by the foliage, and therefore to the calculation of stomatal resistance and consequently for the modelling of transpiration and latent heat flux. For both scenario 6b.2 and the same scenario with the foliage layer placed deep in the canyon (i.e., at 1–5 m), overall foliage absorption of broadband is remarkably constant at ${\approx }70\,\%$ of PAR absorption for the solar zenith angles tested. Hence, substitution of broadband shortwave for PAR in terms of foliage absorption would incur a ${\approx }30\,\%$ error. It is good to note that the separation of the two bands adds little to the computation time, because interception of direct beam PAR, NIR and broadband are identical. Hence, the direct solar scheme need only be run once each time the radiation routine is called, but the shortwave reflection matrix must be solved one or more additional times. The matrix solution represents a minority of the shortwave radiation computation time.

4.2 System Responses: Longwave Radiation

Longwave radiation exchange differs from shortwave in that matter at terrestrial temperatures not only absorbs in this wavelength range, but also emits. Hence this section explores the impacts of sky-view reductions due to buildings and trees on the net longwave exchanges $(L^{*})$ of built surfaces and foliage, i.e. the net rate of gain or loss of thermal radiation energy. Simulations with varying canyon $H$/$W$ and foliage heights and densities are performed. Temperatures of all urban facets and foliage are set to $28^{\circ }\hbox {C}$ (isothermal) and downwelling longwave is 320 W m$^{-2}$, approximating an early evening cooling scenario during mid-latitude summer. Surface and foliage emissivities are 0.95. Canyon and building widths are 12 and 6 m, respectively, and vertical resolution is 1 m.

Computational parameters follow recommendations from the Appendix. Means and standard deviations of 20-member ensembles are presented because all longwave radiation exchanges depend on view factors derived from MCRT, whereas in the shortwave spectrum the majority of the exchange is determined by the receipt of direct shortwave, which does not have a stochastic component. Means of canyon aggregate values have uncertainty estimates based on the standard rules of uncertainty approximation (derived from the patch-level ensemble standard deviations). Simulation results necessarily represent a “snapshot” in time with imposed surface temperatures because the energy balances of patches are not solved by the model.

4.2.1 Net Longwave Exchange: Vertical Distribution

Cumulative vertical profiles of net longwave radiation loss are first assessed, similar to the shortwave scenarios in Sect. 4.1. Specifically, the effects of adding a 4 m thick layer of moderately-high density foliage at different heights in a $H/W = 0.5$ canyon are simulated. The neighbourhood total net longwave flux density differs by less than 2 % for all scenarios (Fig. 9), as the presence of tree foliage in or above the canyon does not significantly alter neighbourhood total net longwave flux density for the isothermal conditions tested here. Differences would likely to be much larger for the common situation where built surface element temperatures are significantly higher than foliage temperatures.

Fig. 9

Cumulative vertical profile (from top) of total neighbourhood net longwave flux for an $H/W = 0.5$ canyon with and without a 4 m thick, ${LAI} = 1.0\,(L_{D} = 0.375\hbox { m}^{2}\hbox { m}^{-3}, \Omega = 0.75)$ tree foliage layer at different heights in the canyon. All values are means of 20-member ensembles

Prior to the addition of tree foliage, the canyon floor has the largest negative $L^{*}$ (i.e., $z = 0{-}1$ m), followed by the roof, and finally the walls (‘No Trees’ in Fig. 9). The addition of the foliage layer in the upper two thirds of the canyon (2–6 m) results in significantly greater longwave loss in the upper part of the canyon (${\approx }45\,\%$ of the total, up from ${\approx }15\,\%$) and reduced longwave loss by the canyon floor (road), as the foliage ‘traps’ thermal radiation in the lower canyon. If the foliage layer is shifted upwards to 4–8 m, and then fully above the canyon at 6–10 m, the centre of longwave loss shifts progressively upwards from the upper canyon and roofs. The foliage layer loses 35, 41, and 43 % of total neighbourhood net longwave at heights of 2–6, 4–8, and 6–10 m, respectively. The corresponding rooftop fraction of $L^{*}$ losses decreases, from 33 to 30 %, and finally to 25 % as the tree foliage exits the canopy (6–10 m). The model predicts, as expected, that the overall effect of tree foliage with sufficient exposure to the sky (e.g., for lower density canyons) is to shift the location of active energy loss upwards and therefore to moderate the nocturnal climate deeper in the canopy. The next section provides a more complete example of the effects of building density and vegetation on canopy climate.

4.2.2 Net Longwave Exchange: Ground and Canyon Fluxes

In this section the model is applied to investigate a well-known relation in urban climatology: the effect of canyon geometry on longwave exchange in the urban canopy. The response of the net longwave balance to canyon height-to-width ratio $(H/W)$ is computed for the canyon floor alone, the canyon walls alone, and for the complete canyon, to elucidate the role of longwave exchange in urban heat island genesis. Foliage addition is also assessed.

Greater canyon $H/W$ decreases the sky-view factor of the canyon floor (streets), which reduces the magnitude of net longwave losses from the surface leading to greater nocturnal street surface temperatures (Oke 1981; Oke et al. 1991). This relation is reproduced correctly in Fig. 10, both by the current model and by the TUF-2D model (Krayenhoff and Voogt 2007).

Fig. 10

The effect of adding a layer of trees into an urban canyon. Ensemble mean $L^{*}$ on the floor of a range of canyons with different cross-sectional geometries $(H/W)$. The tree layer is spread uniformly across the canyon column, in a layer between 2 and 6 m above the floor. Two foliage cases are considered: a layer of foliage with $0.375\hbox { m}^{2}\hbox {m}^{-3}\,(LAI = 1.0)$ and clumping $\Omega = 0.75$; a layer of $0.750\hbox { m}^{2}\hbox { m}^{-3}$ (LAI = 2.0) also with $\Omega = 0.75$. Also, $L^{*}$ of the walls (combined) and the whole canyon (both per m$^{2}$ plan area of canyon) of non-treed canyons. Error bars for floor values are ensemble standard deviations, whereas those for the whole canyon denote overall uncertainty derived from the standard deviations of individual patches. Individual data points are output by the present model. Lines are results for canyons with no trees from the TUF-2D model (Krayenhoff and Voogt 2007). Lines are linear interpolations between discrete results at $H/W = 0.00, 0.25, 0.50, 0.75, 1.00, 1.50, 2.00$ and 2.50

This phenomenon has been postulated to be a leading cause of the nocturnal (canopy-layer) urban heat island. Simple extension of the relation between sky view of individual surfaces and their resulting longwave balance and surface temperature, to the case of screen-level air temperature in the urban canopy as a whole, is not appropriate. For example, several numerical models incorrectly apply reduced sky-view factors to whole canyons, even the whole urban surface, resulting in artificially small magnitudes of urban $L^{*}$ (e.g., Atkinson 2003; Grossman-Clarke et al. 2005).

The canyon floor and walls² each individually have a reduced sky view factor, and therefore reduced exchange with the cold sky. But together, as a canyon system, they exhibit $L^{*}$ (per unit plan area of canyon) of similar or greater magnitude to that of a flat surface, according to both models (‘canyon’ in Fig. 10). This is because the surface area of the walls increases with $H/W$, increasing their total net longwave loss per plan area of canyon, and offsetting the reduced canyon floor $L^{*}$ loss (‘walls’ in Fig. 10). Given that building walls and street surfaces tend to remain warmer than flat ‘rural’ surfaces (as opposed to being equal in temperature, as modelled here), it is apparent that canyon $L^{*}$ magnitude typically exceeds that of more rural areas. Therefore, the only way that neighbourhood-scale average $L^{*}$ could be less than typical rural values is if a sufficiently large fraction of the area is covered with materials possessing low emissivity and/or low thermal admittance (e.g., roofs). The urban structure on its own is not sufficient for this purpose.

Clearly, therefore, the nocturnal urban canopy-layer heat island (in the air) is unlikely to relate to reduced loss of longwave radiation by the urban canopy as a whole. However, it very well may relate to the proximity of the screen-level measurement height to surfaces with reduced loss of longwave radiation (i.e., the canyon floor and lower walls). It might also relate to the increased surface area of urban canopies, which are convoluted relative to rural areas and are thus more available to retain daytime heat, among other factors. It must also be appreciated that the air temperature depends on the heat balance of the air itself not just of nearby surfaces.

The addition of moderately-high tree foliage density in the canyon significantly reduces canyon floor longwave losses (Fig. 10). Reductions of net longwave radiation are ${\approx }50\,\%$ and ${\approx }75\,\%$ for the LAI $=$ 1.0 and LAI $=$ 2.0 scenarios, respectively, irrespective of $H/W$. Hence, the presence of trees reduces the cooling rate of the canyon floor, as expected, an effect that is more pronounced in an absolute sense for lower $H/W$. For the particular conditions considered here, the addition of the neighbourhood-average foliage density of LAI $=$ 1.0 has an impact equivalent to an increase in $H/W$ of 0.75–1.25, and this effect increases to $H/W \ge 1.5$ for the LAI $=$ 2.0 scenario. As for non-treed cases, the total $L^{*}$ of the whole canyon including tree foliage (or the whole neighbourhood for scenarios for which foliage protrudes above the canyon), varies little with $H/W$ (not shown).

Canyon floor $L^{*}$ at $H/W = 0.0$ (no buildings) illustrates the versatility of the model. It has a value of $-139.0\hbox { W m}^{-2}$ without trees, which decreases in magnitude to $-72.2$ and $-42.7\hbox { W m}^{-2}$ with the application of canyon column leaf area densities of $0.375\hbox { m}^{2}\hbox {m}^{-3}$ and $0.75\hbox { m}^{2}\hbox {m}^{-3}$, respectively, between 2 and 6 m. This amounts to a forest-clearing scenario, and the $L^{*}$ of the ground under the forest portions (canyon column) is included for consistency with the built scenarios (i.e., $H/W > 0$) in Fig. 10. $L^{*}$ in the clearings (i.e., the ground level in the building column) has a greater magnitude, as expected: $-96.1\hbox { W m}^{-2}$ for LAI $=$ 1.0 and $-80.3\hbox { W m}^{-2}$ for LAI $=$ 2.0. Finally, extension of the canyon column tree foliage layer into the building column would lead to a continuously forested scenario; hence, the model is potentially able to represent the range of scenarios between forest and completely urban.

To summarize, the new model suggests that both urban structure and tree foliage can substantially decrease the magnitude of net longwave exchange of individual facets, such as the canyon floor. However, the net longwave exchange of canyons or urban neighbourhoods as a whole does not vary significantly with $H/W$ or added foliage for the isothermal conditions modelled here. The latter is likely to depend more on the (distribution of) materials and thermal states of the individual urban elements.

5 Conclusions

A multi-layer urban radiation model with trees is developed that explicitly computes building-tree interaction and represents a substantial improvement over the ‘tile’ approach to urban vegetation simulation. Furthermore, it does so using standard radiative transfer methods: (Monte Carlo) ray tracing for direct shortwave and view-factor determination, and the Bouguer–Lambert–Beer law for attenuation by tree foliage layers. The model is flexible—for trees, any heights, thicknesses, foliage densities and clumping are permitted, and for buildings, any heights and height probability distributions are allowed. The use of ray tracing renders the model less dependent on the complexity of the model geometry, while the initial calculation of inter-element view factors permits a computationally speedier matrix solution to diffuse exchange for the remainder of a mesoscale or urban canopy model simulation.

Model simulations are performed to ensure energy conservation, and subsequently to demonstrate appropriate system responses to varying geometries, foliage characteristics, and solar zenith angle. The effects of different heights and densities of tree foliage on the vertical distribution of shortwave radiation absorption are demonstrated. Furthermore, the partitioning of shortwave absorption between buildings, vegetation and ground is presented. Denser foliage layers exhibiting less clumping absorb more shortwave at the expense of building and ground surfaces, in particular for higher solar zenith angles or when foliage layers are elevated relative to the buildings. Splitting broadband shortwave into separate PAR and NIR bands has moderate implications for total shortwave absorption for some scenarios, but will be essential for coupling with energy/water balance models (e.g., accurate assessment of PAR to model stomatal resistances).

System response scenarios in the longwave spectrum focus on the net exchange. Simulated canyon floor (road), wall and whole canyon net longwave flux densities $(L^{*})$ as a function of canyon $H/W$ are in agreement with an independent radiation model (TUF-2D). The magnitude of canyon floor $L^{*}$ is shown to decrease with deeper canyons and with the addition of canyon foliage. For the isothermal conditions modelled here the $L^{*}$ of the whole canyon system (and of the whole neighbourhood—canyon + roofs) does not vary significantly with canyon $H/W$ and tree foliage in the canyon.

Several future model improvements may be weighed against the additional computational costs of their introduction. While the model permits high resolution in the vertical, it does not do so in the horizontal. If, for example, urban trees are usually located towards the edges of canyons, it may be productive to introduce some additional discretization in the horizontal, or possibly extend the model into three-dimensions. Another improvement to be weighed against additional computation costs is the inclusion of additional wavebands, for example PAR and NIR (and ultra-violet) in the shortwave spectrum and analogous divisions in the longwave; this capability already exists in the model, however, this refinement may be less useful unless sufficient information is available on material and foliage radiative parameters in specific wavebands. Currently sky radiance is isotropic in both shortwave and longwave bands; the introduction of more realistic distributions where possible (e.g., for clear-sky longwave) is perhaps the simplest and most computationally feasible development. Finally, and perhaps most obviously, the model requires testing against ray tracing methods in real three-dimensional urban configurations, and/or full-scale measurements of radiative exchange in treed canyons, once datasets become available.

The new ‘treed’ urban radiation model is intended for use at the local scale, and model fields represent neighbourhood averages. It is designed to simulate any combination of shortwave and longwave radiation bands, and to be portable to any urban surface model based on the urban canyon. The model is sufficiently flexible that it may be extended to forest and forest-clearing scenarios in addition to urban cases with (and without) trees. In an operational mode, the current radiation exchange model will require coupling with the dynamics, energy balance, hydrology and physiology of urban trees in addition to the energy balance of the built surfaces. This coupled, next-generation multi-layer model with integrated trees will benefit local-scale and mesoscale modelling of vegetated urban neighbourhoods. Such a new model will permit advanced assessment of impacts of trees on the urban climate, air quality, human comfort and building energy loads at several scales.

Appendix: Model Sensitivity to Computational Parameters

The model accounts for radiation absorption, scattering and emission by foliage in the canyon column and above rooftops in the building column. For simplicity, parameter sensitivity tests are shown for geometries with tree foliage in the canyon column only. Canyons (i.e., walls and vegetation) in “Direct solar irradiance: number of rays and ray step size and Inter-patch view factors: number of rays” sections in Appendix are resolved with 10 layers unless otherwise stated, as this is a typical number of layers needed to resolve many urban geometries. For a given set of computational parameters, model accuracy is slightly higher (lower) for lower (higher) wall/foliage resolution (not shown). The importance of sufficient resolution for walls and foliage layers is elucidated in the “Building wall and foliage-layer resolution” section in this Appendix, and this has implications for the vertical resolution of multi-layer urban canopy models generally, and in terms of the compromises inherent in the use of single-layer models.

1.1 Direct Solar Irradiance: Number of Rays and Ray Step Size

The trade-off between accuracy and computational expense as a function of number of rays (ni) and input ray step size $(\Delta s_\mathrm{in})$ in the direct shortwave ray tracing module (Sect. 3.2) is explored. A key point is that actual model ray step size depends on layer thickness $\Delta z$ in addition to $\Delta s_\mathrm{in}$ (Eq. 1), whereas the number of rays does not. A canyon with one building height and tree foliage in the canyon column (neighbourhood LAI $=$ 0.50), evenly distributed from the ground to the rooftop level, is chosen. For each $ni, \Delta s_\mathrm{in}$ pair the model is run for 25 scenarios in order to sample a range of urban geometries and solar zenith angles. These 25 scenarios are composed of every combination of the following: five canyon height-to-width $(H/W)$ ratios: 0.25, 0.5, 1.0, 2.0, and 4.0, all having street $(\Delta x_\mathrm{c})$ and building $(\Delta x_\mathrm{b})$ widths of 10 m; and five solar zenith angles: $5^{\circ }, 25^{\circ }, 45^{\circ }, 65^{\circ }$, and $85^{\circ }$. Solar azimuth is perpendicular to the canyon in all cases. The walls and canyon foliage are resolved with 10 layers. Hence, as $H/W$ varies from 0.25 to 4.0, vertical layer thickness $\Delta z$ varies from 0.25 to 4.0 m. All 25 scenarios are also simulated with a suite of “highly accurate” (HA) simulations (ni $=$ 20,000 and $\Delta s_\mathrm{in} = 0.0005$), which serve as the standards of comparison.

Differences from the HA simulations are first examined in aggregate. Fig. 11 displays the maximum over all scenarios of the summed patch-level absolute difference of solar receipt; that is, the total difference relative to incident radiation where positive and negative patch-level differences do not cancel. For ray step sizes less than 0.1 it is clear that the number of rays is of primary importance, suggesting that below a threshold of $\Delta s_\mathrm{in} {\approx } 0.1$ the relation between actual ray step size and layer thickness (Eq. 1) gives sufficient accuracy. There is only further improvement with smaller step size for large numbers of rays ($ni > 1000$).

Fig. 11

Maximum over all scenarios of the summed patch-level differences of direct solar irradiance receipt relative to the highly accurate simulation, as a function of number of rays (ni) and input ray step size $(\Delta s_\mathrm{in})$. Maximum difference is computed over a suite of simulations with canyon resolution of 10 and varying canyon geometry and solar angle. The log of the maximum computation time over all scenarios relative to the highly accurate simulation is given by the dashed white lines (e.g., “$-2$” = 1 % of the computation time, “$-4$” = 0.01 % of the computation time)

The maximum computational time taken by the direct solar ray-tracing scheme across all scenarios, relative to the HA simulations for each ${ni}-\Delta s_\mathrm{in}$ combination, is overlaid on Fig. 11. Maximum overall difference from the HA simulation is ${\approx }1\,\%$ for ni = 500 and $\Delta s_\mathrm{in} = 0.1$, while the maximum computation time across all scenarios at this accuracy is 0.03 % of the HA simulation. At the level of the individual patch (e.g., individual roof levels, foliage layers, etc), a maximum difference at all patches of ${\approx }1\,\%$ is achieved with $\Delta s_\mathrm{in} = 0.1$ and an increase in the number of rays to 1000 (not shown). Using 2000 rays with ray step 0.01 reduces maximum overall difference to ${\approx }0.3\,\%$, but this comes with a 20-fold increase in computation time. Conversely, decreasing ni to ${\approx }200$ with $\Delta s_\mathrm{in} = 0.25$ keeps both mean relative patch-level (not shown) and maximum overall differences (Fig. 11) below 5 % and reduces the computational load to about $10^{-6 }$ % of the HA simulation, or 10 % of the ${ni} = 1000, \Delta s_\mathrm{in} = 0.1$ simulations in the median.

Overall, small patch-level and overall error (i.e., $< 1\,\%$) are achieved with reasonable computation time for 1000 rays with an input ray step size of 0.1; in fact, the product of the maximum overall difference and the maximum computation time is minimized for ${ni} \approx 1000, \Delta s_\mathrm{in} \approx 0.1$. On an Intel CPU, T7200 @ 2.00 GHz, the median and maximum computation time for this accuracy over the 25 scenarios is 0.06 and 0.48 s, respectively. For ni = 200 with $\Delta s_\mathrm{in} = 0.25$ the median and maximum computation times drop to 0.01 s and 0.05 s, respectively. To achieve accuracy significantly better than 1 % difference, both ni and $\Delta s_\mathrm{in}$ must be increased several-fold with resulting computational increases. However, to reduce the computational expense, the solar scheme need only be run every few timesteps when coupled with a mesoscale model.

1.2 Inter-patch View Factors: Number of Rays

View factors between patches are computed only once at the beginning of an urban canopy or mesoscale model simulation, and therefore higher accuracy trumps lower computational time in terms of parameter selection for Monte Carlo ray tracing (MCRT; Sect. 3.3). Tests show the model conserves energy—the sum of view factors from each patch to all other patches equals 1.0 to a high degree of precision in all cases. The model also reproduces view factor reciprocity between patches (Sparrow and Cess 1978). That is, for all pairs of patches (e.g., surface element $P$ at level/layer iz, surface element $Q$ at jz) the following relation is satisfied to a sufficient degree of precision (${\approx }0.001$ view factor difference or less), provided parameter recommendations are followed, viz.

$$\begin{aligned} \psi _{\textit{PQ}} (iz,jz)\,A_{P} (iz)=\psi _{QP} (jz,iz) A_{Q} (jz). \end{aligned}$$

(26)

Subsequently, modelled view factors between patches are evaluated against ‘exact’ values for non-vegetated canyons. View factors are compared to those given by the analytical formulae of Sparrow and Cess (1978) for an $H/W = 1.0$ canyon with one wall patch (“$H/W = 1.0$” in Fig. 12), and to the results of the highly accurate (HA) numerical radiation model TUF-2D (Krayenhoff and Voogt 2007) for an $H/W = 2.0$ canyon with 10 wall patches (“$H/W = 2.0$” in Fig. 12). An input ray step size ($\Delta s_\mathrm{in})$ of 0.01 is chosen, and several values of nk, the number of rays emitted from each patch during the determination of view factors by MCRT, are investigated. The randomness in the selection of ray start location and direction during view factor computation (Sect. 3.3.1) means that ensemble values better approximate average model performance. It is found that the running mean of all view factors converges to within 2 % relative error for ensembles of 20 or larger. Hence, maximum error over all view factors (road-wall, wall-road, wall-wall) in all 20 ensemble members is assumed to give the error a reasonable upper bound for each nk value. Maximum view factor error for the H/W = 1.0 and H/W = 2.0 canyons in Fig. 12 is below 0.01 for all patches for nk $\ge$10,000 for both canyons, and errors appear to drop more slowly with further increases in nk.

Fig. 12

Maximum patch-level view factor difference from the highly accurate (HA) simulation across all patches and all configurations, as a function of number of rays per patch, nk (symbols). The maximum patch difference over an ensemble of 20 simulations is used for each configuration. Also, the maximum patch-level view factor error as a function of number of rays per patch for two configurations (lines). The maximum is over an ensemble of 20 simulations for an $H/W = 1.0$ canyon with a vertical resolution of one patch and an $H/W = 2.0$ canyon with resolution 10 patches, both without foliage

In order to include foliage view factors in the evaluation, model outputs are compared to the ensemble means of a new suite of highly accurate simulations with nk = 50,000 and $\Delta s_\mathrm{in} = 0.01$. This is done for the same canyon LAI, canyon resolution and $H/W$ as for direct solar receipt (“Direct solar irradiance: number of rays and ray step size” section in Appendix). However, larger nk values are tested because rays now travel in all directions and therefore more rays are required for comparable accuracy, and furthermore computational time is a lower priority than for direct solar radiation (which must be computed throughout a mesoscale model run). Input ray step size is fixed at 0.01, because view factor error is found to be insensitive to further decreases of $\Delta s_{in}$. Ensembles of 20 simulations are performed for each scenario and nk value. The maximum ensemble difference from the highly accurate ensemble mean is then determined for each view factor (i.e. each pair of patches). Subsequently, the maximum of these ensemble maximum view factor differences is calculated, yielding a maximum over 11,000 view factor calculations for each data point in the “All” curve in Fig. 12 (i.e., 550 unique view factors multiplied by 20 ensemble members each). This represents an extremely strict test of the model’s ability to compute view factors.

The analysis is completed three times: with all possible view factors between the road, all wall patches and all foliage layers (“All” in Fig. 12); with only those view factors to and/or from foliage patches (“Foliage”), and with only road and wall view factors for an identical canyon without foliage (“Built”). Clearly, view factors between foliage and other elements do not result in maximum errors, and if anything, help to reduce maximum errors; however, recall that $2nk$ rays are fired from each vegetation layer (Sect. 3.3.1). This result may vary somewhat with the resolution and also with the vegetation foliage density. The relatively small input ray step size ($\Delta s_\mathrm{in} = 0.01$) likely also plays a role in the small error induced by foliage; as $\Delta s_\mathrm{in}$ increases, particularly beyond 0.1, errors in vegetation view factors can grow rapidly (not shown).

The tests in Fig. 12 generally indicate a marked drop in maximum view factor error/difference at nk $\approx 10,000$ with smaller decreases beyond that. Hence, nk $\approx 10,000$ with $\Delta s_\mathrm{in} = 0.01$ appears sufficient to achieve excellent accuracy, without excessive computational effort over a range of configurations; for some geometries smaller nk and larger $\Delta s_\mathrm{in}$ may also yield excellent results.

1.3 Building Wall and Foliage-Layer Resolution

The number of layers with which wall and foliage layers are represented becomes important when scattering and reflection are included. It was not as important for computation of view factors or direct solar radiation receipt, particularly in the case of vegetation because the Bouguer–Lambert–Beer law is independent of resolution for vertical uniform leaf area density profiles. That is, a constant density foliage layer will have approximately the same direct solar receipt and area-weighted view factors (i.e. Eq. 18) regardless of the number of layers with which is represented.

Wall resolution is limited to unity by definition for single-layer canopy models. Meanwhile, close attention is rarely paid to wall resolution during the application of multi-layer canopy models. With the addition of vegetation foliage it is critical that the impacts of vertical resolution on model accuracy are assessed. Two tests are performed here, both directed toward shortwave albedo. They assess the impacts of vertical resolution over a range of solar zenith angles for tree foliage only (e.g. a forest), and for a vegetation-free canyon with solar zenith angle chosen to illuminate only part of one wall.

The overall albedo for a continuous canopy of trees (neighbourhood-average LAI = 3.0 with equal foliage density in both model columns, i.e. $L_{DC}=L_{DB}$), with broadband leaf reflection and transmission coefficients of 0.25, demonstrates the importance of sufficient resolution, especially for higher solar zenith angles (Fig. 13). For the two lower solar zenith angles ($0^{\circ }$ and $30^{\circ }$) the albedo converges to within 0.01 of the correct albedo when foliage resolution is $\ge$2, and to within 1 % when foliage resolution $\ge$4. For the higher solar zenith angle $(60^{\circ })$ corresponding resolutions of 3 and 6 are required, respectively. Hence, higher solar zenith angles may require higher resolution; however, solar irradiance tends to be low at these angles and so errors will be less consequential. Clearly it is critical to have at least two layers; a minimum of 4 is recommended here and 6 yields excellent results for all zenith angles tested. Fewer layers may be necessary for layers with lower foliage density.

Fig. 13

Shortwave albedo $(\alpha )$ of a horizontally homogenous layer of foliage as a function of vertical resolution for three different solar zenith angles $(\theta )$. The foliage layer exists from 10 to 20 m with a leaf area density of $0.30\hbox { m}^{2}\hbox { m}^{-3}$ and no clumping $(\Omega = 1.0)$. Leaves absorb 50 % of intercepted radiation and reflect and transmit the remainder equally. Ground albedo is 0.25. Incident shortwave is assumed to be wholly direct beam

Wall resolution is an important consideration for multi-layer models. The effects of wall resolution on canyon albedo for a canyon with a height-to-width ratio $(H/W)$ of 2.0 and wall $(\alpha _\mathrm{W})$ and road $(\alpha _\mathrm{G})$ albedos of 0.25 are presented in Fig. 14. Three solar zenith angles are chosen such that only the upper half $(\theta = 45.0^{\circ })$, upper third ($\theta = 56.3^{\circ })$, or upper fifth $(\theta = 68.2^{\circ })$ of one wall is sunlit (sky-derived diffuse is neglected). One wall patch only (e.g., a single-layer model) results in errors of 0.025–0.052 (29–46 %) in canyon albedo relative to a high resolution simulation by TUF-2D (Krayenhoff and Voogt 2007), and is clearly insufficient to give good results. This is because the model cannot distinguish how much of the wall is sunlit; the same total flux of radiation spread equally over the entire wall (i.e., $\theta = 26.6^{\circ }$) would result in the same canyon albedo. Two, three, and four wall patches are required for absolute error in canyon albedo to drop below 0.01 for $\theta = 45.0^{\circ }, \theta = 56.3^{\circ }$ and $\theta = 68.2^{\circ }$, respectively. As a smaller portion of the wall is sunlit a greater wall resolution is required to contain the error in the canyon albedo; however, this is offset by the decrease in total shortwave irradiance entering the canyon at these higher solar zenith angles.

Fig. 14

Shortwave albedo of a $H/W = 2.0$ canyon as a function of the vertical resolution of the walls. Three solar zenith angles $(\theta )$ with azimuthal angle perpendicular to the canyon axis are modelled. Incident shortwave is assumed to be wholly direct beam. Wall and canyon floor albedos are 0.25

The other obvious feature in Fig. 14 is the oscillation with increasing resolution. This can be explained as follows: the sunlit-shaded boundary coincides with a wall patch boundary for resolutions that are multiples of 2, 3 and 5 for $\theta = 45.0^{\circ }, \theta = 56.3^{\circ }$ and $\theta = 68.2^{\circ }$, respectively, but falls somewhere in the middle of a wall layer in all other cases. Such is the nature of a discrete grid representing a continuous process. Despite the continued oscillation, relative differences from the ‘exact’ solution given by TUF-2D drop consistently below 1 % for a wall resolution of between 6 and 9 for the cases modelled here.

It is clear that resolution is a significant consideration for both wall and foliage layers. A minimum of two layers appears to avoid the very worst of the errors, and further increases in resolution yield declining benefits. Nevertheless, a minimum of four layers for both foliage and walls is recommended, with higher resolutions being recommended in particular for canyons with higher $H/W$ and foliage layers with greater LAI. A previous study encounters similar tradeoffs and recommends similar minimums for urban facet resolution (Krayenhoff and Voogt 2007).

1.4 Computational Parameter Recommendations

Computational parameter recommendations to achieve sufficient accuracy while minimizing computation time are summarized here based on tests performed in “Direct solar irradiance: number of rays and ray step size, Inter-patch view factors: number of rays, and Building wall and foliage-layer resolution” sections in this Appendix. To keep patch (whole canyon) errors below 1 % it is recommended that the solar radiation model have a minimum of 500 (1000) rays and a maximum input ray step size of 0.1, or 10 % of the smallest patch size (e.g., wall patch length). View factor computation, which occurs only once for a given urban configuration, requires a minimum of 10,000 rays and a maximum ray step size of 1 % of the smallest patch size to ensure maximum view factor errors between individual patches are ${\approx }0.01$ or less. Based on the scenarios tested here a minimum resolution of walls and vegetation layers of 4 is recommended; lower (higher) resolution may be appropriate for lower (higher) foliage density and/or canyon $H/W$ than is used here.