Large-Scale Structures over a Single Street Canyon Immersed in an Urban-Type Boundary Layer

Abstract

An analysis of the dynamics of the flow over a street canyon immersed in an atmospheric boundary layer is presented, using particle image velocimetry measurements in a wind tunnel. Care was taken to generate a 1:200 model scale urban type boundary layer that is correctly scaled to the size of the canyon buildings. Using proper orthogonal decomposition (POD) of the velocity field and conditional averaging techniques, it is first shown that the flow above the opening of the canyon consists of a shear layer separating from the upstream obstacle, animated by a coherent flapping motion and generating large-scale vortical structures. These structures are alternately injected into the canyon or shed off the obstacle into the outer flow. It is shown that unsteady fluid exchanges between the canyon and the outer flow are mainly driven by the shear layer. Finally, using POD, the non-linear interaction between the large-scale structures of the oncoming atmospheric boundary layer and the flow over the canyon is demonstrated.

1 Introduction

Understanding street ventilation is of great importance when dealing with air quality issues. Even if simple from a geometrical point of view, the street-canyon model reproduces the main features of most common street configurations. Of particular interest is the case for which the upstream flow is perpendicular to the street axis, the ventilation being mainly driven by the vertical exchanges between the canyon and the flow above.

This configuration has been well-addressed by past studies and the resulting flow regimes have been classified by Oke (1988) as a function of the width to height ratio. The steady organization of the flow within the canyon was investigated first and shown to comprise a single vortex in the case of a square-section canyon (Kovar-Panskus et al. 2002; Kastner-Klein et al. 2004) or a combination of counter-rotating primary recirculations in the case of narrower canyons (Sini et al. 1996; Liu et al. 2004). Several studies have focused on the unsteady dynamics of the flow within and above urban canopies and have shown that, in the case of a street canyon, the instantaneous structure of the flow inside the canopy is far more complex than that of the mean flow (Louka et al. 2000; Michioka et al. 2010). Similar observations have been made in the case of atmospheric flows developing over a regular array of cubical roughness elements. For instance, numerical simulations such as the large-eddy simulation of Kanda (2006) or the direct numerical simulations performed by Coceal et al. (2007b) highlighted the complexity of both the canopy flow and its interactions with the boundary layer that develops above. For cube-array canopies, Takimoto et al. (2011) and Inagaki et al. (2012) have identified two types of coherent events, referred to as flushing and cavity events by these authors, which they found correlated with coherent structures corresponding to large-scale high-speed and low-speed regions in the boundary layer. The large scales present in the logarithmic region of the boundary-layer flow over a smooth wall (Mathis et al. 2009) and in atmospheric flows generally (Drobinski et al. 2004; Inagaki and Kanda 2008) were, indeed, found to interact with the near-surface small-scale structures, favouring the existence of a top-down mechanism.

Michioka et al. (2010) and Salizzoni et al. (2011) investigated the influence of the structure of the atmospheric boundary layer on the turbulent transfers to the canyon. Whereas Michioka et al. (2010) found that pollutant removal from the street is not affected by the large-scale coherent structures that develop above the canyon, being mainly driven by the small-scale structures generated close to the top of the roofs, Salizzoni et al. (2011) showed that the statistics of the turbulent flow in the canyon depend on the characteristics of the oncoming boundary layer. They concluded that turbulent transfers were due to the coupling between the shear layer developing above the canyon and the upstream flow. As shown by Kastner-Klein et al. (2004), and more recently by Kellnerová et al. (2012), the characteristics and the dynamics of the canyon flow are also affected by the roof geometry. Similar conclusions have been drawn from the study of the dynamics of the flow inside and at the top of two-dimensional cavities that have been shown to be strongly influenced by the level of upstream turbulence (Chang et al. 2006; Haigermoser et al. 2008; Kang and Sung 2009). In particular, the ratio between the depth of the cavity and the momentum thickness $\theta$ of the oncoming boundary layer has been found to be a key parameter in the dynamics of the shear layer at the top of the cavity (Kang and Sung 2009). Nevertheless, the computation of $\theta$ requires knowledge of the complete mean velocity profile within and above the canopy, which can be difficult from an experimental point of view.

Studies from the literature have, thus, identified two primary mechanisms that affect street-canyon flows: the shear-layer formation at roof level, the dynamics of which is expected to depend strongly on the nature and the location of its separation point on the upstream canyon building, and the interaction with the oncoming boundary layer. It must be noted here that several studies investigated configurations in which the flow upstream of the canyon has a skimming flow regime combined with the use of upstream roughness made of two-dimensional blocks (Liu et al. 2004; Michioka et al. 2010; Salizzoni et al. 2011; Kellnerová et al. 2012) or configurations in which the canyon is modelled as a two-dimensional cavity cut into the ground (Sini et al. 1996; Kovar-Panskus et al. 2002). They, thus, favoured a certain type of flow regime that promotes the development of thin shear layers above the canyon and two-dimensionality in the oncoming flow that may not be representative of realistic atmospheric flows.

The goal of the present study is, first, to analyze the dynamics of the shear layer that develops above the street-canyon opening and, second, to investigate its relationship with the coherent structures existing in the boundary layer. Particle image velocimetry (PIV) is employed to perform velocity measurements inside and above the street canyon. The oncoming flow is developed using turbulence generators and an array of cubes, in such a manner that it presents the characteristics (in terms of mean velocity profile, energy content, integral length scales and geometric scale ratio) of a properly scaled atmospheric boundary layer developing over an urban terrain. Proper orthogonal decomposition (POD) is used to extract the coherent structures of the flow at and above the roof level and to analyze their dynamics.

2 Experimental Details

In this section, a description of the experimental apparatus and procedures and details of the generated urban boundary layer are provided. In the following, $x,\,y$ and $z$ denote the longitudinal, spanwise and vertical directions, respectively (Fig. 1), and $u,\,v,\,w$ the longitudinal, spanwise and vertical velocity components, respectively. Using the Reynolds decomposition, each instantaneous quantity $u$ can be decomposed as $u=\overline{u}+u^{\prime }$ where $\overline{u}$ denotes the temporal average of $u$ and $u^{\prime }$ its fluctuating part. Multi-component vectors are noted with bold characters (i.e. $\mathbf u =(u,v,w)$).

Fig. 1

Experimental set-up (top elevation view, bottom plan view)

2.1 Experimental Set-up

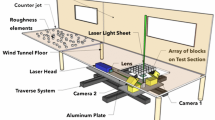
The experiments were conducted in the boundary-layer wind tunnel of the LHEEA Laboratory (Nantes, France), which has a working section of dimensions 24 $\times$ 2$\times$ 2 ${{\text{ m}}^3}$. A 1:200 scale simulation of a suburban-type atmospheric boundary layer was achieved at the test model location by using three vertical, tapered spires over the entire height of the inlet of the working section, a 300-mm high solid fence across the working section located 1.5 m downstream of the inlet, followed by an 18.5-m fetch of staggered cube roughness elements with a plan area density of 6.25 %. The cube height was $h=0.1$ m, while the plan area density of the roughness elements corresponds to a $k$-type rough wall (Jimenez 2004). The boundary-layer mean velocity and turbulence profiles were measured using a crossed hot-wire anemometry system, with a freestream velocity, $U_e$, of 5.9 m s$^{-1}$. The characteristics of the generated boundary layer are described in detail in the following section. The canyon model consisted of two square-section rectangular blocks, placed perpendicular to the flow, whose height was $h$ and length $L/h=14$, with a spacing, representing the street width, of $W/h=1$ (Fig. 1).

Two-component PIV measurements were conducted in a vertical plane aligned with the main flow, in the centre of the canyon. Two sets of 2,000 velocity fields were recorded to enable the computation of the main flow statistics and investigate its large-scale organization in and above the canyon (Fig. 1). The first set spanned the width of the canyon, over a height of 1.6$h$. A 1,344$\times$1,024 pixel 12-bit CCD camera equipped with a 60-mm objective lens was employed to investigate this region. The final spatial resolution of the vector field was 2 mm (0.02$h$), and the temporal sampling frequency used in this experiment was 1 Hz. The second set covered the region $-1.5 \le x/h \le 0.5$ and $1 \le z/h \le 3$ above the upstream obstacle and the canyon. A 2,000$\times$2,000 pixel 12-bit camera equipped with a 105-mm objective lens was employed. This set-up gave a final spatial resolution of 1.55 mm (0.015$h$). The temporal sampling frequency used in this experiment was 7 Hz. A 50 mJ Nd-Yag laser was used to illuminate one or the other region. The flow was seeded with glycol/water droplets (typical size 1 $\upmu$m) using a fog generator. The synchronization between the laser and the camera and the calculation of the PIV velocity vector fields were performed using the DANTEC FlowManager software.

The FFT-based two-component PIV algorithm with sub-pixel refinement was employed. Iterative cross-correlation analysis was performed with an initial window size of 64 $\times$ 64 pixels and with 32 $\times$ 32 final interrogation windows. An analysis window overlap of 50 % was used. Spurious vectors were detected by an automatic validation procedure whereby the signal-to-noise ratio of the correlation peak had to exceed a minimum value and the vector amplitude had to be within a certain range of the local median to be considered as valid. Once spurious vectors had been detected, they were replaced by vectors resulting from a linear interpolation in each direction from the surrounding 3 $\times$ 3 set of vectors.

It should be noted here that, on the one hand, the resultant sampling frequency, which ensures that the acquired velocity samples present a low level of correlation with each other, combined with the relatively large number of samples, provides a good statistical convergence of the second-order statistics (relative error of the velocity variances below 4.5 %). On the other hand, the resultant acquisition frequency, imposed by the fact that no time-resolved PIV system was available, is too low compared to the typical frequencies of the present high Reynolds number turbulent flow. This limitation was overcome here by the use of statistical methods such as conditional averaging and POD analysis that provide information on the spatio-temporal dynamics of the flow despite the absence of time-resolved measurements (see Sects. 3, 4). An estimation of the accuracy of the present measurements has been obtained by comparing the statistics of the velocity measured in the region where the two areas of PIV measurement overlap. In this manner, errors due to the limited statistical convergence, the presence of noise in the PIV measurements and the uncertainty in setting up the different experiments were taken into account. The relative error varies with the location considered but remains below 5 % for the mean longitudinal velocity component and 10 % for the Reynolds stresses. Velocity gradients were computed by using a second-order centred difference scheme that is the best compromise between noise amplification and accuracy when dealing with PIV measurements (Foucaut and Stanislas 2002).

2.2 Approach Flow Boundary Layer

Details of the set-up and the characteristics of the generated boundary-layer flow, together with a discussion on the importance of properly modelling the approaching flow in relation to the geometry of the canyon, can be found in Savory et al. (2013). In the present study, efforts were devoted to the simulation of a boundary layer with aerodynamic roughness length $z_0$ and displacement height $d$ characteristic of suburban terrain. These parameters are used to describe the evolution of the mean longitudinal velocity profile as:

$$\begin{aligned} \frac{\overline{u}}{u_{*}} = \frac{1}{\kappa } \text{ ln} \left( \frac{z-d}{z_0}\right), \end{aligned}$$

(1)

where $u_{*}$ is the friction velocity derived from the wall-shear stress, $z$ is the distance from the wall and $\kappa =0.4$ is the von Kármán constant. The 99 % thickness of the obtained boundary layer was $\delta = 1.1$ m. The measured profile of the mean streamwise velocity component clearly exhibits a logarithmic region that extends over almost $2h$ (Fig. 2, left). The value of $u_{*}$ was derived from the constant shear-stress region exhibited by the flow (Fig. 2, right). These two profiles were used to find the above defined roughness parameters that are summarized in Table 1. The values of $\delta /h$ and of the non-dimensional obstacle height $h^+ = h u_{*}/\nu$ indicate that the effect of the roughness elements will extend far from the wall, ensuring the flow is aerodynamically fully rough, consistent with the behaviour of atmospheric flows (Jimenez 2004). This characteristic is also confirmed by the shape of the profiles and the maximum value of the variance of the streamwise and wall-normal fluctuations (Fig. 2, right). Values of $d/h$ and $z_0/h$ also correspond to flow developing over an urban terrain with low building density (Grimmond and Oke 1999).

Table 1 Characteristics of the upstream boundary layer

Fig. 2

Profiles of the mean streamwise velocity component normalized by $u_{*}$ (left) and Reynolds stresses normalized by $u_{*}^2$ (right) measured in the upstream boundary layer

3 Shear-Layer Dynamics

In this section, both the statistical characteristics and the large-scale dynamics of the flow over and within the canyon are investigated, based on the PIV database.

3.1 One-Point Statistics

Iso-contours of the mean velocity (Fig. 3a, b) are consistent with the presence of a vortex core inside the canyon, the diameter of which is of the order of the height and width of the cavity. These velocity distributions also show the presence of a strong shear layer originating from the top of the upstream obstacle, corresponding to the location of the maximum vertical gradient of the mean longitudinal velocity component. The two-dimensional turbulent kinetic energy $\overline{q}$, evaluated from the two in-plane components and defined as $\overline{q} = 0.5 ( \overline{{u^\prime }^2} + \overline{{w^\prime }^2})$, is also maximum in this region and corresponds to a region of high shear $-\overline{u^\prime w^\prime }$ (Fig. 3c, d). Separation of the upstream flow from the sharp corner of the upstream building generates a strong shear layer, similar to that existing in flow over a $k$-type rod-roughened wall (Cardwell et al. 2011) in which the flow can re-attach between two rods. However, here, the presence of the downstream obstacle reduces the penetration of the flow within the canyon, corresponding more to a skimming flow regime or flow over $d$-type roughness (Jimenez 2004). Moreover, inspection of instantaneous velocity fields showed that this shear layer presents a vertical flapping motion that seems to induce penetrations or ejections of fluid within the canyon combined with large-scale vortices shed from the upstream obstacle that are convected downstream in the boundary layer.

Fig. 3

One-point statistics of the flow obtained from the combination of the two PIV measurement regions. a $\overline{u}/U_e$, b $\overline{w}/U_e$, c $\overline{q}/{U_e}^2$, d $- \overline{u^\prime w^\prime }/{U_e}^2$

3.2 Two-Point Statistics

Investigation of the flow exchange between the canyon and the flow above is studied here via the computation of the two-point coefficient correlation of both the streamwise and the vertical velocity components. These quantities are defined as:

$$\begin{aligned} R_{uu}(x_{ref},z_{ref},x,z) = \frac{\overline{u^\prime (x_{ref},z_{ref})u^\prime (x,z)}}{\sqrt{\overline{{u^\prime }^2(x_{ref},z_{ref})}} \sqrt{\overline{{u^\prime }^2(x,z)}} } \end{aligned}$$

(2)

where $(x_{ref},z_{ref})$ are the coordinates of the fixed point. Correlations of the vertical component $w$ are computed in a similar way. Computation of the correlations within the canyon (not shown here) shows that this region seems to be decoupled from the shear layer and the flow above the shear layer, in agreement with the skimming flow regime. Figure 4 shows an example of correlation maps obtained in the shear-layer region ($z_{ref}/h=1.2$), on the centreline of the canyon. Both $R_{uu}$ and $R_{ww}$ are mainly positive but also exhibit negative levels inside the canyon (black solid lines on Fig. 4 correspond to a correlation level of zero), which is consistent with the clockwise recirculation motion in this region. In addition, $R_{ww}$ shows negative levels above the upstream obstacle, which can be interpreted as being the footprint of large-scale vortical structures developing inside the shear layer emanating from the upstream corner of the upstream building. The origin of the shear layer is the main difference existing between cavity flow configurations where the shear layer starts from the downstream corner (Kang and Sung 2009), and the present configuration. This is confirmed by the investigation of the correlations near the top of the obstacles (not shown here), which indicates that, contrary to many canonical cavity flows (Kang and Sung 2009), large-scale vertical motion of fluid exists in this region rather than well-organized vortex shedding. Correlations computed above the shear layer have a shape and length scales in agreement with those existing in flows developing above urban-like roughness (Coceal et al. 2007b). These characteristics are not addressed in the present study, rather the focus here is on the organization of the shear-layer region.

Fig. 4

Two-point correlation maps obtained for a reference located at $x_{ref}/h = 0,\,z_{ref}/h = 1.2$. Left $R_{uu}(x_{ref},z_{ref},x,z)$, right $R_{ww}(x_{ref},z_{ref},x,z)$. Black solid line zero-contour level, white solid line level used for ellipse fitting

From the above analysis, it appears that the correlation maps have two distinct features: their shape and their inclination. $R_{uu}$ is more elongated in the streamwise direction and exhibits a preferential inclination; $R_{ww}$ tends to be more isotropic, with shorter length scales. To quantify the variation of these characteristics with the location within the flow, ellipses were fitted to a given contour extracted from $R_{uu}$ and $R_{ww}$ calculated for different values of $x_{ref}$ and $z_{ref}$. Given the limited extent of the PIV field of view, rather high values of correlation contours were used here, in comparison to the more common value of 0.4 (Coceal et al. 2007b). Even if this leads to an underestimation in the typical length scales of the flow, the shapes and inclinations are well estimated and allow for a qualitative analysis of the flow structure. Figure 5 shows the result of this analysis, where the ellipses are drawn half of their actual size for clarity. The dashed lines correspond to the limits of the shear layers developing from the upstream obstacle, which were identified from the local maxima of the $\overline{q}$ gradient, $\partial \overline{q}/\partial z$ (Cardwell et al. 2011). In addition to the conclusions that were drawn above, it is noticeable that, in the shear-layer region, the inclination and the length scales of $R_{uu}$, respectively, decrease and increase with the longitudinal distance from the upstream edge of the upstream obstacle, following the growth of the shear layer. Within the shear layer, at a given streamwise location, the length scales are constant with height. Above the shear layer, the characteristic length scales of the correlation appear to progressively increase with height, in accordance with the evolution of length scales in a boundary layer over large roughness elements (Coceal et al. 2007a). This confirms that, on average, three distinct regions exist (with increasing height: inside the canyon, in the shear layer and in the boundary layer developing above), delimited by the shear-layer boundaries emanating from the edges of the upstream building and characterized by different length scales and orientation of the structures.

Fig. 5

Shape of the two-point correlation obtained for different locations of the reference point. Left $R_{uu}$, right $R_{ww}$. For clarity the ellipses are drawn half of their actual size. Dashed line shear-layer boundaries

3.3 Organization of Coherent Structures

In order to investigate the flow transfer processes across the canyon opening that may be induced by the large-scale motion existing in the flapping shear layer, the dynamics of the vertical component $w$ at $z/h = 1$ is studied through the use of the proper orthogonal decomposition (POD). Lumley (1967) proposed the use of POD to identify the coherent structures embedded in turbulent flows as the structure $\mathbf{\phi } (\mathbf{X})$ with the largest mean-square projection onto the velocity field $\mathbf{u} (\mathbf{X},t)$, e.g. with optimal energy content. This maximization process leads to the integral eigenvalue problem

$$\begin{aligned} \int \limits _{\mathcal{D}} R_{ij}(\mathbf{X},\mathbf{X^\prime })\mathbf{\phi }_j^{n}(\mathbf{X^\prime })d\mathbf{X^\prime } = \lambda ^{n}\mathbf{\phi }_i^{n}(\mathbf{X}), \end{aligned}$$

(3)

where the kernel is the two-point velocity correlation tensor over the domain $\mathcal{D}$

$$\begin{aligned} R_{ij}(\mathbf{X},\mathbf{X^\prime }) = \langle \mathbf{u}_i(\mathbf{X},t) \mathbf{u}_j(\mathbf{X^\prime },t)\rangle . \end{aligned}$$

(4)

Here, $\langle \rangle$ is the ensemble average operator, equivalent to the temporal average $\overline{()}$ used in the present study, and the eigenvalue $\lambda ^{n}$ represents the turbulent energy contained in the $n{\text{ th}}$ mode. The velocity field can then be expressed as a linear combination of its POD eigenfunctions $\mathbf{\phi }_i^{n}(\mathbf{X})$:

$$\begin{aligned} \mathbf{u}_i(\mathbf{X},t) = \sum _{n=1}^{\infty }a_{n}(t) \mathbf{\phi }_i^{n}(\mathbf{X}). \end{aligned}$$

(5)

The projection coefficients $a_{n}(t)$ are given by

$$\begin{aligned} a_{n}(t)= \sum _{i=1}^{3} \int \limits _\mathcal{D} \mathbf{u}_i(\mathbf{X},t) \mathbf{\phi }_i^{n}(\mathbf{X}) d\mathbf{X} \end{aligned}$$

(6)

and are uncorrelated

$$\begin{aligned} \langle a_{n}(t)~a_{m}(t) \rangle = \lambda ^{n} \delta _n^m. \end{aligned}$$

(7)

In the present work, following Kang and Sung (2009) who used the same approach to study canonical cavity flows, a one-dimensional POD analysis based on the correlation tensor of $w$ between two points along the line $z=h$ was performed to decompose the vertical velocity component into a set of spatial and temporal eigenmodes $\phi _w^n(x)$ and $a_n(t)$, respectively, such that:

$$\begin{aligned} w(x,t) = \sum _{n=1}^N a_n(t)\phi _w^n(x). \end{aligned}$$

(8)

The spatial modes $\phi _w^n(x)$ form an orthonormal basis of the flow and the temporal coefficients $a_n(t)$ represent the dynamics of the corresponding modes. The eigenvalue $\lambda _w^n=\overline{a_n(t) a_n(t)}$ represents the energy contribution of the $n^{th}$ mode to the total turbulent energy of the vertical velocity component $w$.

The energy content of the first two POD modes, given by the first two eigenvalues (Fig. 6), is found to represent more than 60 % of the total turbulent energy associated with the vertical fluctuations. The spatial shape of these two modes (Fig. 7, left) corresponds to strong penetration or ejection motions through the opening of the canyon. Indeed, given its shape, the first POD mode $\phi _w^1(x)$ will contribute to a global penetration or ejection of fluid throughout the canyon when its temporal coefficient $a_1(t)$ is non-zero. The fact that the fluid movements throughout the canyon are rarely symmetric about the vertical axis $x/h=0$ is accounted for by the non-symmetric nature of the second mode $\phi _w^2(x)$. Velocity fields corresponding to the instants when these two modes contribute the most to the flow energy are likely to resemble the phase-averaged velocity fields shown in Fig. 8. These results are consistent with the analysis of Kang and Sung (2009) who found that the first two POD modes of the vertical velocity $w$ across a cavity of height to width ratio of 1, with a thick turbulent oncoming boundary layer, have a similar shape to those shown here and contain almost 70 % of the kinetic energy associated with the $w$ component. It should be noted here that no direct comparison with the results obtained by Kellnerová et al. (2012) can be made as they did not use POD to study only the vertical velocity $w$ across the canyon but applied it to the entire PIV field of view. Analysis of the higher order modes (not shown here) did not give any information on the possible existence of organized vortex shedding (e.g. very similar spatial modes with a phase difference of a quarter of the pseudo period). These two most energetic modes are also found to contain most of the energy during 70 % of the time (e.g. the maximum mode amplitude is either $a_1(t)$ or $a_2(t)$, 70 % of the time), meaning that the dynamics of the flow is mostly driven by these two modes.

Fig. 6

Energy contribution of POD eigenvalues $\lambda _w^n$ of the corresponding one-dimensionnal POD modes $\phi _w^n(x)$ computed along the line $z=h$

Fig. 7

First two POD modes $\phi _w^1(x)$ and $\phi _w^2(x)$ (left) and phase portrait of POD coefficients $a_1(t)$ and $a_2(t)$ (right)

Fig. 8

Examples of phase-averaged velocity fields (one in every three vectors shown) corresponding to, a and b, penetration of fluid and, c and d, ejection of fluid. The mean velocity field has been subtracted for more clarity. Contours: level of phase-averaged swirling strength $\lambda _{ci}$; white corresponds to zero level, black to high values of $\lambda _{ci}$

The phase portrait of the time-varying coefficients $a_1(t)$ and $a_2(t)$ reveals a complex dynamics, the coefficients taking a wide range of negative and positive values. When selecting samples for which either $a_1(t)$ or $a_2(t)$ is maximum, the phase portrait becomes clearer, as values are then more or less located around a circle (Fig. 7, right). This means that a strong dynamical relationship exists between these two modes and confirms the temporal coherence of the penetration and ejection motions directly observed from the instantaneous velocity fields. This particular distribution also allows the computation of a phase angle between $a_1(t)$ and $a_2(t)$ defined by

$$\begin{aligned} \alpha _{a_1-a_2} = {\arctan }\left(\sqrt{\frac{\lambda _w^1}{\lambda _w^2}} \frac{a_2(t)}{a_1(t)}\right). \end{aligned}$$

(9)

Phase-averaged velocity fields are then computed by averaging instantaneous velocity fields that correspond to the instantaneous angle $\alpha _{a_1-a_2}$ falling into a given range. The whole range of possible angles $\left[ 0,2\pi \right]$ was divided into 18 sub-intervals. Analysis of the 18 phase-averaged velocity fields shows that a strong flapping of the flow exists above the canyon, which corresponds to penetration (Fig. 8a, b) and ejection (Fig. 8c, d) of fluid through the canyon opening. In order to investigate further the organization of the flow, vortical structures, identified by a positive value of the swirling strength $\lambda _{ci}$, are extracted from the instantaneous velocity fields and phase averaged. The swirling strength, computed from the imaginary part of the complex conjugate eigenvalues of the local velocity gradient tensor, has been shown to be frame-independent and able to discriminate compact vortical cores from regions of intense shear (Chakraborty et al. 2005). The phase-averaged $\lambda _{ci}$ distributions show that the vertical fluid motions throughout the canyon opening are accompanied by vortical structures (Fig. 8). This phase averaging procedure shows that the shear layer is animated by a strong coherent flapping motion associated with the shedding of vortices. However, the need to select the events for which either $a_1(t)$ or $a_2(t)$ is maximum to obtain a clear dynamical cycle highlights the strong intermittency of the shear layer above the canyon. The flow associated with the shear layer is, thus, not as regular as that corresponding to a more classical plane mixing layer. As suggested by the results of Kang and Sung (2009) in the case of a two-dimensional cavity, this absence of regular vortex shedding and the strong intermittent character can be attributed to the perturbation and the high level of turbulence induced by the upstream boundary layer.

Based on the occurrence of ejections (referred to as Q2 events defined by the occurrence of $u^{\prime }<0$ and $w^{\prime }>0$) or penetrations (i.e. Q4 defined as $u^{\prime }>0$ and $w^{\prime }<0$), the conditionally-averaged velocity field and swirling strength signed by the vorticity sign $\lambda _{ci}^s$ were computed from the PIV database measured above the canyon. This analysis was performed independently of that discussed above as the two PIV experiments were completely decorrelated. Q2 or Q4 events occurring in the shear-layer region, along the canyon centreline (Fig. 9, left and right, respectively), turn out to be strongly correlated to a clockwise rotating vortical motion ($\lambda _{ci}^s < 0$) existing in the shear layer above the top of the obstacles, in agreement with the previous POD analysis. The flapping motion of the shear layer is also clearly evidenced here. Figure 9, left, also suggests that the vortical structures associated with strong Q2 events in the shear layer are convected downstream and may participate in the generation of vortical structures populating the boundary layer.

Fig. 9

Conditional average of the signed swirling strength distribution $\lambda _{ci}^s$ based on (left) a Q2 event and (right) a Q4 event, occurring at $x/h=0,\,z/h=1.37$

When based on a Q2 or Q4 event occurring well above the shear layer, the conditionally-averaged swirling strength distribution is found to be almost independent of the nature of the conditional event, meaning that the dynamics of the flow just above the canyon is primarily driven by the dynamics of the shear layer separating from the upstream building.

4 Dynamical Link with the Approach Flow Boundary Layer

The results presented in the previous section, based on the analysis of the flow across the opening of the canyon, show that the dynamics of the flow is dominated by the presence of a strong shear layer that emanates from the upstream corner of the upstream building, flaps and sheds vortices inside and above the canyon, in agreement with previous work (Louka et al. 2000; Michioka et al. 2010; Zhang et al. 2011). Analysis of the phase portrait of the POD modes computed at the top of the canyon reveals a more complex dynamics than the regular vortex shedding occurring in the shear layer developing over an open cavity. The complexity of the phenomenon is partly due to the separation of the flow from the upstream building but also to the fact that the canyon is immersed in an atmospheric boundary layer that is appropriately scaled in terms of characteristic parameters (such as boundary-layer thickness to building-height ratio, roughness length, displacement height), energy content and integral length scales (Savory et al. 2013). Great care in modelling the approach flow has been taken to ensure that it will interact with the flow over and inside the canyon in a realistic manner.

This analysis, as well as studies of flow over urban canopies from the literature [see, for instance, Reynolds and Castro (2008), Salizzoni et al. (2011)], based on classical tools such as one- and two-point statistics of first order and second order or conditional analysis, do not reveal a clear influence of the oncoming boundary layer on the canyon flow, and tend to favour a decoupling between the canopy flow and the atmospheric boundary layer. However, recent studies dealing with boundary layers developing over smooth walls [e.g. Hutchins and Marusic (2007), Mathis et al. (2009), Hutchins et al. (2011)] or atmospheric flows (Drobinski et al. 2004; Inagaki and Kanda 2008; Inagaki et al. 2012) show that the large scales present in the logarithmic region of the boundary layer interact with the near-surface small-scale structures. Mathis et al. (2009) demonstrated, in the case of smooth-wall flows, that an amplitude modulation mechanism was responsible for this interaction, pointing out its non-linear character.

The above-mentioned studies are all based on the spectral analysis of the time history of velocity signals to separate large- from small-scales by filtering the signal in the frequency domain. In the present work (based on non-time-resolved PIV measurements), in the absence of such information, the suggested non-linear interaction between the large scales from the boundary-layer flow and the near-surface flow is investigated via the use of POD applied to the flow region above the canyon and the analysis of the contribution of POD modes to third-order statistics of the velocity. The results obtained are presented in the following section.

4.1 POD Analysis of the Flow Above the Canyon

The POD presented in Sect. 3.3 is applied here to $\mathbf u (x,z,t)$ the two-component, two-dimensional velocity fields measured above the canyon (the region where $-1.5 \le x/h \le 0.5$ and $1 \le z/h \le 3$). We recall here that bold characters denote multi-component vectors. The fluctuating velocity vector field $\mathbf{u }^{\prime }(x,z,t)=\mathbf{u }(x,z,t)-\overline{\mathbf{u }(x,z)}$ is, thus, decomposed into a set of temporal and spatial modes such that

$$\begin{aligned} \mathbf u ^{\prime }(x,z,t) = \sum _{n=1}^N b_n(t){\varvec{\varPhi }}^n(x,z). \end{aligned}$$

(10)

The spatial modes ${\varvec{\varPhi }}^n(x,z)$ form an orthonormal basis of the flow and the temporal coefficients $b_n(t)$ represent the dynamics of the corresponding modes. They have the following orthogonality property: $\overline{b_n(t) b_m(t)} = \lambda ^n \delta _n^m$, where $\lambda ^n$ is the eigenvalue of the $n^{th}$ mode and $\delta _n^m=1$ if $n=m$, zero otherwise.

In the present case, it can be seen that the rate of convergence of the POD decomposition in terms of energy content is very fast, with almost 80 % of the total kinetic energy being contained in the first 10 modes (Fig. 10 left). In particular the first POD mode ${\varvec{\varPhi }}^1(x,z)$ contains 46 % of the kinetic energy. Depending on the sign of the corresponding temporal coefficient $b_1(t)$, the vector field corresponding to this mode (Fig. 10 right) corresponds to the presence of a high-speed ($b_1(t)>0$) or a low-speed ($b_1(t)<0$) event in the flow near the building roofs ($z/h<1.5$) as well as in the boundary layer above ($z/h>1.5$). It must be noted here that, with the temporal evolution of this mode being entirely driven by the temporal POD coefficient $b_1(t)$, these two regions, located well above and closer to the roofs, are systematically in phase and highly correlated. Other POD modes (not shown here) exhibit the presence of more complex flow patterns including the presence of vortical structures of smaller scale with increasing mode order. Given its particular shape, attention will be focused here on the contribution of the first POD mode to the flow statistics and its dynamical relationship with the remaining modes.

Fig. 10

Energy contribution of POD eigenvalues $\lambda ^n$ (left) and (right) first POD mode ${\varvec{\varPhi }}^1(x,z)$ (one in every five vectors displayed)

In order to assess the large-scale character of the first POD mode, its contribution to the temporal correlation coefficient of the longitudinal velocity component well above the canyon (at $z/h=2.5$ and $x/h=0$) is computed. To this end, the fluctuating longitudinal velocity component $u^{\prime }(x,z,t)$ is decomposed into a large-scale part $u^{\prime }_L(x,z,t)=b_1(t){\varPhi }^1(x,z)$ represented by the contribution of the first POD mode to the velocity fields and a small-scale part ${u}^{\prime }_S(x,z,t)={u}^{\prime }(x,z,t)-{u}^{\prime }_L(x,z,t)$. Figure 11 shows the temporal correlation coefficient $R_{uu}^{PIV}(\tau ),\,R_{u_L u_L}^{PIV}(\tau )$ and $R_{u_S u_S}^{PIV}(\tau )$ of ${u}^{\prime }(x,z,t),\,{u}^{\prime }_L(x,z,t)$ and ${u}^{\prime }_S(x,z,t)$, respectively, computed from the PIV data, as a function of the time lag $\tau$. Also shown is the temporal correlation coefficient $R_{uu}^{HWA}(\tau )$ of ${u}^{\prime }(x,z,t)$ obtained from the hot-wire measurements performed in the oncoming boundary layer at the same height. It should be noted here that the correlation coefficients estimated either from the well-time-resolved hot-wire measurements or the low frequency PIV data were computed directly in the time domain, i.e. avoiding the use of Fourier transforms. Temporal correlation coefficients of the complete longitudinal velocity $u^{\prime }(x,z,t)$ obtained from both measurement methods are in good agreement at available time lags from the PIV measurements, showing that, despite its low frequency, PIV is able to capture temporal correlation existing in the flow. Integral time scales related to each part of the flow can be roughly estimated from the value of the time lag at which the correlation coefficient reaches the value 0.4. Even if this estimation is almost impossible for $u^{\prime }_S$, it is noticeable that the integral time scale of the large-scale part $u^{\prime }_L$ is twice as large as that of the complete velocity component $u^{\prime }$, whereas $u^{\prime }_S$ has a smaller integral time scale. The results presented in Fig. 11 confirm that the contribution of the first POD mode to the longitudinal velocity component represents large-scale motions, whose typical length is much larger than the PIV field of view and so greater than can be inferred from Fig. 10 right.

Fig. 11

Temporal correlation coefficient of (plus) the longitudinal velocity component $u^{\prime }(z,x,t)$, (open square) its large-scale $u^{\prime }_L(z,x,t)$ and (open circle) its small-scale part $u^{\prime }_S(z,x,t)$, estimated from the PIV measurements at $z/h=2.5$ and $x/h=0$. The temporal correlation coefficient of the longitudinal velocity component $u^{\prime }(z,x,t)$ obtained from hot-wire measurements (solid line) is shown for comparison

Figure 12 shows the contribution of the mode ${\varvec{\varPhi }}^1(x,z)$ to the second-order moments of the velocity in the region above the canyon, computed as the ratio:

$$\begin{aligned} c_{ij}(x,z)= \left( \lambda ^1{\varPhi }_i^1(x,z){\varPhi }_j^1(x,z) \right) \bigg / \left( \overline{u^{\prime }_i u^{\prime }_j}(x,z) \right), \end{aligned}$$

(11)

where $u_i$ is $u$ or $w$ when $i=$ 1 or 3, respectively. Regarding the quantity $\overline{u^{\prime }w^{\prime }}$, it must be noted here that the individual contribution of each POD mode can be positive or negative depending on the sign of the product ${\varPhi }_i^n(x,z){\varPhi }_j^n(x,z)$ at the location considered. However, this product being weighted by the eigenvalue of the corresponding mode, the magnitude of which decreases with increasing mode order, a large value of the ratio $c_{ij}(x,z)$ can still be considered as a reliable indication of the strong contribution of the considered mode to the shear stress. The first POD mode contributes up to 70 % to $\overline{u^{\prime 2}}$ and 35 % to $\overline{w^{\prime 2}}$. The contribution of this mode to $\overline{u^{\prime }w^{\prime }}$ varies from zero to 45 % in the region below $z/h=1.5$ and is comprised of between 70 and 100 % above this height.

Fig. 12

Mode 1 contribution to $\overline{u^{\prime 2}}$ ($c_{11}$, left), $\overline{w^{\prime 2}}$ ($c_{33}$, centre) and $\overline{u^{\prime }w^{\prime }}$ ($c_{13}$, right)

Thus, the first POD mode ${\varvec{\varPhi }}^1(x,z)$ is a large contributor to the shear stress and corresponds to the presence of elongated low- and high-momentum regions (Figs. 10 right, 11) already observed in flows over urban canopies (Castro et al. 2006; Coceal et al. 2007a) but also in channel flows and cannonical boundary layers (Balakumar and Adrian 2007).

4.2 Intermodal Energy Transfers

The findings presented in the previous section motivated the use of the POD decomposition to study the flow dynamics above the canyon and led to a focus on the interaction between the first POD mode ${\varvec{\varPhi }}^1(x,z)$, representing the influence of the presence of elongated regions of low or high speed in the oncoming boundary layer and the rest of the modes that represent the dynamics of the flow associated with the presence of the canyon and the smaller scales of the flow.

Energy transfers between POD modes can be studied through the use of a POD-Galerkin procedure that consists of projecting the Navier-Stokes equations onto the POD basis. By doing so, one obtains a set of ordinary differential equations that describe the dynamics of the temporal POD coefficients $b_n(t)$. This approach is usually used to derive low-order models of turbulent flows. For a detailed presentation of the method, the reader is referred to Aubry et al. (1988). More recently, Couplet et al. (2003) have employed the same POD-Galerkin procedure to obtain balance equations for the fluctuating kinetic energy $K^n=1/2 \lambda ^n b_n(t)^2$ captured by the $n^{th}$ mode. These equations are derived in the same manner as the balance equation of the total fluctuating kinetic energy of the flow from the Navier–Stokes equations, i.e. by multiplying the equation describing the dynamics of the mode $b_n(t)$ by the time derivative $\dot{b}_n(t)$ of $b_n(t)$. The equations obtained are of the form:

$$\begin{aligned} \dot{K}^n = C^n_0 b_n +\sum _{k=1}^N C^n_k b_k b_n +\sum _{k1=1}^N \sum _{k2=1}^N C^n_{k_1,k_2} b_{k1}b_{k2} b_n \end{aligned}$$

(12)

where the computation of the coefficients $C^n_0,\,C^n_k$ and $C^n_{k_1,k_2}$ involves inner products over the three-dimensional space between the spatial POD modes and their spatial derivatives and the three-component velocity field and its spatial derivatives (Couplet et al. 2003). Mean energy exchanges between modes are then evaluated by taking the mean of Eq. 12. A major drawback of POD-Galerkin approaches is that they require detailed knowledge of the flow in a three-dimensional domain in order to be able to properly compute the coefficients $C^n$ present in the above equation. Even if alternative methods have been developed to avoid the direct computation of these coefficients (Perret et al. 2006), they still require information such as the time derivative $\dot{b}_n(t)$ of the temporal coefficients $b_n(t)$ that are not accessible through the database of the present work.

Nevertheless, the form of the general Eq. 12 for the energy captured by the $n^{th}$ mode shows that it involves linear interaction ($C^n_0$), diadic interaction between modes ($C^n_k$) and triadic interactions ($C^n_{k_1,k_2}$) (Couplet et al. 2003). Because of the orthogonality property of POD modes, mean energy exchanges between modes through diadic interactions (i.e. exchanges involving only pairs of modes) are zero. Thus, the energy balance is governed by linear and triadic interactions and depends on the triple products $\overline{b_{k1}b_{k2} b_n }$.

In the present study, detailed computation of Eq. 12 is not feasible due to the fact that measurements are limited to two components of the velocity in a vertical plane. The existence of mean energy transfers between the first POD modes and the remaining flow are investigated via the computation of statistics involving the triple product of the velocity (and, therefore, of POD modes), namely the skewness of the longitudinal velocity component. By decomposing the velocity ${{\varvec{u}}}(x,z,t)$ into a large-scale part ${{\varvec{u}}}_L(x,z,t)=b_1(t){\varvec{\varPhi }}^1(x,z)$ represented by the contribution of the first POD mode to the velocity fields and a small-scale part ${{\varvec{u}}}_S(x,z,t)={{\varvec{u}}}(x,z,t) -{{\varvec{u}}}_L(x,z,t)$, one can write the third moment of the longitudinal velocity component as

$$\begin{aligned} \overline{u^{\prime 3}} = \overline{{u^{\prime }_L}^3} + 3\overline{u^{\prime }_L {u^{\prime }_S}^2} + 3\overline{{u^{\prime }_L}^2 u^{\prime }_S} + \overline{{u^{\prime }_S}^3}. \end{aligned}$$

(13)

Using the expression of ${u^{\prime }}_L(x,z,t)$ and ${u^{\prime }}_S(x,z,t)$ as a function of the POD modes, the term $\overline{u^{\prime }_L {u^{\prime }_S}^2}$ can be rewritten as:

$$\begin{aligned} \overline{u^{\prime }_L {u^{\prime }_S}^2} = \varPhi ^1(x,z)\sum _{k1=2}^N \sum _{k2=2}^N \varPhi ^{k_1}(x,z)\varPhi ^{k_2}(x,z) \overline{b_1 b_{k1}b_{k2}}, \end{aligned}$$

(14)

which shows that $\overline{u^{\prime }_L {u^{\prime }_S}^2}$ bears the footprint of the above-mentioned triadic interactions. Even if $\overline{u^{\prime }_L {u^{\prime }_S}^2}$ does not allow precise quantification of the magnitude and the direction (large toward small scales or small toward large scales) of mean energy transfers, its non-zero value demonstrates the existence of non-linear interactions between scales. Mathis et al. (2011) used the same type of approach but based on a scale decomposition performed in the frequency domain to study the amplitude modulation of near-wall small scales by large-scale structures from the logarithmic layer in a smooth-wall boundary layer. They showed that this mechanism leaves its imprints on the skewness of the longitudinal velocity component through the cross-term $\overline{u^{\prime }_L {u^{\prime }_S}^2}$.

Figure 13 shows the vertical evolution of the different terms in Eq. 14 at three longitudinal locations above the buildings and canyon. In the entire investigated region, there is a strong evolution of the skewness factor with the height, with near-zero negative values far from the building roofs in agreement with those obtained in the upstream boundary layer, high negative values near the upper edge of the shear layer and high positive values near $z/h=1$. This evolution confirms the complexity of the flow above the canyon and the intermittent character of the shear layer, as noted by Barlow and Leitl (2007). What is noticeable here is the very low contribution to the skewness factor of the large- and small-scale terms $\overline{{u^{\prime }_L}^3}$ and $\overline{{u^{\prime }_S}^3}$, respectively, as opposed to the cross-terms $3\overline{u^{\prime }_L {u^{\prime }_S}^2}$ and $3\overline{{u^{\prime }_L}^2 u^{\prime }_S}$. In particular, the cross-term $3\overline{u^{\prime }_L {u^{\prime }_S}^2}$ is the largest contributor in regions of high values of the global skewness factor. Even if no information on the direction of the interactions can be drawn from the signs and values of the different scale contribution to the skewness (Eq. 14), the present analysis clearly shows that non-linear interactions between the first and the other POD modes leave a strong imprint in the skewness factor, in the near-canyon region. Thus, the present analysis supports the hypothesis that the occurrence of a large-scale high or low speed event above the canyon is linked to the intermittent flow close to the canyon through non-linear mechanisms.

Fig. 13

Contribution to the skewness factor at (top left) $x/h=-1$, (top right) $x/h=0$ and (bottom) $x/h=0.5$ (solid line $\overline{u^{\prime 3}},$  open square $\;\overline{{u^{\prime }_L}^3},$  open inverted triangle $\;3\overline{u^{\prime }_L {u^{\prime }_S}^2},$  open triangle $\;3\overline{{u^{\prime }_L}^2u^{\prime }_S},$  open circle $\;\overline{{u^{\prime }_S}^3}$ , normalized by $\left(\overline{u^{\prime 2}}\right)^{3/2}$), (every third point only shown)

5 Discussion and Conclusions

A wind-tunnel experiment has been performed to investigate the dynamics of the large-scale turbulent structures that develop above and within a street canyon model immersed in an urban-like atmospheric boundary layer. The experimental configuration is based on a street-canyon model, of equal height and streamwise width, and the generation of a boundary layer over roughness elements with a plan area density of 6.25 %. Analysis of the PIV database via the computation of two-point spatial correlations and the use of POD and conditional-averaging techniques show that the flow dynamics are different from those expected in canonical cavity flows. The $k$-type regime of the flow upstream of the canyon leads to a strong separation of the flow from the upstream obstacle, leading, in turn, to the formation of a shear layer. This shear layer develops over the top of the two obstacles and the canyon, and generates vortical structures of spanwise vorticity, the length scale of which increases with downstream distance. In addition, the shear-layer region is animated by a flapping motion that is found to be responsible for the unsteady flow exchanges between the canyon and the outer flow. These exchanges consist of intermittent penetrations or ejections of fluid from the canyon, which are combined with vortical structures that irregularly penetrate into the canyon or are shed and convected in the outer flow, respectively. The strong Q2 and Q4 events observed above the canyon opening, which extend up to $z=2h$, are strongly correlated to the shear layer. Analysis of the two-point correlations also revealed that the presence of the shear layer tends to decouple the flow within the canyon from the dynamics of the upstream boundary layer. This first investigation of the flow based on one- and two-point statistics of first and second order was complemented by an analysis of the POD modes associated with the region above the canyon up to the height of $3h$, i.e. in the boundary layer. In the boundary layer above the shear layer, the first POD mode was found to be a major contributor to the kinetic turbulent energy and the shear stress (up to 45 and 90 %, respectively), and to correspond to the presence of large-scale coherent motions in the boundary layer combined with regions of low and high speed close to the top of the canyon. Analysis of the contribution of this mode to the skewness of the longitudinal velocity component provided evidence of a non-linear coupling between the large-scale coherent structures, mainly corresponding to the low and high momentum regions, and the smaller scales represented by the rest of the modes. Even if already observed in previous studies (Takimoto et al. 2011; Inagaki et al. 2012), the coupling has been quantitatively identified here and its non-linear character elucidated, confirming the complexity of the dynamical interaction of the flow. However, the questions of the exact nature of the mechanisms involved and the way that kinetic energy is transferred among the scales remain open.

The present findings have several implications regarding the modelling strategies retained to investigate turbulent flows over and inside urban canopies. Indeed, the present flow configuration corresponds to the combination of a canyon in the skimming flow regime immersed in a flow that belongs in the wake interference regime. This is the main difference with previous numerical and experimental studies (see, for instance, Sini et al. 1996; Kovar-Panskus et al. 2002; Liu et al. 2004; Michioka et al. 2010; Salizzoni et al. 2011; Kellnerová et al. 2012). The most obvious effect is that the flow separates at the upstream corner of the upstream building instead of its downstream corner, leading to the formation of a shear layer of larger vertical extent above the canyon. In the present case, this shear layer is found to be animated by a strong flapping motion and sheds large-scale vortices alternatively inside the canyon and downstream in the flow above the roofs. In canonical plane mixing-layer flows formed by the merging of two parallel flows of different velocities downstream of a splitter plate, the width of the resulting shear layer is usually quantified by the computation of the vorticity thickness $\delta _\omega =\Delta \overline{u} / \left(\partial \overline{u}/\partial z \right)_{\text{ m}ax}$, where $\Delta \overline{u}$ is the velocity difference between the two initial parallel flows and $\left(\partial \overline{u}/\partial z \right)_{\text{ m}ax}$ is the maximum vertical gradient of the mean longitudinal velocity component across the shear layer [see Finnigan (2000) for more details on this parameter]. In street-canyon flows, the vorticity thickness of the shear-layer region can be hard to properly define because of the difficulty of defining the velocity difference $\Delta \overline{u}$ across the shear layer (the canyon being immersed in an atmospheric boundary layer that itself imposes a vertical gradient of longitudinal velocity $\overline{u}$). To circumvent this issue, one can obtain a rough estimate of the thickness of the shear layer by estimating the vertical extent of the region of maximum shear stress $\overline{u^{\prime }w^{\prime }}$ existing at the top of the shear layer. In the present study, this thickness is of the order of $h$ at the centre of the canyon (Fig. 3d). The data from Salizzoni et al. (2011) clearly show that, as the flow upstream of the canyon goes from a wake interference regime to a skimming regime, this region becomes thinner. Canyon flows with skimming upstream flow show a thin shear layer the thickness of which is of the order of $0.2 h$ at $x/h=0$ (Michioka et al. 2010; Salizzoni et al. 2011; Kellnerová et al. 2012). The extreme case of skimming flow corresponds to the case where the canyon is modelled not as a pair of buildings protruding into the boundary-layer flow but as a cavity cut into the ground (Sini et al. 1996; Kovar-Panskus et al. 2002; Liu et al. 2004). Even if very convenient to model, in particular from a numerical point of view, this kind of configuration can be expected to be far from realistic from a dynamical point of view. Although not studied in the present work, it can be inferred that such differences in the shear-layer structure will have a strong impact on the transfer of momentum and scalars between the canyon and the overlying boundary layer.

A second important difference between the present study and several studies found in the literature addressing canyon flows is the use of three-dimensional obstacles as upstream roughness elements to generate the atmospheric boundary layer as opposed to two-dimensional obstacles (Michioka et al. 2010; Salizzoni et al. 2011; Kellnerová et al. 2012). Recent studies based on the direct numerical simulation of boundary-layer flows over rough walls have shown that the geometry of the roughness elements influences the characteristics of the flow in terms of Reynolds stress magnitude and turbulent length scales in the region corresponding to the roughness sub-layer (Volino et al. 2009; Lee et al. 2011). In particular, two-dimensional roughness elements were found to produce larger-scale ejections into the outer boundary layer. It is beyond the scope of the present paper to further discuss differences in the flow structure caused by the nature of the roughness elements, but it must be noted here that the choice of the geometry of the upstream roughness elements will have an impact on the dynamics of the canyon flow. This influence will be through $(i)$ the perturbation of the separation mechanism of the flow from the building roof, as it is known that the development of shear-layer flows is sensitive to initial conditions, and $(ii)$ via the influence of the boundary-layer flow on the canyon through the non-linear interactions identified in the present work.

The present findings lead to several remaining questions regarding the dynamics of the shear layer and its separation mechanism, including the exact nature of the dynamical link with the coherent structures of the upstream boundary layer. In addition, the influence of the geometrical parameters of the canyon such as height to width ratio or length to height on the flow dynamics remains to be studied.