Effects of the Upstream-Flow Regime and Canyon Aspect Ratio on Non-linear Interactions Between a Street-Canyon Flow and the Overlying Boundary Layer

Abstract

Large-scale structures within a rough-wall boundary layer generated over a cube array have recently been linked to small-scale fluctuations close to the roughness through a dynamical mechanism similar to amplitude modulation. Demonstrating the existence of this mechanism for different roughness types is a crucial step towards the development of a generic model for wind fluctuations in the urban canopy. Here the influence of the upstream roughness geometry (two-dimensional (2D) and three-dimensional (3D)) and planform packing density ($\lambda_{p}$) and street-canyon aspect ratio on the non-linear interactions between large-scale momentum regions and the small scales induced by the presence of the roughness is studied within a wind tunnel using combined particle-image velocimetry and hot-wire anemometry. A multi-time delay linear stochastic estimation is used to decompose the flow into large scales that participate in modulation and the remaining small scales. Using three different upstream roughness configurations composed of either 3D cubes or 2D rectangular blocks it is shown that the upstream roughness configuration has an influence on the non-linear interactions in the rough-wall boundary layer. Analysis of the turbulence skewness decomposition shows a change in the location of the maximum of the term $\overline{{u_{L}^{\prime} u_{S}^{\prime 2}}}$, which represents the influence of the large-scale momentum regions on the small scales, whilst the temporal correlation shows a modification of the interaction located closer to the roughness with a change from 3D to 2D roughness. Furthermore, a two-point spatio–temporal correlation demonstrates that the non-linear relationship is significantly modified in the wake-interference-flow regime compared to the skimming-flow regime. Through skewness decomposition and temporal correlations the canyon aspect ratio is shown to have no influence on the non-linear interactions, indicating that the mechanism depends only on the flow developing upstream. Finally, although the upstream roughness configuration is shown to influence the non-linear interactions, the nature of the mechanism remains the same in all configurations.

1 Introduction

The flow associated with street canyons that form the urban-canopy roughness comprises several regions, including the roughness sublayer, whose depth depends on the density and height of the roughness elements, and the inertial layer, which contains large-scale structures influenced by the surface characteristics (Rotach et al. 2005). Within these regions, the flow comprises complex coherent structures that have been identified through direct numerical simulation (DNS) (Coceal et al. 2007; Lee et al. 2011, 2012), wind-tunnel experiments (Castro et al. 2006; Takimoto et al. 2013) and field experiments (Inagaki and Kanda 2008, 2010). These coherent structures consist of large-scale turbulent organized motions of either high or low momentum that form well above the roughness in the inertial layer, shear layers that form within the roughness sublayer along the top of the upstream roughness elements and contain small-scale structures induced by the presence of the roughness, and a recirculation region within the street canyon (Coceal et al. 2007). These structures, especially how they interact with one another, are of particular interest since they govern the intermittent turbulent events, such as ejections (Q2: $u^{\prime} < 0$ and $w^{\prime} > 0$) and sweeps (Q4: $u^{\prime} > 0$ and $w^{\prime} < 0$), that produce the transport of heat, momentum and pollution between the street canyon and the overlying roughness sublayer and inertial layer (Takimoto et al. 2011; Perret and Savory 2013). The present study focuses on the roughness sublayer and lowest region of the inertial sublayer, since this is the region in which scale interactions important to the ventilation of street canyons are expected to occur.

The steady flow regimes of street canyons, with varying aspect ratio AR $=W/h$, where $W$ is the streamwise width and $h$ is the height of the canyon, have been widely studied, including the steady flow regimes: “skimming”, “wake interference” and “isolated roughness” (Oke 1988; Blackman et al. 2015). However, very few studies have examined the influence on the turbulence dynamics of varying the, (i) canyon aspect ratio, and (ii) the geometry (2D or 3D) of the upstream roughness elements (hence, the boundary-layer flow). The configurations used in these studies provide limited information, as they do not use multiple configurations with varying planform area density ($\lambda_{p} =$ the ratio of the plan area of the obstacles to the total plan area) for each type of roughness, 2D and 3D. Recently Blackman (2014) and Blackman et al. (2015) incorporated six different configurations, including three upstream roughness configurations (cubes or 2D bars with different streamwise spacing) and two canyon aspect ratios, and it was found that the geometry of the roughness had an influence on the characteristics of the boundary layer. Above the roughness the mean streamwise velocity component for configurations of equal $\lambda_{p}$ was found to be higher in 3D than in 2D configurations, agreeing with Salizzoni et al. (2011) and Huq and Franzese (2013). It was also shown that the integral length scale is larger in 2D than in 3D cases of equal $\lambda_{p}$ and confirmed that the integral length scale also increases with increasing aspect ratio in 2D configurations, as previously found by Volino et al. (2009). Finally, the canyon-ventilation flow rate was shown to increase from 3D to 2D configurations of equal $\lambda_{p}$, increase with decreasing $\lambda_{p}$, and increase with increasing canyon aspect ratio. This is due to the transition from skimming to wake-interference regimes (Blackman et al. 2015). It is clear that the geometry of both the upstream roughness and the street canyon influence the turbulence and mean flow within the roughness sublayer. However, it is unclear whether these factors have a significant impact on the relationship between the large-scale momentum regions within the inertial layer and the small scales induced by the presence of the roughness (Perret and Savory 2013).

To investigate the interaction between scales in a rough-wall boundary layer one must first use triple decomposition to decompose the instantaneous velocity ($u_{i}$), where $u$ is the streamwise velocity component, $v$ is the spanwise velocity component and $w$ is the vertical velocity component, into a time-averaged mean ($\overline{{u_{i}}}$), large-scale fluctuations ($u_{Li}^{\prime}$) and small-scale fluctuations ($u_{Si}^{\prime}$),

$$ u_{i} = \overline{{u_{i}}} + u_{Li}^{\prime} + u_{Si}^{\prime}. $$

(1)

The non-linear relationship between large-scale structures and near-wall small scales can then be investigated using skewness decomposition as for the streamwise velocity component in

$$ \overline{{u^{\prime 3}}} = \overline{{u_{L}^{\prime 3}}} + 3\overline{{u_{L}^{\prime 2} u_{S}^{\prime}}} + 3\overline{{u_{L}^{\prime} u_{S}^{\prime 2}}} + \overline{{u_{S}^{\prime 3}}}, $$

(2)

where $\overline{{u^{\prime 3}}}$ becomes skewness once normalized by $\sigma_{u}^{3}$, where $\sigma_{u}$ is the standard deviation of the streamwise velocity component, and the cross-terms $\overline{{u_{L}^{\prime} u_{S}^{\prime 2}}}$ and $\overline{{u_{L}^{\prime 2} u_{S}^{\prime}}}$ represent the influence of the large scales on the small scales, and the small scales on the large scales, respectively (Schlatter and Orlü 2010; Mathis et al. 2011b). This analysis has recently been performed in a rough-wall boundary layer consisting of staggered cubes with $\lambda_{p} = 25\%$ (Perret and Rivet 2013; Blackman and Perret 2016). Using skewness decomposition Blackman and Perret (2016) showed that in the near-wall region of the rough-wall boundary layer, the scale interaction occurs through a non-linear mechanism shown in the term $\overline{{u_{L}^{\prime} u_{S}^{\prime 2}}}$ and represents the non-linear influence of the large scales onto the small scales. Furthermore it was demonstrated, using the cross terms of $u_{L}^{\prime}$ with spanwise, $v^{\prime}$, and vertical, $w^{\prime}$, fluctuations, that all three components of velocity interact non-linearly in a similar manner (Perret and Rivet 2013, Blackman and Perret 2016).

Within the smooth-wall boundary layer the non-linear interaction between large and small scales has been linked to a mechanism of amplitude modulation (Hutchins and Marusic 2007; Mathis et al. 2009, 2011a, b; Marusic et al. 2011; Inoue et al. 2012). This mechanism has also been investigated experimentally for a sand-roughened wall (Squire et al. 2016) and numerically using large-eddy simulation (LES) of homogenous roughness (Anderson 2016) and DNS of a 2D-bar roughened wall (Nadeem et al. 2015). Recently, Blackman and Perret (2016) used experimental evidence from a rough-wall boundary layer consisting of staggered cubes with $\lambda_{p}= 25\%$ to investigate the non-linear interactions between large-scale momentum regions and the small scales induced by the presence of the roughness. The use of linear stochastic estimation (LSE) to decompose the flow when temporal information of the near-wall small scales is not available was demonstrated. Two-point spatio–temporal correlations showed positive correlation, confirming that a mechanism similar to amplitude modulation exists in the rough-wall boundary layer resembling that found in the smooth-wall boundary layer. This correlation demonstrates the existence of a time lag between the large-scale momentum regions and their influence on the small scales within the roughness sublayer, agreeing with Anderson (2016). The time lag was found to correspond to the angle of inclination, 11.5°, of typical large-scale momentum regions in the rough-wall boundary layer (Blackman and Perret 2016). Finally, through the use of spatio–temporal correlations, the presence of the roughness elements, which create a recirculation of the flow within the wake of the obstacles, was shown to result in a negative correlation between the large-scale fluctuations and the amplitude of the small-scale near-wall fluctuations thereby modifying the non-linear relationship.

Although the existence of amplitude modulation has been proven experimentally and numerically in a rough-wall boundary layer consisting of homogenous and heterogeneous roughness, previous work is limited to one or two types of roughness (Nadeem et al. 2015; Anderson 2016; Squire et al. 2016; Blackman and Perret 2016). The present work aims to use experimental evidence from six rough-wall boundary-layer configurations consisting of three upstream roughness arrangements (cubes or 2D bars with different streamwise spacing) and two street-canyon aspect ratios with high Reynolds number to answer the following questions:

• 1) What is the quantitative influence of the roughness configuration on the non-linear relationship between large-scale structures in the inertial layer and small-scale structures induced by the presence of the roughness in the roughness sublayer?

• 2) What is the quantitative influence of the street-canyon aspect ratio on this non-linear relationship?

These questions have implications for more realistic heterogeneous urban roughness since if a general dynamical mechanism is shown to exist for different roughness types it will be a significant step towards developing a generic model for velocity fluctuations in the urban canopy. Indeed, we have recently shown, through a simple first-order approach, that the roof-level-ventilation exchange velocity may be estimated from the geometrical characteristics of both the local canyon and the upstream roughness using a generalized model (Perret et al. 2017). The following section outlines the methodologies used including experimental details, boundary-layer characteristics and the stochastic estimation model. Next, the results and discussion, including the influence of both the upstream roughness and the canyon aspect ratio on scale interactions are presented, followed by the conclusions.

2 Methodologies

2.1 Experimental Details

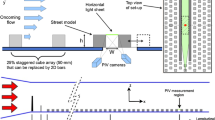
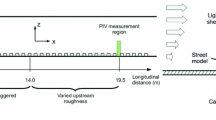
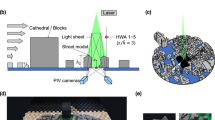
The experiments were conducted in the low-speed, suction type boundary-layer wind tunnel of working section. 2 m (width) $\times\,2\, \hbox{m}$ (height) $\times\,24\, \hbox{m}$ (length) in the Laboratoire de recherche en Hydrodynamique, Énergétique et Environnement Atmosphérique at Ecole Centrale de Nantes. The wind tunnel has a 5:1 inlet ratio contraction and a freestream turbulence intensity within the empty wind tunnel of 0.5% with spanwise uniformity to within ± 5% (Savory et al. 2013). Five 800-mm vertical tapered spires were used immediately downstream of the contraction to initiate the boundary-layer development and were followed by a 200-mm high solid fence located 750 mm downstream of the spires. An initial 13-m fetch of 50-mm staggered cubic roughness elements with a plan area density of $\lambda_{p} \,{=}\, 25\%$ was used to further develop the boundary layer. The roughness elements over the remaining portion of the wind tunnel were either 50-mm cubes (arranged in a staggered array with $\lambda_{p} = 25\%$) or 50-mm square-section, 2D bars that spanned the width of the tunnel, with an element spacing of either 1$h$ ($\lambda_{p} = 50\%$) or 3$h$ ($\lambda_{p} = 25\%$). These configurations result in a 1:200 scaling of a suburban-type atmospheric boundary layer (Blackman et al. 2015). A 2D canyon with length $L= 30$$h$ and height $h= 50$ mm was located 5.5 m downstream of the initial cubic roughness elements. In total six flow configurations were used with canyon widths of $AR= 1$ or 3, and three types of upstream roughness elements as described above (Fig. 1). To simplify the canyons are referred to as C1h and C3h for the canyon aspect ratios of 1h and 3h, respectively. The three upstream roughness configurations are referred to as Rcu for the 25% staggered cube array, R1h for the 2D bars with spacing of 1 $h$ and R3h for the 2D bars with spacing of 3h. By employing an initial 13-m fetch of staggered cubes, the experimental set-up leads to a change in terrain for both the R1h and R3h configurations. The development of an internal boundary layer in these cases has been previously investigated by Blackman et al. (2015) who found that in both configurations an equilibrium state has been reached at the particle-image velocimetry (PIV) measurement location and roughness change effects are negligible. Finally, the experiments were performed with a freestream flow speed $U_{\infty} = 5.8$ m s⁻¹ measured with a pitot-static tube located at $x= 15$ m, $y= 0$ and $z= 1.5$ m, giving a Reynolds number, using the friction velocity $u_{*}$, of Re* = 1.2 × 10³ and 2.3 × 10⁻⁴ based on canyon height h and boundary-layer thickness δ, respectively.

Fig. 1

Canyon and roughness configurations, a C1hRcu and C3hRcu; b C1hR1h and C3hR1h; c C1hR3h and C3hR3h with PIV light sheet (green line) and HWA (red multiple symbol); d stereoscopic PIV set-up

The flow measurements were conducted in the canyon 19.5 m downstream of the wind-tunnel inlet using a Dantec PIV system set up in stereoscopic configuration (Fig. 1d). Water–glycol droplets, which had a diameter with distribution mean of 1 μm, were introduced using a commercially available smoke generator just downstream of the contraction of the wind tunnel to ensure proper seeding of the lower part of the boundary layer. A light sheet generated by a Litron double cavity Nd-YAG laser (2 × 200 mJ) was used in conjunction with two CCD $2048\times 2048$ cameras each equipped with a 60-mm objective lens. Dantec Dynamic Studio software was used to control the synchronization of the cameras and laser as well as to perform PIV analysis of the recorded images. A frequency of 7 Hz was used between pairs of laser pulses and a timestep of 400 μs was set between two images of the same pair. In total 5000 pairs of images were recorded, which corresponds to approximately 12 min of measurements.

The two-component vector fields from each camera were computed using an initial interrogation window size of $256\times 256$ that was reduced to a final interrogation window size of $16 \times 16$ using a multi-pass adaptive correlation algorithm with an overlap of 50%. The final spatial resolution of the measurements was thus 0.83 mm in the longitudinal direction and 1.68 mm in the vertical direction for all configurations. To obtain temporal information of the flow two hot-wire anemometer (HWA) probes were used to measure the streamwise velocity component at heights of $1.2h$ and $4h$ with a sampling frequency of 10 kHz (Fig. 1d). These measurements were conducted at the same time and synchronized with the PIV system to allow for accurate correlation. For further information on the PIV image processing, set-up and synchronization with the HWA measurements, see Blackman and Perret (2016).

The standard deviation $\sigma$ of the main PIV statistics, due to statistical error, is shown in Table 1 at a height of $z/h = 3$ at the centre of the PIV plane for each of the three roughness configurations, based on measurements conducted without a canyon present. The standard deviation was estimated from the number of independent samples under the assumption of a normal distribution, considering that a time separation of two integral time scales between two samples is needed to ensure their independence (Tropea et al. 2007). Shaded areas in Figs. 2, 5, 6 and 10 represent a 99% confidence bound or ± 3σ of the PIV statistics due to statistical error, as listed in Table 1.

Table 1 Standard deviation of PIV statistics due to statistical error

Fig. 2

Spatially-averaged PIV statistics a mean streamwise velocity component normalized by $u_{*}$, b standard deviation of the streamwise velocity component, c vertical component, d spanwise component, e shear stress normalized by $u_{*}$, f skewness of the streamwise velocity component, g vertical component, and h spanwise component

We define the turbulence quantities as follows: the instantaneous velocity components in the $x$, $y$ and $z$ directions are streamwise ($u$), spanwise (v) and vertical (w), respectively. Time averages are denoted with the overbar, spatial averages along the longitudinal direction of width 1h or 3h are denoted as 〈 〉, and $\widetilde{\,\,\,\,}$ denotes a large-scale filter that is further described in Sect. 2.3 below. Using Reynolds decomposition, the velocity is $u_{i} = \overline{{u_{i}}} + u_{i}^{\prime}$, where $\overline{{u_{i}}}$ is the time-averaged velocity and $u_{i}^{\prime}$ is the instantaneous fluctuating velocity. The standard deviation of the velocity is $\sigma_{i} = \sqrt {\overline{{\left({u_{i} - \overline{{u_{i}}}} \right)^{2}}}}$ and the shear stress is $\overline{{u^{\prime}w^{\prime}}} = \overline{uw} - \bar{u}\bar{w}$.

2.2 Boundary-Layer Characteristics

Table 2 lists important flow and scaling parameters measured at $x = 19.5\, \hbox{m}$ except for $U_{\infty}$, which was measured at $x = 15\, \hbox{m}$. For a detailed discussion of these characteristics and their comparison with results published elsewhere, see Blackman et al. (2015). The logarithmic-law parameters, aerodynamic roughness length ($z_{0})$ and displacement height ($d$), were determined by fitting the vertical profile of the streamwise velocity component to the logarithmic law (Blackman et al. 2015) while the friction velocity, $u_{*}$, was estimated from the vertical profile of the Reynolds shear stress in the constant-stress region located just above the roughness elements. Within the wind tunnel a region of constant stress is not typically observed so the shear stress must be approximated by an average of the shear stress over a region, selected based on a combination of the flattest region of the profile and the expected value for the configuration from the literature. Although we recognize that this method of estimating $u_{*}$ does not normally yield accurate results in rough-wall boundary layers the conclusions are unlikely to be affected. For further details, see Blackman (2014).

Table 2 Scaling parameters

The boundary-layer profiles of the three roughness configurations (Rcu, R1h and R3h) including the mean streamwise velocity component, streamwise, vertical and spanwise standard deviations, shear stress $\overline{{u^{\prime}w^{\prime}}}$ and skewness of the streamwise, vertical and spanwise components are shown in Fig. 2. In this figure the measurements were taken within the three roughness configurations with no canyon present using the same PIV configuration as shown in Fig. 1d. As discussed in Blackman et al. (2015) the roughness configuration, whether 3D or 2D, and $\lambda_{p}$ have a significant impact on the turbulence statistics. The skimming-flow regime (R1h) is shown to increase $\bar{u}$, $\sigma_{u}$, $\sigma_{w}$ and $\sigma_{v}$, while $\overline{{u^{\prime}w^{\prime}}}$ decreases compared to the wake-interference regime (R3h). The 3D roughness (Rcu) falls between the skimming-flow and wake-interference-flow regimes except in the case of $\sigma_{w}$ and $\sigma_{v}$, which are similar to wake-interference profiles. Interestingly, other than a difference in magnitude of the skewness of the streamwise component within the shear layer, all three boundary layers have a similar skewness of the streamwise, vertical and spanwise velocity components. Information on momentum transfer events, such as sweeps and ejections, can be obtained from the skewness profiles. Note that all three boundary layers exhibit strong positive skewness of the streamwise component and negative skewness of the vertical component within the shear layer, which has been previously linked to energetic downward sweeping events (Brunet et al. 1994). These events dominate transport within the shear layer but above $z/h = 2$ ejections start to govern transport. Although the R1h configuration exhibits a larger magnitude of skewness within the shear layer and, therefore, a larger relative strength of sweep events, the similarities between the skewness profiles of all three boundary layers suggest that the nature of the mechanism governing transport remains the same.

2.3 Stochastic Estimation Model

A novel application of stochastic estimation has been developed to combine field and wind-tunnel measurements to allow for detailed analysis of flow dynamics (Perret et al. 2016). Recently, stochastic estimation has been used with temporally-resolved HWA measurements and spatially-resolved PIV measurements to predict large-scale temporally- and spatially-resolved flow fields for the investigation of amplitude modulation (Blackman and Perret 2016). The method, fully described in Blackman and Perret (2016), is used herein and a brief description is presented below.

In the stochastic estimation method the approximated near-wall large-scale fluctuating velocity ($\widetilde{{u^{\prime NW}}}$) is calculated at each location of interest from coefficients ($A_{l}^{n}$) and a reference velocity signal ($u_{L}^{\prime BL}$),

$$ \widetilde{{u^{\prime NW}}}\left({x,y,z,t} \right) = \mathop \sum \limits_{l = 1}^{{N_{ref}}} \mathop \sum \limits_{{m = - N_{t}}}^{{N_{t}}} A_{l}^{n} u_{L}^{\prime BL} \left({x_{l},y_{l},z_{l},t + m\Delta \tau} \right). $$

(3)

The time lag $\left({\varDelta \tau} \right)$ is introduced to preserve the time separation between the large-scale boundary-layer event and the maximum correlation contained within the coefficient $A_{l}^{n}$.

The hot-wire anemometer located at $z/h = 4$ is first low-pass filtered to ensure that the reference signal used to run the stochastic estimation contains only low frequency, large-scale fluctuations ($u_{L}^{\prime BL}$) so that the fluctuations predicted by the model are uncorrelated with the small scales, and in agreement with the method of Mathis et al. (2009) and triple decomposition (Hussain 1983, 1986). The cut-off wavelengths for the filter were determined from the spectra of the streamwise velocity component at heights $z = 1.2h$ and $z = 4h$ and were approximately $\ell_{c}=20h$, $31h$ and $24h$ for the Rcu, R1h and R3h configurations, respectively.

The LSE coefficients ($A_{l}^{n}$) are determined from the cross-correlation of the low-pass filtered large-scale fluctuations and the raw near-wall PIV signal at the location in space ($x$, $y$, $z$) that is to be predicted, as well as the autocorrelation of the large-scale signal,

$$ \begin{aligned} &\overline {{{u}^{\prime NW}}\left({x,y,z,t} \right)u_L^{\prime BL}\left({{x_{\jmath}},{y_{\jmath}},{z_{\jmath}},t + m\Delta \tau} \right)} \\ &= \;\;\sum \limits_{l = 1}^{{N_{ref}}} \sum \limits_{n = - {N_t}}^{N_t} A_l^n\overline {u_L^{\prime BL}\left({{x_{\imath}},{y_{\imath}},{z_{\imath}},t + n\Delta \tau} \right)u_L^{\prime BL}\left({{x_{\imath}},{y_{\imath}},{z_{\imath}},t + m\Delta \tau} \right)},\; \\\end{aligned} $$

(4a)

$$ j\;\in\;\left[{1,{N_{ref}}} \right],\;m\;\in\;\left[{-{N_t},{N_t}} \right]. $$

(4b)

A time lag $\varDelta \tau = 0.2\,\hbox{s}$ with a maximum delay of $t = - 1\,\hbox{s}$ to 1 s is introduced to these correlations to preserve the time separation of the conditional and unconditional events so that each coefficient represents the correlation between events at a specific instance in time (Tinney et al. 2006). Once the coefficients are determined they are used, along with the reference low-pass signal ($u_{L}^{\prime BL}$), to predict the large-scale near-wall fluctuations through summation of the velocity predictions at each time ($t$), where $N_{ref}$ is the number of reference locations and $2N_{t} + 1$ is the number of time lags used (Eq. 4).

This process is used to predict the large-scale component of both the streamwise and vertical fluctuating velocity components within the canyon and roughness sublayer up to a height of $z/h = 3$ to include the roughness sublayer and the lower part of the inertial layer where important scale interactions are expected to occur. The spanwise velocity fluctuations are not predicted using this method since the location of the PIV plane lies in the symmetry plane of the cube. This results in statistics such as the correlation between the streamwise velocity component in the overlying boundary layer and the spanwise velocity component within the roughness sublayer that is negligible, thus rendering the stochastic estimation ineffective for decomposing the spanwise velocity component.

3 Results and Discussion

3.1 Influence of the Upstream Roughness Configuration

Previous work using the current LSE model driven by a low-pass filtered reference signal within the overlying boundary layer has demonstrated the ability of the model to estimate large-scale velocity fluctuations correlated with large-scale structures present in the overlying boundary layer while the remaining fluctuations have been shown to be small-scale structures (Blackman and Perret 2016). For further details, see Blackman and Perret (2016) and the analysis presented below.

The statistics presented here are spatially averaged in the x-direction over the width of the PIV measurement region shown in Fig. 1 in each of the three roughness configurations. Spatially averaging the statistics provides better convergence of higher-order statistics while retaining important flow features.

3.1.1 Characteristics of Large-Scale fluctuations

The streamwise length scales ($L_{{\widetilde{{u_{L}}}}}$, where $\widetilde{{u_{L}^{\prime}}}$ is the streamwise velocity fluctuation predicted by the LSE model) are calculated for each of the three upstream roughness configurations using temporal correlation and invoking Taylor’s hypothesis of frozen turbulence, where $\bar{u}\left(z \right)$ is the local streamwise velocity component and $\tau$ is the time delay,

$$ L_{{\widetilde{{u_{L}}}}} \left(z \right) = \int_{0}^{+ \infty} {R_{{\widetilde{{u_{L}}}\widetilde{{u_{L}}}}} \left({z,\tau} \right)d\tau \bar{u}\left(z \right)} . $$

(5)

The sizes of these structures in the streamwise direction are very large compared to the height of the roughness (Fig. 3) and span a streamwise length several times the height of the boundary layer. Furthermore, it is shown that both an increase in packing density and a change from 3D to 2D roughness result in an increase in the size of these structures. The temporal evolution of the estimated fluctuations for each roughness configuration is shown in Fig. 4. Structures that resemble large-scale momentum regions, which are found in both rough-wall and smooth-wall boundary layers (Volino et al. 2007), are shown and span a length on the order of $2\delta$. The angle of inclination ($\theta$) of these structures can be estimated using Fig. 4 with $\theta = { \tan }^{- 1} \left({{\raise0.7ex\hbox{${\Delta z}$} \!\mathord{\left/{\vphantom {{\Delta z} {\left({\Delta \tau U_{\infty}} \right)}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\left({\Delta \tau U_{\infty}} \right)}$}}} \right)$ and is shown to fall between 11° and 15° for the 3D roughness and between 16° and 20° for the 2D roughness. In conclusion, the fluctuations predicted by the linear stocastic estimation represent elongated, large-scale regions of low or high momentum that are present within the overlying boundary layer above the roughness and, thus, the remaining fluctuations represent small-scale structures.

Fig. 3

Spatially-averaged streamwise integral length scales ($L_{{\widetilde{{u_{L}}}}}$) of streamwise velocity fluctuations predicted by the LSE model ($\widetilde{{u_{L}^{\prime}}}$) in Rcu, R1h and R3h roughness configurations

Fig. 4

Temporal evolution of streamwise velocity fluctuations predicted by the LSE model ($\widetilde{{u_{L}^{\prime}}}$) at $x/h =$ 0 for a Rcu, b R1h, c R3h configurations

The linear stochastic estimation model driven by a low-pass filtered reference signal within the overlying boundary layer was able to estimate large-scale velocity fluctuations correlated with large-scale structures present in the overlying boundary layer while the remaining fluctuations are small-scale structures. Figure 5 shows the contribution of the large scales to $\sigma_{u}$, $\sigma_{w}$ and $\overline{{u^{\prime}w^{\prime}}}$ of the three roughness configurations. Within the canopy in all boundary layers the small scales capture the majority of the variance and shear stress while within the overlying boundary layer the large-scale contribution becomes significant for all quantities, but particularly for $\sigma_{u}$. This significance is even larger for the 2D roughness cases, which show a greater than 50% large-scale contribution to $\sigma_{u}$ above a height of $z/h = 1.5$. As well, the R1h configuration is shown to have a greater large-scale contribution (approximately two times) to $\sigma_{w}$ within the canopy. As the spatial averaging in each of these boundary layers covers the extent of the PIV measurement region the R1h and R3h configuration statistics encompass the recirculation region within the canopy as well as flow separation that occurs near the downstream canyon obstacle, whereas the Rcu configuration statistics only encompass the recirculation region.

Fig. 5

Contribution of the large scales, $\widetilde{{u_{L}^{\prime}}}$ to spatially-averaged, a $\langle \sigma_{uL} \rangle$, b $\langle \sigma_{wL} \rangle$, and c $\langle \overline{{u_{L}^{\prime} w_{L}^{\prime}}} \rangle$. Outlying points in $\langle \overline{{u_{L}^{\prime} w_{L}^{\prime}}} \rangle$ are due to normalization by zero

3.1.2 Skewness Decomposition

Skewness decomposition, as outlined in Sect. 1 (Eq. 2), can be used to investigate the existence of non-linear interactions between large and small scales in turbulent flows. Figure 6 shows the spatially-averaged skewness decomposition of the three upstream roughness configurations, Rcu, R1h and R3h, and in all three configurations the decomposed skewness exhibits a maximum within the shear layer forming downstream of a roughness obstacle that is predominately due to $\overline{{u_{S}^{\prime 3}}}$. This suggests that the energetic downward sweeping motions in this region are predominately a result of small-scale fluctuations. The quantity $\overline{{u_{S}^{\prime 3}}}$ becomes negative above the shear layer exhibiting similarities to the skewness profile of a mixing layer, which agrees with Perret and Rivet (2013). The large scales and the cross-term $\overline{{\widetilde{{u_{L}^{\prime 2}}}u_{S}^{\prime}}}$ contribute a negligible amount to the skewness throughout all three boundary layers, which agrees with Mathis et al. (2011b) for a smooth-wall boundary layer. The cross-term $\overline{{\widetilde{{u_{L}^{\prime}}}u_{S}^{\prime 2}}}$ has a significant contribution to the skewness in each of the three boundary layers and the location of its maximum shifts in height depending on the configuration of the roughness. A change from 3D to 2D with the same packing density results in a shift of the maximum from just above the shear layer at $z/h = 1.5$ to within the shear layer at $z/h = 1$. In contrast, increasing packing density shifts the height of the maximum of the cross-term $\overline{{\widetilde{{u_{L}^{\prime}}}u_{S}^{\prime 2}}}$ to $z/h = 1.2$. However, the relative magnitude of this non-linear term is not dependent on the roughness configuration since all three boundary layers have similar magnitudes at the maximum of this term. From this analysis, it is clear that within all three roughness configurations there is a significant influence of the term $\overline{{\widetilde{{u_{L}^{\prime}}}u_{S}^{\prime 2}}}$, which represents the non-linear interaction between the large scales and the small scales and suggests a top-down mechanism such as amplitude modulation.

Fig. 6

Triple decomposition of skewness of the streamwise velocity component, $\langle\overline{{u^{\prime 3}}} \rangle$ (−) including $\langle\overline{{\widetilde{{u_{L}^{\prime}}}^{3}}} \rangle$ (o), $\langle\overline{{u_{S}^{\prime 3}}} \rangle$ (blue left-pointing pointer), $\langle 3\overline{{\widetilde{{u_{L}^{\prime}}}^{2} u_{S}^{\prime}}} \rangle$ (+), $\langle3\overline{{\widetilde{{u_{L}^{\prime}}}u_{S}^{\prime 2}}} \rangle$ (red dotted line) all spatially-averaged and normalized by $\langle\sigma_{u}^{3} \rangle$ for, a Rcu, b R1h, c R3h configurations, spatially-averaged over a width of 3h

Within the literature, it has been previously observed that the non-linear interaction between the large-scale momentum regions and the small scales close to the roughness occurs in a similar manner for all components of the flow (Perret and Rivet 2013; Blackman and Perret 2016). Here the non-linear interaction between the large-scale momentum regions and the spanwise ($\overline{{\widetilde{{u_{L}^{\prime}}}v^{\prime 2}}}$) and vertical fluctuations ($\overline{{\widetilde{{u_{L}^{\prime}}}w^{\prime 2}}}$) are computed for each roughness configuration and compared with $\overline{{\widetilde{{u_{L}^{\prime}}}u_{S}^{\prime 2}}}$ (Fig. 7). In this case the spanwise and vertical fluctuations used are the raw fluctuations with no LSE filtering applied. The results of the 3D cube roughness are in agreement with Perret and Rivet (2013), since all three velocity components have similar profiles particularly within the canopy. This similarity within and above the canopy is reiterated in the 2D roughness cases. However, there is a modification in the flow above the canopy in the R1h configuration, where the spanwise term differs from the streamwise and vertical profiles. This significant difference (confirmed through analysis of the 99% confidence interval, not shown here) is a result of the skimming-flow regime developing over 2D roughness.

Fig. 7

Non-linear skewness terms $3\langle\overline{{\widetilde{{u_{L}^{\prime}}}u_{S}^{\prime 2}}} \rangle$ (−), $3\langle\overline{{\widetilde{{u_{L}^{\prime}}}w^{\prime 2}}} \rangle$ (blue left-pointing pointer) and $3\langle\overline{{\widetilde{{u_{L}^{\prime}}}v^{\prime 2}}} \rangle$ (red multiple symbol) all spatially-averaged and normalized by $\langle\sigma_{{u}} \sigma_{u_{i}}^{2} \rangle$ for, a Rcu, b R1h, c R3h configurations

3.1.3 Temporal Cross-Correlations and Flow Summary

The LSE model used here with HWA measurements of high-temporal resolution allows for the temporal extrapolation of velocity fluctuations. Scale interactions can, thus, also be investigated temporally without having access to the temporal small-scale signal close to the roughness. Using this technique we focus on the cross-correlation of the large-scale component with the squared small-scale fluctuations, $R_{{\widetilde{{u_{L}}}u_{S}^{2}}}$, which represents the non-linear interaction of the scales

$$ R_{{\widetilde{{u_{L}}}u_{S}^{2}}} \left({x_{S},z_{S},x_{L},z_{L},\tau_{L}} \right) = \frac{{\overline{{\widetilde{{u^{\prime}_{L}}}\left({x_{L},z_{L},t + \tau_{L}} \right)u_{S}^{{\prime}2} \left({x_{S},z_{S},t} \right)}}}}{{\sqrt {\overline{{\widetilde{{u_{L}}}^{{\prime}2} \left({x_{L},z_{L}} \right)}}} \sqrt {\overline{{u_{S}^{{\prime}2} \left({x_{S},z_{S}} \right)}}}^{2}}}. $$

(6)

This analysis is performed by introducing time lags to the $\widetilde {u_{L}^{\prime}}$ fluctuations (Eq. 6). Figure 8 shows the temporal evolution of the spatially-averaged cross-correlation, and in all three boundary layers the cross-correlation $R_{{\widetilde{{u_{L}}}u_{S}^{2}}}$ exhibits a significant maximum within the roughness sublayer, which gradually decreases in magnitude with height in the boundary layer. Within the boundary layer over the cubic roughness elements (Rcu) this maximum tends to align with a zero time delay until a height of $z/h = 3$ is reached where the maximum temporally shifts to approximately $\tau U_{\infty}/\delta = 0.5$. However, in the case of 2D roughness, the maximum is located at approximately $\tau U_{\infty}/\delta = 1.5$ and 1.1 and above a height of $z/h = 1.5$ and $z/h = 1$ for the R1h and R3h configurations, respectively. This positive temporal shift of the maximum is a result of small scales interacting with large scales that occur upstream in the flow and has been previously documented (Guala et al. 2011). Although the reason for this shift is unknown it suggests that the behaviour of the non-linear interaction between large- and small-scale structures is modified between the roughness sublayer and above. Here this modification becomes more significant within boundary layers above 2D roughness, especially in wake-interference flow, which shows modification occurring even within the shear layer. The relationship between large- and small-scale structures is also modified within the canopy at $z/h = 0.5$ where a negative correlation exists, occurring consistently in all three boundary layers. In this region, regardless of roughness configuration, there is a recirculation of the flow within the wake where large scales within the canopy are opposite in sign to the large scales above the canopy. This results in a modification of the relationship between large scales and small scales within the canopy.

Fig. 8

Spatially-averaged correlation coefficient $\langle R_{{\widetilde{{u_{L}}}u_{S}^{2}}} \rangle$ where $x_{L} = x_{S}$ and $z_{L} = z_{S}$ of, a Rcu, b R1h, and c R3h configurations

A spatially-averaged two-point spatio–temporal correlation of the term $\widetilde{{u_{L}^{\prime}}}u_{S}^{\prime 2}$ provides further insight into this non-linear interaction (Fig. 9), where the correlation is computed using a small-scale fixed point ($z_{S}$) within the canopy at height $z/h = 0.75$ (Eq. 6).

Fig. 9

Spatially-averaged spatial correlation coefficient $\langle R_{{\widetilde{{u_{L}}}u_{S}^{2}}} \rangle$ where $x_{L} = x_{S}$ and $z_{S} = 0.75$ of, a Rcu, b R1h, and c R3h configurations

At a height of $z/h = 0.75$ in all three boundary layers there is a clear maximum present with positive correlation, even for large time delays. A positive correlation suggests that when large-scale, low momentum, regions are present above the canopy the small scales are suppressed, whereas when large-scale, high momentum, regions are present above the canopy the small scales are amplified. Thus, these results support a top-down mechanism of non-linear interaction. Within the canopy the relationship is modified, and there is a negative correlation between large-scale near-wall fluctuations and the small-scale fluctuations at $z/h = 0.75$. As mentioned above, this is likely caused by the recirculation of the flow within the wake resulting in negative large-scale fluctuations occurring with amplification of the small scales in the shear layer. As noted above a significant modification of the non-linear mechanism occurs in the R3h configuration. The strong maximum at a height of $z/h = 0.75$ and the maximum occurring within the canopy is temporally shifted to approximately $\tau U_{\infty}/\delta = -\,1$, whereas in the other boundary layers this maximum occurs at approximately $\tau U_{\infty}/\delta = -\,0.1$. As well, in all three boundary layers the maximum of correlation tends to shift temporally as the large-scale reference location in the boundary layer increases in height. When the large-scale reference location is close to the small-scale reference at $z/h = \,1$ the maximum occurs at approximately $\tau U_{\infty}/\delta = -\,0.1$ for R1h and Rcu configurations and $\tau U_{\infty}/\delta = -\,0.6$ for the R3h configuration, which becomes $\tau U_{\infty}/\delta = -\,0.6$, − 0.5 and − 1.2 for the Rcu, R1h and R3h configurations, respectively, with large-scale reference at $z/h = \,3$. An inclination angle ($\theta$) can be estimated using Fig. 9 with $\theta = { \tan }^{- 1} \left({{\raise0.7ex\hbox{${\Delta z}$} \!\mathord{\left/{\vphantom {{\Delta z} {\left({\Delta \tau U_{\infty}} \right)}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\left({\Delta \tau U_{\infty}} \right)}$}}} \right)$ and corresponds to approximately 11.5°, 14.4° and 13.8° for Rcu, R1h and R3h configurations, respectively, which agrees well with the angles extracted from Fig. 5.

3.2 Influence of the Canyon Aspect Ratio

The LSE model was used to estimate the large-scale contribution to the total $\sigma_{u}$, $\sigma_{w}$ and $\overline{{u^{\prime}w^{\prime}}}$ for all six configurations (Fig. 10). The large-scale contribution to the total $\sigma_{u}$ within the canyon is similar for all configurations whereas, above the canyon, the large-scale contribution is shown to increase with increasing canyon aspect ratio regardless of the upstream roughness configuration. An increase in canyon aspect ratio also increases the large-scale contribution to $\overline{{u^{\prime}w^{\prime}}}$ above the canyon, but within the canyon there is a significant difference between cases due to the occurrence of negative skewness within the C1h cases. The large-scale contribution to the total $\sigma_{w}$ depends only on the canyon aspect ratio where an increase in aspect ratio results in decreased contribution within the canyon. Finally, in all cases within the canyon, the small scales capture the majority of the component variances and shear stress while within the overlying boundary layer the large-scale contribution becomes significant for all quantities, but particularly for $\sigma_{u}$.

Fig. 10

Contribution of the large scales, $\widetilde{{u_{L}^{\prime}}}$ to a $\langle\sigma_{u} \rangle$, b $\langle\sigma_{w} \rangle$, and c $\langle\overline{{u^{\prime}w^{\prime}}} \rangle$ spatially-averaged over the canyon width, where the measurement canyons are defined as Cnh with n = 1 or 3 and the upstream roughness (R_m) is staggered cubes (m = cu) or 2D bars with m = 1 or 3 h. Outlying points in $\langle\overline{{u_{L}^{\prime} w_{L}^{\prime}}} \rangle$ are due to normalization by zero

The skewness decomposition of the three upstream roughness configurations is discussed in Sect. 3.1, where it is shown that the large scales and the cross-term $\overline{{\widetilde{{u_{L}^{\prime 2}}}u_{S}^{\prime}}}$ contribute a negligible amount to the total skewness. Thus, in this section only the contributions of $\overline{{u_{S}^{\prime 3}}}$ and $\overline{{\widetilde{{u_{L}^{\prime}}}u_{S}^{\prime 2}}}$ are discussed (Fig. 11). It is clear that an increase in canyon aspect ratio decreases the contribution of the small scales to the total skewness suggesting that the wake-interference-flow regime reduces the dominance of energetic downward sweeping motions in the shear layer. The cross-term $\overline{{\widetilde{{u_{L}^{\prime}}}u_{S}^{\prime 2}}}$ is shown to be dependent on upstream roughness that, as discussed above, modifies the location of the maximum of this term. As well, increasing the canyon aspect ratio results in an increase in the contribution of this term suggesting that this non-linear interaction becomes more important in the wake-interference-flow regime.

Fig. 11

Contribution of a $\langle\overline{{u_{S}^{\prime 3}}} \rangle$ and b $3\langle\overline{{\widetilde{{u_{L}^{\prime}}}u_{S}^{\prime 2}}} \rangle$ to the skewness of the streamwise component spatially-averaged over the canyon width and normalized by the value of maximum skewness

Figure 12 shows the non-linear interaction between the large-scale momentum regions and the spanwise ($\overline{{\widetilde{{u_{L}^{\prime}}}v^{\prime 2}}}$) and vertical fluctuations ($\overline{{\widetilde{{u_{L}^{\prime}}}w^{\prime 2}}}$) compared with $\overline{{\widetilde{{u_{L}^{\prime}}}u_{S}^{\prime 2}}}$. As discussed above, previous work has shown that these non-linear interactions occur in a similar manner for all components of the flow (Perret and Rivet 2013; Blackman and Perret 2016). When comparing these profiles for all six configurations studied, it is evident that the canyon aspect ratio has little influence on these relationships, which are predominantly a result of the upstream roughness configuration. Those configurations with R1h roughness upstream have flow developing over 2D roughness, resulting in a different interaction between the large-scale streamwise fluctuations and the small-scale spanwise fluctuations. This phenomenon requires further investigation through additional roughness configurations and measurements to analyze the flow over 2D roughness.

Fig. 12

Non-linear skewness terms $3\langle\overline{{\widetilde{{u_{L}^{\prime}}}u_{S}^{\prime 2}}} \rangle$ (−), $3\langle\overline{{\widetilde{{u_{L}^{\prime}}}w^{\prime 2}}} \rangle$ (blue left-pointing pointer) and $3\langle\overline{{\widetilde{{u_{L}^{\prime}}}v^{\prime 2}}} \rangle$ (red multiple symbol) all spatially-averaged over canyon width and normalized by $\langle\sigma_{{u}} \sigma_{u_{i}}^{2} \rangle$ for, a C1hRcu, b C1hR1h, c C1hR3h, d C3hRcu, e C3hR1h, f C3hR3h configurations

4 Conclusions

We used experimental evidence from six rough-wall boundary-layer configurations consisting of three upstream roughness configurations (cubes or 2D bars with different streamwise spacing) and two street-canyon aspect ratios with high Reynolds number to answer the specific questions listed in Sect. 1.

• 1) The upstream roughness configuration (whether 2D or 3D) and planform packing density have an influence on the non-linear interactions in the rough-wall boundary layer. Through skewness decomposition it is shown that the maximum value of the term $\overline{{u_{L}^{\prime} u_{S}^{\prime 2}}}$, which represents the influence of the large-scale ($u_{L}^{\prime}$) momentum regions on the small scales ($u_{S}^{\prime}$), moves closer to the shear layer with change from 3D to 2D roughness. Previous work has shown that the non-linear interaction occurs similarly through all three velocity components (Perret and Rivet 2013; Blackman and Perret 2016) and this was confirmed except in the case of the closely-spaced 2D bar roughness (R1h) whose skimming-flow regime induces a modification of the non-linear relationship with the spanwise velocity component. Temporal correlation analysis has shown that within the Rcu configuration boundary layer the maximum correlation tends to align with a zero-time delay until a height of $z/h = 3$ is reached. However, in the case of 2D roughness the temporal shift of the maximum occurs above a height of $z/h = 1.5$ and $z/h = 1$ for the R1h and R3h configurations, respectively. This suggests that the non-linear interaction is modified between the roughness sublayer and above, indicating that this modification becomes more significant within boundary layers over 2D roughness, particularly in wake-interference flow. Finally, a two-point spatio–temporal correlation demonstrated that the non-linear relationship is significantly modified in the wake-interference-flow regime. Within the R3h configuration the maximum correlation at a height of $z/h = 0.75$ is temporally shifted to approximately $\tau U_{\infty}/\delta = -\,1$, whereas in the R1h and Rcu configuration boundary layers this maximum occurs at approximately $\tau U_{\infty}/\delta = -\,0.1$.

• 2) The canyon aspect ratio was shown to have minimal influence on the non-linear interactions. An increase in canyon aspect ratio was shown to decrease the dominance of small scales and increase the contribution of the non-linear term $\overline{{u_{L}^{\prime} u_{S}^{\prime 2}}}$ to the total skewness. However, the appearance of the non-linear interaction through the vertical and spanwise velocity components was shown to be only dependent on upstream roughness configuration.

Figure 13 is a qualitative representation of the non-linear relationship in the R1h and R3h configurations; a qualitative representation of the Rcu confguration (not shown here) is available in Blackman and Perret (2016). As discussed by Blackman and Perret (2016), in each of the three boundary layers the inclined large-scale structures within the boundary layer move across the small-scale structures close to the roughness. Thus, small-scale structures experience effects from the large-scale structure that is slightly downstream of them. As the large-scale reference location increases in height the distance in the streamwise direction between the small-scale structure and the low momentum region increases, resulting in an increase in the time delay of the maximum correlation. This confirms that the inclined large-scale structures of high or low momentum detected in the logarithmic layer leave their footprint on the small scales close to the wall through a non-linear relationship. However, a modification of the non-linear relationship occurs close to the roughness. Although the exact cause of this modification is unknown, local differences in the flow, such as the thin shear layer within the skimming-flow regime and the strong flapping shear layer that occurs in the wake-interference regime, probably influences the non-linear relationship. Here it has been demonstrated that the relationship between the large-scale and small-scale structures occurs in each of the different rough-wall configurations, although significant modification of the relationship occurs in the wake-interference 2D roughness case (R3h).

Fig. 13

Qualitative cartoon illustrating influence of large-scale low momentum structure (blue) and high momentum structure (red) on small scales generated by the roughness in, a R1h skimming-flow regime; b R3h wake-interference-flow regime

Our study, in conjunction with Blackman and Perret (2016), has led to significant insight into the nature of the non-linear interaction in the rough-wall boundary layer. Although only limited types of upstream roughness and canyon geometry have been explored, the existence of a non-linear relationship, combined with evidence of this relationship from previous work in smooth-wall (Mathis et al. 2009, 2011a), sand-roughened wall (Squire et al. 2016) and rough-wall (Nadeem et al. 2015; Anderson 2016; Blackman and Perret 2016) boundary layers, suggests that the same basic scale-interaction mechanism exists for different types of boundary layers including different types of roughness configurations. This provides a foundation upon which to build a general predictive model for flow dynamics in the urban canopy.