Effect of Urban Morphology and an Upstream Tall Building on the Scale Interaction Between the Overlying Boundary Layer and a Street Canyon

Abstract

The interaction of large- and small-scale velocity fluctuations between a street canyon flow and the overlying boundary layer, under the influence of a local morphological model and a single upstream tall building, is investigated. The experiments are conducted in a wind tunnel, using Stereoscopic Particle Image Velocimetry (S-PIV) and Hot-Wire Anemometry (HWA). The Proper Orthogonal Decomposition-Linear Stochastic Estimation (POD-LSE) method is applied to decompose the velocity fluctuation scales and estimate the large-scale fluctuations at a high frequency. The amplitude modulation mechanism, which was found to exist for both smooth and homogeneous rough wall boundary layers in previous studies, still applies to the more complex morphological model with a single upstream building having a relative low height, but with some modification. When the upstream building is much higher than the surrounding buildings, the large eddies shed from the tall building may predominate the scale interaction.

1 Introduction

Understanding the dynamic transport of air and pollutants across the shear layers of street buildings to the overlying atmospheric boundary layer is crucial to the enhancement of urban air quality. Urban canopies, which contain the buildings, are usually either modelled by two-dimensional (2D) bars (Salizzoni et al. 2011; Michioka and Sato 2012; Blackman et al. 2015; Jaroslawski et al. 2019; Badas et al. 2020), which are called idealized street canyon models, or by three-dimensional (3D) cubic arrays (Grimmond and Oke 1999; Inagaki and Kanda 2008; Blackman et al. 2015; Jaroslawski et al. 2019). A morphological model can better represent the urban terrain, by incorporating the local topology, such as roof shapes, local tall buildings, etc., thereby enhancing our understanding of more realistic and complex situations. Previous research using morphological models in the urban environment mostly focused on the impact of tall building wakes (Hertwig et al. 2019, 2021) or the local topology (Kastner-Klein and Rotach 2004; Kluková et al. 2021; Mo et al. 2021) on the turbulence statistics or pollutant dispersion in the boundary layer flow. Recent research by Du et al. (2023) focused on the turbulence statistics of the flow within a street canyon and in the overlying boundary layer, downstream of a local tall building. They found lower turbulence intensities and Reynolds shear stresses at the roof-top level of the street canyon with increasing upstream building height. Du et al. (2023) also examined the airflow mass transfer along the street canyon and across the roof-top opening of the street canyon in a morphological model and found that both decreased as the upstream building became higher.

In the case of both a large enough ratio of boundary layer thickness to roughness $\delta /h_1$ and a $\delta ^+ =\delta u_* / \nu )$, the inertial layer (or the log-layer) of an urban-type rough-wall boundary layer has qualitatively similar dynamical and structural properties as smooth-wall turbulent boundary layer flows (Volino et al. 2007; Takimoto et al. 2013; Perret et al. 2019), containing coherent structures such as Large-Scale Motions (LSMs), which are packets of hairpin vortices (Zhou et al. 1999; Adrian et al. 2000), and Very Large-Scale Motions (VLSMs) (Marusic et al. 2010b), which are elongated, low- and high-momentum regions meandering horizontally above the wall.

The interaction between the inner and outer boundary layer was first examined by Rao et al. (1971), Townsend (1976) and Bandyopadhyay and Hussain (1984) for smooth-wall boundary layer flows. Townsend (1976) mentioned a superposition mechanism of the large scales on the near-wall flow, while Rao et al. (1971) found a non-linear relationship between the large scales in the outer boundary layer and the small scales in the inner boundary layer. This non-linear mechanism in the smooth-wall boundary layer was later named ‘amplitude modulation’ (Hutchins and Marusic 2007; Mathis et al. 2009). This mechanism suggested that the footprint of LSMs and VLSMs in the logarithmic region of the smooth-wall turbulent boundary layer modulated the intensity of small-scale streamwise motions in the near-wall region, with the modulation increasing with Reynolds number (Re). The degree of amplitude modulation was represented by the correlation between the large scales and the envelope of the smaller scales and was shown to be a non-linear function of the wall-normal location (Mathis et al. 2009). This theory was later refined by Talluru et al. (2014), who found that the modulation also applied to the spanwise and wall-normal small-scale fluctuations. As for the methods to analyze the scale interaction, the skewness of the streamwise velocity fluctuations was found to be related to amplitude modulation in the smooth-wall boundary layer by Mathis et al. (2009) and confirmed by Schlatter and Örlü (2010). The decomposition of skewness was then applied to observe the non-linear interaction between scales (Mathis et al. 2011a, b). To overcome the limitation of the intrinsically proportional relationship between the velocity skewness and the cross-correlation between the large-scale fluctuations and the envelope of small scales, computed at the same location (Mathis et al. 2009), Bernardini and Pirozzoli (2011) computed the two-point cross-correlation between the large-scale and small-scale velocities at different wall-normal locations to better describe the scale interaction.

Due to the difficulty of measuring velocity fluctuations in the near-wall region, Marusic et al. (2010a) and Mathis et al. (2011a) created a model for predicting the statistics of the small-scale streamwise velocity fluctuations in the wall-bounded flow using the large-scale velocity signature in the outer layer, through superposition and amplitude modulation. This model was utilized by Inoue et al. (2012) to extend the prediction at large Reynolds numbers, and later refined to comprise an increased accuracy at higher Reynolds numbers and be less driven by user input, through spectral linear stochastic estimation by Baars et al. (2016).

Considering the above-mentioned similarity of coherent structures between smooth-wall boundary layer flow and rough-wall boundary layer flow, investigations of the existence of the amplitude modulation mechanism of smooth-wall boundary layers (and its corresponding analysis methods) to rough-wall turbulent boundary layers have been carried out in recent years (Perret and Rivet 2013; Talluru et al. 2014; Nadeem et al. 2015; Anderson 2016; Blackman and Perret 2016; Squire et al. 2016; Blackman et al. 2018; Perret and Kerhervé 2019). The non-linear interaction between the scales occuring above 2D bar roughness was studied by Nadeem et al. (2015) and Blackman et al. (2018), through Direct Numerical Simulation (DNS) and experiments, respectively. Scale interaction over 3D cube roughened walls was investigated by Perret and Rivet (2013), Blackman and Perret (2016), Basley et al. (2018), Blackman et al. (2018), and Perret and Kerhervé (2019) through wind tunnel experiments and Anderson (2016) through Large Eddy Simulation (LES). Blackman and Perret (2016) and Blackman et al. (2018) found that different canopy configurations had a noticeable influence on the non-linear interaction. To further quantify both the superposition and modulation mechanisms when rough wall geometries are significantly different, a predictive model was developed for urban-type boundary layers by Blackman et al. (2019).

However, as far as the present authors are aware, most of the previous research on the scale interaction in a turbulent boundary layer has focused on boundary layers over either a smooth wall or homogeneous idealized roughness arrays. Although Pathikonda and Christensen (2017) and Awasthi and Anderson (2018) researched heterogeneous roughness, their focus was, respectively, on the turbine blade or on topographic features, such as ‘trough’ and ‘crest’, but not on the urban roughness. Based on the differences in the mean statistics observed between the idealized street canyon and a realistic street canyon, and also the effect of a single upstream tall building on the turbulence statistics of a street canyon flow (Du et al. 2023), the nature of the modulation between the scales remains an open question for morphological urban roughness. Furthermore, the presence of large-scale coherent structures in the wake of a local tall building (Wang et al. 2019), which is usually modeled as a wall-mounted rectangular-section prism, could strongly modify the downstream boundary layer (Hertwig et al. 2019; Wang et al. 2022), and, therefore, potentially modify the scale interaction mechanism.

As a crucial step towards predicting the transport dynamics of air and pollutants within the urban canopy, specifically in a street canyon, and the urban-type boundary layer, the present study focuses on analyzing the interaction between the large-scale momentum regions in the boundary layer over a heterogeneous morphological model, with or without a single local tall building upstream of the street canyon, and the small-scale fluctuations at the canyon roof-top and within the street canyon. In the present study, the questions to be addressed are:

• 1. How does the morphology impact the scale interaction in the overlying boundary layer and the street canyon, in comparison with the homogeneous roughness model?

• 2. What is the impact of a single upstream tall building and its height on the scale interaction in the boundary layer and the street canyon?

• 3. Will an irregularly-shaped upstream tall building affect the scale interaction, in comparison with an idealized regular, symmetric building?

The following section outlines the methodologies used, namely the experimental set-up, the oncoming boundary-layer statistics, and the data processing technique adopted to separate the large and small scales. Then, the influences of the heterogeneous morphological model and the upstream tall building on the scale interaction are presented in the results and discussion section, followed by the conclusions.

2 Methodologies

2.1 Experimental Set-Up

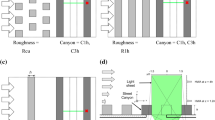
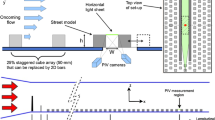
The experiments were conducted in the Atmospheric Boundary Layer Wind Tunnel in the Laboratoire de recherche en Hydrodynamique, Énergétique et Environnement Atmosphérique (LHEEA) at École Centrale de Nantes. This open-loop wind tunnel has test section dimensions of 24 m (length) $\times$ 2 m (width) $\times$ 2 m (height) and a 5:1 ratio inlet contraction. As shown in Fig. 1a, five vertically tapered spires measuring 800 mm in height and 134 mm in base width were positioned at the beginning of the test section, after which a solid fence measuring 200 mm in height and then a 17 m fetch of staggered cubes of height $h_1 = 50$ mm and plan area density $\lambda _{p_1} = 25 \%$ were placed across the test section to fully develop the boundary layer flow.

A 1:200 scale morphographic model centred around the rue de Strasbourg (RdS) in Nantes, France, was placed downstream of the cubic array. The cathedral, as shown in Fig. 1c was identified as the local tall building. The model had a plan area density $\lambda _{p_2} = 44 \%$ and an overall average building ridge height ${\overline{h}}$ of approximately 100 mm (Kastner-Klein and Rotach 2004) (excluding the cathedral). The canyon upstream building ridge height was $h_2$ = 116 mm, while the downstream ridge height was $h_3$ = 114.5 mm, and the width of the street canyon was $W_c$ = 73 mm. Therefore, the canyon aspect ratio in the present paper was $AR_c = W_c/h_2 = 0.63$. Experiments with the cathedral in the morphological model were first performed. The cathedral was then replaced by a set of square cuboids of 200 mm ($W_b$) $\times$ 200 mm cross-sectional area and varying height ($H_b$) of 100, 200, 300, or 600 mm ($AR_b=0.5,1,1.5,3$ and $H_b/\delta =0.1,0.2,0.3.0.6$, respectively), achieved by stacking 1, 2, 3 or 6 blocks, each of which had a height of 100 mm. The different configurations were denoted as Cath, $B1{\overline{h}}$, $B2{\overline{h}}$, $B3{\overline{h}}$, $B6{\overline{h}}$. It should be noted that the symmetry plane of the cathedral was positioned at an angle of approximately 70$^{\circ }$ to the street canyon principal axis (in agreement with the actual building layout in Nantes) and those of the rectangular prisms were placed normal to the canyon. The origin of the coordinate system was at the centre of the street canyon (the intersection line of the XZ and YZ plane) at $z/h_2=0$. The leeward side of the cathedral and the square cuboids were 6.5$h_2$ ($3.8D_b = 3.8W_b$) from the origin of the coordinate system. In this study, only the oncoming wind direction normal to the street canyon principal axis was studied.

Fig. 1

a Wind tunnel set-up; b stereoscopic PIV and HWA set-up for XZ plane; c simplified RdS 3D model with laser sheet in XZ plane; d actual RdS model in the wind tunnel, where the cathedral was replaced by a 3-block building; e view of the cathedral model from downstream (left) and from upstream (right)

A Dantec stereoscopic particle image velocimetry (S-PIV) system was used to measure the 3-component velocity fields throughout the experiments. A Litron double cavity Nd-YAG laser (2 $\times$ 200 mJ) was mounted on the ceiling of the wind tunnel to generate a laser light sheet in the XZ plane. Olive oil droplets of 1 $\upmu$m average diameter generated by a LaVision Laskin-Nozzle aerosol generator were utilized to seed the flow. Two $2048 \times 2048$ CCD cameras with 105 mm objective lenses were installed under the wind tunnel floor on each side of the light sheet and angled at 45$^{\circ }$ towards the sheet. 10,000 pairs of images were recorded at a frequency of 7.4 Hz, with a time delay of 300 $\upmu$s between two images of the same pair. The final spatial resolution for the experiments was 1.6 mm (0.022 $W_c$) and 3.2 mm (0.028 $h_2$) in the streamwise (x) and vertical directions (z), respectively. The Dantec Dynamic Studio software was used to synchronize the cameras and laser, and also to perform the multi-pass cross-correlation PIV processing with a final interrogation window size of 32 $\times$ 32 pixels with an overlap of 50%. Due to limitation of the S-PIV set-up, the regions extending 7.5% of $W_b$ width inward from each wall within the street canyon were not captured. Five single hot-wire anemometer (HWA) probes with a sampling frequency of 15 kHz, were evenly placed in the lateral direction with a spacing of 50 mm (0.25 $W_b$) at $z/{\overline{h}} = 3$ over the centre of the downstream street canyon building, with the middle probe being aligned with the XZ plane (at y = 0), to obtain time-resolved streamwise velocities. The HWA measurements were performed synchronously with the PIV measurements.

2.2 Oncoming Boundary Layer Statistics

All of the experiments were performed with the same oncoming boundary layer, which developed over the fetch of cubic roughness of $h_1 = 50 mm$. The free-stream velocity of $U_e = 5.8$ $\mathrm {m \, s^{-1}}$ was determined from the dynamic pressure measured by a pitot-static tube located at 1.5 m above the wind tunnel floor and 19 m downstream of the start of the wind tunnel working section at the centreline (for details of those boundary layer measurements, see Blackman and Perret 2016; Perret et al. 2019). Since the boundary layer was fully developed, the measured statistics at the present measurement location represent the oncoming boundary layer characteristics. The roughness Reynolds number, based on the upstream fetch height, was $Re_{h_1}= {h_1 u_*}/{\nu }=1.2 \times 10^{3}$, where $u_*$ was the friction velocity of the oncoming boundary layer, and $\nu$ was the kinematic viscosity.

The oncoming boundary layer parameters were documented (Perret et al. 2016; Blackman et al. 2018; Perret et al. 2019; Jaroslawski et al. 2020), as shown in Table 1, where $\delta$, d, $z_0$ and $\partial P / \partial x$ denoted boundary layer thickness, displacement height, roughness length, and longitudinal gradient of the mean static pressure, respectively. The turbulence quantities were defined as follows. The instantaneous streamwise (U), spanwise (V) and vertical (W) velocity components corresponded to those in the x, y and z directions, respectively. The time-averaged mean streamwise flow velocity was denoted as ${\overline{U}}$, and the spatially-averaged mean streamwise velocity was denoted as $\langle {U}\rangle$, which led to the double-averaged streamwise velocity $\langle {{\overline{U}}}\rangle$. The Reynolds decomposition in time $U(x,z,t)={\overline{U}}+u^\prime (x,z,t)$ was applied, where $u^\prime (x,z,t)$ was the instantaneous velocity fluctuation about the mean ${\overline{U}}$ (and similarly for the other two directions). The standard deviation and skewness of the velocities were defined as $\sigma _u=\sqrt{\overline{{(U(x,z,t)-{\overline{U}})}^2}}$, $S_u={(\overline{U(x,z,t)-{\overline{U}})^3}}/{\sigma _u}^3$, respectively. The Reynolds shear stress was denoted as $\overline{u^\prime w^\prime }= \overline{(U(x,z,t)-{\overline{U}}) (W(x,z,t)-{\overline{W}})}$ and the turbulent kinetic energy (TKE) was denoted as ${\overline{k}} = 0.5({\sigma _u}^2+{\sigma _v}^2+{\sigma _w}^2)$. Figure 2 shows the oncoming boundary layer statistics over the cubes. The global turbulence statistics within the street canyon and boundary layer in the present paper can be found in Du et al. (2023).

Table 1 Oncoming boundary layer characteristics

Fig. 2

Spatially averaged oncoming boundary layer statistics. a Mean streamwise velocity normalized by $u_*$; b standard deviation of the streamwise velocity component, vertical component, spanwise component, where $\alpha$ represents u, w, v, respectively, and Reynolds shear stress

Table 2 Standard deviation of PIV statistics in XZ plane due to statistical error at $z/h_2 = 0.5$ and $z/h_2 = 2$

The statistical error-induced standard deviation $\sigma$ of the PIV statistics was estimated at two specific heights $z/h_2 = 0.5$ and $z/h_2 = 2$ on the centreline of the XZ plane, as shown in Table 2. The assumption of a normal distribution and the number of independent samples were used for calculation. The independence was ensured by separating the samples by two integral time scales, determined from the integration of the auto-correlation of the streamwise velocity (Tropea et al. 2007). A 99% confidence bound could be achieved by applying $\pm 3 \sigma$ to the PIV statistics shown in Table 2. In the following, all the presented statistical quantities were computed using the 10,000 PIV samples.

2.3 Low-Pass Filtered and Multi-time Delayed HWA Signals

The present analysis of the interaction between the large scales of the boundary layer or large-building wake and the smaller scales within the canyon uses a scale-separation technique based on the detection of the larger ones in the flow well above the canopy using HWA. Following Blackman and Perret (2016) and Blackman et al. (2018), the HWA signals were low-pass filtered to isolate the large-scale contribution from the local small scales. Figure 3 shows the pre-multiplied power spectrum of the streamwise velocity component measured by HWA at $z/h_2 = 2.58$ and $y/h_2 = 0.86$ for all the measured configurations. The corresponding frequencies of the peak regions in $B1{\overline{h}}$ and $B2{\overline{h}}$ cases are smaller than the other cases, due to the influence of the upstream tall building wake (see Du et al. 2023 for more details). The cut-off frequency for the $B1{\overline{h}}$ and $B2{\overline{h}}$ cases was chosen as 5 Hz ($fW_b/U_e=0.17$), which lays within the cut-off frequency range suggested by Mathis et al. (2009) and Blackman and Perret (2016). Too much information could be filtered out if the same cut-off frequency was applied to the $B3{\overline{h}}$, Cath and $B6{\overline{h}}$ cases, since the peak regions of the pre-multiplied power spectra in these cases were close to 5 Hz. Therefore, the cut-off frequency for the $B3{\overline{h}}$, Cath and $B6{\overline{h}}$ cases was chosen at the same energy level as the $B1{\overline{h}}$ and $B2{\overline{h}}$ configurations, which corresponded to 17.4 Hz ($fW_b/U_e=6$).

Fig. 3

Pre-multiplied spectra of the streamwise velocities captured by HWA at $z/h_2 = 2.58$ and $y/h_2 = 0.86$ in different configurations, in comparison with that above a homogeneous cubic array at $z/h_2 = 1.72$ under the same inlet conditions (Blackman and Perret 2016). The vertical dashed lines correspond to the cut-off frequencies used for scale separation and the horizontal dashed line correspond to the energy level at the cut-off frequency

Fig. 4

Auto-correlation $R_{uu}$ of filtered HWA and PIV measurements at $z/h_2=2.58$ and $x/h_2 = 0$ of a $B1{\overline{h}}$; a $B6{\overline{h}}$. The vertical dashed lines correspond to the maximum time delay, where $R_{uu} \approx 0$, selected for the multi-time delay LSE processing among all the configurations to ensure consistency

As noted by Durgesh and Naughton (2010), multi-time delay Linear Stochastic Estimation (LSE) in the time domain uses the same signal multiple times from the past and future for estimating a conditional event, and, therefore, it performs in the same way as the implementation of a non-causal filter. The temporal auto-correlations of HWA and PIV measurements (Fig. 4), which represent how the average energy containing eddies are correlated with themselves, measured at $z/h_2=2.58$ and $x/h_2 = 0$ in the $B1{\overline{h}}$ and $B6{\overline{h}}$ configurations, showed great agreement with each other and both decreased to around 0 at $t=0.5$ s. Therefore, to be consistent among all the configurations, for a single physical HWA signal in all the measured configurations, 20 time-delayed HWA signals were generated corresponding to linear time-delay increments of 0.05 s from $-$ 0.5 to 0.5 s, where the signal with zero-time delay represents the physical signal. These time-delayed HWA signals (100 in total) could be regarded as imaginary HWA probes, either upstream or downstream of the actual array of the HWA probes. An illustration of the HWA and filtered HWA signals with multiple time delays at $z/h_2 = 2.58$ and $y/h_2 = 0.86$ is shown in the upper right part of Fig. 5.

To apply the Proper Orthogonal Decomposition-Linear Stochastic Estimation (POD-LSE) method (Podvin et al. 2018), the actual and multi-time delayed HWA signals are down-sampled at the synchronized time to achieve the same number of snapshots as the PIV measurements, and, thus, achieve the requirements of linear mapping from the temporal coefficients of the HWA to those of the PIV.

Fig. 5

Flow chart of the POD-LSE method used for scale decomposition in the present study, adopting the method by Podvin et al. (2018)

2.4 Proper Orthogonal Decomposition—Linear Stochastic Estimation Method

The present study employs the POD-LSE method, introduced by Podvin et al. (2018). This approach enables a direct mapping of the POD amplitudes from the measurements to the desired field estimation, all in a single-step procedure. According to Podvin et al. (2018), the computation of POD bases can be performed using either the direct method or the method of snapshots. The snapshot method of POD (Sirovich 1987) is utilized in the derivation presented in this section. A flow chart of the application of the POD-LSE method is shown in Fig. 5. The bold symbols in the following mathematical derivations represent vector quantities, and the plain text symbols represent scalar quantities. In the present study, the velocity fluctuations of the flow field are denoted as ${\varvec{u}}$(${\varvec{x}}$ $,t^n$) at the $n^{\textrm{th}}$ snapshot of the time history and the measurement spatial location of ${\varvec{x}}$, defined in a physical domain $\varOmega$. The POD formalism leads to the following eigenvalue problem that must be solved for the nth eigenmodes $a_n(t)$ and the nth eigenvalue $\lambda _n$,

$$\begin{aligned} \int _{\varOmega }^{}C(t,t^\prime ) a_n(t^\prime ) d\mu (t^\prime )=\lambda _n a_n(t), \end{aligned}$$

(1)

where $d\mu$ is the integration measure. The two-point temporal correlation tensor between the time t and $t^\prime$ is:

$$\begin{aligned} C(t,t^\prime )=\frac{1}{N}\int _{\varOmega }^{}{\varvec{u}} ({\varvec{x}},t){\varvec{u}}({\varvec{x}},t^\prime )d{\varvec{x}}, \end{aligned}$$

(2)

where N is the number of the snapshots of the whole time history, and $t^\prime$ is another snapshot in the time history.

A slice of the velocity fluctuation field measured by PIV (with the subscript P) and multi-time delayed filtered HWA which is down-sampled at 7.4 Hz (with the subscript H) at time $t^n$ can be reconstructed using the temporal POD modes, as shown in Eqs. 3 and 4, where i, either subscript or superscript, represents the index of the POD modes from 1 to the total number of snapshots N:

$$\begin{aligned} {\varvec{u}}_{P} ({\varvec{x}},t^n)= & {} \sum _{i=1}^{N}a_i(t^n)\varvec{\varPhi }^{i}({\varvec{x}}), \end{aligned}$$

(3)

$$\begin{aligned} {\varvec{u}}_{H} ({\varvec{x}},t^n)= & {} \sum _{i=1}^{N}b_i(t^n)\varvec{\varPsi }^{i}({\varvec{x}}), \end{aligned}$$

(4)

where $\varvec{\varPhi }^{i}$ and $\varvec{\varPsi }^{i}$ are the sets of spatial POD modes respectively obtained by back-projection from the PIV or HWA velocity fluctuation field onto the temporal coefficients obtained from the eignevalue problem:

$$\begin{aligned} \varvec{\varPhi }^{i}({\varvec{x}})= & {} \int _{\varOmega }^{}a_i(t^n){\varvec{u}}_{P}({\varvec{x}},t^n)d\mu (t) \cong \sum _{i=1}^{N}a_i(t^n){\varvec{u}}_{P}({\varvec{x}},t^n), \end{aligned}$$

(5)

$$\begin{aligned} \varvec{\varPsi }^{i}({\varvec{x}})= & {} \int _{\varOmega ^\prime }^{}b_i(t^n){\varvec{u}}_{H}({\varvec{x}},t^n)d\mu ^\prime (t) \cong \sum _{i=1}^{N}b_i(t^n){\varvec{u}}_{H}({\varvec{x}},t^n). \end{aligned}$$

(6)

Note that the HWA velocity fluctuation fields are in another physical domain ($\varOmega ^\prime$). A linear operator ${\mathcal {L}}$ is used to represent the relationship between the PIV and HWA-measured velocity fluctuation fields ${\varvec{u}}_{H}={\mathcal {L}}{\varvec{u}}_{P}$ (Podvin et al. 2018). Then, $\varvec{\varPsi }^{i}({\varvec{x}})$ can be rewritten as:

$$\begin{aligned} \varvec{\varPsi }^{i}({\varvec{x}})=\int _{\varOmega ^\prime }^{}{\mathcal {L}} b_i(t^n){\varvec{u}}_{P}({\varvec{x}},t^n)d\mu ^\prime (t) \cong \sum _{j=1}^{N}\varvec{\varPhi }^j({\varvec{x}})\int _{\varOmega ^\prime }^{}{\mathcal {L}}a_j(t^n) b_i(t^n)\varvec{\varPsi }^i({\varvec{x}})d\mu ^\prime ({\varvec{x}}). \end{aligned}$$

(7)

Equations 3 and 4 can be re-formed, using matrix notation, as:

$$\begin{aligned} U_{P}= & {} \varvec{\varPhi } A=\varvec{\varPhi } D_{U,P} {\tilde{A}}, \end{aligned}$$

(8)

$$\begin{aligned} U_{H}= & {} \varvec{\varPsi } B=\varvec{\varPsi } D_{U,H} {\tilde{B}}, \end{aligned}$$

(9)

where $A_{in}=a_i(t^n)$ and $B_{in}=b_i(t^n)$. The mapping matrix from A to B is M. A and B can be normalized to the unitary matrices ${\tilde{A}}$ and ${\tilde{B}}$ by $D_{U,P}$ and $D_{U,H}$, respectively. U is the snapshot matrix where the $n^{\textrm{th}}$ column is the $n^{\textrm{th}}$ snapshot. Using this notation, the Singular Value Decomposition (SVD) method can be applied for snapshot POD in the decomposition of the fields measured by PIV. It should be emphasized here that, in the HWA measurements, the number of spatial locations limits the POD modes rather than the number of available snapshots. Hence, it is recommended to employ the direct method of POD to compute the POD basis associated with the HWA data (Podvin et al. 2018). The modal energy fractions of the HWA and PIV data are shown in Fig. 6. A linear mapping can be found from ${\tilde{A}}$ to ${\tilde{B}}$,

$$\begin{aligned} {\tilde{M}}={\tilde{A}}{\tilde{B}}^T. \end{aligned}$$

(10)

As suggested by Podvin et al. (2018), the linear stochastic estimation is accomplished since the POD amplitudes of the PIV-measured velocity fluctuation fields are linearly linked by a transfer function onto the POD basis of the HWA velocity fluctuation field. Podvin et al. (2018) also mentioned that the number of POD modes of the HWA velocity fluctuation field attained through this method constrain the fluctuating kinetic energy of the PIV fields through mapping and, therefore, the large-scale velocity fluctuation fields can be separated. Unlike the description by Podvin et al. (2018), the ${\tilde{M}}$ and ${\tilde{B}}$ in Eq. 10 are not necessarily unitary matrices, since the number of spatial modes of the HWA data is smaller than the number of HWA snapshots. The subscripts L and S represent the large-scale and small-scale properties, respectively. The $n^{\textrm{th}}$ column of $U_{PIV, L}$ is the $n^{\textrm{th}}$ estimated snapshot of the reconstructed velocity fluctuation field which only contains large-scale fluctuations:

$$\begin{aligned} {\tilde{A}}_{L}= & {} {\tilde{M}}{\tilde{B}}, \end{aligned}$$

(11)

$$\begin{aligned} U_{P,L}= & {} \varvec{\varPhi }D_{U,{P}}{\tilde{A}}_{L}, \end{aligned}$$

(12)

$$\begin{aligned} U_{P,S}= & {} U_{P}-U_{P,L}. \end{aligned}$$

(13)

As shown in Eqs. 12 and 13, the instantaneous small-scale velocity fluctuation field was decomposed by subtracting the reconstructed large-scale fields from the original instantaneous velocity fluctuation field, at the same PIV measurement frequency. To extend the large-scale fluctuations to a higher frequency, the multi-time delayed filtered HWA signals, either at the original measurement frequency or at a down-sampled frequency higher than 7.4 Hz, can be decomposed using the same HWA modes. The subscript hf denotes ‘higher frequency’ in the following equations:

$$\begin{aligned} U_{H,hf}=\varvec{\varPsi } B_{hf}, \end{aligned}$$

(14)

In the reconstruction, the mapping matrix M should be applied. To be consistent with the previous steps, Eqs. 15 and 16 are shown in the normalized form. In the present study, the large-scale fluctuations are estimated at 177.6 Hz using the filtered HWA which is down-sampled at 177.6 Hz. This frequency is selected to be 24 times the PIV measurement frequency so that it contains sufficient temporal information:

$$\begin{aligned} {\tilde{A}}_{L,hf}= & {} {\tilde{M}} D_{U,H}^{-1}B_{hf}, \end{aligned}$$

(15)

$$\begin{aligned} U_{P,L,hf}= & {} \varvec{\varPhi }D_{U,P}{\tilde{A}}_{L,hf}. \end{aligned}$$

(16)

Fig. 6

Relative fraction of fluctuating energy captured by the POD modes corresponding to the filtered HWA and the PIV measurements

3 Results and Discussion

3.1 Characteristics of the Estimated Large-Scale Fluctuations

The temporal evolution of the instantaneous estimated large-scale streamwise velocity fluctuations of all the configurations within the same duration of time is shown in Fig. 7. The high- and low-momentum regions show a general pattern of alternation in all the configurations. The large scales span a shorter period, in general, when the upstream building is higher, in agreement with the spectra shown in Fig. 3. The streamwise length scales of the large-scale streamwise velocity fluctuations are estimated using the temporal auto-correlation $R_{u_L u_L}$ and Taylor’s hypothesis of frozen turbulence,

$$\begin{aligned} L_{u_L}(z)={\overline{U}}(z)\int _{0}^{+\infty }R_{u_L u_L}(z,\tau )d\tau . \end{aligned}$$

(17)

The length scales of the large-scale streamwise velocity fluctuations are shown in Fig. 8. $B1{\overline{h}}$ has an average length scale of $\langle {L_{u_L}}\rangle /h_2=8$, which is around $1\delta$. This length scale is smaller than that reported in Blackman and Perret (2016) and Perret and Kerhervé (2019), but larger than Ferreira and Ganapathisubramani (2021), who used a different method, while maintaining the same magnitude order. The integral length scale decreases as the upstream building height increases, consistent with the earlier discussion regarding the overall pattern and time-span of the fluctuations, as shown in Fig. 6. The contribution of the large scales to the variances $\sigma _u^2$, $\sigma _w^2$, $\sigma _v^2$ and the Reynolds stress $-\overline{u^\prime w^\prime }$ of the three roughness configurations is shown in Fig. 9 (the magnitudes themselves can be found in Du et al. 2023). Within all the canopy layers, the small scales represent the major contribution to all the variances and the Reynolds shear stress, while the large-scale contribution starts to become significant for all the quantities in the overlying boundary layer. The contribution of large scales to $\sigma _v^2$ in the $B6{\overline{h}}$ case shows a linearly increasing pattern, which is different from the other configurations. The turbulent velocity fluctuations of the large-scale structures in the vertical and spanwise direction in the measured plane are higher than the general $B3{\overline{h}}$ case of the same height, at heights above $z/h_2=1.5$, which indicates that the asymmetry of the upstream building can increase the relative energy of the large scales in the wake, especially in the vertical and spanwise direction.

Fig. 7

An excerpt of the temporal evolution of the streamwise velocity fluctuations $u_L^{\prime }$ predicted by the POD-LSE model at $x/h_2=0$ and $y/h_2=0$ at the frequency of 177.6 Hz for a $B1{\overline{h}}$; b $B2{\overline{h}}$; c $B3{\overline{h}}$; d $B6{\overline{h}}$; e Cath configurations

Fig. 8

Spatially-averaged streamwise a integral time scale $t_{u_{L}}$ and b integral length scales $L_{u_{L}}$ of the large-scale streamwise velocity fluctuations predicted by the POD-LSE model

Fig. 9

Contribution of the large scales a $\langle {\sigma _{u_L}^2}\rangle$; b $\langle {\sigma _{w_L}^2}\rangle$; c $\langle {\sigma _{v_L}^2}\rangle$; d $\langle {\overline{u_L^{\prime }w_L^{\prime }}}\rangle$ to the spatially-averaged statistics. The discontinuous spikes in d are due to the zero-value denominators of $\langle {\overline{u^{\prime }w^{\prime }}}\rangle$

3.2 Skewness Decomposition

As shown in Fig. 10, for the $B1{\overline{h}}$ case, $\langle {\overline{{u^\prime }^3}}\rangle$ shows a sharp peak at the roof-top in the shear layer and then constantly decreases at a moderate rate with increasing height until above the shear layer. As explained by Blackman et al. (2018), the steep peak of the skewness correponds to strong downward sweeping motions. For the $B2{\overline{h}}$, $B3{\overline{h}}$ and Cath cases, $\langle {\overline{{u^\prime }^3}}\rangle$ also reaches the maximum magnitude at the roof-top and then decreases in the vertical direction within the shear layer, while a second increase starting from the upper bound of the shear layer can be found. The second increase may be due to the upstream building height since the skewness reaches its maximum at the corresponding height of the upstream buildings. For the $B6{\overline{h}}$ configuration, no obvious increase of $\langle {\overline{{u^\prime }^3}}\rangle$ at the upper bound of the shear layer at the roof-top can be found, but the value continues to decrease at a slower rate above the shear layer.

Fig. 10

Scale-decomposed skewness of the streamwise velocity component $\langle {\overline{u^{\prime 3}}}\rangle$ of a $B1{\overline{h}}$; b $B2{\overline{h}}$; c $B3{\overline{h}}$; d $B6{\overline{h}}$; e Cath configurations

Among all the configurations, whether there is an upstream tall building or not, the $\langle {\overline{{u_{s}^\prime }^3}}\rangle$ term predominates the skewness within the street canyon and the shear layer, as reported by Blackman et al. (2018). One possible explanation for this phenomenon is that the sweep events arise from small-scale fluctuations. For the $B1{\overline{h}}$ case, the skewness of the small-scale fluctuations decreases to become negative above the shear layer, in agreement with Blackman et al. (2018), which may suggest small-scale ejection motions.

The large-scale term $\langle {\overline{{u_{L}^\prime }^3}}\rangle$ and the cross-term $3\langle {\overline{{u_{L}^\prime }^2 u_{s}^\prime }}\rangle$ contribute a negligible amount to the skewness throughout all the boundary layers at heights below $z/h_2=2$. The contribution of the cross-term $3\langle {\overline{u_{L}^\prime {u_{s}^\prime }^2}}\rangle$, which shows the influence of the large-scale fluctuations on the small scales, starts to become non-negligible above a height of $z/h_2=0.75$ for all the configurations. For the $B1{\overline{h}}$, $B2{\overline{h}}$ and $B3{\overline{h}}$ cases, the contribution of $3\langle {\overline{u_{L}^\prime {u_{s}^\prime }^2}}\rangle$ becomes the same as $\langle {\overline{{u_{s}^\prime }^3}}\rangle$ in the upper part of the shear layer, indicating a profound level of scale interaction. For the $B6{\overline{h}}$ and Cath cases, the equivalent contribution happens at a height of $z/h_2=2$. The heights of the peak region of $3\langle {\overline{u_{L}^\prime {u_{s}^\prime }^2}}\rangle$ also correspond to the upstream building height. In addition to the interaction between $u_L^\prime$ and the small-scale streamwise velocity fluctuation $u_S^\prime$, the interaction between $u_L^\prime$ and the small-scale spanwise $v_S^\prime$ or the wall-normal component $w_S^\prime$ is also shown in Fig. 11. Among all the cases, the interactions shows qualitatively similar trends in the wall-normal direction for all three components, which means the large-scale structures influence all the small-scale structures through the same type of mechanism. A similar trend can be found in Blackman et al. (2018). The large-scale structure interacts with the spanwise small scales in a stronger way than in the other two directions in the $B6{\overline{h}}$ case.

Fig. 11

Third-order moments $\langle {\overline{u_L^{\prime } x_S^{\prime }}}\rangle$ normalized by $\langle {\sigma _u \sigma _x^2}\rangle$ of a $B1{\overline{h}}$; b $B2{\overline{h}}$; c $B3{\overline{h}}$; d $B6{\overline{h}}$; e Cath configurations, where x represents u, w or v

3.3 Temporal Cross-Correlations

In order to assess the spatial-temporal structure of the scale-interaction mechanism, the two-point space-time cross-correlation between the large-scale components with the squared small-scale fluctuations is formed, as shown in Eq. 18:

$$\begin{aligned} R_{{u_L}{u_S^2}}(x_S,z_S,x_L,z_L,\tau )=\frac{\overline{u_L^{\prime }(x_L,z_L,t+\tau )u_S^{\prime 2}(x_S,z_S,t)}}{\sqrt{\overline{u_L^{\prime 2}(x_L,z_L)}}\sqrt{\overline{u_S^{\prime 4}(x_S,z_S)}}}. \end{aligned}$$

(18)

Fig. 12

Spatially-averaged cross-correlation coefficient $\langle {R_{{u_L}{u_S^2}}}\rangle$ where $x_L=x_S$ and $z_L=z_S$ of a $B1{\overline{h}}$; b $B2{\overline{h}}$; c $B3{\overline{h}}$; d $B6{\overline{h}}$; e Cath configurations

Figure 12 shows the spatial-temporal cross-correlation $\langle {R_{{u_L}{u_S^2}}}\rangle$ using Eq. 18, where $x_L=x_S=0$ and $z_L=z_S$. For the $B1{\overline{h}}$ configuration, a peak is found in the roughness sublayer and the values decay to zero at around $z/h_2=0.75$ and $z/h_2=2$ in the wall-normal direction. A slight inclination in the positive temporal direction suggests the large-scale fluctuations that occur upstream in the flow interact with the small scales in the shear layer, as found previously (Chung and McKeon 2010; Guala et al. 2011; Baars et al. 2015; Pathikonda and Christensen 2017; Blackman et al. 2018). The hypothesis by Baars et al. (2015) is that a smooth transition between the scale alignment and its bounding phenomena cause the time shift, with the modulation influence near the wall and the intermittent behaviour near the boundary layer edge. Pathikonda and Christensen (2017) think the inclined large-scale motions can be earlier detected at a fixed location, such as a probe, relative to the modulation influences near the wall. For the $B2{\overline{h}}$, $B3{\overline{h}}$, and Cath cases, a strong correlation can still be found at the upper bound of the shear layer, but the peak regions are at the height of the corresponding upstream building. This may suggest that the large-scale motions which develop over the cubic array can be altered by the upstream building and the wakes generated by the buildings may partly join or replace the large-scale motions developed upstream. For the $B6{\overline{h}}$ configuration, the maximum correlation region cannot be identified since the correlated region extends beyond the maximum measurement height.

Fig. 13

Spatially-averaged cross-correlation coefficient $\langle {R_{{u_L}{u_S^2}}}\rangle$ where $x_L=x_S$ and $z_S=0.75h_2$ of a $B1{\overline{h}}$; b $B2{\overline{h}}$; c $B3{\overline{h}}$; d $B6{\overline{h}}$; e Cath configurations

A spatially-averaged two-point spatial-temporal correlation $\langle {R_{{u_L}{u_S^2}}}\rangle$ using Eq. 18, where $x_L=x_S=0$ and $z_S=0.75h_2$, can bring insight into the temporal evolution of the interaction between the large-scale motions and the small-scale fluctuations at a fixed point at in the street canyon, as shown in Fig. 13. For the $B1{\overline{h}}$ case, a positive correlation can be found at the height of $z/h_2=1.2$ and $z/h_2=0.9$ at the corresponding time delays of $\tau U_e/\delta =-1$ and $\tau U_e/\delta =1$, respectively. Blackman and Perret (2016) showed a similar peak value of the cross-correlation, but the peak region was at $z/h_2=0.75$ and $\tau U_e/\delta =0$. The peak of the correlation tends to shift in the negative temporal direction as the large-scale reference location in the boundary layer increases in height. The inclination of the temporal shift is around $\theta =\textrm{tan}^{-1}(\varDelta z/(\varDelta \tau U_e))=13.4^{\circ }$. The positive cross-correlation does not penetrate as deeply as in the idealized street canyon cases (Blackman and Perret 2016; Blackman et al. 2018), which may be explained by the fact that the smaller aspect ratio of the present street canyon makes the penetration of the large-scale motion into the street canyon impossible. Also, the pitched-roof of the street canyons in the present study may impede the movement of the large scales, thereby, creating a tailed cross-correlation region with positive time delays. Therefore, the amplitude modulation mechanism mentioned in the previous research (Blackman and Perret 2016; Blackman et al. 2018) still exists in the $B1{\overline{h}}$ case, but slightly modified. Blackman and Perret (2016) and Blackman et al. (2018) found a negative cross-correlation region in the street canyon which was explained by the correlation of the re-circulation of the flow within the street canyon having negative large-scale fluctuations. However, such a region is not obvious in the present $B1{\overline{h}}$ case.

For the $B2{\overline{h}}$, $B3{\overline{h}}$, and Cath cases, a similar inclination of the peak cross-correlations to the $B1{\overline{h}}$ case can be observed. However, it is harder to estimate the inclination angle since the large scales in the boundary layer are less correlated to the small scales in the street canyon, compared to the $B1{\overline{h}}$ case, and the shape of the correlation in the boundary layer is also less uniform. The main idea of the amplitude modulation mechanism still applies to these cases but is greatly modified.

The cross-correlation is less significant in the $B6{\overline{h}}$ case and shows a remarkably different periodic pattern compared with the configurations with lower upstream buildings. The positive regions repeat around every $\tau U_e/\delta =3$ ($\tau =0.5$s) on average. The Strouhal number for the 6-block building was determined to be $St=fW_b/U_e=0.082$ ($\tau =0.42$s) (Cao et al. 2022; Du et al. 2023), where $W_b=0.2$m is the width of the building. The similar values of $\tau$ suggest that the interaction may be overtaken by the energetic large scales, such as the large eddies shed from the upstream wall-bounded finite-length tall building. However, given the low level of correlation shown in Fig. 13d, these conclusions must be considered with caution. They suggest that the interaction mechanism between the larger scales of the flow and the canyon flow depends on the presence of tall obstacle upstream the canyon but call for further investigation.

An illustrative cartoon depicting the qualitative conclusion is presented in Fig. 14. On the left side, the large-scale high or low momentum regions within the boundary layer have the potential to amplify or suppress small-scale fluctuations at the roof-top, respectively. On the right side, the boundary layer downstream of a tall building can exhibit large-scale eddies, which can amplify or suppress small-scale fluctuations at the roof-top level.

4 Conclusions

A realistic 1:200 scale morphological model of Rue de Strasbourg, Nantes, France was placed in wind tunnel, with a set of upstream buildings of different heights, including the irregularly-shaped cathedral (Cath) or square-based rectangular generic prisms, to investigate the influence of the neighborhood morphology on the interaction between the street canyon flow and the large scales of the flow developing above. The square cuboids were constructed with a cross-sectional area of 200 mm ($W_b$) $\times$ 200 mm and a varying height ($H_b$) of 100, 200, 300, or 600 mm ($AR_b=0.5,1,1.5,3$ respectively), labelled as $B1{\overline{h}}$, $B2{\overline{h}}$, $B3{\overline{h}}$, $B6{\overline{h}}$. Velocity measurements were performed using synchronized PIV and HWA. The Proper Orthogonal Decomposition-Linear Stochastic Estimation (POD-LSE) method was applied to separate the large- and small-scale velocity fluctuations and extend the large-scale fluctuations to a higher frequency.

Fig. 14

Qualitative cartoon illustrating the influence of large-scale low momentum structure (blue) and high momentum structure (red) on small scales generated by the roughness without a presence of a single local tall building (left), and the influence of large-scale tall building wake eddies on the small scales (right)

Referring back to the three key research questions mentioned in the introduction, the three main conclusions from this study are:

• 1. The skewness decompostion for the $B1{\overline{h}}$ case shows a good agreement with the previous idealized street canyon research. A similar cross-correlation $\langle {R_{{u_L}{u_S^2}}}\rangle$ in the $B1{\overline{h}}$ configuration is found as in the idealized street canyon studies, while another cross-correlation peak region at the roof-top level is observed with positive time lags, which can be a result of the pitched-roofs impeding the movement of the large scales. This indicates that, overall, the amplitude modulation mechanism applies to the morphological model, as well as to the smooth and homogeneous rough surface boundary layer flows examined previously.

• 2. The integral length scale of large-scale fluctuations decreases as the upstream building height increases. The small scales comprise the majority of the variances and the Reynolds shear stress, while the large scales start to contribute to the variance and Reynolds shear stress in the overlying boundary layer. The cross-term $3\langle {\overline{{u_{L}^\prime }^2 u_{s}^\prime }}\rangle$ in the skewness decomposition achieves its highest contribution when the height corresponds to that of the upstream building. The large scale fluctuations impact the three velocity components of the small scales. The amplitude modulation mechanism remains applicable to the $B2{\overline{h}}$ and $B3{\overline{h}}$ cases, but less correlated compared to the $B1{\overline{h}}$ case. The correlation is less noticeable in the $B3{\overline{h}}$ case than the $B2{\overline{h}}$ case. The mechanism for the $B6{\overline{h}}$ configuration is greatly altered and its cross-correlation of the large scales in the boundary layer and the small scales at a selected point in the street canyon seems to show a periodic pattern with a frequency close to the shedding frequency computed from the Strouhal number of a 6-block building, indicating that the vortex shedding from the upsteam building in $B6{\overline{h}}$ may dominate the scale interaction.

• 3. The Cath case, with its more complex geometry, shows a smaller integral length scale of the large-scale fluctuations compared to the $B3{\overline{h}}$ case, which is of the same height. The contribution to the variance, Reynolds shear stress, and skewness of the large scales in the Cath case is larger than in the $B3{\overline{h}}$ case. A clearer pattern of the cross-correlation can be found, which means that the amplitude modulation mechanisms is still present in the Cath case, but greatly altered.

Further research will investigate the possibility of predicting the small-scale fluctuations through a new scale interaction mechanism that incorporates the presence of an upstream tall building.