A black-box rational Arnoldi variant for Cauchy–Stieltjes matrix functions

Abstract

Rational Arnoldi is a powerful method for approximating functions of large sparse matrices times a vector. The selection of asymptotically optimal parameters for this method is crucial for its fast convergence. We present and investigate a novel strategy for the automated parameter selection when the function to be approximated is of Cauchy–Stieltjes (or Markov) type, such as the matrix square root or the logarithm. The performance of this approach is demonstrated by numerical examples involving symmetric and nonsymmetric matrices. These examples suggest that our black-box method performs at least as well, and typically better, as the standard rational Arnoldi method with parameters being manually optimized for a given matrix.

1 Introduction

An important problem arising in science and engineering is the computation of the matrix-vector product f(A)v, where A∈ℂ^N×N, v∈ℂ^N, and f is a function such that f(A) is defined. The term f(A) is called a matrix function, and a sufficient condition for f(A) to be defined is that f(z) be analytic in a neighborhood of Λ(A), the set of eigenvalues of A. For more detailed information on matrix functions and their possible definitions we refer to the monograph by Higham [28].

In most applications, A is very large and sparse (e.g., a finite-difference or finite-element discretization of a differential operator), so that explicitly computing and storing the generally dense matrix f(A) is infeasible. In the recent years, polynomial and rational Krylov methods have proven to be the methods of choice for computing approximations to f(A)v efficiently, without forming f(A) explicitly. Rational Krylov methods require the solution of shifted linear systems with A, and the approximations they deliver are rational matrix functions of the form r _n (A)v, with r _n being a rational function of type (n−1,n−1) and n≪N. Polynomial Krylov methods are a special case obtained when r _n reduces to a polynomial. Although each iteration of a rational Krylov method may be considerably more expensive than a polynomial Krylov iteration, rational functions often have superior approximation properties than polynomials, which may lead to a reduction of the overall Krylov iteration number.

An important pitfall, which possibly prevents rational Krylov methods from being used more widely in practice, is the selection of optimal poles of the rational functions r _n . These poles are parameters that should be chosen based on the function f, the spectral properties of the matrix A, and the vector v. While the function f is usually known a priori, spectral properties of A may be difficult to access when A is large. Recently, interesting strategies for the automated selection of the poles have been proposed for the exponential function and the transfer function of symmetric and nonsymmetric matrices, see [18] and [19], respectively. The algorithms proposed in these two papers gather spectral information from quantities computed during the rational Krylov iteration, and they only require some initial rough estimate of the “spectral region” of the matrix A (see [19]). Because the exponential function can be represented as a Cauchy (or Fourier) integral along the imaginary axis, one can motivate that it is natural to choose the poles of the rational Krylov space as mirrored images of rational Ritz values for A with respect to the imaginary axis, and a similar reasoning applies for the resolvent function, see [18, 19]. In the case of functions of Cauchy–Stieltjes (or Markov) type the imaginary axis does not play a prominent role, such that a direct application of the idea of mirrored Ritz values is not helpful. The aim of this paper is to give analysis and numerical evidence for a heuristic pole selection strategy for such functions of non-necessarily symmetric matrices proposed in [26]. Cauchy–Stieltjes functions are of the form

$$ f(z) = \int_{\varGamma}\frac{\mathrm{d}\gamma(x)}{z-x} $$

(1.1)

with a (complex) measure γ supported on a prescribed closed set Γ⊂ℂ. Particularly important examples of such functions are

For instance, certain solutions of the equation

$$A\boldsymbol {u}(t) - \frac{\mathrm{d}^2\boldsymbol {u}}{\mathrm{d}t^2} (t) = g(t)\boldsymbol {v} $$

can be represented as u(t)=f(A)v with f being a rational function of f ₁ and f ₂ (cf. [15, 17]). Functions of this type also arise in the context of computation of Neumann-to-Dirichlet and Dirichlet-to-Neumann maps [3, 16], the solution of systems of stochastic differential equations [2], and in quantum chromodynamics [22]. Another relevant Cauchy–Stieltjes function is

$$f_3(z) = \frac{\log(1+z)}{z} = \int_{-\infty}^{-1} \frac {-1/x}{z-x} \, \mathrm{d}x; $$

see [28] for applications of this function. The variant of the rational Arnoldi method presented here is parameter-free and seems to enjoy remarkable convergence properties and robustness. We believe that our method outperforms (in terms of required iteration numbers) any other available rational Krylov method for the approximation of f(A)v, and we will demonstrate this by a number of representative numerical tests.

This paper is structured as follows. In Sect. 2 we review the rational Arnoldi method and some of its important properties. In Sect. 3 we present our automated version of the rational Arnoldi method for functions of Cauchy–Stieltjes type (1.1). The problem of estimating the error of Arnoldi approximations is dealt with in Sect. 4. In Sect. 5 we study the asymptotic convergence of our method and compare it to other available methods for the approximation of f(A)v. Finally, in Sect. 6 we demonstrate the performance of our parameter-free algorithm for a large-scale numerical example. Throughout this paper, ∥⋅∥ denotes the Euclidian norm, I is the identity matrix of size N×N, and $\overline{\mathbb{C}} = \mathbb{C}\cup\{\infty\}$ is the extended complex plane. Vectors are printed in bold face.

2 Rational Arnoldi method

A popular rational Krylov method for the approximation of f(A)v is known as the rational Arnoldi method. It is based on the extraction of an approximation f _n =r _n (A)v from a rational Krylov space [35, 36]

(2.1)

where the parameters $\xi_{j}\in\overline{\mathbb{C}}$ (the poles) are different from the eigenvalues Λ(A). Note that fractions in (2.1) range over the linear space of rational functions of type (n−1,n−1) with a prescribed denominator q _n−1, and that reduces to a polynomial Krylov space if we set all poles ξ _j =∞. If is of full dimension n, as we assume in the following, we can compute an orthonormal basis V _n =[v ₁,…,v _n ]∈ℂ^N×n of this space. The rational Arnoldi approximation is then defined as

$$ \boldsymbol {f}_n := V_n f(A_n) V_n^{*}\boldsymbol {v}, \quad A_n := V_n^{*} A V_n. $$

(2.2)

If n is relatively small, then f(A _n ) can be evaluated easily using algorithms for dense matrix functions (see [28]). A stable iterative procedure for computing the orthonormal basis V _n is the rational Arnoldi algorithm by Ruhe [36], which we briefly review in the following. Let σ be a finite number different from all ξ _j , and consider the translated operator $\tilde{A}:= A- \sigma I$ and the translated poles $\tilde{\xi}_{j} := \xi_{j}-\sigma$. Note that the rational Krylov space built with the poles $\tilde{\xi}_{j}$ coincides with . We may therefore equally well construct an orthonormal basis for as follows:

Starting with v ₁=v/∥v∥, in each iteration j=1,…,n one utilizes a modified Gram–Schmidt procedure to orthogonalize the vector

$$ \boldsymbol {w}_{j+1} = (I - \tilde{A}/\tilde{\xi}_j )^{-1}\tilde{A} \boldsymbol {v}_j $$

(2.3)

against {v ₁,…,v _j }, yielding the vector v _j+1, ∥v _j+1∥=1 which satisfies

$$ \boldsymbol {v}_{j+1}h_{j+1,j} = \boldsymbol {w}_{j+1} - \sum_{i=1}^j \boldsymbol {v}_i h_{i,j}, \quad h_{i,j} = \boldsymbol {v}_i^{*} \boldsymbol {w}_{j+1}. $$

(2.4)

Equating (2.3) and (2.4), and collecting the orthogonalization coefficients in H _n =[h _i,j ]∈ℂ^n×n, we obtain in the n-th iteration of the rational Arnoldi algorithm a decomposition

$$\tilde{A} V_n \bigl(I_n + H_n \operatorname {diag}\bigl(\tilde{\xi}_1^{-1},\ldots,\tilde{\xi}_n^{-1}\bigr) \bigr) + \tilde{A}\boldsymbol {v}_{n+1} h_{n+1,n} \tilde{\xi}_n^{-1} \boldsymbol {e}_n^T = V_n H_n + \boldsymbol {v}_{n+1} h_{n+1,n}\boldsymbol {e}_n^T, $$

or in more compact form after defining $K_{n}:= I_{n} + H_{n} \mathrm {diag}(\tilde{\xi}_{1}^{-1},\ldots,\tilde{\xi}_{n}^{-1})$,

$$ \tilde{A} V_n K_n + \tilde{A} \boldsymbol {v}_{n+1} h_{n+1,n} \tilde{\xi}_n^{-1} \boldsymbol {e}_n^T = V_n H_n + \boldsymbol {v}_{n+1} h_{n+1,n}\boldsymbol {e}_n^T, $$

(2.5)

where I _n denotes the n×n identity matrix and e _n its last column. Using the convention that $\tilde{\xi}_{n}=\infty$ (i.e., ξ _n =∞, which corresponds to a polynomial Krylov step, cf. [8, 24]), Eq. (2.5) reduces to

$$ \tilde{A} V_n K_n = V_n H_n + \boldsymbol {v}_{n+1} h_{n+1,n} \boldsymbol {e}_n^T. $$

(2.6)

If the matrix H _n appended with the row $h_{n+1,n}\boldsymbol {e}_{n}^{T}$ is an unreduced upper Hessenberg matrix (that is, all the coefficients h _j+1,j of (2.4) are nonzero), then the right-hand side of (2.6) is of full rank n and therefore K _n is invertible. Otherwise, if h _n+1,n =0, then is an A-invariant subspace and we have a lucky early termination. The matrix A _n required for computing the rational Arnoldi approximation (2.2) can be calculated from (2.6) without explicit projection as

$$ A_n = V_n^{*} A V_n = V_n^{*} \tilde{A} V_n + \sigma I_n = H_n K_n^{-1} + \sigma I_n. $$

(2.7)

Note that A _n corresponds to the projection of the non-translated operator A onto the rational Krylov space .

Remark 2.1

In exact arithmetic the rational Arnoldi approximation (2.2) is independent of the choice of the translation σ. However, for numerical stability of the rational Arnoldi algorithm, σ should have a large enough distance to the poles ξ _j relative to ∥A∥, because otherwise the pole and the zero in the fraction of (2.3) may “almost cancel”, causing accuracy loss in the rational Krylov basis [32].

It is well known that the rational Arnoldi approximation f _n defined in (2.2) is (in some sense) a near-optimal approximation for f(A)v from the space (see, e.g., [8, 15, 24]), that is, f _n is very close to the orthogonal projection $V_{n} V_{n}^{*} f(A)\boldsymbol {v}$. Therefore the poles ξ _j need to be chosen such that contains a good approximation to f(A)v, and of course, such a choice depends both on the spectral properties of A and the function f. This necessity for choosing optimal parameters is a serious problem that prevents rational Arnoldi from being used in practice more widely. Before discussing our automated pole selection strategy, we list some well-known properties of the rational Arnoldi approximation (2.2). The interested reader is referred to [8, 24, 25] for further details.

• 1. By the definition of a rational Krylov space 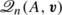(cf. (2.1)), there exists a rational function r _n of type (n−1,n−1) such that

  $$\boldsymbol {f}_n = r_n(A)\boldsymbol {v} = \frac{p_{n-1}}{q_{n-1}}(A) \boldsymbol {v}. $$

• 2. This function r _n is a rational interpolant for f with prescribed denominator q _n−1 and interpolation nodes Λ(A _n )={θ ₁,…,θ _n }, the so-called rational Ritz values. Defining the rational nodal function s _n of type (n,n−1),

  $$ s_n(z) := \frac{{\prod_{k=1}^n (z-\theta_k)}}{q_{n-1}(z)}, $$

  (2.8)

  by the Hermite–Walsh formula for rational interpolants (see, e.g., [39, Theorem VIII.2] or [6]) we have

  $$r_n(z) = \int_{\varGamma} \frac{s_n(z)}{s_n(x)(x - z)} \, \mathrm{d} \gamma(x), $$

  and therefore

  $$ \bigl\| f(A)\boldsymbol {v} - r_n(A)\boldsymbol {v} \bigr\| \leq \bigl\| s_n(A)\boldsymbol {v}\bigr\| \cdot\biggl \Vert \int_{\varGamma} \frac{(xI - A)^{-1}}{s_n(x)} \,\mathrm {d} \gamma(x) \biggr \Vert . $$

  (2.9)

• 3. The term ∥s _n (A)v∥ in (2.9) is minimal among all rational functions of the form $\tilde{s}_{n}(z) = (z^{n} + \alpha_{n-1} z^{n-1} + \cdots+ \alpha_{0} )/q_{n-1}(z)$ (see, e.g., [24, Lemma 4.5]).

3 Automated pole selection

Note that the rational nodal function s _n of (2.8) is explicitly known in the n-th iteration of the rational Arnoldi method: it has poles ξ ₁,…,ξ _n−1, and its zeros are the rational Ritz values Λ(A _n ). The aim of an automated pole selection strategy is, of course, to achieve a smallest possible (bound for the) approximation error ∥f(A)v−f _n ∥ at every iteration of the rational Arnoldi method. In view of (2.9) we will therefore try to make |s _n (x)| uniformly large on Γ (the support of the measure γ in (1.1)) by choosing the next pole ξ _n ∈Γ such that

$$\bigl|s_n(\xi_n)\bigr| = \min_{x\in\varGamma} \bigl|s_n(x)\bigr|. $$

This choice is inspired by the pole selection strategy proposed in [18, 19], where the nodal function has to be large on a negative real interval Γ and small on −Γ (the spectral interval of a symmetric matrix). In our case we do not necessarily have such symmetry, but still we can achieve that our nodal rational function s _n is large on Γ. Recall from above that the term ∥s _n (A)v∥ in (2.9) is guaranteed to be minimal among all rational functions with the prescribed poles. This justifies our strategy to minimize explicitly only the second factor on the right-hand side of (2.9). In Algorithm 1 we summarize our rational Arnoldi method with automated pole selection, see also [26].

Algorithm 1

Rational Arnoldi method for f(A)v with automated pole selection

Remark 3.1

Note that, in contrast to the algorithms presented in [18, 19], Algorithm 1 does not require any estimation for the spectral region of A (except for a very rough estimate of ∥A∥ to choose the parameter σ, see Remark 2.1). In fact, we will demonstrate in Sects. 5 and 6 that our algorithm also performs well for highly nonsymmetric and nonnormal matrices.

Remark 3.2

In a practical implementation of Algorithm 1 one can use an a-posteriori error estimator in Step 8 to halt the iteration if ∥f(A)v−f _j ∥ is below some tolerance. We will discuss such error estimators in Sect. 4.

Remark 3.3

Typically, the cost for orthogonalization of the Krylov basis vectors, equations (2.3) and (2.4), is negligible compared with the cost of solving the shifted linear systems with A. Step 3 of Algorithm 1 corresponds to a polynomial Krylov step (i.e., $\tilde{\xi}_{j}=\infty$) and allows for the cheap computation of the projection matrix $A_{j}=V_{j}^{*} A V_{j}$ in Step 6 using the relation (2.7). Overall two orthogonalizations are required in one iteration of the algorithm. However, techniques for reducing the number of inner products in the rational Arnoldi algorithm using so-called auxiliary vectors could be employed [24, Chap. 6]. Reorthogonalization techniques may be employed as well, however, we have not found this necessary in the numerical experiments presented in this paper.

4 Error criteria

In this section we derive some practical estimates for the approximation error ∥f(A)v−f _n ∥. Some of these techniques were adopted from [14, 24, 31], where they were used for other problems: computation of some non-Markov matrix functions and solution of matrix equations. This section also contains a comparison of these error estimators in Fig. 1 for a simple test matrix.

Fig. 1

Comparison of the error estimators from Sect. 4, given in (4.1), (4.2), (4.3), and (4.4) for a diagonal matrix whose eigenvalues are 10⁴ Chebyshev points in [10⁻³,10³]. The delay integer for the first two error estimators (4.1) and (4.2) is chosen as d=2. Note that the corresponding curves (blue with crosses and red with circles) partly overlay the actual error curve (solid gray). The integrals involved in the other two estimators have been approximated by adaptive Gauss–Kronrod quadrature (Color figure online)

4.1 The difference of iterates

Given some delay integer d, by the triangle inequality ∥f(A)v−f _n ∥≤∥f(A)v−f _n+d ∥+∥f _n+d −f _n ∥. Under the assumption that the rational Arnoldi method converges sufficiently fast so that ∥f(A)v−f _n+d ∥ is relatively small in comparison to ∥f(A)v−f _n ∥, a primitive estimator for the approximation error is

$$ \bigl\| f(A)\boldsymbol {v} - \boldsymbol {f}_n \bigr\| \approx \| \boldsymbol {f}_{n+d} - \boldsymbol {f}_n \|. $$

(4.1)

Note that the Euclidian norm of the difference of two iterates can be computed cheaply using only their coordinates in the orthonormal basis V _n+d and V _n , without forming the long Arnoldi approximation vectors f _n+d and f _n . We warn that this estimator may be too optimistic, in particular, when the approximations f _n (almost) stagnate for d iterations or more. This underestimation of the error can be seen in Fig. 1.

4.2 Exploiting geometric convergence

Another estimate can be derived by assuming that the error is decaying approximately geometrically (as is typically the case, see Sect. 5). A similar estimator has been successfully applied in [14, 31]. One starts by assuming the ideal equalities

$$\| \boldsymbol {f}_n - \boldsymbol {f}_{n+d} \| = c R^{-n} \quad\text{and} \quad \| \boldsymbol {f}_{n+d} - \boldsymbol {f}_{n+2d} \| = c R^{-(n+d)}, $$

and defining χ _j =log∥f _j+d −f _j ∥. Moreover, one defines

$$R = \exp \biggl(\frac{\chi_n - \chi_{n+d}}{d} \biggr) \quad\text{and} \quad c = \exp \biggl(\frac{(n+d)\chi_n - n\chi_{n+d}}{d} \biggr). $$

From

we obtain the estimator

(4.2)

The last equality is only valid if R>1. In practice it may happen that R≤1, in which case this estimator becomes negative or infinite. This typically indicates an error increase or stagnation in the iterates, and one should iterate further to reobtain a reliable estimator. This effect can be seen in Fig. 1, where the curve corresponding to this error indicator shows several “gaps”.

4.3 Approximate error bound

An approximate bound for the approximation error can be derived by replacing A with A _n in the integrand of (2.9), yielding

$$ \bigl\| f(A)\boldsymbol {v} - r_n(A)\boldsymbol {v} \bigr\| \lessapprox \bigl\| s_n(A)\boldsymbol {v}\bigr\| \cdot\biggl \Vert \int _{\varGamma} \frac{(xI_n - A_n)^{-1}}{s_n(x)} \,\mathrm{d} \gamma(x) \biggr \Vert . $$

(4.3)

If A _n is diagonalizable, then this new integral can be approximated by scalar quadrature. We still need to compute ∥s _n (A)v∥. Note that s _n (A)v is just a scalar multiple of v _n+1, say s _n (A)v=δ _n v _n+1. A simple trick to get a hand on this scalar δ _n is to run the rational Arnoldi algorithm with a modified matrix and starting vector

$$\hat{A} = \left [ \arraycolsep=5pt\begin{array}{@{}cc@{}} A & \\ & \tau\\ \end{array} \right ], \qquad \hat{\boldsymbol {v}} = \left [ \begin{array}{c} \boldsymbol {v} \\ 1 \\ \end{array} \right ], $$

where τ∈ℂ is away from Γ and all Ritz values, still performing all inner products only on the first N components (and hence not changing the orthogonality of V _n ). We therefore have

$$s_n(\hat{A})\hat{\boldsymbol {v}} = \left [ \begin{array}{c} s_n(A) \boldsymbol {v} \\ s_n(\tau) \\ \end{array} \right ] = \delta_n \hat{\boldsymbol {v}}_{n+1}. $$

Comparing the last (that is, (N+1)-st) element of $\hat{\boldsymbol {v}}_{n+1}$ with s _n (τ), we obtain the desired scaling factor |δ _n |=∥s _n (A)v∥ as

$$\delta_n = s_n(\tau) / [ \hat{\boldsymbol {v}}_{n+1} ]_{N+1}. $$

The behavior of the resulting approximate upper bound is shown in Fig. 1. Typically, this approximate bound cannot be trusted for small iteration numbers n, but it becomes more reliable in later iterations when more spectral information about A has been captured in A _n .

4.4 Residual-based estimator

As explained in Sect. 2, the matrix $A_{n}=V_{n}^{*} A V_{n}$ required for the Arnoldi approximation (2.2) can be computed via $A_{n} = H_{n} K_{n}^{-1} + \sigma I_{n}$ without explicit projection. This allows us to use a shifted version of the decomposition (2.6) in the form

$$(\tilde{x}I - A) V_n = V_n (\tilde{x}I - A_n) - \boldsymbol {v}_{n+1} h_{n+1,n} \boldsymbol {e}_n^T K_n^{-1}, $$

where $\tilde{x} = x + \sigma$ for an arbitrary x∈ℂ. Let us consider a shifted linear system $(\tilde{x} I - A) \boldsymbol {x}(\tilde{x}) = \boldsymbol {v}$ and the corresponding rational Arnoldi approximation $\boldsymbol {x}_{n}(\tilde{x}) = V_{n} (\tilde{x}I_{n} - A_{n})^{-1} V_{n}^{*} \boldsymbol {v}$. The residual of this approximation satisfies

Using the fact that $V_{n}^{*} \boldsymbol {v} = \|\boldsymbol {v}\|\boldsymbol {e}_{1}$ by construction of the rational Arnoldi algorithm, and $K_{n}^{-1} (\tilde{x}I_{n} - A_{n})^{-1} = (xK_{n} - H_{n})^{-1}$, we obtain

$$\bigl\| \boldsymbol {v} - (\tilde{x}I - A)\boldsymbol {x}_n(\tilde{x})\bigr\| = h_{n+1,n} \|\boldsymbol {v}\| \cdot\bigl| \boldsymbol {e}_n^T (x K_n - H_n)^{-1} \boldsymbol {e}_1 \bigr|. $$

This allows for the definition of a “residual” of a Cauchy–Stieltjes matrix function

$$\mathrm{residual}(f,n) := \boldsymbol {v}_{n+1} h_{n+1,n} \int _{\varGamma -\sigma} \boldsymbol {e}_n^T (x K_n - H_n)^{-1} \boldsymbol {e}_1 \, \mathrm {d}\gamma(x), $$

whose norm is given by

$$ \bigl\| \mathrm{residual}(f,n) \bigr\| = h_{n+1,n} \|\boldsymbol {v} \| \cdot\biggl \Vert \int_{\varGamma-\sigma} \boldsymbol {e}_n^T (x K_n - H_n)^{-1} \boldsymbol {e}_1\, \mathrm{d}\gamma(x)\biggr \Vert . $$

(4.4)

See also [10, 13, 29, 37] for related constructions. In our numerical experiments this appeared to be a good indicator, being almost proportional to the actual error; see again Fig. 1.

5 Convergence studies

  A thorough convergence analysis of our algorithm appears to be complicated by the interaction between the Ritz values Λ(A _n ) (which vary in each iteration) and the selected poles {ξ _j }. Although there is hope of characterizing these two sets asymptotically as equilibrium charges on a condenser (at least in the case of a symmetric matrix A; see our Remark 5.1), we decided to present here a numerical comparison of our method with competing approaches for computing approximations for f(A)v. Our comparison is two-fold. In Sect. 5.1 we compare our method with two other methods, both of which use asymptotically optimal poles computed by assuming knowledge of the spectral properties of A. In Sect. 5.2 we then compare our method to well-established Krylov methods with prescribed pole sequences independent of A, namely the polynomial and extended Krylov subspace methods.

5.1 Comparison with asymptotically optimal pole sequences

Our algorithm can be seen as a strategy for constructing the nodal function s _n of (2.8) such that this function is large on Γ and small on the numerical range $\mathbb{W}(A)$. The numerical range $\mathbb{W}(A):=\{\boldsymbol {x}^{*} A \boldsymbol {x} : \| \boldsymbol {x} \| = 1\}$ is a convenient set for bounding the norm ∥s _n (A)∥: by a theorem of Crouzeix [12] we have

$$ \bigl\|s_n(A)\bigr\| \leq11.08\, \max_{z\in\mathbb{W}(A)} \bigl|s_n(z)\bigr|. $$

(5.1)

Unfortunately, bounds based on the numerical range may be crude, in which case it is not clear on which set Σ⊂ℂ the function s _n actually needs to be small so that ∥s _n (A)∥ is guaranteed to be small. Although the convergence bounds below are given in terms of $\varSigma =\mathbb{W}(A)$, the reader should keep in mind that possibly a smaller set Σ may be relevant for the actual convergence of the Krylov methods under consideration. For example, adaptation of polynomial Krylov methods to the operator spectrum is treated in [30], or in [6] for the rational Krylov case, and improved (theoretical) bounds for ∥s _n (A)∥ may be obtainable by considering sets Σ=Σ _n that shrink as the iteration progresses (see, e.g., [6]), or by considering pseudospectra of A instead of the numerical range (see, e.g., [38]).

Assuming that $\varSigma=\mathbb{W}(A)$ and Σ is disjoint from Γ, we may compare the performance of our automated pole selection strategy with that of explicit selection of (asymptotically) optimal poles ξ _j . One choice of such poles is so-called generalized Leja points (or Leja–Bagby points, see [5]), which are constructed as follows: Starting with a point σ ₁∈Σ such that max _z∈Σ |z−σ ₁| is minimal, the points σ _j+1∈Σ and ξ _j ∈Γ are determined recursively such that with the nodal function

$$s_j(z) = \frac{\prod_{i=1}^j (z-\sigma_i)}{\prod_{i=1}^{j-1} (z-\xi_i)} $$

the conditions

$$\max_{z\in\varSigma} \bigl| s_j(z) \bigr| = \bigl| s_j( \sigma_{j+1}) \bigr| \quad\text {and} \quad \min_{z\in\varGamma} \bigl| s_j(z) \bigr| = \bigl| s_j(\xi_{j+1}) \bigr| $$

are satisfied. Note that the function s _j defined here would agree with the nodal function defined in (2.8) at iteration j of the rational Arnoldi method if all the σ _i were to coincide with Ritz values θ _i , and all the poles ξ _i were the same. Results from logarithmic potential theory [23, 33] assert that there exists a positive number cap(Σ,Γ), called the condenser capacity, such that

$$\limsup_{n\to\infty} \biggl( \frac{\max_{z\in\varSigma} |s_n(z)|}{\min_{z\in\varGamma} |s_n(z)|} \biggr)^{1/n} = e^{-1/\mathrm{cap}(\varSigma,\varGamma)}. $$

Determining the capacity of an arbitrary condenser (Σ,Γ) is a nontrivial problem. The situation simplifies if both Σ and Γ are simply connected sets (and not single points): then by the Riemann mapping theorem (cf. [27, Theorem 5.10h]) there exists a bijective function Φ that conformally maps the complement of Σ∪Γ onto a circular annulus $\mathbb{A}_{R}:=\{w : 1<|w|<R\}$. The number R is called the Riemann modulus of $\mathbb{A}_{R}$ and it satisfies

$$R^{-1} = e^{-1/\mathrm{cap}(\varSigma,\varGamma)}. $$

To relate the asymptotic behavior of s _n to that of the error ∥f(A)v−r _n (A)v∥ we use (2.9) and (5.1), and obtain

$$\limsup_{n\to\infty} \bigl\| f(A)\boldsymbol {v} - r_n(A)\boldsymbol {v} \bigr\|^{1/n} \leq R^{-1}. $$

In the following examples we demonstrate that our adaptive rational Arnoldi method, Algorithm 1, (asymptotically) converges at least with rate R ⁻¹, i.e., not slower than a rational Krylov method with asymptotically optimal poles would converge if the set Σ were known a priori. To this end, we numerically compare our method with two reference methods, both of which are known to converge asymptotically at least with rate R ⁻¹.

The first reference method is the so-called PAIN (poles and interpolation nodes) method, which is a two-term recurrence described in [24]

where the numbers β _j are chosen to normalize the vectors v _j+1, and σ _j and ξ _j are the generalized Leja points for the condenser (Σ,Γ). The corresponding PAIN approximation is defined as

$$\boldsymbol {f}_n^{(\mathrm{P})} := [\boldsymbol {v}_1,\ldots, \boldsymbol {v}_n] f\bigl( R_n L_n^{-1} \bigr) \|\boldsymbol {v} \| \boldsymbol {e}_1, $$

where e ₁∈ℝⁿ denotes the first unit coordinate vector,

$$L_n = \left [ \arraycolsep=5pt\begin{array}{@{}cccc@{}} 1 & & & \\ {\beta_1}/{\xi_1} & 1 & & \\ & \ddots & \ddots& \\ & & {\beta_{n-1}}/{\xi_{n-1}} & 1 \end{array} \right ] \quad\text{and} \quad R_n = \left [ \arraycolsep=5pt\begin{array}{@{}cccc@{}} \sigma_1 & & & \\ \beta_1 & \sigma_2 & & \\ & \ddots & \ddots& \\ & & \beta_{n-1} & \sigma_n \end{array} \right ]. $$

It can be shown that $\boldsymbol {f}_{n}^{(\mathrm{P})} = r_{n}^{(\mathrm{P})}(A)\boldsymbol {v}$, where $r_{n}^{(\mathrm{P})}$ is the rational interpolant for f with prescribed poles ξ ₁,…,ξ _n−1 and interpolation nodes σ ₁,…,σ _n [24]. Note that the PAIN method is not spectrally adaptive: both the poles and the interpolation nodes are chosen a priori and no discrete spectral information about A is taken into account.

The second reference method is the rational Arnoldi method where the poles ξ _j are chosen a priori as generalized Leja points, and we will refer to this as the standard rational Arnoldi method in the following. We denote the corresponding approximations as $\boldsymbol {f}_{n}^{(\mathrm{S})}$. Note that the standard rational Arnoldi method chooses the interpolation nodes spectrally adaptive as Ritz values associated with the rational Krylov space. It is therefore an adaptive method for the interpolation nodes, but still the poles are chosen a priori. The methods under consideration are summarized in Table 1.

Table 1 Overview of the methods to be compared, all of which compute approximations to f(A)v of the form r _n (A)v, where r _n is a rational interpolating function for f

The interval case

Let A be a symmetric matrix with $\varSigma= \mathbb{W}(A) = [a,b]$ being a positive spectral interval. Moreover, let f be a Markov function (1.1) whose generating measure γ is supported on Γ=(−∞,0]. Then the conformal map Φ that carries the complement of Γ∪Σ=(−∞,0]∪[a,b] onto the annulus $\mathbb{A}_{R}$ can be given explicitly in terms of elliptic functions. In particular, the Riemann modulus R is given as (see [23, § 3])

$$ R = \exp \biggl(\frac{\pi}{2}\frac{K(\sqrt{1-\kappa^2})}{K(\kappa )} \biggr), \quad\text{where } \kappa=\frac{\sqrt{b/a}-1}{\sqrt{b/a}+1} $$

(5.2)

and

$$ K(\kappa) = \int_0^1 \frac{1}{\sqrt{(1-t^2)(1-\kappa^2 t^2)}}\, \mathrm{d}t $$

(5.3)

is the complete elliptic integral of the first kind (see [4]).¹

Let f(z)=z ^−1/2 without further mention in this Sect. 5.1. We first consider a diagonal matrix A ₁ with N=10⁴ eigenvalues being scaled and shifted Chebyshev points of the second kind,

$$\lambda_j = a + \frac{\cos(\pi j/(N-1))+1}{2} (b-a), \quad j = 0,1,\ldots,N-1, $$

in the interval [a,b]=[10⁻³,10³], and a vector v whose entries are normally distributed pseudo-random numbers. In Fig. 2 (top left) we show the convergence of our adaptive rational Arnoldi method, Algorithm 1, in comparison with the two reference methods (the PAIN method and standard rational Arnoldi, cf. Table 1). The theoretical convergence rate R ⁻¹ from (5.2) is indicated by the slope of the dashed line. Note that all the three methods converge almost linearly with the predicted rate. The reason for the rational Arnoldi methods behaving like this is that the Chebyshev eigenvalues are denser at the endpoints of the spectral interval, and almost no spectral adaption takes place during the first 50 iterations shown here. In some sense, the rational Krylov methods behave initially as if the spectrum were not discrete; see [6] for a potential theoretic explanation. We expect our adaptive method to choose roughly the same poles as were chosen in the generalized Leja case, and the plot below confirms this expectation by depicting the (smoothed) empirical distribution functions of the first 50 adaptive poles and generalized Leja poles; the two distributions are visually hard to distinguish.

Fig. 2

Left: Convergence curves (top) and distribution of poles (below) when approximating $A_{1}^{-1/2}\boldsymbol {v}$ with different rational Krylov methods. Right: Similar plots for the matrix A ₂

We next consider a diagonal matrix A ₂ with N=10⁴ equispaced eigenvalues

$$\lambda_j = a + j(b-a) / (N-1), \quad j = 0,1,\ldots,N-1, $$

in the interval [a,b]=[10⁻³,10³]. In Fig. 2 (top right) we again show the convergence of the three methods. While the PAIN method still converges linearly with rate R given by (5.2), the standard rational Arnoldi method is somewhat faster because the interpolation nodes (Ritz values) “deflate” some of the left-most eigenvalues of A in early iterations, causing a superlinear convergence speedup (see [6] for an analysis of this effect). The adaptive rational Arnoldi method converges even faster than standard rational Arnoldi, because the poles of the rational Krylov space are selected by taking into account the deflation of left-most eigenvalues. The plot of the pole distribution functions below reveals that the adaptive method has the tendency to place the poles ξ _j somewhat farther away from the origin.

Union of intervals

In Fig. 3 (left) we consider a diagonal matrix A ₃ whose spectrum is the union of 10 Chebyshev points on the interval [10⁻³,10⁻¹] and 9990 Chebyshev points on [10¹,10³]. Note that the PAIN method with poles optimized for the spectral interval [10⁻³,10³] converges linearly. However, our adaptive method changes its slope after a few iterations to converge linearly as if the spectral interval were [10¹,10³]. Both slopes are depicted in this figure. The spectral adaption becomes also visible in the pole distribution function (Fig. 3, bottom left).

Fig. 3

Left: Convergence curves (top) and distribution of poles (below) when approximating $A_{3}^{-1/2}\boldsymbol {v}$ with different rational Krylov methods. Right: Similar plots for the matrix A ₄

Remark 5.1

In view of the behavior of our adaptive rational Arnoldi method for the above symmetric matrices, we believe that the convergence can be asymptotically (that is, for a sequence of symmetric matrices growing larger in size and having a joint limit eigenvalue distribution) compared to min-max rational functions with poles on Γ and zeros on Σ being constrained Leja points in the sense of [11]. The constraint for the zeros is given by the interlacing property of Ritz values associated with symmetric matrices (see, e.g., [7]).

A Jordan block

The matrix A ₄ is a single Jordan block

$$A_4 = \left [ \arraycolsep=5pt\begin{array}{@{}cccc@{}} 1 & 1 & & \\ & 1 & \ddots& \\ & & \ddots& 1 \\ & & & 1 \end{array} \right ]\in\mathbb{C}^{N\times N}, $$

and its numerical range is a disk $\mathbb{W}(A_{4}) = \{ z : | z - 1 | \leq r \}$ with radius r=cos(π/(N+1)). The conformal mapping of the complement of $\mathbb{W}(A_{4})$ in the slit complex plane onto an annulus is known in terms of elliptic functions (see [34, p. 293–294]), and the Riemann modulus of this domain is

$$R = \exp \biggl(\frac{\pi}{4}\frac{K(\sqrt{1-\kappa^2})}{K(\kappa )} \biggr), \quad\text{where } \kappa= \biggl(\frac{c}{r} - \sqrt{\frac {c^2}{r^2} - 1} \biggr)^2, $$

with K(κ) defined in (5.3). The resulting convergence of the three methods is shown in Fig. 3 (right), together with the theoretical rate R ⁻¹. Note that the PAIN method converges as predicted from the bound involving the numerical range, whereas the two rational Arnoldi methods converge faster due to spectral adaption. In particular, our adaptive method converges significantly faster.

5.2 Comparison with fixed pole sequences

In this section we will briefly discuss polynomial and rational Krylov methods with poles prescribed independently of Σ, and therefore not leading to the optimal convergence rate associated with the condenser capacity cap(Σ,Γ).

The simplest of these methods is the polynomial Arnoldi method, which is the special case of rational Arnoldi in which all poles ξ _j are set to infinity. This method has the obvious advantage that no linear system solves are required. If A is Hermitian and we consider the approximation of functions with generating measure supported on Γ=(−∞,0], such as f(z)=z ^−1/2, then the convergence rate of the polynomial Arnoldi method equals that of the CG method, i.e.,

$$\bigl\| f(A)\boldsymbol {v} - \boldsymbol {f}_n\bigr\| \leq C \biggl(\frac{\sqrt{\kappa } - 1}{\sqrt{\kappa} + 1} \biggr)^n \lesssim C \cdot\exp \biggl(-\frac{2n}{\sqrt{\kappa}} \biggr), \quad \kappa= \frac{\lambda_{\mathrm{max}}}{\lambda_{\mathrm{min}}}, $$

where the approximate inequality is valid for large condition numbers κ. Obviously, convergence can be slow if the condition number κ gets large, and therefore many Krylov iterations will be required to approximate f(A)v to a prescribed accuracy. Note that Arnoldi (and also Lanczos) methods for matrix functions require the Krylov basis V _n to be stored for the final computation of the Arnoldi approximation f _n of (2.2), which renders this method impractical if n is large. Although restarted variants of the polynomial Arnoldi method for f(A)v have been proposed, which prevent the dimension of the Krylov space to grow above memory limit (see [1, 20, 21]), the use of finite poles ξ _j typically is a worthwhile alternative if linear systems with shifted versions of A can be solved efficiently.

If the poles alternate between ξ _2j =∞ and ξ _2j+1=0, we obtain the so-called extended Krylov subspace method with convergence (see [15] and [31, Theorem 3.4])

$$\bigl\| f(A)\boldsymbol {v} - \boldsymbol {f}_n\bigr\| \leq C \biggl(\frac{\sqrt [4]{\kappa} - 1}{\sqrt[4]{\kappa} + 1} \biggr)^n \lesssim C \cdot\exp \biggl(-\frac{2n}{\sqrt[4]{\kappa}} \biggr). $$

A computational advantage of the extended Krylov subspace method is that only the actions of A and A ⁻¹ on vectors are required. In particular, if a direct solver is applicable, only one factorization of A needs to be computed. The convergence of the polynomial and extended Krylov subspace methods is illustrated in Fig. 4, and compared with that of our adaptive rational Arnoldi method. In this figure, f(z)=z ^−1/2 and A is the finite-difference discretization of the negative 2D Laplacian with 100 discretization points in each coordinate direction (i.e., N=100²). Note that the predicted convergence rate for the extended Krylov subspace method is only observable in the first few iterations because superlinear convergence effects take place when some rational Ritz values start converging to the left-most eigenvalues of A (which are close to the poles at 0, see [6] for an explanation).

Fig. 4

Comparison of polynomial and rational Arnoldi methods for the approximation of f(A)v=A ^−1/2 v for the negative 2D Laplacian. The dashed lines indicate the expected linear convergence slopes

Our last test is more challenging: We consider the computation of the logarithm log(A)v of a random diagonalizable matrix A∈ℂ^200×200 having eigenvalues in the unit disk under the constraint that the distance of each eigenvalue to Γ=(−∞,0] is at least 0.1. The eigenvalues of this matrix are shown in Fig. 5 (left). We remark that A is highly nonnormal: although the moduli of its eigenvalues are nicely bounded above and below, it has a condition number of ≈2.5×10⁴. To our best knowledge, no existing convergence theory is able to explain why Algorithm 1 converges so robustly even for this matrix (see Fig. 5, right). Note that the usual arguments involving the numerical range $\mathbb {W}(A)$ fail here, as this set is not even disjoint from Γ. We have failed to implement the extended Krylov subspace method in such a way that it reproduces the exact solution at least at iteration n=N=200, as theory predicts. This instability is probably caused by the (n/2)-fold pole 0 being surrounded by eigenvalues of A and lying inside the numerical range.

Fig. 5

Left: Eigenvalues of a highly nonnormal random matrix A∈ℂ^200×200. Right: Convergence of rational Arnoldi for f(A)v=log(A)v, random vector v, with adaptive poles on Γ=(−∞,0]

6 A large-scale numerical example with inexact solves

The following tests are run on a desktop computer with 3.7 GB of RAM, running an AMD Phenom II X3 705e processor at 2.5 GHz. The software environment is Matlab 7.12.0 (R2011a) under Ubuntu Release 10.04.

We shall consider the problem of computing the impedance function f(z)=z ^−1/2 of a discretization A of the convection–diffusion operator

on Ω=[0,1]³. We assume that a is a uniformly positive and bounded function defined on Ω, and b=(b ₁,b ₂,b ₃)^T is a vector function whose components posses the same properties. We have discretized this operator by the standard second-order finite difference scheme with 100 regular interior grid points.

In Fig. 6 (left) we show the convergence behavior of our adaptive method and the extended Krylov subspace method for smooth low-contrast conductivity a ₁ and smooth convective field b, namely

$$ a_1(x,y,z)=1+\exp(x-2y), \qquad b(x,y,z) = \left [ \begin{array}{c} \sin(x+y) \\ \cos(x+y) \\ \sin(y+z) \end{array} \right ]. $$

(6.1)

In Fig. 6 (right) we show the results for piecewise constant high-contrast conductivity a ₂ and the same b as in (6.1),

$$a_2(x,y,z)= \begin{cases} 100, & \text{if } |x|\le0.5 \text{ and } |y|\le0.6, \\ 1 & \text{otherwise}. \end{cases} $$

The resulting discretization matrices are of size 10⁶×10⁶ and are referred to as A ₁ and A ₂, respectively. All components of the vector v are set to 1.

Fig. 6

Left: Convergence curves (top) and distribution of poles (below) when approximating $A_{1}^{-1/2}\boldsymbol {v}$. The iteration is stopped when the relative error is below 10⁻⁴. The linear systems involved are solved with a relative error tolerance of 10⁻⁵. Right: The same plots for the matrix A ₂

All shifted linear systems are solved with a relative error tolerance of 10⁻⁵, which is sufficiently smaller than our target relative error of 10⁻⁴ for the approximation f(A _ℓ )v (ℓ=1,2). The linear system solver is BICGSTAB preconditioned by ILU(0). This combination works quite well for the shifted linear systems under consideration, as is indicated in Table 2. The errors of the linear system solves are estimated by exploiting the almost geometric convergence of BICGSTAB with the estimator presented in Sect. 4.2 (we chose the delay integer d=2). As indicated in the last column of Table 2, the measured errors are typically below 10⁻⁵, or at least of that order. We have also tried other combinations of iterative solvers and preconditioners, such as BICGSTABL, restarted GMRES, GMR, TFQMR, and IDRS(s)² in combination with drop-tolerance ILU or Gauss–Seidel preconditioners. The results of these comparisons are not reported here, but the combination ILU(0) and BICGSTAB consistently outperformed the others. Moreover, BICGSTAB and ILU(0) are parameter-free methods, which is important in our case where we try to develop a black-box method. The initial guess for all linear systems was the vector of all zeroes.

Table 2 Solving linear systems with the matrices A ₁−ξI and A ₂−ξI using BICGSTAB preconditioned by ILU(0). The BICGSTAB iteration is terminated when our estimator of Sect. 4.2 indicated a relative error below 10⁻⁵

Our adaptive shifts ξ _j are chosen by a greedy search on a discretization of the interval [−10⁶,−10⁻⁶] with 10⁵ logarithmically equispaced points. We have found experimentally that this is a sufficiently fine approximation to the continuous set Γ=(−∞,0]: Taking more discretization points or increasing the width of the search interval did not give any visible improvement in the convergence of our adaptive method. As can be seen in Table 2, the computation time of BICGSTAB clearly dominates that of the ILU(0) factorization, the latter being more or less shift-independent. Note how linear systems with a large shift (in modulus) are typically solved faster than systems with a shift of moderate size. The reason for this observation may be the stronger diagonal dominance of systems with larger shifts, which renders the ILU(0) preconditioner to be more effective, a well-known effect [9].

Our adaptive method clearly outperforms the extended Krylov subspace method in terms of required iterations and computation time. For example, in the case of low-contrast conductivity, the adaptive method requires n=7 iterations, whereas the extended Krylov subspace method requires n=24 iterations (see Fig. 6, left). With the conservative assumption that each shifted linear system solve requires about 30 seconds (see Table 2), our adaptive method requires at least 6×30=180 seconds computation time (the first iteration only utilizes the vector v ₁=v/∥v∥ and does not require a linear system solve). The extended Krylov subspace method, on the other hand, requires at least 11×30=330 seconds (only every second iteration of this method requires a linear system solve). Note that we have still neglected the computational costs for orthogonalization and memory management of the long Krylov basis vectors. These costs are larger for the extended Krylov subspace method, because the associated Krylov basis is of higher dimension, but in comparison to the time spent in the BICGSTAB routine these computations are negligible. The gap in iteration numbers between our adaptive method and the extended Krylov subspace method becomes even larger for the example with high conductivity contrast: in this case the methods required 9 versus 43 iterations, respectively (see Fig. 6, right).

We finally remark that the extended Krylov subspace method does not perform well in these examples due to the use of an iterative solver which cannot exploit the fact that only one finite shift ξ=0 appears. The use of direct methods is typically prohibitive for 3D problems. For 2D problems, however, the situation is different and the extended Krylov subspace method in combination with direct solvers may still be competitive with our adaptive method in terms of computation time. In any case, our method tends to require lower-dimensional Krylov subspaces, so that our advantage of lower memory consumption and fewer orthogonalizations still persists.

7 Summary and future work

We have presented a parameter-free rational Arnoldi method for the efficient computation of certain matrix functions f(A) acting on a vector v. We provided numerical evidence that this method converges at least as well as rational Krylov methods using optimal pole sequences constructed with the knowledge of the spectrum. In fact, our new method typically even outperforms such methods due to the spectral adaption of the poles during the iteration. A rigorous convergence analysis, perhaps involving tools from potential theory as in [6, 7], for explaining spectral adaption of this rational Arnoldi variant applied with a symmetric matrix, may be an interesting research problem. The first author also has experienced cases where it seems profitable to take Γ different from the “canonical choice” (−∞,0] when approximating the inverse matrix square root, an observation that will be subject of future investigation.