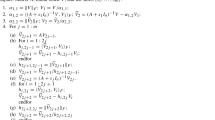Double-shift-invert Arnoldi method for computing the matrix exponential

Abstract

Computing the matrix exponential for large sparse matrices is essential for solving evolution equations numerically. Conventionally, the shift-invert Arnoldi method is used to compute a matrix exponential and a vector product. This method transforms the original matrix using a shift, and generates the Krylov subspace of the transformed matrix for approximation. The transformation makes the approximation converge faster. In this paper, a new method called the double-shift-invert Arnoldi method is explored. This method uses two shifts for transforming the matrix, and this transformation results in a faster convergence than the shift-invert Arnoldi method.

1 Introduction

Evolution equations are used in various fields of science and technology, e.g., the heat equation in building physics [16] and the convection diffusion equation in fluid mechanics and chemistry [10]. Let $\varOmega \subseteq \mathbb {R}^d$ be an open set, $T>0$, and $\mathcal {V}$ be the dense subset of Hilbert space $L^2(\varOmega )$. Let $\mathcal {L}$ be a linear differential operator on $\mathcal {V}$. Explore u(t, x), which satisfies $u(\cdot ,x)\in C^1(0,T)$ for all $x\in \varOmega$, $u(t,\cdot )\in \mathcal {V}$ for all $t\in (0,T]$, and

$$\begin{aligned} \frac{\partial u}{\partial t}=\mathcal {L}u, \end{aligned}$$

(1)

with some appropriate initial and boundary conditions. The following ordinary differential equation with matrices is derived from a spatial discretization of Eq. (1) with the finite element method or finite difference method:

$$\begin{aligned} \left\{ \begin{aligned} M\dot{y}(t)&=Ly(t)+c,\\ y(0)&=v, \end{aligned}\right. \end{aligned}$$

(2)

where $M,L\in \mathbb {R}^{n\times n}$ and $c\in \mathbb {R}^n$. It is assumed that M and L are invertible. The solution of Eq. (2) is represented as:

$$\begin{aligned} y(t)=e^{tM^{-1}L}(v+L^{-1}c)-L^{-1}c. \end{aligned}$$

(3)

Various methods for computing the matrix exponential have been developed [4, 6, 7, 9, 11, 12]. The Krylov subspace methods are efficient, because the matrices resulting from the spatial discretization of problem (1) usually become large and sparse. The Krylov subspace method generates a sequence of approximations of a matrix function and a vector product in the Krylov subspace. The most simple and well-known method is the Arnoldi method. Hochbruck and Lubich [9, Theorem 5] showed that, the Arnoldi method requires a number of iterations if the numerical range of the matrix is widely distributed. The matrices coming from the spatial discretization of problem (1) often have a wide numerical range. Thus, the Arnoldi method needs many iterations until it converges for computing matrix exponentials. In order to resolve this issue, the shift-invert Arnoldi method (SIA) was proposed by Moret and Novati [12]. SIA transforms the matrix using a shift so that the numerical range of the transformed matrix becomes narrow. This results in a faster convergence than the Arnoldi method. However, the error bound of SIA contains the integral, and there is a trade off between the length of the integral contour and the property of the integrand. As shift $\gamma$ becomes larger, the length of the contour becomes shorter, but the property of the integrand becomes worse. This results in the integrated value in the error bound becoming large. Either $\gamma$ is small or large. To resolve this issue, the double-shift-invert Arnoldi method (DSIA) is applied. A similar error bound with the SIA is available for the DSIA. In the DSIA, it can be shown that the length of the contour gets shorter, while keeping the good property of the integrand. This makes the error of the DSIA smaller than the SIA, and results in a faster computation of matrix exponentials. The DSIA uses two shifts instead of a single shift in the SIA. The method which uses multiple shifts for constructing Krylov subspace was originally developed for the eigenvalue problems by Ruhe [13]. This method is called Rational Krylov (RK) method. Using the RK for computing matrix function was proposed by Beckermann and Reichel [2], and it was also proposed by Güttel [6] and Göckler [5]. Generating a basis vector of the Krylov subspace for the SIA or the RK requires the computation of the solution of a linear equation. If the size of matrices are large, the cost of this computation is dominant. The advantage of the RK is the computation of these solutions can be implemented completely in parallel [3]. This is not possible for the SIA, since the new basis vector depends on the basis vectors previously generated. The DSIA uses two shifts, and the computation for two linear equations can be implemented in parallel. On the other hand, the difference with the RK is these two linear equations are for one basis vector. Thus, unlike the RK, we cannot generate the multiple basis vectors in parallel. However, using two shifts for one basis vector reduces the number of basis vectors required for the convergence, compared to using one shift.

In Sect. 2, the SIA for computing the matrix exponential is introduced. The DSIA is proposed in Sect. 3. The results of numerical experiments are shown in Sect. 4 to confirm the effectiveness of our method.

1.1 Notation

The norm is defined as $\Vert \cdot \Vert =\Vert \cdot \Vert _2$. $e_j$ represents the jth column of identity matrix I. Let $\mathbb {C}^{+}:=\{z\in \mathbb {C}\mid \ \mathfrak {R}(z)>0\}$, and $\mathbb {C}^{-}:=\{z\in \mathbb {C}\mid \ \mathfrak {R}(z)<0\}$. Moreover, let $W(A):=\{u^*Au\mid \ u\in \mathbb {C}^n,\ \Vert u\Vert =1\}$ be the numerical range of matrix A.

2 Shift-invert Arnoldi method (SIA)

In this paper, $e^Av$ for $A\in \mathbb {R}^{n\times n}$ and $v\in \mathbb {R}^n$ is computed to simplify the notation. Throughout the following sections, it is assumed that $W(A)\subseteq \mathbb {C}^{-}$.

Let $\beta =\Vert v\Vert$, and $v_1=v/\beta$ be the initial vector. The m-step shift-invert Arnoldi or restricted-denominator (RD) rational Arnoldi process is:

$$\begin{aligned} h_{j+1,j}v_{j+1}&=(\gamma I-A)^{-1}v_j-\sum _{k=1}^jh_{k,j}v_k\,,\\ h_{k,j}&=v_k^*\left[ (\gamma I-A)^{-1}v_j-\sum _{l=1}^{k-1}h_{l,j}v_l\right] \qquad (k=1,\ldots ,j),\\ h_{j+1,j}&=\left\| (\gamma I-A)^{-1}v_j-\sum _{l=1}^jh_{l,j}v_l\right\| \qquad (j=1,\ldots ,m), \end{aligned}$$

where $\gamma >0$ is a shift. This relation is expressed with matrices as:

$$\begin{aligned} V_m^*(\gamma I-A)^{-1}V_m=H_m, \end{aligned}$$

where $V_m=[v_1, \ldots , v_m]$ is an $n\times m$ matrix whose columns are the orthonormal basis of the Krylov subspace generated by the SIA:

$$\begin{aligned} \mathcal {K}_m((\gamma I-A)^{-1},v)={\text {Span}}\Bigg \{v,\ (\gamma I-A)^{-1}v,\ldots , (\gamma I-A)^{-m+1}v\Bigg \}, \end{aligned}$$

where $H_m=[h_{i,j}]$ is an $m\times m$ upper Hessenberg matrix, and $\{v_1, \ldots , v_m\}$ satisfies:

$$\begin{aligned} \text{ Span }\left\{ v_1,\ \ldots ,\ v_m\right\}&=\text{ Span }\left\{ v, (\gamma I-A)^{-1}v, \ldots , (\gamma I-A)^{-m+1}v\right\} \\&=\left\{ r(A)v\mid \ r\in \mathcal {P}_{m-1}/(\gamma -z)^{m-1}\right\} , \end{aligned}$$

where $\mathcal {P}_m$ is the set of polynomials of a degree less than or equal to m. $e^{A}v$ which can be regarded as $f_{\gamma }\left( (\gamma I-A)^{-1}\right) v$, the function of $(\gamma I-A)^{-1}$, where $f_{\gamma }(z):=e^{\gamma -z^{-1}}$. Therefore, the matrix function is:

$$\begin{aligned} e^Av\approx V_mf_{\gamma }\left( V_m^*(\gamma I-A)^{-1}V_m\right) V_m^*v=V_mf_{\gamma }(H_m)V_m^*v=r(A)v, \end{aligned}$$

for some $r\in \mathcal {P}_{m-1}/(\gamma -z)^{m-1}$.

Moret and Novati [12] published a paper on the following theorem about the error bound for the SIA.

Theorem 2.1

Let $S_{\rho ,\theta }:=\{z\in \mathbb {C}\mid |\arg {z}|<\theta ,\ 0<|z|\le \rho \}$, $\mathcal {P}_m$ be the set of polynomials with a degree less than or equal to m, and $\varGamma ^*$ be the contour of any sector $S_{\rho ^*,\theta ^*}$ which satisfies $\rho ^*\ge \rho /(1-\sin (\theta ^*-\theta ))$ and $\theta<\theta ^*<\pi /2$. If

$$\begin{aligned} W((\gamma I-A)^{-1})\subseteq \overline{S_{\rho ,\theta }}, \end{aligned}$$

then the error bound of SIA is

$$\begin{aligned} \Vert e^{A}v-V_mf_{\gamma }(H_m)V_m^*v\Vert \le \frac{\Vert v\Vert }{\pi \sin (\theta ^*-\theta )} \min _{p\in \mathcal {P}_{m-1}}\int _{\varGamma ^*}\left| \frac{f_{\gamma }(\lambda )-p(\lambda )}{\lambda }\right| |d\lambda |. \end{aligned}$$

(4)

From Walsh’s theorem [12, cf. Proposition 2.1], for $\forall \epsilon >0$, $\vert f_{\gamma }(\lambda )-p(\lambda )\vert /\vert \lambda \vert <\epsilon$ is satisfied in approximation (4).

The magnitude of $\int _{\varGamma ^*}\vert f_{\gamma }(\lambda )-p(\lambda )\vert /\vert \lambda \vert \,\vert d\lambda \vert$ depends on the length of $\varGamma ^*$ and the property of $f_{\gamma }$. According to Proposition 3.3, $\rho$ becomes smaller and $\varGamma ^*$ becomes shorter as the shift $\gamma >0$ becomes larger. However, the larger constant $e^{\gamma }$ appears in $f_{\gamma }(\lambda )=e^{\gamma -\lambda ^{-1}}$ as $\gamma$ becomes larger. As a result, the magnitude of the integrated value becomes larger whether $\gamma$ is small or large.

3 Double-shift-invert Arnoldi method (DSIA)

A is transformed into $(\gamma _1 I-A)^{-1}(\gamma _2 I-A)^{-1}$, where $\gamma _1,\gamma _2>0$ instead of $(\gamma I-A)^{-1}$. The m-step Double-shift-invert Arnoldi process is:

$$\begin{aligned} h_{j+1,j}v_{j+1}&=(\gamma _1 I-A)^{-1}(\gamma _2 I-A)^{-1}v_j-\sum _{k=1}^jh_{k,j}v_k\,,\\ h_{k,j}&=v_k^*\left[ (\gamma _1 I-A)^{-1}(\gamma _2 I-A)^{-1}v_j-\sum _{l=1}^{k-1}h_{l,j}v_l\right] \qquad (k=1,\ldots ,j),\\ h_{j+1,j}&=\left\| (\gamma _1 I-A)^{-1}(\gamma _2 I-A)^{-1}v_j-\sum _{l=1}^jh_{l,j}v_l\right\| \qquad (j=1,\ldots ,m). \end{aligned}$$

This relation is expressed with matrices as:

$$\begin{aligned} V_m^*(\gamma _1 I-A)^{-1}(\gamma _2 I-A)^{-1}V_m=H_m, \end{aligned}$$

where $V_m=[v_1, \ldots , v_m]$ is an $n\times m$ matrix whose columns are the orthonormal basis of the Krylov subspace generated by the DSIA:

$$\begin{aligned} \mathcal {K}_m((\gamma _1 I-A)^{-1}(\gamma _2 I-A)^{-1},v), \end{aligned}$$

and $H_m=[h_{i,j}]$ is an $m\times m$ upper Hessenberg matrix. In the DSIA, $e^{A}v$ is regarded as $f_{\gamma _1,\gamma _2}\left( (\gamma _1 I-A)^{-1}(\gamma _2 I-A)^{-1}\right) v$, the function of $(\gamma _1 I-A)^{-1}(\gamma _2 I-A)^{-1}$, where $f_{\gamma _1,\gamma _2}(z):=e^{(\gamma _1+\gamma _2)/2-\sqrt{(\gamma _1-\gamma _2)^2+4z^{-1}}/2}$. The square root $\sqrt{w}$ for $w=re^{i\theta }\in \mathbb {C}{\setminus }(-\infty ,0]\ (r>0,\ -\pi<\theta <\pi )$ is defined as

$$\begin{aligned} \sqrt{w}=\sqrt{r}e^{i\theta /2}\in \mathbb {C}^+. \end{aligned}$$

The matrix function is approximated as:

$$\begin{aligned} e^Av\approx V_mf_{\gamma _1,\gamma _2}\left( V_m^*(\gamma _1 I-A)^{-1}(\gamma _2 I-A)^{-1}V_m\right) V_m^*v=V_mf_{\gamma }(H_m)V_m^*v. \end{aligned}$$

$f_{\gamma _1,\gamma _2}$ is an analytic on $\mathbb {C}{\setminus }(-\infty ,0]$, and setting $f_{\gamma _1,\gamma _2}(0)=0$, it becomes continuous in $\mathbb {C}{\setminus }(-\infty ,0)$. Moreover, the following lemma is deduced.

Lemma 3.1

Let $h(w):=(\gamma _1-w)^{-1}(\gamma _2-w)^{-1}$. If $w\in \mathbb {C}^{-}$, then $f_{\gamma _1,\gamma _2}(h(w))=e^{w}$.

Proof

Let $\gamma _1-w=a+bi$, $\gamma _2-w=c+di\ (a,b,c,d\in \mathbb {R})$. Since $\gamma _1,\gamma _2>0$ and $w\in \mathbb {C}^-$, $a,c>0$, h(w) is represented as $h(w)=(a-bi)(c-di)/(a^2+b^2)(c^2+d^2)$. If $bd=0$ or $bd<0$, then $\mathfrak {R}{(h(w))}>0$, and if $bd>0$, then $\mathfrak {I}{(h(w))}\ne 0$. As a result, $h(w)\in \mathbb {C}{\setminus }(-\infty ,0]$. Therefore, we can define $f_{\gamma _1,\gamma _2}(h(w))$, and $f_{\gamma _1,\gamma _2}(h(w))=e^{w}$ is deduced. $\square$

Lemma 3.1 guarantees the relation $e^A=f_{\gamma _1,\gamma _2}((\gamma _1 I-A)^{-1}(\gamma _2 I-A)^{-1})$.

Concerning the error bound for the DSIA, the following theorem is deduced:

Theorem 3.2

Let $S_{\rho ,\theta }:=\{z\in \mathbb {C}\mid |\arg {z}|<\theta ,\ 0<|z|\le \rho \}$, $\mathcal {P}_m$ be the set of polynomials with a degree less than or equal to m, and $\varGamma ^*$ be the contour of any sector $S_{\rho ^*,\theta ^*}$ which satisfies $\rho ^*\ge \rho /(1-\sin (\theta ^*-\theta ))$ and $\theta<\theta ^*<\pi$. If:

$$\begin{aligned} W((\gamma _1 I-A)^{-1}(\gamma _2 I-A)^{-1})\subseteq \overline{S_{\rho ,\theta }}, \end{aligned}$$

for $\theta <\pi /2$, then the error bound of DSIA is

$$\begin{aligned}&\Vert e^{A}v-V_mf_{\gamma _1,\gamma _2}(H_m)V_m^*v\Vert \nonumber \\&\quad \le \frac{\Vert v\Vert }{\pi \sin (\theta ^*-\theta )} \min _{p\in \mathcal {P}_{m-1}}\int _{\varGamma ^*} \left| \frac{f_{\gamma _1,\gamma _2}(\lambda )-p(\lambda )}{\lambda }\right| |d\lambda |. \end{aligned}$$

(5)

Proof

Let $Z:=(\gamma _1 I-A)^{-1}(\gamma _2 I-A)^{-1}$. It can be shown that $Z^kv=V_mH_m^kV_m^*v$ for $k=0,\ \ldots ,\ m-1$ by induction. Indeed, since $v\in \mathcal {K}_m(Z,v)$, $v=V_mV_m^*v$. For $k=1,\ \ldots ,\ m-1$, since $Z^kv\in \mathcal {K}_m(Z,v)$, the following relation is deduced:

$$\begin{aligned} Z^kv=V_mV_m^*Z^kv=V_mV_m^*ZZ^{k-1}v&=V_mV_m^*ZV_m(V_m^*ZV_m)^{k-1}V_m^*v\\&=V_m(V_m^*ZV_m)^kV_m^*v=V_mH_m^kV_m^*v. \end{aligned}$$

Therefore, the following inequality is satisfied for any $p\in \mathcal {P}_{m-1}$:

$$\begin{aligned}&\Vert e^{A}v-V_mf_{\gamma _1,\gamma _2}(H_m)V_m^*v\Vert \nonumber \\&\quad =\Vert e^{A}v-p(Z)v-V_mf_{\gamma _1,\gamma _2}(H_m)V_m^*v+V_mp(H_m)V_mv\Vert \nonumber \\&\quad \le \Vert f_{\gamma _1,\gamma _2}(Z)v-p(Z)v\Vert +\Vert V_mf_{\gamma _1,\gamma _2}(H_m)V_m^*v-V_mp(H_m)V_mv\Vert \end{aligned}$$

(6)

Since $W(H_m)\subseteq W(Z)\subseteq S_{\rho ^*,\theta ^*}$, and $f_{\gamma _1,\gamma _2}$ are analytic on $S_{\rho ^*,\theta ^*}$ and continuous on $\overline{S_{\rho ^*,\theta ^*}}$, using Cauchy’s integral formula [6, Definition 2.3] yields:

$$\begin{aligned}&f_{\gamma _1,\gamma _2}(Z)v-p(Z)v=\frac{1}{2\pi i} \int _{\varGamma ^*}(f_{\gamma _1,\gamma _2}(\lambda )-p(\lambda ))(\lambda I-Z)^{-1}v\,d\lambda ,\end{aligned}$$

(7)

$$\begin{aligned}&f_{\gamma _1,\gamma _2}(H_m)V_m^*v-p(H_m)V_m^*v\nonumber \\&\quad =\frac{1}{2\pi i}\int _{\varGamma ^*}(f_{\gamma _1,\gamma _2}(\lambda )-p(\lambda ))(\lambda I-H_m)^{-1}V_m^*v\,d\lambda . \end{aligned}$$

(8)

Moreover, since $W(H_m)\subseteq W(Z)$, it is deduced that [15, Theorem 4.1]

$$\begin{aligned} \Vert (\lambda I-Z)^{-1}\Vert&\le 1/{\text {dist}}(\lambda ,W(Z)), \end{aligned}$$

(9)

$$\begin{aligned} \Vert (\lambda I-H_m)^{-1}\Vert&\le 1/{\text {dist}}(\lambda ,W(H_m))\le 1/{\text {dist}}(\lambda ,W(Z)). \end{aligned}$$

(10)

The following inequality is deduced by inequalities (6), (9) and (10), and Eqs. (7) and (8):

$$\begin{aligned}&\Vert e^{A}v-V_mf_{\gamma _1,\gamma _2}(H_m)V_m^*v\Vert \nonumber \\&\quad \le \frac{\Vert v\Vert }{2\pi }\int _{\varGamma ^*}\vert f_{\gamma _1,\gamma _2}(\lambda )-p(\lambda )\vert \,\Vert (\lambda I-Z)^{-1}\Vert \,\vert d\lambda \vert \nonumber \\&\quad +\frac{\Vert v\Vert }{2\pi }\int _{\varGamma ^*}\vert f_{\gamma _1,\gamma _2}(\lambda )-p(\lambda )\vert \,\Vert (\lambda I-H_m)^{-1}\Vert \,\vert d\lambda \vert \nonumber \\&\quad \le \frac{\Vert v\Vert }{\pi }\int _{\varGamma ^*}\vert f_{\gamma _1,\gamma _2}(\lambda )-p(\lambda )\vert \,\frac{1}{{\text {dist}}(\lambda ,W(Z))}\,\vert d\lambda \vert \nonumber \\&\quad \le \frac{\Vert v\Vert }{\pi }\int _{\varGamma ^*}\vert f_{\gamma _1,\gamma _2}(\lambda )-p(\lambda )\vert \,\frac{1}{\lambda \sin (\theta ^*-\theta )}\,\vert d\lambda \vert \quad \left( \because \rho ^*\ge \frac{\rho }{1-\sin (\theta ^*-\theta )}\right) \nonumber \\&\quad \le \frac{\Vert v\Vert }{\pi \sin (\theta ^*-\theta )}\int _{\varGamma ^*}\left| \frac{f_{\gamma _1,\gamma _2}(\lambda )-p(\lambda )}{\lambda }\right| \,\vert d\lambda \vert \end{aligned}$$

(11)

Since $p\in \mathcal {P}_m$ in inequality (11) is arbitrary, Eq. (5) is satisfied. $\square$

The main differences between Eqs. (4) and (5) are the values of $\rho ^*$, $\theta ^*$ and the integrand. Concerning the numerical ranges of $(\gamma I-A)^{-1}$ and $(\gamma _1 I-A)^{-1}(\gamma _2 I-A)^{-1}$, the following proposition is deduced. This result is related to value $\rho ^*$ and $\theta ^*$:

Proposition 3.3

If $W((\gamma _1 I-A)^{-1}(\gamma _2 I-A)^{-1})\subseteq \mathbb {C}^{+}$, then

$$\begin{aligned}&W((\gamma I-A)^{-1})\subseteq \Big \{z\in \mathbb {C}^+\mid \mathfrak {R}{(z)}\le 1/\gamma \Big \}, \end{aligned}$$

(12)

$$\begin{aligned}&W((\gamma _1 I-A)^{-1}(\gamma _2 I-A)^{-1})\subseteq \Big \{z\in \mathbb {C}^+\mid \mathfrak {R}{(z)}\le 1/(\gamma _1\gamma _2)\Big \}. \end{aligned}$$

(13)

Proof

Only inclusion (13) is proven. The proof of inclusion (12) is similar. Let $x\in \mathbb {C}^n$ be an arbitrary vector with $\Vert x\Vert =1$. The following inequality is deduced:

$$\begin{aligned}&\left| x^*(\gamma _1 I-A)^{-1}(\gamma _2 I-A)^{-1}x\right| \le \Vert x\Vert \,\Vert (\gamma _1 I-A)^{-1}(\gamma _2 I-A)^{-1}x\Vert \\&\quad \le \Vert (\gamma _1 I-A)^{-1}\Vert \, \Vert (\gamma _2 I-A)^{-1}\Vert =\frac{1}{\sigma _{{\text {min}}}(\gamma _1 I-A)\sigma _{{\text {min}}}(\gamma _2 I-A)}, \end{aligned}$$

where $\sigma _\mathrm{min}(B)$ is the minimum singular value of matrix B. Concerning $\sigma _{{\text {min}}}(\gamma _1 I-A)$, the following inequality is satisfied for some $y\in \mathbb {C}^n$ with $\Vert y\Vert =1$.

$$\begin{aligned} \sigma _{{\text {min}}}(\gamma _1 I-A)=\Vert (\gamma _1 I-A)y\Vert \ge \vert y^*(\gamma _1 I-A)y\vert \ge \gamma _1 \quad (\because W(A)\subseteq \mathbb {C}^-). \end{aligned}$$

Similarly, $\sigma _{{\text {min}}}(\gamma _2 I-A)\ge \gamma _2$ is satisfied. Therefore, for any $x\in \mathbb {C}^n$ with $\Vert x\Vert =1$, $\left| x^*(\gamma _1 I-A)^{-1}(\gamma _2 I-A)^{-1}x\right| \le 1/(\gamma _1\gamma _2)$ is deduced, and inclusion (13) is satisfied. $\square$

The optimal shift $\gamma$ for the SIA is considered to be order m. Andersson showed that the optimal $\gamma$ for approximating $e^z$ for $z\in (-\infty ,0]$ in $Q_m=\{p(z)/(\gamma -z)^m\mid \gamma >0, p\in \mathcal {P}_m\}$ behaves asymptotically like $m/\sqrt{2}$ [1]. From this fact, the optimal shift for the SIA if A is symmetric, is $m/\sqrt{2}$ as $m\rightarrow \infty$ [17]. Therefore, according to Proposition 3.3, if we set $\gamma _1,\gamma _2\approx \gamma$, the $\rho$ in Eq. (5) will be much smaller than that of Eq. (4). This results in a much smaller $\rho ^*$ in Eq. (5) than in Eq. (4). Although there is a possibility $\theta ^*$ will be larger in the DSIA than in the SIA, the difference of $\rho ^*$ in the DSIA and the SIA will be significant enough to make the contour in Eq. (5) shorter than that of Eq. (4). On the other hand, the integrand in the SIA and the DSIA will be $f_{\gamma }(z)=e^{\gamma -z^{-1}}$ and $f_{\gamma _1,\gamma _2}(z)=e^{(\gamma _1+\gamma _2)/2- \sqrt{(\gamma _1-\gamma _2)^2+4z^{-1}}/2}$. The constants appearing in $f_{\gamma }$ and $f_{\gamma _1,\gamma _2}$ will be almost equal if $\gamma _1,\gamma _2\approx \gamma$. As a result, using the DSIA resolves the trade off between the length of the integral contour and the property of the integrand in the SIA. The DSIA makes the length of the integral contour shorter without making the property of the integrand worse. This results in a faster convergence of the DSIA than the SIA.

In conclusion, Algorithm 3.1 was proposed. The most expensive computation in each Krylov step of the DSIA is solving the linear equation in the third line. This computation is implemented completely in parallel, since $(\gamma _1 I-A)^{-1}(\gamma _2 I-A)^{-1}=[(\gamma _1 I-A)^{-1} -(\gamma _2 I-A)^{-1}]/(\gamma _2-\gamma _1)$, and $(\gamma _1 I-A)^{-1}v_m$ and $(\gamma _2 I-A)^{-1}v_m$ can be solved individually. On the other hand, the most expensive computation in SIA is solving the single linear equation $(\gamma I-A)x=v_m$ for x, and this computation cannot be implemented completely in parallel. Therefore, the cost for computing one step of the Krylov process in the DSIA is much less than twice as expensive as that of the SIA. For this reason, the computation time of the DSIA is faster than that of the SIA. $H_m$ in the tenth line is a small matrix, and $f_{\gamma _1,\gamma _2}(H_m)$ can be computed via a direct method such as the scaling and squaring method [8] inexpensively.

4 Numerical experiments

A few typical numerical experiments have been implemented in this section. These experiments were in a collection of problems to illustrate the effectiveness of the DSIA. All numerical computations of these tests were executed with C on an Intel(R) Xeon(R) X5690 3.47 GHz processor with an Ubuntu14.04 lts operating system. lapack and blas were used with atlas for the computations. In addition, the open mpi was used for parallel computations.

The Galerkin method with an unstructured first order triangle or tetrahedron elements and linear weight functions, were used to discretize the problems. After the discretization, gmres algorithm [14] with an ilu(0) preconditioner were applied to solve the linear equation in the third line of Algorithm 3.1 and in the SIA. We used two processes for computations in both DSIA and SIA. In the DSIA, these two processes were assigned for solving respective linear equations. In the SIA, these processes were assigned for solving the single linear equation. In the SIA, the matrix vector product, which is the most expensive computation of solving the linear equation with gmres, was implemented in parallel.

Example 1

In order to show the advantages of the DSIA, the convection diffusion equation in region $\varOmega =((-1.5,1.5)\times (-1,1)){\setminus }([-0.5,0.5]\times [-0.25,0.25]) \subseteq \mathbb {R}^2$ was implemented:

(14)

where $\partial \varOmega _1=\{-1.5\}\times [-0.5,1]$, $\partial \varOmega _2=\partial \varOmega {\setminus }\partial \varOmega _1$, $\rho =1.3$, $c_v=1000$ and $\lambda =0.025$. After the discretization, Eq. (2) was obtained with n =390,256. In this case, the matrix L is nonsymmetric. The numerical solution of $t=270$ was obtained through computing Eq. (3).

Firstly, Eq. (3) was computed with the SIA. To show the relationship between the shift and the approximation error of SIA explained in Sect. 2, we computed Eq. (3) with different shifts. The results are shown in Fig. 1a. The vertical axis represents the iterations needed for achieving the relative error of $10^{-6}$. The iteration number is smallest when the shift is 40, 50 and 60. If the shift is set smaller or larger than 40–60, more iterations are needed, and the iteration number does not become smaller than 49.

Next, Eq. (3) was computed with the DSIA. We set shifts $\gamma _1=\gamma$, and $\gamma _2=\gamma _1+1$ for each $\gamma$ used in SIA. The results are also shown in Fig. 1a. The iteration number of the DSIA is smaller than that of the SIA, with the exception when $\gamma =20$. Figure 1c and d show the relationship between the iteration number and the relative error when $\gamma =\gamma _1=50$, $\gamma _2=51$ and $\gamma =\gamma _1=100$, $\gamma _2=101$. The faster convergence of the DSIA compared to the SIA is shown in these figures, as well.

Figure 1(b) shows the CPU time of the SIA and the DSIA. As we explained in the last part of Sect. 3 and the beginning part of Sect. 4, two linear equations in each Krylov step of the DSIA is solved completely in parallel. On the other hand, solving the single linear equation for SIA requires a number of communications between processes. Thus, the costs for computing one step of the Krylov process in the DSIA is less than twice as expensive as that in the SIA. In almost all cases, the computation with the DSIA is faster, since its iteration number is smaller than that of the SIA.

Fig. 1

Example 1—numerical results of the convection diffusion equation. a Shifts versus iterations. b Shifts versus CPU time. c Iterations versus relative error ($\gamma =50$). d Iterations versus relative error ($\gamma =100$)

Example 2

The next problem is a heat equation used in fields like metal fitting where $\varOmega \subseteq \mathbb {R}^3$ in Fig. 2a:

(15)

where $\rho =7870$, $c_v=0.442$ and $\lambda =80.3$. After the discretization, Eq. (2) was obtained with $n=1142410$. In this scenario, matrix L is symmetric. The numerical solution of $t=500$ was obtained through computing Eq. (3).

Table 1 shows the CPU times and iteration numbers of the DSIA and the SIA. The shifts were set to $\gamma =50,100,150$ for the SIA, and $\gamma _1=\gamma$, $\gamma _2=\gamma +1$ for the DSIA. Like Table 1, the DSIA computes the solution faster than the SIA. Figure 2b shows the numerical solution obtained by using the DSIA. Equation (15) represents the heat diffusion in the metal fitting made of iron. The temperature in region $\varOmega$ is $0^{\circ }$C at $t=0$, but at this point, the heat begins to flow from $\partial \varOmega _1$ and then diffuses in $\varOmega$. We see the exactness of the computation of the DSIA here.

Fig. 2

Example 2—a heat equation in a field like metal fitting $\varOmega \subseteq \mathbb {R}^3$. a The region $\varOmega$. b Numerical solution

Table 1 Example 2—the CPU time and the iterations of the DSIA and SIA

5 Conclusion

The DSIA was explored in this paper. The DSIA uses two shifts in every Krylov step, and transforms the matrix so that its numerical range becomes small without making the property of the function in the error bound worse. This transformation reduces the iteration number of the DSIA so that it is less than that of the SIA for computing a matrix exponential and a vector product. The most expensive part of the computation in the DSIA can be implemented completely in parallel, while that in SIA cannot be implemented completely in parallel. For these reasons, the DSIA is the choice for faster computation versus the SIA.