1 Introduction

Modeling of the soil-structure interaction (SSI) is meant to be a more accurate and realistic approach to a structural analysis problem; then, a more detailed modeling of the damping phenomenon in the system is warranted in this case. This task is performed by putting aside the convenient assumption that damping is proportional to mass and stiffness, i.e., by doing a nonclassical dynamic analysis. In an SSI system a considerable part of damping, called the radiation damping, is contributed by the totally different medium of soil by letting the structural vibration energy propagate toward infinity from the soil-structure interface, or the foundation. This is unlike the fixed-base systems in which the source of vibration damping is more or less uniquely attributed to the structural system and is hence almost uniform. Therefore, when the flexibility of soil is accounted for in the seismic analysis of structures resting on such a medium, the system damping matrix is no longer taken to be proportional to structure’s mass and stiffness matrices. The damping matrix of such a complex system is a non-uniform combination of structure and soil damping values and therefore is not classical.

On the other hand, when only the maxima of seismic responses are sought (which is the prevailing case), the spectrum analysis can help attain a relatively rapid yet accurate enough design in most problems. A basic assumption in such an analysis is the damping being classical. This makes definition of the damping matrix very easily possible as a combination of mass and stiffness matrices. When there is a doubt on validity of this basic assumption, like in SSI problems as discussed above, availability of a spectrum analysis methodology corrected for nonclassical damping while retaining its simplicity will be very helpful.

Many attempts have been made by different researchers to develop dynamic analysis methods for systems with a nonclassical damping. The first solution for dynamic response of such systems was derived by Foss (1958). His method is known as the extended modal analysis (EMA). While being robust, the complexity of the above method detracted the attention of practical engineers. The work of Veletsos and Ventura (1986) was an important step forward in this regard. They simplified the EMA through giving insight to the physical meaning of different terms of the formulation and converted the complex-valued equations to their real counterparts. They derived equations for determining natural periods and mode shapes of nonclassical systems resulting in free vibration responses and a Duhamel integral formulation for computing the dynamic response.

The response spectrum analysis consists of two steps: computing the maxima in each mode, and, combining the modal maximum responses via a suitable rule like SRSS or CQC. Ziaeifar and Tavousi (2005) developed formulas for calculating the modal values of the response maxima based on the work of Veletsos and Ventura (1986). They applied their formulation to mass-isolated structural systems and studied the conditions requiring such nonclassical analysis. Zhou and Yu (2008) derived formulas for combining the maximum modal responses of non-classically damped linear systems. They used the random vibration theory and accounted for the correlation between the modal displacement and velocity responses of structure. Based on a general modal response history analysis formulation for nonclassical and over-damped systems developed by Song et al. (2008), they derived a response spectrum analysis approach and proposed a general modal combination rule.

To gain attractiveness in practical earthquake engineering, a nonclassical SSI problem should be solved within the frame work of a conventional design spectrum. In the code-based procedures (American Society of Civil Engineers 2010), it is prescribed that for spectral analysis of SSI systems, the fixed-base design spectrum of the code is still used but with the fundamental period and equivalent damping of the SSI system, which are usually larger than those of the fixed-base system. This prescribed analysis is only for the fundamental mode and the effect of SSI on the higher modes is allowed to be ignored.

In the current study, first the SSI base shear and displacements are compared with their fixed-base counterparts using both classical and nonclassical analysis. Then, it is recognized for which cases the higher mode SSI effects are important and in what instances performing the non-classical SSI analysis is necessary. One to 20-story buildings are considered and for each building, two suits of ground motion each containing 10 records, one being recorded at the near field and the other at the far field, selected through a special procedure specifically for each structure are used. Two types of medium and soft soils are also considered.

In the following, first the theory of non-classical spectral analysis of SSI systems is described and then the building-earthquakes cases are identified and the analysis results are presented.

2 Modal analysis of soil-structure systems

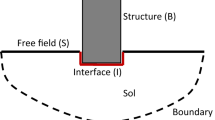
In this section the equations of motion of structures resting on flexible soils are derived and decomposed into its modal components as an extension of (Veletsos and Ventura 1986) to soil-structure systems. To this end, a multistory structure on flexible soil subjected to a horizontal ground motion is considered as shown in Fig. 1.

Fig. 1
figure 1

The multistory structure on flexible soil under lateral movement

Full size image

Without curbing generality, the system is assumed to be a shear building having a single horizontal degree of freedom (DOF) at each floor to retain simplicity. In addition, it is supposed that the supporting medium possesses a horizontal as well as a rotational DOF, and the input motion in the presence of structure is assumed to be identical to the free-field motion.

The equations of motion of the system of Fig. 1 can be written as follows:

$$\left[ M \right] \left\{ {{\ddot{U}}} \right\} + \left[ C \right] \left\{ {\dot{U}} \right\} + \left[ K \right] \{ U\} = p(t)$$
(1)

in which:

$$\left\{ U \right\} = \left\{ {\begin{array}{*{20}c} {\left\{ u \right\}} \\ {u_{b} } \\\uppsi \\ \end{array} } \right\}$$
(2)
$$\left\{ {p\left( t \right)} \right\} = - \left\{ { \begin{array}{*{20}c} {\left\{ m \right\}} & {m_{b} + \mathop \sum \limits_{1}^{n} m_{i} } & {\mathop \sum \limits_{1}^{n} m_{i} h_{i} } \\ \end{array} } \right\}^{T} {\ddot{u}}_{g} \left( t \right)$$
(3)

and the mass, damping and stiffness matrices are shown with \(\left[ M \right],\left[ C \right]\) and \(\left[ K \right]\), respectively, introduced in Eqs. (24–28) in the Appendix. As seen with the vector of degrees of freedom in Eq. (2), the additional two last rows refer to the extra deformations at the base. This in turn results in the fact that the two last rows and columns of the damping matrix pertain to the soil dampings. This property makes the total system damping matrix to be in essence nonclassical, i.e., non-proportional to mass and stiffness matrices. Of course, it can be assumed to be proportional just as an approximate presumption.

As shown in Appendices 2 and 3, the dynamic response including non-proportionality of the damping matrix can be derived as:

$$\{ U\} = \mathop \sum \limits_{j = 1}^{N} \left[ {\left\{ {\alpha_{j}^{v} } \right\} V_{j} \left( t \right) + \{ \beta_{j}^{v} \} \dot{D}_{j} (t)} \right]$$
(4)

in which \(V_{j} (t)\) and \(\dot{D}_{j} (t)\) are the pseudo-velocity and the relative velocity of the jth mode equivalent SDF system with natural frequency \(p_{j}\) and damping ratio \(\zeta_{j}\) (see Eq. 33), N is the total number of degrees of freedom, and \(\left\{ {\alpha_{j}^{v} } \right\}\) and \(\{ \beta_{j}^{v} \}\) are as defined in Eqs. (50) and (45), respectively. \(V_{j} (t)\) and \(\dot{D}_{j} (t)\) are defined as follows:

$$V_{j} \left( t \right) = p_{j} D_{j} \left( t \right) = - p_{j} \int_{0}^{t} {{\ddot{u}}_{g} } \left( \tau \right)h_{j} (t - \tau )d\tau$$
(5)
$$\dot{D}_{j} \left( t \right) = - \int_{0}^{t} {{\ddot{u}}_{g} } \left( \tau \right)\dot{h}_{j} ({\text{t}} - \tau )d\tau$$

The base shear is computed as described in Appendix 4 as the summation of lateral story forces resulting in the following equation:

$$V^{b} \left( {\text{t}} \right) = \mathop \sum \limits_{{{\text{j}} = 1}}^{\text{N}} \left[ {\left( {m_{j}^{\alpha \omega } } \right)p_{\text{j}} V_{j} \left( {\text{t}} \right) + \left( {m_{j}^{\beta \gamma } } \right)p_{\text{j}} \dot{D}_{j} \left( {\text{t}} \right)} \right]$$
(6)

in which:

$$m_{j}^{\alpha \omega } = \alpha_{j}^{Mv} + \omega_{j}^{Mv}$$
$$m_{j}^{\beta \gamma } = \beta_{j}^{Mv} + \gamma_{j}^{Mv}$$
(7)

and \(\left\langle {1_{\text{N}} } \right\rangle = \left\langle {\overbrace {1 \ldots 1}^{\text{n}} 0 \;0_{n + 2} } \right\rangle\), and the quantities on the right side of Eq. (7) are as defined in Eq. (58).

3 The spectrum analysis

In order to calculate the maximum displacements or base shear from Eqs. (4) or (6), respectively, maximum values of \(V_{j} (t)\) and \(\dot{D}_{j} (t)\) are needed noting that these maxima need not to occur simultaneously. One may use the SRSS rule to combine these maxima as:

$$\left\{ U \right\}_{{j_{ \hbox{max} } }} = \sqrt {\left( {\left\{ {\alpha_{j}^{v} } \right\} V_{{j _{\hbox{max} } }} } \right)^{2} \,+\, \left( {\left\{ {\beta_{j}^{v} } \right\}\dot{D}_{{j _{\hbox{max} } }} } \right)^{2} }$$
$$V_{{j_{\hbox{max} } }}^{b} = \sqrt {\left( {\left( {m_{j}^{\alpha \omega } } \right)p_{\text{j}} V_{{j_{\,\hbox{max} } }} } \right)^{2} \,+\, \left( {\left( {m_{\text{j}}^{\beta \gamma } } \right)p_{j} \dot{D}_{{j_{\hbox{max} } }} } \right)^{2} }$$
(8)

in which, an index max shows the maximum value in the jth mode. The following relation can be assumed to exist between the maximum values of \(V_{j} (t)\) and \(\dot{D}_{j} (t)\):

$$\dot{D}_{{j_{\hbox{max} } }} = \eta_{j} V_{{j_{\hbox{max} } }}$$
(9)

There have been different proposals for the conversion factor \(\eta_{j}\) in the above equation. Sinha and Igusa (1995) used an \(\eta_{j}\) = 1 assumption. Zhou and Yu (2008) used the theory of random vibrations to calculate the correlation factors of displacement and velocity functions in each mode. Sadek et al. (2000) proposed the following relation using the period \({\text{T}}_{\text{j}}\) and damping factor \(\upxi_{j}\) of the j-th mode:

$$\eta_{j} = a_{vj} T_{j}^{{b_{vj} }} ,\quad a_{vj} = 1.095 + 0.647\upxi_{j} - 0.382\upxi_{j}^{2}$$
$$b_{vj} = 0.193 + 0.838\upxi_{j} - 0.621\upxi_{j}^{2}$$
(10)

Ziaeifar and Tavousi (2005) based on a work by Pekcan et al. (1999) suggested that:

$$\eta_{j} = f\left( {T_{j} ,\upxi_{j} } \right) = 0.8 - 0.6\upxi_{j} + 0.17{\text{T}}_{j} + 0.4\upxi_{j} {\text{T}}_{j}$$
(11)

The above equation is on the basis of the random vibration analysis of an earthquake ground motion assumed to be a stationary function, and is used in this study.

Substituting (9) in (8) results in:

$$\left\{ U \right\}_{{j_{ \hbox{max} } }} = \sqrt {\left\{ {\alpha_{j}^{v} } \right\}^{2} \,+\, \eta_{j}^{2} \left\{ {\beta_{j}^{v} } \right\}^{2} } V_{{j_{\hbox{max} } }}$$
(12)
$$V_{{j_{\hbox{max} } }}^{b} = \sqrt {\left( {m_{j}^{\alpha \omega } } \right)^{2} \,+\, \eta_{j}^{2} \left( {m_{j}^{\beta \gamma } } \right)^{2} } p_{j} V_{{j_{\hbox{max} } }}$$

Equation (12) can be simplified to give the maximum base shear of the jth mode as:

$$V_{{j_{\hbox{max} } }}^{b} = M_{j} p_{j} S_{{pv_{j} }} \left( {p_{j} ,\xi_{j} } \right) = M_{j} S_{{pa_{j} }} \left( {p_{j} ,\xi_{j} } \right)$$
(13)

in which:

$$M_{j} = \sqrt {\left( {m_{j}^{\alpha \omega } } \right)^{2} \,+\, \eta_{j}^{2} \left( {m_{j}^{\beta \gamma } } \right)^{2} }$$
(14)

where \(S_{pv}\) and \(S_{pa}\) are the spectral values of the jth mode pseudo-velocity and pseudo-acceleration, respectively.

Equation (13) for computing the maximum base shear of a nonclassical SSI system differs from that of the classical (conventional) systems in two ways. First, the pseudo-acceleration \(S_{pa}\) should be calculated using the jth mode period and damping ratio of the nonclassical system, and second, a different modal mass \(M_{j}\) calculated by Eq. (14) is utilized.

4 Numerical modeling

4.1 Design assumptions

For the purposes of this study, special steel moment frame structures being 1, 2, 4, 6, …, 18 and 20 story building are designed. The frames have three bays both ways each spanning 5 m. The floor to floor heights are 3 m. The residential buildings are designed according to ASCE 7-10 (American Society of Civil Engineers 2010) and AISC-ASD (American Institute of Steel Construction 2005). The seismicity of the region is considered to be very high with the effective peak acceleration at the ground surface to be 0.35 g. Two types of underlying soils are considered: a soft soil [soil type D (American Society of Civil Engineers 2010)] and a very soft soil (soil type E). Their characteristics are given in Table 1.

Table 1 Characteristics of the soil types
Full size table

Eleven buildings with the mentioned number of stories are designed with fixed bases for each soils type. Therefore, totally 22 buildings are considered in this study. The design spectra are shown in Fig. 2 for each soil type (American Society of Civil Engineers 2010).

Fig. 2
figure 2

The design spectra for the soil types D and E

Full size image

Natural periods of the buildings in their first three modes of lateral displacement are shown in Table 2.

Table 2 First three natural periods of the fixed-base buildings in lateral motion (s)
Full size table

As seen in Table 2, since the same building is designed using a different spectrum on each soil type, two different buildings with the same height but different periods are resulted. For 1 to 4-story buildings single footings and for 6 to 20-story structures strip foundations are designed. The foundation dimensions are shown in Table 3.

Table 3 Dimensions of the foundations (m)
Full size table

4.2 The earthquake records

After design of fixed-base buildings, they will be analyzed under seismic ground motions for calculating their dynamic responses. For time-history analysis of the buildings under study, earthquake records with the following characteristics are selected out of the PEER NGA database (http://peer.berkeley.edu/peer_ground_motion_database): 6.5 ≤ Magnitude ≤ 7.5, soil type is whether D or E. Two groups of earthquakes are selected for each building on each soil type regarding the epicentral distance, R. Group one, the near-field earthquakes with R ≤ 20 km, and group two, the far-field earthquakes with 20 < R ≤ 50 km. Then the records are scaled according to ASCE7-10 (American Society of Civil Engineers 2010), such that their response spectra does not fall below the design spectrum of Fig. 2 between 0.2T and 1.5T, where T is the fundamental period of the fixed-base buildings. Then 10 records in each distance group with scale factors closer to unity (hence with more similarity to the design spectrum) are retained for dynamic analysis of the same building. Table 4 shows the records selected for each building. Also, for instance, Table 5 shows the records selected for the 10-story building along with their scale factors. Characteristics of the selected records of Table 4 are given in the Appendix.

Table 4 The selected records
Full size table
Table 5 The selected records and their scale factors for the 10 story building
Full size table

4.3 Modeling of soil-structure interaction

For the purposes of this study it is necessary to analyze four different models. Model 1 and Model 2 are two-dimensional (2D) frames representing an interior frame of each of the above buildings developed in SAP2000 (Computers and Structures, Inc. 2014). Model 1 is fixed at base but Model 2 is a flexible base structure. Flexibility of the base in Model 2 is incorporated by adding the body of foundations to the structural model while resting on certain springs. Calculation of the stiffness of the soil springs is described in the next section.

Moreover, an equivalent damping accounting for combination of the dampings of the structure and the soil is determined, as explained in Sect. 4.3.2, and assigned to the flexible-base model. The structural part of the damping is assumed to be of Rayleigh type with a damping ratio of 5 % in all models. Models 3 and 4 are stick models of the same flexible-base 2D frames as above and are developed in Matlab. Models 1–3 are analyzed using the classical modal analysis and Model 4 using the nonclassical procedure described in Sects. 2 and 3. The reason for Model 3 is utilizing it as a basis for comparison, within the needs of this study, with responses determined using the more accurate 2D frame analysis (Model 2) in SAP. This is needed because certain simplifying assumptions are necessary to reduce a 2D model to a stick model. Model 4 is necessary for nonclassical analysis because such an analysis is not possible in commercial engineering softwares. In both models 3 and 4, the flexible base is modeled using a rigid foundation being in dimensions equivalent to the actual foundations of the 2D frames. For strip foundations (in 6 to 20-story buildings), the same dimensions are used. For single footings (in 1 to 4-story buildings), length of the foundation element in Models 3 and 4 is taken to be equal to sum of the single foundation lengths in the corresponding 2D frames. Width of the foundation in this case is mean of the foundation widths in the corresponding frame. The above assumptions are easily validated by doing the same seismic analysis for the Models 2 and 3. It will be shown that the mentioned assumptions are appropriate for the responses targeted in this study.

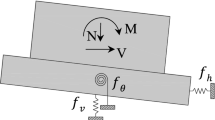
The base of the Models 3 and 4 rests on springs and dampers along the two degrees of freedom in plane as shown in Fig. 3. Characteristics of the springs and dampers are given in the following sections.

Fig. 3
figure 3

Configuration of the stick models (Models 3 and 4)

Full size image

4.3.1 Stiffness of the soil springs

The stiffness of soil springs is a function of the dynamic shear modulus of soil, \(G\). The dynamic shear modulus can be much smaller than the soil shear modulus at small strains, \(G_{0}\), because of the large strains that develop in soil during an earthquake. \(G_{0}\) is given by Eq. (15):

$$G_{0} = \frac{{ \gamma V_{s}^{2} }}{g} = \rho V_{s}^{2}$$
(15)

in which γ is the unit weight of soil, \(V_{s}\) is the shear wave velocity in soil at small strains, and \(g\) is the acceleration of gravity. The ratio \(G/G_{0}\) depends on the soil type and the soil’s shear strain during earthquake. Since the shear strain is somewhat correlated with the peak ground acceleration and the latter with the spectral acceleration, the ratio \(G/G_{0}\) has appeared in the codes as a function also of the effective peak ground acceleration at the ground surface (SDS) for simplicity. SDS is equal to the spectral acceleration at short periods divided by 2.5 (American Society of Civil Engineers 2010). Values of \(G/G_{0}\) for the two soil types are given in Table 6 according to ASCE 7-10 (American Society of Civil Engineers 2010).

Table 6 Values of G/G0
Full size table

Since different ground motions have been selected for different structures, the average SDS of each group of earthquakes mentioned in Table 4 is used for calculation of \({\text{G}}/{\text{G}}_{0}\) on each soil type.

According to ASCE41-13 (American Society of Civil Engineers 2013), before determining the spring stiffnesses, condition of the foundation being flexible or rigid with regard to the underlying soil, must be determined. Then, if the inequalities (16) and (17) hold, the single/mat and strip foundations, respectively, are rigid:

$$4k_{sv} \mathop \sum \limits_{m = 1}^{5} \mathop \sum \limits_{n = 1}^{5} \frac{{\sin^{2} \left[ {\frac{m\pi }{2}} \right]\sin^{2} \left[ {\frac{m\pi }{2}} \right]}}{{\pi^{4} D_{f} \left[ {\frac{{m^{2} }}{{L^{2} }} + \frac{{n^{2} }}{{B^{2} }}} \right]^{2} k_{sv} }} < 0.3$$
(16)
$$D_{f} = \frac{{E_{f} t^{3} }}{{12(1 - \nu_{f} )^{2} }} , \quad k_{sv} = \frac{1.3G}{B(1 - \nu )}$$
$$\frac{{E_{f} I_{f} }}{{l^{4} }} > \frac{2}{3}k_{sv} B$$
(17)

where \(E_{f}\) and \(\nu_{f}\) are respectively the modulus of elasticity and the Poisson’s ratio of foundation material (concrete); B, L and t are width, length, and thickness of foundation, ν and G are the Poisson’s ratio and (dynamic) shear modulus of soil, \(k_{sv}\) is the vertical stiffness of soil (or the modulus of soil reaction) and \(I_{f}\) and l are moment of inertia of the strip foundation’s section and its length shared by one column, respectively.

The above criteria result in all of the foundations of this study resting on the soil type E to be rigid. For the soil type D, only foundations of 1, 2 and 4-story buildings prove to be rigid. This is expected because of the small dimensions of the footings for the shorter buildings and softness of the soil types. In the plane of a 2D frame, introducing the horizontal x and the vertical z translational and the y-axis rocking degrees of freedom at each foundation component suffice. Following the linear procedure of ASCE41-13 (American Society of Civil Engineers 2013), for each foundation, a single horizontal spring is assigned in the x direction. For flexible foundations, a uniformly distributed vertical spring with the stiffness \(k_{sv}\) given in Eq. (16) is utilized.

For rigid foundations, coupling of vertical and rocking degrees of freedom is taken into account using a nonuniform distribution of vertical springs. For this purpose, each foundation is divided to interior and exterior zones. The exterior zones are two rectangles, one at each end of the foundation, with a length of \(B/6\) and a width equal to that of the foundation.

The vertical stiffness of the distributed springs at the middle and end zones, \(k_{mid}\) and \(k_{end}\) respectively, are as follows (American Society of Civil Engineers 2013):

$$k_{end} = \frac{6.83G}{1 - \nu }$$
(18)
$$k_{mid} = \frac{0.73G}{1 - \nu }$$

The distance between the vertical springs is taken to be about 20 cm on average.

4.3.2 Damping

As mentioned at the beginning of Sect. 4.3, an equivalent damping ratio accounting for the effects of base flexibility is used with Model 2. It is calculated using Eq. (19) (American Society of Civil Engineers 2010):

$$\bar{\beta } = \beta_{0} + \frac{\beta }{{\left( \frac{{\overline{{\text{T}}} }}{{\text{T}}} \right)^{3} }}$$
(19)

in which \(\bar{\beta }\) is the equivalent SSI damping ratio of structure, \(\beta_{0}\) is the damping ratio supplied by foundation and soil as being a function of \({\bar{\text{T}}}/{\text{T}}\) and aspect ratio of structure (American Society of Civil Engineers 2010), β is the damping ratio of the fixed-base structure (assumed to be equal to 0.05), \({\bar{\text{T}}}\) is the fundamental period of structure including SSI, and T is the fundamental period of the fixed-base building. Use of Eq. (19) results in \(\bar{\beta }\) values to be as listed in Table 7. According to Sect. 4.3.1, stiffness properties of soil and therefore values of \({\bar{\text{T}}}\) are functions of \(G\), itself being a function of SDS as of Table 6 and its descriptions. Therefore, \(\bar{\beta }\) values are different when analyzing the 2D frames of this study under near and far field earthquakes. Values of \({\bar{\text{T}}}/{\text{T}}\) are given in Sect. 5.2.

Table 7 Values of the equivalent damping ratios of structures including SSI, \(\bar{\beta }\)
Full size table

Design spectra as shown in Fig. 2 are given for a damping ratio of 0.05, as common. For SSI applications, the spectral values will be needed for other damping ratios, as given in Table 7, too. This is usually done using a spectral reduction factor RF. Many versions are available for RF as proposed by different researchers, such as those of Newmark and Hall (1982), Ashour (1987), Wu and Hanson (1989), Ramirez et al. (2002), Lin and Chang (2003) and Bommer and Mendis (2005). The equation given by Bommer and Mendis has been endorsed by several building codes like Eurocode 8 (2003) and is used in this study for spectrum modification. It is given in Eq. (20):

$$RF = \left\{ {\begin{array}{*{20}l} {1 - \left( {1 - \eta } \right)\frac{{{\bar{\text{T}}}}}{{T_{b} }} \quad 0 \le \bar{T} < T_{b} } \hfill \\ { \eta \quad \bar{T} \ge T_{b} } \hfill \\ \end{array} ,\quad \eta = \sqrt {\frac{10}{{5 + 100\bar{\beta }}}} \,\ge\, 0.55 } \right.$$
(20)

in which \(T_{b}\) is the period at which the constant acceleration branch begins in the Newmark spectrum, being equal to \(\frac{1}{8}\) s. According to Fig. 3, for Models 3 and 4 explicit representation of dampers has been adopted. The damping coefficients in the horizontal and rocking degrees of freedom have been given as (Gazetas 1991):

$$C_{uu} = pV_{s} A_{b}$$
(21)
$$C_{\psi \psi } = pV_{la} I_{by} \tilde{c}_{ry}$$

where \(p\) is the unit mass of soil, \(A_{b}\) is the area of foundation in plan, \(I_{by}\) is the moment of inertia of the foundation in plan about the transverse axis, \(V_{la}\) is a wave velocity equal to \(\frac{{3.4 V_{s} }}{\pi (1 - \nu )}\) with \(V_{s}\) being the shear wave velocity, and \(\tilde{c}_{ry}\) is a coefficient beginning from zero for the static case and tending to unity for very large excitation frequencies.

5 The analysis results

In this section, after a comparison between the analytical models, first the natural periods and damping ratios are calculated for the SSI systems. Then, the maxima of base shear and lateral displacement of roof of each building are determined for the all four models of Sect. 4.3. For this purpose, a linear dynamic time history analysis is utilized and the results of each response parameter are averaged between the earthquakes corresponding to each building. Then the responses are shown against the fixed-base natural period.

5.1 Comparison of the flexible-base 2D and stick models responses

As mentioned in Sect. 4.3, two different models, called Models 2 and 3, are used for representing the seismic responses of the flexible base systems, using the classical procedure. Model 2 is a planar frame in SAP including beams, columns, and the single footing of each column or the whole strip footing resting on the vertical springs described in Sect. 4.3.1. Model 3 is a stick model displayed in Fig. 3 with stiffness and damping properties described in Sects. 4.3.1 and 4.3.2. Since the same stick model will be used for the nonclassical analysis procedure too (Model 4, because nonclassical analysis is not possible in SAP), Model 3 is meant to act as a basis of comparison for Model 4. Therefore, Model 3 needs to be justified first with a more accurate system like Model 2.

Figure 4 shows values of the base shear calculated using Model 2 in SAP and Model 3 in Matlab, normalized to the weight of each building. The results are presented separately for the near-field and far-field earthquakes and for different soil types. Average of the maximum response in linear time history analysis of each building is shown for each building on each soil type under near and far field earthquakes by finding its fixed-base natural period on the horizontal axis. Similarly, values of the maximum lateral displacement normalized to the height of each building are shown in Fig. 5.

Fig. 4
figure 4

Values of the base shear for the classical flexible-base 2D and stick models normalized to the building weight, versis the fixed-base period T. a Soil type D, near field earthquakes. b Soil type D, far field earthquakes. c Soil type E, near field earthquakes. d Soil type E, far field earthquakes

Full size image
Fig. 5
figure 5

Values of the maximum roof displacement for the classical flexible-base 2D and stick models normalized to the building height, versis the fixed-base period T. a Soil type D, near field earthquakes. b Soil type D, far field earthquakes. c Soil type E, near field earthquakes. d Soil type E, far field earthquakes

Full size image

As observed, the base shear values calculated by Models 2 and 3 are practically the same. For the maximum roof displacement again a very good similarity is observed, with the relative difference being larger for the taller buildings and reaching a value of about 6 % for the tallest frame. Along the period axis, the displacements are always overestimated by the stick model. Therefore, Model 4 is an appropriate model for nonclassical analysis and Model 3, being almost equivalent to Model 2 and having a similar configuration to Model 4, is a suitable reference for comparison with Model 4.

5.2 The natural periods and damping ratios

Figure 6 shows the values of the first to the third natural periods of the flexible-base systems normalized to the corresponding values of the same systems but fixed at base. The latter values are given in Table 2. Periods of the flexible-base systems have been calculated using Models 3 and 4. Therefore, in each part of the figure results of analysis of classical and nonclassical systems are given together for ease of comparison. Because system stiffness changes also with \({\text{G}}/{\text{G}}_{0}\) (Table 5), values are averaged between the systems corresponding to the near and far field earthquakes. It is observed that period shifting due to SSI is larger for the first mode, the softer soil and the taller buildings and reaches up to 20 %. It decreases sharply as the mode number increases and is negligible for the higher modes. Also, difference of the corresponding periods of the same system but calculated by classical and nonclassical procedures is negligible.

Fig. 6
figure 6

Periods of the flexible-base models normalized to those of the fixed-base systems, versis the fixed-base period T. a First mode. b Second mode. c Third mode

Full size image

Table 8 shows the damping ratios of the first three modes calculated for the nonclassical flexible-base Model 4 using Eq. (33).

Table 8 Damping ratios of the first three modes of the nonclassical SSI systems
Full size table

It is interesting to compare the damping ratios collected in Tables 7 and 8. Values of the code-based damping ratios of Table 7 are essentially for the first mode. They begin from about 10 and 9 % for the 1-story building on the soil types D and E, respectively, and uniformly increase to about 14 % for the 20-story building. On the other hand, the first-mode damping ratios calculated using the equations of non-classical dynamical systems and reported in Table 8, vary from about 10 and 11–6 % for the same cases. There are two important differences here. First, the trend of variation of the damping ratio proves to be descending with the rigorous procedure in contrast to the one predicted by the code. Second, the rigorous damping ratio shows an asymptotic behavior such that from about the 10-story building, it does not change notably. Variation of the code-based ratio is not similar. Although values of damping ratios of the higher modes are larger than those of the first mode, as of Table 8, they show the same trend of variation.

5.3 Responses in the fundamental mode

A modal time history analysis is accomplished in the section. Only response of the first mode is included. Model 1 (see Sect. 4.3) is used for the fixed-base analysis and Models 3 and 4 for the flexible-base classical and nonclassical analysis, respectively. All of the response parameters are shown versus the fixed-base period of each building. Figure 7 shows the averaged maximum lateral displacement of roof normalized to the height of each building. In nonclassical analysis, it is calculated using Eq. (4). The results are presented for each soil type and each earthquake category.

Fig. 7
figure 7

The averaged maximum lateral displacement of roof normalized to the height of each building. a Soil type D, near field earthquakes. b Soil type D, far field earthquakes. c Soil type E, near field earthquakes. d Soil type E, far field earthquakes

Full size image

According to Fig. 7, from a period of about 1 s, lateral displacements of the flexible-base models overtake those of the fixed-base model considerably, for both categories of earthquakes. The relative difference of displacements between models increases with height such that for the soil types D and E it reaches to about 33 and 56 %, respectively, for larger periods. For periods larger than 1 s, difference between the classical and nonclassical approaches for estimating the displacement response can be ignored. It should be noted that in the dynamic analysis of Model 3 the damping matrix is assumed to be proportional to the mass and stiffness matrices and only an equivalent modal damping ratio of 5 % is utilized. On the other hand, in the dynamic analysis of Model 4 that is nonclassical, the damping matrix is explicitly used and the modal damping ratios are calculated to be as reported in Table 8. According to this table, the nonclassical damping ratios of the first mode are about 6 % on both soil types for the periods above 1 s. Therefore, the maximum nonclassically calculated displacements should be slightly smaller than their classical counterparts in this period range, as they are.

For periods smaller than 1 s, difference between the displacements calculated by all of the three models is small and effect of SSI on displacements is negligible. It is interesting that in the same period range, the nonclassical analysis results in displacements smaller than those of the fixed-base and classical flexible-base models. Referring to Table 8, it seems that the damping augmented due to SSI in the nonclassical model is responsible for the smaller displacements in the shorter models. On the other hand, an increased contribution of the rocking motion in taller models overcomes the increased damping effect and results in larger displacements due to SSI. There is no conflict between the classical and nonclassical analysis in the latter case. As Fig. 2 shows, amplification of the structural response due to the soil properties occurs up to a maximum period of 1 s for the softer soil. Therefore larger SSI displacements of Fig. 7 after the 1 s period cannot be attributed to resonance.

The averaged maximum base shear of each system normalized to its weight is shown in Fig. 8. For the nonclassical analysis, it is calculated using Eq. (6).

Fig. 8
figure 8

Averaged maximum base shear normalized to the building weight. a Soil type D, near field earthquakes. b Soil type D, far field earthquakes. c Soil type E, near field earthquakes. d Soil type E, far field earthquakes

Full size image

Figure 8 shows that SSI decreases the base shear on both soil types. The reduction is important from the same 1 s period mentioned in displacement analysis. The more rigorous nonclassical analysis procedure is similar in results to the fixed-base case for periods smaller than 1 s and to the classical procedure for larger periods. The base shear reduction is up to 23 and 38 % for taller buildings.

Comparing Figs. 7 and 8, an important fact emerges. For periods smaller than 1 s, soil-structure interaction may not be taken into account for seismic analysis of structures similar to the ones of this study, i.e., moment frame structures resting on surface foundations. This is because use of the more accurate nonclassical SSI analysis results in response values similar to the fixed-base ones. Therefore, accounting for SSI with classical analysis underestimates the responses in this period range.

Figure 8 actually displays the first-mode spectral accelerations (normalized to g) of the studied buildings because in this figure the base shear is normalized to the building weight. The sample building code ASCE7-10 (American Society of Civil Engineers 2010) in its chapter on soil-structure interaction requires that the spectral acceleration including SSI is calculated using the fixed-base design spectrum but with flexible-base period of the first mode. The resulting value must be modified using the equivalent damping ratio of structure including SSI. Then the modified base shear due to SSI is calculated using Eq. (22):

$$\bar{V} = V - \Delta V$$
(22)

in which \(V\) and \(\bar{V}\) are the base shears without and with considering SSI, respectively, and \(\Delta V\) is portion of the base shear deducted when accounting for SSI. \(\Delta V\) is calculated using Eq. (23):

$$\Delta V = \left[ {C_{s} - \bar{C}_{s} \left( {\frac{0.05}{{\bar{\beta }}}} \right)^{0.4} } \right]\bar{W} \le 0.3V$$
(23)

where \(C_{s}\) and \(\bar{C}_{s}\) are the seismic coefficients determined using the fundamental periods of the fixed-base and flexible-base systems, respectively, and \(\bar{\beta }\) is damping ratio of the SSI system calculated using Eq. (19). With the damping ratios calculated in Sect. 4.3.2 (see Table 7) and the natural periods mentioned in Sect. 5.2, it is now possible to construct a code-based first-mode spectrum including SSI using the fixed-base spectrum of Fig. 8. For this purpose, the spectral ordinate at the fundamental SSI period of each building is taken from the fixed-base spectrum of Fig. 8 and is corrected using the damping ratio of the SSI system (Table 7) by the correction factor of Sect. 4.3.2. The resulting values are depicted against the fixed-base fundamental period of each building and called the SSI-code spectrum. It is illustrated in Fig. 9 after being normalized to the fixed-base responses of the code. The nonclassical spectra of the flexible-base buildings, extracted from Fig. 8 after normalizing to the fixed-base responses in the same figure, are also illustrated for comparison. For the ease of reference, the latter values are averaged between the near and far field earthquakes.

Fig. 9
figure 9

The SSI-code and the flexible base nonclassical spectra averaged between near and far field earthquakes, both normalized to the corresponding rigid-base spectra. a Soil type D. b Soil type E

Full size image

Figure 9 reveals the important fact that how the code-based formula (Eqs. 22 and 23) underestimate the seismic response of an SSI system. While the spectral acceleration ratio using the rigorous method varies between 1 and 0.83 for the soil type D and between 1 and 0.71 for the soil type E as the period increases to about 3 s, similar code-based ratios are between 0.88 and 0.75, and, 0.86 and 0.73, respectively.

5.4 Responses in the higher modes

In Sect. 5.3 only the part of the total response corresponding to the first mode was presented. In the current section sum of the response corresponding to all other modes (called the higher modes) is illustrated. The averaged maximum values of roof displacement and base shear normalized to the building height and building weight, are shown in Figs. 10 and 11, respectively, for the three analysis cases. The values have been also averaged between near and far field earthquakes.

Fig. 10
figure 10

The averaged maximum roof displacement corresponding to the higher modes, normalized to the building height. a Soil type D. b Soil type E

Full size image
Fig. 11
figure 11

The averaged maximum base shear corresponding to the higher modes, normalized to the building weight. a Soil type D. b Soil type E

Full size image

Based on Figs. 10 and 11, it can be said that response in the higher modes can equally be calculated using classical or nonclassical analysis. Therefore, use of nonclassical analysis is not necessary for the higher modes. On the other hand, for the building-soil systems studied and alike, accounting for SSI in the higher modes is important for systems with fixed-base fundamental periods larger than 2.5 s when calculating displacements and larger than 2 s when deriving the base shear. In such ranges, higher mode displacements increase and base shears decrease considerably due to SSI.

5.5 Nonclassical spectral analysis

The nonclassical procedure of spectral analysis developed in Sect. 3 is used in this section to calculate the maximum roof displacement and base shear, using Eq. (12), in comparison with the results of the nonclassical time history analysis, using Eqs. (4) and (6), presented in Sects. 5.3 and 5.4. For spectral analysis, average of the response spectra of the earthquakes associated with each building (Table 4) are used. The spectral ordinates are corrected using the reduction factor introduced in Eq. (20). The CQC rule is used to combine the spectral responses of different modes. Therefore, the nonclassical spectral analysis of this study is approximate with respect to the nonclassical time history analysis, in several aspects: (1) Use of the SRSS rule to combine the maxima of the two terms on the right sides of Eqs. (4) and (6) to calculate the maximum responses presented in Eq. (8); (2) Use of the CQC rule to combine the maximum responses of different modes; (3) Use of an approximate relation between the pseudo-velocity and the relative velocity of the jth mode (Eq. 9); (4) Use of an approximate equation for correcting the spectral values due to a modified damping with SSI (Eq. 20). The response results of this section show the effects of above approximations.

The maximum roof displacement and base shear are illustrated in Figs. 12 and 13, respectively.

Fig. 12
figure 12

Averaged maximum roof displacement normalized to the building height, using nonclassical time history and spectral analysis. a Soil type D, near field earthquakes. b Soil type D, far field earthquakes. c Soil type E, near field earthquakes. d Soil type E, far field earthquakes

Full size image
Fig. 13
figure 13

Averaged maximum base shear normalized to the building weight using nonclassical time history and spectral analysis. a Soil type D, near field earthquakes. b Soil type D, far field earthquakes. c Soil type E, near field earthquakes. d Soil type E, far field earthquakes

Full size image

The maximum relative differences of associated time-history and spectral responses in Figs. 12 and 13 are 12 and 8 % for displacement and base shear, respectively. Therefore, the assumptions made to develop the equations of the nonclassical spectral analysis are justified within the SSI systems studied.

5.6 Correction factors for internal forces and lateral displacements due to SSI

Results of the averaged maximum displacements and base shears of the studied structures presented in Sect. 5.3 suggest that the frame structures can be analyzed as usual on a fixed base and then their lateral displacements and base shears can be increased and decreased, respectively, due to SSI using simple correction factors. Since the spectra of Sect. 5.3 have been plotted using the fixed-base fundamental period of the buildings, the effect of period lengthening has been already included and the correction factors only contain the effect of augmented damping where applicable. On the other hand, the factors are functions of the fixed-base fundamental period of a moment frame structure resting on surface foundations on the soil types D and E. Sections 5.3 and 5.4 present the fundamental and higher mode responses, respectively. Similarly, the total responses could be shown. Then, the correction factors have been calculated both for the fundamental mode responses and the total responses including all modes. According to Sect. 5.4, for the buildings of the type investigated in this study, difference between the two groups of correction factors is considerable only from a period of about 2 s upward. The correction factors are calculated by curve fitting of the fixed-base results of Sect. 5.3 to the more accurate nonclassical responses of the same section in order to have a best fit.

Tables 9 and 10 illustrate equations of the correction factors. They have been determined by averaging between the results of the near and far-field earthquakes and are only necessary to be used for the period range of \(T \ge 1 s\). Out of the mentioned range SSI has minimal effects for the cases studied and may not be taken into account, based on Sect. 5.3. The correction factors can be equally applied to the design spectrum or to the results of spectral analysis including internal forces and deformations of fixed-base moment frame structures, as follows:

$${\text{SSI response}} = {\text{fixed-}} {\text{base response}} \times {\text{correction factor}}.$$
Table 9 Correction factors for the base shear or internal forces, α V
Full size table
Table 10 Correction factors for the lateral displacements and rotations, α U
Full size table

Figures 14 and 15 show the results of correction of the fixed-base total responses, using Tables 9 and 10, in comparison to the nonclassical SSI results of Sect. 5.3. The figures describe the accuracy of the correction process.

Fig. 14
figure 14

Correction of fixed-base base shear (normalized to the building weight) due to SSI. a Soil type D. b Soil type E

Full size image
Fig. 15
figure 15

Correction of the lateral roof displacement (normalized to the building height) due to SSI. a Soil type D. b Soil type E

Full size image

6 Conclusions

In this study the theory of the modal analysis of nonclassical systems was illustrated for systems resting on flexible bases, representative of soil-structure interaction problems. Several structures having one to twenty stories resting on two types of soils, being medium and soft, were analyzed each one under two suits of ten consistent and scaled earthquake motions specific to that structure recorded at near and far distances. Modal time history and spectrum analysis were accomplished in their classical and non-classical versions.

The important results of the study, for the buildings and the soils considered, can be summarized as follows:

  1. 1.

    Period shifting due to SSI is larger for the fundamental mode, the softer soil and the taller buildings and reaches up to 20 %. It decreases gradually as the mode number increases. Periods of flexible-base systems can be almost equally calculated by classical and nonclassical procedures.

  2. 2.

    The first-mode code-based damping ratios begin from about 10 and 9 % for the 1-story building on the soil types D and E, respectively, and uniformly increase to about 14 % for the 20-story building. On the other hand, the first-mode damping ratios calculated using the equations of non-classical dynamical systems, vary from about 10 and 11–6 % for the same cases. Therefore, variation of the damping ratio is descending with the rigorous procedure and ascending according to the code. Also, dissimilar to the code, the rigorous damping ratio shows an asymptotic behavior such that from about the 10-story building, it does not change notably. Values of damping ratios of the higher modes are larger than those of the first mode, and show a trend of variation similar to the first mode.

  3. 3.

    The relative difference of displacements between the associated fixed-base and flexible-base models becomes important from a period of about 1 s and increases with height, and is larger for the softer soil. For periods smaller than 1 s, the nonclassical analysis results in displacements somewhat smaller than those of the fixed-base model.

  4. 4.

    SSI decreases the base shear on both soil types. The reduction is important again from a period of 1 s. Results of SSI analysis with the nonclassical procedure are similar to the fixed-base case for periods smaller than 1 s and to the classical SSI procedure for larger periods. The base shear reduction is up to 23 and 38 % for taller buildings on the soil types D and E, respectively.

  5. 5.

    For periods smaller than 1 s, soil-structure interaction may not be taken into account for seismic analysis of moment frame structures resting on surface foundations.

  6. 6.

    The code-prescribed process of inclusion of SSI underestimates the base shear in the whole period range studied. Underestimation is more critical for the soil type D.

  7. 7.

    Use of nonclassical SSI analysis is not necessary for the higher modes. Accounting for SSI in the higher modes is important for systems with fixed-base fundamental periods larger than 2.5 s when calculating (increased) displacements and larger than 2 s when deriving the (decreased) base shear.

  8. 8.

    The simplifying assumptions for the nonclassical SSI spectral analysis are justified for the SSI systems studied.

  9. 9.

    Maxima of the lateral displacements and base shear can be calculated using conventional spectral analysis of fixed-base structures and converted to the responses including SSI using the simple correction factors presented in this study.

Finally, it should be noted that the mentioned conclusions are only applicable to the cases studied, namely, buildings consisting of moment frames resting on surface foundations. Regarding the soil medium, a uniform halfspace with characteristics representative of soft soils was considered. For the exceptional case of a soft surface layer resting on a very stiff soil the radiation damping of the oscillating structure might diminish. The above limitations should be taken into account when using the results of this study.