Seismic response of nonlinear soil-structure interaction systems through the Preisach formalism: the Messina Bell Tower case study

Abstract

In this paper the seismic response of linear behaving structures resting on compliant soil is addressed through the application of the Preisach formalism to capture the soil nonlinearities. The novel application of the Preisach model of hysteresis for nonlinear soil-structure interaction problems is explored through the study of the seismic response of a real structure. Through a harmonic balance procedure, furthermore, simplified nonlinear springs and dashpots are derived in closed form for a ready and accurate evaluation of the nonlinear soil-structure interaction response. The selected case study is the bell tower of the Messina Cathedral in Italy. The Bell Tower hosts the largest and most complex mechanical and astronomical clock in the world and it has been recently equipped by a permanent seismic monitoring system. A pertinent finite element (FE) model including the superstructure and the soil underneath, has been defined using authentic drawings and engineering design reports. The modal properties of the FE model have been compared with the experimental ones, identified from environmental noise recorded through the seismic monitoring system. Furthermore, the FE model has been validated by means of acceleration time histories recorded at different floors during two independent seismic events. A nonlinear incremental dynamic analysis of the Bell Tower has been also performed. The seismic response obtained by the complete FE analysis, has been compared with the proposed Preisach lumped parameter model, assembled with nonlinear springs and nonlinear dashpots. The results are well in agreement, offering an alternative promising strategy for the nonlinear soil-structure interaction studies.

1 Introduction

Nonlinear dynamic soil–structure interaction (SSI), received particular attention in the last two decades due to the sustained progress in computational analysis and due to the recognition of its relevance by seismic codes and provisions (e.g. Eurocode 8, FEMA-440, 2005, FEMA P-2091, 2020, ASCE/SEI 41–17, 2017). The response of coupled nonlinear soil-structure interaction systems can be determined through what is generally called as “direct method” requiring the solution of the equations of motion after a pertinent Finite Element (FE) or Boundary Element discretization of the soil-structure system. The approach is clearly computational demanding with still open challenges such as the proper modelling of soil and structure nonlinearities, the definition of complex boundary conditions and soil-structure interface elements. Despite those challenges the direct method still remains a key reference for practitioners and researchers to perform detailed analysis of relevant structures. On the other hand, alternative approaches are sought to reduce the computational effort and also to develop a feel for the physical meaning and relative importance of the various factors, with more personal control of calculations (Dobry 2014). The well-known multi-step substructure approach (Kausel and Roesset 1974), requiring the decomposition of the problem into three tasks: (i) site response analysis, (ii) kinematic interaction, and (iii) inertial interaction, cannot be rigorously applied to nonlinear problems; however, it provides accurate results in the case of small nonlinearities. For nonlinear problems, a different approach of the substructuring technique (see e.g. Pecker and Pender 2000) has been proposed. Specifically, it is assumed that the soil medium is divided into two sub-domains: (i) a far field domain, which extends a sufficient distance from the foundation, for which the involved nonlinearities are due mainly to the wave propagation; and (ii) a near field domain, in the vicinity of the foundation where all the geometrical and material non linearities due to soil-structure interaction are concentrated. Following this substructuring approach, Pecker (1998) proposed a simplified rheological model composed of a finite number of springs and Coulomb sliders whose parameters are determined from curve fitting to the non-linear force–displacement (or moment-rotation) backbone curve, determined from a static finite element analysis. More recently, Cavalieri et al. (2020) used the near field/far field substructuring approach for the fragility characterization of buildings with shallow foundations. To model the nearfield subdomain and the inherent nonlinear soil-structure interactions, several approaches can be adopted. Santisi D’Avila and Lopez-Caballero (2018) and Fares et al (2019) modeled the one-directional three-component wave propagation and nonlinear soil-structure interaction using a 1D and a T-shaped soil domain, respectively, in a finite element scheme. A further simplification of the near-field can be obtained through a class of Winkler-type models represented by a system of discrete, closely spaced independent springs characterized by an appropriate constitutive law, which represent the soil medium. In this class can be listed the analytical approach proposed by Siddharthan et al. (1992) to evaluate the moment–rotation response for both uplift- and yield-only conditions of a rigid foundation on a Winkler soil model, further extended by Allotey and El Naggar (2008) as well as the generalized Winkler model for the behavior of shallow foundations proposed by Houlsby et al. (2005). Other contributions exploit the dynamic Beam-on-Nonlinear-Winkler-Foundation (BNWF) model or “dynamic p-y” (see e.g. Boulanger et al. 1999; Tombari et al. 2017) commonly applied to soil-pile interactions but also to to shallow foundations (Raychowdhury and Hutchinson 2009) and to nuclear reactors by Bhaumik and Raychowdhury (2013). Another approach is based on the generally know non‐linear macro‐element (NLME) approach. The basic assumption of this approach is that the footing is considered as a rigid body and entire soil‐foundation system is modelled by a single element with a suitable yield surface and plastic potential function. Various nonlinear macroelements have been proposed in literature with different level of complexity (see e.g., Pecker and Chatzigogos 2010; Chatzigogos et al. 2011; Figini et al. 2012; Cavalieri et al. 2020) aimed to capture specific features of the nonlinear soil-structure interaction. In this regard, a further class of lumped parameter models, modelling the soil-foundation system through a rigid foundation as well as a set of uncoupled nonlinear spring elements, is used to evaluate the nonlinear SSI features such as the equivalent fundamental period of the structure as well as foundation damping. Specifically, nonlinear rocking stiffness have been determined by Gazetas et al. (2013) through an empirical approach based on FE analyses, further extended by Anastasopoulos and Kontoroupi (2014) and applied to motorway bridges by Anastasopoulos et al. (2015). A nonlinear sway-rocking model has been developed by Lu et al. (2016) for shallow foundations. Li et al. (2020) calibrated nonlinear translational and rotational springs through experimental data from centrifuge tests on pile foundations. Following the lumped approach, Cacciola and Tombari (2021) recently proposed the use of the Preisach formalism to model the steady-state response of nonlinear soil structure interaction systems. Through this approach, simplified amplitude-dependent springs and dashpots have been derived through a pertinent harmonic balance.

In this paper, the efficiency of Preisach formalism (Preisach 1935) to model the seismic nonlinear soil-structure interaction of a real structure, is assessed. It is noted, hereinafter, that the nonlinearity is related to the soil hysteretic response only. Geometrical nonlinearities, such as those related to foundation uplifting, and material nonlinearities of the superstructure are not considered in this paper. The selected case study is the Bell Tower of the Messina Cathedral in Italy. The Bell Tower hosts a clock which is unique in the world for its complexity and it has been recently included in the portfolio of structures monitored by the Italian Civil Protection Department. The monitoring system is operational since July 2019 and since then it has recorded two low level ground motion activities. A finite element model of the bell tower and the soil underneath has been developed in ADINA (2020) using authentic drawings, technical reports and modal parameters extracted from environmental noise measurements. A nonlinear finite element model of the soil has been adopted to explore the effectiveness and the efficiency of the Preisach model of hysteresis in simulating the soil nonlinearities. The results from an incremental dynamic analysis conducted on the complete FE model have been compared with a reduced model for which the soil has been replaced by a set of uncoupled nonlinear springs and dashpots determined from the Preisach formalism. The comparisons show the potentiality of this approach as well as the reduced computational effort involved in the analyses.

2 Preisach model of hysteresis for the lumped parameter model of SSI

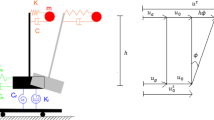
According to the lumped parameter model (Fig. 1) the nonlinear soil-structure interaction is modelled through a set of uncoupled nonlinear spring elements.

Fig. 1

Schematic representation of the lumped parameter model and nonlinear Preisach elements

Under the hypothesis of rigid foundation, the nonlinear force–displacement (or moment-rotation) relationship according to the Preisach formalism is determined by the superposition of an infinite set of elementary hysteresis operators (hysterons or relay operators) $f_{\alpha ,\;\beta }$, having local memory distributed according to a given weight function $\mu \left( {\alpha ,\;\beta } \right)$, that is

$$f_{i,\;H } \left( {x,\;\dot{x}} \right) = \iint\limits_{\alpha \ge \beta } {\mu \left( {\alpha ,\;\beta } \right)f_{\alpha ,\;\beta } \left( {x,\;\dot{x}} \right)d\alpha d\beta },\;i = h,\; \theta \;{\text{and}}\;x = u_{F} ,\; \theta$$

(1)

in which $f_{h,\;H }$ and $f_{ \theta ,\;H }$ are the shear force and the moment at the foundation, while x represents either the foundation generic displacement $u_{F}$ or the rotation $\theta$ degrees of freedom. A dot over a variable indicates the temporal derivative. It is noted that the vertical spring element $f_{{\text{v }}}$ is omitted in the formulation for simplicity’s sake and it is assumed to behave linearly. Typical hysterons are depicted in Fig. 2 and they are defined by following equations (see e.g., Krasnoselʹskiĭ and Pokrovskiĭ 1989; Mayergoyz 1991):

$$f_{\alpha ,\;\beta } \left( {x,\;\dot{x}} \right) = \left\{ {\begin{array}{*{20}c} { + 1} & {{\text{if}}\;x > \alpha \;{\text{or}}\;x > \beta \;{\text{and}}\;{\text{sign}}(\dot{x}) = - 1} \\ { - 1} & {{\text{if}}\;x < \beta \;{\text{or}}\;x < \alpha \;{\text{and}}\;{\text{sign}}(\dot{x}) = + 1} \\ \end{array} } \right.$$

(2)

or also

$$f_{\alpha ,\beta } \left( {x,\dot{x}} \right) = \left\{ {\begin{array}{*{20}c} { + 1} & {{\text{if }}x > \alpha {\text{or }}x > \beta {\text{and sign(}}\dot{x}) = - 1} \\ 0 & {{\text{if }}x < \beta {\text{or }}x < \alpha {\text{and sign(}}\dot{x}) = + 1} \\ \end{array} } \right.$$

(3)

where $\alpha$ and $\beta$ are the variables that define the Preisach plane.

It is noted, also, the velocity assumes the role of events ordering necessary to describe the ascending and descending status in Eqs. (2) and (3), thus keeping satisfied the rate-independence memory of the hysteresis. Moreover, the weight function $\mu \left( {\alpha ,\;\beta } \right)$ can be determined experimentally by the first-order transition curve (see e.g., Mayergoyz 1991) or through the best fitting of relevant experimental or numerical data. Following the first-order transition curve approach, Lubarda et al. (1993) have derived the weight functions in a closed form for certain classical rheological models. In particular for the individual Jenkins model (1962) and for the Iwan-Jenkins model, the weight function assumes the following expressions

$$\mu \left( {\alpha ,\;\beta } \right) = \frac{{k_{J} }}{2}\left[ {\delta \left( {\alpha - \beta } \right) - \delta \left( {\alpha - \beta - 2\frac{{f_{y} }}{{k_{J} }}} \right)} \right]$$

(4)

$$\mu \left( {\alpha ,\beta } \right) = \frac{{k_{J} }}{2}\left\{ {\delta \left( {\alpha - \beta } \right) - \frac{{k_{J} }}{2}\frac{1}{{f_{y,\;\max } - f_{y,\;\min } }}\left[ {H\left( {\alpha - \beta - 2\frac{{f_{y,\;\min } }}{{k_{J} }}} \right) - H\left( {\alpha - \beta - 2\frac{{f_{y,\;\max } }}{{k_{J} }}} \right)} \right]} \right\}$$

(5)

with $\delta \left( \right)$ and $H\left( \right)$ denoting the Dirac delta and the Heaviside functions, respectively. The symbol $k_{J}$ represents the linear stiffness of the individual Jenkins element, and $f_{y}$ is the yielding force (or moment). To derive Eq. (5), it is also assumed that the distribution function in the Iwan-Jenkins model is uniform in the range $f_{y,\;\min } \le f_{y} \le f_{y,\;\max }$.

Fig. 2

Preisach hysterons: a + 1–1 relay operator; b + 1–0 relay operator

Alternative expressions of the weight function have been proposed by Ktena et al. (2001, 2002) through a bivariate Gaussian distribution given by the equation:

$$\mu \left( {\alpha ,\;\beta } \right) = \frac{1}{{2\pi \sigma_{\alpha } \sigma_{\beta } \sqrt {1 - r^{2} } }}\exp \left[ { - \frac{1}{{2\left( {1 - r^{2} } \right)}}\left( {\left( {\frac{{\alpha - \mu_{\alpha } }}{{\sigma_{\alpha } }}} \right)^{2} - 2r\left( {\frac{{\alpha - \mu_{\alpha } }}{{\sigma_{\alpha } }}} \right)\left( {\frac{{\beta - \mu_{\beta } }}{{\sigma_{\beta } }}} \right) + \left( {\frac{{\beta - \mu_{\beta } }}{{\sigma_{\beta } }}} \right)^{2} } \right)} \right]$$

(6)

where $r$, $\mu_{\alpha }$, $\mu_{\beta }$, $\sigma_{\alpha }$ and $\sigma_{\beta }$ are the five parameters defining the model. Alternatively, by setting $r = 0$, $\mu_{\alpha } = \mu_{\beta } = \hat{\mu }$ and $\sigma_{\alpha } = \sigma_{\beta } = \hat{\sigma }$ the simplified two-parameters Gaussian model given by the equation

$$\mu \left( {\alpha ,\;\beta } \right) = \frac{1}{{2\pi \hat{\sigma }^{2} }}\exp \left[ { - \frac{1}{2}\left( {\left( {\frac{{\alpha - \hat{\mu }}}{{\hat{\sigma }^{2} }}} \right)^{2} + \left( {\frac{{\beta - \hat{\mu }}}{{\hat{\sigma }^{2} }}} \right)^{2} } \right)} \right]$$

(7)

has been adopted by Spanos et al. (2004b) for modeling the stress–strain hysteretic behavior of Shape Memory Alloy (SMA) oscillators. From Eq. (1), being $\alpha \ge \beta$, it can be shown (see e.g., Krasnoselʹskiĭ and Pokrovskiĭ 1989; Mayergoyz 1991) that the domain in which the weight function is defined is a triangle bounded by assigned upper limits $\left( {\alpha_{P} ,\;\beta_{P} } \right)$. Therefore, the nonlinear force–displacement (or moment-rotation) relationship given in Eq. (1) can be rewritten (Spanos et al. 2004a) in alternative form for the ascending status

$$f_{i,\;H } \left( {x,\;\dot{x}} \right) = 2\left[ {F\left( {x,\;\beta_{n - 1} } \right) + 2F\left( {0,\;\beta_{P} } \right) - 2F\left( {0,\;\beta_{0} } \right) + \mathop \sum \limits_{j = 2}^{n - 1} F\left( {\alpha_{j} ,\;\beta_{j - 1} } \right) - F\left( {\alpha_{j} ,\;\beta_{j} } \right)} \right] - F\left( {\alpha_{P} ,\;\beta_{P} } \right)$$

(8)

and for the descending status:

$$\begin{aligned} f_{i,\;H } \left( {x,\;\dot{x}} \right) = & 2\left[ {F\left( {\alpha_{n} ,\;\beta_{n - 1} } \right) - F\left( {\alpha_{n} ,\;x} \right) + 2F\left( {0,\;\beta_{P} } \right) - 2F\left( {0,\;\beta_{0} } \right) + \mathop \sum \limits_{j = 2}^{n - 1} F\left( {\alpha_{j} ,\;\beta_{j - 1} } \right) - F\left( {\alpha_{j} ,\;\beta_{j} } \right)} \right] \\ - F\left( {\alpha_{P} ,\;\beta_{P} } \right) \\ \end{aligned}$$

(9)

where

$$F\left( {\alpha_{j} ,\;\beta_{j} } \right) = \mathop \smallint \limits_{{\beta_{j} }}^{{\alpha_{j} }} \mathop \smallint \limits_{{\beta_{j} }}^{\alpha } \mu \left( {\alpha ,\;\beta } \right)d\alpha d\beta$$

(10)

and $\alpha_{j}$ and $\beta_{j}$ represent the j-th dominant maximum and dominant minimum respectively of the foundation displacement (or rotation), respectively. It is noted that the property of non-local memory, typical of hysteretic systems, is evident, herein, by the presence of summation terms in Eqs. (8) and (9) accounting for the previous dominant maxima and minima. This is one of the main features of the Preisach model of hysteresis, generally called as wiping out property, for which the memory of the system is stored only in the dominant maxima (and minima) and not in the whole trajectory. Moreover, from the analysis of Eq. (5) it can be proved that the integral of the first term $\frac{{k_{J} }}{2}\delta \left( {\alpha - \beta } \right)$ over the whole domain leads to a linear elastic zero-memory term $k_{J} x$. To better represent various force–displacement relationships, Spanos et al. (2004b), Spanos et al. (2006), Cacciola and Tombari (2021) proposed to define the complete force–displacement relationships as the superposition of two terms: a zero-memory part $f_{i,\;ZM } \left( {x,\;\dot{x}} \right)$ and a purely hysteretic part, $f_{i,\;H } \left( {x,\;\dot{x}} \right)$, defined though the Preisach formalism, that is

$$f_{i} \left( {x,\;\dot{x}} \right) = f_{i,\;ZM } \left( x \right) + f_{i,\;H } \left( {x,\;\dot{x}} \right);\; i = h,\;\theta \;{\text{and}}\;x = u_{F} ,\; \theta$$

(11)

For the non-hysteretic zero-memory term, $f_{i,\;ZM } \left( x \right)$ a simple cubic polynomial is in general able to capture complex input–output relationships, but in principle any nonlinear function of instantaneous displacements (and rotations) can be adopted.

3 Non-linear spring and dashpot elements

This section is dedicated to a simplified implementation of the Preisach model of hysteresis. The aim is to determine nonlinear equivalent springs and dashpots that can be adopted for practical applications. In this regard a version of the harmonic balance approach is used (Iwan and Spanos 1978; Spanos 1979; Spanos et al. 2004a). The approach assumes that the solution exhibits a pseudo-harmonic behavior, thus the response foundation degrees of freedom and their velocities can be written in the form

$$u_{F} \left( t \right) = a_{h} \left( t \right)\cos \left( {\omega_{n} t + \phi_{h} \left( t \right)} \right),\;\;\dot{u}_{F} \left( t \right) = - a_{h} \left( t \right)\omega_{n} \sin \left( {\omega_{n} t + \phi_{h} \left( t \right)} \right)$$

(12)

and

$$\theta \left( t \right) = a_{\theta } \left( t \right)\cos \left( {\omega_{n} t + \phi_{\theta } \left( t \right)} \right),\;\;\dot{\theta }\left( t \right) = - a_{\theta } \left( t \right)\omega_{n} \sin \left( {\omega_{n} t + \phi_{\theta } \left( t \right)} \right)$$

(13)

in which the amplitudes $a_{h} \left( t \right)$ and $a_{\theta } \left( t \right)$ and the phases $\phi_{h} \left( t \right)$ and $\phi_{\theta } \left( t \right)$ are assumed slowly varying with respect to time. It is noted that the circular frequency $\omega_{n}$ in the case of harmonic excitation can be set equal to the frequency of the input (see e.g. Cacciola and Tombari 2021). For broadband excitation such as the seismic input the frequency $\omega_{n}$ can be approximated by the fundamental frequency of the structural response. Using the approximations given in Eqs. (12) and (13) the nonlinear force–displacement and moment-rotation relationships $f_{h} \left( {u_{F} ,\;\dot{u}_{F} } \right)$ and $f_{\theta } \left( {\theta ,\;\dot{\theta }} \right)$ are appropriately replaced, in a harmonic balance sense, by the expressions:

$$f_{e,\;h } \left( {u_{F} ,\;\dot{u}_{F} } \right) = c_{e,\;h} \left( {a_{h} } \right)\dot{u}_{F} + k_{e,\;h} \left( {a_{h} } \right)u_{F}$$

(14)

where

$$c_{e,\;h} \left( {a_{h} } \right) = - \frac{1}{{\pi \omega_{n} a_{h} }}\mathop \smallint \limits_{0}^{2\pi } f_{h} \left( {a_{h} \cos \vartheta ,\; - a_{h} \omega_{n} \sin \vartheta } \right)\sin \vartheta d\vartheta$$

(15)

and

$$k_{e,\;h} \left( {a_{h} } \right) = \frac{1}{{\pi a_{h} }}\mathop \smallint \limits_{0}^{2\pi } f_{h} \left( {a_{h} \cos \vartheta ,\; - a_{h} \omega_{n} \sin \vartheta } \right)\cos \vartheta d\vartheta$$

(16)

are the equivalent horizontal damping and stiffness, respectively. Similar expressions are determined for the rotational hysteretic element, that is:

$$f_{e,\;\theta } \left( {\theta ,\;\dot{\theta }} \right) = c_{e,\;\theta } \left( \theta \right)\dot{\theta } + k_{e,\;\theta } \left( \theta \right)\theta$$

(17)

where

$$c_{e,\;\theta } \left( {a_{\theta } } \right) = - \frac{1}{{\pi \omega_{n} a_{\theta } }}\mathop \smallint \limits_{0}^{2\pi } f_{\theta } \left( {a_{\theta } \cos \vartheta ,\; - a_{\theta } \omega_{n} \sin \vartheta } \right)\sin \vartheta d\vartheta$$

(18)

and

$$k_{e,\;\theta } \left( {a_{\theta } } \right) = \frac{1}{{\pi a_{\theta } }}\mathop \smallint \limits_{0}^{2\pi } f_{\theta } \left( {a_{\theta } \cos \vartheta ,\; - a_{\theta } \omega_{n} \sin \vartheta } \right)\cos \vartheta d\vartheta$$

(19)

By adapting the weight function defined by Lubarda et al (1993) for the distributed Jenkins-Iwan model to relevant foundation force–displacement (moment-rotation) relationship Cacciola and Tombari (2021) determined closed form solutions of the equivalent stiffness and damping for a particular set of parameters (i.e. $f_{y,\;\min } = 0$ and $f_{y,\;\max } = 2\overline{f}_{y,}$, with $\overline{f}_{y,}$ = average yield force). Those expression are herein rewritten in a more general form taking into account the polynomial counterpart of the zero-memory term and the ultimate shear $V_{u}$ and moment capacity $M_{u}$. Specifically, by setting

$$\mu \left( {\alpha ,\;\beta } \right) = - \eta_{i} \frac{{k_{i}^{2} }}{4}\frac{1}{{f_{u} }} f_{u} = V_{u} ,\;M_{u}$$

(20)

and

$$f_{i,\;ZM } \left( x \right) = k_{i} x + \psi_{i} x^{3}$$

(21)

the horizontal hysteretic element assumes the following form

$$c_{e,\;h} \left( {a_{h} } \right) = \frac{{2 \eta_{h} a_{h} k_{h}^{2} }}{{3\pi \omega_{n} V_{u} }}$$

(22)

and

$$k_{e,\;h} \left( {a_{h} } \right) = k_{h} + \psi_{h} \frac{{3a_{h}^{2} }}{4} - \frac{{\eta_{h} k_{h}^{2} a_{h} }}{{2V_{u} }}$$

(23)

while the rotational element is given by

$$c_{e,\;\theta } \left( {a_{\theta } } \right) = \frac{{2 \eta_{\theta } a_{\theta } k_{\theta }^{2} }}{{3\pi \omega_{n} M_{u} }}$$

(24)

and

$$k_{e,\;\theta } \left( {a_{\theta } } \right) = k_{\theta } + \psi_{\theta } \frac{{3a_{\theta }^{2} }}{4} - \frac{{ \eta_{\theta } k_{\theta }^{2} a_{\theta } }}{{2 M_{u} }}$$

(25)

The parameters $\psi_{i}$ and $\eta_{i}$ are herein introduced to calibrate the model to various hysteretic behaviors. For the particular case of $\psi_{i} = 0$ and $\eta_{i} = 1$ the model reduces to the classical distributed Jenkins-Iwan model used in Cacciola and Tombari (2021). Figure 3 shows some force–displacement loops reproduced by the application of Eqs. (8, 9 and 11) and the comparison with the equivalent spring and dashpot elements (i.e. Equations 14 or 17 at fixed amplitude). From Fig. 3, it is can be seen the versatility of the model and the impact of the key parameters. It can be also appreciated the accuracy of the equivalent springs and damping to match the energy dissipation and the equivalent linear backbone of the loops. Moreover, Cacciola and Tombari (2021) presented a procedure to calibrate the Preisach model to match experimental data, such as stiffness degradation and damping curves. In the following section the Preisach model of hysteresis is applied to a real structure to explore its use in practical applications.

Fig. 3

Illustrative Preisach force displacement loops (black) and equivalent linear (grey) for $\mu \left( {\alpha ,\;\beta } \right) = - \eta /4$ and $f_{i,\;ZM } \left( x \right) = x + \psi x^{3}$; $\alpha_{P} = 1;\;\beta_{P} = - 1$: a $\eta = 1$, $\psi = 0$; b $\eta = 1$, $\psi = - 0$.1; c $\eta = 1$, $\psi = 0$.1; d $\eta = 0.5$, $\psi = 0$; e $\eta = 1.5$, $\psi = 0$; f $\eta = 1.5$, $\psi = 0.5$;

4 The Messina Bell Tower

In this section the Messina Bell Tower (Fig. 4) is selected as a case study. The original Bell Tower dates back to the XII century. After its construction, however, it was severely damaged by a series of natural actions including lightning and several earthquakes. The current structure has been rebuilt shortly after the Messina 1908 earthquake (estimated Magnitude Mw equal to 7.1) by adopting a mixed masonry-reinforced concrete structure that for the bell tower was realized following the innovative confined masonry strategy recommended by a structural code just after the Messina earthquake. Specifically, by using the walls as part of the formwork, the construction strategy marked the birth of the so-called confined masonry buildings (CMB) (Calio’ et al. 2008). The Bell Tower of the Messina Cathedral contains the largest and most complex mechanical and astronomical clock in the world. It has been designed by the firm Ungerer of Strasbourg and it was inaugurated in 1933 and it is nowadays one of the city’s main attraction.

Fig. 4

The Messina Cathedral and its Bell Tower

4.1 Numerical modelling of the Messina Bell Tower

In this section, a numerical model of the Messina Bell Tower is created through the Finite Element (FE) software ADINA (2020). The dimensions of the geometrical model and the properties of the material are derived from the authentic technical drawings and reports owned by the Archdioceses of Messina-Lipari and S.Lucia del Mela.

The main structure of the Bell Tower (Fig. 5) is modelled by using 3D 8-node solid elements for the foundation, 2D 4-node shell elements for the walls and floor slabs, as well as 1D beam elements for the columns and beams. Constraints are set to simulate the rigid floor assumption as well as to connect Hermite 1D beam elements to the Lagrange 2D and 3D finite elements. Material data, reported in Table 1, are derived from the authentic technical documents with the only exception of the mechanical properties of the masonry walls which have been identified to closely match the experimental first natural frequency as reported in the following Sect. 4.2. It is worth mentioning that the low value of the concrete elastic modulus of $15000\;{\text{MPa}}$, is consistent with the Royal Decree Law of the 4th of September 1927 and falls within the expected range of values proposed by Ahmad et al. (2015) for a low compressive strength of 3 MPa as the one considered in the original technical report. Additional masses amounting to $30.8\;{\text{ton}}$, are also added to consider the set of bells and the bronze statues; overall, the total mass of the finite element of the Bell Tower, computed by considering the material densities from standards and building codes, yields to m = 3160.97 ton, which is in line (i.e. less than 1% difference) with the value estimated in the authentic technical report equal to m = 3189.0 ton.

Fig. 5

Numerical a Bell Tower, b coupled soil-structure models

Table 1 Data required to characterize the Finite Element Model of the Bell Tower and soil

Because of the non-negligible soil-structure interaction effects in tall structures (Şafak 1995; Stewart and Fenves 1998; Todorovska 2009), a coupled soil-structure numerical model shown in Fig. 5b, has to be considered. The elastic soil deposit, modelled through 3D 8-node solid elements, is assumed to be characterized by a shear wave velocity of $Vs = 300\;{\text{m}}/{\text{s}}$ (ground type C) and density of $2000\;{\text{kg}}/{\text{m}}^{3}$, because of the lack of information about its soil stratigraphy, and resting above a rigid bedrock at a depth of about 60 m. It is noted that soil stratigraphy might have an impact on the overall system identification, therefore, in absence of an experimentally-evaluated soil profile, the uniform assumption, although academic, has been selected for the scope of this study. The soil model of dimensions 300 × 300 m is determined through a sensitivity analysis to minimize the impact of the reflecting waves from the free lateral artificial boundaries.

4.2 Structural identification of the Messina Bell Tower

In this subsection the tools and the basic steps followed to identify the Messina Bell tower are reported.

4.2.1 Continuous dynamic monitoring system

The continuous dynamic monitoring system (tagged 62CME) has been installed in the Messina Bell Tower in July 2019 and it has been officially included in the Seismic Observatory of Structures (Dolce et al. 2017) on August 1st of the same year. The Seismic Observatory of Structures is a network, created and managed by the Italian Civil Protection Department (DPC), of over 160 civil structures, mostly public buildings, equipped with permanent seismic monitoring systems. The monitoring system, described in Fig. 6, is composed by 5 digital force-balance accelerometers characterized by a dynamic range of $165\;{\text{dB}}$ and a measurement range of $\pm \;2\;{\text{g}}$. Sensors installed at the basement (Sensor 1) and at the floor 7 (Sensor 4–5) are triaxial accelerometers (Fig. 7a), whereas the sensors at the floor 4 (Sensor 2–3) are biaxial (Fig. 7b). The sensor at the basement is connected to the other sensors through an ethernet cable, suppling them with power and providing the common sampling of all the measured data and UTC time through a GPS antenna. Sensor 1 is also equipped with a GSM modem, through which the system can be governed and configured and the recorded data are sent to the server at the DPC headquarters in Rome, Italy. Additionally, to automatically record the vibrations caused by an earthquake, the monitoring system allows, at any time, to obtain data relating to the ambient vibrations of the structure in its normal service conditions, thus allowing to keep under control any variation over time of its modal parameters.

Fig. 6

Layout of the seismic monitoring system of Messina bell tower

Fig. 7

The triaxial accelerometer Sensor 1 (a) and bi-axial accelerometer Sensor 3 (b)

4.2.2 Modal assurance criterion (MAC) assessment

The modal parameters of the Messina Bell Tower have been identified from a measured environmental noise recording of 3600 s on the 4th July 2019 at 5:15 am UTC. The recorded signals have been analyzed to extract the modal parameters in terms of frequencies, damping, and mode shapes. The used identification technique is the one implemented in LMS Test.Lab software, based on a frequency-domain analysis through the Polymax algorithm (Peteers and Van der Auweraer 2005). Polymax is a modal parameter estimation method working in the frequency domain, which is based on the cross-spectra of the recorded signals. The cross-spectra, modelled as the ratio of two complex polynomials, represent, for operational modal analysis, the equivalent of Frequency Response Functions for classical experimental modal analysis.

The structural modes are visible in correspondence of the peaks of the auto (Fig. 8a) and cross-spectra (Fig. 8b). The frequencies and the mode shapes are extracted through stabilization diagrams, which consider as “stable”, and therefore valid, only those modes whose frequencies and damping ratios do not vary sensibly by increasing the order of the model, i.e. the degree of the complex polynomials. In Fig. 8, the auto and cross spectra of the accelerations measured by Sensors 2 and 3, are shown as an example. Seven frequency peaks in the range 0–10 Hz are clearly observable. The first two peaks ($f_{1}^{EXP}$ = 1.37 Hz and $f_{2}^{EXP}$ = 1.43 Hz) correspond to translational modes, whereas the torsional mode can be associated to either of the two very close frequencies ($f_{3a}^{EXP}$ = 3.35 Hz and $f_{3b}^{EXP}$ = 3.53 Hz), as verified by the high value of Modal Assurance Criterion (MAC) between these two mode shapes, equals to 0.99. The cross-spectra highlight as modes 1 and 2 are translations in the X and Y directions, respectively, with their frequency peak that appears only in one direction. On the contrary, mode 4 and 5 ($f_{4}^{EXP}$ = 5.42 Hz and $f_{5}^{EXP}$ = 5.50 Hz), that are translational too, have a diagonal direction, as can be seen by their frequency peak appearing in both X and Y directions. Finally, the experimental mode shape extracted for the peak at frequency $f_{6}^{EXP}$ = 8.58 Hz has not a clear and easy structural interpretation. In conclusion, on the basis of the above considerations, and also of the limited number of the measured degrees of freedom, only the modes corresponding to the frequencies $f_{1}^{EXP}$, $f_{2}^{EXP}$ and $f_{3a}^{EXP}$ have been used to calibrate the mechanical properties of the masonry walls of the FE model described in Sect. 4.1. It is noted that as a difference from masonry structures CMBs are not vulnerable to out-of-plane behavior of the masonry walls and they are not significantly affected by environmental changes if the masonry infills are constituted by solid bricks with cementitious mortar, as in the case of the Bell Tower. The Tower is now continuously monitored, as it has been included in the portfolio of structures monitored by the Italian Civil Protection Department, and no significant change in natural frequencies and modes shapes have been registered with respect to summer–winter environmental conditions.

Fig. 8

a Auto-spectra of measured accelerations in Sensor 2 and b Cross-spectra between accelerations in Sensors 2 and 3

A comparison between the experimental natural frequencies and the ones of the calibrated model are reported in Table 2, which shows as the first two natural frequencies are almost perfectly coincident, whereas for the third one there is a percentage difference below 14%. The first six numerical modal shapes are visualized in Fig. 9.

Table 2 Experimental and numerical natural frequencies

Fig. 9

First 6 mode shapes of the Messina Bell Tower

Once the matching with the first natural frequency is achieved, a Cross- Modal Assurance Criterion or CrossMAC (Pastor et al. 2012) is used to compare the modal shapes between the real Bell Tower and its corresponding Finite Element Model.

The agreement between the ith experimental mode shape $\phi_{i}^{EXP}$ and the jth numerical mode shape $\phi_{j}^{FEM}$ is evaluated through the MAC index (Ewins 2000), which provides a measure of their correlation according to the following equation:

$$MAC\left( {\phi_{i}^{EXP} ,\; \phi_{j}^{FEM} } \right) = \frac{{\left[ {\left( {\phi_{i}^{EXP} } \right)^{T} \left( {\phi_{j}^{FEM} } \right)} \right]^{2} }}{{\left[ {\left( {\phi_{i}^{EXP} } \right)^{T} \left( {\phi_{i}^{EXP} } \right)} \right]\left[ {\left( {\phi_{j}^{FEM} } \right)^{T} \left( {\phi_{j}^{FEM} } \right)} \right]}}$$

(26)

It is worth noting that Eq. (26) leads to a value of 1 to experimental and numerical mode shapes pairs that exactly match, whereas a value of 0 is given to those pairs that are completely uncorrelated.

In Fig. 10 the MAC between experimental and FEM mode shapes is reported for the first three vibrations modes neglecting higher modes which would have required a higher number of sensors to allow their determination. The close to unity values along the main diagonal of the table, testify that the FEM well reproduces the experimentally identified mode shapes.

Fig. 10

Cross- MAC between Experimental and Numerical Modal Properties

From the exam of the mode shapes reported in Fig. 9 (i.e. Mode 1 and Mode 2) it can be observed a non-negligible base rotation. This is also in line with the current literature and with the FEMA P-2091 “rule of thumb test” for which if the soil-to-stiffness ratio, $h^{\prime } /\left( {V_{s} T} \right)$ ($h^{\prime }$ = effective structure height, measured from base of foundation to the centre of mass of the fundamental mode, $V_{s}$ = shear wave velocity and T = fundamental period) is greater than 0.1, the SSI is likely to be significant. Specifically, for the Messina Bell Tower the calculated soil-to-stiffness ratio is equal to 0.1847.

4.2.3 Validation of the Messina Tower Bell numerical model

Further model validation is performed by considering the seismic events recorded by the continuous monitoring system on September 24th, 2020, UTC 05:53:38, of magnitude M = 3.4, and on the 19^th December 2020, UTC 10:57:43, of magnitude M = 3.9. The epicentre of the first event (denominated Event 1) is 35 km far from the Bell Tower at a latitude of 38.1332 and longitude of 15.1643, with depth of the hypocentre of 10 km; the second event (indicated as Event 2) is located at latitude 38.1328 and longitude 15.9537, 35 km away from the Bell Tower and hypocentre depth of 14 km. The time-histories recorded at the foundation (Sensor 1) are used as seismic inputs applied at the same location in the finite element model including the soil underneath as prescribed accelerations, rather than applied to the bedrock after a pertinent back propagation. It is worth emphasising that the signals on the 3 principal directions, recorded at the base do not correspond to the free-field seismic motion at the building location, owing to kinematic and inertial soil-structure interaction effects (Gara et al. 2021), hence, they cannot be applied at the soil bedrock as conventional done in soil-structure interaction analyses. Therefore, the input acceleration time-histories about the 3 principal directions, $\ddot{u}_{x}$, $\ddot{u}_{y}$, and $\ddot{u}_{z}$, are exactly those from the recordings at foundation level, depicted in Fig. 11. A very low structural damping, calibrated through Rayleigh formulation as $\zeta = 0.005$ at the 1.30 Hz and 5.45 Hz, equal to $\alpha = 0.06595$ for the mass-proportional coefficient and $\beta = 2.35785e - 04$ for the stiffness-proportional coefficient is used. Small values of damping are consistent with the low amplitude of the seismic input (Gara et al. 2021), as further confirmed by the damping analysis performed on the recordings. Comparisons between the recordings and the simulated time-histories in acceleration and the related Fourier transforms are shown for each sensor in Figs. 12, 13, 14 and 15. A relatively good match is obtained where the highest difference is observed on the short shift of the second modes about the x- and y- directions as previously identified in Table 2. Moreover, because of the Rayleigh formulation, the values of the Fourier transform of the signal in the z- direction, in-between the frequencies used to calibrate the damping, are slightly smaller than the assumed value of 0.005. Nevertheless, the results for the validation of the model can be considered satisfactory. Similar considerations can be drawn from the analyses carried out on Event 2 as shown in Figs. 16, 17 and 18 for 3 significant locations (Sensors 1–2-5). Because of the higher level of intensity, about 3.5 times the maximum amplitude of Event 1, a further calibration of the damping is required; by considering the same 2 frequencies as before, the Rayleigh coefficients are obtained by setting a damping of $\zeta = 0.02$. A good matching between the numerical results and the recordings is therefore obtained also for Event 2.

Fig. 11

Base input and Fourier Transform accelerations at the foundation (Sensor 1) for Event 1

Fig. 12

Simulated vs Recorded time-histories and Fourier Transform accelerations at floor 4 (Sensor 2) for Event 1

Fig. 13

Simulated vs Recorded time-histories and Fourier Transform accelerations at floor 4 (Sensor 3) for Event 1

Fig. 14

Simulated vs Recorded time-histories and Fourier Transform accelerations at floor 4 (Sensor 4) for Event 1

Fig. 15

Simulated vs Recorded time-histories and Fourier Transform accelerations at floor 7 (Sensor 5) for Event 1

Fig. 16

Base input time-histories and Fourier Transform accelerations at the foundation (Sensor 1) for Event 2

Fig. 17

Simulated vs Recorded time-histories and Fourier Transform accelerations at floor 4 (Sensor 3) for Event 2

Fig. 18

Simulated vs Recorded time-histories and Fourier Transform accelerations at floor 7 (Sensor 5) for Event 2

4.3 Soil-foundation interaction model through Preisach formalism

Direct time integration analyses conducted in Sect. 4.2.3 on the full 3D soil-structure model of Fig. 5b are computationally expensive. The computational time increases when a nonlinear soil model is considered. In order to reduce the time required to perform nonlinear time histories, the soil medium is replaced by an uncoupled lumped parameter model (LPM) made of the approximated Preisach elements governed by Eqs. (22–23) for the translational elements and Eqs. (24–25) for the rotational elements. Accordingly, the Preisach LPM is able to satisfactory capture the nonlinear soil-(massless) foundation interaction through few degrees of freedom substituting the large soil medium as shown in Fig. 19a. In order to implement Eq. (22) and Eq. (23) ($\psi_{h} = 0$; $\eta_{h} = 1$) as Preisach elements specifically for the finite element software ADINA, two 1D trusses about the two principal directions with nonlinear elastic behaviour are used. The translational elements are directly implemented through horizontal truss elements located at the centre of rigidity of the foundation, according to the following force–displacement relationship:

$$F_{e,\;h} = \left( {k_{h} - \frac{{k_{h}^{2} a_{h} }}{{2V_{\max } }}} \right)u_{h}$$

(27)

Fig. 19

FE model of the a Messina Bell Tower with Preisach LPM and b simplified model and c schematics of Preisach elements

At the same centre of rigidity, nonlinear dashpots are added; the damping value is derived from Eq. (22) taking into account the pseudo harmonic behaviour of the response; hence, the following nonlinear damping force – velocity relationships is obtained:

$$F_{d,\;h} = \frac{{2k_{h}^{2} a_{h} }}{{3\pi \omega_{n} V_{\max } }}\dot{u}_{h} \cong \frac{{2k_{h}^{2} }}{{3\pi \omega_{n}^{2} V_{\max } }}\left( {\dot{u}_{h} } \right)^{2}$$

(28)

which represent a quadratic nonlinear viscous dashpot (i.e. damper exponent n = 2). The rotational behaviour is modelled through a couple of vertical 1D truss elements per direction as it can be observed Fig. 19b–c. Each couple of elastic vertical stiffness value, $k_{z,\;\theta }$, is determined as to their sum is equal to the vertical soil-foundation interaction stiffness, $k_{v}$; the distance between the couple of truss elements is derived to obtain the rotational elastic stiffness as follows:

$$l_{b} = \sqrt {\frac{{2k_{\theta } }}{{k_{z,\;\theta } }}}$$

(29)

Therefore, by using Eq. (24), the moment-rotation relationship can be determined as follows:

$$M = \left( {k_{\theta } - \frac{{k_{\theta }^{2} a_{\theta } }}{{2M_{\max } }}} \right)u_{\theta }$$

(30)

or equivalently, in terms of force-vertical displacement ($u_{z}$) of each truss element:

$$F_{e,\;\theta } = \left( {k_{z,\theta } - \frac{{k_{z,\theta }^{2} a_{z} l_{b} }}{{2M_{\max } }}} \right)u_{z}$$

(31)

where $a_{z}$ represents the amplitude of the vertical displacement. Furthermore, the rotational damping can be modelled through a nonlinear rotational dashpot in analogy with the translational case as follows:

$$F_{d,\;\theta } \cong \frac{{2k_{z,\theta }^{2} }}{{3\pi \omega_{n}^{2} M_{\max } }}\left( {\dot{u}_{\theta } } \right)^{2}$$

(32)

In this paper, an elasto-plastic soil model characterized by undrained cohesion of 75 kPa and same elastic properties reported in Table 1, is considered for the modelling of the first 22 m of the soil deposit (corresponding to more the 3.5 times the half-width of the foundation). In order to reduce the computational effort of the complete finite element model the remaining bottom layer is kept as linear material. Therefore, the definition of the Preisach elements requires the determination of the elastic stiffness values, $k_{h}$, $k_{\theta }$, and $k_{v}$, and the ultimate capacity of the foundation, $V_{\max }$ and $M_{\max }$. The elastic values can be found directly from the finite element model of the soil-foundation by applying a unitary displacement and rotation at the foundation level; in this paper the values obtained through this approach have been also verified through the software DYNA6.1 (2020) for dynamic soil-structure interaction analysis. The ultimate capacity of the foundation is obtained through a static pushover analysis of the soil-foundation finite element model; nevertheless, any other design formula might be used. In this paper, the foundation is symmetric and hence, $k_{h}$ and $V_{\max }$ as well as $k_{\theta }$ and $M_{\max }$ are the same for the 2 translational principal directions. Data used to characterize the Preisach elements of the proposed LPM are given in Table 3, whilst the nonlinear elastic behaviour of the Preisach elements for displacement and rotation about the principal direction Y are shown in Fig. 19a–b, respectively.

Table 3 Data required to characterize the Preisach elements of the LPM

It is worth mentioning that the proposed Preisach elements have been derived from the main formulation in Sect. 3 by selecting the characteristic frequency $\omega_{n}$; namely, the first natural frequencies of the Bell Tower in each direction are considered for the definition of $\omega_{n}$ as described in Table 3. The approximation, which arises from this definition of Preisach elements compared to the full formulation, can be appreciated in Fig. 21 where the acceleration of the upper node of the simplified model of the Bell Tower in Fig. 19b is shown. The seismic input of Event 1 is scaled to two factors, 100 × in Fig. 20a and 400 × in Fig. 21b, in order to induce the nonlinear behaviour of the soil. The comparison shows how the difference increases at larger magnitude without compromising sensibly accuracy.

Fig. 20

Capacity curves of the soil-foundation system for a shear force and b moment

Fig. 21

Response of the simplified model assessed by using the full Preisach formalism and the proposed LPM model for input scaled to a 100 × and b 400x

4.4 Nonlinear incremental dynamic analysis

In this section, the accuracy of the proposed Preisach LPM is assessed through a nonlinear incremental dynamic analysis (Vamvatsikos and Cornell 2002). The Event 1 recordings used for the model validation are amplified through 2 scale factors equal to 100 x and 500x, in order to reach a significant peak acceleration of about $9\;{\text{m}}/{\text{s}}^{2}$ at the floor 7 of the Bell Tower at the location of Sensors 4–5. Rayleigh damping factors obtained to validate the linear model are kept constant over the incremental analysis for the sake of simplicity without affecting the analysis’s aim to verify the efficiency and efficacy of the Preisach elements to simulate the nonlinear behaviour of the soil. A preliminary verification of the Preisach LPM is conducted by using the unscaled recordings, which induced a linear behaviour of the response because of their low magnitude. Figures 22 and 23 show the comparison at floors 4 and 7, between the results obtained from the full FEM model (denominated FEM-NLIN) and the Bell Tower model founded on the Preisach LPM; furthermore, the unscaled recordings are plotted to show the accuracy of both models to reproduce the experimental results.

Fig. 22

Comparison of the numerical models with the unscaled recordings at floor 4 (Sensor 3) for Event 1

Fig. 23

Comparison of the numerical models with the unscaled recordings at floor 7 (Sensor 5)

Therefore, further analyses are conducted on both numerical models by scaling the initial recordings by a scale factor of 100 × as shown in Figs. 24 and 25 for floor 4 and 7, respectively. The Preisach model is able to capture well the response of the Tower Bell computed through the full nonlinear FEM. The first peak of the Fourier transform is well matched whilst high frequencies resulted overdamped. Nevertheless, small relative errors of the 2% and 9.9% are obtained between the peak acceleration of the floor 7 for direction X and Y, respectively.

Fig. 24

Comparison between full FEM model and model with Preisach LPM at floor 4 (Sensor 3) for Event 1 scaled with factor 100x

Fig. 25

Comparison between full FEM model and model with Preisach LPM at floor 7 (Sensor 4) for Event 1 scaled with factor 100x

Furthermore, the recordings are scaled to a factor of 500 × to reach a significant peak acceleration on the top of the Bell Tower. Figures 26 and 27 show the comparison between the numerical models in terms of acceleration time histories and Fourier transforms functions. Similarly to the previous case, the Preisach LPM predicts considerably well the seismic response of the soil with relative errors of about 13% for the floor 4 and 16% for floor 7 in both directions. It is worth emphasizing that the time complexity is extremely reduced through the use of the Preisach LPM; 44,605 3D solid elements for the soil medium are eliminated, reducing the total number of equations to be solved from 190,388 to 102,322, hence a 46% reduction of the number of equations leading to faster analyses (about 5 h instead of 12 h by using a workstation with 32 physical cores Intel Xeon at 2.10 GHz and 128 GB of RAM). The reduction is computed by comparing only the two numerical models investigated in this paper. Clearly, a different reduction value would be obtained from the comparison of the computational time with the proposed Preisach LPM by using a different soil-structure modelling approach.

Fig. 26

Comparison between full FEM model and model with Preisach LPM at floor 4 (Sensor 3) for Event 1 scaled with factor 500x

Fig. 27

Comparison between full FEM model and model with Preisach LPM at floor 7 (Sensor 4) for Event 1 scaled with factor 500x

Finally, the incremental dynamics curves of the peak acceleration of the floor 7 are reported in Fig. 28 versus the input scaling factor. The continuous curves represent the peak acceleration obtained at the location of Sensor 5 on the full FE model for both principal directions X and Y.

Fig. 28

Incremental dynamic curves of the unbiased peak acceleration for sensor 5

The dashed curves plot the increment of the peak accelerations at the same location obtained through the model with the Preisach LPM; these curves are purged from the systematic error related to the different modelling at 1x (linear model) and hence, the values of acceleration at 1 x is the same for each direction. It can be observed that an excellent match is obtained between the two numerical modelling proving the efficiency and efficacy of the Preisach LPM to simulate the nonlinearities of the soil medium. To further assess the effects of the nonlinearities on the seismic response of the Bell Tower, a short-time Fourier transform is carried out on the acceleration time histories about the Y direction for the previous cases. Results reported in Table 4 show that the average natural frequency of the system decreases from 1.37 Hz in the linear case to 1.34 Hz for the case scaled to 500x. The shift of the peak frequency can be also observed through the comparison of the Fourier transform functions of the normalized signals depicted in Fig. 29; also, the minimum instantaneous frequency, calculated from the Fourier transform of 40 short time windows in which the signal is subdivided, decreased from 1.37 to 1.20 Hz. Therefore, the soil yielding produces a softening of the soil elastic modulus and therefore a decrement of the natural frequencies along with an increment of the material damping as observed in Fig. 29 by comparing the first peaks obtained for the 1x-signal with respect to the 500x-signal. Moreover, Table 4 shows the equivalent modal damping obtained by best fitting of the Fourier transform of the signal with an equivalent single degree of freedom; the equivalent damping at the first frequency increases from the initial value of $\zeta = 0.005$ to $\zeta = 0.025$ at 500 × because of the soil hysteresis.

Table 4 Effect of the soil properties on the equivalent modal properties

Fig. 29

Comparison of the Fourier transform of the normalized acceleration for sensor 5, y-direction

5 Concluding remarks

In this paper, the seismic response of a linear behaving structure resting on a nonlinear compliant soil has been addressed. The use of the Preisach formalism to capture the hysteretic behaviour of soil and its impact on the nonlinear soil structure interactions has been explored. By using a particular form of the weight function in conjunction with a harmonic balance procedure it was possible to derive closed form expressions of the equivalent stiffness and damping at the foundation. The Preisach springs and damping elements have been applied to a real case study: the Messina Bell Tower in Italy. An accurate FE model has been first developed and validated through experimental data from the permanent monitoring system installed in the Messina Bell tower since July 2019. Furthermore, an incremental dynamic analysis has been performed to explore the nonlinear soil-structure interaction modelled through the Preisach formalism. Excellent agreement has been found from the results determined through the full direct method, performed on the coupled FE model of the Bell Tower and the soil, and through the simplified model replacing the nonlinear soil with the equivalent Preisach springs and dashpots. The results appear promising for future application of the Preisach formalism to more complex hysteretic phenomena in the soil.