1 Introduction

Presently, lunar exploration architecture based on the Lunar Orbital Station (LOS) (Engle et al. 2016; Duggan and Reiley 2015) has been put forward by many countries (Duggan et al. 2016). LOS will be a staging area for assembly and testing for a cislunar transport. Furtherly, as a transportation node in the cislunar space, it can be used to mount expeditions to Mars, and in particular to conduct deep space operations (Smitherman 2016; Davis and Peek 2016). Staging orbit of the LOS have been researched considering the capability of the spacecraft and launch system (Whitley and Martinez 2016), and low lunar orbit (LLO) is concluded as a favorable staging orbit for surface access, including a range of inclinations to access global landing sites (Stanley et al. 2005; Murtazin 2014).

One of the main technical issues of the LOS based architecture is to find Earth-Moon-Earth (Miele and Mancuso 2001) transfer trajectories between the Earth and the LOS. Two-impulse transfer trajectories have been researched and investigated extensively (Topputo 2013; Liang et al. 2016; Qi and Xu 2016; Li et al. 2015; Lv et al. 2017; Cao et al. 2017). The Hohmann transfer represents the easiest way to perform Earth-Moon transfer, but it requires considerable cost to inject the spacecraft into the final orbit about the Moon. Free return trajectories (Peng et al. 2012; Hou et al. 2013; Luo et al. 2013; Li and Baoyin 2015; Bao et al. 2018) are proposed to satisfy the demand to safely return to the Earth in the case of a mission failure. Low energy transfers have been found in the attempt to reduce the total cost for Earth-Moon transfer, which exploit the concept of temporary ballistic capture, or weak capture, which is defined in the framework of n-body problems (Belbruno 2004; Parker and Anderson 2013; Qu et al. 2017; Chupin et al. 2017; Dutt et al. 2018). For the study on the orbit characteristics, Mengali and Quarta (2005) developed a closed-form approximate expression for the total velocity variation under the assumption of minimum \(\Delta \mathrm{v}\) biimpulsive maneuvers. Topputo (2013) constructed a global set of solutions for this problem, which have been characterized and studied in detail. Ground launch windows for high-accuracy free return circumlunar trajectories are systematically established by (Yim et al. 2015).

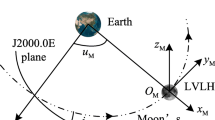
However, in the manned lunar exploration with the LOS, spacecraft is docking at the LOS when astronauts are on the surface of the Moon. Therefore, it is necessary for the selenocentric transfer trajectory to be coplanar with the LOS orbital plane, see in Fig. 1, because maneuvering in the direction of the local velocity maximizes the variations of spacecraft energy (Pernicka et al. 1994). Therefore, LOS orbital plane constraint should be considered in the design of transfer trajectory between the Earth and the LOS. In addition, the LOS orbital plane changes relative to the Earth due to the revolution of the Moon and the orbit precession, shown in Fig. 2, for a fixed epoch, the LOS is on a permanent lunar orbit. Trajectory design with the LOS orbital constraint, or rather its inclination, the right ascension of ascending node (RAAN), and its altitude constraint, will be an interesting problem and the associated characteristics will have different patterns. That is exactly what this article is about.

Fig. 1
figure 1

Spacecraft should be transferred to a lunar orbit coplanar with the LOS, or rather, Earth-LOS transfer trajectories are constrained by the LOS orbital plane

Full size image
Fig. 2
figure 2

The LOS orbit relative to the Earth in one revolution period; the yellow solid lines represent the LOS orbit with inclination 90 deg (not to scale)

Full size image

In this paper, both the Earth-LOS and LOS-Earth transfer trajectories are studied. For the Earth-LOS transfer, only two-impulse transfers are considered. The spacecraft is initially in a low Earth parking orbit. A first impulse \(\Delta \mathrm{v}_{\mathit{tl}}\), assumed parallel to the velocity of the parking orbit, places the spacecraft on the trans-lunar orbit. At the end of the transfer, a second impulse \(\Delta \mathrm{v}_{\mathit{LOI}}\) inserts the spacecraft into the low lunar orbit coplanar with the LOS orbit. This second impulse is also parallel to the velocity of the LOS parking orbit. For the LOS-Earth transfer, only one impulse \(\Delta \mathrm{v}_{te}\) is performed tangentially at the LOS parking orbit to insert the spacecraft into a Moon-Earth transfer that satisfies the reentry condition at the same time.

The paper is organized as follows. After a brief introduction about relationship between the initial and terminal state, a fast-converging iteration method for the design of transfer trajectories between the Earth and the LOS is developed based on the patched conic approach in Sect. 3. On the basis of the method proposed in this paper, transfer trajectories between the Earth and the LOS are explored intensively, including the orbital transfer window, velocity impulse and time of flight. High-fidelity verification is adopted for the correction of the initial value based on the active-set method in Sect. 5.

2 Relationship between the initial and terminal orbital state

Consider two position vectors \(\mathbf{r}_{1}\) and \(\mathbf{r}_{2}\) which locate the points \(P_{1}\) and \(P_{2}\) relative to a center of force fixed at a point \(F\), see in Fig. 3, where \(\theta \) is the transfer angle, \(c\) is the chord length, \(\gamma _{1}, \gamma _{2}\) are the flight path angles at \(P_{1}\) and \(P_{2}\), respectively, that is, the angle between the orbital velocity and the local horizon. Let \(\mathbf{v}_{1}\) at \(P_{1}\) and \(\mathbf{v}_{2}\) at \(P_{2}\) be the velocity vectors for an orbit connecting \(P_{1}\) and \(P_{2}\) with a focus at \(F\). The velocity can be expressed in polar coordinates as

$$ \left \{ \textstyle\begin{array}{l} \mathbf{v}_{1} = v_{r_{1}}\mathbf{i}_{r_{1}} + v_{\theta _{1}} \mathbf{i}_{\theta _{1}} \\ \mathbf{v}_{2} = v_{r_{2}}\mathbf{i}_{r_{2}} + v_{\theta _{2}} \mathbf{i}_{\theta _{2}} \end{array}\displaystyle \right . $$
(1)

The radial component \(v_{r}\) and circumferential component \(v_{\theta} \) of the orbital velocity vector have

$$ \left \{ \textstyle\begin{array}{l} v_{r} = \frac{dr}{dt} = \frac{h}{r}\tan \gamma = \frac{he}{p}\sin f \\ v_{\theta } = r\frac{df}{dt} = \frac{h}{r} \end{array}\displaystyle \right . $$
(2)

where \(p\) is the semi-latus rectum, \(h\) is the norm of angular momentum, \(f\) is the true anomaly and \(e\) is the eccentricity.

Fig. 3
figure 3

Geometry of the boundary value problem. The solid red lines represent the velocity vectors and the dotted red lines represent the local horizon

Full size image

Let \(f_{1}\) and \(f_{2} = f_{1} + \theta \) be the true anomalies of the points \(P_{1}\) and \(P_{2}\), so that

$$\begin{aligned} v_{r_{1}} + v_{r_{2}} &= \frac{he}{p} \bigl[ \sin f_{1} + \sin ( f_{1} + \theta ) \bigr] \\ &= \frac{h}{p} \bigl[ e\cos f_{1} - e\cos ( f_{1} + \theta ) \bigr] \cot \frac{1}{2}\theta \end{aligned}$$
(3)

Using the polar equation of orbit \(e\cos f = p / r - 1\), then

$$ v_{r_{1}} + v_{r_{2}} = ( v_{\theta _{1}} - v_{\theta _{2}} ) \cot \frac{1}{2}\theta $$
(4)

Substituting Eq. (2) into Eq. (4), the relationship between the initial and terminal orbital radii can be written as follows

$$ r_{2}\tan \gamma _{1} + r_{1}\tan \gamma _{2} = ( r_{2} - r_{1} ) \cot \frac{1}{2} \theta $$
(5)

3 Trajectory design method

3.1 Description

In this section, a novel iterative trajectory design method is developed based on the relationship between the initial and terminal state using the patched-conic approach, which analytically satisfies the constraints of the transfer trajectories between the Earth and the LOS.

For the Earth-LOS transfer, constraints are imposed at three points: perigee, perilune and the entry point at the lunar sphere of influence (LSOI). At perigee, the altitude of the Earth parking orbit and the flight-path angle are imposed. Due to the tangential \(\Delta \mathrm{v}_{\mathit{tl}}\) impulse, the flight-path angle is 0 deg; the altitude of the LOS is imposed at the perilune; geocentric state vector \(( \mathbf{R}_{s},\mathbf{V}_{s} ) \) and selenocentric state vector \(( \mathbf{r}_{s},\mathbf{v} _{s} ) \)of the entry point (subscript s) are constrained by the LOS orbital plane.

For the LOS-Earth transfer, constraints are also imposed at three points: perilune, the reentry point and the exit point at the LSOI. At perilune, the radius of the LOS orbit is imposed. The LOS orbital plane also imposes constraints on both the geocentric state vector \(( \mathbf{R}_{\mathit{se}},\mathbf{V}_{\mathit{se}} ) \) and selenocentric state vector \(( \mathbf{r}_{\mathit{se}}, \mathbf{v}_{\mathit{se}} ) \) of the exit point (subscript se). At the reentry point, two constraints are imposed: flight-path angle and altitude. The flight-path angle at the reentry point will always have a negative value. This angle should be selected such that the reentry into the Earth’s atmosphere is within the entry corridor. The reentry corridor of the flight-path angle is typically located at [−7.5 deg, −5.5 deg], similar to the Apollo’s mission.

3.2 Algorithm

A concise and elaborate algorithm is developed to design transfer trajectories between the Earth and the LOS. As shown in Fig. 4, with the free argument of perilune \(\omega _{m}\), initial value of eccentricity \(e_{m}^{0}\) of Moon-phase conics (subscript m) is guessed firstly. Then, the algorithm is implemented to compute the state of the entry point or exit point and update \(e_{m}^{0}\) iteratively, in order to reach the desired value. This process can converge in a few loops.

Fig. 4
figure 4

Algorithm flow charts for design of Earth-LOS transfer (left) and LOS-Earth transfer (right)

Full size image

The input conditions are chosen as \(( r_{p},i_{m},\varOmega _{m}, \omega _{m}, t_{\mathit{se}},e_{m}^{0} ) \) for the LOS-Earth transfer, where \(r_{p}\) is the radius of perilune. \(i_{m},\varOmega _{m}\) are the inclination, RAAN of the Moon-phase conics, respectively. \(t_{\mathit{se}}\) is the arrival time at the exit point. \(\hat{h}_{\mathit{re}},\hat{\gamma }_{\mathit{re}}\) are the normal altitude and flight-path angle of the reentry point (subscript re), which need to be satisfied by solving \(e_{m}^{0}\) iteratively. For the Earth-LOS transfer, \(( i_{m},\varOmega _{m}, \omega _{m},h_{d},\gamma _{d} = 0,t_{s},e_{m}^{0} ) \) are chosen as the input conditions, where \(h_{d},\gamma _{d}\) are the altitude and flight-path angle at the departure point (subscript d), \(t_{s}\) is the arrival time at the entry point. \(\hat{r}_{p}\) is the normal radius of perilune. In the following, the algorithm for the LOS-Earth transfer is described.

(1) With the free parameter \(\omega _{m}\), guess the initial value of eccentricity \(e_{m}^{0}\). With the first four input quantities, the orbital elements of the Moon-phase conics are derived:

$$\begin{aligned} &a_{m} = \frac{r_{p}}{ ( 1 - e_{m}^{0} ) } \end{aligned}$$
(6)
$$\begin{aligned} &\cos f_{\mathit{se},m} = \frac{r_{p} ( 1 + e_{m}^{0} ) - r_{\mathit{se}}}{e _{m}^{0}r_{\mathit{se}}} \end{aligned}$$
(7)

Here, \(r_{\mathit{se}}\) equals to the radius of LSOI. Then, the selenocentric state vector \(( \mathbf{r}_{\mathit{se}},\mathbf{v}_{\mathit{se}} ) \) of the exit point can be expressed as:

$$\begin{aligned} &\mathbf{r}_{\mathit{se}} = r_{\mathit{se}}\cos f_{\mathit{se},m} \cdot \mathbf{P} + r _{\mathit{se}}\sin f_{\mathit{se},m} \cdot \mathbf{Q} \end{aligned}$$
(8)
$$\begin{aligned} &\mathbf{v}_{\mathit{se}} = - \sqrt{\frac{\mu _{M}}{p_{m}}} \sin f_{\mathit{se},m} \cdot \mathbf{P} + \sqrt{\frac{\mu _{M}}{p_{m}}} \bigl( e_{m} ^{0} + \cos f_{\mathit{se},m} \bigr) \cdot \mathbf{Q} \end{aligned}$$
(9)

where

$$\begin{aligned} &\mathbf{P} = \left ( \textstyle\begin{array}{l} \cos \varOmega _{m}\cos \omega _{m} - \sin \varOmega _{m}\sin \omega _{m}\cos i _{m} \\ \sin \varOmega _{m}\cos \omega _{m} + \cos \varOmega _{m}\sin \omega _{m}\cos i _{m} \\ \sin \omega _{m}\sin i_{m} \end{array}\displaystyle \right ) \end{aligned}$$
(10)
$$\begin{aligned} &\mathbf{Q} = \left ( \textstyle\begin{array}{l} - \cos \varOmega _{m}\sin \omega _{m} - \sin \varOmega _{m}\cos \omega _{m} \cos i_{m} \\ - \sin \varOmega _{m}\sin \omega _{m} + \cos \varOmega _{m}\cos \omega _{m} \cos i_{m} \\ \cos \omega _{m}\sin i_{m} \end{array}\displaystyle \right ) \end{aligned}$$
(11)

are unit vectors for eccentricity and semilatus rectum, respectively, \(\mu _{M}\) is the Moon gravity constant, \(p_{m}\) is the semilatus rectum of the Moon-phase conics.

The state of the Moon \(( \mathbf{R}_{M},\mathbf{V}_{M} ) \) at time \(t_{\mathit{se}}\) are obtained from the Jet Propulsion Laboratory DE405 ephemeris. Then, the geocentric state vector \(( \mathbf{R}_{\mathit{se}},\mathbf{V}_{\mathit{se}} ) \) of the exit point are obtained as follows

$$\begin{aligned} &\mathbf{R}_{\mathit{se}} = \mathbf{r}_{\mathit{se}} + \mathbf{R}_{M} \end{aligned}$$
(12)
$$\begin{aligned} &\mathbf{V}_{\mathit{se}} = \mathbf{v}_{\mathit{se}} + \mathbf{V}_{M} \end{aligned}$$
(13)

If the angle \(\theta _{\mathit{se}}\) between the \(\mathbf{R}_{\mathit{se}}\) and \(\mathbf{V}_{\mathit{se}}\) satisfies

$$ \theta _{\mathit{se}} = \arccos \biggl( \frac{\mathbf{R}_{\mathit{se}} \cdot \mathbf{V}_{\mathit{se}}}{ \Vert \mathbf{R}_{\mathit{se}} \Vert \Vert \mathbf{V}_{\mathit{se}} \Vert } \biggr) > \frac{\pi }{2} $$
(14)

Then the Earth-phase transfer trajectory is computed in (2), otherwise change the free variable \(\omega _{m}\).

(2) From \(( \mathbf{R}_{\mathit{se}},\mathbf{V}_{\mathit{se}} ) \), orbital elements of the Earth-phase (subscript \(e\)) transfer trajectory can be calculated (Battin 1999), such as the semi-major radius \(a_{e}\), the eccentricity \(e_{e}\), the semilatus rectum \(p_{e}\). Then, the radius of perigee is

$$ R_{p} = a_{e} ( 1 - e_{e} ) $$
(15)

If

$$ R_{p} > \hat{R}_{\mathit{re}} = \hat{h}_{\mathit{re}} + a_{E} $$
(16)

where \(a_{E}\) is the Earth mean equatorial radius. Then, update the parameters in (3) with the nominal flight path angle \(\hat{\gamma } _{\mathit{re}}\) at reentry point.

If

$$ R_{p} < \hat{R}_{\mathit{re}} $$
(17)

then, the flight-path angle at the reentry point is

$$ \gamma _{\mathit{re}} = \arcsin \biggl( \frac{e_{e}\sin f_{\mathit{re},e}}{\sqrt{1 + 2e _{e}\cos f_{\mathit{re},e} + e_{e}^{2}}} \biggr) $$
(18)

where the true anomaly of the reentry point \(f_{\mathit{re},e}\) has

$$ f_{\mathit{re},e} = 2\pi - \arccos \biggl( \frac{p_{e} - R_{\mathit{re}}}{e_{e}R_{\mathit{re}}} \biggr) $$
(19)

Compare \(\gamma _{\mathit{re}}\) with the nominal value \(\hat{\gamma }_{\mathit{re}}\), if

$$ \vert \gamma _{\mathit{re}} - \hat{\gamma }_{\mathit{re}} \vert < 10^{ - 5} $$
(20)

then, the LOS-Earth transfer trajectory has been obtained, otherwise update the parameters in (3).

(3) The transfer angle \(\Delta f_{e}\) between the exit point and the reentry point can be found by the relationship between the initial and terminal state

$$\begin{aligned} &R_{\mathit{se}}\tan \hat{\gamma }_{\mathit{re}} + \hat{R}_{\mathit{re}}tan \gamma _{\mathit{se}} = ( R _{\mathit{se}} - \hat{R}_{\mathit{re}} ) \cot \biggl( \frac{\Delta f_{e}}{2} \biggr) \\ &\quad {\Rightarrow}\quad \Delta f_{e} = 2arctan \biggl( \frac{R_{\mathit{se}} - \hat{R}_{\mathit{re}}}{R _{\mathit{se}}\tan \hat{\gamma }_{\mathit{re}} + \hat{R}_{\mathit{re}}tan\gamma _{\mathit{se}}} \biggr) \end{aligned}$$
(21)

where

$$ \gamma _{\mathit{se}} = \frac{\pi }{2} - \theta _{\mathit{se}} $$
(22)

Then, the chord length \(c_{e}\) is

$$ c_{e}^{2} = R_{\mathit{se}}^{2} + \hat{R}_{\mathit{re}}^{2} - 2R_{\mathit{se}}\hat{R}_{\mathit{re}}\cos \Delta f_{e} $$
(23)

and the semilatus rectum \(p_{e}^{*}\) of the geocentric transfer orbit is updated as

$$ \frac{p_{e}^{*}}{p_{\min }} = \frac{c_{e}\cos \gamma _{\mathit{se}}}{R_{\mathit{se}} \cos \gamma _{\mathit{se}} - \hat{R}_{\mathit{re}}\cos ( \gamma _{\mathit{se}} + \Delta f _{e} ) } $$
(24)

where \(p_{\min } \) is the semilatus rectum of the minimum-energy orbit.

$$ p_{\min } = \frac{R_{\mathit{se}}\hat{R}_{\mathit{re}}}{c_{e}} ( 1 - \cos \Delta f _{e} ) $$
(25)

Then, the chordal component \(V_{\mathit{se}}^{c}\) and radial component \(V_{\mathit{se}}^{\rho } \) of the velocity vector at the exit point can be expressed in terms of the updated semilatus rectum \(p_{e}^{*}\)

$$ V_{\mathit{se}}^{c} = \frac{c_{e}\sqrt{\mu _{E}p_{e}^{*}}}{\hat{R}_{\mathit{re}}R_{\mathit{se}} \sin \Delta f_{e}} $$
(26)
$$ V_{\mathit{se}}^{\rho } = \sqrt{\frac{\mu _{E}}{p_{e}^{*}}} \frac{1 - \cos \Delta f_{e}}{\sin \Delta f_{e}} $$
(27)

where \(\mu _{E}\) is the Earth gravity constant. Finally, the velocity at the exit point \(V_{\mathit{se}}^{ *} \) in the geocentric coordinate frame is updated as

$$ V_{\mathit{se}}^{*2} = V_{\mathit{se}}^{c2} + V_{\mathit{se}}^{\rho 2} - 2V_{\mathit{se}}^{c}V_{\mathit{se}}^{ \rho } \cos \varphi _{\mathit{se}} $$
(28)

where \(\varphi _{\mathit{se}}\) is the angle between \(V_{\mathit{se}}^{c}\) and \(V_{\mathit{se}} ^{\rho } \)

$$ \varphi _{\mathit{se}} = \arcsin \biggl( \frac{\hat{R}_{\mathit{re}}\sin ( - \Delta f_{e} ) }{c_{e}} \biggr) $$
(29)

(4) Solve the updated geocentric velocity vector \(\mathbf{V}_{\mathit{se}} ^{ *} \), which has

$$ \bar{\mathbf{h}} \cdot \bigl( \mathbf{V}_{\mathit{se}}^{ *} - \mathbf{V}_{M} \bigr) = 0 $$
(30)

where \(\bar{\mathbf{h}}\) is the unit vector parallel to the angular momentum of the Moon-phase conics. In addition, it satisfies

$$ \mathbf{R}_{\mathit{se}} \cdot \mathbf{V}_{\mathit{se}}^{*} = H\tan \gamma _{\mathit{se}} $$
(31)

where \(H = \sqrt{\mu _{E}p_{e}^{*}}\). Therefore, \(\mathbf{V}_{\mathit{se}} ^{*}\) has

$$ \left \{ \textstyle\begin{array}{l} \bar{h}_{x}V_{\mathit{se}}^{*x} + \bar{h}_{y}V_{\mathit{se}}^{*y} + \bar{h}_{z}V_{\mathit{se}} ^{*z} = \bar{\mathbf{h}} \cdot \mathbf{V}_{M} \\ R_{\mathit{se}}^{x}V_{\mathit{se}}^{*x} + R_{\mathit{se}}^{y}V_{\mathit{se}}^{*y} + R_{\mathit{se}}^{z}V_{\mathit{se}}^{*z} = \sqrt{\mu _{E}p_{e}^{*}} \tan \gamma _{\mathit{se}} \\ ( V_{\mathit{se}}^{*x} ) ^{2} + ( V_{\mathit{se}}^{*y} ) ^{2} + ( V_{\mathit{se}}^{*z} ) ^{2} = V_{\mathit{se}}^{*2} \end{array}\displaystyle \right . $$
(32)

where the superscript \(x,y,z\) denote the components of \(\mathbf{V}_{\mathit{se}}^{*}\). Based on the Newton-Raphson method, \(\mathbf{V}_{\mathit{se}}^{*}\) can be found, if

$$ \left \{ \textstyle\begin{array}{l@{\quad}l} \vert \alpha - \beta \vert < \theta \le \alpha + \beta , & 0 < \alpha + \beta \le \pi \\ \vert \alpha - \beta \vert < \theta < 2\pi - ( \alpha + \beta ) , & \pi < \alpha + \beta < 2\pi \end{array}\displaystyle \right . $$
(33)

Herein, \(\alpha = \langle \bar{\mathbf{h}},\mathbf{V} _{\mathit{se}}^{*} \rangle ,\beta = \langle \mathbf{R}_{\mathit{se}}, \mathbf{V}_{\mathit{se}}^{*} \rangle ,\theta = \langle \mathbf{R} _{\mathit{se}},\bar{\mathbf{h}} \rangle \), in which \(\langle \cdot , \cdot \rangle \) denotes the angle between two vectors.

(5) The updated selenocentric velocity vector \(\mathbf{v}_{\mathit{se}}^{*}\) can be found based on Eq. (13). Combined with \(\mathbf{r}_{\mathit{se}}\), the semi-major axis of the Moon-phase conics can be updated as \(a_{m}^{*}\), and the eccentricity can be also updated with

$$ e_{m}^{*} = - \frac{r_{p}}{a_{m}^{*}} + 1 $$
(34)

Then, go to (1), and the process will be repeated until the desired reentry conditions are satisfied. This iterative refinement process converges easily in a few loops.

4 General analysis

Transfer trajectories between the Earth and the LOS generated based on the method in Sect. 3 are analyzed in 2025 and 2034. In 2025, the Moon’s latitude will vary between −28.5∘ and 28.5∘ due to the Moon’s inclination reaching a maximum 28.5 deg. During 2034 it only ranges between −18.5∘ and 18.5∘ due to the Moon’s inclination reaching a minimum of 18.5 deg during a Metonic cycle. For the Earth-LOS transfer, the manned spacecraft is assumed to depart from a low Earth parking orbit with altitude 180 km. For the LOS-Earth transfer, the spacecraft needs to satisfy the reentry conditions at the Earth-reentry interface. Here, \(\hat{h}_{\mathit{re}} = 121~\mbox{km}\), \(\hat{\gamma }_{\mathit{re}} = - 6~\mbox{deg}\), similar to the Apollo reentry conditions. The LOS is assumed to operate at a circular low lunar orbit of which the RAAN is 0 deg at 2025/01/01 00:00:00 (TDT), and changes at a secular rate of

$$ \dot{\bar{\varOmega }} = - \frac{3}{2}J_{2}^{M}\sqrt {\frac{\mu _{M}}{a _{M}^{3}}} \biggl( \frac{a_{M}}{a_{m}} \biggr) ^{\frac{7}{2}} \cos i _{m} $$
(35)

considering the \(J_{2}^{M}\) gravitational perturbation effect of the Moon, \(a_{M}\) is the Moon mean equatorial radius. The convergence of the algorithm and transfer families are investigated. Then, orbital transfer window is discussed with respect to the altitude and inclination of the LOS orbit. At last, variation of the velocity impulse and time of flight during one orbital transfer window for both Earth-LOS and LOS-Earth transfer are analyzed.

4.1 Algorithm convergence and transfer families

In the iterative process, the eccentricity \(e_{m}\) of the Moon-phase conics is a parameter that should be guessed as an initial value. The initial value of eccentricity \(e_{m}^{0}\) should satisfy

$$ 1 < e_{m}^{0} < \alpha ^{2} + 2\alpha $$
(36)

considering the velocity impulse at perilune is limited as \(\Delta \mathrm{v} _{pl} = v_{p} - \sqrt{\mu _{M} / r_{p}} < \alpha \sqrt{\mu _{M} / r _{p}}\) due to the propellant consumption and the hyperbolic nature. Herein, \(\alpha = 1\).

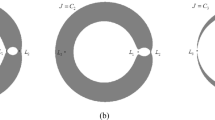
By randomly generating the initial value \(e_{m}^{0}\) that satisfies (36) in the Earth-LOS and LOS-Earth transfer design, the convergence process is shown in Fig. 5(a), and the corresponding transfer trajectories are shown in Fig. 5(b).

Fig. 5
figure 5

The convergence of the iterative Earth-LOS transfer trajectory design algorithm; (a) the initial values of eccentricity converge to two different values in a few iterative loops (2025.01.12 11:00:00 TDT). (b) the corresponding Earth-LOS transfer trajectories

Full size image

It can be seen that the eccentricity converges to two different values in a few loops. The Earth-LOS transfer trajectories shown in Fig. 5(b) corresponding to the two converged values are a prograde and retrograde trajectories, respectively.

Figure 6 shows the iterative process of the LOS-Earth transfer design. It is shown that the algorithm for the LOS-Earth transfer can converge to two different values, which corresponds to two types of LOS-Earth transfer at \(t_{\mathit{se}}\) 2025.01.12 14:00:00 TDT. This is the same as the case in Earth-LOS transfer. It can be concluded that the Earth-LOS and LOS transfer for a fixed time during orbital transfer window have two different types of transfer trajectories, including one prograde trajectory and one retrograde trajectory.

Fig. 6
figure 6

The convergence of the iterative LOS-Earth transfer trajectory design algorithm: (a) the initial values of eccentricity converge to two different values in a few iterative loops (2025.01.12 14:00:00 TDT); (b) the corresponding Earth-LOS transfer trajectories

Full size image

4.2 Orbital transfer window

An orbital transfer window is a time period during which the spacecraft can be transferred to reach its intended target. In the presence of the LOS, spacecraft cannot be transferred between the Earth and the Moon at any time due to the constraint of the LOS orbital plane. Therefore, transfer windows for the Earth-LOS-Earth transfer are analyzed with respect to the LOS orbital inclination and altitude. Herein, Orbital Transfer Window Ratio (OTWR) is defined as the proportion of the total time of orbital transfer windows to the whole year.

  1. (1)

    Earth-LOS transfer

Figure 7 shows the change of the OTWR for the Earth-LOS transfer with the LOS orbital inclination (0 deg ∼ 90 deg) at different orbital altitudes in 2025. It can be seen that the OTWR is associated with the LOS orbital inclination and altitude. When the inclination is 0 deg, the OTWR is the same for different altitude, equal to 41%. The OTWR increases when the inclination is less than 30 deg, and decreases then with the increase of LOS orbital inclination. The OTWR reaches to the maximum when the inclination is near 28.5 deg. When the LOS operates at a polar orbit, the OTWR is only 15%. It is worthy noted that when the LOS operates at LLO with altitude of 3000 km and inclination ranging from 20 deg to 30 deg, spacecraft can be transferred to LOS at any time.

Fig. 7
figure 7

The change of OTWR for the Earth-LOS transfer with LOS orbital inclination at different altitudes in 2025

Full size image

Figure 8 shows the variation of average time of orbital transfer window with the LOS orbital inclination ranging from 0 deg to 90 deg at 200 km altitude. The average time of orbital transfer window reaches the maximum 4.2329 days when the inclination is 20 deg. The number of the orbital transfer window versus inclination is also shown in Fig. 6, and it has at least 26 orbital transfer windows per year.

Fig. 8
figure 8

The average time of the orbital transfer window for the Earth-LOS transfer versus different LOS orbital inclinations at 200 km in 2025

Full size image

Figures 9 and 10 show the change of OTWR and the orbital transfer window statistics for the Earth-LOS transfer in 2034. Overall, the OTWR decreases with the increase of the LOS orbital inclination. The variation tendency is different with respect to the 2025 case due to the different Moon orbit inclination. It can be seen that when the LOS orbital inclination is 10 deg, the OTWR reaches the maximum, namely 50.4%, 48.6%, 57.425% for 200 km, 500 km and 1000 km, respectively. Figure 10 shows that the maximum average time of orbital transfer window occurs when the LOS orbital inclination is 10 deg. The number of orbital transfer window is at least 22 per year.

  1. (2)

    LOS-Earth transfer

Figures 11 and 12 show the change of OTWR for the LOS-Earth transfer trajectories with various LOS orbital inclination and altitude in 2025. The trend is the same as the case of Earth-LOS transfer. It is also noted that the OTWR is larger in the same situation. For example, for the LOS orbit with inclination 28.5 deg and altitude 200 km, the OTWR is 51.6%, which is larger than 28.5% for the Earth-LOS transfer. Figure 12 shows that the average time of orbital transfer window for the LOS-Earth transfer with the inclination 28.5 deg and altitude 200 km, is 7.2412 days, which is the maximum value for different inclinations.

Fig. 9
figure 9

The change of OTWR for the Earth-LOS transfer with LOS orbital inclination at different altitudes in 2034

Full size image
Fig. 10
figure 10

The average time of the orbital transfer window for the Earth-LOS transfer versus different LOS orbital inclinations at 200 km in 2034

Full size image
Fig. 11
figure 11

The change of OTWR for the LOS-Earth transfer with LOS orbital inclination at different altitudes in 2025

Full size image
Fig. 12
figure 12

The average time of the orbital transfer window for the LOS-Earth transfer versus different LOS orbital inclinations at 200 km in 2025

Full size image

The cases that the OTWR and average orbital transfer window change with various inclinations and altitudes in 2034 are shown in Figs. 13 and 14. It is shown that the tendency is also the same as the case of Earth-LOS transfer. The maximum average time of orbital transfer window for the LOS-Earth transfer is 11.293 days, and occurs when the LOS orbital inclination is 10 deg and the altitude is 200 km.

Fig. 13
figure 13

The change of OTWR for the LOS-Earth transfer with LOS orbital inclination at different altitudes in 2034

Full size image
Fig. 14
figure 14

The average time of the orbital transfer window for the LOS-Earth transfer versus different LOS orbital inclinations at 200 km in 2034

Full size image

4.3 Velocity impulse and time of flight

All of the subsequent results in this section are based on the case that LOS is operated on the LLO with altitude of 200 km, inclination of 28.5 deg in 2025 and 18.5 deg in 2034. Figure 15 displays the variation of velocity impulse and the corresponding time of flight for the Earth-LOS transfer as a function of \(t_{s}\) during one orbital launch window in 2025 and 2034. It is shown that the velocity impulse for the Earth-LOS ranges from 3900 m/s to 4800 m/s, and it has a decreasing trend over time. The corresponding time of flight varies from 6.2 days to 1.8 days. It is worth noting that the prograde trajectories need lower velocity impulse than the retrograde trajectories generally.

Fig. 15
figure 15

Variation of velocity impulse and time of flight for the Earth-LOS transfer versus \(t_{s}\) during one orbital transfer window in 2025 (a) and 2034 (b)

Full size image

The magnitudes of trans-earth impulse for the LOS-transfer and the corresponding time of flight versus \(t_{\mathit{se}}\) over an orbital transfer window in 2025 and 2034 are given in Fig. 16. It can be seen that velocity impulse for the LOS-Earth transfer is within 800–1400 m/s, and the corresponding time of flight is between 2 days and 6 days. Contrary to the Earth-LOS transfer, velocity impulse for the LOS-Earth transfer has an increasing trend during one orbital transfer window. Similar to the Earth-LOS transfer, the prograde trajectories also need lower velocity impulse than the retrograde trajectories.

Fig. 16
figure 16

Variation of velocity impulse and time of flight for the LOS-Earth transfer versus \(t_{\mathit{se}}\) during one orbital transfer window in 2025(a) and 2034(b)

Full size image

5 High-fidelity model verification

The accuracy and convergence behavior of the design method for the Earth-LOS and LOS-Earth transfer is verified with high-fidelity model which considers the effect of \(J_{2}\), Earth, Moon, Sun and the atmospheric drag. The dynamics equations of the spacecraft in the J2000 ECI frame can be described as

$$\begin{aligned} &\dot{x} = v_{x} \dot{y} = v_{y} \dot{z} = v_{z} \\ & \begin{aligned}[b] \dot{v}_{x} &= - \frac{\mu _{E}x}{r_{E}^{3}} \biggl[ 1 + \frac{3}{2}J _{2}^{E} \biggl( \frac{a_{E}}{r_{E}} \biggr) ^{2} \biggl( 1 - 5\frac{z ^{2}}{r_{E}^{2}} \biggr) \biggr] \\ &\quad {}- \frac{\mu _{M} ( x - x_{M} ) }{r_{M}^{3}} - \frac{\mu _{S} ( x - x_{S} ) }{r _{S}^{3}} \\ &\quad {}- \frac{\mu _{M}x_{M}}{r_{EM}^{3}} - \frac{\mu _{S}x_{S}}{r_{\mathit{ES}}^{3}} - \frac{1}{2} \biggl( \frac{C_{D}S}{m} \biggr) \rho vv_{x} \end{aligned} \\ & \begin{aligned}[b] \dot{v}_{y} &= - \frac{\mu _{E}y}{r_{E}^{3}} \biggl[ 1 + \frac{3}{2}J _{2}^{E} \biggl( \frac{a_{E}}{r_{E}} \biggr) ^{2} \biggl( 1 - 5\frac{z ^{2}}{r_{E}^{2}} \biggr) \biggr] \\ &\quad {} - \frac{\mu _{M} ( y - y_{M} ) }{r_{M}^{3}} - \frac{\mu _{S} ( y - y_{S} ) }{r _{S}^{3}} \\ &\quad {}- \frac{\mu _{M}y_{M}}{r_{EM}^{3}} - \frac{\mu _{S}y_{S}}{r_{\mathit{ES}}^{3}} - \frac{1}{2} \biggl( \frac{C_{D}S}{m} \biggr) \rho vv_{y} \end{aligned} \\ & \begin{aligned}[b] \dot{v}_{z} &= - \frac{\mu _{E}z}{r_{E}^{3}} \biggl[ 1 + \frac{3}{2}J _{2}^{E} \biggl( \frac{a_{E}}{r_{E}} \biggr) ^{2} \biggl( 3 - 5\frac{z ^{2}}{r_{E}^{2}} \biggr) \biggr] \\ &\quad {}- \frac{\mu _{M} ( z - z_{M} ) }{r_{M}^{3}} - \frac{\mu _{S} ( z - z_{S} ) }{r _{S}^{3}} \\ &\quad {}- \frac{\mu _{M}z_{M}}{r_{EM}^{3}} - \frac{\mu _{S}z_{S}}{r_{\mathit{ES}}^{3}} - \frac{1}{2} \biggl( \frac{C_{D}S}{m} \biggr) \rho vv_{z} \end{aligned} \end{aligned}$$
(37)

where \(( x,y,z,v_{x},v_{y},v_{z} ) \) is the state vector of spacecraft, \(\mu _{S}\) is the Sun gravity constant, \(r_{E},r_{M},r _{S}\) are the distance from spacecraft to the Earth, the Moon, the Sun, respectively, \(r_{EM}\) is the distance from the Earth to the Moon, \(r_{\mathit{ES}}\) is the distance from the Earth to the Sun. \(J_{2}^{E}\) is the gravitational perturbation effect of the Earth. \(\rho \) is the atmospheric density.

The active-set method is used to show the ease of the convergence from the initial estimate (IE) to the feasible solution (FS). The following objective function is used.

$$ f ( x ) = \frac{1}{2}g ( x ) ^{T}g ( x ) $$
(38)

where

$$\begin{aligned} &x_{\mathit{EL}} = \left [ \textstyle\begin{array}{l} \Delta \mathrm{v}_{\mathit{tl}} \\ i_{e} \\ \varOmega _{e} \\ \omega _{e} \end{array}\displaystyle \right ] \end{aligned}$$
(39)
$$\begin{aligned} &x_{\mathit{LE}} = \left [ \textstyle\begin{array}{l} \Delta \mathrm{v}_{\mathit{te}} \\ \omega _{m} \end{array}\displaystyle \right ] \end{aligned}$$
(40)
$$\begin{aligned} &g_{\mathit{EL}} = \left [ \textstyle\begin{array}{l} \frac{i_{m} - i_{m}^{0}}{i_{m}^{0}} \\ \frac{\varOmega _{m} - \varOmega _{m}^{0}}{\varOmega _{m}^{0}} \\ \frac{r_{p} - r_{p}^{0}}{r_{p}^{0}} \end{array}\displaystyle \right ] \end{aligned}$$
(41)
$$\begin{aligned} &g_{\mathit{LE}} = \frac{h_{\mathit{re}} - \hat{h}_{\mathit{re}}}{\hat{h}_{\mathit{re}}} \end{aligned}$$
(42)

are chosen as the optimization variables and constraints for the Earth-LOS (subscript EL) and LOS-Earth (subscript LE) transfer trajectories, respectively.

Simulations for the Earth-LOS and LOS-Earth transfer in the high-fidelity model are presented in Tables 1 and 2. Herein, \(C_{D} = 1.2891, ( S / m ) _{\mathit{EL}} = 2.9 \times 10^{ - 4}, ( S / m ) _{\mathit{LE}} = 2 \times 10^{ - 3}\), similar to the Apollo mission (Graves and Harpold 1972). It can be seen that the differences for the Earth-LOS profile are very small because of the small convergence tolerance between the patched conic model and high-fidelity model. Relatively larger differences exist in the LOS-Earth transfer trajectory verification, because less optimization variables are used to correct the initial estimates.

Table 1 High-fidelity verification for the Earth-LOS transfer
Full size table
Table 2 High-fidelity verification for the LOS-Earth transfer
Full size table

Earth-LOS and LOS-Earth transfer trajectories in the high-fidelity model are shown in Fig. 17 and Fig. 18, respectively, of which the departure time are 2025.01.07 12:40:01.5156 TDT and 2025.01.25 17:09:07.0558 TDT. The inclination and altitude of the LOS in Fig. 17 and Fig. 18 are 90 deg and 200 km, respectively.

Fig. 17
figure 17

Earth-Moon transfer trajectory to the LOS of which the inclination and altitude are 90 deg and 200 km

Full size image
Fig. 18
figure 18

Moon-Earth transfer trajectory from the LOS of which the inclination and altitude are 90 deg and 200 km

Full size image

6 Conclusion

In this paper, a novel and concise iterative algorithm is proposed for the design of transfer trajectories between the Earth and the LOS. The convergence of the proposed algorithm is presented, showing that it can converge in a few loops. Two transfer families are found for the Earth-LOS and LOS-Earth transfer, which correspond to the prograde and retrograde trajectories, respectively. The characteristics of orbital transfer window are analyzed in the typical years 2025 and 2034. The results show that orbital transfer window is associated with the LOS orbital inclination and altitude. In 2025, the maximum OTWR occurs when the inclination is near 28.5 deg. In 2034, the OTWR reaches the maximum when the inclination is 10 deg. This is true for both Earth-LOS and LOS transfer. Velocity impulse and time of flight are also investigated for transfer trajectories between the Earth and the LOS. High-fidelity verification is adopted to eliminate the differences between the initial estimate and a feasible solution based on active-set method, in a high-fidelity model.

The results show that manned lunar exploration based on the LOS will be an important technical approach in the future.