Power-limited low-thrust trajectory optimization with operation point detection

Abstract

The power-limited solar electric propulsion system is considered more practical in mission design. An accurate mathematical model of the propulsion system, based on experimental data of the power generation system, is used in this paper. An indirect method is used to deal with the time-optimal and fuel-optimal control problems, in which the solar electric propulsion system is described using a finite number of operation points, which are characterized by different pairs of thruster input power. In order to guarantee the integral accuracy for the discrete power-limited problem, a power operation detection technique is embedded in the fourth-order Runge-Kutta algorithm with fixed step. Moreover, the logarithmic homotopy method and normalization technique are employed to overcome the difficulties caused by using indirect methods. Three numerical simulations with actual propulsion systems are given to substantiate the feasibility and efficiency of the proposed method.

1 Introduction

The success of the first interplanetary mission propelled by solar electric propulsion (SEP) in Deep Space 1 indicates that SEP as an ion propulsion system (IPS) is very promising for interplanetary missions (Rayman and Williams 2002). This first SEP system is based on the NASA solar electric propulsion technology application readiness (NSTAR) system (Woo et al. 2006). The NSTAR thruster system is also chosen for NASA’s Dawn mission, which proves the advantages of SEP in the interplanetary flight (Dankanich 2010). The more effective IPS based on NASA’s evolutionary xenon thruster (NEXT) (Soulas et al. 2003) is now planned for future space exploration missions. Since IPS is able to produce a higher specific impulse and has lower fuel consumption compared to the chemical propulsion, it can be used in a wide range of applications. Simplified models for the SEP system and its operation have been utilized for previous mission analyses; however, some practical operational details of SEP need to be considered to create an accurate mass budget for a mission design (Gao and Kluever 2005), of which one of the most important details is power constraint: the operating power is generated by the solar arrays, so the available power to the thrusters depends on the distance to the Sun (Bhaskaran et al. 2000). From a theoretical viewpoint, the maximum achievable thrust produced by the limited power can be continuous. Thus far, there are a few studies about low-thrust trajectory optimization concentrated on the continuously variable maximum thrust (Chen et al. 2012; Mengali and Quarta 2005; Senent et al. 2005; Zhang et al. 2014). On this occasion, before the available power achieves the rated input power of the thrusters, the generated thrust is approximately inversely proportional to the square of the distance to the Sun. Once the available power exceeds the rated power, the thrust is full during the flight trajectory. On the other hand, when the power becomes insufficient, the engine is shut down. In the reality, the thrust discretely varies with the limited power. Thus, the discrete power-limited model is closer to actual engineering missions. For Deep Space 1, the IPS based on NSTAR has about 100 throttle levels, with a thrust range of 20 to 90 mN (Bhaskaran et al. 2000). Quarta and Mengali (2011) applied the actual NEXT system to investigate the minimum-time rendezvous problem. This system has 40 available operation points and each point is characterized by a corresponding set of values of thrust, propellant mass flow rate, and power processing unit (PPU) input power. Quarta et al. (2013) employed the actual NEXT model which was discussed in Quarta and Mengali (2011) to find the minimum time optimal direct transfer scenarios for a mission to the circumsolar space. Therefore, regarding to the studies mentioned above, considering the actual power-limited model is vital for accurate low-thrust trajectory design.

Generally, low-thrust trajectory optimization aims to solve two types of problems: time-optimal and fuel-optimal problems. The methods for optimizing low-thrust trajectories are classified into two categories: direct methods and indirect methods. The solutions of indirect methods not only have high accuracy, but are also guaranteed to satisfy the first-order optimality conditions, which are the primary advantages of the indirect methods (Zhang et al. 2014). Moreover, the low dimensionality of the search space of indirect methods enables the random search of initial guesses of the unknowns (Oshima et al. 2017; Russell 2007). In the published papers for power-limited problems, indirect methods which are based on the Pontryagin’s maximum principle, have been widely used (Chen et al. 2012; Chi et al. 2017; Landau et al. 2011; Mengali and Quarta 2005; Woo et al. 2005; Zhang et al. 2014). However, there are two problems with the convergence of indirect methods: (1) the sensitivity of initial guesses of the unknowns and discontinuous bang-bang control for the fuel-optimal problem (2) difficulty for seeking the non-intuitive initial adjoint variables. To overcome the difficulties in convergence caused by bang-bang control, the homotopy method with different homotopy functions has been proposed to find the optimal solutions (Bertrand and Epenoy 2002). Many studies in indirect methods with these techniques have successfully solved the low-thrust trajectory optimization problems. Jiang et al. (2012) applied the homotopy method and proposed the normalization to the initial costates, which can be made to benefit initial guesses. Zhang et al. (2014) developed the homotopy method (Jiang et al. 2012) for the variable-power problems. Yang and Baoyin (2015) investigated the trajectory problems with irregular gravity and also developed the method of Jiang et al. (2012). Chi et al. (2017) proposed a modified homotopy method for variable-specific-impulse trajectory optimization problem. Li et al. (2017) developed the logarithmic homotopy method in solving low-thrust transfer trajectories for multidebris removal missions considering J2 perturbation. The methods for seeking the initial values of adjoint variables include random guess and analytic evaluation. The adjoint variables in the literature mentioned above using indirect methods are almost estimated by the use of random initial guessing. Among analytic evaluation methods, Jiang et al. (2017) applied the linearization of motion equation and solved the simplified optimal control problems around shape-based path to develop the adjoint estimation method.

However, a critical problem has not been addressed in the discretely power-limited low-thrust trajectory optimization problems. As the thrust produced by the limited power varies discretely and has finite operation points, it is hard to guarantee the integration accuracy due to the discontinuous right-hand sides of ordinary equation. To the best of the authors’ knowledge, little research has been conducted about the application of the power detection technique to the power-limited trajectory when the thrust varies discretely. The similar situation is that as the right hand sides of the dynamical equations and Euler-Lagrange equations contain control variables, it is hard to guarantee the integration accuracy for bang-bang control. Jiang et al. (2012) embedded the switching detection (Martinon and Gergaud 2007) in the fourth-order Runge-Kutta algorithm with fixed step size (RK4) to overcome this problem. Other contributions employing this switching detection technique can be found by Zhang et al. (2013, 2014, 2015), Yang and Baoyin (2015). In this paper, a power operation detection technique is proposed to detect the power switching points referring to the ideas of the mentioned switching detection technique. Although among previous studies, Zhang et al. (2014) proposed a method aimed to detect the available input power during the integration to determine the thrust magnitude at each time step. This power detection technique is only used to solve the transfer trajectories for the continuously variable thrust problems. Moreover, on this occasion, only one switching point, i.e., the rated power, was considered. In addition, our proposed power operation detection technique can be applied to the trajectory optimization problems with more than one thrusters.

In this paper, the time and fuel optimizations of SEP-based interplanetary trajectories are considered with practical discrete power constraints. The power operation detection technique is applied to overcome the difficulties caused by the application of the practical discrete power-limited model. With this method, the integration accuracy and the convergence efficiency are both improved. Moreover, the logarithmic homotopy function (Bertrand and Epenoy 2002) and the technique of normalization (Jiang et al. 2012) are employed for the convergence to the optimal solution and the robustness of guessing the initial costates. The experimental data of NSTAR thrusters and the Chinese in-development engine are used to find the optimal transfer trajectories with high precision. Finally, an efficient low-thrust power-limited trajectory optimization method combined with the power operation detection technique is formulated.

The rest of the paper is organized as follows. Section 2 presents the practical solar electric discrete power-limited model. Additionally, in this section, the time-optimal and fuel-optimal control problems are formulated for the low-thrust discrete power-limited problem. And the power operation detection technique is proposed to accurately solve the power-limited problem with finite operation points. In Sect. 3, simulations are carried out to validate the method proposed in Sect. 2. Finally, Sect. 4 concludes the paper.

2 Problem formulation

2.1 Mathematical model

When only considering the solar gravitational force exerted on the spacecraft, the dynamical equations of the low-thrust propelled spacecraft in the heliocentric ecliptic reference frame are (Yang et al. 2015)

$$\begin{aligned} &{\dot{\boldsymbol{r}} = \dot{\boldsymbol{v}}} \end{aligned}$$

(1)

$$\begin{aligned} &{\dot{\boldsymbol{v}} = - \frac{\mu}{r^{3}}\boldsymbol{r} + \frac{T_{\max} u}{m} \boldsymbol{\alpha} } \end{aligned}$$

(2)

$$\begin{aligned} &{\dot{m} = - \frac{T_{\max} u}{I_{\mathrm{sp}}g_{0}} } \end{aligned}$$

(3)

where $\boldsymbol{r}$ and $\boldsymbol{v}$ are the position and velocity vectors, respectively, $m$ denotes the instantaneous mass of the spacecraft, $\mu$ is the solar gravitational constant, which equals to $1.32712440018\times10^{11}~\mbox{km}^{3}/\mbox{s}^{2}$, $u$ ($0 \leq u \leq 1$) denotes the engine thrust ratio and $\boldsymbol{\alpha}$ is the unit vector of the thrust direction, $g _{0} = 9.80665~\mbox{m}/\mbox{s}^{2}$ is the standard value of gravitational acceleration, $T_{\mathrm{max}}$ represents the maximum achievable thrust magnitude, and $I_{\mathrm{sp}}$ is the thruster specific impulse.

A practical SEP system has a finite number of operation points, each one being characterized by a corresponding set of values of thrust, specific impulse and ranges of thruster input power. Assuming that the number of operation points is $N$, consequently, the values of $T_{\mathrm{max}}$ and $I_{\mathrm{sp}}$ in discrete power-limited model are as follows.

$$\textstyle\begin{array}{l@{\ \ }l@{\quad}l} T_{\max} = T_{1},& I_{\mathrm{sp}} = I_{\mathrm{sp},1},& \mbox{when }P_{A} \in [ P_{1},\infty ) \\ \cdots \\ T_{\max} = T_{N - 1},& I_{\mathrm{sp}} = I_{\mathrm{sp}, N - 1},& \mbox{when }P_{A} \in [ P_{N - 2}, P_{N - 1} ) \\ T_{\max} = T_{N},& I_{\mathrm{sp}} = I_{\mathrm{sp}, N},& \mbox{when }P_{A} \in [ P_{N - 1}, P_{N} ) \\ T_{\max} = 0,& I_{\mathrm{sp}} = 0,& \mbox{when }P_{A} \in ( 0,P_{\min} ) \end{array} $$

where $T _{1}, \dots, T_{N-1}, T _{N}$ denote maximum achievable thrust produced by the propulsion system. $I_{\mathrm{sp}, 1}, \dots, I_{\mathrm{sp},N-1}, I_{\mathrm{sp}, N}$ represent the thruster specific impulse by each operation points. $P _{A}$ denotes the available input power to the thrusters. $[P _{0}, P _{1}), \dots, [P_{N-2},P_{N-1}), [P_{N-1}, P_{N})$ are the corresponding ranges of the input power. The operation points are referred to through the value of $P _{0},\dots, P_{N-1}{,} P_{N}$. $P_{\mathrm{min}}$ represents the admissible minimum input power to the thrusters. When the thruster input power is less than $P_{\mathrm{min}}$, the engine is shut down and no longer produces thrust.

The behavior of the SEP system and the way to determine the thruster input power $P_{A}$ are as follows. The solar array power $P _{S}$ is a function of the Sun-spacecraft distance. The evaluation of the available input power to the thrusters $P_{A}$ requires the use of a suitable mathematical model for $P _{S}$ (Quarta and Mengali 2011). In this paper, the more realistic model (Chen et al. 2012) is used for the preliminary analysis of the interplanetary trajectory.

The expression of the solar radiation flux $I$ is

$$ I = I_{ \odot} \biggl( \frac{1}{r} \biggr)^{2} $$

(4)

where the solar constant $I _{\odot}$ is solar radiation energy per unit area at 1 AU. The value of $I_{\odot}$ is $1367~\mbox{W}/\mbox{m}^{2}$. $r$ represents the Sun-spacecraft distance. The solar array power $P_{S}$ can be expressed by

$$ P_{S} = IS\gamma $$

(5)

where $S$ and $\gamma$ denote the area and the efficiency of the solar array.

The available input power is defined as the difference of the solar array output power and the power allocated to operate the spacecraft systems $P_{L}$ (Quarta et al. 2013; Quarta and Mengali 2011). In this paper, $P _{L}$ is assumed to be constant during the whole mission, and represents the power used by all of the on board systems except for the propulsion system. As the available power is a nonnegative quantity, it may be written as (Quarta and Mengali 2011)

$$ P_{A} = \left \{\textstyle\begin{array}{l@{\quad}l} P_{S} - P_{L},& \mbox{if }P_{S} > P_{L} \\ 0,& \mbox{if }P_{S} \le P_{L} \end{array}\displaystyle \right . $$

(6)

Equation (6) indicates that when $P _{S}$ is less than $P _{L}$, the propulsion system is not operational and the spacecraft trajectory follows a Keplerian motion.

The initial mass, initial states, and final states are all fixed. Regarding rendezvous problems, the state variables of the spacecraft satisfy the following boundary conditions (Quarta and Mengali 2011):

$$\begin{aligned} &{\boldsymbol{r}( t_{0}) = \boldsymbol{r}_{0},\qquad \boldsymbol{v}( t_{0}) = \boldsymbol{v}_{0},\qquad m( t_{0}) = 1} \end{aligned}$$

(7)

$$\begin{aligned} &{\boldsymbol{r}( t_{f}) = \boldsymbol{r}_{f},\qquad \boldsymbol{v}( t_{f}) = \boldsymbol{v}_{f}} \end{aligned}$$

(8)

where the values of these parameters should be transformed into those consistent with the non-dimensionalized units.

2.2 Time-optimal control problem

In order to minimize the transfer time, the performance index is formulated as follows

$$ J = \lambda_{0} \int_{t_{0}}^{t_{f}} 1 dt $$

(9)

where $t _{0}$ and $t _{f}$ denote the initial and final times, respectively. $\lambda _{0}$ is a positive parameter which is necessary for the normalization of the costate variables (Jiang et al. 2012). Introducing the costate vector $\boldsymbol{\lambda} \equiv [ \boldsymbol{\lambda}_{\boldsymbol{r}}; \boldsymbol{\lambda} _{\boldsymbol{v}}; \lambda _{m}]$ to the optimal control problem, the Hamiltonian is built as (Zhang et al. 2015)

$$ H = \boldsymbol{\lambda}_{\boldsymbol{r}} \cdot \boldsymbol{v} + \boldsymbol{\lambda}_{\boldsymbol{v}} \cdot \biggl( - \frac{\mu}{r^{3}}\boldsymbol{r} + T_{\max} \frac{u}{m}\boldsymbol{\alpha} \biggr) - \lambda_{m}\frac{T_{\max}}{ I_{\mathrm{sp}}g_{0}}u + \lambda_{0} $$

(10)

where $\boldsymbol{\lambda} _{\boldsymbol{r}}$, $\boldsymbol{\lambda}_{\boldsymbol{v}}$ and $\lambda _{m}$ are vectors adjoint to the position, the velocity and the final mass, respectively. According to Pontryagin’s maximum principle, the direction of the optimal thrust, which minimizes the Hamiltonian, is opposite to the primer vector $\boldsymbol{\lambda} _{\boldsymbol{v}}$, i.e.

$$ \hat{\boldsymbol{\alpha}} = - \frac{\boldsymbol{\lambda}_{\boldsymbol{v}}}{ \Vert \boldsymbol{\lambda}_{\boldsymbol{v}} \Vert } $$

(11)

where the $\Vert \boldsymbol{\lambda}_{\boldsymbol{v}} \Vert$ denotes the 2-norm of $\boldsymbol{\lambda}_{\boldsymbol{v}}$. And the optimal thrust magnitude is determined as

$$ \left \{ \textstyle\begin{array}{l@{\quad}l} \hat{u} = 0,& \mbox{if } \rho > 0 \\ \hat{u} = 1,& \mbox{if } \rho < 0 \\ \hat{u} \in [0,1],& \mbox{if } \rho = 0 \end{array}\displaystyle \right . $$

(12)

where the expression of the so-called switching function $\rho$ is

$$ \rho = - \frac{I_{\mathrm{sp}}g_{0} \Vert \boldsymbol{\lambda}_{v} \Vert }{m} - \lambda_{m} $$

(13)

The equations for the costate variables are called Euler-Lagrange equations (Jiang et al. 2012; Yang et al. 2017). The form of the Euler-Lagrange equations is formulated as

$$\begin{aligned} &{\dot{\boldsymbol{\lambda}}_{\boldsymbol{r}} = - \frac{\partial H}{\partial \boldsymbol{r}} = \frac{\mu}{r^{3}}\boldsymbol{\lambda}_{\boldsymbol{v}} - \frac{3\mu \boldsymbol{r} \cdot \boldsymbol{\lambda}_{\boldsymbol{v}}}{r^{5}} \boldsymbol{r}} \end{aligned}$$

(14)

$$\begin{aligned} &{\dot{\boldsymbol{\lambda}}_{\boldsymbol{v}} = - \frac{\partial H}{\partial \boldsymbol{v}} = - \boldsymbol{\lambda}_{\boldsymbol{r}}} \end{aligned}$$

(15)

$$\begin{aligned} &{\dot{\lambda}_{m} = - \frac{\partial H}{\partial m} = - T_{\max} \frac{u}{m^{2}} \Vert \boldsymbol{\lambda}_{\boldsymbol{v}} \Vert } \end{aligned}$$

(16)

Generally, there is no constraints on the final mass of the spacecraft, i.e. the final mass is free. According to the transversality condition, the mass costate at the final time is zero, i.e.

$$ \lambda_{m}(t_{f}) = 0 $$

(17)

Moreover, the normalization condition (Jiang et al. 2012) is added

$$ \bigl\Vert \boldsymbol{\lambda} ( t_{0} ) \bigr\Vert =1 $$

(18)

where $\boldsymbol{\lambda} (t _{0}) = [ \boldsymbol{\lambda} _{\boldsymbol{r}} (t _{0}), \boldsymbol{\lambda} _{\boldsymbol{v}} (t _{0}), \lambda _{m}(t _{0}), \lambda _{0}]$ is the expanded costate vector. Through this normalization, the solution variables including eight initial costate values are restricted on a unit 8-D hypersphere (Jiang et al. 2012). In addition, Eq. (16) indicates that the derivative of $\lambda _{m}$ with respect to the time is always non-positive. Combining Eqs. (16) and (17), we obtain that $\lambda _{m} (t _{0}) \geq 0$. Therefore, the value of the switching function $\rho$ in Eq. (13) is non-positive and the control variable $u$ takes 1 all the time for the time-optimal problems.

The stationary condition corresponding to the final time is also necessary to be considered for the time-optimal problem

$$ H ( t_{f} ) + \frac{\lambda_{0}\partial \phi}{\partial t_{f}} + \frac{\boldsymbol{\chi} \cdot \partial \boldsymbol{\psi}}{\partial t_{f}} + \frac{\boldsymbol{\kappa} \cdot \partial \boldsymbol{\sigma}}{\partial t_{f}} = 0 $$

(19)

where $\phi$ is the non-integral item of the performance index. $\boldsymbol{\psi}$ is the equality constraint with $p$ components and $\boldsymbol{\sigma}$ is the inequality constraints with $q$ components. $\boldsymbol{\chi}$ and $\boldsymbol{\kappa}$ denote $p$-dimensional and $q$-dimensional numerical multipliers, respectively. In solving this time-optimal problem, $\phi$ and $\boldsymbol{\sigma}$ are non-existent. And $\boldsymbol{\psi}$ contains two boundary equations

$$ \boldsymbol{\psi} = \left[\textstyle\begin{array}{c} \boldsymbol{r}( t_{f}) - \boldsymbol{r}_{f} = \mathbf{0} \\ \boldsymbol{v}( t_{f}) - \boldsymbol{v}_{f} = \mathbf{0} \end{array}\displaystyle \right] $$

(20)

The transversality condition at the final time combined with the above conditions is

$$ - \boldsymbol{\lambda} ( t_{f} ) + \frac{\boldsymbol{\chi} \cdot \partial \boldsymbol{\psi}}{\partial \boldsymbol{x}(t_{f})} = \mathbf{0} $$

(21)

The numerical multiplier $\boldsymbol{\chi}$ is obtained by combining Eqs. (20) and (21)

$$ \boldsymbol{\chi} = \boldsymbol{\lambda} ( t_{f} ) $$

(22)

Substituting Eqs. (20) and (22) into Eq. (19) yields

$$ H ( t_{f} ) - \boldsymbol{\lambda} ( t_{f} ) \cdot \left[ \textstyle\begin{array}{c} \boldsymbol{v}_{f} \\ \boldsymbol{a}_{f} \end{array}\displaystyle \right] = 0 $$

(23)

Consequently, the shooting equation for the equivalent two-point boundary value problem (TPBVP) is extended with nine components

$$\begin{aligned} \boldsymbol{\varPhi} &= \bigl[ \boldsymbol{r}(t_{f}) - \boldsymbol{r}_{f}, \boldsymbol{v}(t_{f}) - \boldsymbol{v}_{f}, \lambda_{m}(t_{f}), \bigl\Vert \boldsymbol{\lambda} (t_{0}) \bigr\Vert - 1, \\ &\quad\ H ( t_{f} ) - \boldsymbol{\lambda}_{r} ( t_{f} ) \cdot \boldsymbol{v}_{f} - \boldsymbol{\lambda}_{v} ( t_{f} ) \cdot \boldsymbol{a}_{f} \bigr]^{T} = \mathbf{0} \end{aligned}$$

(24)

The time-optimal control problem requires the full thrust during all the flight time. So it is relatively easy to solve this problem due to the continuity and differentiability of the right hand sides of the dynamical equations and Euler-Lagrange equations. The more complicated fuel-optimal control problem will be discussed in the next section.

2.3 Fuel-optimal control problem

The expression of the performance index aiming to maximize the final mass and minimize the fuel consumption is as follows

$$ J = \frac{\lambda_{0}T_{\max}}{I_{\mathrm{sp}}g_{0}} \int_{t_{0}}^{t_{f}} u dt $$

(25)

The optimal control problem can be transformed into a TPBVP by the use of Pontryagin’s maximum principle (PMP). So the Hamiltonian is formulated as

$$\begin{aligned} H &= \boldsymbol{\lambda}_{\boldsymbol{r}} \cdot \boldsymbol{v} + \boldsymbol{\lambda}_{\boldsymbol{v}} \cdot \biggl( - \frac{\mu}{r^{3}}\boldsymbol{r} + T_{\max} \frac{u}{m}\boldsymbol{\alpha} \biggr) - \lambda_{m}\frac{T_{\max}}{ I_{\mathrm{sp}}g_{0}}u \\ &\quad{}+ \lambda_{0} \frac{T_{\max}}{ I_{\mathrm{sp}}g_{0}}u \end{aligned}$$

(26)

Then, the optimal thrust direction and magnitude, which minimize the Hamiltonian, take the same forms as Eqs. (11) and (12). But the switching function $\rho$ for the fuel-optimal control problem holds the new form

$$ \rho = 1 - \frac{I_{\mathrm{sp}}g_{0} \Vert \boldsymbol{\lambda}_{v}\Vert }{m} - \lambda_{m} $$

(27)

The sign of the switching function determines the magnitude of thrust. Therefore, the thruster either burns with the full thrust magnitude or it is turned off, which is typical bang-bang control (Zhang et al. 2014). This leads to discontinuities in the shooting function. To avoid direct solving of the bang-bang control problem, a homotopic approach (Bertrand and Epenoy 2002) is employed. The logarithmic homotopy index is given as follows (Li et al. 2017)

$$ J = \lambda_{0}\frac{T_{\max}}{I_{\mathrm{sp}}g_{0}} \int_{t_{0}}^{t_{f}} \bigl\{ u - \varepsilon \ln \bigl[ u ( 1 - u ) \bigr] \bigr\} dt $$

(28)

where the homotopy parameter $\varepsilon$ varies from 1 to 0. With this modified performance index, the Hamiltonian becomes

$$\begin{aligned} H &= \boldsymbol{\lambda}_{\boldsymbol{r}} \cdot \boldsymbol{v} + \boldsymbol{\lambda}_{\boldsymbol{v}} \cdot \biggl( - \frac{\mu}{r^{3}}\boldsymbol{r} + T_{\max} \frac{u}{m}\boldsymbol{\alpha} \biggr) - \lambda_{m}\frac{T_{\max}}{ I_{\mathrm{sp}}g_{0}}u \\ &\quad{}+ \lambda_{0}\frac{T_{\max}}{ I_{\mathrm{sp}}g_{0}} \bigl\{ u - \varepsilon \ln \bigl[ u ( 1 - u ) \bigr] \bigr\} \end{aligned}$$

(29)

The Euler-Lagrange equations under this logarithmic homotopy index are kept the same as before (Eqs. (14)–(16)). The optimal thrust direction is still calculated by Eq. (11). Moreover, the optimal thrust magnitude becomes

$$ \hat{u} = \frac{2\varepsilon}{\rho + 2\varepsilon + \sqrt{\rho^{2} + 4\varepsilon^{2}}} $$

(30)

where the form of the switching function $\rho$ is modified

$$ \rho = 1 - \frac{I_{\mathrm{sp}}g_{0} \Vert \boldsymbol{\lambda}_{v} \Vert }{\lambda_{0}m} - \frac{\lambda_{m}}{\lambda_{0}} $$

(31)

By using logarithmic homotopy function the equations that contain optimal control variables are always continuous and differentiable. Once the solution for the energy-optimal control ($\varepsilon =1$) is obtained, the parameter $\varepsilon$ gradually decreases from 1 to 0 step by step. The optimal solutions obtained at the present step are substituted to the next solving step as the initial values. The fuel-optimal solution is obtained at the final step when $\varepsilon =0$.

Consequently, the optimal control problem yields a TPBVP consisting of eight components (Jiang et al. 2012)

$$ \boldsymbol{\varPhi} = \bigl[ \boldsymbol{r}(t_{f}) - \boldsymbol{r}_{f}, \boldsymbol{v}(t_{f}) - \boldsymbol{v}_{f}, \lambda_{m}(t_{f}), \bigl\Vert \boldsymbol{\lambda} (t_{0}) \bigr\Vert - 1 \bigr]^{T} = \mathbf{0} $$

(32)

Note that the condition $\lambda _{0} > 0$ should also be considered. The conclusion that $\lambda _{m} (t _{0}) \geq 0$ from transversality condition (17) and Euler-Lagrange equation (16) is still established.

2.4 Power operation detection technique

The right hand items of Eqs. (1)–(3) and the Euler-Lagrange equations include $T_{\mathrm{max}}$, and these elements vary rapidly around discrete operation points. In addition, as the number of operation points increases, it is more difficult to guarantee integration accuracy and convergence efficiency. Runge-Kutta methods with adaptive step size but without special handling are not able to solve this problem. Therefore, here we use fourth order Runge-Kutta algorithm (RK4) with fixed step size (Jiang et al. 2012) combined with power operation detection to overcome this problem. For an initial value problem (Jiang et al. 2012)

$$ \dot{\boldsymbol{x}} = f ( t, \boldsymbol{x} ),\quad t_{0} \le t \le t_{f},\quad \boldsymbol{x} ( t_{0} ) = \boldsymbol{x}_{0} $$

(33)

the RK4 iteration algorithm with fixed step $h$ is formulated as follows

$$ \begin{aligned} {}&\boldsymbol{x}_{k + 1} = \boldsymbol{x}_{k} + \frac{h}{6} (\boldsymbol{k}_{1} + 2\boldsymbol{k}_{2} + 3\boldsymbol{k}_{3} + \boldsymbol{k}_{4} ) \\ &\boldsymbol{k}_{1} = \boldsymbol{f} ( t_{k},\boldsymbol{x}_{k} )\qquad \boldsymbol{k}_{2} = \boldsymbol{f} ( t_{k} + h/2,x_{k} +h/2\boldsymbol{k}_{1} ) \\ &\boldsymbol{k}_{3} = \boldsymbol{f} ( t_{k} + h/2,x_{k} +h/2\boldsymbol{k}_{2} ) \\ &\boldsymbol{k}_{4} = \boldsymbol{f} ( t_{k} + h,x_{k} + h\boldsymbol{k}_{3} ) \end{aligned} $$

(34)

The one step iteration result $\boldsymbol{x}_{k+1}$ upon vector function $\boldsymbol{f}(t,\boldsymbol{x})$ is denoted by

$$ \boldsymbol{x}_{k + 1} = \mathrm{RK}4 ( \boldsymbol{f}, t_{k}, \boldsymbol{x}_{k}, h ) $$

(35)

where $t_{k}$ and $\boldsymbol{x}_{k}$ are initial integration time and state. The state vector $\boldsymbol{x} = [\boldsymbol{r};\boldsymbol{v}; m; \boldsymbol{\lambda} _{\boldsymbol{r}}; \boldsymbol{\lambda} _{\boldsymbol{v}};\lambda _{m}]$ includes 14 components. And the vector function $\boldsymbol{f}(t, \boldsymbol{x})$ is the combination of the right-hand sides of the dynamic Eqs. (1)–(3) and the Euler-Lagrange Eqs. (14)–(16).

For the discrete power-limited problems, the switching points refer to the operation points characterized by the thruster input power. If the integration time step $h$ is small enough, the value of the available input power at $k+1$ step $P_{A,k+1}$ can be examined by the value at $k$-th step $P_{A,k}$ using the Taylor expansion:

$$ P_{A, k + 1} = P_{A, k} + \dot{P}_{A, k}h + \frac{1}{2}\ddot{P}_{A, k}h^{2} $$

(36)

Substituting Eqs. (4) and (5) into Eq. (6), the available input power at $k$ step can be expressed by

$$ P_{A, k} = Ar^{ - 2} - P_{L} $$

(37)

where $A$ is the product of $I _{\odot}$, $S$ and $\gamma$.

The first and second derivatives of $P _{A}$ respect to time are determined as

$$\begin{aligned} &{\dot{P}_{A, k} = - 2 \cdot A \cdot r^{ - 3} \cdot \dot{r}} \end{aligned}$$

(38)

$$\begin{aligned} &{\ddot{P}_{A, k} = - 2 \cdot A \cdot \bigl( - 3 \cdot r^{ - 4} \cdot \dot{r} + r^{ - 3} \cdot \ddot{r} \bigr)} \end{aligned}$$

(39)

where $r$ denotes the Sun-spacecraft distance and it can be expressed through three coordinates in the heliocentric ecliptic reference frame: $r = (x ^{2}+y ^{2}+z ^{2})^{1/2}$. The first and second derivatives of $r$ are written as

$$\begin{aligned} &{\dot{r} = \frac{1}{2} \bigl( x^{2} + y^{2} + z^{2} \bigr)^{ - \frac{1}{2}} \cdot ( 2x \cdot \dot{x} + 2y \cdot \dot{y} + 2z \cdot \dot{z} )} \end{aligned}$$

(40)

$$\begin{aligned} &{\ddot{r} = - \bigl( x^{2} + y^{2} + z^{2} \bigr)^{ - \frac{3}{2}} \cdot ( x \cdot \dot{x} + y \cdot \dot{y} + z \cdot \dot{z} )^{2}} \\ &{\phantom{\ddot{r} =}{} + \bigl( x^{2} + y^{2} + z^{2} \bigr)^{ - \frac{1}{2}}} \\ &{\phantom{\ddot{r} =}{}\cdot \bigl( \dot{x}^{2} + \dot{y}^{2} + \dot{z}^{2} + x \cdot \ddot{x} + y \cdot \ddot{y} + z \cdot \ddot{z} \bigr)} \end{aligned}$$

(41)

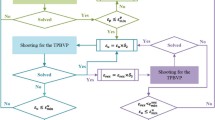
Since the difference of the available input powers at $k$-step and at ($k+1$)-th steps is quite slight, the input power can only be changed in the neighbor two ranges. The arbitrary two neighbor intervals can be denoted as: $[P_{i-1}, P _{i})$ and $[P_{i}, P_{i+1})$ (here $P_{i-1}< P _{i}< P_{i+1}$), so there are three cases with respect to $P_{A,k}$ and $P_{A,k+1}$.

• (1) $P_{A, k}\in[P _{i}, P_{i+1})$, $P_{A,k+1} \in[P_{i-1}, P _{i})$

This means that, the solar distance increases as the spacecraft flies away from the Sun. Meanwhile, the input power is reduced with the distance (decreasing as $1/r^{2}$). Thus, the iteration should be accomplished through two substeps: $x _{m}=\mbox{RK}4(@f(T_{\mathrm{max}, i+1}),t_{k},x_{k},h _{i})$ and then $x_{k+1}=\mbox{RK}4(@f(T_{\mathrm{max}, i}),t_{k}+h_{i},x _{m},h - h _{i})$. $T_{\mathrm{max},i}$ and $T_{\mathrm{max}, i+1}$ are the maximum achievable thrust corresponding to the two power ranges. $h _{i}$ denotes the first substep size, which is obtained by solving the equation $P_{A,k} +\dot{P}_{A, k} h+1/2\ddot{P}_{A, k} h ^{2}= P _{i}$. The result is presented as follows

$$ h_{i} = \frac{2 ( P_{A, k} - P_{i} )}{ - \dot{P}_{A, k} + \sqrt{\dot{P}_{A, k}^{2} - 2\ddot{P}_{A, k} (P_{A, k} - P_{i})}} $$

(42)

• (2) $P_{A,k}\in[P_{i-1},P _{i})$, $P_{A,k+1}\in[P_{i},P_{i+1})$

The process in this case is changed in contrast to the previous case. The input power tends to increase with time because the spacecraft trajectory tends to approach the Sun. So the two-substep iterations are accomplished by the first $x _{m}=\mbox{RK}4(@f(T_{\mathrm{max},i}),t _{k},x _{k},h_{i})$ and then $x_{k+1}=\mbox{RK}4(@f(T_{\mathrm{max},i+1}), t _{k} + h _{i}, x_{m}, h - h _{i})$. The substep size $h _{i}$ is also obtained through

$$ h_{i} = \frac{2 ( P_{A, k} - P_{i} )}{ - \dot{P}_{A, k} - \sqrt{\dot{P}_{A, k}^{2} - 2\ddot{P}_{A, k} ( P_{A, k} - P_{i} )}} $$

(43)

• (3) $P_{A,k}, P_{A,k+1}\in[P_{i-1},P_{i})$ or $P_{A,k},P_{A,k+1}\in[P _{i},P_{i+1})$

In this case, the input power is always moderate and the process is continuous. Thus, the iteration is given by $x_{k+1}=\mbox{RK}4(@f,t _{k},x _{k},h)$.

As the number of the operation points increases, so do the power operation ranges needed to be detected. In order to ensure the accuracy of solution, arbitrary two neighbor power ranges are needed to be taken into account. If the number of the operation points is $N$, there exist $3N$ types of corresponding detected cases. The fixed step integrator RK4 is suitable for this multi-power detection problem as it is easy to embed this detection in it.

3 Numerical examples and results

Three examples of time-optimal and fuel-optimal problems with one or more practical engines are given to substantiate the techniques and theories presented in Sects. 2 and 3, respectively. With the purpose of reducing the numerical sensitivity, a set of canonical units (AU, 149597870.691 km; yr, $365.25\times86400~\mbox{s}$) is used for solving the shooting equation. The tolerance of MinPack-1 is set to $1\times10^{-7}$.

3.1 Mars mission with one NSTAR thruster

The actual NSTAR ion engine is applied for the Earth-Mars mission design. The end-of-life performance of the NSTAR engine over its full throttle range is given in Table 1 (Brophy and Noca 1998). There are six operation points, each one corresponds to the characteristic values of maximum achievable thrust and specific impulse. The total mass of one NSTAR engine is 66.3 kg. The departure time is chosen the same as the mission in Chi et al. (2017). The spacecraft main characteristics have been defined in terms of launch mass $m _{0} = 1000~\mbox{kg}$, area of the solar array $S = 26~\mbox{m}^{2}$, efficiency of the solar array $\gamma = 15\%$, and power allocated to operate the spacecraft systems $P _{L} = 500~\mbox{W}$.

Table 1 Operation level for NSTAR ion engine

In this mission design, the time-optimal and fuel-optimal trajectories have been calculated respectively. The calculated optimal time can be used as the reference of time-constraint for the fuel-optimal trajectory. The initial adjoint variables and the initial value of flight time are estimated by random guessing. The calculated minimum flight time to Mars is about 1017 days. The transfer trajectory is shown in Fig. 1, where the dash lines denote the Earth orbit and Mars orbit. The departure and rendezvous times are labeled on the trajectory. The propellant mass is about 213.5 kg, corresponding to the 21.35% of the initial spacecraft mass. The time histories of the thrust magnitude and the specific impulse are illustrated in Fig. 2 and Fig. 3, respectively. These figures indicate that the transfer trajectory requires the use of 4 different operation points as the Sun-spacecraft distance increases. However, the final two operation levels in Table 1 are not necessary to be used due to the sufficient available power of the first four operation levels in this mission. The spacecraft uses the maximum propelling thrust (92.3 mN) for about 50% of the total flight time in the initial mission phase.

Fig. 1

The time-optimal trajectory for Mars mission with 1 NSTAR engine

Fig. 2

The history of time-optimal control thrust for Mars mission with 1 NSTAR engine

Fig. 3

The history of time-optimal specific impulse for Mars mission with 1 NSTAR engine

The logarithmic homotopy method is applied for solving the fuel-optimal trajectory optimization problem. The decreasing route of $\varepsilon$ consists of 26 steps from 1 to 0, which is [1.0, 0.9, 0.8, 0.7, 0.6, 0.5, 0.4, 0.3, 0.2, 0.15, 0.13, 0.11, 0.07, 0.05, 0.03, 0.02, 0.01, $9.0\times 10^{-3}$, $8.5\times 10^{-3}$, $7.0\times 10^{-3}$, $5.0\times 10^{-3}$, $4.0\times 10^{-3}$, $3.0\times 10^{-3}$, $1.0\times 10^{-3}$, $5.0\times 10^{-4}$, 0.0]. The departure time is also assigned the same as the time in time-optimal problem. The constrained flight time is added 3 days on the basis of the calculated minimum time. “3 days” is not the specified time. The main purpose is to validate the effectiveness of our proposed method in solving fuel-optimal control problems no matter how many days are added. The reason for adding several days is that the fuel consumption of the energy-optimal problem that corresponds to $\varepsilon=1$ is more than that of the fuel-optimal one, so that when assigned the minimum time to the transfer time, the energy-optimal problem, which plays a seed in our solving strategy, has no solution. There are also 4 operation points, which are in accordance to the points in the above time-optimal problem (as demonstrated in Figs. 4, 5 and 6). These figures show the coasting phase in the fuel-optimal bang-bang control problem, which corresponds to that the engine is turned off. The propellant mass is 210.3 kg, about 3 kg less than the propellant mass in time-optimal problem.

Fig. 4

The fuel-optimal trajectory for Mars mission with 1 NSTAR engine

Fig. 5

The history of fuel-optimal control thrust for Mars mission with 1 NSTAR engine

Fig. 6

The history of fuel-optimal specific impulse for Mars mission with 1 NSTAR engine

3.2 Mars mission with two NSTAR thrusters

In order to further investigate the practical application of power-limited propulsion system, two NSTAR ion engines are applied for the Mars mission. In this case, the available input power can be used as much as possible by switching from one engine to two ones. The operation levels for the propulsion system with two NSTAR engines are summarized in Table 2. Each operation point is also characterized by the values of thrust and specific impulse. The thrust magnitude for one operation point is doubled compared with using only one NSTAR ion engine. While the specific impulse keeps unchanged for the same operation point for either one or two engines.

Table 2 Operation level for two NSTAR ion engines

The same Mars mission and departure time are used to validate the application of two practical engines. The minimum-time trajectory is shown in Fig. 7. The calculated minimum time for this mission with 2 engines is about 635 days. Figure 8 shows the first 8 operation points operated on the spacecraft. Different colors correspond to different values of thrust level, as demonstrated in Figs. 7 and 8. The thrust magnitude is increased in the final mission phase as the final rendezvous occurs close to the perihelion of asteroid’s orbit. The specific impulse corresponding to 5 different values is sketched in Fig. 9.

Fig. 7

The time-optimal trajectory for Mars mission with 2 NSTAR engines

Fig. 8

The history of time-optimal control thrust for Mars mission with 2 NSTAR engines

Fig. 9

The history of time-optimal specific impulse for Mars mission with 2 NSTAR engines

After getting the simulation results of the time-optimal trajectories with 1 and 2 NSTAR ion engines, the comparison is needed to be made to measure engineering application of actual power-limited propulsion system. The comparison of the calculated basic parameters for Mars mission with 1 and 2 engines is shown in Table 3. The initial mass is identical for the two missions. As shown in Table 3, the flight time for Mars mission with 2 engines is about 62.5% of the flight time with 1 engine. Meanwhile, the propellant mass with 2 engines is 17 kg less than the fuel consumption with 1 engine. However, the additional mass of loading two NSTAR engines needs to be considered. Therefore, the usable payload mass with 1 engine is about 49 kg more than the payload mass with 2 engines. As a result, in terms of flight time saving, two NSTAR engines are preferred compared to one engine. While considering the usable payload mass, one engine is better.

Table 3 Comparison of the basic performance for Mars mission with 1 and 2 NSTAR engines

As illustrated above, when solving the fuel-optimal problem, the flight time needs to be added several days upon the calculated minimum transfer time of the time-optimal problem. Therefore, the total transfer time is bounded as 640 days, about 5 days longer than the minimum time. The homotopy method with decreasing route of $\varepsilon$ from 1 to 0 with 26 steps is also applied for solving the fuel-optimal trajectory with 2 NSTAR ion engines. Figure 10 shows the calculated fuel-optimal trajectory, where the different colors on the solid lines indicate different operation points in different phases of the whole trajectory. The thrust level corresponding to 8 operation points is illustrated in Fig. 11, while the specific impulse varies among 5 different values, is shown in Fig. 12. The variation trends of thrust magnitude and specific impulse in Fig. 11 and Fig. 12 are almost the same as those in time-optimal simulation results.

Fig. 10

The fuel-optimal trajectory for Mars mission with 2 NSTAR engines

Fig. 11

The history of fuel-optimal control thrust for Mars mission with 2 NSTAR engines

Fig. 12

The history of fuel-optimal specific impulse for Mars mission with 2 NSTAR engines

3.3 Multi-target mission design: Earth–2016 HO₃–Earth Gravity Assist (EGA)–Comet 311P

The practical mission is planned as follows: the spacecraft starts from the Earth, then samples on the near Earth asteroid (NEA) 2016 HO₃, and finally arrives at main-belt comet 311P via EGA. At present multi-target small objects exploration is very promising for space exploration. 2016 HO₃ is currently the smallest, closest, and most quasi-satellite of Earth, attracting particularly interesting from a scientific point of view (Marcos and Marcos 2016). The main-belt comet 311P has a low orbital inclination and always stays outside the orbit of Mars (Jewitt et al. 2015). The instantaneous orbital elements of the Earth, 2016 HO₃ and 311P at 22/09/2006, 16/02/2017 and 25/04/2013, respectively, are obtained from JPL’s database.¹ And their corresponding values are summarized in Table 4.

Table 4 Orbital elements of Earth and target celestial bodies

Using one Chinese in-development engine as a reference thruster for our mission study, 12 operation points are summarized in Table 5. The time constraints of the mission are as follows: the launch date is planned within 2020, the arrival date to 311P is constrained before 2032. The flight altitude of EGA is required not to be less than 200 km. The searching results using impulsive propulsion are employed as the boundary conditions for low-thrust trajectory calculation. In this mission, the value of initial mass is set to $m _{0} = 1000~\mbox{kg}$. The specific impulse $I_{\mathrm{sp}} = 3500~\mbox{s}$ is assumed to be constant during the whole mission. In addition, the area and the efficiency of the solar array are $20~\mbox{m}^{2}$ and 18.3%, respectively. The power allocated to operate the spacecraft systems $P _{L}$ is set to 200 W.

Table 5 Operation level for one Chinese in-development engine

Table 6 gives the calculated results of the low-thrust fuel-optimal trajectory for this mission. The arrival date to 311P satisfies the above-mentioned constraint. In the minimum-fuel trajectory the total propellant mass is 289.1 kg, which corresponds to 28.91% of the initial spacecraft mass. The propellant mass for the transfer trajectory from Earth (EGA) to 311P which is the largest part of the whole trajectory, is 238.16 kg. The thrust profiles for the transfers from Earth to 2016 HO₃, 2016 HO₃ to Earth, and Earth to comet 311P are sketched in Fig. 13–Fig. 15, respectively. In the first two stages (see Figs. 13 and 14), the spacecraft uses the maximum propelling thrust (125 mN) due to the relatively close distance between Earth and NEA 2016 HO₃.

Fig. 13

The history of the optimal thrust for the transfer from Earth to 2016 HO₃

Fig. 14

The history of the optimal thrust for the transfer from 2016 HO₃ to Earth

Fig. 15

The history of the optimal thrust for the transfer from Earth to 311P

Table 6 Simulation results of the fuel-optimal trajectory

Figure 16 shows that the transfer trajectory in the last phase from Earth to 311P requires the use of 10 different operation points. It’s caused by the thrust variation due to the reduction of the solar power, whose value becomes insufficient for the propulsion system to operate at maximum thrust. Consequently, the optimization algorithm selects other operation points with smaller power values. $T = 0$ corresponds to coasting arc and it is shown in Fig. 15. As for the transfer from the Earth to 311P, our proposed techniques are efficiently applied to this discrete multiple-leg power-limited problem, which helps to converge to the optimal solution. The corresponding optimal trajectory is illustrated in Fig. 16. Different colors in this figure corresponding to the different values of the thrust magnitude are labeled in Fig. 15. As shown in Fig. 16, the spacecraft tends to return back to approach the Sun on the way of transfer. This behavior can be explained in this way: the spacecraft needs to be accelerated to reach the target orbit. Therefore, a greater available power is required by the propulsion system to operate at its maximum value.

Fig. 16

The fuel-optimal trajectory from Earth to 311P

4 Conclusion

In this paper, a suite of practical techniques are developed to solve the low-thrust power-limited trajectory optimization problem with actual solar electric model. The time-optimal and fuel-optimal control problems are established to validate the application of the practical propulsion system in the mission design. The homotopy method based on logarithmic homotopy function is applied in fuel-optimal problem to overcome the difficulties in convergence caused by the bang-bang control. In order to guarantee the accuracy of solving the discrete power-limited problem, the power operation detection technique has been proposed to overcome the discontinuity of the integral items caused by the discrete variable thrust.

Numerical simulations of the Earth-Mars transfer mission and multi-target small objects exploration with actual propulsion system have been conducted to validate the application of the proposed techniques.

One NSTAR ion engine and two NSTAR engines have been used in the Mars mission respectively. The results show that the proposed method can be efficiently applied in solving the time-optimal and fuel-optimal problems. The propellant mass in fuel-optimal problem with constrained transfer time, which has added several days upon the minimum time, is less than the fuel consumption in time-optimal problem. These results demonstrate the feasibility and correctness of our proposed method. By comparing the basic performance of using one and two NSTAR thrusters with the same initial mass in time-optimal problem, from a practical point of view it can be concluded that two engines are preferred to use in terms of the flight time, while in our case using one engine has an advantage in usable payload mass.

The more complicated multi-target small objects exploration mission has been designed to validate the application of a Chinese in-development thruster with 12 operation points. In order to better use the mechanism that the available power is proportional to the inverse square of the heliocentric distance, the spacecraft has to return back to approach the Sun to fully accelerate the orbit on the way of transfer. This behavior indicates the characteristics and usefulness of applying the discrete power-limited propulsion system. The results also show that our method can be applied to solve the more complex and more distant interplanetary transfer mission.