1 Introduction

It is interesting to note that as long as in 1924 (Eddington 1924) conceived the idea that our spacetime can be considered as a four dimensional space embedded in a higher-dimensional flat space. This idea has gained quantum of attraction to the scientific community due to the recent proposal by Randall and Sundram (1999) and Anchordoqui and Bergila (2000). The details discussion about the embedding class has been provided by Maurya et al. (2015a).

On the other hand, general theory of relativity (GTR), an outstanding extension of the special theory of relativity with non-uniform reference frame and tensorial presentation of curved spacetime, was put forward by Einstein (O’Connor and Robertson 1996) in the year 1915—a century ago. Till date this is considered as the most profound and effective theory of gravitation. The field theoretical effect of this geometric theory has been described by Wheeler (1990) in a poetic exposition as follows: “Matter tells space–time how to bent and space–time returns the complement by telling matter how to move”.

In the present context we employ GTR as our background canvas to formulate solutions from class 1 metric and thereafter to investigate electromagnetic mass model (EMMM). As the present work is a sequel of our earlier work (Maurya et al. 2015a) so we shall refer that article for detailed discussions on class 1 metric as well as the EMMM.

In connection to the above work on the EMMM it have been specially argued by Maurya et al. (2015a) that most of the investigators (Cooperstock and de la Cruz 1978; Tiwari et al. 1984; Gautreau 1985; Grøn 1985; Tiwari et al. 1986; Ponce de Leon 1987; Tiwari et al. 1991; Tiwari and Ray 1991a,b; Ray et al. 1993, 2007; Ray and Ray 1993; Tiwari and Ray 1997; Ray 2002, 2006, 2007; Ray and Das 2002, 2004; Ray and Bhadra 2004) consider an ad hoc equation of state (EOS) \(\rho + p = 0\) (where \(\rho \) is the matter density and \(p\) is the fluid pressure), which suffers from a negative pressure. In the present investigation, however, for the construction of EMMMs following Maurya et al. (2015a) we also employ a different technique by adopting a special algorithm. We shall see later on that this algorithm will act as a general platform to generate physically valid solutions compatible with the spherically symmetric class one metric.

The plan of the present work can be outlined as follows: we have provided the static spherically symmetric spacetime and the Einstein–Maxwell field equations in Sect. 2 whereas in Sect. 3 based on an algorithm for class one metric we construct a set of new general solutions. In the next Sect. 4 boundary conditions are discussed to find out constants of integration. The Sect. 5 deals with the solutions where critical analysis has been performed to check several physical properties of the model regarding validity with the stellar structure. We have put some remarks in the concluding Sect. 6.

2 The static spherically symmetric spacetime and Einstein–Maxwell field equations

The Einstein–Maxwell field equations can be provided as usual

$$ G_{j}^{i} =R_{j}^{i} - \frac{1}{2} R g_{j}^{i} =-\kappa \bigl(T_{j}^{i} +E _{j}^{i} \bigr), $$
(1)

where \(k = 8\pi \) is the Einstein constant (\(G=c=1\), in the relativistic units).

The matter distribution inside the star is assumed to be locally perfect fluid and consequently \(T_{j}^{i} \) and \(E_{j}^{i}\), the energy-momentum tensors for fluid distribution and electromagnetic field respectively, are defined by

$$\begin{aligned} &T_{j}^{i} =\bigl[(\rho +p)v^{i} v_{j} -p\delta_{j}^{i} \bigr], \end{aligned}$$
(2)
$$\begin{aligned} &E_{j}^{i} =\frac{1}{4\pi } \biggl(-F^{im} F_{jm} +\frac{1}{4} \delta_{j} ^{i} F^{m\, n} F_{m\, n} \biggr), \end{aligned}$$
(3)

where \(v^{i}\) is the four-velocity as \(e^{-\nu (r)/2} v^{i} = \delta _{4}^{i}\).

Now the anti-symmetric electromagnetic field tensor, \(F_{ij}\), satisfies the Maxwell equations

$$\begin{aligned} &F_{ik,j} +F_{kj,i} +F_{ji,k} =0, \end{aligned}$$
(4)
$$\begin{aligned} &\frac{\partial }{\partial x^{k} } \bigl(\sqrt{-g} F^{ik} \bigr)=-4\pi \sqrt{-g} j^{i}, \end{aligned}$$
(5)

where \(g\) is the determinant of quantities \(g_{ij}\) in Eq. (5) and is defined by \(g = - e^{(\nu +\lambda )}r^{4} \sin^{2}\theta \).

The only non-vanishing components of the electromagnetic field tensor are \(F^{41}\) and \(F_{14} \) which describe the radial component of the electric field and are related as \(F^{41} = -F^{14}\). From Eq. (5), we can obtain the following expression for the electric field

$$ F^{41} =e^{-\frac{(\lambda +\nu )}{2} } \frac{q(r)}{r^{2} }, $$
(6)

where \(q(r)\) represents the total charge contained within the sphere of radius \(r\) and is defined by

$$\begin{aligned} q(r) =& r^{2} \sqrt{-F_{14} F^{14} } = r^{2} F^{41} e^{(\lambda + \nu )/2} \\ =& r^{2} E = 4\pi \int_{0}^{r}\sigma \, r^{2} e^{\lambda /2} dr, \end{aligned}$$
(7)

where \(\sigma \) is the charge density.

Now, following the work of Maurya et al. (2015a) here we consider the static spherically symmetric metric in the form

$$ ds^{2} =-e^{\lambda } dr^{2} -r^{2} \bigl(d \theta^{2} +\sin^{2} \theta d \varphi^{2} \bigr)+e^{\nu } dt^{2}. $$
(8)

The above metric represents spacetime of embedding class one if it satisfies the Karmarkar condition (Karmarkar 1948)

$$ R_{1414} =\frac{R_{1212} R_{3434} + R_{1224} R_{1334} }{R_{2323} } $$
(9)

along with the constraint \(R_{2323} \neq 0 \) (Pandey and Sharma 1982). In this connection we note that every gravitational metric of spherical symmetry is in general of class two. Basically through the above mentioned Karmarkar condition (Karmarkar 1948) it was shown that this is a necessary and sufficient condition for the spherically symmetric spacetime to be of class 1. However, later on it was again shown by Pandey and Sharma (1982) that along with the Karmarkar condition (Karmarkar 1948) the constraint \(R_{2323} \neq 0 \) is also needed to impose.

However, in connection to the above condition the components of the Riemann curvature tensor \(R_{hijk}\) (for static case i.e. the derivative with respect to \(t\) is zero) under the metric (8) are as follows:

$$\begin{aligned} &R_{2323}=\sin^{2}\theta r^{2} \bigl[ 1-e^{-\lambda } \bigr] ,\qquad R_{1212}=\frac{1}{2}\lambda 'r, \\ &R_{1224}=0,\qquad R_{1414}=e^{ \nu } \biggl[ \frac{1}{2}\nu ''+\frac{1}{4}{\nu '}^{2}-\frac{1}{4} \lambda '\nu ' \biggr] , \\ & R_{2424}=\frac{1}{4}\nu '\beta ' e ^{\nu -\lambda },\qquad R_{3434}=\sin^{2}\theta \,R_{2424}. \end{aligned}$$

Hence, by inserting the components of \(R_{hijk}\) in Eq. (9), we obtain the following second order differential equation:

$$ \frac{\lambda ' \nu '}{(1-e^{\lambda } )}=-2\bigl(\nu '' +\nu^{\prime 2} \bigr)+ \nu^{\prime 2} +\lambda ' \nu ', $$
(10)

where \(\nu (r)\) and \(\lambda (r)\) are metric potentials and depend only on the radial coordinate \(r\). Here \(e^{\lambda } \neq 1\) with \(r \neq 0\).

The solution of above Eq. (10) can be represented in both the forms with \(e^{\lambda }\) as well as \(e^{\nu }\). The meaning is that if we opt for \(\nu \) then we can determine \(\lambda \) whereas for the option of \(\lambda \) one can determine \(\nu \) of the solution. Therefore, after some manipulation, the solution of the second order differential equation (10), can be obtained in the following forms:

$$ e^{\lambda } =\bigl( 1+K \nu^{\prime 2} e^{\nu }/4\bigr), \quad e^{\nu /2} = A + \frac{1}{\sqrt{K}} \int \sqrt{\bigl(e^{\lambda } - 1\bigr)}dr, $$
(11)

where \(K\) and \(A\) are two non-zero arbitrary constants of integration, \(\nu '(r)\neq 0\), \(e^{\lambda (0)} =1\) and \(\nu '(0)=0\).

For the above spherically symmetric metric (8), the Einstein–Maxwell field equations (1) can be expressed as the following set of ordinary differential equations (Maurya et al. 2015a,b):

$$\begin{aligned} &\frac{\nu '}{r} e^{-\lambda } -\frac{(1-e^{-\lambda } )}{r^{2} } = \kappa p- \frac{q}{r^{4} }^{2}, \end{aligned}$$
(12)
$$\begin{aligned} &\biggl[ \frac{\nu ''}{2} -\frac{\lambda '\nu '}{4} + \frac{\nu ^{\prime\,2} }{4} + \frac{\nu '-\lambda '}{2r} \biggr] e^{-\lambda }=\kappa p+\frac{q}{r^{4} }^{2}, \end{aligned}$$
(13)
$$\begin{aligned} &\frac{\lambda '}{r} e^{-\lambda } +\frac{(1-e^{-\lambda } )}{r^{2}} = \kappa \rho + \frac{q}{r^{4} }^{2}, \end{aligned}$$
(14)

where the prime denotes differentiation with respect to \(r\).

Therefore, by incorporating Eq. (11) in the set of Eqs. (12)–(14), we get

$$\begin{aligned} &\frac{\nu ' }{r^{2} (4+K\nu^{\prime 2} e^{\nu } )} \bigl(4r-K\nu 'e^{ \nu } \bigr)=\kappa p- \frac{q^{2} }{r^{4} }, \end{aligned}$$
(15)
$$\begin{aligned} &\frac{4}{(4+K\nu^{\prime 2} e^{\nu } )} \biggl( \frac{\nu ' }{2r} -\frac{(K \nu ' e^{\nu } -2r) (2\nu '' +\nu^{\prime 2} )}{2r(4+K\nu^{\prime 2} e ^{\nu } )} \biggr) \\ &\quad =\kappa p+\frac{q^{2} }{r^{4} }, \end{aligned}$$
(16)
$$\begin{aligned} &\frac{Ke^{\nu } \nu ' }{r\,(4+K\nu^{\prime 2} e^{\nu } )} \biggl( \frac{4(2 \nu '' +\nu^{\prime 2} )}{(4+K\nu^{\prime 2} e^{\nu } )} +\frac{ \nu ' }{r} \biggr) = \kappa \rho +\frac{q^{2} }{r^{4} }. \end{aligned}$$
(17)

Using the Eqs. (15) and (16), the pressure isotropy condition (Maurya et al. 2015a), and the pressure gradient by Tolman (1939), Oppenheimer and Volkoff (1939) can be written as follows:

$$\begin{aligned} &\biggl( \frac{K\nu ' e^{\nu }}{2r} -1 \biggr) \biggl( \frac{2\nu ' }{r (4+K \nu^{\prime 2} e^{\nu } )} - \frac{4(2\nu '' +\nu^{\prime 2} )}{(4+K \nu^{\prime 2} e^{\nu } )^{2} } \biggr) \\ &\quad =\frac{2q^{2} }{r^{4} }, \end{aligned}$$
(18)
$$\begin{aligned} &\frac{dp}{dr} =-\frac{M_{G} (r)(\rho +p)}{r^{2} } e^{(\lambda -\nu )/2} +\frac{q}{4 \pi r^{4} } \frac{dq}{dr}, \end{aligned}$$
(19)

where \(M_{G}\) is the gravitational mass within the radius \(r\) and is given by

$$ M_{G} (r)=\frac{1}{2} r^{2}\nu ' e^{(\nu -\lambda )/2}. $$
(20)

The above Eq. (19) represents the charged generalization of the Tolman–Oppenheimer–Volkoff (TOV) (Tolman 1939; Oppenheimer and Volkoff 1939) as generally referred to the equation of hydrostatic equilibrium or equation of continuity.

It have been argued by Maurya et al. (2015a) that if charge vanishes in a charged fluid of embedding class one then survived neutral counterpart will only be either the Schwarzschild (1916) interior solution (or its special cases de Sitter universe or Einstein’s universe) or Kohler and Chao (1965) solution otherwise either charge cannot be zero or the survived space–time metric is flat. This means for \(q=0\) in Eq. (18), the first factor of the left hand side gives the Kohler-Chao solution while the second factor gives the Schwarzschild solution.

3 A set of new class of solutions

In general, in the presence of electrical charge, the fluid sphere under consideration can be defined by the following metric functions:

$$\begin{aligned} &e^{-\lambda } = 1-\frac{2m(r)}{r} +\frac{q^{2} }{r^{2} }, \end{aligned}$$
(21)
$$\begin{aligned} &\nu ' =\frac{ ( \kappa r p+\frac{2m}{r^{2} } -\frac{2 q^{2} }{r ^{3} } ) }{ ( 1-\frac{2m}{r} +\frac{q^{2} }{r^{2} } ) }, \end{aligned}$$
(22)

where \(m(r)\) is the mass function where Eq. (21) has been derived with the help of Eqs. (12) and (21) which means \(\lambda \) and \(\nu \) are dependent on each other as also evident from Eq. (11).

Using Eqs. (12)–(14), in terms of the above mass function \(m(r)\) of Eq. (21), an algorithm for constructing electromagnetic mass models of class one metric have been provided by Maurya et al. (2015a).

By plugging Eqs. (11) and (18) into Eq. (21), we get expression of mass function \(m(r)\) as:

$$\begin{aligned} m(r)&= \frac{r\,\nu '(K\nu ' e^{\nu }-2r)}{2(4+K\nu^{\prime 2} e^{ \nu } )} -\frac{r^{2}\,(2\nu '' +\nu^{\prime 2} )(K\nu ' e^{\nu }-2r)}{2(4+K \nu^{\prime 2} e^{\nu } )^{2} } \\ &\quad + \frac{r\,K\,{\nu '}^{2}\,e^{\nu }}{2(4+K \,{\nu '}^{2}\,e^{\nu })} \end{aligned}$$
(23)

For constructing electromagnetic mass model, we consider the following form of metric potential:

$$ \lambda =\log \biggl( \frac{1+a r^{2} }{1+br^{2} } \biggr) , $$
(24)

\(a\) and \(b\) being two real numbers. Here we are opting for \(\lambda \) on the basis of Eq. (18) (i.e. charge should not be zero for that \(\lambda \)).

Then the metric function \(\nu \) can be determined from Eq. (11) as

$$ \nu =2\log \bigl[ A+B\sqrt{1+br^{2} } \bigr], $$
(25)

where \(A\) and \(B\) are two positive constants with

$$ B=\frac{1}{b} \sqrt{\frac{(a-b)}{K} }, $$
(26)

However, the supposition of metric function \(\lambda \) will lead us to a new class of very interesting and physically valid solutions. The explanations for this \(\lambda \) are given as:

3.1:

If \(a=0\), then the present charge fluid reduces to the interior solution of Schwarzschild (1916).

3.2:

If \(a=2b\) and \(A=0\), then the said solution reduces to the interior solution of Kohler and Chao (1965).

3.3:

If \(a \neq 0\) and \(a \neq 2b\), then the charged solution can not reduce to any uncharged solution. But the charged solution in this case can still be uncharged for taking \(a=b\) and reduces to a flat spacetime. Consequently, the charged fluid spheres (for different values of \(a\) and \(b\) with \(a \neq 0\) and \(a \neq 2b\)) represent a class of electromagnetic mass models (Lorentz 1904) as they reduce to the flat spacetime (the pressure and charged density both vanish simultaneously) on the removal of charge.

Therefore, for determining the features of charged fluid as well as to understand concept of the electronic structure, we shall consider the third case i.e. \(a \neq 0\) and \(a\neq 2b\) only.

Hence the expressions for the electric charge and electromagnetic mass respectively can be provided by using the Eqs. (18) and (23) together with Eqs. (24) and (25) as:

$$\begin{aligned} &q(r) = Er^{2} =\sqrt{a}~r^{3}\sqrt{ \biggl[ \frac{C(r) - D(r)}{F(r)} \biggr] }, \end{aligned}$$
(27)
$$\begin{aligned} &m(r) =\frac{1}{2}r^{3} \biggl[ \frac{(a-b)}{1+ar^{2} } + \frac{ar^{2} [C(r) - D(r)]}{F(r)} \biggr] , \end{aligned}$$
(28)

where

$$\begin{aligned} &C(r) = a \bigl(B+bBr^{2} +A\sqrt{1+br^{2} }\bigr),\\ &D(r)= b\bigl(A\sqrt{1+br^{2} } +2B+2Bbr^{2}\bigr),\\ &F(r) = 2\bigl(1+ar^{2}\bigr)^{2}\sqrt{1+br^{2}} \bigl[A+B\sqrt{1+br^{2}}\bigr]. \end{aligned}$$

The expressions for fluid pressure and energy density respectively are obtained by plugging the value of \(\nu \) from Eq. (25) into Eqs. (15) and (17) as:

$$\begin{aligned} &8\pi p= \biggl[ \frac{-a^{2} r^{2}H(r)+2b[H(r)+2B(1+br^{2} )] +a I_{1}}{F(r)} \biggr] , \end{aligned}$$
(29)
$$\begin{aligned} &8\pi \rho = \biggl[ \frac{-6b H(r)+a^{2} r^{2} H(r)+a I_{2}}{F(r)} \biggr] , \end{aligned}$$
(30)

where

$$\begin{aligned} &H(r) = B(1+br^{2} )+A\sqrt{1+br^{2}},\\ &I_{1}= A(-2+br^{2} )\sqrt{1+br^{2} } +2B(-1+br^{2} +2b^{2} r^{4}),\\ &I_{2}=A(6-br^{2} )\sqrt{1+br^{2} } +6B(1+br^{2}). \end{aligned}$$

Therefore, the pressure and density gradients are

$$\begin{aligned} &\frac{ dp}{dr} =\frac{2 r}{8\pi } \biggl[ \frac{p_{1}+p_{2}+p_{3}}{4(1+ar ^{2})^{3} \sqrt{1+br^{2}} [A+B\sqrt{1+b r^{2}}]^{2}} \biggr] , \end{aligned}$$
(31)
$$\begin{aligned} &\frac{ d\rho }{dr} =-\frac{2ar}{8\pi } \biggl[ \frac{\rho_{1}+\rho_{2}+ \rho_{3}}{4(1+ar^{2} )^{3} \sqrt{1+br^{2} } [ A+B \sqrt{1+b r^{2} } ]^{2} } \biggr] , \end{aligned}$$
(32)

where

$$\begin{aligned} &p_{1}=4Ab^{2} B-a b \bigl[ 6A^{2} \sqrt{1+br^{2} } +16B^{2} \bigl(1+br^{2} \bigr)^{3/2}\\ &\phantom{p_{1}=} +AB\bigl(22+15br^{2} \bigr)\bigr], \\ &p_{2}=2a^{3} r^{2} \bigl[ A^{2} \sqrt{1+br^{2} } +B^{2} \bigl(1+br^{2} \bigr)^{3/2}\\ &\phantom{p_{2}=} +2AB\bigl(1+br^{2} \bigr)\bigr], \\ &p_{3}=a^{2} \bigl[ -2A^{2} \bigl(-3+br^{2} \bigr)\sqrt{1+br^{2} }\\ &\phantom{p_{3}=} +AB \bigl(12+2br^{2} -7b^{2} r^{4} \bigr)\\ &\phantom{p_{3}=} - 2B^{2} \bigl(-3+br^{2} +4b^{2} r^{4} \bigr) \sqrt{1+br^{2} } \bigr], \\ &\rho_{1}=-b \bigl[ 22A^{2} \sqrt{1+br^{2} } +24B^{2} \bigl(1+br^{2} \bigr)^{3/2}\\ &\phantom{\rho_{1}=} +AB\bigl(46+47br ^{2} \bigr)\bigr], \\ &\rho_{2}=2a^{2} r^{2} \bigl[ A^{2} \sqrt{1+br^{2} } +B^{2} \bigl(1+br^{2} \bigr)^{3/2}\\ &\phantom{\rho_{2}=} +2AB\bigl(1+br^{2} \bigr)\bigr], \\ &\rho_{3}=a\bigl[ -2A^{2} \bigl(-11+br^{2} \bigr) \sqrt{1+br^{2} } +22B^{2} \bigl(1+br ^{2} \bigr)^{3/2}\\ &\phantom{\rho_{3}=} +AB\bigl(44+42br^{2} -3b^{2} r^{4} \bigr)\bigr]. \end{aligned}$$

4 Boundary conditions

The arbitrary constants \(A\), \(B\) and \(K\) can be obtained by using the boundary conditions. For the above system of equations the boundary conditions that applicable are as follows: the pressure \(p=0\) at \(r=R\), where \(r=R\) is the outer boundary of the fluid sphere [matching the second fundamental form at \(r=R\) i.e. matching of \(\frac{\partial g _{tt}}{\partial r}\) at \(r=R\)]. Actually, the interior metric (8) should join smoothly at the surface of the sphere \((r=R)\) to the exterior Reissner–Nordström metric whose mass is \(m(r=R)=M\), a constant (Misner and Sharp 1964), given by

$$\begin{aligned} ds^{2} =&- \biggl( 1-\frac{2M}{r} +\frac{Q^{2} }{r^{2} } \biggr) ^{-1} dr ^{2}-r^{2} \bigl(d\theta^{2} +\sin^{2} \theta d \phi^{2} \bigr) \\ &{} + \biggl( 1- \frac{2M}{r} +\frac{Q^{2} }{r^{2} } \biggr) dt^{2}. \end{aligned}$$
(33)

This requires the continuity of \(e^{\lambda } \), \(e^{\nu } \) and \(Q\) across the boundary \(r=R\), so that

$$\begin{aligned} &e^{-\lambda (R)} =1-\frac{2M}{R} +\frac{Q^{2} }{R^{2} }, \end{aligned}$$
(34)
$$\begin{aligned} &e^{\nu (R)} = 1-\frac{2M}{R} +\frac{Q^{2} }{R^{2} }, \end{aligned}$$
(35)
$$\begin{aligned} &q(R)=Q, \end{aligned}$$
(36)
$$\begin{aligned} &p_{(r=R)} =0. \end{aligned}$$
(37)

The pressure is zero on the boundary \(r=R\) and hence we obtain

$$ \frac{B}{A} =\frac{ (a-b) (2+aR^{2} )}{[ 6b-a^{2} R^{2} -a (2-4bR^{2} )] \sqrt{1+bR^{2} } }. $$
(38)

Again, at the boundary \(e^{-\lambda (R)} =e^{\nu (R)}\), which gives

$$ A=\frac{(6 b-a^{2} R^{2} -2a+4abR^{2} ) \sqrt{1+bR^{2} } }{(4b+3abR ^{2} ) \sqrt{1+aR^{2} } }. $$
(39)

Also from Eqs. (38) and (39) one can get

$$ B=\frac{(a-b) (2+aR^{2} )}{(4b+3abR^{2} ) \sqrt{1+aR^{2} } }. $$
(40)

For the third constant \(K\), we use Eqs. (26) and (40), which provides the required expression as

$$ K=\frac{ (4b+3abR^{2} )^{2} (1+aR^{2} )}{b^{2} (a-b) (2+a R^{2} )^{2} }. $$
(41)

5 Physical acceptability conditions for the isotropic stellar models

In the present Section we have critically verified our models by performing mathematical analysis and plotting several figures for some of the compact star candidates. All these indicate that the results are fantastically overcome all the barrier of the physical tests.

5.1 Regularity and reality conditions

5.1.1 Case 1

It is expected that the solution should be free from physical and geometrical singularities i.e. the pressure and energy density at the center should be finite and metric potentials \(e^{\lambda (r)}\) and \(e^{\nu (r)}\) should have non-zero positive values in the range \(0 \le r \le R\). We observe that at the center Eqs. (24) and (25) give \(e^{\lambda (0)} =1\) and \(e^{\nu (0)} =(A+B)^{2} \). These results suggest that the metric potentials are positive and finite at the center. These features can be found explicitly from Fig. 1.

Fig. 1
figure 1

Behavior of the metric potentials \(\nu \) and \(\lambda \) with respect to radial coordinate \(r/R\)

Full size image

5.1.2 Case 2

For any physically valid solutions the density \(\rho \) and pressure \(p\) should be positive inside the star. Also the pressure must vanish on the boundary of the fluid sphere \(r=R\). The other physical conditions to be maintained are as follows:

  1. (1)

    \(( dp/dr ) _{r=0} =0 \) and \(( d^{2} p/dr^{2} ) _{r=0} <0\) so that pressure gradient \(dp/dr \) is negative for \(0 \le r \le R\).

  2. (2)

    \(( d\rho /dr ) _{r=0} =0 \) and \(( d^{2} \rho /dr ^{2} ) _{r=0} <0 \) so that density gradient \(d\rho /dr \) is negative for \(0 \le r \le R\).

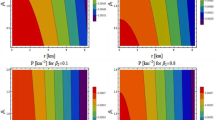
The above two conditions (1) and (2) imply that the pressure and density should be maximum at the center and they should monotonically decrease towards the surface. All these are evident from Fig. 2.

Fig. 2
figure 2

Behavior of the fluid pressure \(p\) and energy density \(\rho \) with respect to radial coordinate \(r/R\), where \(p_{i}=\kappa p\), \(\rho_{i}= \kappa \rho \)

Full size image

We have also shown these features of pressure and density for some specific compact stars in Tables 1 and 2 where we have figured out physical parameters as well as some constants of our models. Actually, the values of Table 1 have been used in Table 2 to find out the energy densities and pressure for different strange star candidates. It is worthwhile to mention that the densities \(\sim 10^{15}~\mbox{gm/cm}^{3}\) and pressure \(\sim 10^{35}~\mbox{dyne/cm}^{2}\) are in good agreement with the observational data of the compact stars, specially Her X-1 (Ruderman 1972; Maurya et al. 2015c).

Table 1 Values of the model parameters for different charged compact stars
Full size table
Table 2 Energy densities and pressure for different charged compact star candidates for the above parameter values of Table 1
Full size table

For specific numerical values of the constant \(\kappa = 8\pi G/c^{4}\) and other physical parameters we have used the data \(G=6.67 \times 10^{-8}~\mbox{cm}^{3}/\mbox{gs}^{-2}\) and \(c=2.997 \times 10^{10}~\mbox{cm/s}\) in the calculations of Table 2.

5.2 Causality and well behaved conditions

Inside the fluid sphere the speed of sound should be less than the speed of light i.e. \(0\leq ( \frac{dp}{d\rho } ) <1 \), which can be observed in Fig. 3. We note from this figure that the velocity of sound monotonically is decreasing away from the center (Canuto 1973).

Fig. 3
figure 3

Behavior of the sound speed \(V\) with respect to radial coordinate \(r/R\)

Full size image

5.3 Energy conditions

It is, in general, argued that a physically reasonable energy-momentum tensor which represents an isotropic charged fluid sphere composed of matter must satisfy the following energy conditions:

  1. 1.

    null energy condition (NEC): \(\rho +\frac{E^{2}}{4\pi } \geq 0\)

  2. 2.

    weak energy condition (WEC): \(\rho -p+\frac{E^{2}}{4\pi } \geq 0\)

  3. 3.

    strong energy condition (SEC): \(\rho -3p+\frac{E^{2}}{4\pi } \geq 0\)

The behaviour of these energy conditions are shown in Fig. 4. This figure clearly indicates that all the energy conditions in our model are satisfied throughout the interior region of the spherical distribution.

Fig. 4
figure 4

Behavior of the energy conditions with respect to fractional radius \(r/R\)

Full size image

5.4 Stability conditions

5.4.1 The Tolman–Oppenheimer–Volkoff equation

The generalized Tolman–Oppenheimer–Volkoff (TOV) equation can be provided as

$$ -\frac{M_{G} (\rho +p_{r} )}{r^{2} } e^{\frac{\lambda -\nu }{2} } - \frac{dp}{dr} +\sigma \frac{q}{r^{2} } e^{\frac{\lambda }{2} } =0, $$
(42)

where \(M_{G} \) is the effective gravitational mass given by

$$ M_{G} (r)=\frac{1}{2} r^{2} e^{\frac{\nu -\lambda }{2} } \nu '. $$
(43)

This Eq. (42) describes the equilibrium condition for a charged perfect fluid subject to the gravitational \((F_{g})\), hydrostatic \((F_{h})\) and electric \((F_{e})\). In summary, we can write it as

$$ F_{g} + F_{h} + F_{e} = 0, $$
(44)

where

$$\begin{aligned} F_{g} &=-\frac{1}{2} (\rho +p)\nu ' \\ &= -\frac{ rbB}{8\pi } \biggl[ \frac{2[A(a-b)\sqrt{1+br^{2}} + B a(1+b r^{2})]}{(1+ar^{2})^{2} (1+br^{2}) [A+B \sqrt{1+br^{2}}]^{2}} \biggr] , \end{aligned}$$
(45)
$$\begin{aligned} F_{h} &=-\frac{ dp}{dr} \\ &=-\frac{2 r}{8\pi } \biggl[ \frac{p1+p2+p3}{4(1+ar^{2} )^{3} \sqrt{1+br ^{2} } [ A+B\sqrt{1+b r^{2} } ]^{2} } \biggr] , \end{aligned}$$
(46)
$$\begin{aligned} F_{e} &=\sigma \frac{q}{r^{2}}e^{\lambda /2} \\ &=\frac{a r}{4\pi } \biggl[ \frac{F_{e1} +F_{e2} +F_{e3} }{4(1+ar^{2} )^{3} \sqrt{1+br^{2} } [ A+B\sqrt{1+b r^{2} } ]^{2} } \biggr] . \end{aligned}$$
(47)

In the above Eq. (47) the symbols used are as follows:

$$\begin{aligned} &F_{e1} =-b \bigl[ 6A^{2} \sqrt{1+br^{2} } +12B^{2} \bigl(1+br^{2} \bigr)^{3/2} \\ &\phantom{F_{e1} =} +AB \bigl(18+19br^{2} \bigr)\bigr], \\ &F_{e2} =2a^{2} r^{2} \bigl[ A^{2} \sqrt{1+br^{2} } +B^{2} \bigl(1+br^{2} \bigr)^{3/2} \\ &\phantom{F_{e2} =} +2AB\bigl(1+br^{2} \bigr)\bigr], \\ &F_{e3} =a \bigl[ -2A^{2} \bigl(-3+br^{2} \bigr) \sqrt{1+br^{2} } \\ &\phantom{F_{e3} =} +AB \bigl(12+6br^{2} -7b ^{2} r^{4} \bigr) \\ &\phantom{F_{e3} =}+2B^{2} \bigl(3+br^{2} -2b^{2} r^{4} \bigr)\sqrt{1+br^{2} } \bigr]. \end{aligned}$$

We have shown the plots for TOV equation in Fig. 5 for different compact strange stars. From figures it is observed that the system is in static equilibrium under three different forces, e.g. gravitational, hydrostatic and electric to attain overall equilibrium.

Fig. 5
figure 5

Behavior of the forces for the compact stars (i) Her X-1 (Top Left), (ii) RX J 1856-37 (Top Right) and (iii) 4U 1820-30 (Middle left), (iv) SAX J1808.4-3658 (SS1) (Middle Right), (v) SAX J1808.4-3658 (SS2) (Bottom left) and (vi) PSR 1937+21 (Bottom Right) with respect to radial coordinate \(r/R\)

Full size image

5.4.2 Electric charge contain

In the present work the expression for electric charge can be given by Eq. (27) and following the work of Maurya et al. (2015a) we can figure out the charge on the boundary as \(1.15295 \times 10^{20}~\mbox{C}\) and at the center it is zero. The charge profile has been shown in Fig. 6 for different compact stars which starts from a minimum value at the center and acquires the maximum value at the boundary. This feature is also evident from the Table 3 and compatible with the result of Ray et al. (2003) where they studied the effect of electric charge in compact stars and found the upper bound as \(\sim 10^{20}\) Coulomb. However, in this connection it is to note that in the Table 3 we have mentioned the data for charge \(q\) for different stars in the relativistic unit Km. Therefore, to convert these values of charge in Coulomb unit, one has to multiply every value by a factor \(1.1659 \times 10^{20}\).

Fig. 6
figure 6

Behavior of electric charge \(q\) with respect to radial coordinate \(r/R\)

Full size image
Table 3 The profile of electric charge for different compact stars in the unit of \(10^{20}\) Coulomb
Full size table

5.4.3 Effective mass-radius relation

Buchdahl (1959) has proposed an absolute constraint on the maximally allowable mass-to-radius ratio \((M/R)\) for static spherically symmetric isotropic fluid spheres which amounts \(2M/R\leq 8/9 \). On the other hand, Böhmer and Harko (2007) proved that for a compact charged fluid sphere there is a lower bound for the mass-radius ratio

$$ \frac{3Q^{2} }{2R^{2} } \frac{ ( 1+\frac{Q^{2} }{18R^{2} } ) }{ ( 1+\frac{Q^{2} }{12R^{2} } ) } \leq \frac{2M}{R}, $$
(48)

for the constraint \(Q < M\).

This upper bound of the mass for charged fluid sphere was generalized by Andréasson (2009) who proved that

$$ \sqrt{M} \leq \frac{\sqrt{R} }{3} +\sqrt{\frac{R}{9} +\frac{Q ^{2} }{3R} }. $$
(49)

In the present model, we find the effective gravitational mass as

$$ M_{eff} =4\pi \int_{0}^{R} \biggl( \rho + \frac{E^{2} }{8\pi } \biggr) r^{2} dr = \frac{1}{2} R \biggl[ \frac{(a-b) R^{2} }{(1+a R ^{2} )} \biggr] . $$
(50)

Note that in the above equation, for the condition \(a=b\), the effective gravitational mass vanishes which is a required feature of electromagnetic mass model.

In terms of the compactness factor \(u=M_{eff}/R\) we now define the surface redshift \(Z\) as

$$ Z =(1-2u)^{-\frac{1}{2} } -1=e^{\frac{1}{2} \lambda (R)} -1= \sqrt{\frac{(1+aR ^{2} )}{(1+bR^{2} )} } -1. $$
(51)

We have demonstrated the behavior of surface redshift \(Z\) with respect to radial coordinate \(r/R\) in Fig. 7 which shows the desirable features (Maurya et al. 2015b).

Fig. 7
figure 7

The behavior of surface redshift \(Z\) with respect to radial coordinate \(r/R\)

Full size image

6 Conclusion

Our sole aim in the present paper was to investigate nature of class 1 metric. For this purpose we have considered matter-energy distribution under the framework of Einstein–Maxwell spacetime. At first we developed an algorithm which has a general nature and thus can be reduced to three special cases, viz. (i) charge analogue of the Kohler and Chao (1965) solution, (ii) charge analogue of the Schwarzschild (1916) solution (i.e. the Reissner–Nordström solution), and (iii) the Lorentz (1904) solution of electromagnetic mass model.

By considering the third case of the Lorentz solution of electromagnetic mass model we have studied its properties through the following two basic physical testing, such as (i) regularity and reality conditions, and (ii) causality and well behaved conditions. Moreover, some other essential testing also have been performed, viz. (i) energy conditions, and (ii) stability conditions. In the case of energy conditions we have seen that the isotropic charged fluid sphere composed of matter satisfy the (i) null energy condition \((\rho +\frac{E^{2}}{4\pi }) \geq 0\), (ii) weak energy condition \((\rho -p+\frac{E^{2}}{4\pi }) \geq 0\), and (iii) strong energy condition \((\rho -3p+\frac{E^{2}}{4\pi }) \geq 0\) (Fig. 4). On the other hand, in connection to stability conditions we critically have discussed the TOV equation, electric charge contain, effective mass-radius relation of the charged spherical distribution. Here also we find that the results are in favor of the physical requirements (Figs. 5 –7).

As a special feature of the models we have presented here an application to stellar structure. The behavior of the compact stars (i) Her X-1, (ii) RX J 1856-37, (iii) 4U 1820-30, (iv) SAX J1808.4-3658 (SS1), (v) SAX J1808.4-3658 (SS2), and (vi) PSR 1937+21 have been demonstrated through two Tables 1 and 2 which are quite satisfactory.