Stability of libration points in the restricted four-body problem with variable mass

Abstract

We have investigated the stability of the Lagrangian solutions for the restricted four-body problem with variable mass. It has been assumed that the three primaries with masses $m_{1}$, $m_{2}$ and $m_{3}$ form an equilateral triangle, wherein $m_{2}=m_{3}$. According to Jeans’ law (Astronomy and Cosmogony, Cambridge University Press, Cambridge, 1928), the infinitesimal body varies its mass $m$ with time. The space–time transformations of Meshcherskii (Studies on the Mechanics of Bodies of Variable Mass, GITTL, Moscow, 1949) are used by taking the values of the parameters $q=1/2$, $k=0$, $n=1$. The equations of motion of the infinitesimal body with variable mass have been determined. The equations of motion of the current problem differ from the ones of the restricted four-body problem with constant mass. There exist eight libration points, out of which two are collinear with the primary $m_{1}$ and the rest are non-collinear for a fixed value of parameters $\gamma (\frac{m \ \text{at time} \ t}{m \ \text{at initial time}}, 0<\gamma\leq1 )$, $\alpha$ (the proportionality constant in Jeans’ law (Astronomy and Cosmogony, Cambridge University Press, Cambridge, 1928), $0\leq\alpha\leq2.2$) and $\mu=0.019$ (the mass parameter). All the libration points are found to be unstable. The zero velocity surfaces (ZVS) are also drawn and regions of motion are discussed.

1 Introduction

In the last few decades, hundreds of articles and reviews have been published on the stability of the libration points in the restricted three-body problem with variable mass. Jeans (1928) has done the pioneer work and studied the two body problem with variable mass. Later, Meshcherskii (1949, 1952) has worked on the mechanics of bodies with variable mass. Thereafter in a series of papers, Shrivastava and Ishwar (1983), Singh and Ishwar (1984, 1985) have done exhaustive work on the restricted three-body problem with decreasing mass. They have determined the equations of motion and investigated the effect of small perturbations in the Coriolis and centrifugal forces on the stability of the triangular libration points. Lu (1990) has extended the work and introduced space–time transformations. He has shown that the regions of stability of equilibrium points do not exist in the restricted problem of three bodies with variable mass. Singh (2003) has studied linear and non-linear stability of the libration points in the restricted three-body problem with variable mass. Singh and Leke (2010) have studied the stability of the photogravitational restricted three-body problem with variable mass of the primaries. They have found that the triangular libration points are stable for $0<\mu<\mu_{c}$ and unstable for $\mu_{c}<\mu<\frac{1}{2}$. The critical value $\mu_{c}$ of the mass parameter depends upon the radiation factor $q_{1}$ and the constant due to the variation in mass $\beta$. They further observed that the collinear libration points are unstable. Letelier and Silva (2010) have determined the particular solutions to the restricted three-body problem where the bodies are allowed to either lose or gain mass to or from a static atmosphere. They have assumed that the masses of the primaries are always in a constant ratio such that all the masses are proportional to the same function of time. They have found that there exist three collinear and two triangular solutions with the relative distance of the bodies changes with time at the same rate by which masses are increasing or decreasing. Zhang et al. (2012) have investigated the triangular libration points in photogravitational restricted three-body problem with variable mass and proved that the motion around the triangular libration points become unstable for the problem with constant mass evolves into the problem with decreasing mass. The photogravitational restricted three-body problem in Zhang et al. (2012) corresponds to the special case of non-isotropic variation of mass, i.e. the mass that falls on (or is ejected from) the small body $P$ has zero momentum (Varvoglis and Hadjidemetriou 2012; Zhang 2012). Recently, Abouelmagd and Mostafa (2015) have studied the dynamics of the third body with change in mass proposed by Jeans’ law. They have obtained an approximation for the locations of the libration points, which are out-of-plane in the special case of a non-isotropic variation of the mass.

There are several celestial bodies which change their masses with time continuously. There are a number of factors which are responsible for this phenomenon like isotropic radiation or absorption in stars which cause their masses as variable. Literature has reported that the mass of Jupiter is increasing gradually (Shrivastava and Ishwar 1983).

In the present scenario, the four-body problem is interesting and important in the dynamical system. Three bodies in co-planarity revolve around their centre of mass, having orbits under the influence of their mutual gravitational attraction. The fourth infinitesimal body is attracted by the above-mentioned three bodies but it never influences their motion. The restricted problem of four bodies is to describe the motion of the fourth body. The three bodies having finite masses are known as primaries. Many mathematicians and astronomers have investigated the restricted four-body problem and have examined the existence of the libration points and their stability. Kalvouridis et al. (2007) have presented 14 families of simple periodic orbits in the restricted four-body problem. They have found that all the orbits are unstable. Papadakis (2007) has studied asymptotic solutions of the restricted planar problem of four bodies. Further, they found the invariant unstable and stable manifolds around the hyperbolic Lyapunov periodic orbits which emanate from the four collinear equilibrium points as well as the invariant manifolds from the triangular libration points. Later, Baltagiannis and Papadakis (2011) have investigated the stability of the libration points in the restricted four-body problem. They have shown that ten libration points exist and out of which two or four are collinear and the remaining are non-collinear. They have also shown that all the equilibrium points are unstable when all the primaries have equal masses. For the case when two of the primaries with equal masses, the equilibrium points are unstable except the collinear libration point $L_{3}$ and non-collinear libration points $L_{5}$ and $L_{6}$ which are stable for a limited interval of $m_{3}$. Papadouris and Papadakis (2013) have studied the photogravitational restricted four body problem (R4BP). They have determined the in-plane and out-of-plane equilibrium points and discussed their stability. They also showed that out-of-plane equilibrium points lie in $(x,z)$ plane in symmetrical position with respect to $(x,y)$ plane. Chand et al. (2015a,b) have studied the R4BP and the photogravitational R4BP when the third primary is either an oblate or prolate body, respectively. They showed that there exists eight libration points or twelve libration points when the third primary is an oblate or prolate body, respectively. They also discussed the stability of these libration points in both the cases. Singh and Vincent (2015a) studied numerically the R4BP under the influence of small perturbation in Coriolis and centrifugal forces. They have considered masses of the primaries $m_{2}$ and $m_{3}$ to be equal. They showed that their exists two collinear and six non-collinear equilibrium points. All these equilibrium points were shown unstable except two non-collinear equilibrium points. Singh and Vincent (2015b) have determined numerically the location of the out-of-plane equilibrium points in the photogravitational R4BP. They have also studied their stability and found that they are unstable. Singh and Vincent (2016) have studied numerically the photogravitational R4BP. Further, they studied the existence of the equilibrium points and their linear stability and found that all these points are unstable when the masses of all these primaries are equal. Arribas et al. (2016) have studied positions and stability of equilibria of the symmetric collinear restricted four-body problem with radiation pressure. None of the above research groups have investigated the restricted four-body problem with variable mass. This paper is an extension of the work of Zhang et al. (2012) and Singh and Vincent (2015a). We have shown the existence of the libration points and determined their locations numerically in the circular restricted four-body problem (CRFBP) with variable mass. Also, space–time inverse transformations of Meshcherskii (1949) are used to investigate the linear stability of the libration points for $\alpha>0$. Further, we have drawn ZVS for different values of the parameters and the energy constant $C$.

2 Equations of motion

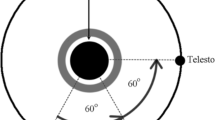
Let there be three masses $m_{1}, m_{2}$ and $m_{3}$ $(m_{1}\geq m_{2}=m_{3})$. The bodies of masses $m_{1}, m_{2}$ and $m_{3}$ are at the vertices of an equilateral triangle $ABC$ of length $l$. They revolve in circular orbits with the angular velocity $\omega$ without rotation about their centre of mass $O$. The angular velocity, $\omega$ satisfies the equation $\omega^{2}l^{2}=G(m_{1}+m_{2}+m_{3})$ (Mccuskey 1963).

The $x$-axis of the synodic system is always the line joining the primary $m_{1}$ and the mid-point of the primaries $m_{2}$ and $m_{3}$. The origin $O$ is taken as the center of mass of the primaries. The $y$-axis is the line perpendicular to the $x$-axis through $O$ in the plane of motion of the primaries. The $z$-axis is the line perpendicular to the plane of motion of the primaries through $O$ (Fig. 1). We have taken the synodic system of coordinates $O\mbox{--}xyz$; initially coincident with the inertial system $O\mbox{--}XYZ$, rotating with the angular velocity $\omega$ about $z$-axis (the $z$-axis is coincident with the $Z$-axis).

Fig. 1

Geometry of the CRFBP when mass of the infinitesimal body is variable

The methodology adopted by Abouelmagd and Mostafa (2015) has been used to determine the following equations of motion, for the infinitesimal variable mass $m$ in the inertial frame of reference under the assumptions that the mass that falls on (or is ejected from) the small body has zero momentum and the variation of the mass originates from one point:

$$\begin{aligned} &\ddot{X}+\frac{\dot{m}}{m}\dot{X}=-\frac{Gm_{1}(X-X_{1})}{{r_{1}}^{3}}- \frac {Gm_{2}(X-X_{2})}{{r_{2}}^{3}} \\ &\phantom{\ddot{X}+\frac{\dot{m}}{m}\dot{X}=} {}-\frac{Gm_{3}(X-X_{3})}{{r_{3}}^{3}}, \\ &\ddot{Y}+\frac{\dot{m}}{m}\dot{Y}=-\frac{Gm_{1}(Y-Y_{1})}{{r_{1}}^{3}}-\frac {Gm_{2}(Y-Y_{2})}{{r_{2}}^{3}} \\ &\phantom{\ddot{Y}+\frac{\dot{m}}{m}\dot{Y}=} {}-\frac{Gm_{3}(Y-Y_{3})}{{r_{3}}^{3}}, \\ &\ddot{Z}+\frac{\dot{m}}{m}\dot{Z}=-\frac{Gm_{1}(Z-Z_{1})}{{r_{1}}^{3}}-\frac {Gm_{2}(Z-Z_{2})}{{r_{2}}^{3}} \\ &\phantom{\ddot{Z}+\frac{\dot{m}}{m}\dot{Z}=} {}-\frac{Gm_{3}(Z-Z_{3})}{{r_{3}}^{3}}, \end{aligned}$$

(1)

where

$$\begin{aligned} &r_{1}^{2}=(X-X_{1})^{2}+(Y-Y_{1})^{2}+(Z-Z_{1})^{2}, \\ &r_{2}^{2}=(X-X_{2})^{2}+(Y-Y_{2})^{2}+(Z-Z_{2})^{2}, \\ &r_{3}^{2}=(X-X_{3})^{2}+(Y-Y_{3})^{2}+(Z-Z_{3})^{2}. \end{aligned}$$

We now assume that $\frac{m_{2}}{m_{1}+m_{2}+m_{3}}=\mu$ and choose units of mass, length and time such that $m_{1}+m_{2}+m_{3}=1,l=1$ and $G=1$ respectively. Thus, angular velocity $\omega=1$, masses $m_{2}=m_{3}=\mu$ and $m_{1}=1-2\mu$. The co-ordinates of the points $A, B$ and $C$ in dimensionless variables are $A(\sqrt{3}\mu,0,0),B(-\frac{\sqrt{3}}{2}(1-2\mu),-\frac{1}{2},0)$ and $C(-\frac{\sqrt{3}}{2}(1-2\mu),\frac{1}{2},0)$ respectively in the synodic system $O\mbox{--}xyz$.

Using the relations between the inertial and rotating coordinates stated in Abouelmagd and Mostafa (2015), from Eq. (1), we obtain the equations of motion in a rotating coordinate system with dimensionless variables for an infinitesimal variable mass $m(x,y,z)$ as

$$\begin{aligned} &\dot{m}(\dot{x}-y)+m(\ddot{x}-2\dot{y})=U_{x}, \\ &\dot{m}(\dot{y}+x)+m(\ddot{y}+2\dot{x})=U_{y}, \\ &\dot{m}\dot{z}+m\ddot{z}=U_{z}, \end{aligned}$$

(2)

where

$$\begin{aligned} &U=\frac{m}{2}\bigl(x^{2}+y^{2}\bigr)+m \biggl( \frac{1-2\mu}{r_{1}}+\frac{\mu }{r_{2}}+\frac{\mu}{r_{3}} \biggr), \\ &{r_{1}}^{2}=(x-\sqrt{3}\mu )^{2}+y^{2}+z^{2}, \\ &{r_{2}}^{2}= \biggl(x+\frac{\sqrt{3}}{2}(1-2\mu) \biggr)^{2}+ \biggl(y+\frac {1}{2} \biggr)^{2}+z^{2}, \\ &{r_{3}}^{2}= \biggl(x+\frac{\sqrt{3}}{2}(1-2\mu) \biggr)^{2}+ \biggl(y-\frac {1}{2} \biggr)^{2}+z^{2}. \end{aligned}$$

Equations (2) are the equations of motion of the restricted problem of four bodies when the infinitesimal mass increases or decreases with respect to time $t$.

Using Jeans’ law (1928)

$$\begin{aligned} \frac{dm}{dt} =&-\alpha m^{n}, \end{aligned}$$

(3)

where $\alpha$ is constant coefficient and the value of exponent $n$ is within the limit $0.4\leq n\leq4.4$ (for the star of the main sequence). For a rocket, $n=1$ and the mass of the rocket which varies exponentially is given by the expression $m=m_{0} e^{-\alpha t}, m=m_{0}$ at $t=0$.

We simplify the equations of motion by using the space–time transformations

$$\begin{aligned} \begin{aligned} &\xi= \gamma^{q} x,\quad\ \ \ \eta= \gamma^{q} y, \quad\ \ \ \zeta= \gamma^{q} z,\quad\ \ \ d\varGamma=\gamma^{k} dt, \\ &r_{1} = \gamma^{-q} \rho_{1}, \quad\ \ \ r_{2} = \gamma^{-q} \rho_{2},\quad\ \ \ r_{3} = \gamma^{-q} \rho_{3}, \end{aligned} \end{aligned}$$

(4)

where

$$\begin{aligned} \gamma =& \frac{m}{m_{0}}. \end{aligned}$$

(5)

Now, following the procedure of Zhang et al. (2012) and taking $q=\frac {1}{2}$, $k=0$, $n=1$, the equations of motion (2) after using (3), (4) and (5) become

$$\begin{aligned} \begin{aligned} &\ddot{\xi}-2 \dot{\eta} = W_{\xi}, \\ &\ddot{\eta}+2 \dot{\xi} = W_{\eta}, \\ &\ddot{\zeta} = W_{\zeta}, \end{aligned} \end{aligned}$$

(6)

where

$$\begin{aligned} \begin{aligned} &W = \frac{1}{2} \biggl(1+\frac{\alpha^{2}}{4} \biggr) \bigl( \xi^{2}+\eta ^{2}\bigr) \\ &\phantom{W =}{}+\gamma^{3/2} \biggl( \frac{1-2\mu}{\rho_{1}}+\frac{\mu}{\rho_{2}}+\frac {\mu}{\rho_{3}} \biggr)+\frac{\alpha^{2}}{8} \zeta^{2}, \\ &{\rho_{1}}^{2} = \bigl(\xi-\sqrt{3}\mu \gamma^{1/2} \bigr)^{2}+\eta ^{2}+ \zeta^{2}, \\ &{\rho_{2}}^{2} = \biggl(\xi+\frac{\sqrt{3}}{2}(1- 2\mu) \gamma ^{1/2} \biggr)^{2}+ \biggl(\eta+\frac{1}{2} \gamma^{1/2} \biggr)^{2}+\zeta ^{2}, \\ &{\rho_{3}}^{2} = \biggl(\xi+\frac{\sqrt{3}}{2}(1- 2\mu) \gamma ^{1/2} \biggr)^{2}+ \biggl(\eta-\frac{1}{2} \gamma^{1/2} \biggr)^{2}+\zeta^{2}. \end{aligned} \end{aligned}$$

(7)

From Eqs. (6), it may be observed that

$$\begin{aligned} \bigl(\dot{\xi}^{2}+\dot{\eta}^{2}+\dot{ \zeta}^{2}\bigr)=2W-C-2 \int_{0}^{t} W_{t} dt, \end{aligned}$$

(8)

where $C$ is similar to Jacobi integral.

3 Libration points

The libration points with variable mass $m$ are obtained by solving the equations:

$$\begin{aligned} W_{\xi} =& 0, \\ W_{\eta} =& 0, \\ W_{\zeta} =& 0, \end{aligned}$$

where

$$\begin{aligned} W_{\xi} =& \biggl(1+\frac{\alpha^{2}}{4} \biggr)\xi - \gamma^{3/2} \biggl\{ \frac{(1-2\mu)(\xi-\sqrt{3}\mu\gamma^{1/2})}{\rho _{1}^{3}} \\ &{}+\mu \biggl(\frac{\xi+\frac{\sqrt{3}}{2}(1-2\mu)\gamma^{\frac {1}{2}}}{\rho_{2}^{3}} \biggr) \\ &{} +\mu \biggl(\frac{\xi+\frac{\sqrt{3}}{2}(1-2\mu)\gamma^{\frac{1}{2}}}{\rho _{3}^{3}} \biggr) \biggr\} , \end{aligned}$$

(9)

$$\begin{aligned} W_{\eta} =& \biggl(1+\frac{\alpha^{2}}{4} \biggr)\eta - \gamma^{3/2} \biggl\{ \frac{(1-2\mu)\eta}{\rho_{1}^{3}} +\mu \biggl(\frac{\eta+\frac{1}{2}\gamma^{\frac{1}{2}}}{\rho_{2}^{3}} \biggr) \\ &{}+\mu \biggl(\frac{\eta-\frac{1}{2}\gamma^{\frac{1}{2}}}{\rho_{3}^{3}} \biggr) \biggr\} , \end{aligned}$$

(10)

$$\begin{aligned} W_{\zeta} =&\frac{\alpha^{2}}{4}\zeta -\gamma^{3/2} \biggl\{ \frac{(1-2\mu)\zeta}{\rho_{1}^{3}} +\frac{\mu\zeta}{\rho_{2}^{3}} +\frac{\mu\zeta}{\rho_{3}^{3}} \biggr\} . \end{aligned}$$

(11)

Here the values of $\rho_{1},\rho_{2}$ and $\rho_{3}$ are given by Eqs. (7). When $\alpha=0$ or $\gamma=1$, Eqs. (9) and (10) are the corresponding ones when $\epsilon=0$ and ${\epsilon}'=0$ presented in Singh and Vincent (2015a). For $\alpha\neq0$, the positions of the libration points are determined numerically for different values of $\alpha$ and $\gamma$. As mentioned in Singh and Vincent (2015a), we have used the value of $\mu=0.019$ throughout this paper. We have calculated few of the libration points for different values of the parameters ($0\leq\alpha\leq2.2$ and $0<\gamma\leq1$). We, now define the collinear libration points, non-collinear libration points and the out-of-plane libration points.

3.1 Collinear libration points

The collinear libration points are the ones lying on $\xi$-axis. These libration points are obtained from Eqs. (9), (10) and (11) by taking $\eta=\zeta=0$. The abscissae of the collinear libration points are the roots of the equation

$$\begin{aligned} g(\xi,0,0) =& \biggl(1+\frac{\alpha^{2}}{4} \biggr)\xi-\gamma^{3/2} \biggl\{ \frac{(1-2\mu)(\xi-\sqrt{3}\mu\gamma^{1/2})}{\mid\xi-\sqrt{3}\mu\gamma ^{1/2}\mid^{3}} \\ &{}+2\mu \biggl(\frac{\xi+\frac{\sqrt{3}}{2}(1-2\mu)\gamma^{\frac {1}{2}}}{ ((\xi+\frac{\sqrt{3}}{2}(1-2\mu)\gamma^{\frac{1}{2}})^{2}+\frac {1}{4}\gamma )^{\frac{3}{2}}} \biggr) \biggr\} =0. \end{aligned}$$

There exist two collinear libration points namely $L_{1}$ and $L_{2}$. In Tables 1, 2 and 3, we have presented the numerical values of these collinear libration points for fixed values of $\gamma=0.1, 0.4, 0.9$ and different values of $\alpha=0.2, 0.4, 0.6, 0.8, 1, 1.15, 2.2$ and $\gamma=1, \alpha=0$, respectively.

Table 1 Libration points in $\xi\eta$-plane

Table 2 Libration points in $\xi\eta$-plane

Table 3 Libration points in $\xi\eta$-plane when $\gamma=1$ and $\alpha =0$ (similar to Singh and Vincent (2015a) when $\varepsilon =\varepsilon'=0$)

3.2 Non-collinear librations points

The non-collinear libration points are the ones lying in $\xi\eta$-plane but not on $\zeta$-axis. The non-collinear libration points are obtained from Eqs. (9), (10) and (11) by taking $\xi\neq0$, $\eta\neq0$ and $\zeta=0$. From Tables 1 and 2, we observe that there exist six non-collinear libration points namely $L_{i}\ (i=3,4,5,6,7,8)$ for wide range of parameters $\gamma$ and $\alpha$, ($0<\gamma\leq1$ and $0\leq \alpha\leq2.2$). In Table 3, we have shown the libration points of Singh and Vincent (2015a).

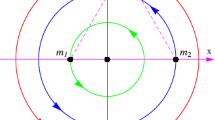
The locations of the collinear and non-collinear libration points are shown in Fig. 2 for various values of parameters $\gamma$ and $\alpha$. In Fig. 2, frame-(a), we have taken $\mu=0.019, \gamma=0.1$ and $\alpha=0.2,0.4,0.6,0.8,1.0,1.15,2.2$. In Fig. 2, frame-(b) and (c), the values of $\gamma$ are taken as 0.4 and 0.9 and $\alpha$ has the same values as in frame-(a).

Fig. 2

The location of eight equilibrium points in the CRFBP with variable mass (a) for $\gamma=0.1$ (b) for $\gamma=0.4$ and (c) for $\gamma=0.9$ and for different values of $\alpha=0.2$ (red, gray), 0.4 (blue, gray), 0.6 (black, gray), 0.8 (green, gray), 1 (purple, gray), 1.15 (orange, gray), 2.2 (magenta, gray). The blue dots show the position of three primaries and black dots show the equilibrium points

It is observed from Fig. 2 that:

• In all the cases, libration point $L_{1}$ is shifted from right to left and the point $L_{2}$ is shifted from left to right towards the bigger primary $m_{1}$ along the $\xi$-axis.

• The non-collinear libration points $L_{3,4}$, $L_{5,6}$ and $L_{7,8}$ are symmetric with respect to $\xi$-axis.

• The libration points $L_{3}$ and $L_{7}$ are located near $m_{3}$ on a dumbbell shaped curve with $L_{3}$ and $L_{7}$ vertically opposite to $m_{3}$. Similar result is observed for $L_{4}$ and $L_{8}$ with respect to $m_{2}$.

• It is also observed from Fig. 2, frames-(a–c), that if $\alpha$ is increased for fix values of $\mu=0.019$ and $\gamma=0.1,0.4$ and 0.9, the points $L_{6}$ and $L_{8}$ move towards the primary $m_{2}$ and the points $L_{5}$ and $L_{7}$ move towards the primary $m_{3}$. The points $L_{3}$ and $L_{4}$ move away from the primaries $m_{3}$ and $m_{2}$ respectively and moving towards the origin.

• It is further observed from Fig. 2 that the locus of $L_{i}\ (i=3,4,\ldots,8)$ are almost a straight line for different values of the parameter $\alpha$.

3.3 Out-of-plane libration points

The libration points which lie in $\xi\zeta$-plane $(\eta=0)$ are called out-of-plane libration points. Moreover, we have determined that the out-of-plane libration points also exist as mentioned by Abouelmagd and Mostafa (2015), (Table 4). The out-of-plane libration points are obtained from Eqs. (9), (10) and (11) by taking $\xi \neq0, \zeta\neq0$ and $\eta=0$. There exist two out-of-plane libration points namely $L_{9}$ and $L_{10}$, which are symmetrical with respect to $\xi\eta$-plane. In Table 4, we have evaluated the numerical values of these out-of-plane libration points for fixed value of $\gamma=0.5$ and different values of $\alpha=0.2, 0.4, 0.6, 0.8, 1, 1.15, 2.2$. Further, we have plotted these points for the above mentioned values of $\gamma$ and $\alpha$ in Fig. 3.

Fig. 3

The location of the out-of-plane libration points $L_{9,10}$ in the CRFBP with variable mass $\gamma=0.5$ (a) for $\alpha=0.4$ (b) for $\alpha=0.2$ (in black), $\alpha=0.4$ (in blue), $\alpha=0.8$ (in red), $\alpha=1.0$ (in green), $\alpha=1.15$ (in magenta) and $\alpha=2.2$ (in purple)

Table 4 Locations of out-of-plane non-collinear libration points on $\xi\zeta$-plane when $\gamma=0.5$

It has been observed that in all the above three cases there is very good agreement between numerical and graphical values.

4 Zero velocity surfaces (ZVS)

Following the procedure given in Abouelmagd and Mostafa (2015), the condition of motion can be written as

$$\begin{aligned} &W(\gamma)\geq C(\gamma) \quad\text{for}\ \frac{\partial W}{\partial\gamma}\geq0, \\ &W(\gamma_{0})\geq C(\gamma_{0}) \quad\text{for}\ \frac{\partial W}{\partial\gamma}\leq0, \end{aligned}$$

where

$$\begin{aligned} &C(\gamma)=\frac{-V_{0}^{2}}{2}+W(\gamma,\xi_{0},\eta_{0}, \zeta _{0}), \\ &V_{0}^{2}=\dot{\xi_{0}}^{2}+\dot{ \eta_{0}}^{2}+\dot{\zeta_{0}}^{2}. \end{aligned}$$

The subscript ‘₀’ denotes the initial value of the corresponding variables. It can be seen that the energy constant $C$ depends upon the value of $\gamma$ and initial conditions.

The quantity in left hand side of Eq. (8) is always non-negative, so for a given value of $C$ the quantity $2W-C-2\int _{0}^{t} W_{t} dt \geq0$ should satisfy for all values of time and initial conditions. In Fig. 4, we have plotted the ZVS using the Eq. (8) for the different values of Jacobian constant $C$ and for fixed value of variable mass parameter $\gamma$ and for fixed value of $\alpha$. The ZVS are classified from the larger to smaller value of Jacobian constant $C$. In Fig. 4, the value of $\mu=0.019$, $\gamma =0.1$ and $\alpha=0.2$ are fixed in all the frames. Frame-(a), shows the ZVS for Jacobian constant $C=0.17$ and reveals that, there exists circular island (in white colour) around each of the primaries and the fourth particle is trapped in this small areas around the primaries, where the motion is possible and the circular strip (in light blue colour) shows the forbidden region. Thus, the fourth body can move around each of the primaries and can not move from one primary to other primary. In frame-(b), we have decrease the value of Jacobian constant $C=0.161$ and observed that the inner circular boundary breaks at $L_{3}$ and $L_{4}$. Hence, the infinitesimal mass $m$ can move freely from one primary to other primary, but the infinitesimal mass is restricted to move outside the outer circular boundary. Frame-(c) is drawn for $C=0.160687$ and observed that there exists two limiting situations and cusps are formed at $L_{7}$ and $L_{8}$. In frame-(d), the curves of zero velocity constitute two branches for Jacobian constant $C=0.157$. The first branch contains $L_{1}$, $L_{5}$ and $L_{6}$ and the other branch contains $L_{2}$. We further, noticed that the fourth body can move from one primary to other primary. The corridor at $m_{2}$ and $m_{3}$ are formed, so that it can move out side the circular boundary as well. For $C=0.151968$ in frame-(e), there exist a limiting situation and a cusp at $L_{1}$ and an island containing $L_{2}$ is formed and the fourth particle is free to move everywhere in white region of the plane. For $C=0.1509$, in frame-(f), the curves split into two parts at $L_{1}$ and shrink to tadpole shaped curves around $L_{5}$ and $L_{6}$. Also an island type region containing $L_{2}$ occurs in the frame. In the last frame (g), the island type region at $L_{2}$ disappears for $C=0.150$. There is only forbidden region around $L_{5}$ and $L_{6}$ in tadpole shaped region and the fourth particle is free to move everywhere in the plane.

Fig. 4

The ZVS of the CRFBP for different values of the energy constant $C$ and for fixed values of $\gamma=0.1$ and $\alpha=0.2$. Here frame-(a) $C=0.17$, frame-(b) $C=0.161$, frame-(c) $C=0.160687$, frame-(d) $C=0.157$, frame-(e) $C=0.151968$, frame-(f) $C=0.1509$ and frame-(g) $C=0.150$. Here black dots represent the eight libration points and the blue dots are the primaries

In Fig. 5, we have determined the ZVS for fixed value of Jacobian constant $C=0.6280687$, $\alpha=0.2$ and different values of $\gamma =0.1, 0.4, 0.9$ in frames-(a, b, c) respectively. In Fig. 6, we have determined the ZVS for fixed value of Jacobian constant $C=0.6280687725$, $\gamma=0.4$ and different values of $\alpha =0.2, 0.6, 0.8$. There is substantial impact of $\alpha$ and $\gamma$ on ZVS.

Fig. 5

The ZVS for the energy constant $C=0.6280687$ in the CRFBP with variable mass (a) for $\gamma=0.1$ (b) for $\gamma=0.4$ and (c) for $\gamma=0.9$ and for fixed value of $\alpha=0.2$. The blue dots show the position of three primaries and black dots show the libration points

Fig. 6

The ZVS in the CRFBP with variable mass for fixed value of $\gamma=0.4$ and the energy constant $C=C_{1}=C_{2}=C_{3}= 0.6280687725$ and for different values of $\alpha=0.2, 0.6, 0.8$. Also $C=C_{4}= 0.6237501$ with $\alpha=0.6$. The blue dots show the position of three primaries and black dots show the libration points

Figure 7 illustrates the out-of-plane ZVS for different values of the energy constant $C$ and for fixed values of $\alpha=0.2$ and $\gamma =0.5$. In Fig. 7, we have drawn ZVS for possible regions of forbidden motion in $\xi\zeta$-plane. Figures (7a, b, c) illustrate the regions of forbidden motion for different values of the energy constant $C$ and fixed values of $\alpha=0.2$ and $\gamma=0.5$. For $C=1.258$ (Fig. 7a), we observe that the infinitesimal mass can only move in the circular white region around $m_{1}$, therefore infinitesimal mass can never approach to the other primaries and vice-versa. For $C=0.757645$ (Fig. 7b), we observe that there is a small opening to the right side of the primary $m_{1}$, so that the infinitesimal mass can move from $m_{1}$ to the other primaries and vice-versa. For $C=0.7$ (Fig. 7c), it is observed that the ZVS constitutes two branches containing the libration points $L_{9}$ and $L_{10}$, so that the infinitesimal mass can move more freely through the corridor around the primary $m_{1}$ to the other primaries and vice-versa.

Fig. 7

The ZVS in the $\xi\zeta$-plane of the CRFBP with variable mass for $\alpha=0.2$, $\gamma=0.5$ (a) for the energy constant $C=1.258$ (b) for the energy constant $C=0.757645$ and (c) for the energy constant $C=0.7$. The blue dot shows the position of the primary $m_{1}$ and black dots show the libration points

In Fig. 8a, we have drawn ZVS for fixed value of energy constant $C=0.757645$, $\gamma=0.5$ and different values of $\alpha=0.2, 0.4, 0.6, 0.8$. We have observed that $\alpha$ has significant impact to the zero velocity surfaces in the $\xi\zeta$-plane. As we increase the value of $\alpha$, the regions of motion also increase. Figure 8b shows the zoom part of the Fig. 8a. It has been observed that as we change $\alpha$ from 0.2 to 0.4 the corridor exists around $m_{1}$, so that the infinitesimal mass can move freely from $m_{1}$ to the other primaries.

Fig. 8

The ZVS in the $\xi\zeta$-plane of the CRFBP with variable mass for the energy constant $C=0.757645$, $\gamma=0.5$. (a) for different values of $\alpha=0.2$ (black), 0.4 (blue), 0.6 (green) and 0.8 (magenta). The blue dot shows the position of the primary $m_{1}$ and black dots show the libration points. (b) the zoomed part of (a) near primary $m_{1}$

5 Stability of the libration points

Now, using the space–time inverse transformations of Meshcherskii (1949) and following the procedure of Zhang et al. (2012), we investigate the linear stability of the libration points.

Displacing $(\xi_{0},\eta_{0},\zeta_{0})$ as

$$\begin{aligned} \begin{aligned} &\xi= \xi_{0}+u, \qquad \eta= \eta_{0}+v,\\ &\zeta= \zeta_{0}+w,\quad (u,v,w \ll 1), \end{aligned} \end{aligned}$$

(12)

where $(\xi_{0},\eta_{0},\zeta_{0})$ is the libration point for a fixed value of time $t$.

Using Eqs. (12) in Eqs. (6), the following variational equations are obtained

$$\begin{aligned} &\ddot{u}-2\dot{v} = (W_{\xi\xi})_{0}u +(W_{\xi\eta})_{0}v +(W_{\xi\zeta })_{0}w, \\ &\ddot{v}+2\dot{u} = (W_{\eta\xi})_{0}u +(W_{\eta\eta})_{0}v +(W_{\eta \zeta})_{0}w , \\ &\ddot{w} =(W_{\zeta\xi})_{0}u +(W_{\zeta\eta})_{0}v +(W_{\zeta\zeta})_{0}w, \end{aligned}$$

(13)

where the subscript ‘0’ in Eqs. (13) indicates that the values are to be calculated at the libration point $(\xi_{0},\eta_{0},\zeta_{0})$ under consideration, where

$$\begin{aligned} W_{\xi\xi} =& \biggl(1+\frac{\alpha^{2}}{4} \biggr)+3 \gamma^{\frac {3}{2}} \biggl\{ (1-2\mu)\frac{(\xi-\sqrt{3}\mu\gamma^{1/2})^{2}}{{\rho _{1}}^{5}} \\ &{}+\mu\frac{(\xi+\frac{\sqrt{3}}{2}(1-2\mu)\gamma^{1/2})^{2}}{{\rho _{2}}^{5}} \\ &{}+\mu\frac{(\xi+\frac{\sqrt{3}}{2}(1-2\mu)\gamma ^{1/2})^{2}}{{\rho_{3}}^{5}} \biggr\} \\ &{}-\gamma^{3/2} \biggl(\frac{1-2\mu}{{\rho_{1}}^{3}}+\frac{\mu}{{\rho _{2}}^{3}}+ \frac{\mu}{{\rho_{3}}^{3}} \biggr), \\ W_{\eta\xi} =&W_{\xi\eta} \\ =&3\gamma^{\frac{3}{2}} \biggl\{ (1-2\mu) \frac {(\xi-\sqrt{3}\mu\gamma^{1/2})\eta}{{\rho_{1}}^{5}} \\ &{} +\mu\frac{(\xi+\frac{\sqrt{3}}{2}(1-2\mu)\gamma^{1/2})(\eta+\frac {\gamma^{1/2}}{2})}{{\rho_{2}}^{5}} \\ &{}+\mu\frac{(\xi+\frac{\sqrt{3}}{2}(1-2\mu)\gamma^{1/2})(\eta-\frac {\gamma^{1/2}}{2})}{{\rho_{3}}^{5}} \biggr\} , \\ W_{\eta\eta} =& \biggl(1+\frac{\alpha^{2}}{4} \biggr)+3\gamma^{\frac {3}{2}} \biggl\{ (1-2\mu)\frac{\eta^{2}}{{\rho_{1}}^{5}} \\ &{}+\mu\frac{(\eta+\frac {\gamma^{1/2}}{2})^{2}}{{\rho_{2}}^{5}}+\mu\frac{(\eta-\frac{\gamma^{1/2}}{2})^{2}}{{\rho_{3}}^{5}} \biggr\} \\ &{} -\gamma^{3/2} \biggl( \frac{1-2\mu}{{\rho_{1}}^{3}}+\frac{\mu}{{\rho _{2}}^{3}}+\frac{\mu}{{\rho_{3}}^{3}} \biggr), \\ W_{\zeta\xi} =&W_{\xi\zeta} \\ =&3\gamma^{\frac{3}{2}}\zeta \biggl\{ (1-2\mu )\frac{(\xi-\sqrt{3}\mu\gamma^{1/2})}{{\rho_{1}}^{5}} \\ &{}+\mu\frac{(\xi+\frac{\sqrt{3}}{2}(1-2\mu)\gamma^{1/2})}{{\rho _{2}}^{5}} \\ &{}+\mu\frac{(\xi+\frac{\sqrt{3}}{2}(1-2\mu)\gamma^{1/2})}{{\rho _{3}}^{5}} \biggr\} , \\ W_{\eta\zeta} =& W_{\zeta\eta} \\ =& 3\gamma^{\frac{3}{2}}\zeta \biggl\{ (1-2\mu)\frac{\eta}{\rho_{1}^{5}} +\mu\frac{(\eta+\frac{\gamma ^{1/2}}{2})}{\rho_{2}^{5}} \\ &{}+\mu\frac{(\eta-\frac{\gamma^{1/2}}{2})}{\rho _{3}^{5}} \biggr\} , \\ W_{\zeta\zeta} =&3\gamma^{\frac{3}{2}}\zeta^{2} \biggl( \frac{1-2\mu}{\rho _{1}^{5}}+\frac{\mu}{\rho_{2}^{5}}++\frac{\mu}{\rho_{3}^{5}} \biggr) \\ &{}- \gamma^{3/2} \biggl(\frac{1-2\mu}{\rho_{1}^{3}}+\frac{\mu}{\rho _{2}^{3}}+\frac{\mu}{\rho_{3}^{3}} \biggr)+\frac{\alpha^{2}}{4}. \end{aligned}$$

(14)

For $\alpha=0$, the system (13) corresponds to a system with constant mass. For $\alpha>0$, the coordinates of the three primaries vary with time $t$ and their distances to the libration point $(\xi_{0},\eta_{0},\zeta_{0})$ decrease with time. Therefore, the linear stability can not be determined by ordinary method. That is why the space–time inverse transformations of Meshcherskii (1949) i.e. $x=\gamma^{-1/2}\xi$, $y=\gamma ^{-1/2}\eta$ and $z=\gamma^{-1/2}\zeta$ have been used. The positions of the primaries are fixed so that their distances to the libration points are invariable.

We, now, write Eqs. (13) in phase-space as

$$\begin{aligned} \begin{aligned} &\dot{u}=u_{1}, \qquad\dot{v}=v_{1}, \qquad\dot{w}=w_{1}, \\ &\dot{u_{1}}-2{v_{1}}=(W_{\xi\xi})_{0}u +(W_{\xi\eta})_{0}v +(W_{\xi\zeta })_{0}w, \\ &\dot{v_{1}}+2{u_{1}}=(W_{\eta\xi})_{0}u +(W_{\eta\eta})_{0}v +(W_{\eta\zeta })_{0}w, \\ &\dot{w_{1}}=(W_{\zeta\xi})_{0}u +(W_{\zeta\eta})_{0}v +(W_{\zeta\zeta})_{0}w. \end{aligned} \end{aligned}$$

(15)

Using Meshcherskii (1949) inverse transformations, and taking

$$\begin{aligned} &x'=\gamma^{-1/2}u, \qquad u'= \gamma^{-1/2}u_{1}, \\ &y'=\gamma^{-1/2}v, \qquad v'= \gamma^{-1/2}v_{1}, \\ &z'=\gamma^{-1/2}w, \qquad w'= \gamma^{-1/2}w_{1}, \end{aligned}$$

the system (15) can be rewritten in the matrix form as follows:

$$\begin{aligned} \left ( \textstyle\begin{array}{c} \frac{dx'}{dt} \\ \frac{dy'}{dt} \\ \frac{dz'}{dt} \\ \frac{du'}{dt} \\ \frac{dv'}{dt} \\ \frac{dw'}{dt} \end{array}\displaystyle \right ) =& \left ( \textstyle\begin{array}{c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c} \frac{\alpha}{2} & 0 & 0 & 1 & 0 & 0 \\ 0 & \frac{\alpha}{2} & 0 & 0 & 1 & 0 \\ 0 & 0 & \frac{\alpha}{2} & 0 & 0 & 1 \\ (W_{\xi\xi})_{0} & (W_{\xi\eta})_{0} & 0 & \frac{\alpha}{2} & 2 & 0 \\ (W_{\eta\xi})_{0} & (W_{\eta\eta})_{0} & 0 & -2 & \frac{\alpha}{2} & 0 \\ 0 & 0 & (W_{\zeta\zeta})_{0} & 0 & 0 & \frac{\alpha}{2} \\ \end{array}\displaystyle \right ) \\ &{}\times \left ( \textstyle\begin{array}{c} {x'} \\ {y'} \\ {z'} \\ {u'} \\ {v'} \\ {w'} \\ \end{array}\displaystyle \right ). \end{aligned}$$

(16)

As the positions of the primaries are fixed and their distances to the libration points are invariable, the stability of (16) and (6) is consistent with each other. In the original null solution, when $\alpha=0$, the solution get changed to a non-trivial solution (Lu 1990). Thus, the linear stability of this solution depends on the existence of stable region of the libration point, which in turn depends on the boundedness of the solution of linear and homogeneous system of Eqs. (16). Herein, we have determined the linear stability of the libration points, by finding the characteristic roots of the coefficient matrix of Eqs. (16) numerically.

The characteristic equation corresponding to the libration point under consideration is

$$\begin{aligned} &\lambda^{6}-3\alpha\lambda^{5}+ \biggl(\frac{15}{4}\alpha^{2}+P \biggr)\lambda^{4}- \biggl(\frac{5}{2}\alpha^{3}+P\alpha \biggr)\lambda^{3} \\ &\quad {}+ \biggl(\frac{15}{16}\alpha^{4} +\frac{3}{2}P\alpha^{2}+Q \biggr)\lambda^{2} \\ &\quad {}- \biggl(\frac{3}{16}\alpha ^{5}+\frac{1}{2}P \alpha^{3}+Q\alpha \biggr)\lambda \\ &\quad {}+ \biggl(\frac{1}{64} \alpha^{6}+\frac{1}{16}P\alpha^{4}+\frac{1}{4}Q \alpha^{2}+R \biggr)=0, \end{aligned}$$

(17)

where

$$\begin{aligned} &P = 4-(W_{\xi\xi})_{0}-(W_{\eta\eta})_{0}-(W_{\zeta\zeta})_{0}, \\ &Q = (W_{\xi\xi})_{0}(W_{\zeta\zeta})_{0}+(W_{\eta\eta})_{0}(W_{\zeta\zeta })_{0}+(W_{\xi\xi})_{0} (W_{\eta\eta})_{0} \\ &\phantom{Q =}{}-4(W_{\zeta\zeta})_{0}-\bigl[(W_{\xi\eta})_{0} \bigr]^{2}, \\ &R = -(W_{\xi\xi})_{0}(W_{\eta\eta})_{0}(W_{\zeta\zeta})_{0}+(W_{\zeta\zeta })_{0} \bigl[(W_{\xi\eta})_{0}\bigr]^{2}, \end{aligned}$$

the values of $(W_{\xi\xi})_{0}$, $(W_{\eta\eta})_{0}$, $(W_{\zeta\zeta })_{0}$ and $(W_{\xi\eta})_{0}$ are given by Eqs. (15).

The characteristic roots of Eq. (17) have been calculated at various libration points in the range $0<\gamma\leq1$, $0\leq\alpha\leq2.2$ and $\mu=0.019$. It has been observed that there always exist at least one positive real characteristic root at each libration point. Hence, it can be concluded that all the libration points are unstable for $\alpha>0$.

6 Conclusion

The existence and stability of the libration points in the restricted four-body problem with variable mass and the primaries with masses $m_{1}$, $m_{2}$ and $m_{3}$ $(m_{1}\geq m_{2}=m_{3})$ have been investigated. It has been found that there exist eight libration points, out of which $L_{1}$ and $L_{2}$ are collinear with the primary $m_{1}$ and the rest $L_{i}\ (i=3,\ldots,8)$ are non-collinear. We have found that the out-of-plane libration points namely $L_{9}$ and $L_{10}$ also exist which are symmetrical with respect to $\xi\eta$-plane (Table 4). We have also observed that the non-collinear libration points are symmetric about $\xi$-axis (Tables 1–3). In all cases, all the libration points are unstable for $\alpha>0$. For $\alpha>0$, the positions of all the libration points $L_{i}\ (1,2,\ldots,10)$ are shown in Figs. 2 and 3.

Our results are different from Zhang et al. (2012) in some aspects like, (i) they have studied the existence and the stability of the libration points in the photogravitational restricted three-body problem with variable mass, whereas we have studied the existence and the stability of the libration points in the restricted four-body problem with variable mass; (ii) they have determined only non-collinear libration points, whereas we have determined collinear, non-collinear and out-of-plane libration points; (iii) they have determined that there are two non-collinear libration points and these points are time dependent, whereas in our case there are six non-collinear libration points and these are also time dependent; (iv) in their case, the libration points are symmetrical about $\xi$-axis and approaches towards origin with the increase of $\alpha$ or with the decrease of $\gamma$. In our case, all the libration points move towards the primaries except $L_{3}$ and $L_{4}$ which move away from masses $m_{3}$ and $m_{2}$ respectively. However, all the libration points are found to be unstable in restricted three-body problem (Zhang et al. 2012) and in our restricted four-body problem for $\alpha>0$.

On comparing our results with the results of Singh and Vincent (2015a), our results are different from their in several aspects: (i) they have studied the restricted four-body problem with constant mass, whereas we have studied the restricted four-body problem with variable mass; (ii) they have determined that there are eight libration points which are independent of time, whereas we have also determined that there exist eight libration points which are time dependent; (iii) they have reported that there exist two collinear and six non-collinear libration points, we have also observed the same, but in our case the libration points are time dependent; (iv) they have determined the linear stability of the libration points and found that all the libration points are unstable except two non-collinear libration points, while in our case all the libration points are unstable due to variable mass; (v) from the ZVS, we observe that lesser energy is required in our case to achieve the same regions of motion.

The results of Singh and Vincent (2015a) can be verified from our results by taking $\gamma=1$ or $\alpha=0$ in our case and $\epsilon=0$ and ${\epsilon}'=0$ in their case. It has been observed that the problems with variable mass destroy the stability.

From the results in Fig. 4, we conclude that for different values of the energy constant $C$, we have different trapped areas in which the fourth body can move. Furthermore, we observe that the fourth body can move free around the primaries for smaller-and-smaller values of Jacobian constant $C$. It is obvious that Jacobian constant $C$ has substantial impact on the areas where the fourth body can move. From Fig. 5, it is evident that the variable mass parameter $\gamma$ have significant impact on the topology of the ZVS in the $\xi\eta$-plane. As we increase the value of $\gamma$, the forbidden region decreases. Figure 6 reveals that the parameter $\alpha$ also have significant impact on the topology of the zero velocity surfaces in the $\xi\eta$-plane. As we increase the value of $\alpha$, the forbidden region decreases. In Figs. 7 and 8, we have plotted the ZVS in $\xi\zeta$-plane and observed that as the value of the energy constant decreases, the region of possible motion increases (Fig. 7) and as the value of $\alpha$ increases the regions of possible motion also increases (Fig. 8). We have also observed that as we increase the values of $\alpha$, the libration points $L_{9}$ and $L_{10}$ move towards the primary $m_{1}$. Therefore, we can conclude that variable mass parameter $\gamma$ has substantial effect on the regions of motion.