1 Introduction

Wormholes are exciting objects predicted by general relativity which are topological tunnel-like structures of the spacetime playing a role of bridge connecting disconnected regions in one or different universes. The first traversable general relativistic wormhole solution has been obtained by Ellis (1973) and its properties have been studied by Morris et al. (1988), Morris and Thorne (1988) (for the comprehensive review please look to Visser 1995). The discussed wormhole solutions were obtained in the framework of general relativity, if some standard conditions on the energy-stress tensor are modified, due to e.g. quantum effects or so. However, there are some attempts to obtain wormhole solutions in modified gravity due to the corrections introduced by the modifications (Harko et al. 2013). Possible ways to observationally distinguish wormholes from other compact gravitational objects, in particular, through the effect of gravitational lensing are extensively discussed in the literature (see e.g. Chetouani and Clement 1984; Clément 1984; Perlick 2004; Nandi et al. 2006; Dey and Sen 2008; Tsukamoto and Harada 2013; Kardashev et al. 2007; Cramer et al. 1995; Harko et al. 2009; Tsukamoto et al. 2012; Bambi 2013a). It is interesting to mention that the traversable wormholes have recently been attractive from point of view of scientific fiction (James et al. 2015b,a). Kleihaus and Kunz (2014) have recently provided the first numerical globally regular rotating wormhole solutions and analysed their physical properties.

It is believed that the most strong evidence of the existence of the black hole can be achieved only through the direct observation of its image. Due to this reason the study of the shadow of the black hole has received much attention in the recent years motivated by the presence of the supermassive black holes (SMBH) at the galactic centers and the high resolution of the current and future telescopes as Event Horizon Telescope (EHT),Footnote 1 International Space Very Long Baseline Interferometry (VLBI) project RadioAstron and future Cosmic Radio-interferometers as Millimetron etc.

EHT project consists in phasing up millimetre and sub-millimetre telescopes scattered over the world, which together will form an effective high-resolution Earth-sized telescope.

The orbital motion of the stars surrounding SMBH Sgr A*, which is the compact radio source at the center of the Milky Way, indicates that its mass is \(4\times10^{6} M_{\odot}\) (Ghez et al. 2008; Genzel et al. 2010). Dexter et al. (2012) have calculated the structure surrounding the supermassive black hole candidate at the centre of M87 which drives an ultra-relativistic jet visible on kiloparsec scales. M87 is also one of the two largest black holes on the sky (along with the Galactic Center SMBH candidate, Sgr A*). Its mass is \(\simeq 6.4 \times10^{9} M_{\odot}\) (Gebhardt et al. 2011), which is 1600 times larger than Sgr A*. At a distance of 16 Mpc, the angular size is about \(4/5\) that of Sgr A*. Recent VLBI observations at 1.3 mm have detected source structure in Sgr A* on event horizon scales (Fish et al. 2011), allowing a direct comparison between observations and black hole accretion theory. These observations also have the potential to detect the black hole shadow (Bardeen 1973; Falcke et al. 2000), which would provide the first direct evidence for an event horizon.

In Table 1 adopted from Cherepashchuk (2014) one can find masses of some stellar and supermassive black holes, distances to them and the corresponding linear and angular diameters of their shadows. One can see that angular sizes of the shadows of the stellar mass black holes are very small (less than nanoarcseconds). However, the angular Schwarzschild radius of the supermassive black hole Sgr A* is about \(10~\upmu\mbox{as}\) and thus the angular diameter of the shadow is of the order of \(50~\upmu\mbox{as}\) which can be obtained from the rough evaluation of the shadow as \(2.6 r_{S}\) where \(r_{S} = 2GM/c^{2}\) is the Schwarzschild radius, \(c\) is the speed of light and \(G\) the gravitation constant, using the values of the distance of Sgr A* from the Sun as 8 kpc, and the mass of Sgr A*. The angular size of the shadow of SMBH at the center of M87 is of the same order i.e. about \(40~\upmu\mbox{as}\). The current resolution is therefore not yet sufficient to get an image of the shadow of the black hole, but it is quite close. Adding more baselines to the EHT array will thus improve the resolution so that the shadow of Sgr A* should be observed in the very near future.

Table 1 Masses, distances and estimated diameters of the shadows of the various black holes (Cherepashchuk 2014)
Full size table

Motivated by the fact that imaging the shadow of a wormhole will allow one to develop observational test of distinguishing the wormhole among other compact objects in the relativistic astrophysics, Ohgami and Sakai (2015) have recently developed the images of wormholes surrounded by optically thin dust. Imaging supermassive confined-exotic-matter wormholes has been studied by Azreg-Aïnou (2015). Here we consider rotating wormhole shadow surrounded by plasma with the power law density since it may allow setting additional constraints on the parameters of the wormhole and its plasma environment. The shadow of the spherically-symmetric Ellis wormholes surrounded by plasma has been studied by Perlick et al. (2015). The gravitational lensing and images of black hole in plasma environment has been recently studied in Bisnovatyi-Kogan and Tsupko (2010), Tsupko and Bisnovatyi-Kogan (2012), Morozova et al. (2013), Perlick et al. (2015), Er and Mao (2014), Atamurotov et al. (2015), Rogers (2015). The transfer of radiation in an isotropic refractive, and dispersive medium using the Hamiltonian approach in a curved spacetime is studied in Bicak and Hadrava (1975) by applying the general-relativistic kinetic theory. The optical properties of the Kerr superspinars and black holes in braneworld have been considered in Stuchlík and Schee (2010), Schee and Stuchlík (2009).

This paper is organized as follows. Section 2 gives brief description of the wormhole spacetime and the photon motion around it in the presence of the plasma with the power-law density. In Sect. 3 the shadow caused by the wormhole surrounded by plasma has been considered. The summary of the research is given in Sect. 4.

Throughout the paper, we use a space-like signature \((-,+,+,+)\) and a system of units in which \(G = 1 = c\). Greek indices are taken to run from 0 to 3 and Latin indices from 1 to 3; covariant derivatives are denoted with a semi-colon and partial derivatives with a comma.

2 Wormhole surrounded by plasma

The axially symmetric solution of wormhole within standard Einstein theory of gravity was first proposed by Teo (1998)Footnote 2 and in Boyer-Linquist coordinates \((t,r,\theta, \phi)\) has the following general form

$$\begin{aligned} ds^{2} =& - N^{2}dt^{2} + \biggl( 1-\frac{b}{r} \biggr) ^{-1} dr^{2} \\ &{} +r^{2}K^{2} \bigl[ d\theta^{2}+ \sin^{2}\theta(d\phi-\omega_{\mathrm{LT}} dt)^{2} \bigr] , \end{aligned}$$
(1)

where in general the metric functions \(N\), \(b\), \(K\) and \(\omega _{\mathrm{LT}}\) are functions of both \(r\) and \(\theta\) coordinates. Function \(K(r, \theta)\) is a positive, nondecreasing function that determines the “proper radial distance” \(R\) measured at \((r, \theta)\) from the origin, \(N(r,\theta)\) is the so-called lapse function. The spacetime metric (1) is regular on the symmetry axis \(\theta= 0, \pi\) and has no event horizons or curvature singularities.

In the limit of zero rotation and spherical symmetry the expression (1) is going to Morris and Thorne spacetime metric (Morris et al. 1988; Morris and Thorne 1988):

$$\begin{aligned} &N(r,\theta) \rightarrow e^{\varLambda(r)}, \end{aligned}$$
(2)
$$\begin{aligned} &b(r,\theta) \rightarrow b(r), \end{aligned}$$
(3)
$$\begin{aligned} &K(r,\theta) \rightarrow 1, \end{aligned}$$
(4)
$$\begin{aligned} &\omega_{\mathrm{LT}}(r,\theta) \rightarrow 0. \end{aligned}$$
(5)

\(\varLambda(r)\) is the radial function, \(b(r)\) is the shape function and two identical, asymptotically flat regions joined together at throat \(r = b\). The neck of the wormhole corresponds to the minimum \({r}={r}_{0}=b({r}_{0})\) where \(\partial b/\partial r|_{r_{o}}\leq1\). For the traversable wormhole there is requirement for the lapse function \(N\) so that it should be finite and nonzero everywhere.

For the selection of Teo (1998) the metric functions are

$$\begin{aligned} &N = K=1+\frac{(4J\cos\theta)^{2}}{r}, \end{aligned}$$
(6)
$$\begin{aligned} &b = 1, \end{aligned}$$
(7)
$$\begin{aligned} &\omega_{\mathrm{LT}} = \frac{2 J}{r^{3}}. \end{aligned}$$
(8)

Coordinate \(r\) is asymptotically the proper radial distance and by making transformations to the Cartesian coordinates, it can be checked that \(J\) is the total angular momentum of the wormhole of total mass \(M\), \(\omega_{\mathrm{LT}}(r)=2J/r^{3}\) is known as Lense-Thirring angular velocity of dragging of inertial frames. Proper radius \(R = 1+(4J \cos\theta)^{2}\) is at throat \(r = 1\). One can introduce new radial coordinate as

$$ l=\pm\bigl[\sqrt{r(r - 1)}+\ln(\sqrt{r}+\sqrt{r-1})\bigr]. $$
(9)

If the rotation of the wormhole is sufficiently fast, the metric function \(g_{t\phi} = (N^{2}\omega_{\mathrm{LT}}^{2}r^{2} \sin^{2} \theta )\) becomes positive in some region outside the throat, indicating the presence of an ergoregions where particles can no longer remain stationary with respect to infinity. This occurs when \(r^{2} = |2a \sin\theta| > 1\) and \(|a| > 1/2\). However, the ergoregions does not completely surround the throat, but forms a tube around the equatorial region instead of ergosphere in Kerr metric. This is characteristic of traversable wormholes: the ergoregion would necessarily intersect an event horizon at the poles, but since the latter is ruled out by definition, the ergoregion cannot extend to the poles. Consequently, it has not character of the traditional ergosphere, but rather of ergotorus due to non-existence of the event horizons for the wormhole. Similar behavior on transition from the ergosphere to ergotorus was observed for superspinning Kerr naked singularities due to disappearance of the event horizons (de Felice 1974; Stuchlik 1980).

According to Nedkova et al. (2013) the selection of the metric functions is the following. (i) In order for the wormhole to be traversable, the redshift function \(N\) should be finite and nonzero, so that no curvature singularities and event horizons occur. (ii) The shape function \(b\) is assumed to be non-negative, and contains an apparent singularity at \(r=b\geq0\) which corresponds to the throat of the wormhole. The function \(b\) is also required to be independent of the coordinate \(\theta\) at the throat, i.e \(\partial_{\theta}b(r,\theta)=0\), because otherwise curvature singularity is present. Consequently, for a regular solution the throat represents a 2-dimensional surface located at some constant radius \(r=r_{0}\). A further condition \(\partial_{r} b(r, \theta)<1\) at the throat is imposed on the function \(b\) to ensure that the wormhole possesses the characteristic shape. (iii) The remaining metric function \(K\) is a regular, positive and non-decreasing function determining the proper radial distance \(R = rK\), while the function \(\omega\) is connected with the angular velocity of the wormhole. (iv) To ensure that the metric is nonsingular on the rotation axis \(\theta=0\) and \(\theta= \pi\) the derivatives of \(N\), \(K\) and \(b\) with respect to \(\theta\) should vanish on it. (v) As a result the described metric represents two identical regions joined together at the throat \(r = b=r_{0}\). The radial coordinate takes the range \(r_{0}\leq r < \infty\), and the limit \(r\rightarrow\infty\) corresponds to the physical infinity. By physical reasons the described wormhole solution is assumed to be asymptotically flat. Therefore, the metric functions should possess the asymptotically flat behavior at \(r\rightarrow \infty\) and consequently one can have (Teo 1998; Nedkova et al. 2013)

$$\begin{aligned} &N = 1-\frac{M}{r}+\mathcal{O}\bigl(r^{-2}\bigr), \end{aligned}$$
(10)
$$\begin{aligned} &K = 1+\mathcal{O}\bigl(r^{-1}\bigr), \end{aligned}$$
(11)
$$\begin{aligned} &1-\frac{b}{r} = 1+\mathcal{O}\bigl(r^{-1}\bigr), \end{aligned}$$
(12)
$$\begin{aligned} &\omega_{\mathrm{LT}} = \frac{2 J}{r^{3}}+\mathcal{O}\bigl(r^{-4}\bigr). \end{aligned}$$
(13)

The constants involved in the asymptotic expansions correspond to the conserved charges of the solution. Except for the described restrictions necessary for the regularity and the physical relevance of the solution, the metric functions \(N\), \(K\), \(b\) and \(\omega\) can be chosen at will, and the obtained solution (Nedkova et al. 2013) represents a particular case of rotating traversable wormhole and one may consider the class of solutions, when all the metric functions depend only on the radial coordinate \(r\). These solutions reduce to the Morris-Thorne wormhole in the limit of zero rotation \(\omega= 0\).

Consider a plasma surrounding the central axially symmetric wormhole. The refraction index of the plasma has the form \(n=n(x^{i}, \omega)\) and the \(\omega\) is the photon frequency measured by observer with velocity \(u^{\alpha}\). Then the effective energy of photon has the form \(\hbar\omega= - p_{\alpha}u^{\alpha}\). General expression for the refraction index of the plasma depending on the photon four-momentum has the following form (Synge 1960)

$$ n^{2}=1+\frac{p_{\alpha}p^{\alpha}}{ ( p_{\beta}u^{\beta} ) ^{2}}. $$
(14)

Note that in the vacuum case one has the value for the refraction index as \(n=1\). Hereafter we will use the Hamiltonian for the photon moving around the axial symmetric wormhole surrounded by plasma in the standard form

$$ H\bigl(x^{\alpha}, p_{\alpha}\bigr)=\frac{1}{2} \bigl[ g^{\alpha\beta} p_{ \alpha}p_{\beta}- \bigl(n^{2}-1\bigr) \bigl( p_{\beta}u^{\beta} \bigr) ^{2} \bigr] =0 . $$
(15)

Following to Rezzolla and Ahmedov (2004) one can assume that the spacetime around the wormhole is stationary and allows existence of a timelike Killing vector \(\xi^{\alpha}\) obeying to the Killing equations (see e.g. Tsukamoto and Bambi 2015a,b). One can introduce two frequencies of the photon with null wave-vector \(k^{\alpha}\). Photon frequency

$$ \omega\equiv-k^{\alpha}u_{\alpha} $$
(16)

is measured by an observer with four-velocity \(u^{\alpha}\). An alternate photon frequency

$$ \omega_{\xi}\equiv-k^{\alpha}\xi_{\alpha} $$
(17)

is associated with the timelike Killing vector \(\xi^{\alpha}\). Since the frequency (16) depends on the position and the frequency (17) is conserved along the photon trajectory, we can define the radial dependence of the frequency due to the gravitational redshift. Assuming the components of the timelike Killing vector as

$$ \xi^{\alpha}\equiv (1,0,0,0 ), $$
(18)

one can find that \(\omega_{\xi}=-k_{0}=\mbox{const}\). Comparing this with the frequency of the photon detected by the observer with four-velocity \(u^{\alpha}\{1/\sqrt{-g_{00}},0,0,0\}\) one can easily obtain that

$$ \sqrt{-g_{00}}\omega(r)=\omega_{\xi}=\mbox{const} . $$
(19)

One may introduce a specific form for the plasma frequency for analytic processing, assuming that the refractive index has the general form

$$ n^{2}=1- \frac{\omega_{e}^{2}}{\omega^{2}}, $$
(20)

where \(\omega_{e}\) is usually called plasma frequency.Footnote 3

We will consider the Lagrangian for the particle in order to get the equation of motion in the following form

$$\begin{aligned} {\mathcal{L}}=\frac{m^{2}}{2} \bigl[ g_{\alpha\beta}u^{\alpha }u^{\beta}- \bigl(n^{2}-1\bigr) ( u_{0}/\sqrt{-g_{00}})^{2} \bigr] , \end{aligned}$$
(21)

where we have assumed that the plasma is a stationary and inhomogeneous medium having four-velocity \(V^{0}=1/\sqrt{-g_{00}}\), \(V^{i}=0\). Plasma itself is rotating due to the effect of frame dragging of inertial frames. Using the Euler-Lagrange equation

$$\begin{aligned} \frac{\partial{\mathcal{L}}}{\partial x^{\alpha}} = \frac{d}{dt} \frac{ \partial{\mathcal{L}}}{\partial u^{\alpha}}, \end{aligned}$$
(22)

for the case when \(\alpha=0, 3\), we can obtain the following equations of motion

$$\begin{aligned} N^{2}\frac{dt}{d\sigma} =& n^{2} E- \omega_{\mathrm{LT}}L, \end{aligned}$$
(23)
$$\begin{aligned} N^{2} \frac{d\phi}{d\sigma} =& \omega_{\mathrm{LT}} (E+ \omega_{\mathrm{LT}} L)+\frac{N ^{2}}{r^{2} K^{2} \sin^{2}\theta} L, \end{aligned}$$
(24)

where conserved quantities \(E\) and \(L\) correspond to the energy and angular momentum of the particles, respectively.

Now we will use the Hamilton-Jacobi equation to obtain the equation of motion of massless particles around wormhole in the presence of plasma

$$ \frac{\partial S}{\partial\sigma} =\frac{1}{2} \bigl[ g^{\alpha \beta} p_{\alpha}p_{\beta}-\bigl(n^{2}-1\bigr) ( p_{0} /\sqrt {-g_{00}} ) ^{2} \bigr] . $$
(25)

The four momentum of the photon is related to the action \(S\) in the form \(p_{\alpha}=\partial S/\partial x^{\alpha}\). Using the fact of existence of two conserved quantities \(E\) and \(L\) one can choose the action for photons in the following form

$$ S=\frac{1}{2} m^{2}\sigma- Et +L\phi+ S_{r} (r) +S_{\theta}(\theta ), $$
(26)

where \(m\) is the mass of the particle which is zero for the photon. Then the equations of motion of photons around the wormhole surrounded by plasma take the following form

$$\begin{aligned} &N^{2}\frac{dt}{d\sigma} = n^{2} E- \omega_{\mathrm{LT}} L, \end{aligned}$$
(27)
$$\begin{aligned} &\frac{N}{\sqrt{1-b/r}}\frac{dr}{d\sigma} = \sqrt{R}, \end{aligned}$$
(28)
$$\begin{aligned} &r^{2}K^{2}\frac{d\theta}{d\sigma} = \sqrt{\varTheta} , \end{aligned}$$
(29)
$$\begin{aligned} &N^{2} \frac{d\phi}{d\sigma} = \omega_{\mathrm{LT}} (E+\omega_{\mathrm{LT}} L)+\frac{N^{2}}{r^{2} K^{2} \sin^{2}\theta} L, \end{aligned}$$
(30)

where the following notations

$$\begin{aligned} &R = (E-\omega_{\mathrm{LT}} L)^{2} - Q\frac{N^{2}}{r^{2}K^{2}} - \bigl(1-n^{2}\bigr) E^{2}, \end{aligned}$$
(31)
$$\begin{aligned} &\varTheta = Q-\frac{L^{2}}{\sin^{2}\theta} \end{aligned}$$
(32)

are introduced with \(Q\) being the Carter constant. The selected rotating wormhole spacetime allows calculations of the Carter constant (Nedkova et al. 2013).

Now we will introduce the effective potential being a useful tool for describing the photon motion which is necessary for considering the wormhole shadow. One may rewrite the radial equation of motion of the photons around wormhole surrounded by plasma in the form

$$ \frac{1}{2} \dot{r}^{2} + V_{eff} = 0, $$
(33)

with the effective potential

$$ V_{eff} = \frac{1-b/r}{2N^{2}} \biggl[ (E-\omega_{\mathrm{LT}} L)^{2} - Q\frac{N ^{2}}{r^{2}K^{2}} -\bigl(1-n^{2}\bigr) E^{2} \biggr] . $$
(34)

In order to get the real images for the radial dependence of the effective potential of radial motion of the photons around wormhole surrounded by plasma we consider the particular solution of the general class of the solutions given in Nedkova et al. (2013) as

$$\begin{aligned} &N = \exp \biggl( -\frac{r_{0}}{r}- \alpha \biggl( \frac{r_{0}}{r} \biggr)^{\delta} \biggr) , \end{aligned}$$
(35)
$$\begin{aligned} &b(r) = r_{0} \biggl( \frac{r_{0}}{r} \biggr) ^{\gamma}, \end{aligned}$$
(36)
$$\begin{aligned} &K = 1, \end{aligned}$$
(37)

where \(r_{0}\) and \(J\) are quantities related to the mass and angular momentum of the wormhole, respectively. The constants \(\alpha\geq0\), \(\delta\geq0\), and \(\gamma\geq0\) are real numbers (Harko et al. 2009; Bambi 2013a,b).

The radial dependence of the effective potential of the radial motion of the photons are shown in Fig. 2 for the particular case when the constants in metric function parameters (35)–(37) have the following values: \(\alpha=\delta=\gamma=0\). The ergoregions around the throat of the wormhole for this particular choice of the metric parameters are shown in Fig. 1. From the plots one can observe that the ergoregion around the rotating wormholes increases with the increasing the angular momentum of the wormholes and consists of tube around equatorial plane. In Fig. 2 the plots from the left to right correspond to the different values of the angular momentum of the wormhole as \(J/M^{2}=0.01\), \(J/M^{2}=0.1\) and \(J/M^{2}=0.7\), respectively. The solid, dashed and dotted lines in the plots correspond to the values of \(k/M= 0, 0.2, 0.4\), respectively. From the obtained dependence one can conclude that the presence of the plasma decreases the inner radius of the circular photon orbits around rotating wormhole. This can be caused by the effect of wormhole’s rotation (the peak of the plots decreases with increase of the spin parameter of the rotating wormhole). This is analogous to the effect of dragging of inertial frames in the Kerr spacetime.

Fig. 1
figure 1

The cross-section of ergotorus around the throat of the wormhole for the different values of the angular momentum of the wormhole. The grey areas correspond to the throat of the wormhole. The solid blue lines correspond to the static limit defined as a surface \(g_{tt}=0\)

Full size image
Fig. 2
figure 2

The radial dependence of the effective potential of the radial motion of the photons around wormhole surrounded by plasma for the different values of plasma parameter \(k/M\). Here we set \(\omega_{e}^{2}/\omega^{2} = k/r\). The solid, dashed and dotted lines in the plots correspond to the values of \(k/M= 0, 0.2, 0.4 \), respectively. The plots from the left to right correspond to the different values of the angular momentum of the wormhole as \(J/M^{2}=0.01\), \(J/M^{2}=0.1\) and \(J/M^{2}=0.7\), respectively

Full size image

3 Shadow of the wormhole

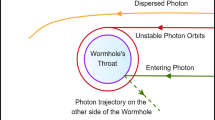
In this section we study the shadow cast by the wormhole in plasma environment. Assume that one of the two regions of the spacetime connected by the wormhole illuminated by a far source of light. Then an observer at the infinity will observe the photons scattered away from the second visible region of the spacetime which, as a model assumption, is considered not containing the light source. The photon orbits plunging into the wormhole and passing through its throat cannot be observed by the observer and this causes the dark spot on the observed image which corresponds to the wormhole’s shadow.

In order to describe the apparent shape of the wormhole one needs to consider the closed orbits around wormhole surrounded by plasma which depend on the integration constants \(E\), \(L\) and the Carter constant \(Q\). The equation of motion of the photons can be parametrized using the normalised parameters \(\xi=L/E \) and \(\eta= Q/E^{2}\). The boundary of the shape of the shadow of the wormhole surrounded by plasma can be found using the conditions

$$\begin{aligned} R(r)=0=\partial R(r)/\partial r . \end{aligned}$$

Using these equations one can easily find the expressions for the parameters \(\xi\) and \(\eta\) in the form

$$\begin{aligned} &\xi = \frac{B}{2A} +\sqrt{\frac{B^{2}}{4 A^{2}} -\frac{C}{A}}, \end{aligned}$$
(38)
$$\begin{aligned} &\eta = \frac{r^{2} K^{2}}{N^{2}} \bigl[ (1-\omega_{\mathrm{LT}}\xi)^{2}-1+n^{2} \bigr], \end{aligned}$$
(39)

where we have introduced the following notations

$$\begin{aligned} &A = \varSigma\omega_{\mathrm{LT}}^{2}-\omega_{\mathrm{LT}}\omega_{\mathrm{LT}}' , \end{aligned}$$
(40)
$$\begin{aligned} &B = 2 \omega_{\mathrm{LT}} \varSigma-\omega_{\mathrm{LT}}' , \end{aligned}$$
(41)
$$\begin{aligned} &C = \varSigma\bigl(n^{2}-1\bigr) -n n', \end{aligned}$$
(42)
$$\begin{aligned} &\varSigma = \frac{1}{2} \frac{d}{dr}\log \biggl(\frac{N^{2}}{r^{2} K^{2}} \biggr) , \end{aligned}$$
(43)

and prime denotes the differentiation with respect to radial coordinate \(r\).

The boundary of the wormhole’s shadow can be fully determined through the expression (38)–(39). However, observer will observe the shadow on ‘his sky’, thus usually one needs to introduce the celestial coordinates related to real astronomical measurements. The celestial coordinates are defined as (Bardeen et al. 1972; Hioki and Maeda 2009)

$$\begin{aligned} &\alpha = \lim_{r_{0}\rightarrow\infty} \biggl(-r_{0}^{2}\sin\theta _{0}\frac{d\phi}{dr}\biggr) , \end{aligned}$$
(44)
$$\begin{aligned} &\beta = \lim_{r_{0}\rightarrow\infty}r_{0}^{2}\frac{d\theta}{dr} . \end{aligned}$$
(45)

Using the equations of motion (27)–(30) one can easily find the relations for the celestial coordinates for the case of wormhole surrounded by plasma in the form

$$\begin{aligned} &\alpha = -\frac{\xi}{n\sin\theta}, \end{aligned}$$
(46)
$$\begin{aligned} &\beta = \frac{\sqrt{\eta-\xi/\sin^{2}\theta}}{n} . \end{aligned}$$
(47)

For the particular case when the constant parameters in metric functions (35)–(37) have the values as \(\alpha=\delta=\gamma= 0\) the images for the shadow of wormhole surrounded by plasma are shown in Fig. 3. For the comparison we also plot shadows for the vacuum case (solid lines in the plots). The dashed lines in plots correspond to the wormhole surrounded by plasma, where the plasma refraction index has been chosen in the way that \(\omega_{e}^{2}/ \omega^{2} = k/r\) and \(k/M = 0.9\). The comparison of the shadow of the wormhole with the one of Kerr black hole has been extensively studied in Nedkova et al. (2013). The plasma influence on the black hole shadow images has been recently studied in our paper (Atamurotov et al. 2015). From the plots in Fig. 3 one can easily see that the influence of the plasma on wormhole shadow images are essential. Particularly, the plasma influence is dominated in the left side of the shadow when the angular momentum of the wormhole is relatively small. The plasma influence is strong on the right side of the shadow when the angular momentum of the wormhole is relatively large. Recall, that the shadow of the compact objects within general relativity in the presence of the rotation shifts from the left to the right and its shape is distorted from a circle by being flattened at the left side (Hioki and Maeda 2009). The shifting of the shadow is due to opposite dragging of prograde and retrograde orbits, while the distortion on the left side is due to difference of the curvature of the rightmost and leftmost points. With the increase of the angular momentum of the wormhole the curvature of the rightmost point of the shadow changes due to the presence of plasma. When the angular momentum of the wormhole is small then one can observe that presence of the plasma prevents the shadow to be highly distorted. The same effects can be seen for the different values of the inclination angle between observer plane and axis of rotation.

Fig. 3
figure 3

The shadow of wormhole surrounded by plasma with the refraction index to be chosen in the way that \(\omega_{e}^{2}/\omega ^{2} = k/r\) and \(k/M = 0.9\) (dashed lines). The solid lines correspond to the case when wormhole is in vacuum. Here we take the metric parameter to be as \(\alpha=\delta=\gamma=0\)

Full size image

As the next example we can get the parameters in metric function (35)–(37) to be as \(\alpha=1\), \(\delta=1\), \(\gamma=0\). For this particular case the images for the shadow of wormhole surrounded by plasma are shown in Fig. 4. As in previous case we take the vacuum case (solid lines in the plots) the case when wormhole surrounded by plasma (dashed lines), where the plasma refraction index has been chosen in the way that \(\omega_{e}^{2}/ \omega^{2} = k/r\) and \(k/M = 0.9\). In this case one can observe the increase of the radius of the shadow of the wormhole due to change in the lapse function and the influence of the plasma becomes relatively weak.

Fig. 4
figure 4

The shadow of wormhole surrounded by plasma with the refraction index to be chosen in the way that \(\omega_{e}^{2}/\omega^{2} = k/r\) and \(k/M = 0.9\) (dashed lines). The solid lines correspond to the case when wormhole is in vacuum. Here we take the metric parameter to be as \(\alpha=1\), \(\delta=1\), \(\gamma=0\)

Full size image

4 Conclusions

In this paper we have studied shadow of rotating wormhole in the presence of plasma with radial power-law density. The obtained results can be summarized as follows.

  1. i)

    The analysis of the equation of motion of photons around wormhole in the plasma environment shows that the presence of the plasma decreases the inner radius of the circular orbits of photons around wormhole.

  2. ii)

    In the presence of plasma the shape and size of the wormhole shadow is changed depending on i) plasma parameters, ii) wormhole rotation and iii) inclination angle between observer plane and axis of rotation of wormhole.

  3. iii)

    We have shown that the influence of the plasma on wormhole shadow images is essential. Particularly, the plasma influence is dominated in the left hand side of the wormhole shadow when the angular momentum of the wormhole is relatively small. The plasma influence is strong on the right hand side of the shadow when the angular momentum of the wormhole is relatively large (see Fig. 3).

  4. iv)

    It has also been shown that due to the presence of plasma the increase of the angular momentum of the wormhole changes the curvature of the rightmost point of the shadow. In the case when the angular momentum of the wormhole is small the presence of the plasma prevents the shadow to be highly distorted. The analogous effects can be observed for the different values of the inclination angle between observer plane and axis of rotation of the wormhole.

In the future work we plan to study the optical properties of the traversable wormholes surrounded by plasma, such as weak and strong gravitational lensing and dependence of optical properties of the wormholes from the frequency of the electromagnetic radiation which may lead to dispersion and absorption of the electromagnetic radiation.