1 Introduction

To search and understand deeply physical aspects of the astrophysical and cosmological phenomena there still remain several challenging and intrigued problems for the theoretical physicists. Einstein’s theory of gravitation, though has been always a very fruitful tool for uncovering hidden mysteries of Nature, does not meet all the criteria to explain the current paradigm of astrophysics and cosmology. As a result, several alternative theories of gravity have been proposed time to time. Recently, two generalized functional theories, namely, \(f(R)\) gravity and \(f(T)\) gravity, received more attention as an alternative theories of Einsteinian gravitational theory.

However, \(f(T)\) theory of gravity is more controllable than \(f(R)\) theory because the field equations in the former one are restricted to the second order differential equations whereas the later case is relatively difficult to handle as those are of fourth order differential equations (Böhmer et al. 2011). Obviously one can take help from the Palatini approach to make \(f(R)\) theory a second order system of differential equations (Durrer and Maartens 2010; De Felice and Tsujikawa 2010; Sotiriou and Faraoni 2010). Another general feature of \(f(T)\) gravity is that its construction is associated with a generalized Lagrangian (Bengochea and Ferraro 2009; Linder 2010).

In connection to application of \(f(T)\) gravity we note that most research have been oriented to cosmology—theoretical presentation as well as observational verification (Wu and Yu 2010a, 2010b, 2011; Tsyba et al. 2011; Dent et al. 2011; Chen et al. 2011; Bengochea 2011; Yang 2011; Zhang et al. 2011; Li et al. 2011; Bamba et al. 2011). However, later on astrophysical applications also can be observed in the following works (Böhmer et al. 2011; Deliduman and Yapiskan 2011; Wang 2011; Daouda et al. 2011; Abbas et al. 2015). Among these works we are specially interested to the works of Böhmer et al. (2011) and Deliduman and Yapiskan (2011). Deliduman and Yapiskan (2011) claimed that relativistic stars in \(f(T)\) theory of gravity do not exist whereas Böhmer et al. (2011) proved that they do exist. In the present work we shall follow the result of Böhmer et al. (2011) by considering the problem in \(f(T)\) gravity along with conformal Killing vector field. There are some other standard works on \(f(T)\) gravity which one may consult for further studies with various physical aspects (De Andrade et al. 2000; Ferraro and Fiorini 2011; Tamanini 2012; Tamanini and Böhmer 2012; Aldrovandi and Pereira 2013; Aftergood and DeBenedictis 2014).

The conformal Killing vectors (CKV) provide inheritance symmetry which conveniently makes a natural relationship between geometry and matter through the Einstein field equations. In favor of the prescription of this mathematical technique CKV, Rahaman et al. (2015a) mention the following features: (1) it provides a deeper insight into the spacetime geometry and facilitates the generation of exact solutions to the Einstein field equations in a more comprehensive forms, (2) the study of this particular symmetry in spacetime is physically very important as it plays a crucial role of discovering conservation laws and to devise spacetime classification schemes, and (3) because of the highly non-linearity of the Einstein field equations one can reduce easily the partial differential equations to ordinary differential equations by using CKV.

Therefore, several works have been performed by use of the technique of conformal motion as can be seen available in the literature. A few interesting applications of conformal motion to astrophysical field can be found in Ray et al. (2008), Rahaman et al. (2010a, 2010b, 2014, 2015b, 2015c), Usmani et al. (2011) and Bhar (2014). In this line of investigations some special mention are of the very recent works of Rahaman et al. (2015a) and Bhar et al. (2015). Search for a new wormhole solution inspired by noncommutative geometry with the additional condition of allowing conformal Killing vectors was performed by Rahaman et al. (2015a) whereas Bhar et al. (2015) have shown that a new class of interior solutions for anisotropic stars are possible by admitting conformal motion in higher-dimensional noncommutative spacetime. Interior solutions admitting conformal motions also have been studied extensively in the past by Herrera and his co-workers (Herrera et al. 1984; Herrera and Ponce de Leon 1985a, 1985b, 1985c).

Under this background, therefore, in the present work our main aim or motivation is to construct a set of stellar solutions under \(f(T)\) theory of gravity by admitting conformal motion of Killing Vectors. The outline of the investigation is as follows: in Sect. 2 we provide the basic mathematical formalism of \(f(T)\) theory whereas in Sect. 3 the CKVs are formulated. The Einstein field equations under \(f(T)\) gravity and CKVs have been provided along with their solutions in Sect. 4. We have tested physical validity of the model by using Tolman–Oppenheimer–Volkoff (TOV) equation in Sect. 5. Lastly, in Sect. 6 we pass some concluding remarks.

2 The \(f(T)\) theory: basic mathematical formalism

The action of \(f(T)\) theory is taken as (for geometrical units \(G=c=1\))

$$ S\bigl[e^{i}_{\mu}, \phi_{A} \bigr] = \int d^{4}x \biggl[ \frac{1}{16 \pi} f(T) + L_{\mathit{matter}} ( \phi_{A}) \biggr] . $$
(1)

Here, \(\phi_{A}\) indicates matter fields and \(f(T)\) is an arbitrary analytic function of the torsion scalar \(T\). The torsion scalar is constructed from torsion and cotorsion as follows:

$$ T = S_{\sigma}^{ \mu\nu} T^{\sigma}_{ \mu\nu}, $$
(2)

where

$$\begin{aligned} &T^{\sigma}_{ \mu\nu} = \varGamma^{\sigma}_{ \mu\nu}- \varGamma^{\sigma}_{ \nu\mu} = e_{i}^{\sigma}\bigl( \partial_{\mu}e^{i}_{\nu}- \partial_{\nu}e^{i}_{\mu}\bigr), \end{aligned}$$
(3)
$$\begin{aligned} &K_{\sigma}^{ \mu\nu} = -\frac{1}{2} \bigl( {T^{\mu\nu}}_{\sigma}- {T^{\nu\mu}}_{\sigma} -T^{ \mu\nu}_{\sigma} \bigr), \end{aligned}$$
(4)

are torsion and cotorsion respectively with newly defined tensor components

$$ S_{\sigma}^{ \mu\nu} = \frac{1}{2} \bigl( {K^{ \mu\nu}}_{\sigma}+ \delta_{\sigma}^{\mu}{T ^{ \beta \nu}}_{\beta}- \delta_{\sigma}^{\nu}{T^{ \beta \mu }}_{\beta} \bigr). $$
(5)

Here, \(e^{i}_{\mu}\) are the tetrad by which it is possible to define any metric as \(g_{\mu \nu} = \eta_{ij} e^{i}_{\mu}e^{j}_{\nu}\), where \(\eta_{ij} = \operatorname{diag} ( -1,1,1,1 )\) and \(e_{i}^{\mu}e^{i}_{\nu}= \delta_{\nu}^{\mu}\), \(e= \sqrt{-g} = \operatorname{det}(e^{i}_{\mu})\).

If one varies the action (1) with respect to the tetrad, one can get the field equations of \(f(T)\) gravity which can be given by

$$\begin{aligned} &S_{i}^{ \mu \nu}f_{TT} \partial_{\mu}T + e^{-1} \partial_{\mu}\bigl( e S_{i}^{ \mu \nu} \bigr) f_{T} -T^{\sigma}_{ \mu i}S_{\sigma}^{ \nu \mu} f_{T} + \frac{1}{4} e_{i}^{\nu}f \\ &\quad{} = 4 \pi \varUpsilon_{i}^{\nu}, \end{aligned}$$
(6)

where

$$S_{i}^{ \mu \nu} =e_{i}^{\sigma}S_{\sigma}^{ \mu \nu},\qquad f_{T} =\frac{\partial f}{\partial T}\quad \mbox{and}\quad f_{TT} = \frac{\partial^{2} f}{\partial T^{2}} $$

and \(\varUpsilon_{i}^{\nu}\) denotes the energy stress tensor of the anisotropic fluid as

$$\varUpsilon_{\nu}^{\mu}= ( \rho + p_{r})u^{\mu}u_{\nu} - p_{r} g^{\mu}_{\nu}+ (p_{t} -p_{r} )\eta^{\mu}\eta_{\nu}, $$

with

$$u^{\mu}u_{\mu} = - \eta^{\mu}\eta_{\mu} = 1. $$

3 Conformal Killing vector

To search for a natural relationship between geometry and matter Einstein’s general relativity provides a rich arena to use symmetries. Various symmetries that arising either from geometrical point of view or physical relevant quantities are known as collineations. The greatest advantageous collineations is the conformal Killing vectors (CKV) which provide a deeper insight into the spacetime geometry. In mathematical point of view, conformal motions or conformal Killing vectors (CKV) are motions along which the metric tensor of a spacetime remains invariant up to a scale factor. Another advantage to use the CKV is that it facilitates generation of exact solutions to the field equations. This is achieved by reducing the highly nonlinear partial differential equations of Einstein’s gravity to ordinary differential equations through the technique of CKV.

The CKV can be defined as

$$ L_{\xi} g_{ij} = \xi_{i;j}+ \xi_{j;i} = \psi g_{ij}, $$
(7)

where \(L\) is the Lie derivative operator of the metric tensor and \(\psi\) is the conformal factor. It is supposed that the vector \(\xi\) generates the conformal symmetry and the metric \(g\) is conformally mapped onto itself along \(\xi\). However, it is to note that neither \(\xi\) nor \(\psi\) need to be static even though one considers a static metric (Böhmer et al. 2007, 2008). Further, one should note that (i) if \(\psi=0\) then Eq. (7) gives the Killing vector, (ii) if \(\psi= \mbox{constant}\) it gives homothetic vector, and (iii) if \(\psi=\psi(\textbf{x},t)\) then it yields conformal vectors. Moreover, for \(\psi=0\) the underlying spacetime becomes asymptotically flat which further implies that the Weyl tensor will also vanish. Therefore, CKV has an intrinsic property to provide a deeper insight of the underlying spacetime geometry. Basically the Lie derivative operator \(L\) describes the interior gravitational field of a stellar configuration with respect to the vector field \(\xi\).

Let us therefore assume that our static spherically symmetric spacetime admits an one parameter group of conformal motion, so that the metric

$$ ds^{2}=-e^{\nu(r)}dt^{2}+e^{\lambda(r)}dr^{2}+r^{2} \bigl(d\theta^{2}+\sin^{2}\theta d\phi^{2} \bigr), $$
(8)

is conformally mapped onto itself along \(\xi\).

Here Eq. (7) implies that

$$ L_{\xi}g_{ik} =\xi_{i;k}+ \xi_{k;i} = \psi g_{ik}, $$
(9)

with \(\xi_{i} = g_{ik}\xi^{k}\).

From Eqs. (8) and (9), one can get the following expressions (Herrera and Ponce de Leon 1985a, 1985b, 1985c; Böhmer et al. 2011)

$$\begin{aligned} &\xi^{1} \nu^{\prime}=\psi, \\ &\xi^{4} = \mathrm{constant}, \\ &\xi^{1} = \frac{\psi r}{2}, \\ &\xi^{1} \lambda ^{\prime}+ 2 \xi^{1} _{,1} =\psi, \end{aligned}$$

where 1 and 4 stand for the spatial and temporal coordinates \(r\) and \(t\) respectively.

The above set of equations imply

$$\begin{aligned} &e^{\nu}= C_{0}^{2} r^{2}, \end{aligned}$$
(10)
$$\begin{aligned} &e^{\lambda}= \biggl[\frac{C}{\psi} \biggr]^{2}, \end{aligned}$$
(11)
$$\begin{aligned} &\xi^{i} = C_{1} \delta_{4}^{i} + \biggl[\frac{\psi r}{2} \biggr]\delta_{1}^{i}, \end{aligned}$$
(12)

where \(C\), \(C_{0}\) and \(C_{1}\) all are integration constants.

4 The field equations and their solutions

Let us define tetrad matrix for the metric (8) as follows:

$$ e^{i}_{ \mu} = \operatorname{diag} \Bigl[ \sqrt {C_{0}^{2} r^{2}}, e^{\frac{\lambda}{2}}, r, r \sin\theta \Bigr]. $$
(13)

Therefore, the torsion scalar can be determined as

$$ T(r) = - \frac{6 e^{-\lambda}}{r^{2}}. $$
(14)

Inserting this and the components of the tensors \(S_{i}^{ \mu \nu}\) and \(T_{i}^{ \mu \nu}\) in Eq. (6) we obtain

$$\begin{aligned} &4 \pi \rho = \frac{ e^{-\lambda}}{r} T^{\prime} f_{TT} - \biggl[ \frac{T}{2} + \frac{ 1}{2r^{2}} + \frac{ e^{-\lambda}}{2r} \biggl( \frac{2}{r} + \lambda^{\prime}\biggr) \biggr]f_{T} \\ &\phantom{4 \pi \rho =\,}+ \frac{f}{4}, \end{aligned}$$
(15)
$$\begin{aligned} &4 \pi p_{r} = \biggl[ \frac{T}{2} + \frac{ 1}{2r^{2}} \biggr]f_{T} - \frac{f}{4}, \end{aligned}$$
(16)
$$\begin{aligned} &4 \pi p_{t} = -\frac{e^{-\lambda}}{r} T^{\prime} f_{TT} + \frac{T }{4} f_{T} -\frac{e^{-\lambda}}{2} \biggl[ \frac{1}{ r^{2}} -\frac{\lambda^{\prime}}{r} \biggr]f_{T} \\ &\phantom{4 \pi p_{t} =\,}-\frac{f}{4}. \end{aligned}$$
(17)

Due to Böhmer et al. (2011), one of the possible way to get back general relativistic result is \(f_{TT} = 0\), although its general relativity form has no meaning in the present context. Therefore, we are now seeking solutions using

$$ f(T) = T $$
(18)

and

$$ f(T)=aT+b, $$
(19)

which immediately follows from \(f_{TT} = 0\). Here \(a\) and \(b\) are two purely constant quantities. For a fluid distribution consisting of normal matter, we have

$$ p_{r} = \omega \rho, $$
(20)

where \(\omega\) is an equation of state parameter.

4.1 CASE I: \(f(T)=T\)

4.1.1 \(p_{r} = p_{t} = p\)

Now, using Eqs. (14)–(18), we obtain the following solutions (Herrera et al. 1984; Herrera and Ponce de Leon 1985c):

$$\begin{aligned} &e^{-\lambda(r)}= \biggl( \frac{1}{2}+ F r^{2} \biggr), \end{aligned}$$
(21)
$$\begin{aligned} &T(r) = - \biggl[\frac{3}{r^{2}}+6F \biggr], \end{aligned}$$
(22)
$$\begin{aligned} &4 \pi \rho(r)= -\frac{1}{4r^{2}}+\frac{3}{2}F, \end{aligned}$$
(23)
$$\begin{aligned} &4 \pi p =-\frac{1}{4r^{2}}-\frac{3}{2}F, \end{aligned}$$
(24)
$$\begin{aligned} &\psi= C \biggl[ \frac{1}{2}+Fr^{2} \biggr]^{\frac{1}{2}}, \end{aligned}$$
(25)

where \(F\) is an integration constant.

The sound velocity \({v_{s}}^{2}\) can be found out as

$$ \frac{dp}{d\rho}= 1. $$
(26)

4.1.2 \(p_{r} \neq p_{t}\)

Now, using Eqs. (14)–(18) and (20), we obtain the following solutions (Herrera et al. 1984; Herrera and Ponce de Leon 1985c):

$$\begin{aligned} &e^{-\lambda(r)}= \biggl[\frac{\omega+1}{\omega+3} \biggr] +Dr^{- [\frac{\omega+3}{\omega} ]}, \end{aligned}$$
(27)
$$\begin{aligned} &T(r) = - \biggl[\frac{6(\omega+1)}{(\omega+3)} \biggr]r^{-2} -6Dr^{- [\frac{3(\omega+1)}{\omega} ]}, \end{aligned}$$
(28)
$$\begin{aligned} &4 \pi \rho(r)=- \biggl[\frac{ 3D}{2\omega} \biggr]r^{- [\frac{3(\omega+1)}{\omega} ]}- \biggl[ \frac{1}{\omega+3} \biggr]r^{-2}, \end{aligned}$$
(29)
$$\begin{aligned} &4\pi p_{r}=- \biggl[\frac{3D}{2} \biggr]r^{- [\frac{3(\omega+1)}{\omega} ]}- \biggl[\frac{\omega}{\omega+3} \biggr]r^{-2}, \end{aligned}$$
(30)
$$\begin{aligned} &4 \pi p_{t}= \biggl[\frac{3D}{2\omega} \biggr]r^{- [\frac{3(\omega+1)}{\omega} ]}- \biggl[\frac{(\omega+1)}{2(\omega+3)} \biggr]r^{-2}, \end{aligned}$$
(31)
$$\begin{aligned} &\psi= C \biggl[ \biggl(\frac{\omega+1}{\omega+3} \biggr) +Dr^{- (\frac{\omega+3}{\omega} )} \biggr]^{\frac{1}{2}}, \end{aligned}$$
(32)
$$\begin{aligned} &\frac{dp_{t}}{d\rho}= \frac{-\frac{9D (\omega+1 )}{2\omega^{2}}r^{- (\frac{\omega+3}{\omega} )}+ (\frac{\omega+1}{\omega+3} )}{ \frac{9D (\omega+1 )}{2\omega^{2}}r^{- (\frac{\omega+3}{\omega} )}+ (\frac{2}{\omega+3} )}, \end{aligned}$$
(33)

where \(D\) is an integration constant.

4.2 CASE II: \(f(T)=aT+b\)

4.2.1 \(p_{r} = p_{t} = p\)

Now, using Eqs. (14)–(17) and (19), we obtain the following solutions (Herrera et al. 1984; Herrera and Ponce de Leon 1985c):

$$\begin{aligned} &e^{-\lambda(r)}= \biggl( \frac{1}{2}+H r^{2} \biggr), \end{aligned}$$
(34)
$$\begin{aligned} &T(r) = - \biggl[\frac{3}{r^{2}}+6H \biggr], \end{aligned}$$
(35)
$$\begin{aligned} &4 \pi \rho(r)= -\frac{a}{4r^{2}}+\frac{3}{2}aH+\frac{b}{4}, \end{aligned}$$
(36)
$$\begin{aligned} &4 \pi p =-\frac{a}{4r^{2}}-\frac{3}{2}aH-\frac{b}{4}, \end{aligned}$$
(37)
$$\begin{aligned} &\psi= C \biggl[ \frac{1}{2}+Hr^{2} \biggr]^{\frac{1}{2}}, \end{aligned}$$
(38)

where \(a\) and \(b\) are two purely constant quantities as mentioned earlier and \(H\) is an integration constant.

As before the sound velocity \({v_{s}}^{2}\) can be given by

$$ \frac{dp}{d\rho}= 1. $$
(39)

4.2.2 \(p_{r} \neq p_{t}\)

Now, using Eqs. (14)–(17), (19) and (20), we obtain the following solutions (Herrera et al. 1984; Herrera and Ponce de Leon 1985c):

$$\begin{aligned} &e^{-\lambda(r)}= \biggl[\frac{\omega+1}{\omega+3} \biggr] +Er^{- [\frac{\omega+3}{\omega} ]}- \frac{br^{2}}{6a}, \end{aligned}$$
(40)
$$\begin{aligned} &T(r) = - \biggl[\frac{6(\omega+1)}{(\omega+3)} \biggr]r^{-2} -6Er^{- [\frac{3(\omega+1)}{\omega} ]}+ \frac{b}{a}, \end{aligned}$$
(41)
$$\begin{aligned} &4 \pi \rho(r)=- \biggl[\frac{ 3aE}{2\omega} \biggr]r^{- [\frac{3(\omega+1)}{\omega} ]}- \biggl[ \frac{a}{\omega+3} \biggr]r^{-2}, \end{aligned}$$
(42)
$$\begin{aligned} &4 \pi p_{r}=- \biggl[\frac{ 3aE}{2} \biggr]r^{- [\frac{3(\omega+1)}{\omega} ]}- \biggl[\frac{a\omega}{\omega+3} \biggr]r^{-2}, \end{aligned}$$
(43)
$$\begin{aligned} &4 \pi p_{t}= - \biggl[\frac{ a(\omega+1)}{2(\omega+3) } \biggr]r^{-2} + \biggl[ \frac{3aE}{2\omega} \biggr]r^{- [\frac{3(\omega+1)}{\omega} ]}, \end{aligned}$$
(44)
$$\begin{aligned} &\psi= C \biggl[ \biggl(\frac{\omega+1}{\omega+3} \biggr) +Er^{- (\frac{\omega+3}{\omega} )}- \frac{br^{2}}{6a} \biggr]^{\frac{1}{2}}, \end{aligned}$$
(45)
$$\begin{aligned} &\frac{dp_{t}}{d\rho}= \frac{-\frac{9aE (\omega+1 )}{2\omega^{2}}r^{- (\frac{\omega+3}{\omega} )}+ (\frac{a(\omega+1)}{\omega+3} )}{ \frac{9aE (\omega+1 )}{2\omega^{2}}r^{- (\frac{\omega+3}{\omega} )}+ (\frac{2a}{\omega+3} )}, \end{aligned}$$
(46)

where \(E\) is an integration constant.

5 Physical features of the model

5.1 Energy conditions

Now, let us check whether all the energy conditions are satisfied or not for the present model under \(f(T)\) gravity. For this purpose, we should consider the following inequalities:

  1. (i)

    \(\mathit{NEC}: \rho+p_{r}\geq 0,~\rho+p_{t}\geq 0\),

  2. (ii)

    \(\mathit{WEC}: \rho+p_{r}\geq 0,~\rho\geq 0,~\rho+p_{t}\geq 0\),

  3. (iii)

    \(\mathit{SEC}: \rho+p_{r}\geq 0,~\rho+p_{r}+2p_{t}\geq 0\).

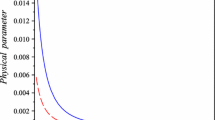
Among all the above CASES I and II of \(f(T)\) gravity it is revealed that only the solutions of sub-case with isotropic condition (\(p_{r} = p_{t} = p\)) under CASE II i.e. \(f(T)=aT+b\) (4.2.1) are physically valid (see Fig. 3 for energy conditions). The other cases are not physically interesting the energy conditions being violated there (Figs. 1, 2 and 4).

Fig. 1
figure 1

Variation of \(\rho + p\) (Top) and \(\rho + 3p\) (Bottom) are shown with respect to radial coordinate for isotropic case

Full size image
Fig. 2
figure 2

Variation of \(\rho + p_{t}\) (Top) and \(\rho+p_{r}+2p_{t}\) (Bottom) are shown with respect to radial coordinate for anisotropic case

Full size image
Fig. 3
figure 3

Variation of \(\rho\) (Top), \(p\) (Upper Middle), \(\rho+p\) (Lower Middle) and \(\rho+3p\) (Bottom) are shown with respect to radial coordinate for isotropic case

Full size image
Fig. 4
figure 4

Variation of \(\rho + p_{t}\) (Top) and \(\rho+p_{r}+2p_{t}\) (Bottom) are shown with respect to radial coordinate for anisotropic case

Full size image

5.2 TOV equation

The Generalized Tolman–Oppenheimer–Volkoff (TOV) equation can be written in the form

$$ -\frac{M_{G}(r)(\rho+p_{r})}{r^{2}}e^{\frac{\lambda-\nu}{2}}-\frac{dp_{r}}{dr}+\frac{2}{r}(p_{t}-p_{r})=0, $$
(47)

where \(M_{G}(r)\) is the gravitational mass within the sphere of radius \(r\) and is given by

$$ M_{G}(r)=\frac{1}{2}r^{2}e^{\frac{\nu-\lambda}{2}} \nu'. $$
(48)

Substituting Eq. (48) into Eq. (47), we obtain

$$ -\frac{\nu'}{2}(\rho+p_{r})-\frac{dp_{r}}{dr}+ \frac{2}{r}(p_{t}-p_{r})=0. $$
(49)

The above TOV equation describe the equilibrium of the stellar configuration under the joint action of the different forces, viz. gravitational force (\(F_{g}\)), hydrostatic force (\(F_{h}\)) and anisotropic force (\(F_{a}\)) so that eventually as an equilibrium condition one can write it in the following form:

$$ F_{g}+F_{h}+F_{a}=0, $$
(50)

where

$$\begin{aligned} &F_{g}=-\frac{\nu'}{2}(\rho+p_{r}), \\ &F_{h}=-\frac{dp_{r}}{dr}, \\ &F_{a}=\frac{2}{r}(p_{t}-p_{r}). \end{aligned}$$

In case of \(p_{r} = p_{t}\) and \(f(T)=aT+b\) the gravitational and hydrostatic forces are given by

$$ F_{g} = \frac{a}{8\pi r^{3}} $$
(51)

and

$$ F_{h} = - \frac{a}{8\pi r^{3}}. $$
(52)

We have plotted the feature of TOV equation for sub-case 4.2.1 in Fig. 5 (we don’t need to include TOV equation in sub-case 4.1.1 as the model does not exist the energy conditions being violated). In sub-case 4.2.1 we observe that static equilibrium has been attained by the forces through balancing of the stresses between them. However, it can be found out that anisotropic forces have no contribution to equilibrium i.e. \(F_{a} =0\) as \(p_{r} =p_{t}\).

Fig. 5
figure 5

The three different forces, viz. gravitational force \((F_{g})\), hydrostatic force \((F_{h})\) and anisotropic force \((F_{a})\) are plotted against \(r\) (km) for sub-case 4.2.1

Full size image

5.3 Stability issue

We shall now turn our attention to the stability issue of model. According to the cracking technique proposed by Herrera (1992) the squares of the sound speed should be within the limit \([0,1]\). Fig. 6 satisfies Herrera’s criterion i.e. \({v_{s}}^{2} \geq 0\) within the matter distribution and therefore our model maintains stability.

Fig. 6
figure 6

Profile of sound velocity is shown which actually remains constant

Full size image

5.4 Nature of the star

We have drawn a plot to show radius of our stellar model. It can be seen by the clear ‘cut’ on X-axis which is turned out to be 1.445 km (Fig. 7). This is very small and indicates towards a compact star with ultra-compactness. A tally of this value with the already available data set immediately reveals that the star is nothing but either a quark/strange star (see Table 1 of Bhar et al. 2015) or a brown dwarf star of type F5 (see the Link: http://www.world-builders.org/lessons/less/les1/StarTables.html).

Fig. 7
figure 7

Radius of the star is given where \(p\) cuts \(r\) axis

Full size image

This value of \(R=1.445~\mbox{km}\) immediately provoke us to figure out the surface density of the stellar system. As \(r\) tends to zero, \(\rho\) goes to infinity and therefore, we are not in position to comment on the central density. However, we can estimate the surface density of the star by plugging \(G\) and \(c\) in the expression of \(\rho\) which eventually yields the numerical value as \(4.847 \times 10^{16}~\mbox{gm/cc}\). Therefore, this very high density in the order \(10^{16}~\mbox{gm/cc}\) with a very small radius \(R=1.445~\mbox{km}\) really indicates that the model under \(f(T)\) gravity represents an ultra-compact star (Ruderman 1972; Glendenning 1997; Herjog and Roepke 2011).

6 Conclusions

We have studied in detail the \(f(T)\) gravity for the two specific cases \(f(T)= T\) and \(f(T)=aT+b\). It has specially been observed that among all the CASES I and II of \(f(T)\) gravity only the solutions of sub-case 4.2.1 with isotropic condition (\(p_{r} = p_{t} = p\)) under CASE II, i.e. \(f(T)=aT+b\) are physically valid. In general, our observation is that under \(f(T)\) gravity anisotropy doesn’t exist as well as all the energy conditions become jeopardized. Obviously, in favor of this conclusion further studies are needed to perform several other aspect of the \(f(T)\) theory of gravity.

In connection to features and hence validity of the model we have studied several physical aspects based on the solutions and all these being very interesting advocate in favor of physically acceptance of the model. We would like to summarize all these results as follows:

(i) Energy conditions

Our study reveals that only the solutions of sub-case 4.2.1 with isotropic condition under CASE II i.e. \(f(T)=aT+b\) are physically valid as in the other cases energy conditions are seen to be violated.

(ii) TOV equation

The plot for the generalized TOV equation shows that static equilibrium has been attained by the different forces, viz. gravitational force (\(F_{g}\)), hydrostatic force (\(F_{h}\)) and anisotropic force (\(F_{a}\)). However, it is also observed that anisotropic forces have no role for equilibrium of the system.

(iii) Stability issue

By employing the cracking concept of Herrera (1992) we have demonstrated through plot that the squares of the sound speed remains within the limit \([0,1]\) and hence shown our model is a stable one.

(iv) Nature of the star

The model with very high density (\(4.847 \times 10^{16}~\mbox{gm/cc}\)) and small radius (\(R=1.445~\mbox{km}\)) suggests that the present investigation under \(f(T)\) theory of gravity is a representative of an ultra-compact star.

We note an interesting work on the \(f(T)\) gravity in connection to Krori and Barua (1975) metric parameters as done by Abbas et al. (2015). The present work therefore may be extended to that line of thinking in a future project.