1 Introduction

Noncommutative geometry aims to place General Relativity and the Standard Model on the same footing in order to describe gravity and the electro-weak and strong forces as gravitational forces in a unified spacetime [1]. It is based on the realization that coordinates may become noncommutative operators on a D-brane [2, 3]. The result is a fundamental discretization of spacetime due to the commutator [x μ, x ν] = i θ μν, where θ μν is an antisymmetric matrix. Noncommutativity replaces point-like structures by smeared objects [4–7] and is intended to eliminate the divergences that normally appear in General Relativity. It is an intrinsic property of spacetime and does not depend on any particular features such as curvature.

A standard way to model the smearing effect is by using a Gaussian distribution of minimal length \(\sqrt {\theta }\) due to the uncertainty. So the energy density of the static, spherically symmetric and particle-like gravitational source has the form [4, 8]

$$ \rho = \frac{M}{(4\pi\theta)^{\frac{3}{2}}}e^{-\frac{r^{2}}{4\theta}}, $$
(1)

where M is the total mass of the source which here could be considered as a diffused centralized object such as a wormhole [6].

A number of studies inspired by noncommutative geometry can be found in the literature [9–11]. Thus Rahaman et al. [9] showed that a noncommutative-geometry background is able to account for producing stable circular orbits, as well as attractive gravity, without any need for exotic dark matter. Garattini and Lobo [10] obtained a self-sustained wormhole in noncommutative geometry. Under their semi-classical approach the energy density of the graviton one loop contribution to a classical energy in a traversable wormhole background and the finite one loop energy density is considered as a self-consistent source for these wormhole geometries. Kuhfittig [11] showed that a special class of thin-shell wormholes possess small regions of stability around a thin shell, even though they are unstable in classical general relativity. Some other works on wormholes, in connection with their origin and development (with or without noncommutative-geometry), can be looked at in the following references [12, 13]. On the other hand, for Lorentzian traversable wormhole, where it would allow travel in both directions from one part of the spacetime of this universe or the another universe, one has to go through the seminal papers of Thorne and his coworkers [14, 15].

Our starting point is the search for a natural relationship between the wormhole geometry and the matter source supporting such a wormhole, with the help of the Einstein field equations. So we turn to the well-known inheritance symmetry contained in the set of conformal Killing vectors (CKV) [16–20]

$$ L_{\xi} g_{ik} =\xi_{i;k}+ \xi_{k;i} = \psi g_{ik}. $$
(2)

Here L is the Lie derivative operator and ψ the conformal factor. The vector ξ generates the conformal symmetry, while the metric tensor g i k is conformally mapped into itself along ψ. Over time, CKV’s have provided ever deeper insights into the spacetime geometry. In the process these conformal symmetries assist in generating exact solutions of the Einstein field equations that may, in turn, be used to model various relativistic, astrophysical, and cosmological phenomena [21–24].

To obtain the desired connection to the relativistic as well as astrophysical modeling of a wormhole in the framework of noncommutative geometry, our principal aim is the construction of a stable configuration fueled by a suitable amount of exotic matter. To this end, we have introduced conformal Killing vectors and basic equations in Section 2. The important properties of the wormhole thus obtained have been examined in Section 3, including studies on (i) active gravitational mass, (ii) TOV equation, and (iii) total gravitational energy, explored and discussed in several Sub-sections. A succinct summary of these results is provided in Section 4.

2 Conformal Killing Vectors and Basic Equations

In this section we turn our attention to traversable wormholes, starting with the static spherically symmetric metric

$$ ds^{2}=- e^{\nu(r)} dt^{2}+e^{\uplambda(r)} dr^{2} +r^{2}(d\theta^{2}+{sin}^{2}\theta\, d\phi^{2}). $$
(3)

Here ν and λ are the metric potentials of the spacetime and function of radial coordinate r only.

The Einstein field equations are stated next:

$$ e^{-\uplambda} \left[\frac{{\uplambda}^{\prime}}{r} - \frac{1}{r^{2}} \right]+\frac{1}{r^{2}}= 8\pi \rho, $$
(4)
$$ e^{-\uplambda} \left[\frac{1}{r^{2}}+\frac{\nu^{\prime}}{r}\right]-\frac{1}{r^{2}}= 8\pi p_{r}, $$
(5)

and

$$ \frac{1}{2} e^{-\uplambda} \left[\frac{1}{2}(\nu^{\prime})^{2}+ \nu^{\prime\prime} -\frac{1}{2}{\uplambda}^{\prime}\nu^{\prime} + \frac{1}{r}({\nu^{\prime}- {\uplambda}^{\prime}})\right] =8\pi p_{t}, $$
(6)

where ρ, p r and p t are respectively the matter-energy density, radial and tangential pressures of the fluid distribution.

Equation (2) now implies the following:

$$\begin{array}{@{}rcl@{}} \xi^{1} \nu^{\prime} &=&\psi; ~~~ \xi^{4} = C_{1} = ~constant;\\ \xi^{1} &=& \frac{\psi r}{2}~~~ and ~~~ \xi^{1} {\uplambda}^{\prime} + 2 \xi^{1}_{,1} =\psi. \end{array} $$
(7)

These, in turn, imply that

$$ e^{\nu} ={C_{2}^{2}} r^{2}, $$
(8)
$$ e^{\uplambda} = \left(\frac {a} {\psi}\right)^{2}, $$
(9)

and

$$ \xi^{i} = C_{1} {\delta_{4}^{i}} + \left(\frac{\psi r}{2}\right){\delta_{1}^{i}}, $$
(10)

where C 2 and a are integration constants. We note from the (8) and (9) that to get the explicit forms of the metric potentials we have to fix the values of the constants C 2 and a, and also the conformal factor ψ. However, to find out solvable pattern of the Einstein equations (4)-(6) we can, at first hand, transform these in terms of ψ. Thus using solutions (8) and (9), equations (4)-(6) take the forms as follows:

$$ \frac{1}{r^{2}}\left[1 - \frac{\psi^{2}}{a^{2}} \right]-\frac{2\psi\psi^{\prime}}{ra^{2}}= 8\pi \rho, $$
(11)
$$ \frac{1}{r^{2}}\left[1 - \frac{3\psi^{2}}{a^{2}} \right] = - 8\pi p_{r}, $$
(12)
$$ \frac{\psi^{2}}{a^{2}r^{2}} +\frac{2\psi\psi^{\prime}}{ra^{2}} =8\pi p_{t}. $$
(13)

At this point it is necessary to assume relationships between the physical parameters ρ, p r and p t . There are two possibilities: either (1) to choose a suitable form of ρ or (2) to choose a suitable relation between p r and p t . Following Nicolini et al. [4], we concur that the first choice is clearly preferable.

3 Model of a Wormhole and its Properties

It has been argued by several authors [25, 26] that noncommutative geometry offers conjecture of smeared or diffused objects to eliminate point-like structures. To get this smearing effect we choose the mass density of a static, spherically symmetric, diffused, particle-like gravitational source as provided in (1).

Thus, using (1), (11) becomes

$$ \frac{1}{r^{2}}\left[1 - \frac{\psi^{2}}{a^{2}} \right]-\frac{2\psi\psi^{\prime}}{ra^{2}}= 8 \pi \left( \frac{M}{(4\pi\theta)^{\frac{3}{2}}}e^{-\frac{r^{2}}{4\theta}} \right). $$
(14)

Solving this equation, we get

$$ \psi^{2} = a^{2}-\left (\frac{4 M a^{2} }{r \sqrt{4 \pi \theta}}\right )\left[ -r e^{-\frac{r^{2}}{4\theta}} + \sqrt{\theta \pi}~ erf\left(\frac{r}{2 \sqrt{\theta}}\right)\right]-\frac{Da^{2}}{r}, $$
(15)

where D a 2 is an integration constant.

Using this result, we get the exact analytical form for all the parameters, stated next:

$$ p_{t} = \frac{1}{8 \pi} \left[ \frac{1}{r^{2}} - \frac{8 \pi M }{(4 \pi \theta)^{\frac{3}{2}}} e^{-\frac{r^{2}}{4\theta}}\right], $$
(16)
$$ p_{r} =-\frac{1}{8 \pi r^{2}} \left[1- 3\left\{ 1-\left (\frac{4 M }{r \sqrt{4 \pi \theta}}\right )\left( -r e^{-\frac{r^{2}}{4\theta}} + \sqrt{\theta \pi}~ erf\left(\frac{r}{2 \sqrt{\theta}}\right)\right)-\frac{D}{r}\right\} \right], $$
(17)
$$ e^{\nu} ={C_{2}^{2}} r^{2}, $$
(18)

and

$$ e^{\uplambda} = \frac{1}{1-\left (\frac{4 M } {r \sqrt{4 \pi \theta}}\right )\left(-r e^{-\frac{r^{2}}{4\theta}} + \sqrt{\theta \pi}~ erf\left(\frac{r}{2 \sqrt{\theta}}\right)\right)-\frac{D}{r}}. $$
(19)

If the metric coefficient e λ is written in terms of shape function b(r), i.e., if

$$ e^{\uplambda} = \frac{1}{1-\frac{b(r)}{r}}, $$
(20)

then b(r) takes the form

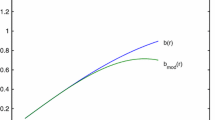
$$ b(r)= \left (\frac{4 M}{\sqrt{4 \pi \theta}}\right )\left[-r e^{-\frac{r^{2}}{4\theta}} + \sqrt{\theta \pi}~ erf\left(\frac{r}{2 \sqrt{\theta}}\right)\right]+D. $$
(21)

We have assumed the particle-like gravitational source in (1), which is positive and therefore results in a shape function that is monotone increasing, so b′(r) > 0 (Fig. 1). The throat of the wormhole is located at r = r 0, where b(r) − r cuts the r-axis, shown in Fig. 2. We also observe that for r > r 0, b(r) − r < 0, which implies that b(r)/r < 1, an essential requirement for a shape function. Finally, since b(r) − r is decreasing for r > r 0, b′ (r 0) < 1, which is the flare-out condition.

Fig. 1
figure 1

Diagram of the shape function of the wormhole for specific values of the parameters: θ = 0.1, M = 1

Full size image
Fig. 2
figure 2

The throat of the wormhole, occurs where b(r) − r cuts the r-axis

Full size image

One can note that Fig. 3 shows the asymptotic behavior b(r)/r → 0 as r → ∞. Unfortunately, the redshift function does not approach zero as r → ∞ due to the conformal symmetry. So the wormhole spacetime is not asymptotically flat and will therefore have to be cut off at some radial distance and joined to an exterior vacuum solution.

Fig. 3
figure 3

Asymptotic behavior of the shape function of the wormhole given in Fig. 1

Full size image

From (8), the redshift function is given by

$$ \frac{1}{2}\nu(r)=ln(C_{2}r). $$
(22)

So we match our interior solution to the exterior Schwarzschild solution at a junction interface r = R. Using this matching condition, we can determine the constant C 2:

$$ C_{2}=\frac{e^{\nu(R)/2}}{R}. $$
(23)

So, obviously the redshift function is finite in the region r 0 < r < R, as required.

Finally, let us check whether the material threading the wormhole violates the energy conditions. According to Fig. 4, the Null Energy Condition (NEC) and the Weak Energy Condition (WEC) are violated, conditions that are necessary to hold a wormhole open. It is interesting to note that the Strong Energy Condition (SEC) is met away from the throat. By contrast, when dealing with noncommutative wormholes that do not admit conformal motion, the SEC is violated [7].

Fig. 4
figure 4

Variation of the left-hand sides of the respective expressions for the energy conditions plotted against r

Full size image

3.1 The Tolman-Oppenheimer-Volkoff (TOV) Equation

At this point let us consider the equilibrium stage that can be achieved for matter threading the wormhole. To that end, we write the TOV equation as derived by solving the Einstein equations for a general time-invariant, spherically symmetric metric in the following form [27–29]:

$$ -\frac{M_{G}\left(\rho+p_{r}\right)}{r^{2}}e^{\frac{\uplambda-\nu}{2}} -\frac{dp_{r}}{dr} +\frac{2}{r}\left(p_{t}-p_{r}\right)=0, $$
(24)

where M G =M G (r) is the effective gravitational mass within the region (from r 0 up to the radius r), and is given by

$$ M_{G}(r)=\frac{1}{2}r^{2}e^{\frac{\nu-\uplambda}{2}}\nu^{\prime}. $$
(25)

The TOV (24) describes the equilibrium condition for the wormhole, subject to the gravitational force F g (due to gravitating mass), the hydrostatic force F h (due to hydrostatic fluid), and the anisotropic force F a (due to anisotropy of the system). To study the equilibrium of the physical system, we write (24) suitably in the following form

$$ F_{g}+ F_{h} + F_{a}=0, $$
(26)

where

$$\begin{array}{@{}rcl@{}} F_{g} &=&-\frac{\nu^{\prime}}{2}(\rho+p_{r})\\ &=& \frac{1}{8 \pi r^{3}}\left[1- 3\left\{1-\left(\frac{4 M}{r\sqrt{4 \pi \theta}}\right) \left(-r e^{-\frac{r^{2}}{4\theta}} +\sqrt{\theta \pi}~ erf \left(\frac{r}{2\sqrt{\theta}}\right)\right)\right\}\right]\\ &&-\frac{M}{r(4\pi\theta)^{\frac{3}{2}}}e^{-\frac{r^{2}}{4\theta}}, \end{array} $$
(27)
$$F_{h}= -\frac{dp_{r}}{dr}= \frac{1}{2 \pi r^{3}} +\left(\frac{3M}{\sqrt{ 4\pi\theta}}\right) \left(\frac{e^{-\frac{r^{2}}{4\theta}}}{r^{3}}\right) +\left(\frac{3M}{2\pi\sqrt {4\pi\theta}}\right)e^{-\frac{r^{2}}{4\theta}}$$
$$ +\left(\frac{3M}{4 \theta\sqrt {4\pi\theta}}\right)\left(\frac{e^{-\frac{r^{2}}{4\theta}}}{r}\right) -\left(\frac{9M\sqrt {\theta \pi}}{2\pi \sqrt {4\pi \theta}}\right)\left(\frac{erf (\frac{r}{2\sqrt\theta})}{r^{4}}\right), $$
(28)

and

$$F_{a}= \frac{2}{r}(p_{t}-p_{r}) = \frac{1}{4\pi r} \left[ \frac{1}{r^{2}}- \frac{8\pi M }{(4\pi \theta)^{\frac{3}{2}}} e^{-\frac{r^{2}}{4\theta}} \right]$$
$$ +\frac{1}{4\pi r^{3}}\left[1- 3 \left\{1- \left(\frac{4M}{r\sqrt{4\pi \theta}}\right) \left( -r e^{-\frac{r^{2}}{4\theta}}+ \sqrt{\theta \pi}\;\;erf (\frac{r}{2\sqrt\theta})\right)\right \}\right]. $$
(29)

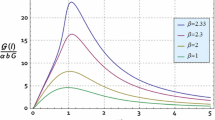
The profiles of F g , F h , and F a are shown in Fig.5. Since the gravitational force is by far the weakest, the counterbalancing is accomplished mainly by the hydrostatic and anisotropic forces outside the throat. Fig.5 indicates that the overall equilibrium can indeed be achieved by these forces, as a consequence of the conformal motion and the noncommutative geometry.

Fig. 5
figure 5

Three different forces acting on the fluid elements in static equilibrium plotted against r

Full size image

3.2 Total Gravitational Energy

We have already observed that the material composing the wormhole violates the NEC and WEC, and must therefore be of the exotic rather than normal type. The total gravitational energy of a structure composed of normal baryonic matter is negative. So it is important to determine the nature of the gravitational energy in a wormhole setting.

Lynden-Bell et al. [30] prescribed the formula for the total gravitational energy of any stationary spacetime (considering absence of black holes) as follows: E g =M a c t i v e − E M , where M a c t i v e is the total mass as defined earlier and E M is the gravitational binding energy. However, following Nandi et al. [31], we can obtain an expression for this total gravitational energy in it’s explicit form, applied particularly to a wormhole:

$$ E_{g}= \frac{1}{2} {\int}_{r_{0}}^{r} [ ~1 -\sqrt{g_{rr}}~] \rho r^{2} dr + \frac{r_{0}}{2}. $$
(30)

Here \(g_{rr} = \left [1- \frac {b(r)}{r}\right ]^{-1}\) as defined in terms of shape function b(r), and the quantity \(\frac {r_{0}}{2}\) is associated with the effective gravitational mass [31]. It can be argued that since \(\sqrt {g_{rr}} > 1\), then E g < 0 (attractive) if \({T^{0}_{0}} > 0\) and that E g > 0 (repulsive) if \({T^{0}_{0}} < 0\) [31, 32]. We are now interested to evaluate E g and hence take the range of the integral to be from the throat r 0 to the embedded radial space of the wormhole geometry. So the total gravitational energy of the wormhole is given by

$$ E_{g}= \left[-\frac{.0129 r^{2}}{\theta^{\frac{3}{4}}} + \frac{.0037 r^{3}}{\theta^{\frac{3}{2}}} +\frac{.0011 r^{4}}{\theta^{\frac{7}{4}}} +0(r^{5})\right]^{r}_{r_{0}} + \frac{r_{0}}{2}. $$
(31)

Due to complicated nature of the integrand, we cannot obtain an exact analytical form and must therefore approximate the total gravitational energy graphically. The plot for total gravitational energy, obtained by retaining terms up to fourth order in (31), indicates that E g > 0. Note that we get E g > 0 here in spite of \({T_{0}^{0}}>0\). This is because the matter distribution that supported the wormhole structure violates the NEC and WEC. In other words, there is a repulsion around the throat (See Fig. 6). This repulsive nature or positivity of E g is very much expected in a physically valid wormhole.

Fig. 6
figure 6

Plot of E g as a function of r

Full size image

4 Concluding Remarks

In this paper we investigate traversable wormholes admitting conformal motion that are also supported by a noncommutative-geometric matter source. Some of the important features of the present investigation can be formulated as follows:

  1. (1)

    Since, due to the conformal symmetry, the spacetime is not asymptotically flat, it was necessary to cut off the material and to match the interior wormhole solution to an exterior Schwarzschild spacetime at a junction interface r = R.

  2. (2)

    We also calculated the active gravitational mass in the region extending from r = r 0 to r = R, and then observed that at a certain stage the active mass, M a c t i v e , tends to the total mass, M, of the system. This effect then indicates that a distant observer would not be able to distinguish between the gravitational nature of the wormhole and a compact mass of the source.

  3. (3)

    This is followed by a discussion of the TOV equation describing the effect of the conformal motion on the equilibrium stage for the wormhole in terms of the gravitational force F g , the hydrostatic force F h , and the anisotropic force F a .

  4. (4)

    It is shown that the total gravitational energy is positive, attributable to the repulsion around the throat.

  5. (5)

    Finally, in the framework of wormhole construction, the matter violating the NEC condition plays a significant role in avoiding the collapse of the tunnel. Given that this type of matter constitutes a sharp departure from the behavior of normal matter, we are justified in considering a Gaussian distribution for modeling the matter distribution in the sense that it succeeds in supplying fuel for constructing the wormhole.