1 Introduction

There is a large body of exact solutions to the Einstein field equations describing spherically symmetric, static matter distributions available in the literature. A systematic study of these solutions reveal that only a small subset of them are physically viable (Finch and Skea 1995). Various approaches have been adopted to solve the Einstein field equations in the hope that these solutions describe physically realizable stellar structures. These approaches range from ad-hoc assumptions that lead to mathematical tractable solutions through to the imposition of physical requirements on the spacetime geometry and matter content. Nearly all spherically symmetric static solutions of the Einstein field equations were obtained using curvature coordinates. Recently, there have been attempts at finding exact solutions for perfect fluid spheres in isotropic coordinates. Mak and Harko (2005) presented a matrix method for generating relativistic solutions which describe compact objects in isotropic coordinates. Ivanov (2012), through his study of collapsing shear-free fluid spheres with heat flow was able to show a strong link between the solution-generating method for static, isotropic spheres and collapsing, radiating spheres. Lake (2003) has presented an algorithm which generates all static spherically symmetric perfect solutions by choosing a single monotone function (subject to boundary conditions). Herrera et al. (2008) extended Lake’s algorithm to locally anisotropic fluids. In this case one requires two generating functions (as opposed to one in the isotropic case) in order to obtain solutions to the Einstein field equations. A general framework to study axially symmetric static fluids was provided by Herrera et al. (2013). They were able to generate an exact solution representing a constant density spheroid which degenerates into the Schwarzschild incompressible sphere in the spherically symmetric limit. A general formalism to generate solutions of the Einstein field equations representing static polytropes with unequal stresses was set up by Herrera and Barreto (2013). In their investigation, they considered two types of polytropic equations of state which in the Newtonian limit become the generalised Lane-Emden equation for anisotropic matter distributions.

The role of anisotropic stresses in bounded gravitating systems has been investigated in two comprehensive papers by Dev and Gleiser (2002, 2003) in which they (I) obtained exact anisotropic star models by specifying various equations of state and (II) investigated the stability of these solutions under radial perturbations. Herrera and Santos (1997) provided an excellent review of the role of anisotropy in self-gravitating systems for both static and non-static spherical mass distributions.

Observational data on the compactness of astrophysical bodies such as Her X-1, SAX J1808.4-3658 amongst others, point to the possibility that these objects may actually be strange stars. An alternative model to the MIT bag model \((p = \frac{1}{3}(\rho - 4B))\) which relates the isotropic pressure \(p\) to the energy density \(\rho\) and the bag constant \(B\) was provided by Dey et al. (1998). It was shown that the equation of state (EOS) for strange stars developed by Dey et al. (1998) can be approximated to a linear form, \(p = n(\rho - \rho_{s})\) where \(n\) is a constant and \(\rho_{s}\) is the surface density (Sharma and Maharaj 2007). The role played by a linear equation of state in the stability of charged compact objects was studied by Ngubelanga et al. (2015b). By utilising isotropic coordinates, they were able to show that their solutions were well-behaved and adequately described the physical features of a star like PSR J1614-2230. Pant and coworkers have investigated various relativistic, charged anisotropic spheres in isotropic coordinates (Pant et al. 2014a, 2014b, 2015b). They were able to obtain a large class of new, exact solutions of the Einstein-Maxwell field equations. Their indepth study of the physical properties of these solutions indicates that these solutions describe physically viable models of neutron and self-bound strange quark stars. Recently, there have been numerous attempts at modeling strange stars with exotic equations of state. One simple generalisation of the linear barotropic equation of state is the so-called quadratic equation of state in which the energy density and pressure of the stellar fluid are related by \(p_{r} = \eta\rho^{2} + \alpha \rho - \beta\). This EOS was shown to adequately describe strange star candidates with the quadratic term playing a significant role in the predicted mass and radius profiles of these stellar objects (Maharaj and Takisa 2012; Takisa et al. 2014). In a more recent study Ngubelanga et al. (2015a) studied charged static spheres obeying a quadratic equation of state. By assuming a particular form for one of the gravitational potentials and specifying the behaviour of the electric field intensity, they were able to solve the Einstein-Maxwell system to obtain new exact solutions in isotropic coordinates. These models were used to regain the masses of the stars PSR J1614-2230, 4U 1608-52, PSR J1903+0327, EXO 1745-248 and SAX J1808.4-3658. Thirukkanesh and Ragel (2014) utilised a Van der Waals EOS to model an anisotropic compact star. These models were shown to satisfy the regularity, stability and boundary conditions thus rendering them ideal candidates for modeling highly compact objects within the framework of general relativity. A more recent study of static compact objects was carried out by Ngubelanga and Maharaj (2013) in which they used a transformation due to Kustaanheimo and Qvist (1948) to model charged, static spheres in comoving isotropic coordinates. Their approach reduced the problem to a Bernoulli equation which they were to able to integrate for the case of a conformally flat, static sphere. Pant et al. (2015a) modeled anisotropic compact objects in isotropic coordinates by assuming particular forms for the anisotropic parameter. By assuming a surface density of \(2 \times 10^{14}~\mbox{g}.\mbox{cm}^{-3}\), they were able to show that their model describes a super dense quark star with a maximum mass of approximately 1.35 solar masses and a radius of \(R= 12.58~\mbox{km}\). In a recent study of static compact spheres in comoving isotropic coordinates Thirukkanesh et al. (2015) presented an intriguing model of a sphere with vanishing radial stresses in the in the interior. They showed that stability is achieved via the tangential stresses and that these models adequately describe strange star candidates such as Her. X-1, SAX J1808.4-3658(SS2), SAX J1808.4-3658(SS1) and PSR J1614-2230.

In this paper we present an algorithm for generating solutions of the Einstein field equations in isotropic coordinates describing static, anisotropic spheres with a linear EOS of the form \(p_{r} =\alpha \rho - \beta\). As in the Lake algorithm, only one metric function is required to generate the complete gravitational field within the gravitating sphere. We illustrate the validity of our algorithm by obtaining the constant density solution in isotropic coordinates as well as a particular model of a conformally flat static sphere. The physically viability of our solution-generating method is carried out for a particular model describing a spherically symmetric static star.

2 Spherical symmetry

In this paper we consider a model which represents a spherically symmetric, anisotropic fluid configuration obeying a linear equation of state. The interior spacetime of the stellar model takes the form

$$ ds^{2} = -A^{2}(r)dt^{2} + B^{2}(r) \bigl[dr^{2} + r^{2}d\varOmega^{2} \bigr], $$
(1)

where \(d\varOmega^{2} = d\theta^{2} + \sin^{2}{\theta}d\phi^{2}\) and the metric functions, \(A(r)\) and \(B(r)\) are yet to be determined. For our model the energy-momentum tensor for the stellar fluid is

$$ T_{ab} = \operatorname{diag} (-\rho, p_{r}, p_{t}, p_{t} ), $$
(2)

where \(\rho\), \(p_{r}\) and \(p_{t}\) are the proper energy density, radial pressure and tangential pressure respectively. The fluid four-velocity \(\mathbf{u}\) is comoving and is given by

$$ u^{a} = \frac{1}{A} \delta^{a}_{0} . $$
(3)

The Einstein field equations for the line element (1) are

$$\begin{aligned} &{\rho = - \frac{1}{B^{2}} \biggl( 2\frac{B''}{B} - \frac{{B'}^{2}}{B^{2}} + \frac{4}{r}\frac{B'}{B} \biggr),} \end{aligned}$$
(4a)
$$\begin{aligned} &{p_{r} = \frac{1}{B^{2}} \biggl[\frac{{B'}^{2}}{B^{2}} + 2 \frac{A'}{A}\frac{B'}{B} + \frac{2}{r} \biggl(\frac{A'}{A} + \frac{B'}{B} \biggr) \biggr],} \end{aligned}$$
(4b)
$$\begin{aligned} &{p_{t} = \frac{1}{B^{2}} \biggl[\frac{A''}{A} + \frac{B''}{B}- \frac{{B'}^{2}}{B^{2}}+\frac{1}{r} \biggl(\frac{A'}{A}+ \frac{B'}{B} \biggr) \biggr] ,} \end{aligned}$$
(4c)

where primes represent differentiation with respect to the radial coordinate \(r\). In generating the above field equations we have utilised geometrized units where the coupling constant and the speed of light are taken to be unity. The system (4a)–(4c) comprises three independent equations with five variables (\(A(r)\), \(B(r)\), \(\rho\), \(p_{r}\) and \(p_{t}\)). The mass contained within a sphere of radius \(r\) is defined as

$$ m(r)= \frac{1}{2}\int_{0}^{r} \omega^{2} \rho(\omega)d\omega, $$
(5)

where \(\omega\) is an integration variable. The study of relativistic stars with a linear equation of state has received widespread attention amongst astrophysicists. Sharma and Maharaj (2007) modeled a strange star with quark matter by imposing a linear equation of state of the form

$$ p_{r} =\alpha \rho - \beta, $$
(6)

where \(\beta = \alpha \rho_{s}\), \(0\leq \alpha \leq 1\) and \(\rho_{s}\) is the density at the surface \(r = r_{\varSigma}\). They presented a class of solutions in curvature coordinates which were well-behaved and described physical objects such as the X-ray pulsar SAX J 1808.4-3658. Substituting (4a) and (4b) into (6) we obtain the master equation

$$\begin{aligned} &{2\alpha\frac{B''}{B}+(1 - \alpha)\frac{{B'}^{2}}{B^{2}} + \frac{2}{r} \biggl(\frac{A'}{A} + (1 + 2\alpha)\frac{B'}{B} \biggr)} \\ &{\quad {}+ 2\frac{A'}{A}\frac{B'}{B} + \beta B^{2}=0,} \end{aligned}$$
(7)

the solution of which yields the gravitational behaviour of our model. Equation (7) can be written as

$$ \frac{A'}{A}= \frac{- [2\alpha\frac{B''}{B}+(1 -\alpha) \frac{{B'}^{2}}{B^{2}} + 2(1 + 2\alpha)\frac{1}{r}\frac{B'}{B}+ \beta B^{2} ]}{2 [\frac{1}{r}+\frac{B'}{B} ]}. $$
(8)

On integrating (8) we obtain

$$ A= d \exp \biggl[-\frac{1}{2}\int F(r) \,dr \biggr], $$
(9)

where

$$ F(r) = \biggl( \frac{ 2\alpha\frac{B'' }{B}+(1 - \alpha) \frac{B^{\prime2} }{B^{2}} + 2(1 +2\alpha) \frac{1}{r}\frac{B' }{B}+ \beta B^{2}}{\frac{1}{r}+\frac{B'}{B}} \biggr) $$
(10)

and \(d\) is a constant of integration. Hence the line element (1) can be written as

$$\begin{aligned} ds^{2} =& -d^{2} \exp \biggl[-\int F(r)\, dr \biggr] dt^{2} \\ &{}+ B^{2} \bigl[dr^{2} + r^{2}d \varOmega^{2} \bigr] , \end{aligned}$$
(11)

where \(F(r)\) is given in (10). Hence, any solution describing a static spherically symmetric anisotropic matter distribution with linear equation of state in isotropic coordinates can be easily determined by a single generating function \(B(r)\).

3 Uniform density sphere

If we assume that the density of the interior matter distribution is constant, \(\rho = \mu = \mbox{constant}\), (4a) becomes

$$ \mu = - \frac{1}{B^{2}} \biggl( 2\frac{B''}{B} - \frac{{B'}^{2}}{B^{2}} + \frac{4}{r}\frac{B'}{B} \biggr) . $$
(12)

This equation admits the solution

$$ B=\frac{2\sqrt{3}~c}{\sqrt{\mu}(1+c^{2}r^{2})}, $$
(13)

where \(c\) is an arbitrary constant. This solution was first derived by Wyman (1946). Substituting (13) in (9) we obtain

$$ A=d \biggl[\frac{1+c^{2}r^{2}}{1-c^{2}r^{2}} \biggr]^{\frac{\mu (1+3\alpha)-3\beta}{2 \mu}} , $$
(14)

where \(d\) is an integration constant. In this case the metric (1) take a particular form

$$\begin{aligned} ds^{2} =& -d^{2} \biggl[\frac{1+c^{2}r^{2}}{1-c^{2}r^{2}} \biggr]^{\frac{\mu (1+3\alpha)-3\beta}{\mu}}dt^{2} \\ &{} + \chi^{2} \bigl[dr^{2} + r^{2}d\varOmega^{2} \bigr] , \end{aligned}$$
(15)

where \(\chi^{2} = \frac{12c^{2}}{\mu (1+c^{2}r^{2})^{2}}\). The Bowers and Liang (1974) solution in curvature coordinates is a generalisation of the constant density Schwarzschild sphere to include anisotropic pressure. They showed that it was possible to obtain arbitrarily large surface redshifts by including large anisotropies within the stellar fluid. A model of dissipative gravitational collapse was constructed by Kramer (1992) in which he transformed the interior Schwarzschild solution into comoving, isotropic coordinates and then allowed the mass parameter to evolve with time. The temporal evolution of the collapsing sphere was obtained from the boundary condition and the subsequent dynamics of the model was investigated (Maharaj and Govender 1997). As pointed out by Ivanov (2012), Kramer’s approach is a special case of a more general method of constructing shear-free, radiating spheres from known static solutions of the Einstein field equations in comoving, isotropic coordinates.

4 Conformally flat spheres

The nonvanishing components of the Weyl tensor \(C_{abcd}\) for the line element (1) are

$$\begin{aligned} C_{2323} =& \frac{r^{4}}{3}B^{2}\sin^{2}{\theta} \biggl[ \biggl(\frac{A'}{A} - \frac{B'}{B} \biggr) \biggl( \frac{1}{r} + 2\frac{B'}{B} \biggr) \\ & {} - \biggl(\frac{A''}{A} - \frac{B''}{B} \biggr) \biggr], \end{aligned}$$
(16a)
$$\begin{aligned} C_{2323} =& -r^{4} \biggl(\frac{B}{A} \biggr)^{2}\sin^{2}{\theta}C_{0101} \end{aligned}$$
(16b)
$$\begin{aligned} =& 2r^{2} \biggl(\frac{B}{A} \biggr)^{2} \sin^{2}{\theta}C_{0202} \\ =& 2r^{2} \biggl(\frac{B}{A} \biggr)^{2}C_{0303} \end{aligned}$$
(16c)
$$\begin{aligned} =& -2r^{2}\sin^{2}{\theta}C_{1212} = -2r^{2}C_{1313}. \end{aligned}$$
(16d)

If we now impose the condition of conformal flatness, then this would imply vanishing of all the Weyl tensor components. From the above relations we note that this condition is fulfilled if we demand

$$ r \biggl(\frac{A''}{A} - \frac{B''}{B} \biggr) - \biggl( \frac{A'}{A} - \frac{B'}{B} \biggr) \biggl(1 + 2r\frac{B'}{B} \biggr) = 0. $$
(17)

Equation (17) can be easily integrated to give

$$ A = \bigl[C_{1}r^{2} + 1\bigr]B, $$
(18)

where \(C_{1}\) is a constant of integration. Substituting (18) into (7) we obtain

$$\begin{aligned} &{2\alpha\frac{B''}{B}+(3 - \alpha)\frac{{B'}^{2}}{B^{2}} + \frac{4B'}{B} \biggl(\frac{1+\alpha}{r}+\frac{C_{1}r}{1+C_{1}r^{2}} \biggr)} \\ &{\quad {}+\frac{4C_{1}}{1+C_{1}r^{2}} + \beta B^{2}=0,} \end{aligned}$$
(19)

which is highly non-linear and difficult to integrate in general. However, if we place some restrictions it is possible to integrate Eq. (19). For example, when \(C_{1}=0\) (i.e., \(A=B\)) and \(\beta =0\) (i.e., \(p_{r}=\alpha \rho\)), Eq. (19) reduces to a convenient form

$$ \frac{B''}{B}+\frac{(3 - \alpha)}{2\alpha}\frac{{B'}^{2}}{B^{2}} + \frac{2(1+\alpha)}{\alpha}\frac{1}{r} \frac{B'}{B}=0. $$
(20)

This equation can be written as

$$ \frac{B''}{B'}+\frac{(3 - \alpha)}{2\alpha}\frac{B'}{B} + \frac{2(1+\alpha)}{\alpha}\frac{1}{r}=0, $$
(21)

which can be easily integrated to yield

$$ B= \bigl[b +c r^{ (\frac{-(2+\alpha)}{\alpha} )} \bigr]^{\frac{2\alpha}{3+\alpha}}, $$
(22)

where \(b\) and \(c\) are constants of integration. In this case the metric (1) take a particular form

$$ ds^{2} = - \bigl[a +b r^{ (\frac{-(2+\alpha)}{\alpha} )} \bigr]^{\frac{4\alpha}{3+\alpha}} \bigl[dt^{2} + dr^{2} + r^{2}d\varOmega^{2} \bigr] . $$
(23)

Radiating gravitational collapse with vanishing Weyl stresses were studied by many authors using comoving and isotropic coordinates (Herrera et al. 2004, 2006; Maharaj and Govender 2005).

5 Example

Variety of choices can be made for the gravitational potential \(B\) for integrate (9) to obtain the potential \(A\). However, the choices must be physically reasonable to model a realistic stellar object. Consequently, as example, we choose a form for the gravitational potential \(B\) as

$$ B=\frac{a}{\sqrt{1+br^{2}}}, $$
(24)

where \(a\) and \(b\) are real constants. The potential chosen in (24) is regular at the center and a similar form potential has been used in curvature coordinates to model compact sphere (Schwarzschild 1916; Einstein 1917; de Sitter 1917). Substituting (24) into (9) and integrate we obtain

$$ A=d \bigl(1 +br^{2}\bigr)^{\frac{(1+5 \alpha)}{4}} \exp \biggl[\frac{ [b(1 +\alpha)- a^{2} \beta](1 + br^{2}) }{4b} \biggr]. $$
(25)

In this case the matter variables can be explicitly written as

$$\begin{aligned} &{\rho = \frac{b(6+br^{2})}{a^{2}(1+br^{2})}, } \end{aligned}$$
(26)
$$\begin{aligned} &{p_{r} = \alpha \frac{b(6+br^{2})}{a^{2}(1+br^{2})} -\beta ,} \end{aligned}$$
(27)
$$\begin{aligned} &{\textstyle\begin{array}[b]{@{}rcl} p_{t} &=& \dfrac{1}{4a^{2}(1+br^{2})} \bigl\{ b \bigl[24\alpha +br^{2}\bigl[br^{2}(1+\alpha) \\ && {}\times \bigl(4(2+3\alpha) +(1+\alpha)br^{2} \bigr)+4\bigl(3+ \alpha(8+9\alpha)\bigr)\bigr] \bigr] \\ && {}+a^{2}\beta^{2} r^{2}\bigl(1+br^{2}\bigr)^{2} -2a^{2}\beta\bigl(1+br^{2}\bigr) \\ && {}\times \bigl[2+br^{2}\bigl(4+6\alpha+(1+\alpha)br^{2} \bigr)\bigr] \bigr\} , \end{array}\displaystyle } \end{aligned}$$
(28)
$$\begin{aligned} &{\textstyle\begin{array}[b]{@{}rcl} \Delta &=&\dfrac{r^{2}}{4a^{2}(1+br^{2})} \bigl\{ b^{2} \bigl[(1+\alpha)br^{2} \\ && {}\times\bigl(4(2+3\alpha)+(1+\alpha)br^{2}\bigr) \\ && {}+4\bigl(3+\alpha (7+9\alpha)\bigr) \bigr]+a^{4} \beta^{2}\bigl(1+br^{2}\bigr)^{2} \\ && {} -2a^{2}b \beta \bigl(1+br^{2}\bigr) \bigl(2(2+3 \alpha)+(1+\alpha)br^{2}\bigr) \bigr\} , \end{array}\displaystyle } \end{aligned}$$
(29)

where \(\Delta =p_{t}-p_{r}\) is the measure of anisotropy. It is noted that the matter variables are given in terms of elementary functions that facilitate for a detailed physical analysis of the model. Substituting (26) into (5) we obtain

$$ m(r)=\frac{br^{3}+15 (r-\frac{\arctan [\sqrt{b}r]}{\sqrt{b}} )}{6a^{2}}. $$
(30)

6 Physical analysis

We are now in a position to discuss the physical features of the model generated in Sect. 5. In order to describe a realistic stellar structure our model must satisfy the following physical requirements:

  1. (i)

    regularity of the gravitational potentials at the origin;

  2. (ii)

    positive definiteness of the energy density and the radial pressure at the origin;

  3. (iii)

    monotonic decrease of the energy density, the radial pressure and the tangential pressure with increasing radial distance;

  4. (iv)

    the square of speed of sound \(V_{S}^{2}=|(dp_{t}/d\rho)^{2}-(dp_{r}/d\rho)^{2}|\leq 1\) throughout the interior of star;

  5. (v)

    the continuity of the extrinsic curvature across the matching hypersurface, \(K^{-}_{ij} = K^{+}_{ij}\). Continuity of the extrinsic curvature across the matching hypersurface, \(r=R\) yields

    $$ (p_{r})_{(r=R)} = 0; $$
    (31)
  6. (vi)

    the ratio of trace of stress tensor to energy density, \((p_{r}+2p_{t})/\rho\), must decrease outward;

  7. (vii)

    matching conditions: we must match the interior spacetime \((\mathcal{M}_{-})\) to the exterior spacetime \((\mathcal{M}_{+})\) described by the exterior Schwarzschild solution in comoving isotropic coordinates (Bonnor et al. 1989)

    $$\begin{aligned} ds^{2} =& - \frac{ ( 1 - \frac{M}{2r} )^{2}}{ ( 1 + \frac{M}{2r} )^{2}} dt^{2} +\biggl( 1+ \frac{M}{2r} \biggr)^{4} \\ & {}\times \bigl[dr^{2}+ r^{2} \bigl(d\theta^{2} +\sin^{2}\theta d \phi^{2}\bigr)\bigr], \end{aligned}$$
    (32)

    where \(M\) is the mass within a sphere of radius \(R\).

We now show that the models generated in Sect. 5 satisfy the above listed physical properties.

  1. (i)

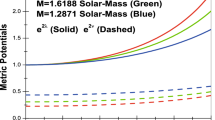
    Since \(A^{2}(0)=d^{2} e^{[b(1+\alpha) -a^{2}\beta]/2b}\), \(B^{2}(0)=a^{2}\) which are constants and \((A^{2}(r))'=(B^{2}(r))'=0 \) at the origin \(r=0\), the gravitational potentials are regular at the origin.

  2. (ii)

    Since \(\rho(0)= \frac{6b}{a^{2}}\) and \(p_{r}(0)=\frac{6\alpha b}{a^{2}}-\beta\), the energy density and radial pressure are positive at the origin.

  3. (iii)

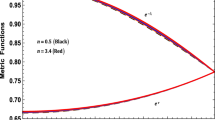
    Since \(\frac{d\rho}{dr}=-\frac{10b^{2}r}{a^{2}(1+br^{2})^{2}} <0\), the energy density is a decreasing function of \(r\). The radial pressure \(p_{r}\) is also a decreasing function as \(p_{r}\) and \(\rho\) are related on a linear equation of state. The decreasing features of the tangential pressure \(p_{t}\) is illustrated in Fig. 3 for particular choice of parameters.

  4. (iv)

    In general it is difficult to obtain the constraints on the parameters \(a, b, \alpha\) and \(\beta\) to satisfy \(V_{S}^{2}=|(dp_{t}/d\rho)^{2}-(dp_{r}/d\rho)^{2}|\leq 1\). However it is possible for a particular set of values of parameters as shown in Fig. 5.

  5. (v)

    At the hypersurface, the condition \((p_{r})_{(r=R)}=0\) implies \(R=\sqrt{\frac{6\alpha b-a^{2}\beta}{b(a^{2}\beta -\alpha b)}}\) which is finite for appropriate choice of parameters \(a, b, \alpha\) and \(\beta\).

  6. (vi)

    In addition to the monotonic decreasing trend of the radial and tangential pressures we require that the ratio of trace of the stress tensor to energy density from center to the surface also decrease as illustrated in Fig. 6.

  7. (vii)

    Matching of interior metric (1) and exterior metric (32) at the boundary \(r=R\) leads to the constraints

    $$\begin{aligned} A(R) =&\frac{ (1 -\frac{M}{2R} )}{ (1 +\frac{M}{2R} )}, \end{aligned}$$
    (33)
    $$\begin{aligned} B(R) =& \biggl(1 +\frac{M}{2R} \biggr)^{2}, \end{aligned}$$
    (34)

    where

    $$ M=m(R)=\frac{bR^{3}+15 (R- \frac{\arctan [\sqrt{b}R]}{\sqrt{b}} )}{6a^{2}}. $$
    (35)

    The condition (33) imposes the following restriction on the constant of integration

    $$\begin{aligned} d =&\frac{12a^{2}R - [bR^{3} +15 (R- \frac{\arctan [\sqrt{b}R]}{\sqrt{b}} ) ]}{12a^{2}R + [bR^{3} +15 (R- \frac{\arctan [\sqrt{b}R]}{\sqrt{b}} ) ]} \\ &{}\times\bigl(1+bR^{2}\bigr)^{-\frac{(1+5 \alpha)}{4}} \\ &{}\times \exp \biggl[-\frac{[b(1+\alpha)- a^{2} \beta](1+ bR^{2})}{4b} \biggr]. \end{aligned}$$

    The condition (34) implies

    $$ \frac{a}{\sqrt{1+b R^{2}}}= \biggl[1 +\frac{ bR^{3}+15 (R-\frac{\arctan [\sqrt{b}R]}{\sqrt{b}} )}{12a^{2}R} \biggr]^{2} . $$
    (36)

    This imposes a restriction on the parameters \(a, b\) which can be determined if we specify the radius of the sphere. For example, the model parameter values chosen to prepare Table 1. satisfy all these boundary conditions.

    Table 1 Radial pressure (Central), density (central and surface) and mass for different anisotropic stellar models
    Full size table

To illustrate the radial dependence of the physical quantities of our model, Figs. 1–8 were plotted for the same parameter values utilised in Table 1 corresponding to the strange star candidate PSR J1614-2230 with radius \(R = 15\) km. For these parameter values we have plotted the behaviour of the energy density \(\rho\), the radial pressure \(p_{r}\) and the tangential pressure \(p_{t}\) in Figs. 1, 2 and 3 respectively. These figures show that the energy density, the radial pressure, the tangential pressure decrease monotonically with increasing radial distance. Moreover, as seen in Figs. 1, 2 and 3, density and tangential pressure are non-zero at the surface while the radial pressure vanishes, which is physically acceptable (Herrera and Santos 1997). The measure of anisotropy is plotted in Fig. 4 which is outward or repulsive (\(\Delta > 0\)) throughout the interior of the star. The square of speed of sound is plotted in Fig. 5 shows that \(V_{S}^{2}=|(dp_{t}/d\rho)^{2}-(dp_{r}/d\rho)^{2}|\leq 1\) which is a requirement for an anisotropic model (Herrera and Santos 1997). Figure 6 shows that the ratio of trace of stress tensor to energy density, \((p_{r}+2p_{t})/\rho\), is decreasing outwards. The surface redshift is given by

$$ Z_{R} = \biggl[1-\frac{bR^{3}+15 (R-\frac{\arctan[\sqrt{b}R]}{\sqrt{b}} )}{3a^{2}R} \biggr]^{-1/2}-1. $$
(37)

Figure 7 shows that the surface redshift is an increasing function of the radius of the star. Figure 8 illustrates the compactness of the star. For the isotropic case, Buchdahl (1959) has shown that the maximum allowed mass-to-radius ratio for a static sphere in equilibrium is \(\frac{M}{R} < \frac{4}{9}\). Figure 8 shows that our model satisfies the Buchdahl inequality for the maximum allowable mass-to-radius ratio.

Fig. 1
figure 1

Energy Density

Full size image
Fig. 2
figure 2

Radial Pressure

Full size image
Fig. 3
figure 3

Tangential Pressure

Full size image
Fig. 4
figure 4

Measure of anisotropy

Full size image
Fig. 5
figure 5

Square of sound speed

Full size image
Fig. 6
figure 6

Ratio of trace of stress tensor to energy density

Full size image
Fig. 7
figure 7

Surface redshift as a function of \(R\)

Full size image
Fig. 8
figure 8

\(\frac{M}{R}\) as a function of \(R\)

Full size image

In order to illustrate the physical viability of our model-generating algorithm we have computed the relevant physical parameters for various strange star candidates namely, Her. X-1, SAX J1808.4-3658(SS2), SAX J1808.4-3658(SS1) and PSR J1614-2230 as presented in Table 1. In the calculation of numerical values for the physical parameters in Table 1 we use values for the parameters such that the physical requirements given in (i)–(vii) are satisfied. Moreover, our calculated masses for the strange star candidates Her. X-1, SAX J1808.4-3658(SS2) and SAX J1808.4-3658(SS1) are compatible with the values of Tikekar and Jotania (2007) while the values for PSR J1614-2230 is compatible with the values of Muñoz-Darias et al. (2009). In particular, Table 1 confirms the observed mass to radius ratio for Her. X-1 is \(0.121\mbox{--}0.128~M_{\odot}.\mbox{km}^{-1}\) (Leahy 2004) and the observed mass range is \(1.07 \pm 0.360~M_{\odot}\) (Rawls et al. 2011) to good approximation. We compare the compactness parameter (mass-to-radius ratio) in Tikekar and Jotania (2007): \(u > 0.3\) for pulsars SAX J1808.4-3658 (SS1 & SS2) and PSR J1614-2230 suggests they are strange stars of type I, and Her X-1 are of type II \((0.2 < u < 0.3)\), and the \(u\) value for neutron star counterparts are considered to be still lower.

7 Conclusion

We have provided an algorithm to generate solutions of the Einstein field equations in comoving, isotropic coordinates which describe anisotropic, static spheres obeying a linear equation of state. All solutions can be obtained by specifying the behaviour of a single function. Our algorithm allows us to obtain the constant density solution first derived by Wyman as well as a class of conformally flat, static spheres. With the aid of a specific model we demonstrate the physical viability of our solution-generating method and its applicability to modeling physically realizable stellar structures such as strange stars.