1 Introduction

The modeling of astrophysical compact objects has been a challenge and continuous interest among the relativistic community. Analysis emanating from experimental observations (Demorest et al. 2010; Freire et al. 2011; Pons et al. 2002; Dey et al. 1998; Li et al. 1999; Xu et al. 1999) on astrophysical compact objects predict densities that significantly exceed the equilibrium density of nuclear matter exotica, ρs≃2.7×1014 g cm−3 (or ns≃0.16 baryons fm−3). To explain such observed compactness of pulsars, strange quark stars (SQS) have been proposed in recent past (Weber 2005; Angeles Perez-Garcia et al. 2010; Rodrigues et al. 2011). Strange stars are expected to form during the collapse of the core of a massive star after the supernova explosion. In the extreme of such high densities, a deconfined quark-gluon phase is possible at the core of a compact star, as predicted by Quantum chromodynamics. It has already been conjectured that strange quark matter (SQM) might be the true ground state of hadrons (Witten 1984; Farhi and Jaffe 1984). It has been articulated that SQM made of up, down and strange quarks is absolutely stable with a lower charge-to-baryon ratio compared to the nuclear matter, and compression of which to sufficiently high density would trigger a phase transition converting virtually the entire star into SQM. Such a SQS is more stable and self-bound as opposed to being gravitationaly bound as in normal neutron star. One expects configurations of quark stars with macroscopic properties quite different from neutron stars (Hansel et al. 1986; Alcock et al. 1986; Kettner et al. 1995) and are not compatible with the standard neutron star models. However, it has so far been difficult to identify sites from astrophysical observations (e.g. photon or neutrino observations, or radio binary pulsar timing measurements) that could unambiguously distinguish a SQS from the normal neutron star because self-bound stars have similar radii, moments of inertia, and neutrino emissivities and opacities to that of moderate mass neutron stars.

The SQS, founded from quark matter theory, consists of too many unsolved puzzles which are usually involved in the physics of these high density relativistic objects and hence prohibits considering all physical and astrophysical properties simultaneously. Therefore, most of the SQS studies have been performed within the framework of quark matter MIT-Bag models (Hansel et al. 1986; Kettner et al. 1995; Müller 1997; Burgio et al. 2002; Mak and Harko 2004; Di Toro et al. 2006; Nicotra et al. 2006; Komathiraj and Maharaj 2007). In the quark bag model (Chodos et al. 1974), it is assumed that breaking of physical vacuum takes place inside hadrons. As a result, vacuum energy densities inside and outside a hardron becomes essentially different and the vacuum pressure on the bag wall equilibrates the quark pressure thus stabilizing the system. In the simplified version of the bag model, the equation of state relating the total pressure p and energy density ρ is given by \(p =\frac{1}{3} (\rho - 4B)\) (Witten 1984; Sotani et al. 2004), where B is known as the Bag constant. The stability of the SQS is due to the long range effects of confinement of quarks, represented by B (Hansel et al. 1986; Chodos et al. 1974), which is the universal pressure on the surface of any region containing quarks. The equation of state formulated by Dey et al. (1998) can also be approximated to a linear form (Gondek-Rosińska et al. 2000) that describes the quark interaction in a SQS by an interquark vector potential originating from gluon exchange and a density dependent scalar potential which restores chiral symmetry at high density. Therefore, linearity in equation of state appears to be a most convincing feature in the composition of compact objects such as SQS.

Moreover, in modeling such ultra-compact SQS, anisotropy is expected to play a crucial role as first shown by Ruderman (1972) where nuclear interactions need to be treated relativistically. Since the pioneering work of Bowers and Liang (1974), there has been extensive literature devoted to the study of anisotropic, spherically symmetric, static relativistic matter distributions in which radial pressure (pr) is not equal to tangential pressure (pt). On similar physical grounds that quark phase inside the core is best described by linear bag model, there have been studies reported with different forms for one of the gravitational potentials (Maharaj et al. 2014; Mafa Takisa and Maharaj 2013; Feroze 2012; Thirukkanesh and Ragel 2013; Thirukkanesh and Maharaj 2008). Through this work, we seek new class of solution to the Einstein system in static spherically symmetric spacetime, modeling anisotropic SQM by imposing a linear barotropic equation of state with one of the potentials having Tolmann IV form (Tolman 1939). The physically admissible Tolmann IV type potential (Delgaty and Lake 1998) has been previously used to model anisotropic fluids and solved numerically without specifying an equation of state (Cosenza et al. 1981). The feature of this work as described above is that we characterize a linear barotropic equation of state in the MIT-Bag model to signify SQM. We motivate that the generated model represents a wider physical scenario by showing in Sect. 4 the model reduces to previously known models, and in Sect. 6 that the model parameters corroborate well with experimental observations of realistic stars. Through a physical analysis in Sect. 5, the generated models are shown to be physically viable (Delgaty and Lake 1998): regularity of the gravitational potentials at the origin, positive definiteness of the energy density and the radial pressure at the origin, vanishing of the pressure at some finite radius, and monotonic degrease of the energy density, the radial pressure with increasing radius, and the generated interior metric match smoothly with the Schwarzschild exterior metric at the boundary of stellar object. Moreover, Motivated by significant experimental developments in recent years with attempts on measuring the radii and masses of dense astrophysical objects (Thorsett and Chakrabarty 1999; Link et al. 1999; Heinke et al. 2006; Ho Wynn and Heinke 2009), we attempt to provide physical significance to the model with relation to compactness, which provides a vital clue to distinguish different stars such as white dwarf, neutron stars and strange stars from one another (Tikekar and Jotania 2007). Stellar objects such as SAX, Her.X-1 and other low mass X-ray binaries have been differently interpreted at times (Li et al. 1999) and hence compaction parameter is suggested to be a good measure in this study to differentiate compact stellar objects.

2 Anisotropic model

The gravitational field for static, spherically symmetric spacetime can be describe by the line element

$$\begin{aligned} ds^{2} = -e^{2\nu(r)} dt^{2} + e^{2\lambda(r)} dr^{2} + r^{2}\bigl(d\theta^{2} + \sin^{2}{\theta} d\phi^{2}\bigr) \end{aligned}$$
(1)

in Schwarzschild coordinates (xa)=(t,r,θ,ϕ). We assume the energy momentum tensor for an anisotropic imperfect fluid sphere to be of the form

$$\begin{aligned} T_{ij}=\operatorname{diag}(-\rho, p_r, p_t, p_t). \end{aligned}$$
(2)

The energy density ρ, the radial pressure pr and the tangential pressure pt are measured relative to the comoving fluid velocity \(u^{i} = e^{-\nu}\delta^{i}_{0}\). For the line element (1) and matter distribution (2) the Einstein field equations can be expressed as

$$\begin{aligned} &\rho = \frac{1}{r^{2}} \bigl[ r\bigl(1-e^{-2\lambda}\bigr) \bigr]', \end{aligned}$$
(3)
$$\begin{aligned} &p_r = - \frac{1}{r^{2}} \bigl( 1-e^{-2\lambda} \bigr) + \frac{2\nu'}{r}e^{-2\lambda}, \end{aligned}$$
(4)
$$\begin{aligned} &p_t = e^{-2\lambda} \biggl( \nu'' + \nu'^{2} + \frac{\nu'}{r}- \nu' \lambda' - \frac{\lambda'}{r} \biggr), \end{aligned}$$
(5)

where primes denote differentiation with respect to r. In the field equations (3)–(5), we employ the coupling constant \(\frac{8\pi G}{c^{4}}=1\) and the speed of light c=1. This system of equations govern the behaviour of the gravitational field for an anisotropic imperfect fluid sphere.

The mass contained within a radius r of the sphere is defined as

$$\begin{aligned} m(r)= \frac{1}{2}\int_0^r \omega^2 \rho(\omega)d\omega. \end{aligned}$$
(6)

If we introduce the transformation

$$\begin{aligned} x = r^2,\qquad Z(x) = e^{-2\lambda(r)}\quad \mbox{and}\quad y^{2}(x) = e^{2\nu(r)}, \end{aligned}$$
(7)

the system (3)–(5) takes the form

$$\begin{aligned} &\rho = \frac{1-Z}{x} - 2\dot{Z}, \end{aligned}$$
(8)
$$\begin{aligned} &p_r = 4Z\frac{\dot{y}}{y} + \frac{Z-1}{x} , \end{aligned}$$
(9)
$$\begin{aligned} &p_t = 4x Z \frac{\ddot{y}}{y} +(4 Z+ 2 x \dot{Z}) \frac{\dot{y}}{y} + \dot{Z}, \end{aligned}$$
(10)

where dots denote differentiation with respect to the variable x. The mass function (6) becomes

$$\begin{aligned} m(x)=\frac{1}{4} \int_0^x \sqrt{w}\rho(w)dw, \end{aligned}$$
(11)

in terms of the new variables in (7).

For a physically realistic relativistic star we expect that the matter distribution should satisfy a barotropic equation of state pr=pr(ρ). As motivated in the introduction, we assume a linear EOS to represent SQM:

$$\begin{aligned} p_r = \alpha \rho - \beta, \end{aligned}$$
(12)

where α and β are constants. With the inclusion of (12) the general solution to the Einstein system (3)–(5) can be expressed as

$$\begin{aligned} &e^{2\lambda}= \frac{1}{Z} \end{aligned}$$
(13)
$$\begin{aligned} &e^{2\nu}= y^2 \end{aligned}$$
(14)
$$\begin{aligned} &\rho=\frac{1-Z}{x}-2 \dot{Z}, \end{aligned}$$
(15)
$$\begin{aligned} &p_r = \alpha \rho -\beta, \end{aligned}$$
(16)
$$\begin{aligned} &p_t = p_r +\Delta, \end{aligned}$$
(17)
$$\begin{aligned} &\Delta = 4 x Z \frac{\ddot{y}}{y} + \dot{Z} \biggl(1+ 2x \frac{\dot{y}}{y} \biggr)+\frac{1-Z}{x} \end{aligned}$$
(18)

in terms of the gravitational potential Z, where the quantity Δ=pt−pr is the measure of anisotropy,

$$\begin{aligned} y=d x^{\frac{-(1+\alpha)}{4}}Z^{\frac{- \alpha}{2}} \exp \biggl[\int \biggl(\frac{1+\alpha -\beta x}{4xZ} \biggr)dx \biggr] \end{aligned}$$
(19)

and d is the constant of integration. Therefore the line element (1) takes the form

$$\begin{aligned} ds^{2} =& -d^2 r^{-(1+\alpha)}Z^{- \alpha} \exp \biggl[\int \biggl(\frac{1+\alpha -\beta r^2}{rZ} \biggr)dr \biggr]dt^{2} \\ &{}+ Z^{-1} dr^{2} + r^{2}\bigl(d\theta^{2} + \sin^{2}{\theta} d\phi^{2}\bigr). \end{aligned}$$

Hence, any solution describing static spherically symmetric anisotropic matter distribution with linear equation of state can be easily determined by the generating function Z(r). It is noted that this matter distribution may be modeled by means of two generating functions irrespective of specifying an equation of state (Herrera et al. 2008).

3 Particular model

To investigate the physical significant of the matter quantities, the solution must be given in simple elementary functions without an integral. Variety of choices can be made for the gravitational potential Z, however the choices must be physically reasonable to model a realistic stellar object. Consequently, we choose a form for the gravitational potential Z as

$$\begin{aligned} Z=\frac{(1+ a x)(1-bx)}{(1+2 a x)}, \end{aligned}$$
(20)

where a and b are real constants. A similar form of the gravitational potential (20) had been used to study a relativistic compact sphere with isotropic matter distribution by Tolman (1939) and satisfy all the physical requirements (Delgaty and Lake 1998). For the choice (20) the solution (13)–(18) takes the form

$$\begin{aligned} & e^{2\lambda}=\frac{(1+2 a x)}{{(1+ a x)(1-bx)}} \end{aligned}$$
(21)
$$\begin{aligned} &e^{2\nu}= d^2(1+2ax)^{\alpha} (1+ax)^{\frac{a-(a+2b)\alpha +\beta}{2(a+b)}} \\ &\phantom{e^{2\nu}=\,}\times (1-bx)^{- \frac{b \alpha (4a+3b)+(b-\beta)(2a+b)}{2b(a+b)}} \end{aligned}$$
(22)
$$\begin{aligned} &\rho= \frac{3(a+b)+(2a+7b)ax+6a^2bx^2}{(1+2ax)^2} \end{aligned}$$
(23)
$$\begin{aligned} & p_r =\alpha \rho -\beta, \end{aligned}$$
(24)
$$\begin{aligned} &p_t = p_r +\Delta, \end{aligned}$$
(25)
$$\begin{aligned} &\Delta =\frac{-x}{4(1+ax)(1+2ax)(1-bx)} \\ &\phantom{\Delta =\,}\times \bigl\{ \bigl[\beta -3b(1+\alpha)\bigr] \bigl[b(1+3\alpha)-\beta \bigr] \\ &\phantom{\Delta =\,} +4a^3x \bigl[-3{\alpha}^2 -b^2x^2(1+3 \alpha) (8+7\alpha) \\ &\phantom{\Delta =\,}-2(1-2\beta x)^2 +\alpha(9+10 \beta x) \\ &\phantom{\Delta =\,}+2bx\bigl[-2(2+\alpha) (1+4 \alpha)+(9+13\alpha)\beta x\bigr] \bigr] \\ &\phantom{\Delta =\,}+ a^2 \bigl[-3\bigl(1+3 {\alpha}^2\bigr)-b^2x^2\bigl[33+\alpha (146+85\alpha)\bigr] \\ &\phantom{\Delta =\,}+4\beta x(5-6\beta x) +28\alpha (1+\beta x) \\ &\phantom{\Delta =\,}+2bx\bigl[-3(1+3\alpha) (4+3\alpha) +2\beta x(16+23\alpha)\bigr] \bigr] \\ &\phantom{\Delta =\,}+4a^4x^2 \bigl[2\alpha -1 +4\beta x-3b^2 x^2 (1+\alpha) (1+3\alpha) \\ &\phantom{\Delta =\,}-(\alpha -2\beta x)^2+2bx\bigl[2(2\beta x -1) \\ &\phantom{\Delta =\,}-\alpha (7+3\alpha -6\beta x)\bigr] \bigr]+2a \bigl[-b^2x\bigl[8+3\alpha(13+7 \alpha)\bigr] \\ &\phantom{\Delta =\,}+\beta (2+3\alpha-4\beta x) \\ &\phantom{\Delta =\,}+b\bigl[-3+13\beta x+\alpha(-2-9\alpha+19\beta x)\bigr] \bigr] \bigr\} \end{aligned}$$
(26)

The solution (21)–(26) is given in simple elementary function so that it is more convenient to study the physical behaviour of SQS.

In this case mass function (11) takes the form

$$\begin{aligned} m(x)=\frac{x^{3/2}[b^2+a^2(1+b^2x)]}{2(1+2a^2x)}. \end{aligned}$$
(27)

4 Known solutions

It is interesting to observe that for particular parameter values we can regain anisotropic and isotropic models from our solution (21)–(26). We regain the following particular cases of physical interest:

4.1 Lobo model

If we set β=b=0 then we regain the equation of state studied by Lobo (2006)

$$\begin{aligned} p_r=\alpha \rho \end{aligned}$$

and generate the metric

$$\begin{aligned} ds^2 =& -\bigl(1+ar^2\bigr)^{(1- \alpha)/2} \bigl(1+2ar^2\bigr)^{\alpha}dt^2 \\ &{}+ \biggl(\frac{1+2ar^2}{1+ar^2} \biggr)dr^2+ r^{2}\bigl(d \theta^{2} + \sin^{2}{\theta} d\phi^{2}\bigr). \end{aligned}$$
(28)

The line element (28) corresponds to the anisotropic model of Lobo (2006). Lobo (2006) showed that the line element (28) describes as an interior solution for dark energy stars with \(\alpha < - \frac{1}{3}\) and proved that stability regions exist for dark energy stars by selecting particular values of α using a graphical analysis.

4.2 Isotropic models

In general the measure of anisotropy Δ≠0 so that the model remains anisotropic. However for particular parameter values we can show that Δ vanish in the relevant limit in the general solution (21)–(26). If we set \(a=-\frac{1}{R^{2}}\), \(b=\frac{2}{R^{2}}\) and β=0 then we obtain

$$\begin{aligned} \Delta = \frac{3x}{4R^2(R^2-x)}(1+\alpha) (1+3\alpha). \end{aligned}$$
(29)

If we set Δ=0 in (29), then two different cases arise α=−1 and \(\alpha =- \frac{1}{3}\).

In the first case (α=−1) equation of state becomes pr(=pt)=−ρ. In this case the line element becomes

$$\begin{aligned} ds^2 =& - \biggl(1-\frac{r^2}{R^2} \biggr)dt^2 + \biggl(1-\frac{r^2}{R^2} \biggr)^{-1}dr^2 \\ &{} + r^{2}\bigl(d\theta^{2}+ \sin^{2}{\theta} d \phi^{2}\bigr). \end{aligned}$$
(30)

The metric (30) corresponds to the familiar isotropic de Sitter model.

In the second case (\(\alpha =-\frac{1}{3}\)), equation of state becomes \(p_{r} (=p_{t})=-\frac{1}{3}\rho\). In this case the line element becomes

$$\begin{aligned} ds^2 =& -A^2dt^2 + \biggl(1- \frac{r^2}{R^2} \biggr)^{-1}dr^2 \\ &{}+ r^{2}\bigl(d \theta^{2} + \sin^{2}{\theta} d\phi^{2}\bigr). \end{aligned}$$
(31)

The metric (31) corresponds to the well known isotropic Einstein model.

5 Physical analysis

In this section, we show that the solutions generated in Sect. 3 is physically viable to model an anisotropic strange star. At the origin (r=0), e2ν(0)=d2,e2λ(0)=1, which are constants and (e2ν(r))′=(e2λ(r))′=0. Hence the gravitational potentials are regular at the origin. Since ρ(0)=3(a+b) and pr(0)=3α(a+b)−β, it is possible to make both the energy density and radial pressure to be positive at the origin for appropriate choices of the parameters a,b,α and β. Vanishing of radial pressure (pr) at some finite radius r=s gives

$$\begin{aligned} s =& \biggl\{ \frac{1}{4a(3b\alpha -2\beta)} \bigl[4\beta -\alpha (2a+7b)\\ &{}+\sqrt{\alpha (a+b) \bigl[\alpha(2a-23b) +16\beta\bigr]} \bigr] \biggr\} ^{1/2}. \end{aligned}$$

Since \(\frac{d\rho}{dr}=-\frac{2ar(2a+b)(5+2ar^{2})}{(1+2ar^{2})^{3}} <0\), for suitable choice of parameters a and b, the energy density is a decreasing function of r. For the same choice of parameters the radial pressure pr is also a decreasing function as pr and ρ are related on a linear equation of state. Therefore, our generated model is stable for appropriate choice of parameters (Herrera et al. 2008).

Moreover, the solution generated must smoothly match with the Schwarzschild exterior metric:

$$\begin{aligned} ds^2 =& - \biggl( 1 - \frac{2M}{r} \biggr) dt^2 + \biggl( 1 - \frac{2M}{r} \biggr)^{-1} dr^2 \\ &{}+ r^2 \bigl(d\theta^2 +\sin^2\theta d \phi^2\bigr) \end{aligned}$$

across the boundary r=s, where M is the total mass of the sphere. This leads to the constrains

$$\begin{aligned} &\biggl(1 -\frac{2M}{s} \biggr) =\frac{(1+ a s^2)(1-bs^2)}{(1+2 a s^2)} \end{aligned}$$
(32)
$$\begin{aligned} &\biggl(1 -\frac{2M}{s} \biggr) = y^2 \bigl(s^2\bigr) \end{aligned}$$
(33)

The condition (32) does not impose any restrictions on the parameters. However the condition (33) impose the restriction on the constant of integration d as

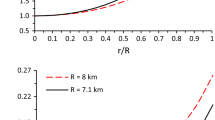
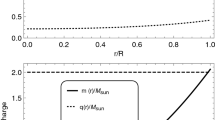
$$\begin{aligned} d =&\pm \bigl(1+as^2\bigr)^{\frac{(1+\alpha)(a+2b)-\beta}{4(a+b)}} \bigl(1+2as^2 \bigr)^{-\frac{(1+\alpha)}{2}}\\ &{}\times \bigl(1-bs^2\bigr)^{\frac{(1+\alpha)b(3b+4a)-\beta (2a+b)}{4b(a+b)}} \end{aligned}$$

We demonstrate that the matter variables are well behaved throughout the interior of the star by plotting the radial dependence of physical quantities: Figs. 1–4 represent the energy density, the radial pressure, the tangential pressure and the measure of anisotropy respectively. The graphs has been plotted for a particular choice of parameters a=0.0225, b=0.00776, \(\alpha =\frac{1}{3}\) and β=0.0083 with stellar boundary set at r=7.07 km. Figs. 1 and 2 show that the energy density and the radial pressure decreases continuously with increasing radius. Moreover, as seen in Figs. 1, 2 and 3, density and tangential pressure are non-zero at the surface and the radial pressure vanishes, which is physically acceptable (Herrera 1997). It is noted that an ideal isotropic fluid with non-vanishing surface pressure cannot be concentrated in a thin layer and in most cases this layer is composed of dust. Hence, in the scenario of anisotropic fluid, the absence of radial pressure with non-zero density at the surface has been explained by assumption of particles moving on circular orbits (Lake 1979; Maeda and Sato 1983), and hence the tangential pressure of a surface layer is related to surface tension (Schmidt 1984). In fact, Mak and Harko (2002) show that the anisotropic pressure distribution leads to an increase in the maximum radius and mass of the quark star. As seen in Fig. 4, the measure of anisotropy Δ remains finite and continuous in the interior, and the anisotropy is directed inward or attractive (i.e. Δ<0) in the region 0<r<3.55 km, and the anisotropy is outward or repulsive (i.e. Δ>0) in the region r>3.55 km, which indicates instabilities in the internal substance in the radial direction (Chan et al. 1993).

Fig. 1
figure 1

Energy density

Full size image
Fig. 2
figure 2

Radial pressure

Full size image
Fig. 3
figure 3

Tangential pressure

Full size image
Fig. 4
figure 4

Measure of anisotropy

Full size image

6 Stellar structure

In this section we show that the solutions generated in this paper can be used to describe realistic compact objects. In particular we seek to compare our results with the observational results. In this model, the parameters a and b has the dimension of length−2. For simplicity, we introduce the transformation

$$\begin{aligned} \tilde{a}=a S^2,\quad \mbox{and}\quad \tilde{b}=bS, \end{aligned}$$

where S is a parameter which has the dimension of length. Under this transformation the energy density becomes

$$\begin{aligned} \rho =\frac{1}{S^2}\frac{3({\tilde{a}}+{\tilde{b}})+{\tilde{a}}(2 {\tilde{a}}+7{\tilde{b}})\frac{r^2}{S^2}+6 {\tilde{a}}^2 {\tilde{b}} \frac{r^4}{S^4}}{ [1+2 {\tilde{a}} \frac{r^2}{S^2} ]^2}, \end{aligned}$$
(34)

and the mass contained within a radius s has the form

$$\begin{aligned} M=\frac{S}{2}\frac{ [{\tilde{b}} +{\tilde{a}} (1+{\tilde{b}}\frac{s^2}{S^2} ) ]\frac{s^3}{S^3}}{ [1+2{\tilde{a}} \frac{s^2}{S^2} ]}. \end{aligned}$$
(35)

In view of comparing our model with realistic stellar objects, we choose S=1 km, α=1/3 with stellar boundary r=s to calculate values of model parameters and the relevant physical parameters for strange star candidates SAX J1808.4-3658(SS1), SAX J1808.4-3658(SS2) and 4U 1820-30 respectively are given in Table 1. Our calculated masses 1.44M⊙ and 1.32M⊙ for radii 7.07 km and 6.35 km respectively, well corroborates with values emanating from the theoretical model reported analyzing pulsars SAX J1808.4-3658 (SS1 & SS2) (Li et al. 1999), in which it was also shown to be consistent with observational data and remarkable accord with the strange star models (Li et al. 1999). Our calculated values for surface densities for SAX J1808.4-3658 (SS1 & SS2) in Table 1 are about 5–6 times of nuclear saturation density ρn, suggesting the chargeless beta-stable (u,d,s) quarks may form the surface of the compact star with central core density being in the order of ∼20ρn, which substantiate the reported claim for strange star. Moreover, our calculations of surface and central densities of 4U 1820-30 show ρ(s)=2.6ρn and ρ(0)=12.8ρn, which suggests it to be a strange star candidate, corroborating with mass-radius relation studies using theoretical models analyzing X-ray burst spectra of 4U 1820-30 (Bombaci 1997).

Table 1 Density (central and surface) and mass for different anisotropic stellar models
Full size table

Moreover, our calculated masses for respective strange star candidates coincide with the values of Tikekar and Jotania (2007). Therefore we compare the compaction parameter (mass-to-radius ratio) in Tikekar and Jotania (2007): U>0.3 for pulsars SAX J1808.4-3658 (SS1 & SS2) and 4U 1820-30 suggests they are strange stars of type I.

7 Conclusion

There have been studies reported with MIT-Bag model treating strange matter with linear equation of state with different forms of gravitational potentials. By motivating Tolmann IV type for one of the gravitational potentials, we find new class of solutions to the Einstein system in static spherically symmetric spacetime, modeling anisotropic strange quark matter by imposing a linear barotropic equation of state. The models generated can be reduced to previously known anisotropic dark energy star model of Lobo (2006), and isotropic models of de Sitter and Einstein. The physical analysis with graphical illustration indicate that the model satisfy all the major physical requirements of a realistic star and calculations with specific model parameters well corroborates with experimental observations on strange star candidates such as SAX J1808.4-3658 and 4U 1820-30. Hence, the models generated will be useful to describe a wider physical scenario of strange matter.