1 Introduction

Dusty plasmas occur in several situations of astrophysical interest such as cometary tails, asteroid zones, planetary rings, interstellar medium, nebulas, earth’s ionosphere and magnetosphere, etc. (Goertz 1989; Mendis and Rosenberg 1994; Horanyi 1996; Verheest 2000; Shukla and Mamun 2002). Beside these, dust particles have been observed in low temperature plasmas, like those used in plasma processing and plasma crystal. The consideration of charged dust grains in a plasma does not only modify the existing plasma wave spectra (Angelis et al. 1988; Shukla and Stenflo 1992), but also introduces a number of new novel eigenmodes, such as dust acoustic (DA) waves (Rao et al. 1990; Barkan et al. 1995), dust ion acoustic (DIA) waves (Shukla and Silin 1992; Barkan et al. 1996), dust lattice waves (Melands 1996; Homann et al. 1997), etc. Rao et al. (1990) were the first to report theoretically the existence of extremely low phase velocity DA waves in an unmagnetized dust plasma whose constituents are an inertial, charged dust fluid with Boltzmann-distributed electrons and ions. Thus, in dust-acoustic waves, the dust particle’s mass provides the inertia whereas the restoring force comes from the pressures of electrons and ions with no inertia. In a very interesting and influential paper, Mamun et al. (1996) showed that a dusty plasma with inertial dust fluid and Boltzmann distributed ions admits only negative solitary potentials associated with nonlinear DA waves. Kakati and Goswami (1998) studied nonlinear shock-like DA waves considering nonisothermal ions and adiabatic dust charge variations using the reductive perturbation technique. The obliquely propagating solitary DA holes in a hot magnetized two-temperature-ion dusty plasma has been studied by Mamun (1999). El-Labany et al. (2002) revisited the same problem and studied the critical density solitary waves and small amplitude DA waves in a hot dusty plasma with nonisothermal ions. The effect of nonadiabatic dust charge variations on nonlinear DA waves with nonisothermal ions has been investigated by Ghosh et al. (2002). El-Shewy et al. (2011) investigated the nonlinear properties of DA solitary waves in Saturn F-ring’s region.

On another side, the formation of double layers has been a topic of great interest. A double layer (DL) is a narrow, isolated region with abrupt potential jump or trough in the amplitude due to a localized dipole sheet of space charge surrounded by large regions of effectively uniform potential. DLs are found in a variety of laboratory plasmas such as in constricted plasmas (Langmuir 1929), mercury discharges (Stangeby and Allen 1973), Q-machines (Sato et al. 1976), triple plasma devices (Coakley et al. 1978) etc. The role of DLs in astrophysics is also considerable as they are thought to be present in the magnetosphere and responsible for the acceleration or deceleration of electrons onto the upper atmosphere, creating the fantastic aurora (Alfven 1958). The formation of DLs in plasmas has been studied by several authors (Temerin et al. 1982; Kim 1987; Raadu 1989; Sakanaka and Shukla 2000; Sahu and Roychoudhury 2004; Verheest et al. 2006; Saharia and Goswami 2007; Verheest and Pillay 2008; Boubakour et al. 2009; Amour and Tribeche 2009). Roychoudhury and Chatterjee (1999) investigated arbitrary amplitude DLs in dusty plasma. They investigated the region of existence of DLs theoretically and numerically. El-Labany et al. (2004) studied DA solitary waves and DLs in a dusty plasma with two-temperature trapped ions.

Over the last two decades, a great deal of attention has been paid to a non-extensive generalization of the Boltzmann-Gibbs-Shannon (BGS) entropy, first recognized by Renyi (1955) and subsequently proposed by Tsallis (1988). Due to an increasing amount of experimental and theoretical evidences showing that the BGS formalism fails to describe systems with long range interactions and memory effects, Tsallis (1988) proposed a new entropy. The latter and the ensuing generalized statistics have been employed with success in plasma physics (Silva et al. 1999; Lima et al. 2000; Leubner 2004; Du 2004; Liu et al. 2009; Tribeche et al. 2010; Tribeche and Djebarni 2010). Because of the lack of a formal derivation, a non-extensive approach to the kappa-distributions has been suggested by Leubner (2004). It has been shown that the plasma particle distribution functions very close to the kappa distribution could be a consequence of the generalized entropy favored by a non-extensive statistics. To the best of our knowledge, DA-DLs with nonextensive ions have never been addressed in the dusty plasma literature.

2 Theoretical model

Let us consider a homogeneous, collisionless, unmagnetized plasma having nonextensive ions and inertial fluid negatively charged dust particles of density n i and n d , respectively. The electron number density is assumed sufficiently depleted owing to the charging process of the dust grains and, thus, to the attachment of the background plasma electrons on the surface of the dust grains. In many laboratory and space dusty plasma situations, most of the background electrons could stick onto the dust grain surface during the charging processes and as a result one might encounter a significant depletion of the electron number density in the ambient dusty plasma. This scenario is relevant to a number of space dusty plasma systems, for example, planetary rings (particularly, Saturn’s F-ring), and laboratory experiments. It should be noted here that a complete depletion of the electrons is not possible, because the minimum value of the ratio between the electron and ion number densities turns out to be the square root of the electron to ion mass ratio when electron and ion temperatures are approximately equal and the grain surface potential approaches zero.

To model the nonextensive ions, we refer to the following q-distribution function (Tribeche and Merriche 2011).

$$ f_i(u)=C_q \biggl\{1-(q-1) \biggl(\frac{m_iu^2}{2T_i}+ \frac{e\phi }{T_i} \biggr) \biggr\}^{1/(q-1)} $$
(1)

where ϕ, T i , m i and e denote the electrostatic potential, the ion temperature, the ion mass and the magnitude of the electron charge, respectively. Note that f i (u) is the particular distribution that minimizes the Tsallis entropy and therefore conforms to the laws of thermodynamics. The constant of normalization C q is given by

$$ C_q= \begin{cases} n_{i0} \frac{\varGamma(\frac{1}{1-q} )}{\varGamma(\frac {1}{1-q}-\frac{1}{2} )} \sqrt{\frac{m_i(1-q)}{2\pi T_i}}, &\mbox{for}\ -1<q<1\\ \noalign{\vspace{3pt}} n_{i0}(\frac{1+q}{2})\frac{\varGamma(\frac{1}{q-1}+\frac {1}{2} )}{\varGamma(\frac{1}{q-1} )}\sqrt{\frac {m_i(q-1)}{2\pi T_i}}, &\mbox{for}\ q>1 \end{cases} $$
(2)

Here, the parameter q denotes the strength of nonextensivity and the quantity Γ is the standard gamma function. It may be useful to note that for q<−1, the q-distribution Eq. (1) is unnormalizable. In the extensive limiting case (q→1), distribution Eq. (1) reduces to the well known Maxwell-Boltzmann velocity distribution. Integrating f i (u) over the velocity space and noting that for q>1, the distribution function exhibits a thermal cutoff on the maximum value allowed for the velocity of the particles, given by

$$ u_{\mathit{max}}=\sqrt{\frac{2T_i}{m_i(q-1)}-\frac{2e\phi}{m_i}} $$
(3)

we get

(4)

The nonlinear dynamics of low-phase velocity dust acoustic waves is governed by

(5)
(6)
(7)

In the above equations, the ion and dust densities n i and n d , the dust fluid velocity u d , and the electrostatic potential ϕ are normalized, respectively, to their corresponding equilibrium densities n i0 and n d0, \(C_{d}=\sqrt{Z_{d}T_{i}/m_{d}}\), and T i /e, where Z d is the number of charges residing on the dust particles. Time and space variables are normalized in units of the dust plasma period \({\omega_{pd}}^{-1}=\sqrt{m_{d}/4 \pi n_{d0}Z_{d}^{2}e^{2}}\), and the Debye length \(\lambda_{Dd}= \sqrt{T_{i}/4 \pi Z_{d} n_{d0}e^{2}}\), respectively. In equilibrium, we have n i0=Z d n d0.

To obtain a travelling wave solution we make all the dependent variables depend on a single independent variable ξ=x−Mt, where M is the Mach number i.e., the velocity of solitary wave. Now, under the appropriate boundary conditions, viz. u d →0, n d →1, ϕ→0 as ξ→±∞, Eqs. (5) and (6) can be integrated to give

$$ n_d=\frac{1}{\sqrt{1+\frac{2\phi}{M^2}}} $$
(8)

To obtain the pseudopotential ψ(ϕ), we notice that Eq. (7) can be expressed as

$$ \frac{1}{2} \biggl(\frac{d \phi}{d \xi} \biggr)^2+\psi(\phi)=0 $$
(9)

where ψ(ϕ), the pseudopotential (Sagdeev 1966), is given by

(10)

In deriving Eq. (10), the following boundary conditions are used. n d →1, u d →0, ϕ→0 and \(\frac{d \phi}{d \xi}\rightarrow0\) at ξ→±∞.

In the small amplitude limit, ϕ≪1, Eq. (10) can be written as

$$ \psi(\phi)=A_1\phi^2+A_2 \phi^3+A_3\phi^4+0\bigl(\phi^5 \bigr) $$
(11)

where

Now for DLs creation, we have 2ϕ m =−A 2/A 3 and the Sagdeev’s potential ψ(ϕ) is given by ψ(ϕ)=A 3 ϕ 2(ϕ m −ϕ)2. The DL solution can be obtained as

$$ \phi=\frac{\phi_m}{2} \biggl[1-\tanh\biggl(\frac{2\xi}{\Delta } \biggr) \biggr] $$
(12)

where \(\Delta=\frac{\sqrt{-8/A_{3}}}{|\phi_{m}|}\) represents the width of the DL provided A 3<0, i.e.,

$$ M> \biggl\{\frac{120}{(q+1)(3-q)(5-3q)} \biggr\}^{1/6} $$
(13)

It is to be noted from Eq. (12) that the nature of the DL depends upon the sign of A 2, i.e. for A 2>0 a compressive DL exists, whereas for A 2<0 we would have a rarefactive DL.

To deal with the nature of small-amplitude DA-DLs, one has to distinguish two cases.

Case 1: −1<q<3:

In this case

  • A 2>0 for M>M c , compressive DLs

  • A 2<0 for M<M c , rarefactive DLs

where M c (by virtue of A 2=0) is given by

$$ M_c= \biggl\{\frac{12}{(q+1)(3-q)} \biggr\}^{1/4} $$
(14)

Case 2: q>3:

In this case, A 2 is always negative and we have only rarefactive DA-DLs.

Note that in each case, one has to keep in mind the following constraints A 3<0 and A 1<0 (the latter comes from ψ″(0)<0 and gives the true dust-acoustic velocity in the plasma under consideration). Strictly speaking, the critical Mach number M c (see Eq. (14)) represents the Mach number for which the cubic term (when expanding the arbitrary amplitude Sagdeev potential to third order) changes sign: when the cubic term is negative, there is a double-layer on the negative side, and when the cubic term is positive, there is a double-layer on the positive side. At this critical value, one could encounter (in the arbitrary amplitude regime) coexistence of rarefactive and compressive structures.

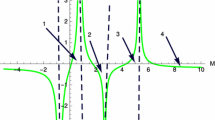
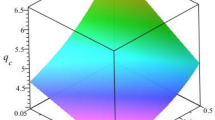
Let us now numerically analyze the effects of ion nonextensivity on the properties of the DA-DLs. Figure 1 displays rarefactive DA-DLs for different values of the ion nonextensive parameter q=−0.7 (solid line), −0.69 (dotted line), −0.68 (dashed line), as is evident from the structure of the Sagdeev potential (Fig. 2). It can be seen that as the nonextensive parameter q increases, the DL strength decreases leading ultimately to the development of compressive DLs (Figs. 3 and 4). The latter become wider as q→1, i.e., as the ions evolve towards their Maxwellian equilibrium. Physically, increasing the DL strength means that the potential drop across the double-layer enhances, and then more particles will be either accelerated or decelerated. Owing to ion nonextensivity, our plasma model may therefore admit compressive as well as rarefactive DA-DLs. Figure 5 illustrates the coexistence of the compressive and rarefactive small amplitude DLs. In Fig. 6 we have plotted the region for existence domain of the compressive and rarefactive DA-DLs. For M>M c only rarefactive DA-DLs are observed and for M<M c only compressive DA-DLs are observed. It is found that the value of the critical mach number M c decreases as q increases.

Fig. 1
figure 1

The electrostatic potential ϕ of DL is plotted against ξ for different values q (solid line for q=−0.7, dotted line for q=−0.69 and dashed line for q=−0.68), where M=1.7

Full size image
Fig. 2
figure 2

Variation of Sagdeev potential ψ(ϕ) for rarefactive DL structures against ϕ for different values of q (solid line for q=−0.7, dotted line for q=−0.69 and dashed line for q=−0.68), where M=1.7

Full size image
Fig. 3
figure 3

The electrostatic potential ϕ of DL is plotted against ξ for various values q (solid line for q=−0.2, dotted line for q=−0.1 and dashed line for q=0.1), where M=1.7

Full size image
Fig. 4
figure 4

Variation of Sagdeev potential ψ(ϕ) for compressive DL structures against ϕ for various values of q (solid line for q=−0.2, dotted line for q=−0.1 and dashed line for q=0.1), where M=1.7

Full size image
Fig. 5
figure 5

Variation of Sagdeev potential ψ(ϕ) for compressive and rarefactive DL structures against ϕ for several values of q (solid line for q=−0.75, dotted line for q=−0.73, dashed line for q=0.2 and dot-dashed line for q=0.1), where M=1.7

Full size image
Fig. 6
figure 6

Region plot for existence domain of compressive and rarefactive DL

Full size image

3 Conclusion

In this paper, we have addressed the problem of DA-DLs in a plasma having inertial fluid dust grains and nonextensive ions. Our results show that in such a plasma, DL structures the onset of which depends sensitively on the ion nonextensivity, can exist. In particular, it may be noted that owing to the non-Maxwellian nature of the ions, our plasma model may admit compressive as well as rarefactive DA-DLs. Our results should assist in the interpretation of the nonlinear DLs that may occur in Saturn’s ring. Depending on the nature (rarefactive or compressive) of these DLs, their associated electric fields are thought to be responsible for particle acceleration or deceleration.