1 Introduction

Dusty plasma is well known as complex plasma due to its new and unusual behavior relative to the ordinary two-component plasma. It is well-known that the presence of grain particulates may give rise to either new or modified waves in the dusty plasmas. It has been shown that the dust dynamics introduces new eigenmodes, whereas the presence of static charged dust grains may modify the existing plasma wave spectra. The well-known new or modified dust eigenmodes are the dust-acoustic (DA) mode (Rao et al. 1990; Barkan et al. 1995), the dust-ion acoustic (DIA) mode (Shukla and Silin 1992), the dust-cyclotron mode (Shukla and Rahman 1998), the dust-drift mode (Shukla et al. 1991) and the dust-lattice mode (Melandso 1996; Shahmansouri and Farokhi 2012). Rao et al. (1990) have first predicted the existence of a new low-frequency DA wave in a multi-component dusty plasma. Subsequently, Barkan et al. (1995) (and also Thompson et al. 1999) have experimentally observed DA waves in laboratory experiments. It must be noted that the DA phase velocity is much smaller than the electron and ion thermal speeds. The nonlinear properties of the DA waves have been studied by a number of authors due to their fundamental importance both in laboratory, astrophysical and space environments (Rao et al. 1990; Melandso et al. 1993; Rosenberg 1993; Barkan et al. 1995; D’Angelo 1995; Mamun 1999a, 1999b; Ghosh et al. 2001; Verheest et al. 2005; El-Labany et al. 2010; Baluku and Helberg 2008; Rahman et al. 2008; Das and Devi 2010; Eslami et al. 2011; Alinejad 2011; Alinejad and Mamun 2011; Amour et al. 2012; Shahmansouri and Tribeche 2012a, 2012b; Sahu and Tribeche 2012). Space plasma observations indicate that astrophysical and space plasmas have non-Maxwellian particle distribution functions (Vasyliunas 1968; Leubner 1982). Nevertheless, most of the above cited studies on nonlinear DA waves have been confined to Maxwell-Boltzmann distributed particles. It must be noted that it is now recognized that the Maxwellian velocity distribution may be inadequate for the description of systems with long-range interactions. A suitable nonextensive generalization of the Boltzmann-Gibbs (BG) statistics (by introducing an additional parameter q measuring the strength of nonextensivity) has then been successfully applied to a number of plasma systems endowed with long-range interactions (Tribeche and Shukla 2011; Sahu 2011; El-Awady and Moslem 2011; Alinejad and Shahmansouri 2012). To model particle nonextensivity effects, the following power law q-distribution function (Silva et al. 1998)

(1)

has been widely used, where ϕ is the electrostatic potential, and j=i,e,d denotes, respectively, ions, electrons, and dust grains. Here and in the following, Q j are the electric charges, m j the masses, T j the temperatures, and q j the strength of particle nonextensivity. It must be noted that f e,i (v) is the distribution function that maximizes the Tsallis entropy and hence conforms to the thermodynamics laws. The constant of normalization is given by

$$ C_{q_{e,i}} = \left\{ \begin{array}{l@{\quad}l} n_{e,i0}\frac{\varGamma (\frac{1}{1 - q_{e,i}})}{\varGamma (\frac{1}{1 - q_{e,i}} - \frac{1}{2})}\sqrt{\frac{m_{e,i}(1 - q_{e,i})}{2\pi T_{e,i}}} \\[6pt] \quad \mbox{for}\ - 1 < q_{e,i} < 1, \\[6pt] n_{e,i0}\frac{1 + q_{e,i}}{2}\frac{\varGamma (\frac{1}{q_{e,i} - 1} + \frac{1}{2})}{\varGamma (\frac{1}{q_{e,i} - 1})}\sqrt{\frac{m_{e,i}(q_{e,i} - 1)}{2\pi T_{e,i}}} & \mbox{for}\ q_{e,i} > 1, \end{array} \right. $$
(2)

where Γ refers to the standard Gamma function. For q e,i <−1, the q-distribution (1) is not normalizable. The well known Maxwell-Boltzmann distribution function is recovered in the extensive limiting case (q e,i →1).

Recently, Tribeche and Merriche (2011) investigated the nonextensive DA solitary waves in an electron depleted dusty plasma. They found that depending on whether q is positive or negative, their plasma model may admit either compressive (for q<0) or rarefactive (for q>0) DA solitary waves. Small amplitude DA solitary waves in dusty plasmas with nonextensive ions and electrons have been studied by Eslami et al. (2011). More recently, Sahu and Tribeche (2012) have considered a nonextensive electron depleted dusty plasma in nonplanar geometry. They investigated the effects of ion nonextensivity and dust kinematic viscosity on the basic features of DA solitary and shock waves. On another side, the effect of charge fluctuation on DA solitary waves in a dusty plasma with nonextensive electrons has been examined by Bacha and Tribeche (2012). To complement and provide new insights into previously published work on nonextensive DA solitary waves, we propose here to study arbitrary amplitude DA solitary waves in an unmagnetized, collisionless dusty plasma with electrons and ions featuring Tsallis distribution. The structure of this paper is as follows. The basic set of dynamical equations governing our dusty plasma model is presented in Sect. 2. A discussion of our numerical results is provided in Sect. 3. Our findings are summarized in Sect. 4.

2 Formulation of the problem

Let us consider the propagation of DA waves in a three component, homogeneous, unmagnetized and collisionless dusty plasma consisting of nonextensive electrons, singly charged nonextensive ions, and negatively charged dust particles. In consequence of the fact that the typical dust charging time scale is more longer than the DA time scale, it is anticipated that dust charge fluctuations have not essential effect on the DA mode (Shukla and Mamun 2002), and so we assume that the dust charge is constant. The same negative charge q d =−Z d e has been considered for all of dust grains, where Z d is the number of charge residing on the dust grain. At equilibrium, the charge neutrality reads as n e0+Z d n d0=n i0, where n e0,n i0 and n d0 are the equilibrium density of electrons, ions and dust grains, respectively. The subscript “0” stands for equilibrium quantities. From the charge neutrality condition, we define f=n e0/n i0=1−Z d n d0/n i0. The dynamics of the low phase velocity DA wave is governed by the following normalized equations

(3)
(4)
(5)

where use has been made of the following non-dimensional variables x→x/λ Dd , t→tω pd , n j →n j /n j0, u j →u j /c d , and ϕ→eϕ/T i , where \(\omega_{pd} = \sqrt{4\pi n_{d0}e^{2}Z_{d0}^{2}/m_{d}}\) is the dust plasma frequency, \(c_{d} = \sqrt{T_{i}Z_{d0}/m_{d}}\) the dust-acoustic speed, λ Dd =c d /ω pd the dust Debye length, and the other variables have their usual meaning. The actual dust acoustic speed in our plasma model can be shown to be c d,κ =ω pd λ d,κ , where the global Debye length takes the form

$$ \lambda_{d,\kappa } = \frac{1}{\sqrt{2\pi e^{2}}} \frac{1}{\sqrt{\frac{n_{e0}}{T_{e}}(1 + q_{e}) + \frac{n_{i0}}{T_{i}}(1 + q_{i})}}. $$
(6)

In the limit of the Maxwellian behavior, (6) reduces to the usual Debye length, i.e., \(\lambda_{d} = 1/\sqrt{4\pi e^{2}(n_{e0}/T_{e} + n_{i0}/T_{i})}\).

Integrating the q-distribution function (1) over all velocity space, we get the following normalized electron and ion number densities (Tribeche and Merriche 2011)

(7)
(8)

where σ=T i /T e .

3 Arbitrary amplitude DA solitons

To study the time-independent arbitrary amplitude DA solitary waves, we suppose that all the dependent variables in Eqs. (3)–(5) depend only on a single variable ξ=x−Mt, where M is the solitary wave speed normalized by the DA speed. Thus, Eqs. (3) and (4) yield the following dust number density

$$ n_{d}(\phi) = \biggl(1 + \frac{2\phi}{M^{2}} \biggr)^{ - 1/2}. $$
(9)

Now substituting Eqs. (7), (8) and (9), along with the new coordinate, into Eq. (5) we obtain

(10)

Multiplying both side of Eq. (10) by dϕ/dξ, and integrating once, we obtain the following energy integral

$$ \frac{1}{2}\biggl(\frac{d\phi}{d\xi} \biggr)^{2} + \psi(\phi) = 0, $$
(11)

where the Sagdeev potential (Sagdeev 1966) for our purpose reads as

(12)

To obtain Eq. (11), we have imposed the appropriate boundary conditions, namely, (ϕ,dϕ/dξ)→0 as ξ→±∞. In the extensive limiting case (q i,e →1), the Sagdeev potential (12) reduces to Eq. (21) of Rao et al. (1990). For an electron depleted dusty plasma with nonextensive ions f→0, our results are in accordance with the results of Tribeche and Merriche (2011). The existence of solitary wave solutions requires that

  1. (i)

    ψ(ϕ=0)=ψ(ϕ max)=(∂ψ/∂ξ)| ϕ=0=0,

  2. (ii)

    (∂ 2 ψ/∂ξ 2)| ϕ=0<0, so that the fixed point at the origin is unstable,

  3. (iii)

    ψ(ϕ)<0 when 0<ϕ<ϕ max for compressive solitary waves and ψ(ϕ)<0 when ϕ min<ϕ<0 for rarefactive solitary waves, where ϕ max(ϕ min) is the maximum (minimum) value of ϕ for which ψ(ϕ)=0.

Equation (12) satisfies the first condition. The second condition (which is often called the soliton condition), yields the following constraint

$$ M_{\min } = \frac{\sqrt{2(1 - f)}}{\sqrt{f\sigma (1 + q_{e}) + 1 + q_{i}}} < M, $$
(13)

where M min is the lower limit of the Mach number, above which solitary waves may be excited. In the Maxwellian limit; i.e., when q i,e →1, Eq. (13) reduces to the expression obtained for the Maxwellian electrons and ions, namely, \(M_{\min} = \sqrt{(1 - f)/[f\sigma + 1]}\) (Verheest et al. 2005). It is evident that the lower limit of M is greater than its Maxwellian counterpart (q i,e →1) in the case of superextensivity (q i,e <1), whereas M min is smaller than its Maxwellian counterpart in the case of subextensivity (q i,e >1). The upper limit of M,M max, can be found by the condition ψ(ϕ c )>0, where \(\phi_{c} = - M_{\max}^{2}/2\) is the extremum value of ϕ for which the dust density is real. Thus we have

(14)

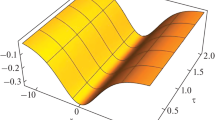
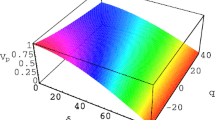
The existence domains of DA solitons are depicted in Fig. 1, for different values of electron and ion nonextensivity (Fig. 1a), and different temperature ratios (Fig. 1b). In each figure, the lower (upper) curve depicts the variation with f of M min (M max). It can be seen that the domain of allowable Mach numbers becomes smaller as f increases, i.e., as the dust number density is depleted. An increase of the nonextensive character of the plasma leads to a shift of this domain towards higher values of the Mach number (Fig. 1a). A decrease of the temperature ratio σ=T i /T e leads to qualitatively similar results (Fig. 1b). As expected, for f=0 (electron depleted dusty plasma) and q e,i →1 (Maxwellian limit), the well-known domain 1<M<1.58 is recovered. The nature of the DA solitary waves can be found by expanding the Sagdeev potential to the third order in a Taylor series in ϕ. The critical value of M is that which corresponds to the vanishing of the quadratic term. At this time, if the cubic term is negative, there is a potential well on the negative side, and if the cubic term is positive, there is a potential well on the positive side. Therefore, by expanding ψ around ϕ=0, the critical value of M, at which the second derivative changes sign, can be found as

$$ M_{\mathit{crit}} = \frac{\sqrt{2(1 - f)}}{\sqrt{f\sigma (1 + q_{e}) + 1 + q_{i}}} , $$
(15)

and at this critical value, the cubic term reads as

(16)

Variation of the pseudo- potential with respect to the electrostatic potential is shown in Figs. 2a–b for different values of the ion and electron nonextensive parameter. Figure 2a (2b) shows the development of rarefactive DA solitary waves the amplitude of which increases as the ions (electrons) evolve toward their Maxwellian equilibrium. Interestingly and for certain values of the electron and ion nonextensivity, Fig. 3 indicates that our plasma model may admit compressive DA solitary waves. Their amplitude increases as f→1. We have then performed a systematic numerical investigation and found that:

  1. (a)

    for 0<q e and q i <1, only rarefactive DA solitons may be excited in our plasma model (Fig. 4a),

  2. (b)

    for −1<q e and q i <0, DA solitons with both polarities may appear in our plasma model (Fig. 4b).

These results are qualitatively and quantitatively different from that obtained for DA solitons in dusty plasmas with either Maxwellian electrons and ions, or kappa-distributed electrons and ions. This may be attributed to the functional form of the electrons/ions distribution. For instance, it is shown here that both negative and positive DA solitary waves could be excited, while only negative DA solitons are observed for negative dust and Maxwellian (Rao et al. 1990) or kappa-distributed (Baluku and Helberg 2008; Tribeche et al. 2009) electrons and ions.

Fig. 1
figure 1

Existence domains for DA solitons. (a) For different values of the nonextensive parameters q e =q i =0.6 (solid lines), q e =q i =0.8 (dashed lines), and q e =q i =0.98 (dotted lines), with σ=0.01. (b) For different temperature ratios σ=0.01 (solid lines) and σ=0.5 (dashed lines), q e =q i =0.6

Full size image
Fig. 2
figure 2

Profile of the pseudo-potential, for different values of the ion and electron nonextensivity. (a) q i =0.6 (dotted-line), q i =0.8 (dashed-line), and q i =0.95 (solid-line), with q e =0.6, M=1.2, f=0.2 and σ=0.01. (b) q e =0.6 (dotted-line), q e =0.8 (dashed-line), and q e =0.95 (solid-line), with q i =0.6, M=1, f=0.5 and σ=0.01

Full size image
Fig. 3
figure 3

Profile of the pseudo-potential for different values of number density ratio, f. Where f=0.7 (dotted-line), f=0.8 (dashed-line), f=0.95 (solid-line), σ=0.01, q e =q i =−0.8, and M=3

Full size image
Fig. 4
figure 4

Behavior of the cubic term in the case of (a) negative values of q e and q i , (b) positive values of q e and q i . Where σ=0.5 and f=0.5

Full size image

4 Conclusion

In the present study, the properties and formation of arbitrary amplitude DA solitary waves in a nonextensive dusty plasma have been described. It is found that the nonextensivity effects may drastically influence the spatial patterns of the DA solitary waves. Interestingly, we found that our plasma model supports the formation of compressive as well as rarefactive DA solitons. The DA solitary wave profile is highly sensitive to the strength of electron and ion nonextensivity. It has been observed that due to the particle nonextensivity, the allowable Mach numbers are greater than their Maxwellian counterpart. Rarefactive DA solitons are observed for 0<q e and q i <1 in our plasma model, while DA solitons with both polarities may appear for −1<q e and q i <0.

The present study may be of wide relevance to astronomers and space scientists working on interstellar dusty plasmas where non-Maxwellian distributions are turning out to be a very common and characteristic feature. Also these results should provide a better fit of the space observations due to the flexibility provided by the nonextensive q-parameter.