1 Introduction

The fact that the universe is expanding at every point in space has become the most popular issue in cosmology. It is found that the universe is nearly spatially flat and consists of about 74 % dark energy (DE) (Perlmutter et al. 1997, 1998; Riess et al. 1998) and the remaining 26 % corresponds to matter. Dark energy has positive energy density with large negative pressure in order to derive the acceleration of the universe. There are many proposals which serve as a candidate of the DE in spite of lack of best fit model for this acceleration. Modified theories of gravity (Nojiri and Odintsov 2007; Paul et al. 2009) has played an important role during last decades to explain this accelerated expansion. The generalized teleparallel theory of gravity (Bengochea and Ferraro 2009; Linder 2010; Yang 2011; Ferraro and Fiorini 2011; Myrzakulov 2011; Tsyba et al. 2011) dubbed as f(T) gravity is commonly used to explore the insights of the universe with T as the torsion scalar.

There are several cosmological ingredients in the universe including radiations, dark matter and DE. The properties of these ingredients are well specified by the equation of state (EoS) parameter ω which is the ratio of pressure to energy density of the universe. The radiation dominated phase corresponds to ω=1/3, whereas ω=0 represents the matter dominated phase. The DE dominated phase inherits different regions with the help of EoS parameter including the quintessence region for −1<ω<−1/3, vacuum energy due to the cosmological constant for ω=−1 and phantom region for ω<−1. The EoS parameter for f(T) gravity also corresponds to these regions in different scenarios. Recently, we have reconstructed the f(T) models using EoS parameter for the above mentioned cases and explored the accelerated expansion of the universe (Sharif and Rani 2011a). Also, the relationship between f(T) gravity and k-essence model has been discussed with the help of this parameter to present the evolving universe (Sharif and Rani 2011b).

Bamba et al. (2011) examined the EoS parameter in this gravity by taking into account exponential, logarithmic and their combined models which result different DE regions. Karami and Abdolmaleki (2012) investigated the validity of generalized second law of thermodynamics (GSLT) for Hubble horizon in f(T) gravity using power-law and exponential models. They concluded that GSLT holds for both these models from early to present universe, while it is violated in the future epoch. Bamba and Geng (2011) explored the thermodynamics in equilibrium and non-equilibrium descriptions for apparent horizon in f(T) gravity. Bamba et al. (2012) studied the finite time singularities, Little Rip, Pseudo-Rip cosmologies and thermodynamics for the apparent horizon bounded universe for this gravity.

The nonlinear electrodynamics (NLED) has gained an increasing revival during last years. This was firstly proposed by Born and Infeld (1934) who determined an electron of finite radius. After this achievement, the effects of NLED have been studied in several papers. De Lorenci et al. (2002) investigated the consequences of NLED which indicate a universe in the radiation phase. Novello et al. (2007) determined three different phases of the universe, bounce, matter and DE phases using NLED. Câmara et al. (2004) derived the general nonsingular solution supported by a magnetic field plus a cosmic fluid and also a non-vanishing vacuum energy density, which may exhibit the inflationary dynamics of the universe. Nashed (2011) constructed regular charged spherically symmetric solutions with NLED coupled to teleparallel theory of gravity. Bandyopadhyay and Debnath (2011) considered a universe with magnetic field and matter in NLED and checked the validity of GSLT for magnetic universe bounded by Hubble, apparent, particle and event horizons. They concluded that the GSLT violates initially but holds for later times.

This work provides a motivation to consider a universe with matter, magnetic field and DE contributions to the energy-momentum tensor. In this paper, we assume matter in the form of dust and magnetic field in f(T) gravity, while torsion serves as the DE component. We evaluate EoS as well as deceleration parameters to explore the accelerated expansion of the universe. We also check the validity of the GSLT in this scenario. The format of the paper is as follows: In Sect. 2, we present the preliminaries of the generalized teleparallel gravity along with NLED for FRW universe. Section 3 is devoted to construct some cosmological parameters and the rate of change of total entropy in the universe for Hubble and event horizons. We discuss all these results by constructing f(T) models for polelike and power-law forms of scale factor. The validity of GSLT in this scenario is investigated in Sect. 4. The last section summarizes all the results.

2 Basics of f(T) gravity and NLED

In this section, we provide the basic formulation of the generalized teleparallel gravity and NLED.

2.1 Generalized teleparallel gravity

The Riemann-Cartan spacetime is the general structure that possesses both curvature and torsion tensors. There are two main subclasses of this spacetime, i.e., the Riemannian spacetime and the Weitzenböck spacetime. The torsion tensor becomes zero in the Riemannian spacetime due to symmetric properties of the Levi-Civita connection defined by the metric tensor. Using this connection with scalar curvature R, Einstein theory of gravity and its modifications are formed such as \(f(R),~f(R,\mathcal{G}),~f(R,\mathcal{T})\) (De Felice and Tsujikawa 2010; Harko et al. 2011; De Felice et al. 2011) etc. gravity theories, where \(\mathcal{G}\) and \(\mathcal{T}\) are the Gauss-Bonnet invariant and trace of the energy-momentum tensor. By setting curvature tensor zero, Weitzenböck spacetime is obtained, which gives rise to TPG and its generalized forms f(T) (Bengochea and Ferraro 2009; Yang 2011; Ferraro and Fiorini 2011; Myrzakulov 2011; Tsyba et al. 2011; Linder 2010) and f(R,T) (Myrzakulov 2012; Chattopadhyay 2012; Sharif et al. 2012), depending upon the tetrad field and the torsion scalar T.

The basic element in the structure of f(T) gravity is the tetrad field h a (x μ), where the Latin alphabets (a,b,…=0,1,2,3) denote the tangent space indices and the spacetime indices are represented by Greek alphabets (μ,ν,…=0,1,2,3). This field forms an orthonormal basis for the tangent space at each point x μ of the manifold and can be identified by its components \(h_{\mu}^{a}\) such that \(h_{a}=h^{\mu}_{a} \partial_{\mu}\). These components satisfy the following properties

$$ h^{a}_{\mu}h^{\mu}_{b}= \delta^{a}_{b},\qquad h^{a}_{\mu}h^{\nu}_{a}= \delta^{\nu}_{\mu}. $$
(1)

The relationship between tetrad field and metric tensor g μν is given by \(g_{\mu\nu}=\eta_{ab}h_{\mu}^{a}h_{\nu}^{b}\), where \(\eta_{ab}=\operatorname{diag}(1,-1,\allowbreak -1,-1)\) is the Minkowski metric for the tangent space. With the help of Weitzenböck connection (\({\varGamma^{\lambda}}_{\mu\nu}=h_{a}^{\lambda}\partial_{\nu}h^{a}_{\mu}\)), the torsion tensor T ρ μν and the tensor S ρ μν are defined as follows (Sharif and Amir 2006, 2007; Sotirious et al. 2011)

(2)
(3)

and \({K^{\mu\nu}}_{\rho}=-\frac{1}{2}({T^{\mu\nu}}_{\rho} -{T^{\nu\mu}}_{\rho}-{T_{\rho}}^{\mu\nu})\) is the contorsion tensor. These tensors inherit the antisymmetric property and give the torsion scalar as T=S ρ μν T ρ μν .

The action of f(T) gravity is given by (Bengochea and Ferraro 2009; Yang 2011; Ferraro and Fiorini 2011; Myrzakulov 2011; Tsyba et al. 2011)

$$ S=\frac{1}{2\kappa^2}\int d^{4}x\bigl[ef(T)+L_m \bigr], $$
(4)

where \(e=\sqrt{-g},~\kappa^{2}=8\pi G,~G\) is the gravitational constant and L m is the matter Lagrangian density inside the universe. The corresponding field equations are obtained by varying this action with respect to tetrad as

(5)

where f T =df/dT, f TT =d 2 f/dT 2 and \(T^{\nu}_{\rho}\) is the energy-momentum tensor of perfect fluid. The flat FRW universe is described by

$$ ds^{2}=dt^{2}-a^{2}(t) \bigl(dx^{2}+dy^{2}+dz^{2}\bigr), $$
(6)

where a is the time dependent scale factor. The corresponding tetrad components are \(h^{a}_{\mu}=\operatorname{diag}(1,a,a,a)\), which satisfy Eq. (1). The modified Friedmann equations are

(7)
(8)

where \(H=\dot{a}/a\) is the Hubble parameter and ρ t , p t are the total energy density and pressure of the universe, dot represents derivative with respect to time.

2.2 Nonlinear electrodynamics

The standard cosmological model is successful in resolving many issues but still there are some issues which remain to be solved. One of the issues is the initial singularity (big bang) which leads to a troubling state of affairs because at this point, all known physical theories break down. It has been claimed that very strong electromagnetic field might help in avoiding the occurrence of spacetime singularities. Here we give some general properties of the nonlinear electrodynamics (Born and Infeld 1934; De Lorenci et al. 2002; Câmara et al. 2004; Novello et al. 2007; Nashed 2011; Bandyopadhyay and Debnath 2011) in cosmology and discuss its particular case. The FRW universe model (6) requires an averaging procedure in electrodynamics to maintain its geometry. For this purpose, the volumetric spatial average of an arbitrary quantity Y is defined by

$$ \overline{Y}=\lim_{V\rightarrow V_{0}}\frac{1}{V}\int Y \sqrt{-g}d^{3}x, $$
(9)

where g is the determinant of the metric tensor, \(V=\int \sqrt{-g}d^{3}x\) and V 0 stands for a sufficiently large time dependent volume of the whole space. This procedure sets up the mean values of the electric E i and magnetic B i fields as follows

$$ \everymath{\displaystyle} \begin{array}{@{}l} \overline{E_{i}}=0, \qquad \overline{B_{i}}=0, \qquad \overline{E_{i}B_{i}}=0, \\[2mm] \overline{E_{i}E_{j}}=- \frac{1}{3}E^{2}g_{ij},\qquad \overline{B_{i}B_{j}}=- \frac{1}{3}B^{2}g_{ij}. \end{array} $$
(10)

We consider the extended Maxwell electromagnetic Lagrangian density up to second order terms in the field invariants F and F ∗ as

$$ \mathcal{L}=-\frac{1}{4}F+\omega_{0}F^{2}+ \eta_{0}F^{\ast2}, $$
(11)

with \(F=F_{\mu \nu}F^{\mu \nu}=2(B^{2}-E^{2}),~F^{\ast}\equiv F^{\ast}_{\mu \nu}F^{\mu \nu}=-4\textbf{E}\cdot\nobreak \textbf{B}\), ω 0 and η 0 are arbitrary constants. The Maxwell term (first term) dominates in the radiation era while the quadratic terms dominates during very early epoch of the evolving universe. The corresponding energy-momentum tensor takes the form

$$ T_{\mu \nu}=-4\mathcal{L}_{F}F_{\mu}~^{\alpha}F_{\alpha \nu}+ \bigl(F^{\ast}\mathcal{L}_{F^{\ast}}-\mathcal{L}\bigr)g_{\mu \nu}, $$
(12)

where \(\mathcal{L}_{F}\) and \(\mathcal{L}_{F^{\ast}}\) represent the partial derivatives of the nonlinear Lagrangian with respect to field invariants. Using the average values given in Eq. (10), the comparison of the energy-momentum tensor (12) with that of perfect fluid, T μν =(ρ+p)u μ u ν −pg μν , yields the general form of energy density ρ and pressure p as

(13)
(14)

We assume the case of homogenous electric field in plasma which gives non-vanishing magnetic field whereas the electric field rapidly decays and becomes zero. The nonlinear term F 2 with only magnetic field helps to avoid the initial singularity by inducing the universe to bounce (Novello et al. 2007). The vanishing E 2 helps to neglect the viscosity terms in the electric conductivity of the primordial plasma while its presence removes the bounce which results a universe with a singular state. Inserting the corresponding values in Eqs. (13) and (14), the magnetic energy density and pressure take the form

(15)
(16)

When ω 0=0=η 0, Eqs. (11) and (12) reduce to the linear Maxwell electromagnetic Lagrangian and energy-momentum tensor as follows

$$ \mathcal{L}=-\frac{1}{4}F, \qquad T_{\mu\nu}=F_{\mu}~^{\alpha}F_{\alpha \nu}+ \frac{1}{4}Fg_{\mu\nu}. $$
(17)

For the Lagrangian with the energy-momentum tensor and the same assumptions as for nonlinear process, we obtain

$$ \rho=3p=\frac{1}{2}\bigl(E^2+B^2\bigr), $$
(18)

which shows that the universe is composed of ordinary radiations with positive pressure. For the homogeneous electric field case, it yields \(p=\frac{1}{3}\rho=\frac{1}{6} B^{2}\).

3 Cosmological parameters and thermodynamics

In this section, we construct the EoS and deceleration parameters as well as the GSLT for Hubble and event horizons. Jamil et al. (2010) checked the validity of GSLT for a universe composed of DE interacting with dark matter and radiation fluid. Karami et al. (2011) studied GSLT for non-flat FRW universe containing the same fluids for apparent horizon. Here we assume a universe where the three generic sources fueled its spatial sections including the pressureless cold dark matter, DE as modified form of torsion scalar and NLED. The first two sources relate with the late-time evolution of the universe. The third component is important for avoiding initial singularity and behaves like standard radiation field at later times. Thus these contributions develop the budget of energy density of the universe according to recent observations (i.e., 72.8 % is DE, 22.7 % is dark matter and 4.5 % is ordinary matter) (Komatsu et al. 2011).

The field equations (7) and (8) can be written as

(19)

where ρ t =ρ m +ρ B +ρ T , p t =p m +p B +p T . The subscripts m, B and T denote the matter, magnetic and torsion contributions to the total energy density and pressure of the universe with ρ T and p T as

(20)
(21)

For the sake of simplicity, we take dust like matter, i.e., p m =0. The corresponding energy conservation equations take the form

(22)
(23)
(24)

Equation (22) gives

$$\rho_{m}=\rho_{m0}a^{-3}, $$

where ρ m0 is an arbitrary constant. Inserting Eqs. (15) and (16) in (23), we obtain

$$B=\frac{B_0}{a^2}, $$

where B 0 is an arbitrary constant. This shows that the evolution of energy density of the magnetic field decays with the expansion of the universe and corresponds to the early phase for small values of the scale factor (Novello et al. 2004) as well as to radiation phase in linear case.

Now we investigate the behavior of the universe inheriting magnetic field and dust matter with f(T) gravity as the DE source. The EoS parameter is

(25)

The deceleration parameter is the measure of the cosmic acceleration of the expanding universe and is given by

$$ q=-1-\frac{\dot{H}}{H^2}. $$
(26)

The negative value of q corresponds to the accelerated regime, for positive q decelerated and q=0 leads to constant expansion of the universe. In the present case, it becomes

$$q_t=\frac{1}{2}(1+3\omega_{t}), $$

hence

(27)

Equations (25) and (27) represent the general form of the EoS and the deceleration parameters in terms of f(T). We may check the behavior of these cosmological parameters for some viable f(T) models.

It has been interesting to study the GSLT in the context of modified theories of gravity (Akbar and Cai 2006; Sadjadi 2007; Sheykhi and Wang 2009; Karami and Khaledian 2011, 2012; Karami and Abdolmaleki 2012; Karami et al. 2012). This law states that the sum of entropy of total matter inside the horizon and entropy of the horizon does not decrease with time. Using the first law of thermodynamics, the Clausius relation is obtained as, −dE=T X dS X , where \(S_{X}=\frac{A}{4G}\) is the Bekenstein entropy, \(A=4\pi R_{X}^{2}\) is the area of horizon with X as an arbitrary horizon and \(T_{X}=\frac{1}{2\pi R_{X}}\) is the Hawking temperature. Miao et al. (2011) found that the first law of thermodynamics violates in f(T) gravity due to local Lorentz invariance (Li et al. 2011) which results in addition a entropy production term S P . However, its validation takes place if f TT is very small and entropy horizon becomes \(S_{X}=\frac{Af_{T}}{4G}\) with vanishing S P in this case. We use the general approach (i.e., independent of f TT condition) to study the GSLT in magnetic f(T) scenario along with Gibbs’ equation (Bandyopadhyay and Debnath 2011; Cai and Kim 2005; Bamba et al. 2013). The time derivative of the entropy on the horizon is

$$ \frac{dS_{X}}{dt}+\frac{dS_{P}}{dt}=\frac{\pi R_{X}}{G}(2 \dot{R}_{X}f_T+R_X\dot{T}f_{TT}). $$
(28)

If the condition f TT ≪1 does not satisfy, then we have to find out the entropy production term (Bamba et al. 2013).

The Gibbs’ equation is used to find the rate of change of normal entropy S I of the horizon

$$ \frac{dS_{I}}{dt}=\frac{1}{T_X} \biggl(\frac{dE_{I}}{dt}+p_t \frac{dV}{dt} \biggr), $$
(29)

where \(E_{I}=\rho_{t} V,~V=\frac{4}{3}\pi R_{X}^{3}\) is the volume of the horizon. Inserting the values in Eq. (29), it follows that

$$ \frac{dS_{I}}{dt}=\frac{4\pi R_{X}^{2}}{T_X}(\dot{R}_{X}-HR_{X}) (\rho_t+p_t). $$
(30)

Combining Eqs. (28) and (30), we obtain the time derivative of total entropy for the arbitrary horizon as

(31)

The validity of the GSLT (\(\dot{S}_{X}+\dot{S}_{I}+\dot{S}_{P}\geq0\)) on the horizon of radius R X for viable f(T) models can be investigated. Here we discuss two forms of cosmological horizons widely used in literature (Bak and Rey 2000; Li 2004; Sharif and Jawad 2013).

Hubble horizon

Let us assume that the boundary of the thermal system of the FRW universe is occupied by the apparent horizon (Bak and Rey 2000) in equilibrium state. For the flat FRW, it reduces to the Hubble horizon with radius R H as

$$ R_{H}=\frac{1}{H}, \qquad \dot{R}_{H}=- \frac{\dot{H}}{H^2}. $$
(32)

Inserting these values (X→H) in Eq. (31), we obtain

(33)

This is the rate of change of total entropy of all the fluids (dust matter, magnetic and torsion contributions) in the universe for Hubble horizon.

Event horizon

The radius of event horizon is given by (Li 2004)

$$ R_{E}=a\int^{\infty}_{t} \frac{dt}{a}, \qquad \dot{R}_{E}=HR_{E}-1. $$
(34)

The convergence of this integral leads to the existence of the event horizon. Basically, it is the distance of light traveling from present time to infinity. If Big Rip singularity occurs at some future time denoted by t s , then we must replace ∞ by t s . Using Eq. (34) in (31) and replacing X by E, it follows that

(35)

This represents the rate of change of total entropy in the universe for event horizon in equilibrium state and its validity depends upon the viable f(T) model. Sadjadi (2007) investigated the validity of GSLT for event horizon in f(R) gravity which also depends upon some viable f(R) model. In the following, we construct some f(T) models to check the behavior of cosmological parameters ω t , q t and validity of GSLT for Hubble and event horizons in a universe composed of dust, magnetic and torsion contributions.

4 f(T) model: an example

Since there are mainly two possible ways of working with cosmological equations of motion, either postulating a theory with matter content of the universe and then solving corresponding equation to discuss the cosmological time behavior of the model under consideration. Or, vice versa, postulating a theory with desired time behavior of the model deriving information about the matter content. Novello et al. (2007) investigated the removing of initial singularity by NLED and resulted a power-law form of scale factor in the corresponding scenario. Here we adopt the second method by assuming the following polelike type scale factor (Sadjadi 2006; Nojiri and Odintsov 2006)

$$ a(t)=a_{0}(t_{s}-t)^{-h},\quad h>0, \ t_{s}\geq t $$
(36)

where a 0 is the present value of the scale factor. This scale factor indicates the superaccelerated universe with a Big Rip singularity at t=t s . Using above scale factor, Hubble parameter, torsion scalar and \(\dot{H}\) become

$$ H=\frac{h}{t_s-t}, \qquad T=-\frac{6h^2}{(t_s-t)^{2}}, \qquad \dot{H}= \frac{h}{(t_s-t)^{2}}. $$
(37)

Inserting these values in the first equation of modified Friedmann equations (19), we obtain the f(T) model as

(38)

which shows the contributions from dust matter and magnetic field with nonlinear terms of torsion scalar. Here c 1 is an integration constant and can be found through a boundary condition. For this purpose, Eq. (7) can be rewritten as follows

$$H^2=\frac{8\pi G}{6f_T} \biggl(\rho_t- \frac{f}{16\pi G} \biggr). $$

This equation implies that the gravitational constant G has to be replaced by an effective gravitational constant (time dependent), G eff for nonlinear f(T) model (Capozziello et al. 2011; Wei et al. 2012). For a linear f(T), G eff should reduce to the present day value of G which yields the condition f T (T 0)=1, where \(T_{0}=-6H_{0}^{2}\) and H 0 is the present day value of Hubble parameter. Applying this condition in model (38), we obtain

(39)

Also, the model (38) satisfies the condition \(\frac{f}{T}\rightarrow 0\) at high redshift T→∞ to be a realistic model representing accelerated expansion of the universe. This is consistent with the primordial nucleosynthesis and cosmic microwave background constraints (Wu and Yu 2010; Karami and Abdolmaleki 2012).

We check the behavior of the expanding universe along with GSLT for this model by adopting \(z=\frac{a_{0}}{a}-1\). Inserting the above values in Eqs. (25) and (27), we obtain

(40)
(41)

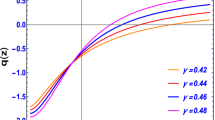
The graphical behavior of the cosmological parameters ω t and q t versus z is shown in Fig. 1. We use a 0=1=κ 2, H 0=74.2 Km s−1 Mpc−1 for h=2,3,5 and fix the values ω 0=0.05, B 0=0.8 for the magnetic contribution. In the left graph, ω t shows the phantom dominated universe as z decreases for all values of h. Approximately at z=0.75,0.95,1.2, the graph shows the crossing of phantom divide line and converges to phantom era of the expanding universe which is consistent with the recent observations (Sadjadi and Vadood 2008). The EoS parameter converges to ω t =−2.7,−2.5,−2.3 for h=2,3,5 respectively. The range z>1.2 does not correspond to the accelerated phase of the universe. As we increase the value of h, the graph shifts towards phantom divide line but it crosses the line for higher value of z. The deceleration parameter remains negative for decreasing z as shown in the right graph. The graph of this parameter becomes negative in the range, z<1.3 and shows the accelerated expansion of the universe. For higher values of redshift, roughly z≥1.3, the positive behavior of q t indicates the positive decelerated expansion of the universe. This implies that for decreasing z, the torsion contribution overcomes the magnetic contribution completely.

Fig. 1
figure 1

Plot of EoS parameter ω t (left) and deceleration parameter q t (right) versus z for polelike type scale factor

Full size image

Now to check the validity of GSLT, we first see the behavior of second derivative of the model (38) given by

(42)

Its plot versus z is shown in Fig. 2 indicating that f TT ≪1 for z<0.2. Thus we take the entropy production term to zero in Eqs. (33) and (35). Using Eqs. (37) and (38) in (33), the rate of change of total entropy in terms of redshift for the Hubble horizon turns out to be

(43)

Figure 3 (left graph) represents the plot of the rate of change of total entropy versus redshift keeping the same values of the constants as in the previous figure. This shows the positive behavior of \(\dot{S}_{H}+\dot{S}_{I}\) as z decreases. Thus the GSLT always holds for the Hubble horizon in the magnetic f(T) scenario.

Fig. 2
figure 2

Plot of f TT versus z for polelike type scale factor

Full size image
Fig. 3
figure 3

Plot of the rate of change of total entropy versus redshift for polelike type scale factor. The left graph is for \(\dot{S}_{H}+\dot{S}_{I}\) versus z for Hubble horizon and the right graph is for \(\dot{S}_{E}+\dot{S}_{I}\) versus z for event horizon

Full size image

For the event horizon, inserting Eqs. (37) and (38) in (35), the rate of total entropy becomes

(44)

The plot of \(\dot{S}_{E}+\dot{S}_{I}\) versus z is shown in Fig. 3 (right graph). This also represents positive behavior of the total entropy as z decreases indicating the validity of GSLT for the event horizon in the magnetic f(T) gravity. It is interesting to mention here that the time derivative of total entropy always remains positive for Hubble and event horizons and GSLT holds for all values of z. For the magnetic universe only (Bandyopadhyay and Debnath 2011), the GSLT remains valid for Hubble horizon whereas its validity is investigated up to a certain level along z for event horizon.

There is another type of scale factor in the exact power-law form as, a(t)=a 0(t s −t)h (Sadjadi 2006; Nojiri and Odintsov 2006; Setare and Darabi 2012) which is simply obtained by replacing h with −h in Eq. (36) and gives the inverse power-law expansion. Debnath et al. (2012) investigated the validity of GSLT in general relativity using this scale factor (in the limit t→t s −t) along with some other forms of a(t) without using the first law of thermodynamics. We analyze the behavior of ω t , q t and time derivative of total entropy for the Hubble and event horizons using the same approach as for polelike scale factor. The corresponding f(T) model is given by

(45)

where c 2 is an integration constant which can be found by applying the same boundary condition as for polelike scale factor, and is given by

(46)

This model does not satisfy the condition for a realistic model (Wu and Yu 2010; Karami and Abdolmaleki 2012) at high redshift. It may give some relativistic results for \(h<\frac{1}{4}\) but this range does not represent accelerated expansion of the universe (h>1). However, this model satisfies the condition f(T)→0 as T→0 (Rastkar et al. 2012; Chattopadhyay and Pasqua 2013). By comparing this model with Eq. (38), the only difference is the sign of h. Thus omitting the expressions for ω t ,q t and time derivative of total entropy for the Hubble and event horizons, we discuss graphically these phenomena.

The EoS and deceleration parameters represent a phantom dominated accelerated phase of the universe for decreasing values of z as shown in Fig. 4. It shows the same behavior of these parameters as for polelike type scale factor. However, ω t crosses the phantom divide line at z=0.4,0.65,0.9 and becomes convergent at ω t =−1.3,−1.5,−1.7 for h=2,3,5. As we decrease the value of h, the graph of ω t shifts towards −1. For the chosen values of h with z<1.4, the deceleration parameter shows negative behavior. It converges to q t =−1.5,−1.85,−2.1 for z<0.7 and corresponds to the accelerated expansion of the universe.

Fig. 4
figure 4

Plot of EoS parameter ω t (left) and deceleration parameter q t (right) versus z for power-law scale factor

Full size image

The second derivative of model (45) is also satisfies the condition f TT ≪1 as shown in Fig. 5. Thus we take S P =0 and check the validity of GSLT for Hubble and event horizons. The time derivative of total entropy for Hubble and event horizons using Eqs. (33) and (35) in terms of redshift. The time derivative of total entropy of Hubble horizon shows positive behavior for z>0.7 as shown in Fig. 6 (left), hence the GSLT holds. The quantity \(\dot{S}_{H}+\dot{S}_{I}\) becomes negative at z≤0.7 violating the GSLT in the magnetic f(T) scenario for h=2,3 whereas it remains positive for h=5. In the right graph, \(\dot{S}_{E}+\dot{S}_{I}\) represents negative behavior in the limit z≤0.95, showing the violation of GSLT while it holds when z>0.95 for all chosen values of h in this scenario.

Fig. 5
figure 5

Plot of f TT versus z for exact power-law scale factor

Full size image
Fig. 6
figure 6

Plot of the rate of change of total entropy versus redshift for exact power-law scale factor. The left graph is for \(\dot{S}_{H}+\dot{S}_{I}\) versus z for Hubble horizon and the right graph is for \(\dot{S}_{E}+\dot{S}_{I}\) versus z for event horizon

Full size image

5 Concluding remarks

We have studied the NLED in the framework of f(T) gravity using FRW universe containing DE, dust matter and magnetic field contribution. An averaging procedure is adopted to preserve the isotropy of spacetime in the NLED. In this scenario, we have evaluated EoS and deceleration parameters for the total energy density and pressure of the universe. The time derivative of the total entropy for the Hubble and event horizons are developed to investigate the validity of GSLT using horizon entropy and Gibbs’ equation. Dias and Moraes (2005) investigated that torsion affects the magnetic field only in the topological defect and found that it spirals up the magnetic field lines along defect axis. The NLED serves to remove the initial singularity and becomes standard radiation phase in later times. We have constructed f(T) models using polelike and power-law forms of scale factor. The graphical behavior is discussed for some particular model parameters. The results of the paper are summarized as follows.

  • The cosmological parameters for the first constructed f(T) model by polelike scale factor represent a phantom dominated universe with acceleration for z≤1.3 as shown in Fig. 1. For higher values of z, the expansion rate reduces and magnetic field dominates the torsion contribution representing a decelerated universe.

  • The time derivative of total entropy for Hubble and event horizons are plotted versus z to discuss the validity of GSLT for this model satisfying the condition f TT ≪1 (Fig. 2). The GSLT holds for all the values of z for both these horizons (Fig. 3).

  • Using the second constructed f(T) model from the exact power-law scale factor, plots of ω t and q t versus z (Fig. 4) indicate the same behavior as the first model.

  • The second model also meets the condition f TT ≪1 as shown in Fig. 5 to discuss the GSLT with the help of first law of thermodynamics. Figure 6 shows the positive behavior of time derivative of the total entropy for both horizons upto a certain range. For Hubble horizon, the GSLT is valid for z≥0.7, while it holds for z≥0.95 in case of event horizon.

It is interesting to mention here that for the magnetic universe (Bandyopadhyay and Debnath 2011) only, the time rate of the total entropy stays positive when z≥−0.1 for event horizon and becomes negative after this range. On the other hand, in our case, it remains in the positive region for all values of z in the magnetic f(T) framework for this horizon with polelike scale factor. The Hubble horizon shows the similar behavior of the time derivative of total entropy in both scenarios. For higher values of redshift, the cosmological parameters indicate a universe where torsion contribution has become faint as compared to the magnetic field. It is pointed towards early decelerated phase of the universe.