Thermodynamic study in modified $f(T)$ gravity with cosmological constant regime

Abstract

This study is conducted to examine the validity of thermodynamical laws in a modified $f(T)$ gravity involving a direct coupling of torsion scalar with matter contents. For this purpose, we consider spatially flat FRW geometry with matter contents as perfect fluid and formulate the first thermodynamical law in this gravity at apparent horizon. It is found that equilibrium description of thermodynamics exists in this modified gravity in a similar way to Einstein and other gravities. Further we discuss generalized second law of thermodynamics at apparent horizon of FRW universe for three different $f(T)$ models using Gibbs law as well as the assumption that temperature of matter within apparent horizon is similar to that of horizon. It is found that for some particular cosmologically consistent values of coupling parameters, GSLT remains valid in observationally consistent cosmic eras.

1 Introduction

After the astronomical evidences of speedy cosmic expansion, the investigation of complete historical picture of cosmos (from beginning inflationary epochs to final fate of universe) has become one of the most fascinating issue of this century. In this regards, many cosmological and gravitational developments like rapid cosmos expansion in late eras and its responsible factor dark energy (an unusual sort of energy), DE candidates including modified gravities are proposed by the scientists (Bamba et al. 2012; Capozziello and Faraoni 2011; Felice and Tsujikawa 2010; Sotiriou and Faraoni 2010). On the basis of comparison among various DE candidates, the modified gravitational theories like Gauss-Bonnet theory, $f(R)$ and $f(R,T)$ theories, scalar-tensor theories emerge as the most successful tool for discussing numerous cosmic aspects. Such gravitational modifications are obtained by introducing either minimal or non-minimal couplings between different fields like higher-order curvature correction terms, matter and scalar fields as well as torsion scalar.

In contrast to Einstein’s relativity and its proposed modifications where the source of gravity is determined by curvature scalar terms, another formulation is presented since the time of Einstein himself which comprises torsional formulation as gravity source (Einstein 1928; Maluf 2013). This theory is labeled as TEGR (teleparallel equivalent of general relativity) and is determined by Lagrangian density involving curvature less Weitzenböck connection instead of torsion less Levi-Civita connection with the vierbein as a fundamental tool. This theory is then further extended to a generalized form by the inclusion of $f(T)$ function in the Lagrangian density and has been tested cosmologically by numerous researchers (Bamba et al. 2011; Bengochea and Ferraro 2009; Ferraro and Fiorini 2008, 2011; Linder 2010; Jamil et al. 2012; Wei et al. 2012). Later, Harko et al. (2014) proposed a comprehensive form of this theory by involving a non-minimal torsion matter interaction in the Lagrangian density. In a recent paper Zubair and Waheed (2015), have investigated the validity of energy constraints for some specific $f(T)$ models and discussed the feasible bounds of involved arbitrary parameters. Another interesting modifications of this theory have also been discussed in literature (Chandia and Zanelli 1997; Harko et al. 2014; Kofinas and Saridakis 2014a, 2014b) on cosmological landscape.

On the basis of fundamental study of black holes thermodynamics that was carried in 1930, it is found that the assumption of proportionality between horizon area and entropy together with the condition $dQ=TdS$ ($Q$, $S$, $T$ are notations for energy flux, entropy and temperature) leads to the formulation of dynamical equations of Einstein’s relativity (Bekenstein 1973; Bardeen et al. 1973; Hawking 1975). In this arena, the pioneer work was presented by Jacobson (1995) in which he verified such connection for Rindler model by considering the observer (measuring such quantities) is also in motion within the horizon. In BH thermodynamics, BHs are assumed as thermodynamical systems whose quantities like temperature and entropy are interconnected with geometrical terms like surface gravity and horizon area. Gibbons and Hawking (1977) explored these thermodynamical characteristics for de Sitter model. Frolov and Kofman (2003) studied the connection of gravity and thermodynamics for the flat quasi de-Sitter inflationary model of cosmos and found that Friedmann equations can be recovered from $dE=TdS$ in case of slowly rolling scalar field. Such connection has also been investigated for spherically symmetric BHs by Padmanabhan (2002) who proved that field equations can be written in the form $dE+PdV=TdS$. While in the context of braneworld, it is shown (Cai and Cao 2007) that at apparent horizon, Friedmann equations can corresponds to first thermodynamical law. This work is then also extended to warped DGP braneworld (Sheykhi et al. 2007a) and Gauss-Bonnet braneworld (Sheykhi et al. 2007b).

The investigation about the validity of thermodynamical laws in GR as well as modified theories has been carried out by numerous researchers in literature. In this regards, Sharif and Zubair (2013a) developed some constraints on coupling parameter for the validity of first and second thermodynamical laws by considering apparent horizon of FRW geometry in $f(R,T,R_{\mu\nu}T^{\mu\nu})$ theory. They have also discussed thermodynamical properties for some modified $f(R,T)$ theories (Sharif and Zubair 2012, 2013b, 2013c). Debnath and Chattopadhyay (2013) discussed thermodynamical laws by taking FRW geometry with dark matter and new holographic DE as matter contents for both event and apparent horizon. Abdolmaleki and Najafi (2015) examined the validity of generalized second thermodynamical law for two different $f(G)$ models in modified Gauss-Bonnet gravity by assuming FRW universe with matter and radiations for dynamical apparent horizon. Cai et al. (2008) studied the thermodynamical properties of generalized Vaidya spacetime at apparent horizon by considering effective energy-momentum tensor in dynamical equations as well as unified first law in Einstein relativity and they discussed an entropy expression for this horizon.

In this context, thermodynamic laws are studied by Eling et al. (2006) in $f(R)$ gravity. They concluded that non-equilibrium description of thermodynamics needed, whereby an additional entropy term $d_{\jmath}{S}$ is appeared in Clausius relation resulting in the form $\delta{Q}=T(dS+d_{\jmath}{S})$. Karami et al. (2012) discussed thermodynamical laws for ordinary matter FRW geometry in $f(R)$ theory by taking a well famed $f(R)$ model. It is concluded that for the validity of GSLT in early epochs, a specific range of equation of state parameter is required while it is valid for all values in final cosmic epochs. Farajollahi et al. (2011) explained the validity of thermodynamical laws by considering perfect fluid FRW model for dynamical apparent horizon in chameleon cosmology. The question about the validity of thermodynamical laws in Brans-Dicke theory has been investigated by Bhattacharya and Debnath (2011) for constant BD parameter with power law scalar field on apparent horizon of FRW geometry. Mazumder and Chakraborty (2011) examined the validity of GSLT for FRW model with matter contents as a mixture of perfect fluid and the holographic dark energy in a generalized scalar-tensor gravity at the event horizon. In the presence of magnetized fluid, Sharif and Waheed (2013a, 2013b) explored the validity of thermodynamical laws in some scalar-tensor gravities by taking FRW and Bianchi geometries at different horizons with entropy corrected formulas.

In this study, we are focused on the validity of thermodynamical laws in a modified $f(T)$ gravity involving a direct interaction between torsion scalar and matter field. The present paper is coordinated in this format. In Sect. 2, we give a brief introduction of this gravity and the respective field equation for FRW geometry with perfect fluid as matter contents. In Sect. 3, the first law of thermodynamics at apparent horizon is defined for this theory. The validity of GSLT at apparent horizon for three different $f(T)$ models is investigated in Sect. 4. Last section presents an outlook of all findings.

2 Modified $f(T)$ gravity with non-minimal torsion-matter coupling

In this section, we explain some basics of the theory under consideration. A more general $f(T)$ gravity involving non-minimal coupling between torsion scalar and matter Lagrangian is defined by the action (Harko et al. 2014)

$$ \mathcal{A}=\frac{1}{2{\kappa}^{2}} \int{dx^{4}e\bigl\{ T+f_{1}(T)+\bigl[1+ \lambda{f_{2}(T)}\bigr] \mathcal{L}_{m}\bigr\} }, $$

(1)

where $\kappa^{2}=8\pi{G}$, $f_{i}(T)~(i=1,2)$ are arbitrary functions of torsion scalar, $\lambda$ is the coupling parameter of torsion scalar with geometry (taken as a positive constant) and $\mathcal{L}_{m}$ denotes the Lagrangian density corresponding to matter part. The field equations in non-minimal $f(T)$ theory can be determined by varying the action with respect to the tetrad $e^{\mu}_{i}$ and are given as follows

$$\begin{aligned} &{\bigl(1+f'_{1}+\lambda{f}'_{2} \mathcal{L}_{m}\bigr) \bigl[e^{-1}\partial_{\mu}\bigl(ee_{i}^{\sigma}{S}_{\sigma}^{\rho\mu}\bigr) -e^{\sigma}_{i}T^{\mu}_{\nu\sigma}S^{\nu\rho}_{\mu}\bigr]} \\ &{\qquad {}+\bigl(f''_{1}+\lambda {f}''_{2}\mathcal{L}_{m}\bigr) \partial_{\mu}{T}e^{\sigma}_{i}S_{\sigma}^{\rho\mu}+ \frac {1}{4}e^{\rho}_{i}(f_{1}+T)} \\ &{\qquad {}- \frac{1}{4} \lambda{f}'_{2}\partial_{\mu}{T}e^{\sigma}_{i}S_{\sigma}^{(m)\rho\mu}+ \lambda {f}'_{2}e^{\sigma}_{i} S_{\sigma}^{\rho\mu}\partial_{\mu}{\mathcal{L}}_{m}} \\ &{\quad {}=4\pi {G}(1+\lambda{f_{2}})e^{\sigma}_{i}T_{\sigma}^{(m)\rho},} \end{aligned}$$

(2)

where $S_{i}^{(m)\rho\mu}=\frac{\partial{\mathcal{L}_{m}}}{\partial\partial_{\mu}{e}^{i}_{\rho}}$ and prime denotes the differentiation with respect to torsion scalar. Equation (2) reduces to the respective dynamical equation in $f(T)$ gravity for the choice $\lambda=0$ or $f_{2}(T)=0$. The contribution to the energy momentum tensor of matter is taken as perfect fluid defined by the following form

$$T_{{\mu}{\nu}}=({\rho}_{m}+p_{m})u_{\mu}u_{\nu}-p_{m}g_{{\mu}{\nu}}. $$

We set the matter Lagrangian density as $L_{m}=-\rho_{m}$, which further implies $S_{i}^{(m)\rho_{m}\mu}=0$.

We consider the homogeneous and isotropic flat FRW metric defined by

$$ ds^{2}=dt^{2}-a^{2}(t)d \mathbf{x}^{2}, $$

(3)

where $a(t)$ represents the scale factor and $d\textbf{x}^{2}$ contains the spatial part of the metric and corresponding tetrad components are $e^{i}_{\mu}=(1,a(t),a(t),a(t))$. In such settings, the modified Friedmann equations are obtained as follows

$$\begin{aligned} &{3H^{2}=8\pi{G}\bigl[1+\lambda\bigl(f_{2}+12H^{2}f'_{2} \bigr)\bigr]\rho_{m} -\frac{1}{6}\bigl(f_{1}+12H^{2}f'_{1} \bigr),} \\ \end{aligned}$$

(4)

$$\begin{aligned} &{\dot{H}=-\frac{4\pi{G}(\rho_{m}+p_{m})[1+\lambda (f_{2}+12H^{2}f'_{2})]}{1+f'_{1}-12H^{2}f''_{1}-16\pi{G}\lambda\rho_{m} (f'_{2}-12H^{2}f''_{2})},} \end{aligned}$$

(5)

where $H=\dot{a}/a$ is the Hubble parameter and dot denotes the derivative with respect to cosmic time $t$. Equations (4) and (5) can be rewritten as

$$\begin{aligned} 3H^{2}=8\pi{G}\rho_{\mathit{eff}},\quad-\bigl(2 \dot{H}+3H^{2}\bigr)=p_{\mathit{eff}}, \end{aligned}$$

(6)

where the effective energy density and effective pressure of dark components are given by

$$\begin{aligned} \rho_{\mathit{eff}} =&\bigl[1+\lambda\bigl(f_{2}+12H^{2}f'_{2} \bigr)\bigr]\rho_{m}-\frac{1}{2\kappa ^{2}}\bigl(f_{1}+12H^{2}f'_{1} \bigr), \\ \end{aligned}$$

(7)

$$\begin{aligned} p_{\mathit{eff}} =&(\rho_{m}+p_{m}) \\ &{}\times \frac{[1+\lambda (f_{2}+12H^{2}f'_{2})]}{1+f'_{1}-12H^{2}f''_{1}-2\kappa^{2}\lambda\rho_{m} (f'_{2}-12H^{2}f''_{2})} \\ &{}+\frac{1}{2\kappa ^{2}}\bigl(f_{1}+12H^{2}f'_{1} \bigr) \\ &{}-\bigl[1+\lambda\bigl(f_{2}+12H^{2}f'_{2} \bigr)\bigr]\rho_{m}. \end{aligned}$$

(8)

3 Thermodynamic laws in modified $f(T)$ gravity

This section comprises of thermodynamic laws in the background of non-minimally coupled $f(T)$ gravity. It is interesting to explore the description of thermodynamical laws in modified $f(T)$ gravity involving non-minimal coupling between torsion and matter Lagrangian. In particular, we address the issue of non-equilibrium description of thermodynamics, which appears in modified theories involving curvature matter coupling like $f(R,T),f(R,T,Q)$ and $f(R,L_{m})$ (Sharif and Zubair 2012, 2013a, 2013b, 2013c). In our recent papers (Sharif and Zubair 2012, 2013a, 2013b, 2013c), we have discussed the non-equilibrium thermodynamics in non-minimally coupled modified gravity theories.

3.1 First law of thermodynamics

Here we define first law of thermodynamics in this modified gravity and examine the equilibrium picture of thermodynamics. The radius of dynamical apparent horizon is defined by $h^{\alpha\beta}\partial_{\alpha}\tilde{r}_{A}\partial_{\beta}\tilde{r}_{A}=0$, where $h^{\alpha\beta}$ denotes $h_{\alpha{\beta}}=\operatorname{diag}(-1,a^{2}/(1-kr^{2}))$. It is mentioned that we have considered the apparent horizon in this thermodynamic study however one can also see the future event horizon which is given by

$$ R_{h}=a(t) \int^{\infty}_{t}{\frac{d\hat{t}}{a(\hat{t})}} =a(t) \int^{\infty}_{a}{\frac{da'}{Ha^{\prime 2}}}. $$

In de Sitter space time $R_{H}=1/H$ and the future event horizon becomes the same as the de Sitter (Hubble) horizon. The role of future event horizon has been discussed in various perspectives (Setare 2006, 2007; Setare and Vagenas 2008; Jamil et al. 2010a, 2010b).

In case of flat FRW geometry, this turns out to be

$$ \tilde{r}_{A}=\frac{1}{H}. $$

(9)

Differentiating with respect to time, it results into the following equation

$$ \frac{\tilde{r}^{-3}_{A} d\tilde{r}_{A}}{dt}=H\dot{H}. $$

Substituting the above result in Eq. (5), we get

$$\begin{aligned} &{\frac{1}{2\pi\tilde{r}_{A}} \biggl(\frac{2\pi\tilde{r}_{A}d\tilde {r}_{A}}{G} \biggr)} \\ &{\quad {}= 4\pi \tilde{r}_{A}^{3}Hdt(\rho_{m}+p_{m})\bigl\{ 1+\lambda\bigl(f_{2}+12H^{2}f'_{2} \bigr)\bigr\} /\bigl\{ 1+f'_{1}} \\ &{\qquad {} -12H^{2}f''_{1}-2 \kappa^{2}\lambda\rho_{m} \bigl(f'_{2}-12H^{2}f''_{2} \bigr)\bigr\} .} \end{aligned}$$

(10)

Multiplying the whole Eq. (10) by the factor $(1-\frac{\dot{\tilde{r}}_{A}}{2H\tilde{r}_{A}} )$, leads to

$$\begin{aligned} TdS =&\bigl(4\pi\tilde{r}_{A}^{3}H-2\pi \tilde{r}_{A}^{2}\dot{\tilde{r}}_{A}\bigr) ( \rho_{m}+p_{m})\bigl\{ 1+\lambda\bigl(f_{2} \\ &{}+12H^{2}f'_{2} \bigr)\bigr\} /\bigl\{ 1+f'_{1}-12H^{2}f''_{1} \\ &{}-2 \kappa^{2}\lambda\rho_{m} \bigl(f'_{2}-12H^{2}f''_{2} \bigr)\bigr\} dt, \end{aligned}$$

(11)

where $T=\frac{|\kappa_{sg}|}{2\pi}$ represents the temperature of apparent horizon with $\kappa_{sg}=\frac{1}{\tilde{r}_{A}}(1-\frac{\dot{\tilde{r}}_{A}}{2H\tilde{r}_{A}})$ being the surface gravity and $A=4\pi{\tilde{r}^{2}_{A}}$ is the area of apparent horizon. Moreover, the Bekenstein-Hawking entropy relation (Bekenstein 1973; Bardeen et al. 1973; Hawking 1975) $S=A/4G$ is employed in Eq. (11) to set the first law of thermodynamics (FLT) in this gravity.

The matter energy density inside a sphere of radius $\tilde{r}_{A}$ at the apparent horizon is defined by the relation $E={V}\rho_{\mathit{tot}}$ with $V=4/3\pi\tilde{r}_{A}^{3}$. In modified $f(T)$ gravity, we have

$$\begin{aligned} dE =&4\pi{\tilde{r}}_{A}^{2}(\rho_{m}+ \rho_{\mathit{DE}}){d}\tilde{r}_{A}-4\pi\tilde {r}_{A}^{3}( \rho_{m}+p_{m}) \\ &{}\times Hdt \bigl\{ 1+\lambda\bigl(f_{2}+12H^{2}f'_{2} \bigr)\bigr\} /\bigl\{ 1+f'_{1} \\ &{}-12H^{2}f''_{1}-2 \kappa^{2}\lambda\rho _{m}\bigl(f'_{2}-12H^{2}f''_{2} \bigr)\bigr\} . \end{aligned}$$

(12)

Putting $dE$ in Eq. (11), we get

$$ TdS=-dE+2\pi\tilde{r}_{A}^{2}( \rho_{m}+\rho_{\mathit{DE}}-p_{m}-p_{\mathit{DE}})d \tilde{r}_{A}. $$

(13)

Now introducing the total work density which is defined as (Hayward 1998; Hayward et al. 1999)

$$ W=-\frac{1}{2}T^{(tot)\alpha\beta}h_{\alpha\beta}= \frac{1}{2} (\rho_{\mathit{tot}}-p_{\mathit{tot}}). $$

(14)

Finally, Eq. (13) takes the standard form of FLT given by

$$ TdS=-dE+dW, $$

(15)

which is FLT in modified $f(T)$ gravity involving non-minimal torsion-matter coupling. We conclude that equilibrium description of thermodynamics exists in this modified gravity and results are identical to that in Einstein, Gauss-Bonnet and Lovelock gravities (Padmanabhan 2002; Cai and Cao 2007; Sheykhi et al. 2007a, 2007b).

4 GSLT in modified $f(T)$ gravity

Here we investigate the validity of GSLT in the context of modified $f(T)$ gravity. It states that the sum of the horizon entropy and entropy of ordinary matter fluid components always increases in time (Wu et al. 2008). The validity of GSLT has been tested in modified gravities including $f(R)$, $f(R)$ theory involving matter geometry coupling, $f(T)$, $f(R,T)$, $f(R,T,Q)$, $f(R,L_{m})$ and scalar tensor theories. The Gibb’s equation which relates the entropy of matter and energy sources inside the horizon $S_{\mathit{in}}$ to the density and pressure in the horizon is defined by the relation

$$ T_{\mathit{in}}dS_{\mathit{in}}=d(\rho_{m}V)+p_{m}dV. $$

(16)

Equation (16) can be rewritten as

$$ T_{\mathit{in}}\dot{S}_{\mathit{in}}=4\pi{\tilde{r}^{2}_{A}}( \rho_{m}+p_{m}) (\dot{\tilde {r}}_{A}-H \tilde{r}_{A}). $$

(17)

One can find $\rho_{m}$ and $p_{m}$ from Eqs. (4) and (5), and hence using in Eq. (17), it results in

$$\begin{aligned} T_{\mathit{in}}\dot{S}_{\mathit{in}} =&4\pi{\tilde{r}^{2}_{A}}( \dot{\tilde{r}}_{A}-H\tilde {r}_{A})\frac{1}{\kappa^{2}(1+\lambda(f_{2}+12H^{2}f'_{2}))} \\ &{}\times \biggl[3H^{2}+\frac{1}{2}\bigl(f_{1}+12H^{2}f'_{1} \bigr) \\ &{}-2\dot {H}\bigl(1+f'_{1}-12H^{2}f''_{1} \bigr) \\ &{}+\frac{3H^{2}+\frac{1}{2}(f_{1}+12H^{2}f'_{1})}{ \kappa^{2}(1+\lambda(f_{2}+12H^{2}f'_{2}))} \\ &{}\times\biggl\{ 2\kappa^{2}\lambda\bigl(f'_{2}-12H^{2}f''_{2} \bigr)\dot{H} \\ &{}-\frac{\kappa^{2}}{2} \bigl(1+\lambda\bigl(f_{2}+12H^{2}f'_{2} \bigr)\bigr)\biggr\} \biggr]. \end{aligned}$$

(18)

Using the horizon entropy relation, one can find

$$ T_{h}\dot{S}_{h}=\frac{1}{2\tilde{r}_{A}HG}\bigl(2H \tilde{r}_{A}\dot{\tilde {r}}_{A}-\dot{\tilde{r}}^{2}_{A} \bigr). $$

(19)

Now we discuss the validity of GSLT which requires $(\dot{T}_{h}\dot{S}_{h}+\dot{T}_{\mathit{in}}\dot{S}_{\mathit{in}})\geqslant0$. It is natural to assume a relation between the temperature of apparent horizon and entire contents within the horizon. In this setting, we limit our discussion to hypothesis of thermal equilibrium so that energy would not flow in the system and horizon temperature is more or less equal to temperature inside the horizon i.e., $T_{\mathit{in}}=T_{h}$.

Using Eqs. (9), (18) and (19), GSLT takes the following form

$$\begin{aligned} T_{h}\dot{S}_{\mathit{tot}} =&\frac{-\dot{H}}{2GH^{4}} \bigl(2H^{2}+\dot{H}\bigr)-\frac{4\pi }{H^{4}}\bigl(H^{2}+\dot{H}\bigr) \\ &{} \times\frac{1}{\kappa^{2}(1+\lambda(f_{2}+12H^{2}f'_{2}))} \biggl[3H^{2}+\frac {1}{2} \bigl(f_{1} \\ &{}+12H^{2}f'_{1}\bigr) -2 \dot{H}\bigl(1+f'_{1}-12H^{2}f''_{1} \bigr) \\ &{}+\frac{3H^{2}+\frac {1}{2}(f_{1}+12H^{2}f'_{1})}{\kappa^{2}(1+\lambda(f_{2}+12H^{2}f'_{2}))} \biggl\{ 2\kappa^{2}\lambda \bigl(f'_{2} \\ &{}-12H^{2}f''_{2}\bigr)\dot {H}-\frac{\kappa^{2}}{2} \bigl(1+\lambda\bigl(f_{2}+12H^{2}f'_{2} \bigr)\bigr)\biggr\} \biggr]. \end{aligned}$$

(20)

Equation (20) represents the constraint for examining the validity of GSLT in modified $f(T)$ gravity. We are interested to explore this condition for particular functional forms of $f_{1}(T)$ and $f_{2}(T)$.

• $f_{1}(T)=-\varLambda+\alpha_{1}T^{2}$, $f_{2}(T)=\beta_{1}T^{2}$

In the first place, we examine the case for which $f_{1}(T)=-\varLambda+\alpha_{1}T^{2}$ and $f_{2}(T)=\beta_{1}T^{2}$, where $\alpha_{1}$, $\beta_{1}$ are model parameters and $\varLambda>0$ is a constant. These functions involve quadratic contribution from $T$ and appear as corrections to teleparallel theory. The derivatives of these functions are defined as $f'_{1}=2\alpha_{1}T$, $f''_{1}=2\alpha_{1}$, $f'_{2}=2\beta_{1}T$ and $f''_{2}=2\beta_{1}$. Since torsion is defined in terms of Hubble parameter so we can change the functional dependence from $T$ to $H$ as $f_{1}(T)\equiv f_{1}(H)=-\varLambda+\alpha{H}^{4}$ and $f_{2}(T)\equiv f_{2}(H)=\beta{H}^{4}$, where $\alpha=36\alpha_{1}$, $\beta=36\beta_{1}$. For the derivatives of $f_{1}$ and $f_{2}$, we have $f'_{1}(H)=-\alpha{H}^{2}/3$, $f''_{1}(H)=\alpha/18$, $f'_{2}(H)=-\beta{H}^{2}/3$ and $f''_{2}(H)=\beta/18$.

In this case, GSLT takes the form

$$\begin{aligned} T_{h}\dot{S}_{\mathit{tot}} =&\frac{-\dot{H}}{2GH^{4}} \bigl(2H^{2}+\dot{H}\bigr)-\frac{4\pi }{H^{4}}\bigl(H^{2}+\dot{H}\bigr) \\ &{} \times\frac{1}{\kappa^{2}(1-3\lambda\beta{H}^{4})} \biggl[3H^{2}-\frac{1}{2}\bigl( \varLambda+3\alpha{H}^{4}\bigr) \\ &{} -2\dot{H}\bigl(1- \alpha{H}^{2}\bigr)+\frac{3H^{2}-\frac{1}{2}(\varLambda+3\alpha {H}^{2})}{\kappa^{2}(1-3\lambda\beta{H}^{4})} \\ &{}\times \biggl\{ -2\kappa^{2} \lambda\beta{H}^{2}\dot{H} -\frac {\kappa^{2}}{2}\bigl(1-3\lambda\beta{H}^{4} \bigr)\biggr\} \biggr]. \end{aligned}$$

(21)

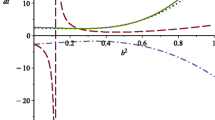
In literature, Harko et al. (2014) explored the time variation of Hubble function $H(t)$, scale factor $a(t)$, matter energy density $\rho_{m}(t)$, deceleration parameter $q(t)$ and equation of state parameter $\omega_{\mathit{DE}}$ for the above model in modified $f(T)$ gravity. They set the particular model parameters and show that this model favors the cosmological constant regime. Following Harko et al. (2014), we choose the model and coupling parameters to show the evolution of EoS parameter $\omega_{\mathit{DE}}$ versus cosmic time. Left plot in Fig. 1 indicates that $\omega_{\mathit{DE}}$ favors the cosmological constant regime. For this choice of parameters, we explore the validity of GSLT and find that GSLT can be met for these specific choices of parameters for small positive range of cosmic time only as shown in right plot of Fig. 1. Further, we assume the power law solutions given by $a(t)=a_{0}t^{m}$, where $m>0$ is a constant. We set $m>1$ with matter contents as dust $\rho=\rho_{0}t^{-3m}$ and see the validity of GSLT as shown in Fig. 2. In left and right plots, we show the evolution of GSLT versus the model parameters $\alpha$ and $\beta$ respectively. Figure 3 shows the variation of GSLT versus $\varLambda$ and $t$. It is seen that the range of cosmic time for which the GSLT remains valid can be increased only if we chose large values of $\alpha$ parameter when other parameters are fixed as shown in left plot of Fig. 2. In right plot we find that GSLT can be satisfied only for small values of $\beta$. In a similar fashion, one can vary the time interval and find that GSLT is satisfied for $\varLambda>0$.

• $f_{1}(T)=-\varLambda$, $f_{2}(T)=\alpha_{2}T+\beta_{2}T^{2}$

In this example, we consider the model defined by the following functions (Harko et al. 2014)

$$\begin{aligned} f_{1}(T)=-\varLambda,\quad f_{2}(T)= \alpha_{2}T+\beta_{2}T^{2}, \end{aligned}$$

(22)

where $\alpha_{2}$ and $\beta_{2}$ are parameters for the model (22). We express the functions $f_{1}$ and $f_{2}$ in terms of $H$ as $f_{1}(H)=-\varLambda$, $f_{2}(H)=\alpha{T}+\beta{T}^{2}$, where $\alpha=-6\alpha_{2}$ and $\beta=36\beta_{2}$. Similarly, the derivatives of $f_{1}$ and $f_{2}$ are given by $f'_{1}(H)=f''_{1}(H)=0$, $f'_{2}(H)=-\gamma/6-\delta{H}^{2}/3$ and $f''_{2}(H)=\delta/18$. The constraint for validity of GSLT is found as

$$\begin{aligned} T_{h}\dot{S}_{\mathit{tot}} =&\frac{-\dot{H}}{2GH^{4}} \bigl(2H^{2}+\dot{H}\bigr)-\frac{4\pi }{H^{4}}\bigl(H^{2}+ \dot{H}\bigr) \\ &\times\,\frac{1}{\kappa^{2}(1-\lambda(\alpha{H}^{2}+3\beta{H}^{4}))} \biggl[3H^{2}-\frac{\varLambda}{2}-2\dot{H} \\ &+\,\frac{3H^{2}-\frac{\varLambda}{2}}{\kappa^{2}(1-\lambda(\alpha{H}^{2}+3\beta{H}^{4}))} \biggl\{ -2 \kappa^{2}\lambda\biggl(\frac{\alpha}{6}+\beta{H}^{2} \biggr) \\ &-\,\frac{\kappa ^{2}}{2}\bigl(1-\lambda \bigl(\alpha{H}^{2}+3 \beta{H}^{4}\bigr)\bigr)\biggr\} \biggr]. \end{aligned}$$

(23)

Fig. 1

Evolution of $\omega_{\mathit{DE}}$ and GSLT for non-minimally coupled $f(T)$ model $f_{1}(T)=-\varLambda+\alpha_{1}T^{2}$, $f_{2}(T)=\beta_{1}T^{2}$. We set the parameters as $\varLambda=0.002$, $\alpha=1.01$, $\beta =2.01$, $\lambda=0.003$ (black curve), $\varLambda= 0.0024$, $\alpha=1.02$, $\beta=2.02$, $\lambda=0.0034$ (blue curve) and $\varLambda= 0.0028$, $\alpha= 1.023$, $\beta=2.023$, $\lambda=0.0038$ (red curve)

Fig. 2

Evolution of GSLT for non-minimally coupled $f(T)$ model $f_{1}(T)=-\varLambda+\alpha_{1}T^{2}$, $f_{2}(T)=\beta_{1}T^{2}$ in power law cosmology. In left plot, we show the variation for parameter $\alpha$ and set $\varLambda=0.01$, $m=5$, $\beta=0.001$, $\lambda=0.2$ and in right plot, we fix $\varLambda=0.01$, $m=5$, $\alpha=2$, $\lambda=0.2$ to show the variation for parameter $\beta$

Fig. 3

Evolution of GSLT for non-minimally coupled $f(T)$ model $f_{1}(T)=-\varLambda+\alpha_{1}T^{2}$, $f_{2}(T)=\beta_{1}T^{2}$ in power law cosmology versus $\varLambda$ with $m=5$, $\alpha=2$, $\beta=0.001$, $\lambda=0.2$

In this case, we set the model parameters to show the crossing of phantom divide line in non-minimally coupled $f(T)$ gravity. In left plot of Fig. 4, we show the variation of equation of state parameter of DE versus cosmic time for some specified model parameters. One can see that equation of state crosses the phantom divide line from phantom phase ($\omega_{\mathit{DE}}<-1$) to quintessence phase ($\omega_{\mathit{DE}}>-1$) and then evolves to cosmological constant regime $\omega_{\mathit{DE}}=-1$. In right plot, we show the evolution of GSLT for the cosmological constant regime. It is observed that GSLT remains valid only for a short interval of cosmic time for the selected choice of model parameters.

Fig. 4

Variation of equation of state parameter and GSLT for non-minimally coupled $f(T)$ model $f_{1}(T)=-\varLambda$, $f_{2}(T)=\alpha _{2}T+\beta_{2}T^{2}$. Here, we set $\varLambda=1$, $\alpha=0.1$, $\beta=0.2$, $\lambda=1$ (black curve), $\varLambda=1.3$, $\alpha=0.13$, $\beta=0.23$, $\lambda=1.3$ (blue curve) and $\varLambda=1.6$, $\alpha=0.15$, $\beta=0.3$, $\lambda=1.5$ (red curve)

We also discuss the evolution of GSLT versus coupling parameters $\alpha$ and $\beta$ in power law cosmology and show the evolution in Fig. 5. It is observed that GSLT may be valid for all values of $\alpha>0$ for fixed values of other parameters as shown in left plot of Fig. 5. It is also seen that GSLT also remains valid for small as well as large values of $\beta$ parameter as indicated in right plot of Fig. 5.

Fig. 5

Evolution of GSLT for non-minimally coupled $f(T)$ model $f_{1}(T)=-\varLambda$, $f_{2}(T)=\alpha_{2}T+\beta_{2}T^{2}$. In left plot, we set, $\varLambda=0.01$, $m=5$, $\beta=30$, $\lambda=0.2$ to show evolution versus $\alpha$ and $t$, whereas right plot shows the variation versus $\beta$ and $t$ for the values $\varLambda=0.01$, $m=5$, $\alpha=30$, $\lambda=0.2$

4.1 Exponential model

In this section, we discuss a specific case of non-minimal coupling to show the difference in evolution of $f(T)$ model with minimal coupling. We set $f_{1}(T)=0$ and $f_{2}(T)=f(T)$, so that action (1) takes the following form

$$ \mathcal{A}=\frac{1}{2{\kappa}^{2}} \int{dx^{4}e\bigl\{ T+\bigl(1+\lambda{f(T)}\bigr) \mathcal{L}_{m}\bigr\} }. $$

(24)

In this case, one can find the relations for energy density and Hubble parameter in this form

$$\begin{aligned} &{\rho_{m}(t)=\frac{3H^{2}}{1+\lambda(f+12H^{2}f')},} \end{aligned}$$

(25)

$$\begin{aligned} &{2\dot{H}=-\frac{\{1+\lambda(f+12H^{2}f')\}\{\frac{3H^{2}}{1+\lambda (f+12H^{2}f')}+p_{m}\}}{ 1-\frac{6H^{2}(f'-12H^{2}f'')}{1+\lambda(f+12H^{2}f')}}.} \end{aligned}$$

(26)

Here we are interested to discuss the exponential model in non-minimal $f(T)$ gravity. We consider the following exponential $f(T)$ model, initially proposed by (Linder 2010)

$$ f(T)=\alpha{T}\bigl(1-e^{pT_{o}/T}\bigr),\quad\alpha=- \frac{1-\varOmega_{m0}}{1-(1-2p)e^{p}}. $$

(27)

Linder (2010) explored the effective equation of state $\omega$ versus scale factor $a(t)$ for the model (27). It is shown that $\omega$ crosses $\omega=-1$ from $\omega>-1$ to $\omega<-1$ and then asymptotically approaches a de Sitter fate. In Bamba et al. (2011), Bamba et al. discussed the evolution of exponential model $f(T)$ model and conclude that the phantom crossing cannot be realized in this case as it results in $\omega=-1$. Such type of models has also been tested with the varying fine structure “constant” $\alpha=e^{2}/\hbar{c}$ (Wei et al. 2011). We integrate Eq. (26) for different values of parameters $p$ and $\varLambda$ to find the evolution of Hubble parameter as shown in Fig. 6. The variation of $H(t)$ is similar to that in Harko et al. (2014) for the non-minimally coupled $f(T)$ models. $H(t)$ is decreasing function of $t$ which approaches to a constant value in future evolution. In right plot, we show the evolution of equation of state parameter $\omega_{\mathit{DE}}$ for varying values of $p$ with $\lambda=4$ $\omega_{m0}=0.315$ and $H_{0}=67.3$ (Ade et al. 2014). In this plot, we find that $\omega_{\mathit{DE}}$ represents the quintessence regime as compared to its evolution in minimally coupled $f(T)$ gravity (Bamba et al. 2011; Linder 2010). Such behavior of $\omega_{\mathit{DE}}$ is consistent with the recent observations (Ade et al. 2014) $\omega=-1.13^{+0.24}_{-0.25}$, (95% Planck + BAO + WP). In this setting, we also test the validity of GSLT and its evolution is shown in Fig. 7. It can be observed that the GSLT remains valid for the range of cosmic time approaching to zero with increasing values of $p$ parameter.

Fig. 6

Evolution of $H(t)$ and $\omega_{\mathit{DE}}$ for the exponential model $f(T)=\alpha{T}(1-e^{pT_{o}/T})$, $\alpha=-\frac{1-\varOmega _{m0}}{1-(1-2p)e^{p}}$. Here we set $H_{0}=67.3$, $\omega_{m0}=0.315$ with $p=.009$ (blue curve), $p=.006$ (black curve) and $p=.003$ (red curve)

Fig. 7

Evolution of GSLT for the exponential model $f(T)= \alpha{T}(1-e^{pT_{o}/T})$, $\alpha=-\frac{1-\varOmega _{m0}}{1-(1-2p)e^{p}}$. Here we set $H_{0}=67.3$, $\omega_{m0}=0.315$ with $p=.009$ (blue curve), $p=.006$ (black curve) and $p=.003$ (red curve)

5 Concluding remarks

In the present paper, we have discussed the thermodynamical laws in the context of modified $f(T)$ theory, where $T$ denotes the torsion scalar. Here we have taken flat FRW geometry filled with dust fluid and discussed the FLT and GSLT at apparent horizon. Firstly, we have presented the equilibrium picture of thermodynamics in such gravity at the apparent horizon of FRW model. Further we have investigated the validity of GSLT at apparent horizon using Gibbs relation. For the purpose, we have taken two cosmologically consistent models of $f(T)$ gravity namely

• $f_{1}(T)=-\varLambda+\alpha_{1}T^{2}$, $f_{2}(T)=\beta_{1}T^{2}$;

• $f_{1}(T)=-\varLambda$, $f_{2}(T)=\alpha_{2}T+\beta_{2}T^{2}$.

We have developed the constraints for the validity of GSLT in terms of Hubble parameter and in terms of cosmic time using power law model and check its evolution graphically. We have also discussed the solutions and validity of GSLT model for exponential model of $f(T)$ gravity as proposed by Linder. The obtained results can be summarized as follows

• In modified $f(T)$ gravity involving non-minimal torsion-matter coupling, the gravitational dynamical equations can lead to standard form of FLT given by $TdS=-dE+dW$. We have concluded that equilibrium description of thermodynamics exists in this modified gravity and results are identical to that in Einstein, Gauss-Bonnet and Lovelock gravities.

• In first example, we have found the dynamical behavior of EoS parameter $\omega_{\mathit{DE}}$ versus cosmic time numerically by choosing appropriate selection of the model and coupling parameters as indicated in Fig. 1 which favors the cosmological constant regime. For the same choice of free parameters, we have investigated the validity of GSLT graphically and it is found that GSLT can be met only for small positive range of cosmic time closer to 0. Further, we have considered the power law model of scale factor for which the continuity equation leads to $\rho=\rho_{0}t^{-3m}$ and explored the validity of GSLT graphically as given in Figs. 2 and 3. It is seen that the range of cosmic time for which the GSLT remains valid can be increased only if we choose large values of $\alpha$ parameter when other parameters are taken fixed while for other choices of $\beta$ and $\varLambda$, the GSLT remains valid only on a short small interval of cosmic time.

• In second example, we have explored the variation of $\omega_{\mathit{DE}}$ versus cosmic time for some specified selection of model parameters. It is concluded that crossing of phantom divide line from phantom phase ($\omega_{\mathit{DE}}<-1$) to quintessence phase ($\omega_{\mathit{DE}}>-1$) is admissible and finally it evolves to cosmological constant regime $\omega_{\mathit{DE}}=-1$. Further we have investigated the evolution of GSLT which indicates that it remains valid only for a short interval of cosmic time closer to 0 for the specified model parameters. We have also determined the evolution of GSLT versus coupling parameters $\alpha$ and $\beta$ graphically using power law cosmology. It is shown that GSLT may be valid for all values of $\alpha$ with cosmic time satisfying $t\geq6$ by taking other parameters fixed. It is also seen that GSLT also remains valid for small as well as large values of $\beta$ parameters with cosmic time satisfying $t\geq2$.

• In case of exponential $f(T)$ model, we have found numerical solution for Hubble parameter by taking different values of parameters $p$ and $\varLambda$. It is concluded that the $H(t)$ is decreasing function of cosmic time which approaches to a constant value in future evolution which is similar to that in Harko et al. (2014) for the non-minimally coupled $f(T)$ models. Further, we have explored the evolution of $\omega_{\mathit{DE}}$ for varying values of $p$ with some cosmologically consistent values of $\lambda$, $\omega_{m0}$ and $H_{0}$. It is seen that $\omega_{\mathit{DE}}$ represents the quintessence regime as compared to its evolution in minimally coupled $f(T)$ gravity (Bamba et al. 2011; Linder 2010) which is also consistent with the recent observations (Ade et al. 2014) $\omega=-1.13^{+0.24}_{-0.25}$, (95% Planck + BAO + WP). For such selection of parameters, we have also discussed the validity of GSLT graphically. It is concluded that the GSLT remains valid for the range of cosmic time approaching to zero with increasing values of $p$ parameter.