Helical Structures in the Near Field of a Turbulent Pipe Jet

Abstract

We perform a finely resolved Large-eddy simulation to study coherent vortical structures populating the initial (near-nozzle) zone of a pipe jet at the Reynolds number of 5300. In contrast to ‘top-hat’ jets featured by Kelvin-Helmholtz rings with the non-dimensional frequency S t≈0.3−0.6, no high-frequency dominant mode is observed in the near field of a jet issuing from a fully-developed pipe flow. Instead, in shear layers we observe a relatively wide peak in the power spectrum within the low-frequency range (S t≈0.14) corresponding to the propagating helical waves entering with the pipe flow. This is confirmed by the Fourier transform with respect to the azimuthal angle and the Proper Orthogonal Decomposition complemented with the linear stability analysis revealing that this low-frequency motion is not connected to the Kelvin-Helmholtz instability. We demonstrate that the azimuthal wavenumbers m=1−5 contain the most of the turbulent kinetic energy and that a common form of an eigenmode is a helical vortex rotating around the axis of symmetry. Small and large timescales are identified corresponding to “fast” and “slow” rotating modes. While the “fast” modes correspond to background turbulence and stochastically switch from co- to counter-rotation, the “slow” modes are due to coherent helical structures which are long-lived and have low angular velocities, in agreement with the previously described spectral peak at low S t.

1 Introduction

Jet-like flows are encountered in many technological applications. Moreover, because of their rich physics and simple configuration, jets have been considered as the paradigm of free shear flows and one of the basic research topics in hydrodynamics [1]. Coherent structures sustained by the flow instabilities are closely linked to the mixing and noise-generating characteristics. The knowledge of the flow response to an external forcing and variation of initial conditions gives the opportunity to control some properties of jets [2–4].

Jets produced with a ‘top-hat’ velocity profile using smoothly contracting nozzles are the usual target in the literature [5]. The close-to-laminar inflow consists of a uniform flow in the center and a thin boundary layer near the wall. The near field, apart from the Reynolds number, is mainly governed by the ratio of the nozzle diameter D to the initial momentum thickness 𝜃. The third controlling criterium is the incoming level of turbulence. These parameters influence the development of the Kelvin-Helmholtz instability close to the nozzle edge resulting in the formation of the energetic axisymmetric vortical rings [6] which are induced by the inflexional instability of a thin shear layer [7, 8]. The initial growth of a vortex ring can be described by the linear stability theory followed by the non-linear interaction between vortices such as pairing [9]. Yule [9] schematically described the evolution of the jet downstream, associated with the formation of laminar vortex rings very close to the nozzle, the azimuthal instabilies provoking the transition to three-dimensional flow leading to its turbulization.

The shear-layer instability is the most amplified at frequencies which scale with 𝜃. As the local momentum thickness grows further downstream from the nozzle, the characteristic scale of the energetic instabilities corresponding to the interaction between the opposite shear layers becomes the width of the jet (jet-column instability). Crow and Champange [7] first observed this low-frequency instability at x/D=4 appearing as ‘a more tenuous train of large-scale vortex puffs’ existing with the average non-dimensional frequency, i.e. the Strouhal number, S t _D ∼0.3 based on D and U _b which is the inflow bulk velocity. They called it the preferred mode, which was later extensively studied by a number of authors showing that S t _D falls into a range of values [10] due to different initial conditions. The recent analysis of the global linear frequency response to some artificial forcing performed by Garnaud et al. [11] shows that the dominant perturbations appearing with S t _D ≈0.45 are spatially located in the end of the potential core covering the attached shear-layers as well. Thus, the connection of the shear-layer and jet-column instabilities together with high sensitivity to the inflow conditions of ‘top-hat’ jets make the study of the inherent low-frequency instabilities problematic.

In the spirit of Crow and Champange who tripped the boundary layer inside the nozzle to destroy the energetic axisymmetric vortex rings in order ‘to isolate the large-scale pattern’ (sinusoidal perturbations of the jet column) we propose to study a canonical jet induced by a fully developed turbulent pipe flow. This case is defined by only one governing parameter, i.e. the Reynolds number, as it completely determines the inlet conditions. The fully developed inflow suppresses the development of the quasi-laminar Kelvin-Helmholtz rings making pipe jets a natural object to study instability modes of the jet core. Relevant publications [12–14] report on comparison of mean and spectral characteristics between ‘top-hat’ and pipe jets. A number of authors [15–18] performed pipe jet experiments at relatively high Reynolds numbers including the study of temperature and concentration fields. Visualizations [19] and extensive measurements [20–22] were recently conducted at lower Reynolds numbers.

Using Large-eddy simulation (LES) we study the flow at R e = U _b D/ν=5300, where ν denotes the kinematic viscosity. The aim is to provide the lacking information on vortical structures populating the near-nozzle area of a pipe jet. We report on the non-Kelvin-Helmholtz-type low-frequency coherent motion with S t _D ≈0.14 originating from the propagating helical waves existing in the pipe flow [23]. Two common techniques supplementing each other are used to probe the typical coherent structures of the flow, i.e. the Proper Orthogonal Decomposition (POD) and local linear stability analysis [24–26].

The application of POD, originally proposed by Lumley [27] in the context of turbulence, advances the understanding of coherent structures. POD is a tool to identify the most energetic motions in the form of a series expansions with respect to spatial eigenmodes and their temporal amplitudes. This technique has been mostly applied to ‘top-hat’ jets using the velocity fields measured in a plane normal to the jet (2D or ‘slice’ POD). Cintriniti and George [28] performed POD analysis using information from an array of simultaneously operating hot-wire anemometer probes. Based on the streamwise velocity they found that five Fourier modes with azimuthal wavenumbers m=(0,3,4,5,6) were necessary to represent the dynamics at x/D=3. Jung et al. [29] and Gamard et al. [30] analysed the near and far fields using multiple ‘slices’ in the range 2≤x/D≤6 and 15≤x/D≤69, respectively. They found that the symmetric mode m=0 vanished rapidly after few diameters downstream in the near field, while m=2 became the most energetic by the end of the potential core. In the far field the mode m=2 was also dominant, while m=0 and 1 were less energetic. Note that the above described investigations relied only on the information about the streamwise velocity. Iqbal and Thomas [31] showed that when all three velocity components were taken into account m=1 overweighed m=2. Similar results were demonstrated for the far-jet [32]. In the present work we employ ‘slice’ POD and use all three velocity components.

Numerical time-resolved simulations are widely used to extract coherent structures using some filtering approach such as POD. As stated above, the ‘top-hat’ jets have been mainly in focus. A database from the direct numerical simulations (DNS) of a high subsonic jet at R e=3600 [33] was employed by Freund and Colonius [34] to perform POD showing that energetic axisymmetric (m=0) and helical (m=1) modes are present at the end of the potential core which is a particularly important area for the noise radiation [35]. Vuorinen et al. [36] studied the influence of the nozzle pressure ratios on the jet as encountered in the internal combustion engines showing the connection of POD modes and observed pressure fluctuations. LES/DNS databases [37, 38] were recently analysed by Ryu and co-authors [26, 39] with the main emphasis on the noise generation and supersonic jets complementing the analysis with linear stability tools.

The present work addresses the near field of a turbulent pipe jet at R e=5300. We combine POD and linear stability analysis to probe the typical coherent structures in the flow. The observed low-frequency spectral peak of velocity fluctuations and its connection to the fully developed turbulent inflow conditions is the main focus of the paper which is arranged as follows. Section 2 provides computational details and flow configuration. In Section 3 we describe the linear stability analysis and the POD algorithm. The main results are presented in Section 4 followed by conclusions.

2 Problem Formulation and Computational Details

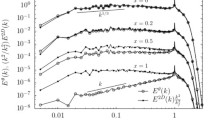
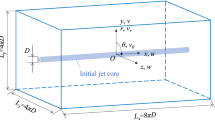
We consider a canonical jet induced by a fully developed turbulent pipe flow at R e=5300. The computational domain represents a cylinder of 12D in diameter and 16D in length. Figure 1 shows the instanteneous passive scalar field together with the computational domain organization and boundary conditions. Vortices are visualized by constant levels of the Q-criterium where Q=(Ω _{i j} Ω _{i j} −S _{i j} S _{i j} )/2, with Ω _{i j} and S _{i j} being the rotation rate and the rate-of-strain tensors, respectively. The pipe flow supplies the streamwise streaky structures which can be traced close to the nozzle. They interact with the shear layer forming hairpin-like vortices which have a complex dynamics and breakdown further downstream. In contrast to ‘top-hat’ jets, no high-frequency dominant mode is observed in the time power spectrum close to the nozzle [12], while low-frequency range distinctly shows the existence of energy-containing motion (see Fig. 1). This peak occurs at the Strouhal number S t = f D/U _b ≈0.14, where f is the frequency, and is not connected to the Kelvin-Helmholtz instability as shown below from the spectral analysis and linear stability theory. To the best of authors’ knowledge this issue has never been reported before in the literature. We use POD to find the spatial form of the coherent structures corresponding to the observed low-frequency peak.

Fig. 1

Left: Half of the computational domain, cylindrical coordinate system (r,ϕ,x) and boundary conditions. The instanteneous field is visualized by a passive scalar. Cyan lines indicate walls of 1D pipe fragment. Right: Two subsequent samples of vortical structures near the nozzle are visualized using two isosurfaces of the Q-criterium with Q=0.5 (transparent violet) and Q=1.5 (orange). The inset shows the time power spectrum E at x/D=1 and r/D=0.5 averaged over azimuthal angle together with the radial profile of turbulent kinetic energy k at x/D=1. The blue arrow indicates the low-frequency peak at S t=0.14

LES is performed with the convective outflow imposed at the exit boundary, while constant pressure is imposed on the open lateral boundary. A small co-flow of U _{c o} =0.04U _b is set at the bottom x=−1D. The mesh has a DNS-like resolution in the near-nozzle area and consists of 252×282×264 cells (∼16.7×10⁶) in the radial, axial and azimuthal directions, respectively, with the majority clustered in the shear layers and near-wall regions with the stretching factor being less than 5 percent. The minimum axial spacing Δx=0.005D is at the nozzle exit resulting in the following near-wall cell dimensions Δr ⁺=0.5, (DΔ𝜃/2)⁺=5.58 and Δx ⁺=2.51 expressed in terms of wall units ν/u _τ , where u _τ is the pipe-wall friction velocity (see Fig. 2 for mesh spacing). Earlier [40] we showed that LES of a coaxial swirling jet flow at R e=11250 is well-resolved on a similar mesh of 12.3×10⁶ cells satisfying the criterium Δ/η<12 [1], where Δ=(rΔrΔ𝜃Δx)^1/3 is the cell size and η=(ν ³/𝜖)^1/4 the Kolmogorov scale and 𝜖 the kinetic energy dissipation rate. Moreover, with the use of the dissipation profile from the pipe flow DNS [41], the calculated ratio Δ/η appears to be around unity (or less) inside the pipe (see the inset in Fig. 2). To generate proper unsteady inflow conditions we perform a separate precursor LES simulation of a periodic pipe flow with a cylinder length of 5D. The mesh consisted of 2.8×10⁶ cells providing excellent agreement of the first- and second-order statistics with the available DNS data of [41] and [42].

Fig. 2

The variations of axial grid spacing with x. The inset shows the ratio Δ/η inside the pipe fragment

The LES was carried out with the TU Delft unstructured finite-volume computational code T-FlowS. The filtered Navier-Stokes and continuity equations for incompressible fluid are closed by the dynamic Smagorinsky subgrid-scale model. The diffusion and convection terms in the momentum equations are discretized by the second-order central-difference scheme, whereas the time-marching is performed using a fully-implicit three-level time scheme. The velocity and pressure are coupled with the SIMPLE algorithm.

Figure 3 gives an overview of the time-averaged field of the axial velocity and turbulent kinetic energy. Close to the pipe exit at x/D=−1 the profiles of U _x and k correspond to a fully developed pipe flow. Due to the shear close to the nozzle the turbulent kinetic energy rapidly grows between x/D=1−3 but then begins to decay. The velocity profile transforms to a self-similar Gaussian-shaped one by x/D=10. The k field distinctly shows the presence of a “preserving core” region which is similar to the potential core for jets with the turbulent inlet [21]. This region spans until the point where the mixing layers merge on the axis near x/D=4.

Fig. 3

Fields of the time-averaged axial velocity U _x and turbulent kinetic energy k. The azimuthally averaged radial profiles (solid black-in-white lines) of U _x and k are shown at selected axial positions (dashed lines). The axes are not to scale

According to the conservation law of the axial momentum, the time-averaged velocity along the centreline at some distance becomes inversely proportional to the axial coordinate. At the same time, the width of the jet grows linearly with the distance downstream. These dependencies are expressed as follows:

$$\begin{array}{@{}rcl@{}} && \frac{{U_{c}^{e}}}{U_{c}} = \frac{1}{K} \frac{x - x_{0}}{D}, \;\;\;\;\;\;\; \frac{r_{1/2}}{D} = K_{r} \frac{x - x_{0r}}{D}. \end{array} $$

(1)

where U _c = U _x (x,r=0) is the time-averaged axial velocity along the centreline, ${U_{c}^{e}}$ corresponds to U _x (x=0,r=0) and r _1/2 denotes the radius at which the velocity is half its maximum value. The parameter x ₀ represents the coordinate of the virtual origin of the jet, while x _0r is the so-called “geometrical” virtual origin [21]. Although in the present work we focus on the near field of the jet, it is instructive to calculate the self-similar parameters from the obtained data. Table 1 and Fig. 4 show the comparison of R e, K, x ₀ and K _r with other studies together with the variation of the centreline axial velocity and half-width of the jet downstream. We find good agreement for K and K _r with the data from the literature [14, 15, 21, 43], while the negative value of the virtual origin is probably due to the considered short near-nozzle axial range.

Fig. 4

Left: The inverse time-averaged axial velocity along the centreline, U _c . Right: The half-width r _1/2 against x. Dashed lines correspond to the appropriate linear fit

Table 1 Comparison of self-similar characteristics with pipe jet experiments at various Reynolds numbers

Another lengthscale often used in the analysis of jets and mixing layers is the momentum thickness. The following definitions are used in the present study:

$$\begin{array}{@{}rcl@{}} && \theta_{co} = \int \frac{U_{x} - U_{co}}{U_{c} - U_{co}} \left( 1 - \frac{U_{x} - U_{co}}{U_{c} - U_{co}} \right) dr, \end{array} $$

(2)

$$\begin{array}{@{}rcl@{}} && \theta^{*}_{co} = \frac{2}{D}\int \frac{U_{x} - U_{co}}{U_{c} - U_{co}} \left( 1 - \frac{U_{x} - U_{co}}{U_{c} - U_{co}} \right) r dr, \end{array} $$

(3)

where the asterix denotes the definition accounting for cylindrical geometry while the subscript ‘co’ indicates that the non-zero co-flow is taken into account. Note that inside the pipe 𝜃 = 𝜃 _{c o} and $\theta ^{*} = \theta ^{*}_{co}$ since U _{c o} =0. The inflow provides a relatively high momentum thickness corresponding to D/𝜃≈22.3 and D/𝜃 ^∗≈30.8. Figure 5 (left) shows the direct comparison of the inflow velocity profile of the present pipe jet simulation to ‘top-hat’ jets used by Kim and Choi [44]. The slope of the pipe jet axial velocity at the wall falls between the ‘top-hat’ inflow profiles with D/𝜃=80 and 120. Below we compare the pipe jet with the data for ‘top-hat’ jets with D/𝜃=80 at similar Reynolds numbers. The growth of 𝜃 _{c o} with x can be well approximated by a linear function, while $\theta ^{*}_{co}$ increases more rapidly. Up to x/D=2, $\theta ^{*}_{co}$ can be accurately represented by a parabola while further it seems to grow linearly.

Fig. 5

Left: The time-averaged inflow axial velocity profile from the present LES (solid line) against the profiles from LES of the ‘top-hat’ jet [44] (dashed lines). Note that the ‘top-hat’ profiles have also been normalized with the bulk velocity. Right: The momentum thickness calculated according to Eqs. 2 and 3. Thin dashed lines correspond to the appropriate linear fit

To validate the computation we compare the time-averaged axial velocity U _x , the root-mean-square (rms) axial and radial fluctuations normalized by U _b with DNS of Sandberg et al. [45] at a close Reynolds number and PIV experiments of Capone et al. [22] in a range of Reynolds numbers, Fig. 6. A comparison is shown in the near-nozzle region of few diameters (0≤x/D≤3) with DNS with a much stronger co-flow (U _{c o} >0.2U _b , M46-c1 case) compared to the present case with U _{c o} =0.04U _b affecting the statistics further downstream. Experiments and LES show good agreement for U _x . Note that the level of fluctuations u x′ is slightly higher in experiments compared to LES and DNS while $u^{\prime }_{r}$ is in excellent agreement. Higher level of $u^{\prime }_{x}$ may indicate that the pipe flow in experiments does not completely correspond to the fully developed one. The LES computations [44] of a ‘top-hat’ jet with D/𝜃=80 for two Reynolds numbers are also shown for comparison. Despite the different incoming velocity profile, the decay of the axial velocity has a similar slope for R e=8750 to the present LES.

Fig. 6

Profiles of the mean axial velocity U _x , fluctuations $u^{\prime }_{x}$ and $u^{\prime }_{r}$ along the centreline against the DNS with co-flow (Sandberg et al. [45]) and PIV experiments (Capone et al. [22]). Note that ‘top-hat’ LES results [44] for the jet with D/𝜃=80 and R e=3150 (brown squares) and R e=8750 (violet triangles) are also shown for comparison

3 Description of Tools

3.1 Linear stability analysis

With a focus on coherent motion, we start from the triple decomposition of the velocity field

$$ \mathbf{u} = \mathbf{U} + \widetilde{\mathbf{u}} + \mathbf{u}^{\prime\prime}, $$

(4)

where u, U are the instanteneous and time-averaged velocity and $\widetilde {\mathbf {u}}$, u ^″ represent periodic (coherent) and stochastic fluctuating (turbulent) part, respectively. Note that velocity fluctuations in the traditional Reynolds decomposition are $\mathbf {u^{\prime }} = \widetilde {\mathbf {u}} +\mathbf {u^{\prime \prime }}$. We are interested in the govering equation for the coherent part of the velocity field. After the substitution of the triple decomposition into the Navier-Stokes equations and further manipulations, we arrive to the following equation

$$ \frac{{\partial} \widetilde{\mathbf{u}}}{{\partial} t} + \widetilde{\mathbf{u}} \cdot \mathbf{\nabla} \mathbf{U} + \mathbf{U} \cdot \mathbf{\nabla} \widetilde{\mathbf{u}} = -\frac{1}{\rho} \mathbf{\nabla} \widetilde{p} + \frac{1}{Re} \mathbf{\nabla}^{2} \widetilde{\mathbf{u}} - \mathbf{\nabla} \cdot \mathbf{\tau}, \;\;\;\;\;\; \mathbf{\nabla} \widetilde{\mathbf{u}} = 0, $$

(5)

where the constituents of the stress tensor $\tau = \widetilde {\mathbf {u}} \widetilde {\mathbf {u}} - \overline { \widetilde {\mathbf {u}} \widetilde {\mathbf {u}}} + \widetilde {\mathbf {u}^{\prime \prime } \mathbf {u}^{\prime \prime }}$ represent different interactions of the mean, coherent and turbulent fields. While the coherent contribution in τ is neglected due to the assumption of the small-amplitude perturbations, the stochastic stresses are expressed using the linear eddy viscosity model [46]

$$ \tau_{ij} = \nu_{t} \left( \frac{{\partial} \widetilde{u}_{i}}{{\partial} x_{j}} + \frac{{\partial} \widetilde{u}_{j}}{{\partial} x_{i}} \right), \;\;\;\; \nu_{t} = - \overline{u_{r}^{\prime} u_{x}^{\prime}} / \left( \frac{{\partial} U_{x}}{{\partial} r} + \frac{{\partial} U_{r}}{{\partial} x} \right), $$

(6)

resulting in linear differential equations governing the coherent part of fluctuations of velocity and pressure, $\widetilde {\mathbf {u}}$ and $\widetilde {p}$. The local linear stability framework is used to supplement the analysis of the numerical data to provide information (frequency and wavelength) of the most unstable modes. The mean velocity field U = U _x e _x is assumed to be unidirectional with U _x = U _x (r) profile taken from LES at a given axial position corresponding to the quasi-parallel approach. The coherent velocity field is decomposed into the normal modes with respect to axial and azimuthal homogeneous directions

$$ \widetilde{\mathbf{u}}(r, \phi, x, t) = \hat{\mathbf{u}}(r) e^{i (k x + m \phi - \omega t)} + c.c., \;\;\;\; \widetilde{p}(r, \phi, x, t) = \hat{q}(r) e^{i (k x + m \phi - \omega t)} + c.c. $$

(7)

Here k = k _{r e} + i k _{i m} denotes the complex streamwise wavenumber, ω the angular frequency and m the real azimuthal wavenumber. The solution of Eqs. 5–7 with the appropriate boundary conditions provides the dispersion relation k = k(ω).

Within the normal mode ansatz we obtain a system of linear ordinary differential equations for $\hat {\mathbf {u}}$ and $\hat {q}$ depending only on r. The spatial stability analysis approach gives the complex-valued k, determined for a certain real-valued ω. A disturbance is exponentially amplified at a given ω provided k _{i m} (ω)<0. A well-established Chebyshev pseudospectral collocation technique is used to discretize and solve the obtained eigenvalue problem [25, 47]. The performance of the algorithm is verified against the data of other authors (see Table 2).

Table 2 Comparison of the eigenvalue spectrum and convergence for spatial stability of the Poiseuille pipe flow with R e=10000 and ω=0.5. N _{c o l} is the number of Chebyshev terms used to represent the flow variables

3.2 Fourier analysis and proper orthogonal decomposition

As in the local linear stability analysis described above for a fixed axial location we perform the Fourier transform with respect to azimuthal angle ϕ of the instanteneous velocity field u(r,ϕ,t) in r−ϕ plane. The LES snapshots of u at some x position are decomposed into complex Fourier coefficients u(r,m,t) yielding

$$ \mathbf{u}(r, m, t) = \frac{1}{2 \pi} {\int}_{0}^{2\pi} \mathbf{u}(r, \phi, t) e^{i m \phi} d\phi. $$

(8)

To get the spectral characteristics of the flow one proceeds with the analysis in the wavenumber-frequency space. The corresponding complex-valued Fourier coefficients are

$$ \mathbf{u}(r, m, f) = \frac{1}{T} {{\int}_{0}^{T}} \mathbf{u}(r, m, t) e^{-2 \pi f t} dt. $$

(9)

The power spectral density E _m =|u(r,m,f)|² shows the amount of turbulent kinetic energy in a single azimuthal mode [48].

We further apply POD for each azimuthal wavenumber m to an ensemble of N instantaneous ϕ-Fourier-decomposed fields $[\mathbf {u}^{m}_{1}, \mathbf {u}^{m}_{2}, ..., \mathbf {u}^{m}_{N}]$ corresponding to time instants t = t ₁,...,t _N :

$$ \mathbf{u}^{m}_{i}(r) = \mathbf{u} (r, m, t_{i}) = \sum\limits_{q=1}^{N} {a^{m}_{q}}(t_{i}) \lambda^{(m)}_{q} \mathbf{V}^{m}_{q}(r), $$

(10)

where $\mathbf {V}^{m}_{q}(r)$ and ${a^{m}_{q}}(t)$ are the non-dimensional complex-valued spatial eigenfunctions and time coefficients (temporal amplitudes) satisfying

$$ \frac{1}{D^{2}} {\int}_{0}^{\infty} \mathbf{V}^{m}_{i}(r) \mathbf{V}^{m}_{j}(r) r dr = \delta_{ij}, \;\;\;\;\;\; \frac{1}{N}\sum\limits_{n=1}^{N} {a^{m}_{i}}(t_{n}) {a^{m}_{j}}(t_{n}) = \delta_{ij}, $$

(11)

$\lambda ^{(m)}_{q}$ are the real eigenvalues and δ _{i j} is the Kronecker delta. The functions $\mathbf {V}^{m}_{q}(r)$ together with ${a^{m}_{q}}(t)$ and $\lambda ^{(m)}_{q}$ are to be determined from a variational problem so that the basis maximizes the mean-square projection on the velocity vector. The solution of the Fredholm integral equation of the second kind provides the optimal basis of this variational problem, where the kernel of the integral operator is a two-point cross-correlation function between the instantaneous velocity fields $B_{ij}(r, r^{\prime },m) = \sqrt {r} \; \mathbf {u}_{i}^{m}(r) \mathbf {u}_{j}^{m}(r^{\prime }) \sqrt {r^{\prime }}$. Note that each velocity component is multiplied by $\sqrt {r}$ to make the kernel Hermitian symmetric [28]. To reduce the computational cost of the algorithm, we use Singular Value Decomposition [49] of a set of N Fourier-decomposed velocity vectors $[\mathbf {u}^{m}_{1}, \mathbf {u}^{m}_{2}, ..., \mathbf {u}^{m}_{N}]$ multiplied by $\sqrt {r}$ used to obtain the eigenvalues $\lambda ^{(m)}_{q}$, basis functions $\mathbf {V}^{m}_{q}$ and temporal amplitudes ${a^{m}_{q}}$.

4 Results

4.1 General observations

To highlight the difference between the ‘top-hat’ jet produced by a contracting nozzle and a fully developed pipe jet we again compare the results with Kim and Choi [44]. They presented the axial velocity fluctuations for a particular azimuthal wavenumber m integrated over a cross-section

$$ E_{xx}^{m} = \int \overline{(u^{\prime}_{x} u^{\prime}_{x})}^{\; m} r dr $$

(12)

as a function of the axial station. Figure 7 shows $E_{xx}^{m}$ for m=0−3 from both computations. The quasi-laminar ‘top-hat’ inflow with the chosen flow parameters provides the development of vortex rings at x/D=2−4 with subsequent turbulization. The growth rate of $E_{xx}^{m=0}$ is exponential for the inflow produced by the contraction, while other modes also experience rapid increase at the same axial distance. On the contrary, the fully developed inflow produces linear growth of energy which is weak compared to the burst-like increase for the laminar inflow. The maximum amplitudes of the ‘laminar’ profiles of $E_{xx}^{m}$ are 2−3 times higher than for the fully developed pipe jet. At the same time, the values at x/D=15 from Kim and Choi are comparable with that from the present LES at x/D=10.

Fig. 7

The integrated energy of axial velocity fluctuations $E_{xx}^{m}$ along the axial direction. Dashed lines show the data of [44] for D/𝜃=80

The turbulent kinetic energy spectrum and the peak at S t=0.14 observed in Fig. 1, which motivated the present study is further analyzed for different velocity components. According to Fig. 8, the axial velocity component is responsible for low-frequency energetic motion. It turns out that this is a footprint of the propagating helical waves which are present in the pipe flow, as was shown by Duggleby et al. [23]. Indeed, in Fig. 8 we see the same peak at S t=0.14 in the power spectrum of the axial velocity fluctuations denoted by a blue line in the periodic pipe flow (or at x/D=−1). Further below we investigate this issue. At the same time, the tangential velocity fluctuations do not have a pronounced spectral peak at high frequencies, while radial fluctuations possess a bump at S t≈0.78 at the considered axial station. As discussed below, this frequency is well-represented by a neutral wave solution (with k _{i m} =0) in the framework of the linear stability theory.

Fig. 8

Blue lines show the time power spectrum at x/D=−1 and r/D=0.46 for each velocity component averaged over azimuthal angle, while black lines correspond to x/D=1 and r/D=0.5. Red lines denote the moving average

As mentioned above, the distribution of the turbulent kinetic energy inside the pipe flow strongly affects the spectral characteristics in the near field of the jet. Figure 9 depicts the distribution of the turbulent kinetic energy contained in individual m obtained from the pipe flow precursor simulation. While in the centre of the pipe the energy is exclusively stored in m=0 (fluctuations of the axial velocity) and m=1 (radial and tangential velocity fluctuations), a very broad range of m contributes to the near-wall peak. Note that the main contribution comes from m=9 corresponding to the statistically average spanwise distance between the near-wall streaky structures at this Reynolds number. The ‘slice’ POD agrees well with the conclusions of Duggleby et al. [23] who performed a three-dimensional analysis and revealed the dynamical significance of the propagating helical waves. The most energetic POD mode obtained in [23] with m=5 at R e≈4300 rotates with the frequency of S t≈0.165 confirming the above discussed peak in the power spectrum.¹ For the pipe flow we obtain a wide range of POD modes of comparable energy. The eigenvalue (namely, λ ²/2) is connected to the turbulent kinetic energy integrated over the considered area. The first POD mode (q=1) with m=3 contains the most energy, i.e. 2.47 percent from the total energy, while q=1 with m=0 is ranked 14th with 1.35 percent. The spatial spotty distribution of the axial velocity for various modes is also shown in Fig. 9.

Fig. 9

Fourier and POD analysis of the periodic pipe flow. Left: Radial profiles of the turbulent kinetic energy for different azimuthal Fourier mode m. Right: Axial velocity corresponding to the first POD mode (q=1) for various m. Dashed lines mark zero axial velocity, while red/blue colors denote positive/negative values

4.2 Identification of helical waves

As a first step we track the evolution of the power spectra along the axial coordinate for various m starting from the fully developed pipe flow, see Eq. 9. The velocity field decomposed into helical waves of the form e ^{i(mϕ−2πft)} shows the azimuthal modes rotating with the constant angular velocity, Oberleithner et al. [48]. Figure 10 presents E _m for several axial locations calculated in the shear layer. The dynamics inside the pipe is mainly concentrated around the frequency S t≈0.14 with a mild scatter. The modes with m=3,4,5,6,8 can be easily identified. Another group of high wavenumber modes (m≥7) focuses around zero frequency corresponding to the so-called ‘non-propagating’ sub-class employed by Duggleby et al. [23]. These modes resemble the features of the near-wall streaky structures existing in the wall-bounded turbulent flows. The same trends are observed at x/D=1 with additional energy present in the high-frequency range due to the shear layer instabilities. Further downstream the turbulent kinetic energy is transferred to low m and low frequencies. At x/D=6 with S t=0.14 being the highest with m=1,2,3 contributing the most, there are several other low-frequency peaks.

Fig. 10

The time power spectrum for various azimuthal modes at several axial locations. For x/D=−1 the spectrum is calculated at r/D=0.46 while for other stations we used r/D=0.5 position

Further we perform POD at 32 axial locations starting from x/D=0 with the last position at x/D=10. The spatial step close to the nozzle is Δx/D=0.25, while at the end of the domain it is fixed to Δx/D=0.5. Figure 11 (left) shows the turbulent kinetic energy of the first POD mode for different m against the axial position. Along 0≤x/D≤10 there is a competition between the eigenvalues for different m. The most energetic modes correspond to low wavenumbers m=1−5. The distribution of the relative turbulent kinetic energy between various (m,q) modes at x/D=6 can be observed in Fig. 11 (right). The cumulative energy of (m=0−7,q=1) modes contributes around 25 % of the total energy. If the modes are ranked among all m and q then the first 15 modes carry around 40 % of energy, while 40 and 120 modes contribute around 60 % and 80 %, respectively. It is interesting to compare the distribution of energy between the pipe- and ‘top-hat’ jets. For high Reynolds numbers ‘top-hat’ jet Jung et al. [29] calculated the fraction of energy stored in the first POD modes summed among all m. At x/D=6 in the first (q=1), the first two (q=1,2) and the first three (q=1−3) modes contribute around 66 %, 83 % and 92 %, respectively, while in our case it is 30 %, 47 % and 57 %. Further in Section 4.4 we employ POD to analyze dynamical features investigating temporal amplitudes of the most energetic modes.

Fig. 11

Left: The energy in the first POD mode $(\lambda ^{(m)}_{q=1})^{2}/2$ against x/D. Right: The columns show the energy (normalized with the total value of the turbulent kinetic energy) of the first 5 POD modes q and first 10 azimuthal modes m at x/D=6. The dashed black line shows the cumulative energy content of first 5 POD modes (summation of columns from left to right). The solid blue line shows the cumulative energy of the ranked among all m and q POD modes. Note that both cumulative curves are scaled down by a factor of 10

4.3 Local linear stability analysis of the mean flow

Although above we show that the spectral characteristics of a wall-bounded pipe flow determines the dynamical features of the jet, it is instructive to compare results with the linear stability analysis (LSA). The local LSA relies on the mean velocity profiles at a fixed axial station and eddy-viscosity concept to account for the background turbulence where coherent fluctuations may develop. Figures 12 and 13 show the growth rate −k _{i m} against the frequency f = ω/(2π) at x/D=1 and 10, respectively. We perform two sets of calculations for comparison. The dashed lines indicate results using the laminar model velocity profiles (see Table 3), whereas the solid lines correspond to the LES velocity profiles with the turbulent viscosity taken into account. At x/D=1 the velocity gradient in shear layers is relatively steep giving rise to unstable modes with m=0 and 1.

Fig. 12

The growth rate −k _{i m} calculated with linear stability analysis against the non-dimensional frequency S t at x/D=1. The upper inset shows the spectrum E at r/D=0.5 from LES. The lower inset depicts the LES and model velocity profiles used for stability analysis with the profile of the turbulent viscosity

Fig. 13

The same as in Fig. 12 at x/D=10

Table 3 Two profiles common in the literature [51, 52] are used to obtain the reference dispersion curves k = k(ω)

The frequency corresponding to the maximum spatial growth rate (S t≈0.39 and 0.47) is not observed in the turbulent kinetic energy spectrum while the frequency of the neutral eigensolution (with −k _{i m} =0) describes well the Kelvin-Helmoltz instability. At x/D=1 the power spectrum of the radial velocity component gives a peak at S t≈0.78 (see Fig. 8), while LSA provides the value of S t≈0.76 for m=0. This is in agreement with Petersen and Samet [50] who showed that the spectral peak value of a ‘top-hat’ jet agrees well with the one corresponding to the neutral growth rate solution at some distance downstream. At the pipe exit the sinusoidal mode m=1 also provides unstable high-frequency solutions close to those for m=0. At the same time, the low-frequency peak is around S t≈0.14 and is not captured by the linear stability analysis confirming that it is not connected to the Kelvin-Helmholtz instability but is a pipe flow legacy. At x/D=10 only m=1 remains unstable with the peak frequency S t≈0.019 (see Fig. 13). Again the neutral mode appearing at S t≈0.041 is in excellent agreement with the energy spectrum.

Figure 14 shows the variations of spectral peaks obtained with LSA and LES. The Kelvin-Helmholtz peak (orange dashed line) derived from the radial velocity power spectrum can be tracked for x/D≤2 with the frequency value well approximated by a linear fit S t=1.25−0.4x/D. This peak is closely described by LSA up to x/D≤1. After x/D=1 the cut-off of the axisymmetric instabilities takes place due to the spreading of the velocity profile. No unstable modes for m=0 can be found with LSA for x/D≥1.6. The frequencies of the maximum growth rate solutions and neutral waves are all presented in Fig. 14 following a power-law decrease with the axial distance. A blue dashed line denotes the peak S t≈0.14 tracable along 0≤x/D≤10. The shaded area schematically presents other low-frequency motion/peaks (see, for example, inset in Fig. 13).

Fig. 14

The evolution of spectral peaks from the LSA results and LES power spectra against the axial position

4.4 Propagating helical waves: POD analysis

The above analysis is supplemented with direct observations from POD. To be able to separate helical patterns rotating in opposite directions, we follow the approach of Davoust et al. [53] (see also [23, 54–56] for a similar analysis in the channel and pipe flows). Recently, they successfully described flapping and helical motion of the ‘top-hat’ jet at x/D=3 based on the information about the temporal amplitudes. We analyse the complex-valued temporal amplitudes ${a^{m}_{q}}(t)$ starting from the following representation:

$$ a(t) = \beta(t) e^{2 \pi i \gamma(t)}, $$

(13)

where β and γ are the time sequences of N real numbers. Particular combinations of β and γ correspond to helical and flapping motion [53]. The ideal helix represents a rotation of the jet core with constant angular velocity at some fixed distance from the x-axis. Thus, one expects β to be constant and γ to grow in time linearly. In terms of two azimuthal waves with opposite m values this means that one mode is present while the other is not. For the flapping motion both modes are present with the same rotation speed but opposite directions. This results in a more complicated behaviour of β and γ.

Figure 15 shows γ(t) during 150 time units for the first several q and m. A striking feature of γ is that it contains very long time intervals over which it varies linearly. As pointed out above, this means that the corresponding spatial mode rotates around the jet core with some precession frequency. This fact was first observed by Sirovich and co-authors in the 3D POD results of the channel flow DNS database [54] and recently in a pipe flow [23]. The linear variation of the phase in time led to coining the term ‘propagating wave’. We also show the slope of γ(t) for some characteristic regions (dashed lines). This slope is in fact the non-dimensional angular velocity Ω of the mode rotation. For example, three typical regions are shown in Fig. 15 for m=1 with Ω≈−0.87, −0.14 and 0.08. For Ω≈−0.14 and γ=Ωt the corresponding POD mode turns around in seven time units according to Eq. 13. These curves of γ(t) for m=1 show changes of rotation direction within short time intervals (say, t<25 with the typical value of t=5−10), while in a long run the average rotation is non-zero. For m=2 the slope of γ is bounded between −0.167 and 0.14, while Ω≈0.08 is visible in the plot of m=2, 3 and 4. Similar patterns can be recognised for higher wavenumbers. Note that one of the insets in Fig. 15 (m=4) shows the time power spectrum at x/D=6 of the turbulent kinetic energy calculated in the shear layer. We observe two peaks in the low-frequency range, i.e. S t=0.08 and 0.14, which are explained by typical slopes of γ(t) corresponding to the low average |Ω|. However, in Fig. 15 we also observe a quite common steep slope with |Ω|∼1.0. We interpret it as a superposition of “fast” and “slow” rotation. While the “fast” rotation appears stochastic with short time scales, the “slow” rotation can last for up to a hundred of non-dimensional time units. Although we have considered in detail only the axial position x/D=6, the mentioned features can be found along the whole considered near-nozzle area. Coming back to the Fourier analysis summarized in Fig. 10 and LSA shown in Fig. 14 the results are in line with the POD. The Spectral Fourier analysis shows noticeable peaks at S t≈0.04, 0.08 and 0.14 for x/D=6 (see Fig. 10). All three slopes (or Ω) are readily observed in the time series of the phase γ. Furthermore, at this axial distance LSA for m=1 shows the maximum growth rate at S t≈0.037, while neutral mode solution corresponds to S t≈0.09. These two values bound two peaks at S t≈0.04 and 0.08 observed in the spectral Fourier analysis.

Fig. 15

The time history of the phase γ(t) for different m and q at x/D=6. The inset in m=3 plot shows the zoomed area indicating sufficient time resolution. The inset in m=4 figure displays the time power spectrum of the turbulent kinetic energy at x/D=6 and r/D=0.5

Figure 16 shows some additional observations during t∈[49;52.5] for m=1 and q=4. This region, as mentioned above, has a slope −0.87 pointing at a relatively fast rotation of a POD structure. The left graph demonstrates a sample of the trajectory of $a^{m = 1}_{q = 4}(t)$ in a complex plane. A typical pattern here is an ellipse due to oscillations of β(t) around the mean value β=0.9. We employ Taylor’s hypothesis to reconstruct a three-dimensional structure. The convective velocity is adopted as U _{c o n v} = U _c /2, where U _c =1.01U _b is the local mean centreline axial velocity at x/D=6. Figure 16 on the right shows an isosurface of the Q-criterium for the velocity field, which is the sum of the mean field and q=4, m=1 POD mode. Apparent helical motion is explicitly detected. Although this mode represents only a relatively small fraction of the total turbulent kinetic energy (1.26 %), propagating wave motion appears to be a typical building block among POD modes according to Fig. 15. A preliminary three-dimensional POD analysis fully supports the presented results and conclusions, thus, giving the confidence that helical structures are indeed present and are not the consequence of the Taylor’s hypothesis.

Fig. 16

Left: Sample of a(t) in the complex plane corresponding to q=4, m=1 at x/D=6 and the time interval t∈[49;52.5], where Ω≈−0.87 as in Fig. 15. The trajectory is colored with black, blue and red indicating (almost) full turnovers in the form of an ellipse. The inset shows β(t). Right: The isosurface of Q=0.0012 based on the sum of q=4, m=1 POD mode and mean velocity fields. Three-dimensional information is recovered with the use of Taylor’s hypothesis in the same time interval t∈[49;52.5] (see the text for details). The jet flows upwards

Further we inspect if separate POD modes resemble the actual flow features. Figure 17 shows the velocity magnitude time sequence corresponding to the sum of a number of POD modes. Every row in Fig. 17 can be compared with the instanteneous velocity field shown at the bottom. We start with the most energetic mode m=1 and q=1 with 5.77 % of the total turbulent kinetic energy. Only one mode traces the local velocity maximum but hardly represents the complex dynamics of the whole field. However, the sum of two modes with m=1 and q=1,2 resembles the flow more accurately (second row in Fig. 17). Obviously, the larger the number of modes in the sum, the closer we approach the instanteneous field. To compare we sum up 12, 18, 48 and 930 modes with the latter corresponding to the instanteneous field. The important conclusion here is that few modes are needed to trace the dynamics of the flow with even one mode sufficient to track the main features.

Fig. 17

A time sequence of the velocity magnitude field reproduced using different number of POD modes at x/D=6. Six rows correspond to 1, 2, 12, 18, 48 and 930 modes, respectively. For each sum the resolved part of the total turbulent kinetic energy (in %) is indicated on the left

5 Conclusions

We performed LES, linear stability analysis and ‘slice’ POD to get an insight into the coherent motion in the near-nozzle area (x/D≤10) of a canonical pipe jet at R e=5300. The main conclusions can be summarized as follows.

• The near-wall streaky structures supplied by the pipe and observed only close to the pipe exit (“nozzle”) suppress the growth of Kelvin-Helmholtz vortex rings that characterize and dominate in ‘top-hat’ jets. In contrast to the exponential growth of the turbulent kinetic energy in the latter, the pipe jet features a linear growth rate for low azimuthal wavenumbers, which are found to be the most energetic (m=1−5).

• A low-frequency peak (S t≤0.14) detected in the time power spectrum corresponds to the propagating helical waves which are present in the pipe flow. The linear stability analysis confirmed that this motion is not connected to the Kelvin-Helmholtz instability.

• The analysis of the dynamic features based on the temporal amplitudes obtained from POD identifies clearly two types of the dominant helical structures: the “fast” and “slow” rotations. They differ in the characteristic time scales of the process with t<25 (or, more pronounced, for t=5−10) for the former and with up to t=150 (or more) for the latter. The “slow” modes are due to the coherent helical structures (propagating waves) which are long-lived and have low angular velocities of rotation around the axis of symmetry while the “fast” modes correspond to the background stochastic turbulence