Mixing and entrainment in the near field of turbulent round jets

Abstract

Results from experiments on the near field of a turbulent circular pipe jet at Reynolds numbers between 3,000 and 30,000 are compared to analytical models derived from assuming a perfect balance between axial and radial flow rates. This assumption is proved to be valid on average by taking measurements on both longitudinal and transverse planes and by direct evaluation of axial and radial flow rates. The experimental campaign is carried out by performing measurements by means of high-speed particle image velocimetry. The analytical models describe approximately the behavior of measured average radial velocities and entrainment rates with indications of a significant Reynolds number dependence which disappears for values larger than 10,000. This behavior is also confirmed by velocity rms and integral scale results.

1 Introduction and motivation

Jet flows have been widely considered in turbulence research due to their relatively simple geometry coupled with the huge variety of large- and small-scale phenomena involved. Restricting the investigations to relatively low Reynolds number conditions (less than 50,000), as those considered in this paper, jets are largely employed in engineering devices for mixing, combustion, propulsion, biomedical, ventilation and energy production purposes. One of the main directions of investigation was to find asymptotic behaviors which could enable a description of the flow field as much as possible independent of the details of each experiment (Xu and Antonia 2002; Hussein et al. 1994).

In such a description, several geometrical, kinematic and dynamical parameters are involved. Restricting the analysis to single-phase, low-Mach number, isothermal steady jets, it is possible to summarize these parameters under the frameworks inlet conditions (IC), boundary conditions (BC) and Reynolds number (based on pipe diameter and exit velocity, Re). In the moderate-far jet field (x/D > 15, where x is the streamwise coordinate starting from the jet exit and D is the jet diameter) and for rather high Reynolds numbers (Re > 50,000), the hypothesis of self-similarity (self-preservation) holds (Malmstrom et al. 1997; Hussein et al. 1994; Wygnanski and Fiedler 1969). Prediction of the jet centerline velocity self-similar streamwise decay is given by Pope (2000)

$$ \frac{U_0}{U_x(x)} = \frac{1}{K_u}\left[\frac{(x-x_p)}{D}\right] $$

(1)

where U ₀ is the jet exit velocity, U _x (x) is the local centerline axial velocity and x _p is the so-called virtual origin of the jet. Similarly, the streamwise behavior of the jet half-width $R_\frac{1}{2}$ (where the axial velocity is one half that at the centerline) is

$$ \frac{R_\frac{1}{2}(x)}{D} = K_d\left[\frac{(x-x_p)}{D}\right] $$

(2)

The values of the constants K _u and K _d in (1) and (2) have been examined by several authors, and typical values are 6 and 0.1, respectively (Malmstrom et al. 1997). Simultaneously, along the radial direction, r, the axial velocity exhibits a Gaussian behavior (Malmstrom et al. 1997)

$$ U_x(x,r) = U_x(x){\text {e}}^{-\eta^2} $$

(3)

where η = K _u r/(x − x _p ) is the radial rescaled coordinate. The self-similar analysis can be further extended to turbulent Reynolds stresses along axial and radial directions (Kuang et al. 2001). It is rather established that (1), (2), (3) are almost independent on IC, BC and Reynolds number, providing the conditions of far field (x/D > 15) and Re > 50,000 to hold. It is worth pointing out that these conditions correspond to those required for establishing local isotropy of the turbulent flow field. However, in many engineering applications, the interest is focused onto the jet near field and to regimes with Re < 50,000, so that previous issues regarding asymptotic behavior rise up again. For example, there were robust indications on a linear dependence of K _u on Reynolds number, for Re < 50,000 (Malmstrom et al. 1997), which could reflect the simultaneous reduced jet spread as a function of Reynolds number as shown in Hussein et al. (1994). The LES investigations on the circular pipe jet made by Kim and Choi (2009) pointed out that the behavior of mean and rms axial velocity along the streamwise direction is strongly dependent on the combined effects of Reynolds number and IC (namely the momentum thickness at the jet outlet). This has been derived also by Bogey and Bailly (2009) and is in agreement with early observations by Zaman and Hussain (1981) and Crow and Champagne (1971). Such a variation was not observed by Fellouah and Pollard (2009) on a contraction jet at Reynolds numbers between 6,000 and 100,000. There is also a certain degree of variation due to the BC, specifically if the jet originates from a pipe, a contraction or an orifice (Xu and Antonia 2002; Quinn 2006, 2007; Mi et al. 2007; Deo et al. 2007a, b; Romano 2002). It is thus desirable to separate the contribution of the previous effects to establish specifically if there is a Reynolds number dependence. In particular, the dependence on Reynolds number should be considered within the entire picture of jet flow behavior along the streamwise and orthogonal directions, being the phenomena under observation fully three-dimensional. Indeed, this point is connected to the subtle argument underlying the self-similarity hypothesis, that is, that the flow was described by a single length (and velocity) scale (Burattini et al. 2005). However, if IC, BC and Reynolds number influenced self-similarity, it should be expected that this will not be the case and the number of relevant scales would increase. Thus, it is rather important to establish the effect of IC, BC and Re on the relation between longitudinal (axial) and transverse (radial) phenomena.

2 Relations between axial and radial flows

In the case of constant density jets, it is useful to start from the definitions of axial and radial volumetric flow rate, respectively Q _a and Q _r, and relating them to the entrainment rate as in Wygnanski and Fiedler (1969), Crow and Champagne (1971) and Liepmann and Gharib (1992). The mass balance on the differential control volume shown in Fig. 1 can be written as

$$ \frac{{\partial Q_{{\text{a}}} }}{{\partial x}}{\text{d}}x = - {\text{d}}Q_{{\text{r}}} (x,R), $$

(4)

thus, it is possible to write

$$ Q_{\hbox{a}}(x + {\hbox{d}}x,R) - Q_{\hbox{a}}(x,R) = - {\hbox{d}}Q_{\hbox{r}}(x,R) $$

(5)

Fig. 1

Schematic of volumetric flow rate balance

Therefore, using the axial and radial volumetric flow rates expressions

$$ Q_{\hbox{a}}(x,R) = \int\limits_{0}^{2\pi}\int\limits_{0}^{R}U_x(x,r,\theta) r {\hbox{d}}r {\hbox{d}}\theta $$

(6)

$$ {\hbox{d}}Q_{\hbox{r}}(x,R)=\left(\int\limits_{0}^{2\pi} U_{\hbox{r}}(x,R,\theta) R {\hbox{d}}\theta\right){\hbox {d}}x $$

(7)

the following descends from relation (5).

$$ \frac{\hbox{d}}{{\hbox{d}}x}\int\limits_{0}^{2\pi}\int\limits_{0}^{R}U_x(x,r,\theta) r {\hbox{d}}r {\hbox{d}}\theta = - R \int\limits_{0}^{2\pi} U_{\hbox{r}}(x,R,\theta){\hbox{d}}\theta $$

(8)

where R is a generic radius over which integration is performed which could be also a function of the axial distance x,  U _r is the radial velocity component and θ is the azimuthal angle. This equation establishes a relationship between axial and radial velocities, at each downstream distance, as also a means to derive the entrainment rate (which is just the left-hand side of the equation) from radial velocity distribution along a circle centered on the jet axis. For large R (in comparison with local jet radius defined in 2), the integral will reach an asymptotic value (Liepmann and Gharib 1992), whereas for small R, the dependence on the radial coordinate will be outlined. In the following, the dependence on the azimuthal angle θ will be relaxed on the basis of the results presented in this paper, to focus the attention on axial and radial behaviors. Thus, we can insert in (8) the expression for the axial velocity component derived from combining (1) and (3), that is, we are considering the self-similar region, to obtain

$$ \frac{U_0D}{2K_u} \frac{\hbox{d}}{{\hbox{d}}x}[(x-x_p)(1-{\hbox{e}}^{-H^2})] = -RU_{\hbox {r}}(x,R) $$

(9)

where H = K _u R/(x − x _p ). Therefore,

$$ \frac{U_{\hbox {r}}(x,R)}{U_0} = - \frac{1}{2H(x-x_p)/D} \frac{\hbox{d}}{{\hbox{d}}x}[(x-x_p)(1-{\hbox{e}}^{-H^2})] $$

(10)

where the dependence of H(x) should be specified (through R(x)). If we assume that along the axial distance, the generic radius R scales as in (2), the quantity H is a constant along x and it is derived from (10) that

$$ \frac{U_{\hbox {r}}(x,R)}{U_0} = - \frac{1}{2(x-x_p)/D} \frac{(1-{\hbox{e}}^{-H^2})}{H}, $$

(11)

whereas without such an assumption the outcome is the following

$$ \frac{U_{\hbox {r}}(x,R)}{U_0} = - \frac{1}{2(x-x_p)/D} \frac{(1-{\hbox{e}}^{-H^2}(1+2H^2))}{H} $$

(12)

This is a well-defined behavior with negative values, that is, positive entrainment, along the axial distance (decreasing as 1/x) in both model equations. Considering relation (8), in the potential core, that is, with U _x ≈ U ₀ and R(x) equal to a constant (D/2), it descends that U _r(x,R) = 0 (no entrainment). Along the radial direction, the hypothesis on H to be independent of x or its relaxation leads to different behaviors up to H = 2.5. In particular, for H < 1.2, a positive radial velocity is predicted by Eq. (12) as opposed to (11) as shown in Fig. 2 which displays (11) and (12) versus H. Similarly, the behavior of axial and radial flow rates in the self-similar region can be derived from (5) and (6)

$$ \frac{Q_{\hbox {a}}(x,R)}{Q_0} = \frac{4}{K_u} \frac{(x-x_p)}{D} (1-{\hbox {e}}^{-H^2}) $$

(13)

$$ \frac{{\hbox {d}}Q_{\hbox {r}}(x,R)}{Q_0} = - \frac{4}{K_u} (1-{\hbox {e}}^{-H^2}) \frac{{\hbox {d}}x}{D} $$

(14)

the latter taking the following form in case no assumption is made about R scaling

$$ \frac{{\hbox {d}}Q_{\hbox {r}}(x,R)}{Q_0} = - \frac{4}{K_u} (1-{\hbox {e}}^{-H^2}(1+2H^2)) \frac{{\hbox {d}}x}{D} $$

(15)

where Q ₀ = π D ² U ₀/4 is the flow rate at the jet nozzle. Along the streamwise direction x, from (13), the well-known linear increase in the axial flow rate can be derived. On the other hand, the radial flow rate from being zero at the nozzle attains a negative constant value for increasing axial distance. In the potential core, from (6), (7) and (8), the initial values of the flow rates are Q _a = Q ₀ and Q _r = 0. The behavior along the radial direction is much more interesting, and it is shown in arbitrary units in Fig. 2 as a function of H (which depends on both the radial and axial coordinates) for model Eqs. (11), (14) (hereafter equations A) and (12), (15) (hereafter equations B). In this figure, the parameters K _u and x _p are taken, respectively, equal to 6 and 0 as in Malmstrom et al. (1997) for similar IC and a Reynolds number equal to 42,000. The entrainment rate (dQ _r(x, R)/dx) starts from zero for H = 0 and attains an asymptotic negative value for both models A and B (in arbitrary units equal to −1). For intermediate values of H, a region of negative entrainment is present in model B, as for the radial velocity, ending at nearly H = 1.2. This behavior is the same for the axial flow rate with opposite sign.

Fig. 2

Radial velocity and entrainment rate model equations versus H = K _u R/(x − x _p ) given in arbitrary units

Starting from these models, the objective of the present paper is to highlight the connections between phenomena on longitudinal and transverse planes and their effects on mixing in the near field of a circular turbulent jet by focusing the attention on their dependence on Reynolds number. To this end, high-speed particle image velocimetry (PIV) measurements on longitudinal and transverse planes are performed. The relevant quantities for this analysis are axial, radial and azimuthal velocities and their spatial behaviors, the axial and radial flow rates, entrainment rate calculations and velocity fluctuations. In Sect. 4, the results obtained in longitudinal planes are carefully verified and compared to existing results to investigate whether the Reynolds number dependence could be connected to the mixing transition in jet flows, reported by Dimotakis (2000), Hill (1972) and Liepmann and Gharib (1992). For Reynolds numbers below 10,000, the cited authors report a rather strong dependence on Reynolds number which almost disappears for Re > 10,000. In Sect. 5, the results on cross-planes are examined to establish if the simplified models descending from far field behavior here presented are able to capture the essentials of the highly three-dimensional phenomena involved in turbulent jets near field. The possibility of acquiring data on both longitudinal and transverse planes is used in Sect. 6 to verify the correctness of the hypothesis of perfect balance between axial and radial flow rates which is the basis for the derived simplified models.

3 Experimental set-up, data acquisition and analysis

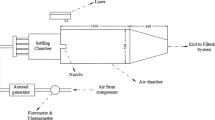
The water jet apparatus is detailed in Fig. 3; the facility consists of a long pipe with a round section of diameter D = 2.2 cm ending nearly 7 cm inside the observation tank. Being the pipe nozzle not flush with the tank’s wall, the flow is characterized by a free-slip condition (Romano 2002). The pipe is about 100D long, which is enough to observe fully developed turbulent flow conditions. The observation tank is approximately 40D high and wide, approximately 60D long and is made of glass for full optical access. Due to the limited size of the tank, the jet is considered as confined rather than free. It should be pointed out that this work focuses on the near field region of the jet where the cross-sectional area of the jet flow estimated as three times the jet half-width $R_\frac{1}{2}$ is below 2D and then small compared to the observation tank width whose effect on the flow is thus negligible (Cater and Soria 2002). The flow is driven by constant head provided by an elevated tank which is constantly supplied by a pump. At the bottom of the observation tank, opposite the pipe outlet, a discharge hole is located which was kept closed during measurements in order not to introduce disturbances in the flow.

Fig. 3

Experimental set-up

A high-speed PIV system is set up by means of a high-speed 8-bit BW, Photron APX CMOS camera with 1, 024 × 1, 024 pixels resolution at 1 KHz frame rate. The camera objective used for all the acquisitions was a Nikon F 50 mm focal length with maximum aperture of 1.2. Lighting is provided by a continuous Spectra Physics Ar-ion laser, 488–514 nm in wavelength, with a maximum power equal to 7 W, and flow seeding was attained with neutrally buoyant 10μm diameter hollow glass spheres (Dantec HGS-10).

Two types of image acquisition were carried out, based on the position of the camera. The first set of acquisitions, hereafter streamwise acquisitions, was performed by placing the camera laterally with respect to the main flow (denoted as Position 1 in Fig. 3), whereas the second image set, hereafter crosswise acquisitions, was obtained by setting the camera facing on transversal planes (labelled as Position 2 in Fig. 3).

Streamwise measurements covered an area equal to 6D from the nozzle exit, resulting in a pixel resolution of 0.12 mm corresponding to 0.006D. In order to collect data from the jet’s far field, complementary streamwise acquisitions were performed by composing a series of close-up measurements covering each approximately 3D and reaching 18D in the far field.

Transverse, crosswise acquisitions covered a squared area with side equal to 3D with a pixel spatial resolution of 0.12 mm. Measurements were carried out on planes lying within a range from 0.75 to 4.5D from nozzle exit.

In the experimental campaign, the jet Reynolds number based on the jet bulk velocity U ₀ ranged from 3,200 to 32,000 for both acquisition types. For each Reynolds number, typically 5,000 image pairs were collected. Streamwise measurements acquisition rate was 0.5 or 1 KHz corresponding to a δ _t between image pairs of, respectively, 0.002 and 0.001 s. Shutter time was set according to the flow speed in order to keep the maximum distance traveled by the seeding particles in a time frame well below 0.4 mm, corresponding to 3 pixels. In Table 1, acquisition parameters for streamwise measurements are reported. Crosswise measurements were carried out with an acquisition rate of 1 KHz. Laser sheet thickness was approximately 1 mm. A sample image for the streamwise acquisitions, obtained at Re = 10,000, is given in Fig. 4.

Table 1 Streamwise measurements acquisition parameters

Fig. 4

Sample streamwise PIV image at Re = 10,000. Pipe outlet is visible at the far left of the picture

A commercial PIV software, that is DaVis by LaVision Gmbh, has been employed for instantaneous vector field computation. The advanced image deformation multi-pass PIV cross-correlation algorithm with window offset, adaptive window deformation and Gaussian sub-pixel approximation is thoroughly described in Stanislas et al. (2008), together with features and overall performances. Minimum window size adopted was 32 × 32 and 16 × 16 pixels for streamwise and crosswise measurements, respectively. In both cases, overlap was set to 75 %, thus the spacing between velocity vectors was 8 and 4 pixel corresponding to a spatial velocity resolution of approximately 0.045D for all acquired data.

As described in detail in Falchi and Romano (2009), data collected via high-speed PIV systems have a high degree of correlation in time. Thus, the high temporal resolution of the present measurements (0.001 and 0.002 s, respectively; 0.04 and 0.08 integral time scales) allows to derive correlation functions. Integral time scale was derived by the integral length scales measured from correlation functions in the far field, that is, L = 10 mm, divided by the local mean velocity, about 0.4 m/s. At the same time, the typical acquisition time window for the streamwise case was 10 or 20 s, depending on the Reynolds number, and covered as much as 400 integral time scales so that reported data are also almost statistically independent to attain statistical convergence (Falchi and Romano 2009). An example of that is given in Fig. 5 where the relative difference to the final value for the mean and rms of streamwise velocity is given versus number of samples N. Data are taken at a point within the shear layer in the jet far field (x/D = 5) at a Reynolds number of 3,200 and 22,000 and show a good overall behavior in both cases, with both mean and rms within 15 % relative difference already for N > 1,000 and within 2 % for N = 4,000.

Fig. 5

Relative differences to final values for the first two statistical moments of the streamwise velocity components as a function of the number of samples. Data from upper shear layer (y/D = 0.5) in jet’s far field (x/D ≈ 5) at Re = 3,200 and Re = 22,000. Dashed lines indicate a relative difference of ±15 %

4 Results on streamwise decay and validation

In Fig. 6, the horizontal decay of average axial velocity is reported and compared to that provided by Amielh et al. (1996) obtained by means of laser Doppler anenometry at a Reynolds number of 22,000 and to low Reynolds number data from O’Neill et al. (2004). The present data covered a range of Reynolds number from 3,200 to 28,000 reaching up to x/D = 9. For the largest Reynolds number, data were collected by composing three slightly overlapping close-up runs, each of nearly 3D length, thus reaching as far as 9D and adding a further series in the jet’s far field up to approximately 18D. Data have been trimmed at the border of each imaged region to account for the intrinsic loss of accuracy of PIV algorithm at the boundaries. Capital and lowercase letters are used respectively for mean and fluctuating quantities and a ′ represents rms values.

Fig. 6

Average normalized axial velocity versus downstream distance in log scale for different Reynolds numbers compared to (x/D)⁻¹ profile, LDA data from Amielh et al. (1996) and low Reynolds number data from O’Neill et al. (2004)

For increasing Reynolds numbers, the decay of normalized streamwise velocity along the jet’s axis given in Fig. 6 approaches the one of LDA data and shows a satisfactory continuity between near and far field measurements. Such decay exhibits also the expected (x/D)⁻¹ behavior described in Liepmann and Gharib (1992). Measurements up to 6D for different Reynolds numbers show a similar decay profile which moves downstream as the Reynolds number increases, as displayed in figure inset. Comparison to the results reported in O’Neill et al. (2004), obtained at a Reynolds number of 1,030, confirms the reported trend of axial velocity decay even at low Reynolds numbers.

Normalized profiles of axial and vertical velocity rms versus downstream position are depicted, respectively, in Figs. 7 and 8, where a quite good agreement with LDA data is noticeable at high Reynolds numbers for the axial velocity. The decay of the profile is slightly above LDA data at 5–6D, where the shear layers begin to merge. At lower Reynolds numbers, this merging is attained farther from the nozzle, and an increase in rms is observed. In Fig. 9, normalized axial and vertical velocity rms values taken at x/D = 5 are shown as a function of Reynolds number. This position is approximately that of maximum rms as shown in Figs. 7 and 8. The observed decrease is in agreement with a −1/4th power of the Reynolds number, thus suggesting that the rms fluctuations scale as Re ^3/4.

Fig. 7

Rms of axial velocity, that is, at y/D = 0, versus downstream distance compared to LDA from Amielh et al. (1996)

Fig. 8

Rms of vertical velocity versus downstream distance at y/D = 0 compared to LDA from Amielh et al. (1996)

Fig. 9

Normalized rms of axial and vertical velocity versus Reynolds number at x/D = 5 compared to Re ^−1/4 slope

Present data are also validated with respect to radial velocity profile very close to the nozzle (x/D = 0.2). Comparison to LDA data and to empirical fully developed pipe flow power law $\left(1-2r/D\right)^{1/n}$ with n = 6.5 described in Mi et al. (2001) is shown in Fig. 10 with collected data matching fairly well the reference profiles. The smooth ends at the jet’s boundaries (r/D = 0.5) are also a consequence of the free-slip condition due to the nozzle not flushing with the tank wall, as described in Romano (2002). These findings confirm the hypothesis of completely developed turbulent pipe flow at the nozzle exit.

Fig. 10

Mean velocity profile at x/D = 0.2 and Re = 22,000 compared to experimental data from other authors and empirical power law for turbulent pipe flows

5 Crosswise instantaneous and mean velocity fields

The fluid mechanics phenomena taking place on longitudinal planes considered in previous section are closely related to those on crosswise planes leading to fully three-dimensional vortical structures (Klaasen and Peltier 1988; Liepmann and Gharib 1992; Sbrizzai et al. 2004). In axisymmetric jets, the ejection of secondary transverse fluid related to Kelvin-Helmholtz shear layer primary instabilities allows the formation of secondary double counter-rotating structures, resembling a mushroom shape in the plane perpendicular to the main flow (Liepmann and Gharib 1992; Romano 2002; Sbrizzai et al. 2004). Secondary instabilities are here investigated by measuring the velocity field on cross-planes from x/D = 0.75 up to x/D = 4.5, approximately where the potential core vanishes.

The high-speed acquisition method allowed the visualization of the transient secondary structures evolution, as shown in the series of pictures given in Fig. 11. The snapshots represent a close-up on the upper-left area of the cross-plane where the formation of a mushroom-like structure takes place, that is at x/D = 2.5, for two different Reynolds numbers, namely 3,200 and 14,500. For the sake of clarity, only one image every 0.008 s, nearly 0.3 integral time scales, was displayed in the picture for Re = 3,200, whereas one image each 0.15 integral scales was used for Re = 14,500 data. The formation and evolution of the two counter-rotating vortices can be appreciated; in particular, the life time of such structures is approximately equal to 1 integral time scale. The picture is similar for the data at Re = 14,500. The vector field averaged over 5,000 images (about 10 s, i.e. more than 100 integral time scales) at x/D = 1.5 and Re = 4,800 is presented at the top of Fig. 12. The empty central area is the effect of a computation mask which was set prior to PIV processing to avoid the large velocities at the jet centerline which give almost uncorrelated image pairs. The actual pipe outlet shape is depicted as the gray circle. The circular area close to the pipe outlet characterized by low velocities values is due to the travelling vortex rings. As the vortex passes by in fact, fluid is ejected; this process is compensated by the subsequent ring’s roll up during which a strong fluid entrainment takes place, thus leading to the observed average velocity field. For large radial distances (around 1D), on the other hand, there is a negative radial velocity, that is a positive entrainment stemming from secondary instabilities, as shown in instantaneous plots and predicted by the model presented in Sect. 2 (Fig. 2). It is also interesting to note that the velocity field under investigation is not affected by major swirling.

Fig. 11

Snapshots of cross-plane transient structures for x/D = 2.5,  Re = 3, 200 (first four pictures at the top) and Re = 14,500 (four pictures at the bottom). T _s represents the integral time scale. Displayed data have been downsampled respectively to 0.125 and 0.250 KHz, roughly 0.3T _s  (0.15T _s ), in order to allow a clearer visualization. U ₀ for Re = 3,200 case has been used as a reference for both figures

Fig. 12

Mean velocity field for x/D = 1.5 at Re = 4,800 (top) and Re = 19,300 (bottom). U ₀ for Re = 4,800 case has been used as a reference for both figures. Blue circle represents pipe outlet’s rim

For increasing Reynolds numbers, a similar field is noticeable as shown at the bottom of Fig. 12, for Re = 19,300, where fluid entrainment is again visible up to the border of the imaged area. As expected, the average velocity field magnitude is considerably larger than the Re = 48,00 case and the region around the pipe outlet where the velocity field is attenuated is less evident. The resulting radial and azimuthal mean velocities are presented in Fig. 13 for Re = 14,500 with positive U _r pointing outward. The mean U _r field, displayed on the left side of Fig. 13, normalized by the flow velocity U ₀, reveals a strong dependence on the downstream distance: up to x/D = 1, the field shape is still unaffected by secondary structures, and vortex rings action is predominant. From x/D = 1.5 up to 2.5, instabilities of the potential core begin to be visible, and consequently, the velocity field shows an increasing dependence of the radial velocity on the azimuthal angle. In the last downstream position, x/D = 4.5, the presence of secondary vortex structures is substantial and modifies the velocity field’s shape up to r/D = 2. The absolute value of the radial component U _r increases considerably with x/D, both outward up to −0.25U ₀ and inward up to 0.25U ₀. On the other hand, the mean U _θ (azimuthal velocity) distribution is quite independent from x/D as may be seen in the right side of Fig. 13. In particular, for high x/D, the field retains its shape and no far field modification is evident. This behavior may be related to the counter-rotating features of vortical structures that cancels out the U _θ component on average. It is important to point out that the azimuthal velocity attains average values which are as small as ±0.001U ₀ at all downstream distances. The behavior of average velocity components as a function of Reynolds number is summarized in Fig. 14 at four downstream positions. Those values have been obtained by sorting positive (fluid ejection) and negative (fluid entrainment) motions and by averaging the data over the entire region under investigation. All velocity components at the different distances decrease with respect to Reynolds number not far from the −1/4 slope (depicted as reference in Fig. 14). This is the same behavior derived for the rms velocities on a longitudinal plane (Fig. 9), thus indicating that on the average, the secondary instabilities on cross-planes are driven by the same mechanism (at least with respect to Reynolds number effects) which gives rise to primary instabilities on longitudinal planes. On a statistical basis, this mechanism can predict the ones from the others and viceversa.

Fig. 13

Normalized U _r and U _θ mean field for Re = 14,500 at various x/D. The gray circle represents the pipe outlet’s rim. For the sake of conciseness, only three x/D positions have been shown

Fig. 14

Radial (U _r) and azimuthal (U _θ ) average velocity versus Reynolds number at different downstream positions. Positive values refer to velocity pointing outward (fluid ejection). Triangle and diamond symbols represent, respectively, positive and negative U _r, circle and square positive and negative U _θ

The behavior of velocity fluctuations provides further insight into the phenomenon. In Fig. 15, radial profiles of rms values for radial and azimuthal velocities are presented for Re = 14,500. Radial rms were obtained by averaging four data sets lying on two mutually perpendicular axes passing by the pipe outlet’s geometric center. The values of turbulent fluctuations, while decreasing with the radial distance, are almost constant with x/D up to x/D = 3.5, where an increase is observed, matching the onset of fully three-dimensional instability as reported by Liepmann and Gharib (1992). In comparison with u _r fluctuations, those in u _θ appear to attain lower values (less than 1/20) and consequently seem to be weakly related to jet’s mixing. The $u^{'}_{r}$ and $u^{'}_{\theta}$ rms curves at fixed x/D for different Reynolds numbers are depicted in Fig. 16. Radial velocity data are characterized by the following pattern: the rms level decreases up to Re = 9,600 and then increases for higher Reynolds numbers, in particular for r/D < 0.5, that is close to the pipe outlet’s rim. A similar behavior was pointed out in Liepmann and Gharib (1992), for a Reynolds number of approximately 10,000; it was related to jet’s initial boundary layer transition to turbulence. Azimuthal velocity rms profile shows a similar behavior, although with much smaller values.

Fig. 15

Rms of radial velocity u _r (top) and azimuthal velocity u _θ (bottom) versus radial distance in cross-planes at Re = 14,500 for various downstream distances x/D

Fig. 16

Rms of radial velocity u _r (top) and azimuthal velocity u _θ (bottom) versus Reynolds number at x/D = 1.5

5.1 Mean entrainment rates

The observations made in the previous sections confirm the average relationships between longitudinal and transverse vortical structures. Thus, the entrainment rate introduced in Sect. 2 can be evaluated by combining Eqs. (5), (6) and (7)

$$ \frac{{\hbox {d}}(Q_{\hbox {r}}(x,R)/Q_0)}{{\hbox {d}}(x/D)}=\frac{D}{Q_0}\int\limits_{0}^{2\pi}R U_{\hbox {r}}(x,R) \hbox{d}\theta $$

(16)

with the already mentioned normalization. The above formulation states that the mean entrainment rate at a specific downstream distance x/D will be derived by integrating the radial velocity U _r along a circular path centered on the pipe’s outlet. It is of interest to assess how for R < 2 D, the entrainment rate is affected by the radial coordinate as it can provide a good insight into the role of different vortical structures in such process. The entrainment rate derived by the average radial velocity field U _r is displayed in Fig. 17 at downstream position x/D = 0.75 for different Reynolds numbers. For r/D < 0.5, the curves feature a slightly negative rate, whereas for larger radial distances, the entrainment rate level becomes positive and increases up to an almost asymptotic value. The features of the reported profiles can be explained, considering that the effect of primary instability structures is predominant at this downstream position and vortex rings affect noticeably the entrainment. As shown in Fig. 12, for radial distances shorter than 0.5D, there is still an ejection of flow which is responsible for the negative peak. On the other hand, the increase achieved for r/D in the range 0.6–0.8 stems from the primary vortex rings roll up, whose effect is most relevant in a limited flow region and vanishes in the cross-plane far field (r/D > 1). For large r/D, the entrainment rate is expected to be a constant independent from radial distance, and this is confirmed by the results shown in Fig. 17. Figure 17 provides also information on Reynolds number effect on entrainment, in particular on the negative entrainment r/D < 0.5 region and the asymptotic behavior of normalized entrainment rate. About the latter effect, it is worth pointing out that the effect of secondary instabilities is less evident at higher Reynolds number regimes, as suggested also by Fig. 13.

Fig. 17

Normalized entrainment rate at downstream position x/D = 0.75 for different Reynolds numbers. Data were obtained by mean radial velocity U _r

These observations, combined with the results from Fig. 13, confirm that for cross-planes farther away from the nozzle, secondary vortical structures become more efficient at entraining fluid and, when the potential core ends, they take full control of the entraining process.

The initial negative entrainment region visible in Fig. 17, which was also reported by Hassan and Meslem (2010) at r/D = 0.8 for x/D = 4, shows a strong dependence on Reynolds number almost vanishing for Re > 14,500.

In Sect. 2, the balance between axial and radial volumetric flow allowed to derive model equations for the average radial velocity as well as for the entrainment rate in the form of model equations A and B depicted in Fig. 2. Comparison of the proposed models against experimental data is shown in Fig. 18 where average radial data and entrainment rate at x/D = 4.5 and at different Reynolds numbers were plotted against H = K _u R/(x − x _p ). Such a downstream position was chosen to verify as much as possible the assumption of self-similarity even in such a region close to the jet outlet. The parameters K _u and x _p are taken respectively equal to 6 and 0 as in Malmstrom et al. (1997).

Fig. 18

Average radial velocity (top) and entrainment rate (bottom) versus H = K _u R/(x − x _p ) at x/D = 4.5. Error bars obtained as standard deviation of the mean. Model Eqs. (11, 14) (blue lines, Model A) and (12, 15) (red lines, model B) show predicted profiles

Experimental data show that for the radial velocity, the agreement is rather poor, especially for Re ≤ 14,500 and H > 1. However, the simple models seem to account for the main features of measured data and relative error bars for Re > 14,500 and H < 1. Specifically, model A seems to be more suited for data around Re ≈ 20,000, while model B is better describing the other data. Results for the entrainment rate show that model B prediction of an initial negative entrainment region followed by a positive negative entrainment region is confirmed by experimental data for Re < 10,000. For Re > 10,000, model B does not recover the sign of entrainment rate for H < 1.3, predicted by model A, while following satisfactorily the experimental data for H > 1.3.

Clearly, the choice of the parameters in the model (K _u and x _p ) could be one of the reasons for the observed differences in comparison with data.

5.2 Velocity correlation

The analysis of transverse structures can explain some of the features observed in previous sections in relation to the effect of Reynolds number as also investigated by Liepmann and Gharib (1992). These authors found that the number of secondary structures grows up to Re = 10,000 (while dropping for larger values), whereas their size appears to be inversely proportional to Reynolds number up to Re = 10,000 (and nearly constant for larger values). In the present work, a preliminary visual investigation of the flow features did not show an evident increase in the number of counter-rotating vortical structures in cross-planes with Reynolds number. The reason lies in the different inlet conditions of the present work, that is a long pipe as opposed to a smooth contraction in Liepmann and Gharib (1992). The average size of cross-planes vortical structures was assessed by means of radial and azimuthal velocity correlation functions defined respectively as

$$ R_{{{\text{rr}}}} (x_{0} ,r) = \left\langle {u_{{\text{r}}} (x_{0} )u_{{\text{r}}} (x_{0} + r)} \right\rangle $$

(17)

$$ R_{{\theta \theta }} (x_{0} ,r) = \left\langle {u_{\theta } (x_{0} )u_{\theta } (x_{0} + r)} \right\rangle $$

(18)

where the reference position x ₀ was set right inside the pipe’s outlet rim (at r/D ≈ 0.45), and r direction represents the radial position with respect to pipe’s outlet center. Correlation functions were then normalized to their initial value, R _rr(x ₀,0) and R _{θ θ} (x ₀,0), and were subsequently spatially averaged from four data sets lying on two mutually perpendicular axis passing by the pipe’s center, as for rms calculations presented in Figs. 15 and 16. Figure 19 shows such correlation functions calculated at x/D = 3.5 for different Reynolds numbers. The radial correlation profiles show a dependence on Reynolds number with decreasing levels of correlation as Reynolds number increases. For Re ≤ 4, 800,  R _rr retains 50 % of its starting value up to r/D ≈ 0.65, whereas at the same radial distance for the Re = 32,200 case, it is as low as 25 %. Furthermore, R _rr is above 10 % of its initial value up to r/D≈ 1 for lower Reynolds numbers, whereas such relative value is reached already at r/D ≈ 0.7 at Re = 32,200. These findings confirm that the average spatial extension in the radial direction of counter-rotating, secondary vortical structures decreases with growing Reynolds number for Re < 10,000 followed by an asymptotic behavior.

Fig. 19

Normalized radial (top) and azimuthal (bottom) velocity correlation functions at x/D = 3.5 for different Reynolds numbers. The horizontal axis has been shifted so as to align it to actual nozzle’s outlet rim, thus the horizontal axis’ origin has been set to r/D = 0.4

Similarly, at the bottom of Fig. 19, the profile of R _{θ θ} for different Reynolds numbers is provided. Differently from the radial correlation, the azimuthal correlation shows negative values due to the vortical structures which roll up inward and is related to the spatial extension of such structures in the azimuthal direction. For increasing Reynolds number, the radial position at which the anti-correlation peak is attained decreases confirming again the shrinking of vortices. R _{θ θ} is less subject to this effect than R _rr, arguably because of the double counter-rotating nature of the structures under investigation, which dampens the azimuthal component of velocity in the spatial-averaging process.

A further insight into the dependence of velocity correlation functions on Reynolds number is given by Fig. 20, where normalized integral scales obtained by previous functions have been plotted as a function of Reynolds number. Radial and azimuthal integral scales show both the same profile, confirming the decrease of the average spatial extension of secondary vortical structures for increasing Reynolds numbers with similar results found at other downstream positions. Therefore, a Reynolds number, in which length scales on cross-planes and rms fluctuating velocities are considered, is derived to be a function close to the Reynolds number based on the jet diameter and jet outlet velocity at the power 1/2. The given results bear an important resemblance to entrainment rate findings presented in the previous paragraph as to the Reynolds number dependency. The entrainment rate appears in fact to be affected by the velocity spatial correlation induced in cross-planes by the secondary structures. The efficiency at entraining fluid relatively to a reference velocity decreases with Reynolds number and attains an asymptotic state for Re > 10,000 as also reported in Figs. 17 and 18.

Fig. 20

Integral scales derived by azimuthal and radial velocity correlation functions versus Reynolds number. Re ^−1/4 and Re ^−1/8 slopes are also shown as a reference

6 Axial and radial flow rate

To establish if the main hypothesis of the proposed simplified models of a perfect balance between axial and radial flow rates holds as presented in Sect. 2, data derived from measurements on both longitudinal and transverse planes are considered. In order to match the volume flux, entrainment calculations carried out in the previous paragraph from transverse planes (Figs. 17, 18) are compared to those regarding axial flow rate on longitudinal planes. The radial volume flux, Q _r, is obtained by the entrainment rate results by averaging over radii larger than that corresponding to the maximum entrainment. In this way, the effect of an onset of asymptotic radial value is considered. On the other hand, the average longitudinal volume flux, Q _a, is derived from the streamwise velocity profile at the corresponding crosswise x/D locations. The results are given in Fig. 21, where the ratio Q _r = Q _a is displayed versus x/D for different Reynolds numbers. The ratio, which in case of perfect balance should be equal to one, as from Eq. (5), shows large oscillations with some indication that for x/D < 2.5 it is Q _a > Q _r, whereas for x/D > 2.5 is Q _r > Q _a. Even if error bars are very large, this trend seems to increase with increasing Reynolds number. This means that the average balance between axial and radial flow rates shows a defect of radial rate for x/D < 2.5 and an overestimate for x/D > 2.5, which is in agreement with observations from Figs. 17 and 18. Close to the jet outlet, there is a positive radial flow rate (toward the external part of the jet) balanced by a slight reduction in the axial flow rate. On the other hand, far from the jet, there is a negative radial flow (inward, corresponding to a positive entrainment) balanced by an increase in the axial flow. While the second of these results is well known, the first clearly build on the simple result for the potential core in which the radial flow rate is simply zero with a constant axial rate. In any case, the results displayed in Fig. 21 confirm that the main hypothesis used to derive the models presented in Sect. 2 is quite closely satisfied from the present data.

Fig. 21

Volume flux balance versus downstream position for comparable Reynolds numbers. Q _r and Q _a respectively represent volume flux derived from radial and longitudinal acquisitions

7 Conclusions

The present work focuses on the effect of Reynolds number on the relation between primary and secondary structures developing in a fully developed turbulent pipe jet and in particular on the effects on entrainment rate.

The results on the axial plane confirm those obtained by other authors, showing that potential core extension increases with Reynolds number, whereas rms of velocity components decreases according to a Reynolds number power law of −0.25.

Simple analytical models for radial velocity and entrainment rate, derived in Sect. 2, are compared to experimental data in Fig. 18.

Models agreement to data is rather poor for radial velocity, whereas entrainment rate curve is better predicted, in particular by Model B for Re > 14,500 and H > 1. This considered, it is important to stress that model B predictions of positive radial velocity and negative entrainment rate for H < 1 and Re < 10,000 and model A predictions of positive entrainment rate for H < 1 for Re > 10,000 are correctly recovered by data.

Velocity correlation results suggest a link between the size of transverse secondary vortical structures and their mixing efficiency.

The previous indications confirm that the dependence on Reynolds number of the near field axisymmetric jet statistics descending from both longitudinal and transverse phenomena is high for values lower than 10,000, suggesting an asymptotic behavior for larger Reynolds numbers.