1 Introduction

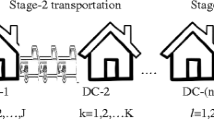
The traditional kind of a Transportation Problem (TP) is a type of decision making problem which minimizes the transportation cost for transporting the goods from origin to destinations satisfying some restrictions according to the feasibility of the problem. But, it is not exactly true that the TP only minimizes the transportation cost. In addition to this, it can have applications in a decision making problem like minimizing the purchasing cost and maximizing the profit, etc. In a TP, sometimes it is also to be considered that before transporting the goods in the destinations from the sources, goods are to be stored at warehouses from sources. So, the Decision Maker (DM) utilizes the concept for managing Two-Stage transportation in his position which maximizes the profit. A TP is called a Two-Stage transportation problem, if it consists of transporting the goods by two Stages, namely, One-Stage transportation problem and in Another-Stage transportation problem. The TP which is considered in two stages of collecting the goods in warehouses is called an One-Stage transportation problem; the TP considered in Another Stage of distributing the goods is referred to as an Another Stage transportation problem. In Fig. 1, a network is considered to illustrate a Two-Stage transportation problem.

Fig. 1
figure 1

Network represents a Two-Stage transportation problem

Full size image

Here, the DM has three warehouses such as S1, S2 and S3 which collect the goods from two cities: D1 and D2 (One-Stage transportation problem). Again the goods are supplied to four cities: C1, C2, C3 and C4 (Another-Stage transportation problem) by the help of the DM. So, the goods are in and out at the warehouses S1, S2 and S3 by two-times transportation, and so it is a Two-Stage transportation problem. Again, there may be more than one objective function in a Two-Stage transportation problem which makes it a multi-objective Two-Stage transportation problem. In this situation, taking decision is not an easy task for the DM unless he or she selects some proper goals for the objective functions. So, we make a connection between the goals and the objective functions of a multi-objective Two-Stage transportation problem.

Goal Programming (GP) is a decision making tool for the MOTP. In most of the cases, a GP is used to produce a better solution of the MOTP under the assumption of certain goals. Later on, RMCGP is also introduced to improve the solution of the MOTP by a GP program. In both methods, certain goals are to be chosen by the DM and the solution is obtained satisfying the optimal values of the goals. But, it is difficult for the DM to guess the possible goals of the objective functions in connection with the methodologies of GP or RMCGP.

Because of the globalization of the markets, the supply and demand in a TP are not always fixed; hence they are considered to be uncertain numbers or, more specifically, grey numbers. A grey number means a number which is not known exactly. An interval grey number can be treated as continuous and discrete. It may be a discrete number within certain range or any number within a range of lower and upper limits. Again, if the number is not known precisely, but is taken from a set of numbers, then it becomes a multi-choice grey number. In a real-life TP, the capacity of supply (a) may not be a fixed number always, but there exists an upper limit \((\bar{a})\) of supply that can be utilized. Again, it is also noticed that the supply cannot be less than an amount which is the lower limit \((\underline{a})\) of supply. Then the upper and lower limits of supply describe the situation of interval grey supply (\(\underline{a},\bar{a}\)) in a TP. Again, if the supply is not a fixed number and it is considered from a set of multi-choice numbers \(\{a^1,a^2,\ldots ,a^p\}\), then the supply becomes a multi-choice grey supply. The demands (b) at the destinations may not be fixed in advance; it also has an upper limit (\(\bar{b}\)) according to the market situation concerned. Therefore, it has a lower limit (\(\underline{b}\)) also. In that situation, we may assign an interval grey demand \((\underline{b},\bar{b}\)) in our proposed study. Furthermore, if the possible demands are multi-choice real numbers which belong to the set of multi-choice values \(\{b^1,b^2,\ldots , b^q\}\), then demand also becomes a grey demand. Here we use two types of greyness in our model, namely, interval grey number and multi-choice grey number.

Based on the above discussions, realizing the real-life situations, we allow for the supply and demand constraints of a TP as grey supply and demand constraints. Again, a real-life TP has many dimensions; so to accommodate these phenomena, here we employ the multi-objective TP. Thereafter, we define the goal space for the objective functions. Then we solve a Two-Stage MOTP for optimal selection of goals from the goal space to the objective functions through a utility function for proper choice of goals and optimal solution of the MOTP.

The residue of this article can be depicted as follows: An updated review on research in related areas connected to this proposed study, problem environment and theoretical background of our proposed study are presented in Sects. 1.1, 1.2 and 1.3, respectively. Section 2 contains the mathematical model along with two subsections. A reduction procedure from grey supply and demand to real numbers is presented in Sect. 2.1. An algorithm for solving the proposed MOTP is offered in Sect. 2.2. A numerical example to justify our study and a sensitivity analysis are carried out in Sects. 3 and 4. The article ends with the conclusion and an outlook of the study which are presented in Sect. 5.

1.1 Review on research in related areas

The basic transportation problem was originally initiated by Hitchcock (1941) and later on by Kantorovich (1960), who has given an algorithm for obtaining the solution of the transportation problem. He developed a procedure to solve the transportation problem, which has a close connection with the simplex method for solving TP as the primal simplex transportation method. Aneya and Nair (1979) resolved a bi-criteria transportation problem. A large number of research works on transportation problems has been done by several researches such as Bhatia et al. (1977), Sharma and Swarup (1997), Szware (1971), Liu (2003), Roy and Mahapatra (2014), Palanci et al. (2015), Sharma et al. (2015). Damci-Kurt et al. (2015) solved a TP with market choice. A study on time-dependent fuzzy random location-scheduling programming for hazardous materials has been conducted by Meiyi et al. (2015). Maity and Roy (2015) presented a solution procedure for multi-objective TP using a utility function approach. Lei et al. (2015) solved a problem on transportation cost allocation under the consideration of a fixed route. Reisach et al. (2016) employed a study on special areas of operational research problems.

Goal Programming (GP) is used widely as a tool to solve the MOTP, and it is accepted by many researchers and industrialists due to its easiness of use, adaptability and efficiency to provide the most appropriate solutions in multi-objective decision making problems. Charnes and Cooper (1961) developed a goal programming model for linear programming problems in which conflicting goals were incorporated as constraints. Later on, Ignizio and Perlis (1979) introduced a solution approach of GP, known as sequential GP method. Tamiz et al. (1998), Romero (1991) and Lee et al. (2010) presented some useful studies in decision making problems under a goal environment. Chang (2007) proposed a multi-choice goal programming approach to solve mathematical programming problems. Again, later on, Chang (2008) offered another multi-choice goal programming approach in a revised form. Liao and Kao (2010) described a method based on quality function development, fuzzy-extended analytic hierarchy process and Multi-Segment GP (MSGP). Paksoy and Chang (2010) studied on revised multi-choice goal programming in a multi-period, multi-stage inventory management problem. Roy et al. (2013), Mahapatra et al. (2013) and Roy (2014) discussed a multi-choice stochastic TP involving exponential distribution, extreme-value distribution and Weibull distribution in which the multi-choice concept is involved only in the cost parameters of the objective function. Roy and Mahapatra (2011) also considered a solid TP under the multi-choice environment. Zhanga et al. (2009) introduced the multi-depot concept in truck transport TP. Maity and Roy (2014) suggested the multi-choice concept on study of multi-objective TP under a utility-function approach. A study on single-sink fixed-charge, multi-objective, multi-index stochastic TP was developed by Midya and Roy (2014). Maity and Roy (2016) studied on a multi-objective transportation problem with nonlinear cost and multi-choice demand. Recently, a study on solving MOTP using conic scalarization approach has been introduced by Roy et al. (2016).

The concept of Grey Numbers emerged as an effective model for systems with partial information only known. Liu (1989) proposed a study on forming a new algebraic system of grey numbers. Palanci et al. (2016) studied on uncertainty under grey goals in a cooperative game. An investigation on interval grey numbers to solve grey multi-attribute decision making problem was introduced by Honghua and Yong (2013). Liu et al. (2010) proposed a study on interval grey number which suggested some knowledge on the degree of greyness of grey numbers. A work on general grey numbers and their operations was given by Liu et al. (2011). Xie and Liu (2010) presented novel methods on comparing grey numbers. Mi et al. (2007) introduced a study on GSOM model based on interval grey numbers.

Many researchers adopted various methodologies for analyzing multi-criteria decision making problems and MOTPs. Nevertheless, to the best of our knowledge, the existing approaches are not sufficient to tackle the MOTP when the supply and demand are interval grey numbers, and to answer the question of how to select goal values corresponding to the objective functions. To tackle such a type of MOTP, we propose a new approach for solving a Two-Stage MOTP problem which could be of a great impact for the scientific community, especially, in Operational Research.

1.2 Problem environment

A large number of investigations have been accommodated by different researchers for solving MOTP with goals through the objective functions. But, in many cases, we observe that the objective function is considered associated with the goals, and then solution procedures are developed to find solutions to the best according to decision maker’s choice. In our research, we formulate a mathematical model on the MOTP which is a Two-Stage transportation problem. Here, a Two-Stage transportation problem refers to a TP in which goods are collected at some warehouses, and then the goods are delivered to several destinations. So, the warehouses are the demand points for sources and the supply points for destinations. Goods are transported at two Stages, i.e., for gathering and distributing, and the whole system is managed by only one decision maker. The DM wishes to maximize his benefit and to minimize the transportation costs. The data regarding the demand and the supply are not necessarily exact in TP due to the globalization of markets or other conditions like weather conditions, seasonal effects, etc. So, without loss of generality, these are taken as grey numbers in the MOTP. The grey numbers may be interval-valued numbers, multi-choice numbers, stochastic numbers, fuzzy numbers, etc. Here, we consider two types of grey numbers, namely, interval grey numbers and multi-choice grey numbers in our proposed MOTP. Another important notion for this MOTP is that if the DM wishes to maximize his profit without considering the transportation cost, then the customers will be affected. In this situation, the optimal goals for the objective functions and the corresponding solutions are not specified in the literature until now. Based on all these ideas, we propose a new way to select the optimal goals for the objective functions of a regarded MOTP.

1.3 Theoretical background

Goal programming is a branch of Multi-Objective Optimization (MOO). It is also considered as a section of optimization problem in multi-criteria decision analysis. It can be treated as an extension or generalization of linear programming to handle multiple, usually conflicting objective measures. Each of these measures is given a goal or target value to be achieved. Unwanted deviations from this set of target values are then minimized through an achievement function. This can be a vector or a weighted sum, depending on the goal programming used. The mathematical model for solving a Multi-Objective Decision Making (MODM) problem using a GP can be considered in the subsequent form:

$$\begin{aligned} \text{ minimize }&\sum _{i=1}^{K}w_i|Z^i(x)-g_i|\\ \text {subject to}&x \in F, \end{aligned}$$

where F is the feasible set and \(w_i\) are the weights attached to the deviation of the achievement function. Here, \(Z^i(x)\) is the i-th objective function of the i-th goal and \(g_i\) is the aspiration level of the i-th goal. Here, \(|Z^i(x)-g_i|\) represents the deviation of the i-th goal.

Weighted goal programming allows for direct trade-offs among all unwanted deviational variables by placing them in a weighted, normalized single achievement function. In fact, weighted goal programming is also termed as non-preemptive goal programming in the literature. Mathematically, Weighted Goal Programming (WGP) can be displayed in the following form:

$$\begin{aligned} \text{ minimize } ~~&\sum _{i=1}^{K}w_i(d_i^++d_i^-)\\ \text {subject to} ~~&Z^i(x)-d_i^++d_i^-=g_i~~~(i=1,2,\ldots ,K),\\&d_i^+\ge 0,d_i^-\ge 0 ~~(i=1,2,\ldots ,K),\\&x \in F, \end{aligned}$$

where \(d_i^+\) and \(d_i^-\) signify over and under achievements of the i-th goal, respectively.

However, the conflicts of resources and the lack of available information make it almost impossible for the DM to set the specific aspiration levels and to choose a better decision when there is a multi-choice of goals connecting with the objective functions. To tackle this situation, Chang (2008) proposed the mathematical model on RMCGP to solve a MODM problem. The mathematical model of a MODM using RMCGP is prescribed as follows:

RMCGP

$$\begin{aligned} \text{ minimize }&\sum _{i=1}^{K}\left[ w_i(d_i^++d_i^-)+\alpha _i(e_i^++e_i^-)\right] \\ \text {subject to}&Z^i(x)-d_i^++d_i^-=y_i~~~(i=1,2,\dots ,K),\\&y_i-e_i^++e_i^-=g_{i,max} \text{ or } g_{i,min}~~~(i=1,2,\dots ,K),\\&g_{i,min}\le y_i\le g_{i,max}~~(i=1,2,\dots ,K),\\&d_i^+,d_i^-,e_i^+,e_i^-\ge 0~~(i=1,2,\dots ,K),\\&x \in F, \end{aligned}$$

where \(y_i\) is the continuous variable associated with i-th goal which is restricted between the upper \((g_{i,max})\) and lower \((g_{i,min})\) bounds, and \(e_i^+\) and \(e_i^- \) are positive and negative deviations attached to the i-th goal of \(|y_i-g_{i,max}|\) and \(\alpha _i\) is the weight attached to the deviation of \(|y_i-g_{i,max}|\); the other variables are defined as in a WGP. To show the efficiency of the variables \(d_i^+\) and \(d_i^-\), \(e_i^+\) and \(e_i^-\), here we use \(d_i^+\) and \(d_i^-\) to minimize the deviation in the objective function of RMCGP; and \(e_i^+\) and \(e_i^-\) are introduced in the model to optimize the goals according to the type of the objective functions, either being of maximization or of minimization type. Again, we formulate the model for both maximization and minimization type functions; so we consider \(e_i^+\) and \(e_i^-\). However, if the type of some objective function is known in advance, then one of the variables \(e_i^+\) and \(e_i^-\) may be omitted according to the type of objective function, of maximization or minimization, respectively.

Theorem 1

WGP is a modification of GP for solving an MODM problem and RMCGP produces better results than GP and WGP.

Proof

The mathematical model of the GP for solving a MODM problem is considered as follows:

GP

$$\begin{aligned} \text{ minimize }&\sum _{i=1}^{K}w_i|Z^i(x)-g_i| \end{aligned}$$
(1.1)
$$\begin{aligned} \text {subject to}&x \in F. \end{aligned}$$
(1.2)

Let us take \(d_i^+=Z^i(x)-g_i\) if \(Z^i(x)\ge g_i\), and \(d_i^+=0\) otherwise (\(i=1,2,\ldots ,K\)). Also, we put \(d_i^-=g_i-Z^i(x)\) if \(Z^i(x)\le g_i\), and \(d_i^-=0\) otherwise. Then, \(Z^i(x)-g_i=d_i^+-d_i^-\), which implies that \(Z^i(x)-d_i^++d_i^-=g_i\). Furthermore, \(|Z^i(x)-g_i|=d_i^++d_i^-\).

Thus, the GP model reduces to the model WGP as follows:

WGP

$$\begin{aligned} \text{ minimize }&\sum _{i=1}^{K}w_i(d_i^++d_i^-)\\ \text {subject to}&Z^i(x)-d_i^++d_i^-=g_i~~~(i=1,2,\ldots ,K),\\&d_i^+\ge 0,d_i^-\ge 0 ~~(i=1,2,\ldots ,K),\\&x \in F. \end{aligned}$$

According to the above discussion, we see that the mathematical model GP is a function of the decision variables along with the weights and goals, whereas the objective function in the mathematical model of WGP consists of the variables which are the goal deviations \((d_i^+\) and \(d_i^-)\). Both the models GP and WGP produce the same result, but the WGP model is easier to handle than GP as its objective function contains a minimum number of variables when compared to the GP model.

If the goal (\(g_i\)) for the i-th objective function is not prescribed by a fixed value but it is considered as a range [\(g_{i,min},g_{i,max}\)], then for a better solution of a maximization type objective function \(g_i\) should attain the maximum value of the range, and for a minimization type objective function it should take its minimum value over the specified range.

In that case, we introduce a new variable \(y_i\) in model WGP as \(Z^i(x)-d_i^++d_i^-=y_i\), and the deviation variables such as \(e_i^+\) and \(e_i^-\) are indeed similar to \(d_i^+\) and \(d^-_i\), respectively, along with the constraint \(y_i-e_i^++e_i^-=g_{i,max}\;\text{ or }\;g_{i,min}\). Then, the objective function is changed into the following form:

$$\begin{aligned} \hbox {minimize}\quad \left[ \sum _{i=1}^{K}w_i(d_i^++d_i^-)+\sum _{i=1}^{K}\alpha _i(e_i^++e_i^-)\right] , \end{aligned}$$

where \(\alpha _i\) are weights corresponding to the goal deviations. Using this objective function we formulate the model RMCGP. In fact, this model RMCGP minimizes both the deviations (\(d_i^++d_i^- \)) and (\( e_i^++e_i^-\)), whereas the problem GP only minimizes the deviation of the objective function value, i.e., \((d_i^++d_i^-) \). Thus, in the course of time of minimizing the objective function in RMCGP model, the second part of the objective function \(\sum _{i=1}^{K}\alpha _i(e_i^++e_i^-)\) is also minimized. This implies that the value of \(y_i\) tends to \(g_{i,max}\) for a maximizing type objective function, and \(y_i\) tends to \(g_{i,min}\) for a minimizing type objective function. In WGP or GP, the goal deviations are only minimized, which does not consider the type of objective function. Here, the additional variables \(e_i^+\) and \(e_i^-\) tackle the situation that minimizes the deviations according to the nature of the objective function. Hence, we conclude that RMCGP produces a better result than WGP or GP models.

Again, in the RMCGP model, if we treat the goal deviations \(e_i^+\) and \(e_i^-\) as 0, then it takes the form of a WGP which is a modification of the model GP. Herewith, it is clear that the solution of RMCGP is better than the solution of WGP and GP. Hence, the arguments evince the proof of the theorem. \(\square \)

Considering real-world practical problems, we present the situation where supply and demand are taken as grey numbers. Basically, grey numbers are used to represent any situation where the supply and demand are not known exactly. Sometimes supply or demand may be a number among a set of values which indicates supply or demand follow multi-choice values. Again, supply or demand may be considered as interval valued. Therefore, different types of uncertain supply and demand situations may occur in an MOTP, which are considered as grey supply and grey demand in our proposed model.

Utility function The term “utility” is measured (Berger 1985; Blanchard and Fischer 1989) to be correlative as “Desire” or “Want”. It has been argued already that desire cannot be measured directly, but only indirectly, by the outward phenomena in which the context is presented.

Definition 1.1

A utility function describes a function \(U:X\longrightarrow \mathbb {R}\) which assigns a real number in such a way that it captures the DM’s preference over the desired goals of the objectives, where X is the set of feasible points.

Satisfaction of goals does not always mean a better selection of goals for the objective function as well as the solution for the objective functions with respect to the goals. There may occur situations to compare the solutions corresponding to the goals. Here, to introduce a better goal, we include a utility function, whose value indicates to optimize the proposed problem through optimal selection goals.

2 Mathematical model

Generally, a transportation problem is a type of decision making problem in which the main objective is to minimize the transportation cost and it is defined subsequently:

Model 1

$$\begin{aligned} \text{ minimize }&Z = \sum _{i=1}^{m}\sum _{j=1}^{n}C_{ij}x_{ij}, \end{aligned}$$
(2.1)
$$\begin{aligned} \text {subject to}&\sum _{j=1}^{n}x_{ij}\le a_i\quad (i=1,2,\ldots , m), \end{aligned}$$
(2.2)
$$\begin{aligned}&\sum _{i=1}^{m}x_{ij}\ge b_j\quad ( j=1,2,\ldots , n), \end{aligned}$$
(2.3)
$$\begin{aligned}&x_{ij} \ge 0~~ \forall \;i \text { and}\;j, \end{aligned}$$
(2.4)

where \(x_{ij}\) \((i=1,2,\ldots ,m; j=1,2,\ldots ,n)\) is the decision variable and \(C_{ij}\) \((i=1,2,\ldots ,m;\) \(j=1,2,\ldots ,n)\) is the transportation cost per unit commodity from the i-th origin to the j-th destination. Here, \(a_i\) \((i=1,2,\ldots ,m)\) and \(b_j\) \((j=1,2,\ldots ,n)\) are availability and demand at the i-th origin and the j-th destination, respectively, and the feasibility condition is \(\sum _{i=1}^{m}a_i\ge \sum _{j=1}^{n}b_j\).

The mathematical model of the MOTP can be posed as follows:

Model 2

$$\begin{aligned} \text {minimize/maximize}&Z^{s} = \sum _{i=1}^{m}\sum _{j=1}^{n} C^{s}_{ij}x_{ij}~~(s=1,2,\ldots ,K) \end{aligned}$$
(2.5)
$$\begin{aligned} \text {subject to} ~~~~~~~~~~~~~&\sum _{j=1}^{n} x_{ij}\le a_{i}~~(i=1,2,\ldots ,m), \end{aligned}$$
(2.6)
$$\begin{aligned}&\sum _{i=1}^{m} x_{ij}\ge b_{j}~~(j=1,2,\ldots ,n), \end{aligned}$$
(2.7)
$$\begin{aligned}&x_{ij}\ge 0\quad \forall \; i\; \text{ and }\; j. \end{aligned}$$
(2.8)

The objective functions in MOTP are conflicting to each other, so even if sometimes they are of the same type, i.e., two objective functions are of minimization type or maximization type, they cannot be summed up to a single objective function. For example, if the transportation cost and production cost are considered as two objective functions in MOTP, then both are of minimization type but they cannot be combined to make a single objective function as the costs are dealt by two decision makers, namely, by the customer and by the seller, respectively. Again, it is true that a maximization problem can be reduced easily to a minimization problem. But this is not what we are considering, because such a reduction of a maximization to a minimization problem turns the goals from positive to negative numbers; however, in real-life situations, negative goals are not considered since they are regarded as meaningless. Based on these phenomena, we do not convert the maximization problem into the minimization in our proposed model.

According to real-world situations, considering the ambiguity that exists in the supply and demand parameters, we incorporate grey supply and grey demand in our study and we depict the MOTP in Model 3.

Model 3

$$\begin{aligned} \text{ maximize/minimize }&Z^{s} = \sum _{i=1}^{m}\sum _{j=1}^{n} C^{s}_{ij}x_{ij}~~(s=1,2,\ldots ,K) \end{aligned}$$
(2.9)
$$\begin{aligned} \text {subject to} ~~~~~~~~~~~~&\sum _{j=1}^{n} x_{ij}\le \hat{a}_i~~(i=1,2,\ldots ,m), \end{aligned}$$
(2.10)
$$\begin{aligned}&\sum _{i=1}^{m} x_{ij}\ge \hat{b}_j~~(j=1,2,\ldots ,n), \end{aligned}$$
(2.11)
$$\begin{aligned}&~~~x_{ij}\ge 0 \quad \forall \; i\;\text{ and }\; j, \end{aligned}$$
(2.12)

where \(\hat{a}_i\) and \(\hat{b}_j\) are the grey supply and grey demand, respectively. In our proposed approach, we consider the grey supply \(\hat{a}_i\) as any interval grey numbers \(\hat{a}_i=[\underline{a}_i,\bar{a_i}]\) or multi-choice grey numbers \(\hat{a}_i=(a_i^1,a_i^2,\ldots , a_i^p)\); here, p is the number of possible multi-choice supplies at i-th origin. Again, demand is also addressed by interval grey numbers \(\hat{b}_j=[\underline{b}_j,\bar{b_j}]~~(j=1,2,\ldots ,n)\) or multi-choice grey numbers \(\hat{b}_j=(b_j^1,b_j^2,\ldots , b_j^q)\); here, q is the number of possible multi-choice demand at the j-th destination. In fact, \(\underline{a}_i\) and \(\overline{a}_i\) are lower and upper bounds of grey supply at the i-th origin; \(\underline{b}_j\), \(\overline{b}_j\) are the bounds of grey demand at the j-th destination, and \(\sum _{i=1}^{m}\bar{a}_i\ge \sum _{j=1}^{n}\underline{b}_j\) is the feasibility condition.

We introduce the following assumptions to formulate a mathematical model (for Model 4) of a Two-Stage multi-objective TP as:

  • Consider m sources \(D_i ~(i=1,2,\ldots , m\)) with interval grey supply \([\underline{a}_i,\bar{a_i}] ~(i=1,2,\ldots , m\)) and p destinations \(C_{j'}~(j'=1,2,\dots , p\)) with interval grey demand \([\underline{b}_{j'},\bar{b_{j'}}] ~(j'=1,2,\ldots , p\)), and there are no direct links between sources and destinations.

  • Assume n nodes \(S_j~ (j=1,2,\ldots , n)\) with equal interval grey supply and demand \([\underline{d}_{j},\bar{d_{j}}] ~(j=1,2,\ldots , n\)) to interact between sources \(D_i\) and destinations \(C_{j'}\); this has the capacity of taking goods from sources \(D_i\) and delivering goods to the destinations \(C_{j'}\).

  • We consider that there are no goods left after the completion of a particular time of transportation in the nodes \(S_j\).

  • We treat T objective functions for One-Stage transportation, i.e., transportation from sources \(D_i\) to destination \(S_j\); \(y_{ij}\) is taken as a decision variable and \(P^t_{ij}\) is the cost parameter for the t-th objective function.

  • We describe K objective functions for Another-Stage transportation, i.e., transportation from sources \(S_j\) to destination \(C_{j'}\); here, \(x_{i'j'}\) is taken as a decision variable and \(C^k_{i'j'}\) is the penalty parameter for the k-th objective function. In fact, the penalty parameter may be the transportation cost per unit item, production cost per unit item of goods, selling cost per unit item of goods, etc.

Then, our mathematical model can be designed in the following form:

Model 4

$$\begin{aligned} \text{ minimize/maximize }&W^t = \sum _{i=1}^{m}\sum _{j=1}^{n} P^t_{ij}y_{ij}~~(t=1,2,\ldots ,T), \end{aligned}$$
(2.13)
$$\begin{aligned} \text{ minimize/maximize }&Z^k = \sum _{i'=1}^{n}\sum _{j'=1}^{p} C^k_{i'j'}x_{i'j'}~~(k=1,2,\ldots ,K) \end{aligned}$$
(2.14)
$$\begin{aligned} \text {subject to} ~~~~~~~~~~~~&\sum _{j=1}^{n} y_{ij}\le \hat{a}_i ~~(i=1,2,\ldots ,m), \end{aligned}$$
(2.15)
$$\begin{aligned}&\sum _{i=1}^{m} y_{ij}\ge \hat{d}_j \;(j=1,2,\ldots ,n), \end{aligned}$$
(2.16)
$$\begin{aligned}&\sum _{j'=1}^{p} x_{i'j'}\le \hat{d}_{i'}~~(i'=1,2,\ldots ,n), \end{aligned}$$
(2.17)
$$\begin{aligned}&\sum _{i'=1}^{n} x_{i'j'}\ge \hat{b}_{j'}~~(j'=1,2,\ldots ,p), \end{aligned}$$
(2.18)
$$\begin{aligned}&\sum _{i=1}^{m} y_{il}=\sum _{j'=1}^{p}x_{lj'}~~~(l=1,2,\ldots , n), \end{aligned}$$
(2.19)
$$\begin{aligned}&y_{ij}\ge 0~~\forall ~ i,~ j;\quad ~x_{i'j'}\ge 0~~\forall ~ i',~ j'. \end{aligned}$$
(2.20)

Here, \(\hat{a}_i\), \(\hat{d}_j\), \(\hat{d}_{i'}\) and \(\hat{b}_{j'}\) are the grey supply and demand parameters as defined in Model 3. Also, \(\sum _{i=1}^{m}\bar{a}_i\ge \sum _{j'=1}^{p}\underline{b}_{j'}\) is the feasibility condition. Although this condition can be made according to the choice of DM, we consider a possibly very large feasible region for the multi-objective Two-Stage TP.

In Model 4, constraints (2.15) and (2.16) represent availability and demand at the origins and destinations of One-Stage transportation, respectively. Again, constraints, (2.17) and (2.18) represent availability and demand at the origin and destinations of Another-Stage transportation, respectively. Finally, constraints (2.19) represent that the amount of goods stored at the destination of One-Stage transportation will all be distributed to the destinations of Another-Stage of transportation.

The objective functions \(W^t~(t=1,2,\ldots ,T)\) are of conflicting nature which we consider at the first stage of Model 4; so these functions are not summed up, even if they are of same type. A similar concept is adopted for the objective functions at the subsequent stage of Model 4. Also, there are different agents to pay the cost at different stages of transportation. Due to this fact, we consider the objective functions separately in Model 4.

Usually, the DM determines the goals into the objective functions and, thereafter, the solution is obtained according to the best fit of the goals. Here, our main interest is to constitute the way of assignment of goals to the objective functions. When there are more than one objective function, conflicting in nature, in many cases optimal solutions of the objective functions occur at different points. So, consideration of specific goals and the corresponding solution are a complex task for the DM.

Now, some useful definitions regarding our proposed study in the goal space are presented. The following definitions are given with respect to s objective functions.

Definition 2.1

(Feasible goal) Let \(Z^t\) be the t-th objective function of the MOTP. Then the feasible goal for the objective function \(Z^t\) refers to all the possible values of the objective function \(Z^t\) which is an interval \(I^t=[\min ~Z^t, \max ~ Z^t]\). Here, \(\min ~Z^t\) and \(\max ~ Z^t\) are obtained under supply and demand constraints of the MOTP along with the nonnegativity conditions.

Definition 2.2

(Feasible goal region) Let \(I^t\) be the feasibility of goal for t-th objective function of the MOTP. Then the subset \(I^1\times I^2\times \ldots \times I^s\) of \(\mathbb {R}^s\) is the feasibility goal region for the MOTP with respect to s objective functions.

Definition 2.3

(Optimum goal region) In the usual way of the MOTP, each objective function is either of maximization type or of minimization type. Each can be solved with respect to the constraints separately to get its individual optimal solution. Let \(X_1^*, X_2^*,\ldots ,X_s^*\), be the respective ideal solutions of s objective functions. Evaluating all these objective functions at all the ideal solutions, we construct a pay-off matrix of format \(s\times s\) as stated in Table 1.

$$\begin{aligned} \text {Then, we find}\quad I_o^i=\left[ \;\min _{\begin{array}{c} j=1,2,\ldots ,s \end{array}}\; Z^i(X_j^*),\max _{\begin{array}{c} j=1,2,\ldots ,s \end{array}}\; Z^i(X_j^*)\right] \; \;(i=1,2,\ldots ,s). \end{aligned}$$

The subset \(I^1_o\times I^2_o\times \cdots \times I^n_o\) of \(\mathbb {R}^s\) is the optimum feasibility goal region for the MOTP with respect to the given objective functions.

Table 1 Pay-off Matrix for ideal solutions of the objective functions
Full size table

Again, presence of grey numbers in the constraints of Model 4 makes the model non-deterministic, and we use a reduction procedure to make the MOTP become a deterministic one by the following rule.

2.1 Reduction of grey supply and demand parameters to real parameters

In most of the real-life cases, it is seen that, if the number of units of goods transported to some destination is of a rather small amount already, then the transportation cost may even be around a minimal value. Herewith, the demand in the classical TP could be considered with a minimum value among all the uncertain possibilities through grey numbers for an optimum solution. However, in the situation of minimizing transportation cost and maximizing profit through transporting the goods, it is not predictable how much an amount of goods is needed to be transported for an optimum solution; it may be any one among the possible values of the grey demands. Again, if the supply amount of goods is of a high value, then total transportation cost reduces as the customers purchase goods from those origins in which the transportation cost per unit item is about its minimum. But, it is often not useful to provide the satisfactory level of supply at all the origins; so we follow a reduction procedure in which the optimum solution is obtained through the optimum selection of grey supply, according to the goals of the objective functions.

If the interval grey supply is taken as \([\underline{a}_i,\bar{a}_i]\), then it reduces to a real number by considering the following reduction technique:

figure a

where \(0\le \lambda \le 1\).

Similarly, the interval grey demand can also be reduced to a real number as

figure b

where \(0\le \lambda \le 1\), when the interval grey demand is \([\underline{b}_j,\bar{b}_j]\). Again, \(\lambda \) is considered as a real free parameter, whose value determines the possible supply and demand by the DM. The value of \(\lambda \) is obtained from the solution according to the best goals assigned about the optimal demand and supply in the proposed problem.

Again, if the supply or demand quantity is a multi-choice grey number, then we use a reduction procedure by employing binary variables in the following way.

If there are two possible values of \(a_i\), namely, \(a_i^1\) and \(a_i^2\), then using one binary variable we reduce the multi-choice grey number to a crisp number in the subsequent manner:

\(a_i^{'}=a_i^1z_1+ a_i^2(1-z_1)\), where \(z_1=0\) or 1.

If there are three possible values of \(a_i\), namely, \(a_i^1,~a_i^2\) and \(a_i^3\), then we use two binary variables to reduce the greyness in the following manner:

\(a_i^{'}=a_i^1z_1z_2+ a_i^2(1-z_1)z_2+a_i^3(1-z_2)z_1\), where \(z_1,z_2=0\) or 1, and \(z_1+z_2\ge 1\).

Furthermore, for four possible values \(a_i^1,~a_i^2,~a_i^3\) and \(a_i^4\), of \(a_i\), we use the following reduction formulae:

\(a_i^{'}=a_i^1z_1z_2+ a_i^2(1-z_1)z_2+a_i^3(1-z_2)z_1+a_i^4(1-z_1)(1-z_2)\), where \(z_1,z_2=0\) or 1.

One issue to be noted is that the number of binary variables is r, when \(2^{r-1}<p\le 2^r\), where p is the number of multi-choice numbers in grey supply \((a_i^1,a_i^2,\ldots , a_i^p)\). For more details about a general transformation technique, we refer to Roy et al. (2016). In a similar way, the multi-choice grey uncertainty can be reduced for demand parameters, too.

2.2 Algorithm for selection of goals to the objective functions in Two-Stage transportation problem

The following steps are proposed for the selection of goals to the objective functions in our Two-Stage MOTP with interval grey demand and supply:

Step 1: First, we reduce the constraints with grey numbers to deterministic constraints with real numbers by the help of the procedure described in Sect. 2.1.

Step 2: We solve each of the objective functions corresponding to a One-Stage TP under the restriction of proposed problem. As a result, we obtain the solutions, \(Y_1^*, Y_2^*,\ldots ,Y_T^*\). Again, we solve each of the objective functions corresponding to a Another-Stage TP under the restriction of our proposed problem and we calculate the solutions, \(X_1^*, X_2^*,\ldots ,X_K^*\). These solutions are called as ideal solutions; often, they are known as Pareto optimal solutions.

Step 3: Using the ideal solutions obtained in Step 2, we formulate pay-off matrices, one is of format \(T\times T\), and the other one is of format \(K\times K\), according to Definition 5.3.

Step 4: Obtaining \(I_o^i=[\text{ min }_j ~W^i(Y_j^*),\text{ max }_j~ W^i(Y_j^*)]\)   (\(i=1,2,\ldots ,T\)), we then find the optimum feasibility goal region \(I^1_o\times I^2_o\times \cdots \times I^T_o\) of \(\mathbb {R}^T\) for the One-Stage MOTP. In a similar way, we define \(G_o^i=[\text{ min }_j~ Z^i(X_j^*),\text{ max }_j~ Z^i(X_j^*)]\)   (\(i=1,2,\ldots ,K\)), and derive the optimum feasibility goal region \(G^1_o\times G^2_o\times \cdots \times G^K_o\) in \(\mathbb {R}^K\) for the Another-Stage MOTP.

Step 5: We consider \(p_t\) as the goal value to each of the objective functions \(W^t\) and \(g_k\) as the goal value to each of the objective functions \(Z^k\). Based on the goal values, we construct a utility function \(E=E(p_1,p_2,\ldots ,p_T;g_1,g_2,\ldots ,g_K)\) and, then, we optimize the value of E within the feasible goal regions \(I^1_o\times I^2_o\times \cdots \times I^T_o\) in \(\mathbb {R}^T\) and \(G^1_o\times G^2_o\times \cdots \times G^K_o\) in \(\mathbb {R}^K\). If \(p_1^*,p_2^*,\ldots ,p_T^*;g_1^*,g_2^*,\ldots ,g_K^*\) are the optimal solutions of E, then these are the optimal goals to the objective function of the MOTP.

Step 6: We formulate a single objective function whose solution optimally accommodates the goals and, it also yields the solution of the MOTP.

Step 7: Based on the results of optimal goals and possible optimized values of the objective functions, we design an RMCGP model to obtain the optimal solution.

Step 8: Stop.

Construction of utility function The utility function regarding all of the goals can be formed according to the choice of the DM. We propose the function E of the goals in such a way that the value of E approaches to zero when the function of the MOTP is minimized or maximized according to the choice of the DM. Let us define

figure c

Here, \(\alpha _t~(t=1,2,\ldots ,T)\) and \(w_i~(i=1,2,\ldots ,K)\) are the weights. Weights are mainly used for the preference of the respective objective functions in the MOTP. Basically, in MOTP the weights are chosen by the DM, which reflects the priority levels of respective objective functions. In most of the cases, weights are taken in normal form, i.e., the sum of all weights is considered as 1. We also present the weights in normal form by considering the percentages of preferences corresponding to the objective functions in a unit scale. Furthermore, \(u_t\) (\(t=1,2,\ldots , T\)) is the utility function for the t-th objective function with respect to the goal \(p_t\) (\(t=1,2,\ldots ,T\)), and \(u_i\) (\(i=1,2,\ldots , K\)) is the utility function for the i-th objective function with respect to goal \(g_i\).

The objective function is considered by two types, namely, maximization type and minimization type. The utility function is regarded in such a way that the goal of a maximization type objective function is increased and the goal value corresponding to a minimization type objective function is minimized. So the utility function \(u_i\) \((i=1,2,\ldots ,K\)) is defined as follows:

figure d

Again, the utility function \(u_t(p_t)\) (\(t=1,2,\ldots , T\)) is defined in a very similar way as the function \(u_i(g_i)\) has been introduced.

3 Numerical example

Now, we present a real-life Two-Stage TP to show the effectiveness of our proposed study. A reputed company wishes to select proper goals for objective functions and the corresponding solution. The company has three stores: S1, S2 and S3, and it purchases goods from two market cities: D1 and D2. Thereafter, the company supplies the goods to four cities: C1, C2, C3 and C4. During the purchasing of items from the marketed cities D1 and D2, the company mainly considers two criteria: one is transportation cost, and other is purchasing cost of goods. Here, the transportation of goods from D1 and D2 to the warehouses S1, S2 and S3 is a One-Stage TP. In this situation, the company would like to minimize both the value of the objective functions. Again, during the selling time, the company tackles the transportation of goods with the motivation that it wishes to minimize the transportation cost and to maximize the profit. Here, the transportation of goods from S1, S2 and S3 to C1, C2, C3 and C4 is considered as Another-Stage TP. Indeed, the company is interested to proceed in such a way that the stored amount will all be delivered. Then, the capacities of supply at D1 and D2 and the intake capacity at S1, S2 and S3 are chosen according to the requirement of the cities C1, C2, C3 and C4, which are considered as interval grey numbers. The supplied data of the problems are shown in Tables 2 and 3.

Table 2 Transportation cost (in \(\$ \)) for transporting the amount of goods per item
Full size table
Table 3 Purchasing cost (in \(\$ \)) for amounting of goods per item
Full size table

Here, we assume that the One-Stage transportation system is maintained by the supplier and, therefore, the transportation cost is treated by the supplier; the purchasing cost is taken into account by the buyer. So, we cannot add them to a single objective function, because the objective functions are of conflicting nature. Due to the globalization of the market, the intake amount of goods to the center D1 is followed by an interval grey number which is the [1500, 1600] unit, and the capacity of supply items of D2 is also assessed as an interval grey number, the [1550, 1750] unit. In the TP, there are certain demands at the destinations S1, S2 and S3. Demand is always varying through the market scenario, so it is unpredictable. We consider that the intake amount of goods will be delivered completely for the destinations S1, S2 and S3. Let the capacity of supply at S1, S2 and S3 be [900, 1000], [1100, 1150] and [1000, 1100], respectively. Due to fluctuation in the market, the demands at the cities C1, C2, C3 and C4 are represented by interval grey numbers. The transportation has been made in Two-Stage form, namely, D1 and D2 to S1, S2 and S3 and, then, S1, S2 and S3 to C1, C2, C3 and C4. Here, the decision maker tries to minimize the Two-Stage transportation cost and would like to maximize the profit for distributing goods from S1, S2 and S3 to C1, C2, C3 and C4. For this case, the DM assigns the profit for transferring goods which are given in Table 4, and the transportation costs from S1, S2 and S3 to C1, C2, C3 and C4 are presented in Table 5.

Table 4 Profit (in $) of selling goods per amount
Full size table
Table 5 Transportation cost (in $) per amount of goods for selling time
Full size table

Without loss of generality, we assume that the demands at the destinations C1, C2, C3 and C4 are grey numbers and they are taken as [750, 800], [850, 900], {600, 650, 700} and {690, 700, 750, 850}. Here, we mainly concentrate on the following approach:

  • We fix the optimum goals for minimizing transportation cost and maximizing the profit.

  • The optimum amount of goods will run over the stores S1, S2 and S3.

  • We find an optimum solution for the proposed goals of the MOTP.

We formulate the mathematical model in which \(W^1\) and \(W^2\) are the objective functions of minimization type for One-Stage transportation (i.e., for keeping the goods at the stores S1, S2 and S3), and \(Z^1\) and \(Z^2\) are objective functions of maximization and minimization type, respectively, for Another-Stage transportation (i.e., for supplying the goods to the destination C1, C2, C3 and C4). Obviously, this problem is a multi-objective Two-Stage grey transportation problem. So, based on the supplied data, we formulate the subsequent mathematical model.

Model 5

$$\begin{aligned} \text{ minimize }&W^1=12y_{11}+11y_{12}+10y_{13}+9y_{21}+8y_{22}+9y_{23}, \end{aligned}$$
(3.1)
$$\begin{aligned} \text{ minimize }&W^2=25y_{11}+30y_{12}+20y_{13}+25y_{21}+20y_{22}+22y_{23}, \end{aligned}$$
(3.2)
$$\begin{aligned} \text{ maximize }&Z^1=4.5x_{11}+5.0x_{12}+6.0x_{13}+6.5x_{14}+4.0x_{21}+5.5x_{22}\nonumber \\&~~~~~~ \quad +5.5x_{23}+4.5x_{24}+5.0x_{31}+4.5x_{32}+5.0x_{33}+5.5x_{34}, \end{aligned}$$
(3.3)
$$\begin{aligned} \text{ minimize }&Z^2=8x_{11}+9x_{12}+6.5x_{13}+7.5x_{14}+10x_{21}+8.0x_{22}\nonumber \\&~~~~~~ \quad +5.0x_{23}+6.5x_{24}+6x_{31}+9.5x_{32}+6.0x_{33}+7.0x_{34} \end{aligned}$$
(3.4)
$$\begin{aligned} \text {subject to}&y_{11}+y_{12}+y_{13}\le [1500,1600], \end{aligned}$$
(3.5)
$$\begin{aligned}&y_{21}+y_{22}+y_{23}\le [1550,1750], \end{aligned}$$
(3.6)
$$\begin{aligned}&y_{11}+y_{21}\ge [900,1000], \end{aligned}$$
(3.7)
$$\begin{aligned}&y_{12}+y_{22}\ge [1100,1150], \end{aligned}$$
(3.8)
$$\begin{aligned}&y_{13}+y_{23}\ge [1000,1100], \end{aligned}$$
(3.9)
$$\begin{aligned}&x_{11}+x_{12}+x_{13}+x_{14}\le [900,1000], \end{aligned}$$
(3.10)
$$\begin{aligned}&x_{21}+x_{22}+x_{23}+x_{24}\le [1100,1150], \end{aligned}$$
(3.11)
$$\begin{aligned}&x_{31}+x_{32}+x_{33}+x_{34}\le [1000,1100], \end{aligned}$$
(3.12)
$$\begin{aligned}&x_{11}+x_{21}+x_{31}\ge [750,800], \end{aligned}$$
(3.13)
$$\begin{aligned}&x_{12}+x_{22}+x_{32}\ge [850,900], \end{aligned}$$
(3.14)
$$\begin{aligned}&x_{13}+x_{23}+x_{33}\ge (600~\text{ or }~ 650~\text{ or }~ 700), \end{aligned}$$
(3.15)
$$\begin{aligned}&x_{14}+x_{24}+x_{34}\ge (690 ~\text{ or }~ 700~\text{ or }~ 750~\text{ or }~ 850), \end{aligned}$$
(3.16)
$$\begin{aligned}&y_{11}+y_{21}=x_{11}+x_{12}+x_{13}+x_{14}, \end{aligned}$$
(3.17)
$$\begin{aligned}&y_{12}+y_{22}=x_{21}+x_{22}+x_{23}+x_{24}, \end{aligned}$$
(3.18)
$$\begin{aligned}&y_{13}+y_{23}=x_{31}+x_{32}+x_{33}+x_{34}, \end{aligned}$$
(3.19)
$$\begin{aligned}&x_{i'j'}\ge 0,~y_{ij}\ge 0~~~ \forall ~ i',\quad j=1,2,3;\quad i=1,2; j'=1,2,3,4.\nonumber \\ \end{aligned}$$
(3.20)

To solve Model 5, using the reduction procedure of grey numbers to real numbers as presented in Sect. 2.1, we reduce the constraints (3.5)–(3.16), which contain grey numbers, to deterministic constraints as follows:

$$\begin{aligned}&y_{11}+y_{12}+y_{13}\le (1-a_1)1500+a_11600, \end{aligned}$$
(3.21)
$$\begin{aligned}&y_{21}+y_{22}+y_{23}\le (1-a_2)1550+a_21750, \end{aligned}$$
(3.22)
$$\begin{aligned}&y_{11}+y_{21}\ge (1-a_3)900+a_31000, \end{aligned}$$
(3.23)
$$\begin{aligned}&y_{12}+y_{22}\ge (1-a_4)1100+a_41150, \end{aligned}$$
(3.24)
$$\begin{aligned}&y_{13}+y_{23}\ge (1-a_5)1000+a_51100, \end{aligned}$$
(3.25)
$$\begin{aligned}&x_{11}+x_{12}+x_{13}+x_{14}\le (1-b_1)900+b_11000, \end{aligned}$$
(3.26)
$$\begin{aligned}&x_{21}+x_{22}+x_{23}+x_{24}\le (1-b_2)1100+b_21150, \end{aligned}$$
(3.27)
$$\begin{aligned}&x_{31}+x_{32}+x_{33}+x_{34}\le (1-b_3)1000+b_31100, \end{aligned}$$
(3.28)
$$\begin{aligned}&x_{11}+x_{21}+x_{31}\ge (1-b_4)750+b_4800, \end{aligned}$$
(3.29)
$$\begin{aligned}&x_{12}+x_{22}+x_{32}\ge (1-b_5)850+b_5900, \end{aligned}$$
(3.30)
$$\begin{aligned}&x_{13}+x_{23}+x_{33}\ge 600 z_1z_2+650(1-z_1)z_2+700(1-z_2)z_1, \end{aligned}$$
(3.31)
$$\begin{aligned}&x_{14}+x_{24}+x_{34}\ge 690z_3z_4+700(1-z_3)z_4+750z_3(1-z_4)\nonumber \\&\qquad +850(1-z_3)(1-z_4), \end{aligned}$$
(3.32)
$$\begin{aligned}&z_1+z_2\ge 1;~~z_1,~z_2,~z_3,~z_4=0~\text{ or }~1, \end{aligned}$$
(3.33)
$$\begin{aligned}&0\le a_r\le 1,~0\le b_s\le 1~~(r=1,2\ldots ,5;s=1,2,\ldots ,5). \end{aligned}$$
(3.34)

Now, we minimize the objective functions \(W^1\) and \(W^2\) independently with respect to the constraints (3.17)–(3.34), and we construct the pay-off matrix (using Definition 2.3) which is shown in Table 6.

Table 6 Pay-off Matrix for \(W^1\) and \(W^2\)
Full size table

Table 7 represents the pay-off matrix (using Definition 2.3) which is designed by solving each objective functions \(Z^1\) and \(Z^2\) with respect to the same constraints (3.17)–(3.34).

Table 7 Pay-off Matrix for \(Z^1\) and \(Z^2\)
Full size table

Using the pay-off matrices from Tables 6 and 7 and also using equations (C) and (D), we formulate Model 6 with a utility function as follows:

Model 6

$$\begin{aligned} \text{ minimize }&0.25u_1+0.25u_2+0.25u_3+0.25u_4 \\ \text{ subject } \text{ to }&u_1=\frac{W^1-28,050}{30,700-28,050};~~~u_2=\frac{W^2-68,500}{73,250-68,500};\\&u_3=\frac{18400-Z^1}{18,400-14,400};~~~u_4=\frac{Z^2-22,500}{22,500-19,075};\\&0\le u_i\le 1~~(i=1,2,3,4); \\&\text {and constraints }(3.17)-(3.34). \end{aligned}$$

Solving Model 6, we derive the optimal value of each objective function as follows:

\(W^1=30,700,~W^2=72583.3;~~Z^1=16800;~Z^2=20600.\) These solutions provide the subsequent optimal goal regions: [28050, 30700] for \(W^1\), [68,500, 72,583.3] for \(W^2\), [16,800, 18,400] for \(Z^1\), and [19,075, 20,600] for \(Z^2\). Referring to the optimal goal regions in RMCGP model, we construct the following model:

Model 7

$$\begin{aligned} \text{ minimize }&0.25(d_1^++d_1^-)+0.25(d_2^++d_2^-)+0.25(d_3^++d_3^-)+0.25(d_4^++d_4^-)\\&~~~+0.25(e_1^++e_1^-)+0.25(e_2^++e_2^-)+0.25(e_3^++e_3^-)+0.25(e_4^++e_4^-)\\ \text {subject to}&W^1-d_1^++d_1^-=y_1;~y_1-e_1^++e_1^-=28,050; \\&W^2-d_2^++d_2^-=y_2;~y_2-e_2^++e_2^-=68,500;\\&Z^1-d_3^++d_3^-=y_3;~y_3-e_3^++e_3^-=18,400;\\&Z^2-d_4^++d_4^-=y_4;~y_4-e_4^++e_4^-=19,075; \\&28,050\le y_1\le 30,700;~68,500\le y_2\le 72,583.3;\\&16,800\le y_3\le 18,400;~19,075\le y_4\le 20,600;\\&d_i^+\ge 0,~d_i^-\ge 0,~e_i^+\ge 0,~e_i^- \ge 0~~(i=1,2,3,4);\\&\text {and constraints }(3.17)-(3.34). \end{aligned}$$

Finally, we obtain the optimal solution by solving Model 7 as follows:

\(W^1=30,700;~W^2=68,500;~Z^1=16,800;~Z^2=20,600.\)

The values of the decision variables are

$$\begin{aligned} y_{11}= & {} 500;y_{12}=1100;y_{13}=0;y_{21}=400;y_{22}=0;y_{23}=1000;\text { and}\\ x_{11}= & {} 0;x_{12}=0;x_{13}=450;x_{14}=450;x_{21}=0;x_{22}=850;x_{23}=250;x_{24}=0;\\ x_{31}= & {} 750;x_{32}=0;x_{33}=0;x_{34}=250. \end{aligned}$$

Again, the amount of goods are stocked or delivered in or from the warehouses S1, S2 and S3 are 900, 1100 and 1000 units, respectively. The amount of goods which are purchased from sources D1 and D2 are 1600 units and 1400 units, respectively. The amount of goods that are sold to the destinations C1, C2, C3 and C4 are 750 units, 850 units, 700 units and 700 units, respectively.

4 Sensitivity analysis

RMCGP is a technique to solve the MOTP having the goals related to each of the objective functions. As a matter of fact, the main drawback of a RMCGP model is about how the DM would select the possible goals of the objective functions. In real-life problems, if the goal values of the objective functions are not defined properly, then the RMCGP method will have failed to produce the best result. In this study, we describe the scenarios of a Two-Stage TP and select the goals to each of the objective functions. In the meantime, we accommodate our situation by removing the drawback of RMCGP for selecting the goals by proposing a new algorithm. With the proposed algorithm, we first determine the optimal goal values for the objective functions; then we use RMCGP to find a better compromise solution. Following the proposed example, we select the goal arbitrarily and if the selected goal does not lie in the optimal goal region, then we cannot get any feasible solution. As an example, if the DM needs a solution with the following interval goals: [22,000, 24,000] for \(W^1\),  [60,450, 62,700] for \(W^2\), [18,700, 20,000] for \(Z^1\), and [13,710, 16,050] for \(Z^2\); then the RMCGP fails to produce a feasible solution. So, RMCGP does not provide any definite conclusion for selecting the interval goals of the choices of the DM. Under this circumstance, our proposed methodology helps to seek out the optimal goal region as well as the optimal solution of the MOTP. Again, one issue should be noticed, namely, that the solutions and optimal goal regions depend on the choice of weights (\(w_i\)) also. These weights are the preferences of the objective functions by the DM. If the weights are changed according to the choice of the DM, then the optimal goal region will be changed, too.

In our reflections, the supply and demands are taken as interval grey numbers. From the obtained solution, we see that the amount of goods purchased from the sources D1 and D2 are 1600 units and 1400 units, respectively. In that case, the DM addresses the upper bound of grey supply at D1 and an amount less than the minimum supply capacity at D2. If the DM wishes to prepare a model by considering the minimum capacity of supply rather than grey supply, then the purchasing cost would be increased which may cause a smaller profit. So, the choice about the amount of goods to be purchased from the sources are cleared by our proposed technique through grey supply, whereas the existing methods fail to select a better choice when greyness is involved in the supply. Here, the amount of goods transported to the destinations C1, C2, C3 and C4 are 750 units (lower limit of demand), 850 units (lower limit of demand), 700 units (maximum among multi-choice of demand) and 700 (one value among the multi-choice of demand), respectively, for an optimal solution. Hence, for a better solution of our proposed MOTP, the selling amount of goods regarding an optimal solution is produced by our technique when demands are grey numbers.

In most of the real-life MOTPs, we just directly address origins and destinations, but here we add a new concept by proposing a Two-Stage TP. In the modern-days business economy, the DM wishes to find the optimal solution by keeping the minimum transportation cost. But, here the DM gets a platform to fix the goals in some situations of gathering the goods in the warehouses and, in time, of distributing the goods from the warehouses. It suggests that the specific value of some storing items in the warehouses is produced with the optimal profit by the DM.

Again, the proposed study may be a good foundation for making decision in managerial problems on the scheduling traffic flow in an urban city. In this regard, we relate our approach for solving the problem investigated by Anderluh et al. (2016). Consider D1 and D2 as the depots of vans and cargo bikes with an anticipation of number of vans and cargo bikes, respectively, as supply in these origins. We choose the variables which are involved in our model as the number of vans and cargo bikes supplied through the routes. Thereafter, we anticipate the possible numbers of vans and cargo bikes passing through the stoppages S1, S2 and S3, and we treat these as the demands with the nodes in our proposed model. Furthermore, we select the flow of them to the centers C1, C2, C3 and C4 satisfying the proper demands of vans and cargo bikes at these centers by solving the model which is formulated under aforementioned schedule of parameters and variables in our proposed model. Again the constraints may be redesigned according to the conditions supplied in the problem. Thereafter, we can consider different costs for transport along different routes by vans and cargo bikes and imposing carbon emission by different vehicles [cf. Letmathe et al. (2011) for related work] as an objective function. Then, we find the compromise solution according to restrictions which should preserve the health of nature. In this process, our method is very useful to determine the flow of traffic by minimum cost of transportation along with the minimization of carbon emission. Herewith, the study of Anderluh et al. (2016) may be accommodated using goals according to our study in order to provide a better result in multi-objective environments.

5 Conclusion and outlook

In this paper, we have proposed a Two-Stage MOTP with two interesting characteristics, that one being about the goal preferences of the DM and another one consists in the selection of particular values of supply and demand from grey supply and grey demand. Solution of the MOTP under these goals through RMCGP has provided a technique for multi-objective decision making. But, the main drawback of RMCGP consists in how the DM would select the goals for the objective functions. The core content of our proposed study has removed this difficulty by selecting the goals of the objective functions through an algorithm. We have constructed a utility function (choice by the DM) for selecting the optimal goal region. After this selection, we have solved the proposed problem by our RMCGP approach. Our suggested multi-objective Two-Stage TP has provided a new direction to select proper goals for real-life multi-objective transportation problems under the environment of grey supply and grey demand. A numerical example has been given to show the applicability and suitability of our way of solving MOTP and fixing the proper goals for the objective functions.

In the future scope of our study, we can address different kinds of uncertainty related to the data, such as fuzzy, stochastic, etc., and test several examples, such as route selection problem with consideration of a real-life Two-Stage TP, technology selection problem, plant location selection problem, etc., using our proposed methodology. In this paper, we especially provided the research direction of associating our approach with the method by Anderluh et al. (2016) on scheduling traffic flow in a city. In addition to all the aforementioned, we can employ our study for selecting optimal goals in inventory optimization, supply chain management and other areas.