1 Introduction

In recent years, mobile robots are extensively used in industry and for tasks in dangerous and harsh environments, such as space exploration, military, rescue in the event of natural disasters, and nuclear areas, etc. the ability to track a planned path and perform tasks in these environments autonomously is still among the main challenges facing researchers in the intelligent mobile robot’s field. Significant recent studies have been focused on trajectory tracking control. Most of the proposed control strategies are using the kinematic model which produces a reference velocity based on position errors [1,2,3,4,5].

Recently, many studies have been done on the artificial intelligence application in mobile robot control such as fuzzy logic (FLC) and neural network (NN). The Fuzzy control (FLC) uses linguistic information based on human expertise, as a result, the FLC has several advantages such as stability, robustness, no models are required (free model), using expert knowledge and the IF-THEN rules algorithm [6, 7]. Thus, the FLC has attracted more attention in mobile robot control research. In [8], Castillo et al. designed a dynamic fuzzy logic controller for mobile robot trajectory tracking with membership functions optimization using Ant Colony algorithm. In [9], Huq et al. proposed a behaviour-modulation technique which combined the state-based formalism of discrete event system (DES) with the deterministic fuzzy decision making. In [10], Hou et al. proposed adaptive control via fuzzy approach and backstepping for mobile robot control. In [11], Bencherif and Chouireb presented a sensors data fusion based on the fuzzy logic technique for navigation of wheeled mobile robot in an unknown environment. In [7], Hagras. presented a control architecture using type-2 FLC for mobile robot navigation in dynamical unknown environments.

Previous studies achieved the main control objectives and thus have a huge impact on mobile robot control. But on the other hand, the fuzzy logic needs a human expertise knowledge information (there is no learning ability) and Fuzzy rule derivation is often difficult [12]. Recently, much research is interested in the development and applications neural network (NN) for control and system identification. In [13], Bencherif and Chouireb proposed a new training method for a neural network which is based on a combination between Levenberg-Marquardt optimisation method and iterated Kalman Filter for mobile robot trajectory tracking control. In [14], Yacine et al. presented the design of a kinematic controller for wheeled mobile robot trajectory tracking based on an adaptive neural network (ADALINE). In [15], Li et al. proposed an incorporating Neural-Dynamic optimisation based on predictive model control approach for mobile robot tracking control. In [16], Shojaei et al. presented mobile robots formation trajectory tracking control of type (m, s) by using neural adaptive feedback.

More recently, there has been much research that discusses incorporating the behaviours of fuzzy logic (FLSs) and neural networks (NNs). The fuzzy neural networks (FNNs) get their learning ability from NNs, and their inference technology from fuzzy systems, FNNs are an effective tool for mobile robot control. FNNs include, the adaptive network based fuzzy inference system (ANFIS) [17, 18] with a fixed structure and all parameters are tuned with a backpropagation or a hybrid learning algorithms and use for the consequent part the Takagi-Sugeno-Kang (TSK) type. The self-constructing neural fuzzy inference network (SONFIN) [19] uses the Mamdani type for the consequent part. The recurrent FNN (RFNN) [20, 21] takes the form of self-feedback connections used as internal memories and are done by returning the output of each membership function (MF) back as an input.

Moreover, all of the aforementioned FNNs and RFNN are based on type-1 fuzzy sets. In recent years, type-2 fuzzy logic systems (FLSs) have drawn much attention in many studies, the type-2 fuzzy logic introduced by Zedah in [22]. The use of type-2 fuzzy sets in nonlinear dynamic systems that are exposed to a variety of internal and external perturbations shows that type-2 methods have more potential than type-1 methods. However, the theory of type-2 FLS is more complicated than type-1 FLS theory. The interval type-2 fuzzy sets have been proposed in [23] to remove complexity and improve the type-2 fuzzy sets theory. The interval type-2 FNN has attracted a great attention in [12, 24,25,26,27,28,29,30,31,32,33], and proposed a learning process for an interval type-2 FNN system with uncertain means Gaussian membership functions. In [24], Abiyev and Kaynak described the design of IT2FNN using gradient descent learning algorithm for identification and control of time varying systems. In [25, 26], the authors proposed a self-learning IT2FNN with a fixed structure using sliding mode (SM) theory for parameters learning . In [27], Lin et al. used IT2FNN with adaptive control law for motion control. Castro et al. [28] proposed a hybrid learning algorithm for IT2FNN. In [12, 29], the authors proposed a self-evolving interval type-2 FNN (SEIT2FNN)uses interval type-2 fuzzy sets with type-2 Gaussian MFs uncertain means in the antecedent parts and Takagi-Sugeno-Kang (TSK) fuzzy sets in the consequent parts. Also, it uses the structure learning process to self-structure evolving for the IT2FNN and parameter learning to tuned the antecedent parameters using gradient descent algorithm. The consequent parameters are learned by using a rule-ordered Kalman filter. In [30], Juang et al. proposed a RSEIT2FNN for Dynamic nonlinear Systems, the antecedent part of RSEIT2FNN forms a local internal feedback connections loop by feeding the firing strength of each rule back to itself. In [31], Lin et al. applied a functional-link network (FLN) to the self-evolving IT2FNN for identification and control time-varying plants. In [32], Lin et al. designed a self-organisation T2FNN using gradient descent for parameters learning and the particle swarm optimization (PSO) method to find the optimal learning rates, applied for antilock braking systems. In [33], Lin, Y et al. proposed a simplified interval type-2 fuzzy neural networks with design factors qr and ql are learned to set the upper and lower values to avoid using K-M iterative method to find L and R points.

The motivation of this paper is to construct a self evolving recurrent TSK interval type 2 FNN for mobile robot trajectory tracking. A self evolving algorithm gives the ability to achieve the suitable structure of RTSKIT2FNN during the online learning, and the varied learning rates algorithm VLR is used to find the optimal learning rates of the gradient descent algorithm and to guarantee a good stability convergence of the control system which is proved using the discrete Lyapunov function. The major contributions of the proposed control are summarized as:

  1. (1)

    Successful apply a recurrent frame into interval type-2 FNN structure by using internal-feedback loops in the antecedent part are formed by feeding the interval output of each membership function back to itself.

  2. (2)

    A type-reduction process in the RTSKIT2FNN is performed by fixing the design factors ql and qr to reduce the computational time.

  3. (3)

    The online structure and parameters learning algorithms are used to ameliorate the learning performances of the RTSKIT2FNN-VLR. Initially, the rule base in the RTSKIT2FNN is empty, and all rules are generated online by the structure learning algorithm. Concurrently to structure learning all the consequent and the antecedent parameters of the RTSKIT2FNN are learned by gradient descent algorithm.

  4. (4)

    The design of the varied learning rates algorithm VLR to adjust the learning rates of the gradient descent algorithm to guarantee the robustness and the stability convergence of the system.

  5. (5)

    In addition, experimental results were conducted to verify the proposed control RTSKIT2FNN-VLR performances by a comprehensive comparison with type-1 FNN and RFNN and other type 2 IFNN’s.

The rest of this paper is organized as follows. Section 2 introduces the Kinematics model of the mobile robot. Section 3 presents the RTSKIT2FNN structure. In Section 4, the online structure and parameter learning for RTSKIT2FNN are described in detail. Section 5 presents the experimental results, and Section 6 contains the conclusion.

2 Kinematics model

The unicycle mobile robot kinematics model is the basis of many types of nonholonomic Wheeled Mobile Robots WMRs. For this reason, it has attracted much theoretical attention of researchers.

Unicycle WMRs have usually two driving wheels, one mounted on each side of their center, and a free rolling wheel for carrying the mechanical structure. These two wheels have the same radius r and separated by 2R and are driven by two electrical actuators for the motion and orientation, and the free rolling wheel is a self-adjusted supporting wheel. It is assumed that this mobile robot is made up of a rigid frame and non-deformable wheels, and they are moving in a horizontal 2D plane with the global coordinate frame (O, X, Y). The configuration is represented by vector coordinates: q = [x, y, 𝜃], that is, the position coordinates of the point q the centre of the WMR in the fixed coordinate frame OXY, and its orientation angle as shown in Fig. 1. The linear velocity of the wheels represented by v and the angular velocity of the mobile robot is w. The kinematics model (or equation of motion) of the mobile robot is then given by:

$$ \left( \begin{array}{l} {\dot{x}} \\ {\dot{y}} \\ {\dot{\theta }} \end{array}\right)=\left( \begin{array}{l} {v\text{ cos(}\theta \mathrm{)}} \\ {v\text{ sin(}\theta \mathrm{)}} \\ {w} \end{array}\right) $$
(1)

To consider a trajectory tracking problem, a reference trajectory should be generated. The reference trajectory is:

$$ \left( \begin{array}{l} {\dot{x}_{r} } \\ {\dot{y}_{r} } \\ {\dot{\theta }_{r} } \end{array}\right)=\left( \begin{array}{l} {v_{r} \text{ cos(}\theta_{r} \mathrm{)}} \\ {v_{r} \text{ sin(}\theta_{r} \mathrm{)}} \\ {w_{r} } \end{array}\right) $$
(2)

The error coordinates represented by the world coordinates are:

$$ q_{r} -q=\left( \begin{array}{l} {x_{r} -x} \\ {y_{r} -y} \\ {\theta_{r} -\theta } \end{array}\right) $$
(3)

In the view of moving coordinates, the error coordinates are transformed into:

$$ \left( \begin{array}{l} {x_{e} } \\ {y_{e} } \\ {\theta_{e} } \end{array}\right)=\left( \begin{array}{ccc} {\text{cos}\left( \theta \right)} & {\sin\left( \theta \right)} & {0} \\ {\sin\left( \theta \right)} & {\text{cos}\left( \theta \right)} & {0} \\ {0} & {0} & {1} \end{array}\right)\left( \begin{array}{l} {x_{r} -x} \\ {y_{r} -y} \\ {\theta_{r} -\theta } \end{array}\right) $$
(4)
Fig. 1
figure 1

Model description of a unicycle robot

Full size image

3 Recurrent TSK interval type-2 fuzzy neural networks description

This section introduces the structure of a RTSKIT2FNN. This multi-input single-output (MISO) system consists of n inputs and one output. Figure 2 shows the proposed six-layered network which realizes an interval type-2 fuzzy neural network using Takagi-Sugeno-Kang (TSK) type for the consequent part. The basic functions of each layer are described as follows.

Layer 1:

(Input layer): Each node in this layer represents an input variable xj, j = 1,..., n and there are no weights to be modified in this layer.

Layer 2:

(Fuzzification Layer or membership function layer): each node in the membership layer performs a recurrent interval type-2 MF to execute the fuzzification operation.

The input of the membership layer can be represented by:

$$ {r_{j}^{i}} (t)=x_{j} (t)+\mu_{\overline{A}_{j}^{i} } (t-1){\alpha_{j}^{i}} $$
(5)

Where t denotes the number of iterations, \({\alpha _{i}^{j}} \)represents the weight of the self-feedback loop,\(\mu _{\overline {A}_{j}^{i} } (t-1)\) represents the output signal of layer 2 in the time (t-1) and is defined with Gaussian membership functions as

$$ net_{i} ({r_{j}^{i}} )=-\frac{1}{2} \left( \frac{{r_{j}^{i}} -{m_{j}^{i}} }{{\sigma_{j}^{i}} {}^{} } \right)^{2} $$
(6)
$$ \begin{array}{@{}rcl@{}} \mu_{\overline{A}_{j}^{i} } &=&\exp (net_{i} ({r_{j}^{i}} )) \\ &\equiv& N({m_{j}^{i}} ,{\sigma_{j}^{i}} ,{r_{j}^{i}} ),{m_{j}^{i}} \in \left[m_{j1}^{i} ,m_{j2}^{i} \right] \end{array} $$
(7)

Each MF of the premise part can be represented as a bounded interval in terms of upper MF, \(\overline {\mu }_{j}^{i}\), and a lower MF,\(\underline {\mu }_{j}^{i} \), where

$$ \overline{\mu }_{j}^{i} ({r_{j}^{i}} )=\left\{\begin{array}{l} {N(m_{j1}^{i} ,{\sigma_{j}^{i}} ,{r_{j}^{i}} ),{r_{j}^{i}} <m_{j1}^{i} } \\ {1,\begin{array}{ccc} {} & {} & {\begin{array}{cc} {} & {m_{j1}^{i} \le {r_{i}^{i}} \le m_{j2}^{i} } \end{array}} \end{array}} \\ {N(m_{j2}^{i} ,{\sigma_{j}^{i}} ,{r_{j}^{i}} ),{r_{j}^{i}} >m_{j2}^{i} } \end{array}\right. $$
(8)

And

$$ \underline{\mu }_{j}^{i} ({r_{j}^{i}} )=\left\{\begin{array}{l} {N(m_{j1}^{i} ,{\sigma_{j}^{i}} ,{r_{j}^{i}} ),{r_{i}^{i}} \le \frac{m_{j1}^{i} +m_{j2}^{i} }{2} } \\ {N(m_{j2}^{i} ,{\sigma_{j}^{i}} ,{r_{j}^{i}} ),{r_{j}^{i}} >\frac{m_{j1}^{i} +m_{j2}^{i} }{2} } \end{array}\right. $$
(9)

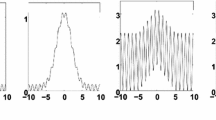
And thus, the output of this layer can be represented as an interval \([\overline {\mu }_{j}^{i} ,\underline {\mu }_{j}^{i} ]\) as shown in Fig. 3 .

Layer 3 (Firing Layer)::

In this layer, there are M nodes each node represents one fuzzy rule, and it computes the firing strength using the values that it receives from layer 2 and an algebraic product operator adopted in fuzzy meet operations, to generate the spatial firing strength Fi, and is computed as follows

$$ {\underline f^{i}} = \prod\limits_{j = 1}^{n} {\underline \mu_{j}^{i}},{\overline f^{i}} = \prod\limits_{j = 1}^{n} {\overline \mu_{j}^{i}} \text{~and~} F^{i} = [\underline f^{i} ;\overline f^{i} ] \ $$
(10)
Layer 4 (Consequent Layer)::

In this layer, each node represents a TSK-type consequent node, for each rule node in layer 3 there is a corresponding consequent node in layer 4. The output is an interval type-1 set and can be represented as \([{w_{l}^{i}} ,{w_{r}^{i}} ]\) where l and r indices represent the left and right limits respectively, the node output can be expressed as

$$ [{w_{l}^{i}} ,{w_{r}^{i}} ]=[{c_{0}^{i}} -{s_{0}^{i}} ,{c_{0}^{i}} +{s_{0}^{i}} ]+\sum\limits_{j=1}^{n}[{c_{j}^{i}} -{s_{j}^{i}} ,{c_{j}^{i}} +{s_{j}^{i}} ]x_{j} $$
(11)

that is

$$ {w_{l}^{i}} =\sum\limits_{j=0}^{n}{c_{j}^{i}} x_{j} -\sum\limits_{j=0}^{n}\left|x_{j} \right| {s_{j}^{i}} $$
(12)

and

$$ {w_{r}^{i}} =\sum\limits_{j=0}^{n}{c_{j}^{i}} x_{j} +\sum\limits_{j=0}^{n}\left|x_{j} \right| {s_{j}^{i}} $$
(13)

where x0 ≡ 1.

Layer 5 (Output Processing Layer)::

Each node in this layer computes an interval output [yl, yr] by using the output from layer 4 and the firing strength Fi from layer 3, and the design factors [ql, qr] proposed in [33] to adjust the upper and lower values without using the Karnik-Mendel iterative method. In this paper, ql and qr are non-adjustable values and set to 0.5. The outputs of this layer can be computed by

$$ y_{l} =\frac{(1-q_{l} ){\sum}_{i=1}^{M}\underline{f}^{i} {w_{l}^{i}} +q_{l} {\sum}_{i=1}^{M}\overline{f}^{i} {w_{l}^{i}} }{{\sum}_{i=1}^{M}\underline{f}^{i} +\overline{f}^{i} } $$
(14)

And

$$ y_{r} =\frac{(1-q_{r} ){\sum}_{i=1}^{M}\overline{f}^{i} {w_{r}^{i}} +q_{r} {\sum}_{i=1}^{M}\underline{f}^{i} {w_{r}^{i}} }{{\sum}_{i=1}^{M}\underline{f}^{i} +\overline{f}^{i} } $$
(15)
Layer 6 (output layer)::

The node in this layer computes the output variable of the RTSKIT2FNN using a sum operation of the output interval of layer 5 yl and yr. In this paper the output of this layer is given by

$$ y=\frac{y_{l} +y_{r} }{2} $$
(16)
Fig. 2
figure 2

Structure of the RTSKIT2FNN

Full size image
Fig. 3
figure 3

Interval type-2 fuzzy set of Gaussian shape

Full size image

4 Online learning algorithm

This section presents the two-phase learning scheme algorithm for RTSKIT2FNN. The objective of the first phase is structure learning that discusses how to construct the RTSKIT2FNN rules. The learning starts with empty rule-base in the RTSKIT2FNN and all fuzzy rules are evolved by an online structure learning scheme. The second phase is the parameter learning phase that uses a gradient descent algorithm with varied learning rates for online parameters learning.

4.1 Structure learning

The structure learning used the rule firing strength variation as a criterion for rule generation, this idea was used for type-1 fuzzy rule generation in [19], and developed to type-2 fuzzy rule generation [12, 33] by using the interval firing strength Fi in (10), the structure learning of the proposed RTSKIT2FNN is introduced as follows.

For the first incoming data point \(\overrightarrow x \) is used to generate the first fuzzy rule with mean, width, centre and the weight of the self-feedback loop of recurrent interval type 2 fuzzy set as

$$ \begin{array}{@{}rcl@{}} [m_{j1}^{1} ,m_{j2}^{1} ]&=&[x_{j} -{\Delta} x,x_{j} +{\Delta} x] ,\\ {\sigma_{j}^{1}} &=&\sigma_{fixed} \text{~and~} {\alpha_{j}^{1}} =\alpha_{fixed} \end{array} $$
(17)

where σfixed is a predefined threshold, Δx indicates the width of the uncertain mean region. If Δx is too small, then the type-2 fuzzy set approximates a type-1 fuzzy set and if Δx is too large, then a type-2 fuzzy set will cover most of the input domain. In this paper Δx and σfixed are set to 0.1 and 0.3 respectively and αfixed is set to 0.1.

For each subsequent of incoming data \(\overrightarrow x \), we compute the firing strengths interval in (10) then we compute the mean or centre value of firing strength for each rule i denoted as

$$ {f_{c}^{i}} =\frac{\bar{f}^{i} +\underline{f}^{i} }{2} $$
(18)

\({f_{c}^{i}}\) the spatial firing strength centre is a rule generation criterion to generate a new rule based on a predetermined threshold fth . For each new incoming data,

$$ I=\arg {\underset{1\le i\le M(t)}{\max }} {f_{c}^{i}} $$
(19)

With M(t) is the number of generated rules at time t. If \({f_{c}^{I}}\le f_{th} \), then new fuzzy rules will be generated M(t+ 1)=M(t)+ 1; this condition means that the data point does not match well from any existing rules, so the new fuzzy rule evolved. The uncertain means, width and centre of type 2 fuzzy set related to the new fuzzy rule are defined in the same manner as the first rule

$$ [m_{j1}^{M(t)+1} ,m_{j2}^{M(t)+1} ]=[x_{j} -{\Delta} x,x_{j} +{\Delta} x] \text{~,~} \alpha_{j}^{M(t)+1} =0.1 $$
(20)

and

$$ \sigma_{j}^{M(t)+1} =\beta \left|x_{j} -\frac{m_{j1}^{I} +m_{j2}^{I} }{2} \right| $$
(21)

where β > 0 determines the overlap degree between fuzzy sets. Equation (21) denotes that the width is equal to Euclidean distance between the average centres of the new fuzzy set and fuzzy set I. The high overlapping between fuzzy sets is obtained when β is too large, and there is no overlapping if β is too small. In this paper is set to 0.5; this indicates that the width is equal to the half distance between fuzzy sets

The initial consequent parameters \({c_{j}^{1}}\) with j = 1,.., n in the first rule are set to very small values 0.05, and \({s_{j}^{1}}\) are defined as the initial output interval range are set to very small values 0.002. For the new generated rules the consequent parameters are assigned to the same values as the first rules

$$ {c_{j}^{1}} =c_{j}^{M\left( t+1\right)} =0.05 j=1,{\ldots} n $$
(22)
$$ {s_{j}^{1}} =s_{j}^{M\left( t+1\right)} =0.002 $$
(23)

The structure learning and fuzzy rules generation algorithm as follows:

figure a

Parameters of each evolved rules are modified by the parameter-learning algorithm introduced in the next section.

4.2 Parameter learning

Parameter learning is performed concurrently with the structure learning process. Parameter Learning tunes all parameters for each fuzzy rule, including the current fuzzy rule and that was newly generated. To describe the parameter learning, we define the objective function as

$$ E=\frac{1}{2} \left( y_{d} \left( t+1\right)-y\left( t+1\right)\right)^{2} $$
(24)

where yd(t + 1) is the desired output and y(t + 1) is the output of RTSKIT2FNN. The updated parameters based on gradient descent algorithm are given by the following equations:

$$ m_{j1}^{i} \left( t+1\right)=m_{j1}^{i} \left( t\right)-\eta_{m_{1} } \frac{\partial E}{\partial m_{j1}^{i} } $$
(25)
$$ m_{j2}^{i} \left( t+1\right)=m_{j2}^{i} \left( t\right)-\eta_{m_{2} } \frac{\partial E}{\partial m_{j2}^{i} } $$
(26)
$$ {\sigma_{j}^{i}} \left( t+1\right)={\sigma_{j}^{i}} \left( t\right)-\eta_{\sigma } \frac{\partial E}{\partial {\sigma_{j}^{i}} } $$
(27)
$$ {\alpha_{j}^{i}} \left( t+1\right)={\alpha_{j}^{i}} \left( t\right)-\eta_{\alpha } \frac{\partial E}{\partial {\alpha_{j}^{i}} } $$
(28)
$$ {c_{j}^{i}} \left( t+1\right)={c_{j}^{i}} \left( t\right)-\eta_{c} \frac{\partial E}{\partial {c_{j}^{i}} } $$
(29)
$$ {s_{j}^{i}} \left( t+1\right)={s_{j}^{i}} \left( t\right)-\eta_{s} \frac{\partial E}{\partial {s_{j}^{i}} } $$
(30)

where ηm1, ηm2, ησ, ηα, ηc, ηs are the learning rates , j = 1,., n and i = 1,, M, n and M are the number of inputs and rules respectively . The derivation of the premise part in (25)–(28) can be expressed by the following:

$$ \begin{array}{@{}rcl@{}} \frac{\partial E}{\partial m_{j1}^{i} } &=&(y-y_{d} )\times \left( \left( \frac{\partial y_{l} }{\partial \bar{f}^{i} } + \frac{\partial y_{r} }{\partial \bar{f}^{i} } \right)\frac{\partial \bar{f}^{i} }{\partial m_{j1}^{i} }\right.\\ &&\qquad\qquad\qquad\left.+\left( \frac{\partial y_{l} }{\partial \underline{f}^{i} } +\frac{\partial y_{r} }{\partial \underline{f}^{i} } \right)\frac{\partial \underline{f}^{i} }{\partial m_{j1}^{i} } \right) \end{array} $$
(31)
$$ \begin{array}{@{}rcl@{}} \frac{\partial E}{\partial m_{j2}^{i} } &=&(y-y_{d} )\times \left( \left( \frac{\partial y_{l} }{\partial \bar{f}^{i} } + \frac{\partial y_{r} }{\partial \bar{f}^{i} } \right)\frac{\partial \bar{f}^{i} }{\partial m_{j2}^{i} } \right.\\ &&\qquad\qquad\qquad\left.+\left( \frac{\partial y_{l} }{\partial \underline{f}^{i} } + \frac{\partial y_{r} }{\partial \underline{f}^{i} } \right)\frac{\partial \underline{f}^{i} }{\partial m_{j2}^{i} } \right) \end{array} $$
(32)
$$ \begin{array}{@{}rcl@{}} \frac{\partial E}{\partial {\sigma_{j}^{i}} } &=&(y-y_{d} )\times \left( \left( \frac{\partial y_{l} }{\partial \bar{f}^{i} } +\frac{\partial y_{r} }{\partial \bar{f}^{i} } \right)\frac{\partial \bar{f}^{i} }{\partial {\sigma_{j}^{i}} } \right.\\ &&\qquad\qquad\qquad\left.+\left( \frac{\partial y_{l} }{\partial \underline{f}^{i} } +\frac{\partial y_{r} }{\partial \underline{f}^{i} } \right)\frac{\partial \underline{f}^{i} }{\partial {\sigma_{j}^{i}} } \right) \end{array} $$
(33)
$$ \begin{array}{@{}rcl@{}} \frac{\partial E}{\partial {\alpha_{j}^{i}} } &=&(y-y_{d} )\times \left( \left( \frac{\partial y_{l} }{\partial \bar{f}^{i} } +\frac{\partial y_{r} }{\partial \bar{f}^{i} } \right)\frac{\partial \bar{f}^{i} }{\partial {\alpha_{j}^{i}} } \right.\\ &&\qquad\qquad\qquad\left.+\left( \frac{\partial y_{l} }{\partial \underline{f}^{i} } +\frac{\partial y_{r} }{\partial \underline{f}^{i} } \right)\frac{\partial \underline{f}^{i} }{\partial {\alpha_{j}^{i}} } \right) \end{array} $$
(34)

The derivation of \(\frac {\partial y}{\partial f}\) can be expressed by the following equations :

$$ \frac{\partial y_{l} }{\partial \bar{f}^{i} } =\frac{(1-q_{l} )w_{l} -y_{l} }{\sum \bar{f}^{i} +\underline{f}^{i} } $$
(35)
$$ \frac{\partial y_{l} }{\partial \underline{f}^{i} } =\frac{q_{l} w_{l} -y_{l} }{\sum \bar{f}^{i} +\underline{f}^{i} } $$
(36)
$$ \frac{\partial y_{r} }{\partial \bar{f}^{i} } =\frac{q_{r} w_{r} -y_{r} }{\sum \bar{f}^{i} +\underline{f}^{i} } $$
(37)
$$ \frac{\partial y_{r} }{\partial \underline{f}^{i} } =\frac{(1-q_{r} )w_{r} -y_{r} }{\sum \bar{f}^{i} +\underline{f}^{i} } $$
(38)

Now, we calculate the derivatives of firing functions with respect to the premise parameters

$$ \frac{\partial \bar{f}^{i} }{\partial m_{j1}^{i} } =\frac{\partial \bar{f}^{i} }{\partial \overline{\mu }_{j}^{i} } \frac{\partial \overline{\mu }_{j}^{i} }{\partial m_{j1}^{i} } =\left\{\begin{array}{l} {\bar{f}^{i} \times \frac{{r_{j}^{i}} -m_{j1}^{i} }{({\sigma_{j}^{i}} )^{2} } ,{r_{j}^{i}} <m_{j1}^{i} } \\ {0\begin{array}{ccc} {} & {} & {\begin{array}{cc} {} & {\begin{array}{cc} {} & {otherwise} \end{array}} \end{array}} \end{array}} \end{array}\right. $$
(39)
$$ \frac{\partial \underline{f}^{i} }{\partial m_{j1}^{i} } =\frac{\partial \underline{f}^{i} }{\partial \underline{\mu }_{j}^{i} } \frac{\partial \underline{\mu }_{j}^{i} }{\partial m_{j1}^{i} } =\left\{\begin{array}{l} {\underline{f}^{i} \times \frac{{r_{j}^{i}} -m_{j1}^{i} }{({\sigma_{j}^{i}} )^{2} } ,{r_{j}^{i}} >\frac{m_{j1}^{i} +m_{j2}^{i} }{2} } \\ {0\begin{array}{ccc} {} & {} & {\begin{array}{cc} {} & {\begin{array}{cc} {} & {otherwise} \end{array}} \end{array}} \end{array}} \end{array}\right. $$
(40)
$$ \frac{\partial \bar{f}^{i} }{\partial m_{j2}^{i} } =\frac{\partial \bar{f}^{i} }{\partial \overline{\mu }_{j}^{i} } \frac{\partial \overline{\mu }_{j}^{i} }{\partial m_{j2}^{i} } =\left\{\begin{array}{l} {\bar{f}^{i} \times \frac{{r_{j}^{i}} -m_{j2}^{i} }{({\sigma_{j}^{i}} )^{2} } ,{r_{j}^{i}} >m_{j2}^{i} } \\ {0\begin{array}{ccc} {} & {} & {\begin{array}{cc} {} & {\begin{array}{cc} {} & {otherwise} \end{array}} \end{array}} \end{array}} \end{array}\right. $$
(41)
$$ \frac{\partial \underline{f}^{i} }{\partial m_{j2}^{i} } =\frac{\partial \underline{f}^{i} }{\partial \underline{\mu }_{j}^{i} } \frac{\partial \underline{\mu }_{j}^{i} }{\partial m_{j2}^{i} } =\left\{\begin{array}{l} {\underline{f}^{i} \times \frac{{r_{j}^{i}} -m_{j2}^{i} }{({\sigma_{j}^{i}} )^{2} } ,{r_{j}^{i}} \le \frac{m_{j1}^{i} +m_{j2}^{i} }{2} } \\ {0\begin{array}{ccc} {} & {} & {\begin{array}{cc} {} & {\begin{array}{cc} {} & {otherwise} \end{array}} \end{array}} \end{array}} \end{array}\right. $$
(42)
$$ \frac{\partial \bar{f}^{i} }{\partial {\sigma_{j}^{i}} } =\frac{\partial \bar{f}^{i} }{\partial \overline{\mu }_{j}^{i} } \frac{\partial \overline{\mu }_{j}^{i} }{\partial {\sigma_{j}^{i}} } =\left\{\begin{array}{l} {\bar{f}^{i} \times \frac{({r_{j}^{i}} -m_{j1}^{i} )^{2} }{({\sigma_{j}^{i}} )^{3} } ,{r_{j}^{i}} <m_{j1}^{i} } \\ {\bar{f}^{i} \times \frac{({r_{j}^{i}} -m_{j2}^{i} )^{2} }{({\sigma_{j}^{i}} )^{3} } ,{r_{j}^{i}} <m_{j2}^{i} } \\ {0\begin{array}{ccc} {} & {} & {\begin{array}{cc} {} & {\begin{array}{cc} {} & {otherwise} \end{array}} \end{array}} \end{array}} \end{array}\right. $$
(43)
$$ \frac{\partial \underline{f}^{i} }{\partial {\sigma_{j}^{i}} } =\frac{\partial \underline{f}^{i} }{\partial \underline{\mu }_{j}^{i} } \frac{\partial \underline{\mu }_{j}^{i} }{\partial {\sigma_{j}^{i}} } =\left\{\begin{array}{l} {\underline{f}^{i} \times \frac{({r_{j}^{i}} -m_{j2}^{i} )^{2} }{({\sigma_{j}^{i}} )^{3} } ,{r_{j}^{i}} \le \frac{m_{j1}^{i} +m_{j2}^{i} }{2} } \\ {\underline{f}^{i} \times \frac{({r_{j}^{i}} -m_{j1}^{i} )^{2} }{({\sigma_{j}^{i}} )^{3} } ,{r_{j}^{i}} >\frac{m_{j1}^{i} +m_{j2}^{i} }{2} } \end{array}\right. $$
(44)
$$ \begin{array}{@{}rcl@{}} \frac{\partial \bar{f}^{i} }{\partial {\alpha_{j}^{i}} } &=&\frac{\partial \bar{f}^{i} }{\partial \overline{\mu}_{j}^{i}} \frac{\partial \overline{\mu}_{j}^{i}}{\partial {\alpha_{j}^{i}}} =\frac{\partial \bar{f}^{i}} {\partial \overline{\mu}_{j}^{i}} \left( \frac{\partial \overline{\mu}_{j}^{i}}{\partial {r_{j}^{i}}} \frac{\partial {r_{j}^{i}}}{\partial {\alpha_{j}^{i}}} \right)\\ &=&\left\{\begin{array}{l} {\bar{f}^{i} \times \frac{{r_{j}^{i}} -m_{j1}^{i} {~}^{~} }{({\sigma_{j}^{i}} )^{2} } \times \overline{\mu }_{j}^{i} (t-1),{r_{j}^{i}} <m_{j1}^{i} } \\ {\bar{f}^{i} \times \frac{{r_{j}^{i}} -m_{j2}^{i} }{({\sigma_{j}^{i}} )^{2} } \times \overline{\mu }_{j}^{i} (t-1),{r_{j}^{i}} <m_{j2}^{i} } \\ {0\begin{array}{ccc} {} & {} & {\begin{array}{cc} {} & {\begin{array}{cc} {} & {otherwise} \end{array}} \end{array}} \end{array}} \end{array}\right. \end{array} $$
(45)
$$ \begin{array}{@{}rcl@{}} \frac{\partial \underline{f}^{i} }{\partial {\alpha_{j}^{i}} } &=&\frac{\partial \underline{f}^{i} }{\partial \underline{\mu }_{j}^{i} } \frac{\partial \underline{\mu }_{j}^{i} }{\partial {\alpha_{j}^{i}} } =\frac{\partial \underline{f}^{i} }{\partial \underline{\mu }_{j}^{i} } \left( \frac{\partial \underline{\mu }_{j}^{i} }{\partial {r_{j}^{i}} } \frac{\partial {r_{j}^{i}} }{\partial {\alpha_{j}^{i}} } \right)\\ &=&\left\{\begin{array}{l} {\underline{f}^{i} \times \frac{{r_{j}^{i}} -m_{j2}^{i} }{({\sigma_{j}^{i}} )^{2} } \times \underline{\mu }_{j}^{i} (t-1),{r_{j}^{i}} \le \frac{m_{j1}^{i} +m_{j2}^{i} }{2} } \\ {\underline{f}^{i} \times \frac{{r_{j}^{i}} -m_{j1}^{i} }{({\sigma_{j}^{i}} )^{2} } \times \underline{\mu }_{j}^{i} (t-1),{r_{j}^{i}} >\frac{m_{j1}^{i} +m_{j2}^{i} }{2} } \end{array}\right. \end{array} $$
(46)

Then the derivation of consequent parameter in (29–30) can be expressed by the following:

$$ \begin{array}{@{}rcl@{}} \frac{\partial E}{\partial {c_{j}^{i}} } \!&=&\!(y-y_{d} )\!\times\! \left( \left( \frac{\partial y}{\partial y_{l} } \frac{\partial y_{l} }{\partial {w_{l}^{i}} } \frac{\partial {w_{l}^{i}} }{\partial {c_{j}^{i}} } \right)+\left( \frac{\partial y}{\partial y_{r} } \frac{\partial y_{r} }{\partial {w_{r}^{i}} } \frac{\partial {w_{r}^{i}} }{\partial {c_{j}^{i}} } \right)\right) \\ \!&=&\!(y-y_{d} )\!\times\! \left( \frac{(1-q_{l} )\underline{f}^{i} +q_{l} \overline{f}^{i} }{2{\sum}_{i=1}^{M}\underline{f}^{i} +\overline{f}^{i} } x_{j} \right.\\ &&\qquad\qquad\qquad\left. +\frac{(1-q_{r} )\overline{f}^{i} +q_{r} \underline{f}^{i} }{2{\sum}_{i=1}^{M}\underline{f}^{i} +\overline{f}^{i} } x_{j} \right)\\ \mathrm{ }\!&=&\!(y-y_{d} )\!\times\! \left( \frac{x_{j} }{2{\sum}_{i=1}^{M}\underline{f}^{i} +\overline{f}^{i} } \right)(1 - q_{l} +q_{r} )\underline{f}^{i} \\ &&\!+(1 - q_{r} +q_{l} )\overline{f}^{i} \end{array} $$
(47)
$$ \begin{array}{@{}rcl@{}} \frac{\partial E}{\partial {s_{j}^{i}} } \!&=&\!(y-y_{d} )\times \left( \left( \frac{\partial y}{\partial y_{l} } \frac{\partial y_{l} }{\partial {w_{l}^{i}} } \frac{\partial {w_{l}^{i}} }{\partial {s_{j}^{i}} } \right)+\left( \frac{\partial y}{\partial y_{r} } \frac{\partial y_{r} }{\partial {w_{r}^{i}} } \frac{\partial {w_{r}^{i}} }{\partial {s_{j}^{i}} } \right)\right) \\\!&=&\!(y-y_{d} )\times \left( \frac{(1-q_{r} )\overline{f}^{i} +q_{r} \underline{f}^{i} }{2{\sum}_{i=1}^{M}\underline{f}^{i} +\overline{f}^{i} } \left|x_{j} \right|\right.\\ &&\qquad\qquad\qquad\left. -\frac{(1-q_{l} )\underline{f}^{i} +q_{l} \overline{f}^{i} }{2{\sum}_{i=1}^{M}\underline{f}^{i} +\overline{f}^{i} } \left|x_{j} \right|\right) \\ \!&=&\!(y-y_{d} )\times \left( \frac{\left|x_{j} \right|}{2{\sum}_{i=1}^{M}\underline{f}^{i} +\overline{f}^{i} } \right)(1-q_{r} -q_{l} )\overline{f}^{i}\\ &&-(1-q_{l} -q_{r} )\underline{f}^{i} \end{array} $$
(48)

The structure of the global online learning process is presented in the flowchart Fig. 4.

Fig. 4
figure 4

Flowchart of the online learning of the RTSKIT2FNN

Full size image

4.3 Convergence analysis

In this section, we propose the varied learning rates of parameter learning to assure the convergence of the tracking errors based on the analysis of a discrete-type Lyapunov function. Consider the objective function in (24) as the discrete Lyapunov function.

The derivative of the proposed discrete Lyapunov function can be written as

$$ {\Delta} E\left( t\right)=E\left( t+1\right)-E\left( t\right) $$
(49)

The linearized model of (49) can be calculated via (25)–(30) as follow

$$ \begin{array}{@{}rcl@{}} E\left( t+1\right)&=&E\left( t\right)+{\Delta} E\left( t\right) \\ &\approx& E\left( t\right)-{\sum}_{j=1}^{n}\eta_{m_{1} } \left( \frac{\partial E}{\partial m_{j1}^{i} } \right)^{2} +\eta_{m_{2} } \left( \frac{\partial E}{\partial m_{j2}^{i} } \right)^{2} \\ &&+\eta_{\sigma } \left( \frac{\partial E}{\partial {\sigma_{j}^{i}} } \right)^{2} +\eta_{c} \left( \frac{\partial E}{\partial {c_{j}^{i}} } \right)^{2} +\eta_{s} \left( \frac{\partial E}{\partial {s_{j}^{i}} } \right)^{2} \\ &&+\eta_{\alpha } \left( \frac{\partial E}{\partial {\alpha_{j}^{i}} } \right)^{2} \end{array} $$
(50)

Then E(t + 1) can be expressed as

$$ \begin{array}{@{}rcl@{}} E\left( {t + 1} \right) &=& \left( {\frac{1}{6}E\left( t \right) - {\eta_{{m_{1}}}}{{\sum\limits_{j = 1}^{n} {\left( {\frac{{\partial E}}{{\partial m_{j1}^{i}}}} \right)} }^{2}}} \right) \\ &&+\left( {{\text{ }}\frac{1}{6}E\left( t \right) - {\eta_{{m_{2}}}}\sum\limits_{j = 1}^{n} {{{\left( {\frac{{\partial E}}{{\partial m_{j2}^{i}}}} \right)}^{2}}} } \right)\\ &&+\left( {\frac{1}{6}E\left( t \right) - {\eta_{\sigma} }\sum\limits_{j = 1}^{n} {{{\left( {\frac{{\partial E}}{{\partial {\sigma_{j}^{i}}}}} \right)}^{2}}} } \right) {\text{ }}\\ &&+\left( {\frac{1}{6}E\left( t \right) - {\eta_{c}}\sum\limits_{j = 1}^{n} {{{\left( {\frac{{\partial E}}{{\partial {c_{j}^{i}}}}} \right)}^{2}}} } \right)\\ &&+ \left( {\frac{1}{6}E\left( t \right) - {\eta_{s}}\sum\limits_{j = 1}^{n} {{{\left( {\frac{{\partial E}}{{\partial {s_{j}^{i}}}}} \right)}^{2}}} } \right) \\ &&+ \left( {\frac{1}{6}E\left( t \right) - {\eta_{\alpha} }\sum\limits_{j = 1}^{n} {{{\left( {\frac{{\partial E}}{{\partial {\alpha_{j}^{i}}}}} \right)}^{2}}} } \right) \end{array} $$
(51)

where ηm1, ηm2, ησ, ηα, ηc, ηs are the learning rates parameters. The derivatives of the objective function in (51) are calculated in parameter learning Section 4.2. The learning-rate parameters of the RTSKIT2FNN are designed as

$$ \eta_{m_{1} } =\frac{E\left( t\right)}{6\left[{\sum}_{j=1}^{n}\left( \frac{\partial E}{\partial m_{j1}^{i} } \right)^{2} +\varepsilon \right]} $$
(52)
$$ \eta_{m_{2} } =\frac{E(t)}{6\left[{\sum}_{j=1}^{n}\left( \frac{\partial E}{\partial m_{j2}^{i} } \right)^{2} +\varepsilon \right]} $$
(53)
$$ \eta_{\sigma } =\frac{E\left( t\right)}{6\left[{\sum}_{j=1}^{n}\left( \frac{\partial E}{\partial {\sigma_{j}^{i}} } \right)^{2} +\varepsilon \right]} $$
(54)
$$ \eta_{\alpha } =\frac{E\left( t\right)}{6\left[{\sum}_{j=1}^{n}\left( \frac{\partial E}{\partial {\alpha_{j}^{i}} } \right)^{2} +\varepsilon \right]} $$
(55)
$$ \eta_{c} =\frac{E(t)}{6\left[{\sum}_{j=1}^{n}\left( \frac{\partial E}{\partial {c_{j}^{i}} } \right)^{2} +\varepsilon \right]} $$
(56)
$$ \eta_{s} =\frac{E(t)}{6\left[{\sum}_{j=1}^{n}\left( \frac{\partial E}{\partial {s_{j}^{i}} } \right)^{2} +\varepsilon \right]} $$
(57)

where ε is positive constant, then (51) can be rewritten as

$$ E\left( t+1\right)\approx \varepsilon \left( \eta_{m_{1} } +\eta_{m_{2} } +\eta_{\sigma } +\eta_{c} +\eta_{s} +\eta_{\alpha } \right) $$
(58)

Applying the learning rates values from (52–57) into the (58) we have

$$ E(t + 1)\!<\!\frac{E(t)}{6} +\frac{E(t)}{6} +\frac{E(t)}{6} +\frac{E(t)}{6} +\frac{E(t)}{6} +\frac{E(t)}{6} =E(t) $$
(59)

From (59), we can guarantee that the error represented in (24) will converge to zero with varied learning rates designed in (52)–(57). Moreover, the mobile robot with the proposed RTSKIT2FNN control system has the ability to track the reference path stably.

5 Experimental results

5.1 Robot description and control architecture

Herein, we present experimental results to validate the control performance of the proposed RTSKIT2FNN with online structure and parameter learning for stable path tracking of mobile robots. In this paper, a Pioneer 3-DX mobile robot is used as an example to verify the effectiveness of the proposed trajectory tracking control scheme shown in Fig. 5.

Fig. 5
figure 5

RTSKIT2FNN control scheme for a unicycle wheeled mobile robot

Full size image

Pioneer 3-DX mobile robot is shown in Fig. 6. The platform is assembled with motors featuring 500-tick encoders, 19 cm wheels, tough aluminum body, 8 forward-facing ultrasonic (sonar) sensors, 1, 2 or 3 hot-swappable batteries, and a complete software development kit. The base Pioneer 3-DX platform can reach speeds of 1.6 meters per second. The Pioneer 3-DX robot is an all-purpose base, used for research and applications involving mapping, teleportation, localization, monitoring, reconnaissance, and other behaviors.

Fig. 6
figure 6

Experimental test with Pioneer 3-DX mobile robot

Full size image

5.2 Results

For RTSKIT2FNN’s, the used parameters are chosen as follows. The RTSKIT2FNN for linear velocity has two inputs \((x_{e} ,\dot {x}_{e} )\) and one output v, the spatial firing strength threshold is set to fth = 0.6. The RTSKIT2FNN for angular velocity has two inputs (ye, 𝜃e) and one output w, the spatial firing strength threshold is fth = 0.3. For the fixed learning rates FLR are set to ηv = 0.5 for linear velocity and ηw = 0.01 for the angular velocity. For the varied learning rates VLR the positive constant ε is set to 0.01 and 0.00001 for the linear and angular velocities respectively. The objective functions for parameters learning of the two RTSKIT2FNN’s are chosen as follows

$$ E_{v} =\frac{1}{2} \left( v_{r} \left( t+1\right)-v\left( t+1\right)\right)^{2} $$
(60)
$$ E_{w} =\frac{1}{2} \left( w_{r} \left( t+1\right)-w\left( t+1\right)\right)^{2} $$
(61)

The sampling time (ts) is 0.01s. In order to exhibit the superiority of the proposed RTSKIT2FNN control system, seven different network structures including ANFIS [17], RFNN [34], IT2FNN [24], IT2FNN-SM [26], SOT2FNN-PSO [32], SEFT2FNN [31] and SIT2FNN in [33] are considered. The SIT2FNN, SEFT2FNN and SOT2FNN-PSO are also examined with the same structure and learning parameters in RTSKIT2FNN with FLR. As a performance criterion, we evaluate the root mean square error (RMSE)

$$ RMSE=\sqrt{\frac{1}{n} \sum\limits_{i=1}^{n}\left( X(i)-X_{r}(i) \right)^{2} } $$
(62)

Experimental results are shown in Figs. 7, 8, 9, 10, and Tables 1, 2, 3 and 4. Figures 7 and 8 show the reference paths Lemniscate and sinusoidal respectively with the real tracked path of the mobile robot using RTSKIT2FNN with varied learning rates (VLR), the dashed red line is the reference trajectory; the solid blue line is the trajectory followed by the mobile robot with RTSKIT2FNN-VLR. Figure 9 presents the position coordinates x, y and 𝜃 of the mobile robot with reference coordinates for the Lemniscate trajectory, the tracking errors xe, ye and 𝜃e are shown in the Fig. 10. From these figures, we can see that, the effectiveness of the proposed control scheme using RTSKIT2FNN -VLR for mobile robot trajectory tracking with stable speed and high accuracy.

Fig. 7
figure 7

Tracking response of a mobile robot with RTSKIT2FNN controllers for Lemniscate trajectory with initial position X0 = [0;− 0.3;π]

Full size image
Fig. 8
figure 8

Tracking response of a mobile robot with RTSKIT2FNN controllers for Sinusoidal trajectory with initial position X0 = [0;0.1;π/4]

Full size image
Fig. 9
figure 9

The position coordinates for lemniscate trajectory

Full size image
Fig. 10
figure 10

Tracking errors

Full size image
Table 1 Comparison results between FLR and VLR
Full size table
Table 2 Influence of fthv on the performance of RTSKIT2FNN with fthw = 0.3
Full size table
Table 3 Influence of fthw on the performance of RTSKIT2FNN with fthv = 0.6
Full size table
Table 4 Comparison results of networks RMSE
Full size table

Table 1 studies the RTSKIT2FNN performances with varied and fixed learning rates for two cases of trajectories. The performances are evaluated using the RMSE of the position (x, y) and the orientation 𝜃. The obtained results show that the RTSKIT2FNN with VLR has better performances than RTSKIT2FNN with FLR. The table shows the difficulty to ensure the good convergence and tracking stability during the online learning by using fixed learning rates (FLR) because the choice of fixed learning rate values is not necessarily appropriate to all of the cases and conditions of tracking control in real time and it may cause in some cases the divergence of the system. On the other hand, the varied learning rates VLR guaranteed the stability, robustness and the good parameters adaptation of the RTSKIT2FNN during the online learning, this VLR property changes the learning rates according to the objective function represented in (60) and (61) to guarantee the convergence of tracking errors.

Additionally, Tables 2 and 3 show the influence of firing strength thresholds fthv and fthw for linear and angular velocity respectively on the performance of RTSKIT2FNN. Table 2 represents the influence of fthv with a fixed fthw and the opposite in Table 3. We notice that larger values of fthv or fthw generate larger numbers of rules and improve the performance of RTSKIT2FNN in general. However, when the value of fthv or fthw is too large, the performance saturates for reason that the online learning process achieved the local minimum, and also the number of rules change according to the learning algorithm types VLR and FLR as shown in Table 4 for the same network. From the two tables the small RMS errors are obtained when fthv = 0.6 and fthw = 0.3.

Table 4 compares the RMSE values and generated rules number for other related networks ; we can note that the T2FNN networks have the smaller RMSE compared to T1FNN which is represented by two structures ANFIS and RFNN. This note shows the high superiority of T2FNN structure for the mobile robot trajectory tracking. The T2FNN is divided into two types in terms of learning principle: static and evolving. For the static type we have two algorithms IT2FNN-SM that uses sliding mode for learning and IT2FNN which uses the gradient descent. For the evolving learning type we have SOT2FNN-PSO, SEFT2FNN, SIT2FNN, RTSKIT2FNN-FLR, and RTSKIT2FNN-VLR. We can note that the IT2FNN-SM has the smaller RMSE than IT2FNN with gradient descent algorithm, and we can note also that the evolving algorithms have lower RMSE than the static algorithms; this demonstrates the superiority of the evolving algorithms. For the evolving algorithms, the proposed RTSKIT2FNN-VLR has the smaller RMSE compared to the other evolving algorithms. This result shows the high superiority and the effectiveness of the proposed algorithm, we can also note that RTSKIT2FNN-VLR and SEFT2FNN have the largest number of generated rules and the lower RMSE this demonstrates, the relationship between the generated rule and the effectiveness of the evolving algorithms.

6 Conclusion

This paper proposed a recurrent TSK Interval Type-2 Fuzzy Neural Networks with online structure and parameters learning control scheme for path tracking of mobile robots. The proposed RTSKIT2FNN has successfully incorporated the recurrent frame of internal-feedback loops into the interval Type-2 Fuzzy Neural Networks. The online learning of RTSKIT2FNN, there is no need to determine an initial network structure for the reason that the structure learning algorithm enables the network to evolve online and generate the required network structure and rules based on the rule firing strength. The structure learning is performed concurrently with parameter learning using the proposed gradient descent algorithm with varied learning rates (VLR) to tune all parameters of the RTSKIT2FNN, the learning convergence and the stability of the control system are proved using the discrete-type Lyapunov function. The experimental results have shown the obvious superiority of the proposed control method for mobile robot trajectory tracking compared to the other control methods.