1 Introduction

The antilock braking system is a safety–critical system in modern cars, which was first invented for the aviation industry in 1920 [1]. During the braking action, ABS helps maintain the steerability of the car by limiting the longitudinal slip. The challenging problem in designing an ABS is that the vehicle braking dynamics are highly nonlinear and the environmental parameters are unknown. Since most commercial ABS control methods do not have an adaptive function to deal with this problem, their performance is often degraded under harsh road conditions [2, 3]. Recently, many intelligent control methods such as fuzzy control, neural network control, sliding mode control, hybrid control and cerebellar model articulation controller (CMAC) have been applied in ABS to improve the performance [3–11]. In 2010, Sharkawy presented a fuzzy self-tuning PID controller for ABS [5]. In 2012, Corno et al. [7] provided hybrid ABS control using force measurement. Following that, in 2013, Lin and Li introduced a self-organizing function-link fuzzy CMAC for ABS [8], where CMAC is a type of neural network based on a model of the mammalian cerebellum [12]. In 2016, Peric et al. [9] presented an ABS control using a quasi-sliding mode control with neural network estimator. However, some of the above methods are complex, and their parameters adjusting laws are not effective enough; furthermore, most control performance can be further improved. In this paper, a self-organizing interval type-2 fuzzy neural network control system will be proposed to control ABS. The proposed controller incorporates the advantages of sliding mode control to enhance stability and performance of the control system [13].

In recent years, the type-2 fuzzy logic system (T2FLS) has attracted many researchers in many application fields such as control problem, system identification, prediction and classification [14–22]. The fuzzy set was first introduced by Zadeh in 1965 [23], and shortly thereafter, it was applied in many fields due to its advantageous properties such as flexibility, intuitive knowledge and easy computation. However, in many cases, this type-1 fuzzy logic system has difficultly achieving optimal performance because it cannot effectively deal with the uncertainty coming from the internal and external disturbances of the plant [14]. To solve this problem, in 1975 Zadeh developed the concept of type-2 fuzzy sets [24], which are potentially more suitable for the plant with uncertainty. Moreover, a T2FLS has the potential to outperform a T1FLS, because it has more design degrees of freedom. The T1FLS can be viewed as a special case of T2FLS. In T2FLS, if the means and variances of upper and lower membership functions are the same, then it can be reduced to a T1FLS. So T2FLS is more general than T1FLS. The T2FLS with more complex computation led to the appearance of interval type-2 fuzzy logic systems (IT2FLS), which is a special case of T2FLS simplifying the computation operations in the fuzzification and defuzzification of fuzzy logic systems [25]. By combining the fuzzy logic system with a neural network, several fuzzy neural systems have been presented [26–29]. However, in the design of fuzzy neural systems, it is often difficult to determine a suitable network size, so some papers have dealt with the self-organization of fuzzy neural systems [8, 30].

In many adaptive controllers, the learning rates are highly influential to the system performance. Most papers in the literature often need to use a trial-and-error method to determine the learning rates of parameter adaptive laws, but it is difficult to obtain the most suitable value and it always takes a long time. The PSO algorithm is an optimization technique first introduced in 1995 by Kennedy and Eberhart [31]. It optimizes a problem by modifying each candidate solution based on the best performance of the swarm. In the beginning, the particles (set as learning rates) will be initialized with a group of random solutions. At each iteration, the best solution can be shared among other particles and every particle will move to follow the best solution. The PSO algorithm is especially effective in solving nonlinear problems in control systems; so in the last decade, it has been widely used to optimize the parameters for many controllers such as PID, LQR, fuzzy and neural network [32–36]. In 2011, Bingül and Karahan [35] proposed PSO fuzzy logic controller for a 2 DOF robot. In their study, the PSO algorithm was used to tune the antecedent and consequent parameter of fuzzy law, which used fixed structure of type-1 fuzzy system. The advance of this method is its simplicity in calculation, so it is easier to be implemented than other traditional methods. However, because of with fixed structure, it led to difficulty to determine the suitable size of fuzzy membership functions and fuzzy rules. In [37], a self-evolving algorithm for an interval type-2 fuzzy neural network (IT2FNN) has been established, which can auto-generate the network structure. The advance of this approach is the initial rule-based and membership function can be empty initially and then can be constructed by itself, but one cannot use the knowledge about the system to design the initial membership function and the initial rule to obtain better result; furthermore, one also cannot apply off-line PSO algorithm to train the network. In [38], a self-organizing IT2FNN was introduced, which can self-construct the network size. Nevertheless, in this paper, the learning rate in adaptive law is fixed and chosen by the trial-and-error method.

The motivation of this study is to construct a self-organizing type-2 fuzzy neural network by applying a self-organizing algorithm for the type-2 fuzzy neural systems, and the PSO algorithm will be applied to find the optimal learning rates of SOT2FNN; and this network is referred to as a PSO-SOT2FNN. Then, it is applied to control the antilock braking systems. The main contributions of this paper are (1) successful apply off-line and online PSO algorithm to find the optimal learning rates of the adaptive laws of SOT2FNN, (2) the self-organizing algorithm is used to achieve the suitable structure of IT2FNN, (3) all the adaptive laws are designed based on the gradient descent method, and the stability of the control system is proved by the Lyapunov function and (4) the simulation results illustrate that the proposed control system can effectively achieve braking responses for the ABS under different road conditions.

The remainder of this paper is as follows. The problem formulation of ABS is formulated in Sect. 2. The design of the PSO-SOT2FNN control system is presented in Sect. 3. The simulation results are provided in Sect. 4 to demonstrate the effectiveness of the proposed approach, and a conclusion is given in Sect. 5.

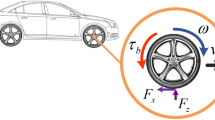
2 Formulation of ABS

In antilock braking systems, the control objective is to regulate the wheel slip to maximize the coefficient of friction between the wheel and the road for any given road surface. In general, the coefficient of friction \(\mu\) during a braking operation can be described as a function of the slip \(\lambda\), which is defined as

$$\lambda \left( t \right) = \frac{{\omega_{\text{v}} \left( t \right) - \omega_{\omega } \left( t \right)}}{{\omega_{\text{v}} \left( t \right)}}$$
(1)

where \(\omega_{\text{v}} \left( t \right)\) and \(\omega_{\omega } \left( t \right)\) are the angular velocity of vehicle and the wheel, respectively.

The relationship between the braking coefficient of friction \(\mu\) and the wheel slip \(\lambda\) depends on the tire–road conditions and has been measured in [39], as shown in Fig. 1 [3, 6]. From (1), it is obvious when \(\omega_{\text{v}} \left( t \right) = \omega_{\omega } \left( t \right)\), the slip \(\lambda\) is 0% representing the free rolling wheel condition, while when \(\omega_{\omega } \left( t \right) = 0\), the slip \(\lambda\) is 100% corresponding to the wheel being completely locked. The angular velocity is defined as

$$\omega_{\text{v}} \left( t \right) = \frac{{V_{\text{v}} \left( t \right)}}{{R_{\omega } }}$$
(2)

where \(R_{\omega }\) is the radius of the wheel, \(V_{\text{v}} \left( t \right)\) is the velocity of the vehicle. Applying Newton’s law, the dynamic equations for the wheel and the vehicle during a nominal braking are derived [3, 6]. The acceleration of the vehicle is determined by summing the total forces applied.

$$\dot{V}_{\text{v}} \left( t \right) = \frac{ - 1}{{M_{\text{v}} }}\left[ {4F_{\text{t}} \left( t \right) + B_{\text{v}} V_{\text{v}} \left( t \right) + F_{\theta } \left( \theta \right)} \right]$$
(3)

where \(M_{\text{v}}\) is the mass of the vehicle, \(B_{\text{v}}\) is the vehicular viscous friction, \(F_{\text{t}} \left( t \right)\) is the tractive force and \(F_{\theta } \left( \theta \right)\) is the force applied to the car which results from a vertical gradient in the road so

$$F_{\theta } \left( \theta \right) = M_{\text{v}} g{ \sin }\left( \theta \right)$$
(4)

where \(\theta\) is the angle of inclination of the road, and g is the gravitational acceleration constant. The tractive force \(F_{\text{t}} \left( t \right)\) is given by

$$F_{\text{t}} \left( t \right) = \mu \left( \lambda \right)N_{\text{v}} \left( \theta \right)$$
(5)

where \(N_{\text{v}} \left( \theta \right)\) is the nominal reaction force applied to the wheel. For this model, assume the vehicle has four wheels and the weight of the vehicle is evenly distributed between these wheels. Then, the nominal reaction force on each wheel \(N_{\text{v}} \left( \theta \right)\) can be expressed by

$$N_{\text{v}} \left( \theta \right) = \frac{{M_{\text{v}} g}}{4}{ \cos }\left( \theta \right)$$
(6)
Fig. 1
figure 1

Relation between road–wheel friction coefficients (μ) and slip (λ) for various road surfaces [3, 39]

Full size image

The wheel dynamic is determined by summing the rotational torque to yield

$$\dot{\omega }_{\omega } \left( t \right) = \frac{1}{{J_{\omega } }}\left[ { - T_{\text{b}} \left( t \right) - B_{\omega } \omega_{\omega } \left( t \right) + T_{\text{t}} \left( t \right)} \right]$$
(7)

where \(J_{\omega }\) is the rotational inertia of the wheel, \(B_{\omega }\) is the viscous friction of the wheel, \(T_{\text{b}} \left( t \right)\) is the braking torque and \(T_{\text{t}} \left( t \right)\) is the torque generated due to the slip between the wheel and the road surface. In general, \(T_{\text{t}} \left( t \right)\) is the torque generated by the tractive force \(F_{\text{t}} \left( t \right)\) as

$$T_{\text{t}} \left( t \right) = R_{\omega } F_{\text{t}} \left( t \right)$$
(8)

Taking the derivative from (1)

$$\dot{\lambda }\left( t \right) = \frac{{\left( {1 - \lambda \left( t \right)} \right)\dot{\omega }_{\text{v}} - \dot{\omega }_{\omega } }}{{\omega_{\text{v}} }} = \frac{{ - \dot{\omega }_{\text{v}} }}{{\omega_{\text{v}} }}\lambda \left( t \right) + \frac{{\dot{\omega }_{\text{v}} - \dot{\omega }_{\omega } }}{{\omega_{\text{v}} }}$$
(9)

Substituting (2), (3) and (7) into (9) gives

$$\dot{\lambda }\left( t \right) = f\left( {\lambda ;t} \right) + g\left( t \right)u\left( t \right)$$
(10)

where \(f = \frac{{4F_{\text{t}} + B_{\text{v}} R_{\omega } \omega_{\text{v}} + F_{\theta } }}{{M_{\text{v}} R_{\omega } \omega_{\text{v}} }}\lambda - \frac{{\left( {4F_{\text{t}} + B_{\text{v}} R_{\omega } \omega_{\text{v}} + F_{\theta } } \right)J_{\omega } - \left( {B_{w} \omega_{w} - T_{\text{t}} } \right)M_{\text{v}} R_{\omega } }}{{M_{\text{v}} R_{\omega } \omega_{\text{v}} J_{\omega } }}\) and \(g = \frac{1}{{J_{\omega } \omega_{\text{v}} }}\) is the control gain, \(u = T_{\text{b}}\) is the control effort. This equation is nonlinear and involves uncertainties in the parameters. When uncertainties and measurement noise are under consideration, (10) can be reformulated as

$$\begin{aligned} \dot{\lambda }\left( t \right) & = \left[ {f_{0} \left( {\lambda ;t} \right) +\Delta f\left( {\lambda ;t} \right)} \right] + \left[ {g_{0} \left( t \right) +\Delta g\left( t \right)} \right]u\left( t \right) + n\left( t \right) \\ & = f_{0} \left( {\lambda ;t} \right) + g_{0} \left( t \right)u\left( t \right) + \beta \left( {\lambda ;t} \right) \\ \end{aligned}$$
(11)

where \(f_{0} \left( {\lambda ;t} \right)\) and \(g_{0} \left( t \right)\) are the nominal parts of \(f\left( {\lambda ;t} \right)\) and \(g\left( t \right)\), respectively, \(\Delta f\left( {\lambda ;t} \right)\) and \(\Delta g\left( t \right)\) are the uncertainties of system, \(n\left( t \right)\) denotes the measurement noise, \(\beta \left( {\lambda ;t} \right)\) is referred to as the lumped uncertainty and is defined as

$$\beta \left( {\lambda ;t} \right) =\Delta f\left( {\lambda ;t} \right) +\Delta g\left( t \right)u\left( t \right) + n\left( t \right)$$
(12)

In the case that the lumped uncertainty is known exactly, then an ideal controller can be designed as follows:

$$u^{*} \left( t \right) = g_{0}^{ - 1} \left( t \right)\left[ {\dot{\lambda }_{\text{d}} \left( t \right) - f_{0} \left( {\lambda ;t} \right) - \beta \left( {\lambda ;t} \right) + k\lambda_{\text{e}} \left( t \right)} \right]$$
(13)

where k is a gain, and \(\lambda_{\text{e}} \left( t \right)\) is defined as

$$\lambda_{\text{e}} \left( t \right) = \lambda_{\text{d}} \left( t \right) - \lambda \left( t \right)$$
(14)

where \(\lambda_{\text{d}} \left( t \right)\) is the desired slip trajectory.

The goal of the controller produces a control signal \(u\left( t \right)\), which can force the system output \(\lambda \left( t \right)\) to track the reference trajectory \(\lambda_{\text{d}} \left( t \right)\) to maximize the road/wheel friction, regardless of variations in vehicular speed. The desired slip is usually set at 20% based on Fig. 1 to meet the maximum friction coefficient. Substituting (13) into (11), the error dynamics can be obtained as

$$\dot{\lambda }_{\text{e}} \left( t \right) + k\lambda_{\text{e}} \left( t \right) = 0$$
(15)

From (15), it is obvious if \(k\) is selected to correspond to the coefficients of the Hurwitz polynomial, then the tracking error can approach zero \(\mathop { {\text{lim}}}\limits_{t \to \infty } \lambda_{\text{e}} \left( t \right) = 0\), and then, the system can follow the desired slip trajectory \(\lambda_{\text{d}} \left( t \right)\). However, the lumped uncertainty \(\left( {\varvec{x}\left( t \right)} \right)\) cannot be precisely known in practical applications. Therefore, the ideal controller in (13) is unobtainable. Thus, a PSO-SOT2FNN control system is proposed in the following section to achieve the desired control performance.

3 PSO-SOT2FNN Control System

The structure of the PSO-SOT2FNN control system is shown in Fig. 2, consisting of an SOT2FNN controller and a robust compensation controller. The SOT2FNN is the main controller, and its parameters can be adjusted based on the derived adaptive law; and the learning rates in adaptive laws can be updated using the PSO algorithm.

Fig. 2
figure 2

Block diagram of PSO-SOT2FNN control system

Full size image

3.1 Interval Type-2 Fuzzy Neural Network

This section introduces the structure of an interval type-2 fuzzy neural network (IT2FNN), consisting of an input layer, a membership layer, a rule layer, a type reduction layer and an output layer, as shown in Fig. 3. The IF–THEN rule for IT2FNN has the following form:

$$\begin{aligned} & {\text{Rule i:}}\quad {\text{IF}}\quad x_{1} \, {\text{is}} \,\tilde{X}_{1}^{i} \quad {\text{and}} \ldots {\text{and}} x_{n} \,is\,\tilde{X}_{n}^{i} \\ & {\text{THEN}}\quad w\, {\text{is}}\, \tilde{W}^{i} \quad i = 1, \ldots , M \\ \end{aligned}$$
(16)

where \(\tilde{X}_{j}^{i}\) and \(\tilde{W}^{i}\) are the interval type-2 fuzzy membership function input and output, respectively. M is the total number of rulers and \(j = 1, \ldots , n\) where n is the number of the inputs in the first layer.

Fig. 3
figure 3

Structure of an IT2FNN

Full size image

The signal propagation and basic function in each layer are described as follows.

  1. 1.

    Layer 1 (Input Layer): there are no weights in this layer, and each node is an input variable which will be transmitted directly to layer 2. In this study, the inputs are the error and the derivative of the error.

  2. 2.

    Layer 2 (membership function layer): each node in this layer defines an interval type-2 membership function (IT2MF) to perform the fuzzification operation. The IT2MF \(\tilde{X}_{j}^{i}\) is defined by an interval type-2 Gaussian membership function, which has a standard deviation \(\sigma\) and an uncertain mean \(m \in \left[ {m_{1} , m_{2} } \right]\) (Fig. 4); and it can be described as:

    $$\mu_{{\tilde{X}_{j}^{i} }} = { \exp }\left\{ { - \frac{1}{2}\left( {\frac{{x_{j} - m_{j}^{i} }}{{\sigma_{j}^{i} }}} \right)^{2} } \right\} \equiv O\left( {m_{j}^{i} , \sigma_{j}^{i} ,x_{j} } \right)$$
    (17)
    Fig. 4
    figure 4

    Interval type-2 fuzzy Gaussian membership function

    Full size image

    The footprint of uncertainty (FOU) of IT2MF can be represented as a bounded interval denoted by \(\bar{\mu }_{j}^{i} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\mu }_{j}^{i}\) the upper and lower membership function (UMF and LMF), respectively. The output of each node in this layer can be represented as an interval \(\left[ {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\mu }_{j}^{i} , \bar{\mu }_{j}^{i} } \right]\) and is given by

    $$\bar{\mu }_{j}^{i} \left( {x_{j} } \right) = \left\{ {\begin{array}{*{20}l} {O\left( {m_{j1}^{i} , \sigma_{j}^{i} ,x_{j} } \right) , } \hfill & {x_{j} < m_{j1}^{i} } \hfill \\ {1,} \hfill & {m_{j1}^{i} \le x_{j} \le m_{j2}^{i} } \hfill \\ {O\left( {m_{j2}^{i} , \sigma_{j}^{i} ,x_{j} } \right) ,} \hfill & {x_{j} > m_{j2}^{i} } \hfill \\ \end{array} } \right.$$
    (18)
    $$\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\mu }_{j}^{i} \left( {x_{j} } \right) = \left\{ {\begin{array}{*{20}l} {O\left( {m_{j2}^{i} , \sigma_{j}^{i} ,x_{j} } \right) , } \hfill & {x_{j} \le \frac{{m_{j1}^{i} + m_{j2}^{i} }}{2}} \hfill \\ {O\left( {m_{j1}^{i} , \sigma_{j}^{i} ,x_{j} } \right) ,} \hfill & {x_{j} > \frac{{m_{j1}^{i} + m_{j2}^{i} }}{2}} \hfill \\ \end{array} } \right.$$
    (19)
  3. 3.

    Layer 3 (rule layer): each node in this layer is a rule node and performs the fuzzy firing operation using an algebraic product t-norm operation. The output of a rule node is a firing strength \(F^{i}\), which is an interval type-1 fuzzy set. The firing strength is computed as follows [25]:

    $$F^{i} = \left[ {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{f}^{i} , \bar{f}^{i} } \right]$$
    (20)

    where

    $$\bar{f}^{i} = \mathop \prod \limits_{j = 1}^{n} \bar{\mu }_{j}^{i} , \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{f}^{i} = \mathop \prod \limits_{j = 1}^{n} \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\mu }_{j}^{i}$$
    (21)
  4. 4.

    Layer 4 (type reduction layer): In this layer, the center of set type reduction and the Karnik–Mendel (KM) algorithms are used to compute the interval output \(\left[ {y_{l} , y_{r} } \right]\) [40], which can be derived from the consequent centroid set \(\left[ {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{w}^{i} , \bar{w}^{i} } \right]\) and firing strengths \(\left[ {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{f}^{i} , \bar{f}^{i} } \right]\). The left and right outputs \(y_{l}\) and \(y_{r}\) can be computed by

    $$y_{l} = \frac{{\mathop \sum \nolimits_{i = 1}^{M} f_{l}^{i} \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{w}^{i} }}{{\mathop \sum \nolimits_{i = 1}^{M} f_{l}^{i} }}$$
    (22)
    $$y_{r} = \frac{{\mathop \sum \nolimits_{i = 1}^{M} f_{r}^{i} \bar{w}^{i} }}{{\mathop \sum \nolimits_{i = 1}^{M} f_{r}^{i} }}$$
    (23)

    where \(f_{l}^{i}\) and \(f_{r}^{i}\) are chosen as

    $$f_{l}^{i} = \left\{ {\begin{array}{ll} \bar{f}^{i} ,&\quad i \le L \\ \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{f}^{i} ,&\quad i > L\\ \end{array} } \right.$$
    (24)
    $$f_{r}^{i} = \left\{ {\begin{array}{ll} \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{f}^{i} ,&\quad i \le R \\ \bar{f}^{i} ,&\quad i > R \\ \end{array} } \right.$$
    (25)

    where L and R are the left and right switch points, respectively.

  5. 5.

    Layer 5 (output layer): this layer performs the defuzzification operation from the interval set in the output of layer 4, and the output can be computed by the average of \(y_{l}\) and \(y_{r}\). Finally, the output of IT2FNN can be expressed as

    $$y = \frac{{y_{l} + y_{r} }}{2}$$
    (26)

3.2 Self-Organizing for Type-2 Fuzzy Neural Network

In the design structure of IT2FNN, it is difficult to determine the number of rules for the system to obtain favorable performance, and many previous published papers used a trial-and-error method to determine the rule’s number. However, using this method takes a long time and the performance cannot be guaranteed. The idea of a self-organizing IT2FNN is to use the firing strength of each rule to determine whether a new rule needs to be generated or an inappropriate existing rule needs to be deleted.

Consider the process of generating the new rules. The mathematical description of a rule can be expressed as a cluster, and the degree of input data that belongs to a cluster can be considered according to its firing strength. The center of interval firing strength can be computed by

$$f_{c}^{i} = \frac{1}{2}\left( {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{f}^{i} + \bar{f}^{i} } \right)$$
(27)

If \(\left( {f_{\text{c}}^{I} \le f_{\text{th}} } \right)\) means a new input data fall outside the boundary of all existing clusters, then the SOT2FNN will generate a new rule to cover it, where \(f_{\text{th}}\) is the prespecified threshold and \(f_{\text{c}}^{I}\) is the maximum value of the center interval firing strength and I is the index of the maximum value given by

$$I = \arg \mathop {\hbox{max} }\limits_{i} \left[ {f_{\text{c}}^{1} ,f_{\text{c}}^{2} , \ldots f_{\text{c}}^{M} } \right]$$
(28)

In the new rule, the initial values for the uncertain mean and the variance of the type-2 fuzzy system are defined as

$$\left[ {m_{j1}^{M\left( t \right) + 1} ,m_{j2}^{M\left( t \right) + 1} } \right] = \left[ {x_{j} \left( t \right) -\Delta x, x_{j} \left( t \right) +\Delta x } \right]\quad j = 1, \ldots , n$$
(29)
$$\sigma_{j}^{M\left( t \right) + 1} = \beta .\left| {x_{j} \left( t \right) - \left( {\frac{{m_{j1}^{I} + m_{j2}^{I} }}{2}} \right)} \right|$$
(30)
$$\left[ {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{w}^{i} , \bar{w}^{i} } \right] = \left[ {0, 0} \right]$$
(31)

where M(t) is the total number of rules at time t, \(\Delta x\) is a half of the uncertainty mean value. If the chosen \(\Delta x\) is extremely small, it will be similar to a type-1 fuzzy set. For an extremely large value of \(\Delta x\), the uncertainty will cover most of the input domain and cover other existing IT2MFs. The positive parameter \(\beta\) decides the initial cluster width. A large \(\beta\) value leads to a large overlapping degree between these fuzzy sets and generates a smaller number of rules [15]. Conversely, if \(\beta\) is an extremely small value, it will lead to a small overlapping degree between these fuzzy sets and will generate a huge number of rules.

Choosing the values of \(\Delta x\) and \(\beta\) is the design of the initial values for the uncertainty mean and variance. This paper sets \(\Delta x = 0.1\) and \(\beta = 0.5\) based on the adaptive law designed in the following, and the uncertainty mean and the variance can be updated to a suitable value.

Another process of self-organizing is to delete the existing rules. The rules will be deleted if they contribute less than the predefined deleting threshold value \(K_{\text{del}}\). The ratio used to evaluate the contribution of the ith rule in IT2FNN is defined as

$$K_{l}^{i} = \frac{{f_{l}^{i} \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{w}^{i} }}{{y_{l} }}\quad {\text{and}}\quad K_{r}^{i} = \frac{{f_{r}^{i} \bar{w}^{i} }}{{y_{r} }}$$
(32)

If \(K_{l}^{i} < K_{\text{del}}\) and \(K_{r}^{i} < K_{\text{del}}\), then the ith rule in the left or in the right is deleted. With this automatic way of generating and pruning, the proposed self-organizing IT2FNN can obtain the most suitable number of rules.

3.3 Adaptive Type-2 Fuzzy Neural Network Controller Design

Since the lumped uncertainty in (11) is unknown, assume there is an optimal SOT2FNN controller \(u_{\text{SOT2FNN}}^{*}\) to approximate the ideal controller \(u^{*} \left( t \right)\) in (13)

$$u^{*} \left( t \right) = u_{SOFT2NN}^{*} \left( {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{w}^{*} , \bar{w}^{*} ,m_{j1}^{*} ,m_{j2}^{*} ,\sigma_{j}^{*} ,t} \right) + \varepsilon (t)$$
(33)

where \(\varepsilon (t)\) denotes the approximation error, and \(\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{w}^{*} , \bar{w}^{*} ,m_{j1}^{*} ,m_{j2}^{*} {\text{and}} \sigma_{j}^{*}\) are the optimal parameters of \(\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{w} ,\bar{w},m_{j1} {\text{and}} \sigma_{j}\), respectively. However, the optimal controller \(u_{\text{SOT2FNN}}^{*}\) cannot be obtained. Thus, an estimation controller \(\hat{u}_{\text{SOT2FNN}}\) can be designed to online estimate \(u_{\text{SOT2FNN}}^{*}\), and the overall controller can be designed as

$$\hat{u}\left( t \right) = \hat{u}_{\text{SOT2FNN}} \left( {\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{w} },\hat{\bar{w}},\hat{m}_{J1} ,\hat{m}_{J2} ,\hat{\sigma }_{j} ,t} \right) + \hat{u}_{R} \left( t \right)$$
(34)

where \(\hat{u}_{R}\) is a robust compensation controller used to cope with the approximation error between the estimation controller \(\hat{u}_{\text{SOT2FNN}}\) and the optimal controller \(u_{\text{SOT2FNN}}^{*}\); and \(\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{w} },\hat{\bar{w}},\hat{m}_{J1} ,\hat{m}_{J2} ,\hat{\sigma }_{j} ,t\) are the estimation of \(\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{w}^{ *} , {\bar{\text{w}}}^{ *} ,m_{j1}^{*} ,m_{j2}^{*} ,\sigma_{j}^{*}\), respectively.

A sliding surface s(t) is defined as

$$s\left( t \right) \triangleq \lambda_{\text{e}} \left( t \right) + k\mathop \int \limits_{0}^{t} \lambda_{\text{e}} \left( \tau \right){\text{d}}\tau$$
(35)

Taking the derivative of (35) and using (11), (14) and (34), yields

$$\dot{s}\left( t \right) = \dot{\lambda }_{\text{e}} \left( t \right) + k\lambda_{\text{e}} \left( t \right) = - f_{0} \left( {\lambda ;t} \right) - g_{0} \left( x \right)\left( {\hat{u}_{\text{SOT2FNN}} \left( t \right) + \hat{u}_{R} \left( t \right)} \right) + \dot{\lambda }_{\text{d}} \left( t \right) - \left( {\lambda ;t} \right) + k\lambda_{\text{e}} (t)$$
(36)

Choosing a Lyapunov cost function as \(V_{1} \left( {s\left( t \right)} \right) = \frac{1}{2}s^{2} \left( t \right)\), take the derivative of the cost function \(\dot{V}_{1} \left( {s\left( t \right)} \right) = s\left( t \right)\dot{s}\left( t \right)\). The aim is to tune the parameter values \(\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{w} },\hat{\bar{w}},\hat{m}_{J1} ,\hat{m}_{J2} ,\hat{\sigma }_{j}\) so \(\dot{V}_{1} \left( {s\left( t \right)} \right)\) is minimized to achieve rapid convergence of \(s\left( t \right)\). Using the gradient descent method, the parameters of type-2 fuzzy system can be updated by the following equations:

$$\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{w} }^{i} \left( {t + 1} \right) = \hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{w} }^{i} \left( t \right) - \hat{\eta }_{w} \frac{{\partial s\left( t \right)\dot{s}\left( t \right)}}{{\partial \hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{w} }^{i} }}$$
(37)
$$\hat{\bar{w}}^{i} \left( {t + 1} \right) = \hat{\bar{w}}^{i} \left( t \right) - \hat{\eta }_{w} \frac{{\partial s\left( t \right)\dot{s}\left( t \right)}}{{\partial \hat{\bar{w}}^{i} }}$$
(38)
$$\hat{m}_{j1}^{i} \left( {t + 1} \right) = \hat{m}_{j1}^{i} \left( t \right) - \hat{\eta }_{m} \frac{{\partial s\left( t \right)\dot{s}\left( t \right)}}{{\partial \hat{m}_{j1}^{i} }}$$
(39)
$$\hat{m}_{j2}^{i} \left( {t + 1} \right) = \hat{m}_{j2}^{i} \left( t \right) - \hat{\eta }_{m} \frac{{\partial s\left( t \right)\dot{s}\left( t \right)}}{{\partial \hat{m}_{j2}^{i} }}$$
(40)
$$\hat{\sigma }_{j}^{i} \left( {t + 1} \right) = \hat{\sigma }_{j}^{i} \left( t \right) - \hat{\eta }_{\sigma } \frac{{\partial s\left( t \right)\dot{s}\left( t \right)}}{{\partial \hat{\sigma }_{j}^{i} }}$$
(41)

where \(\hat{\eta }_{w} ,\hat{\eta }_{m} ,\hat{\eta }_{\sigma }\) are the learning rates with positive number and they can be obtained by PSO algorithm, and the detail of PSO will be presented in the following Sect. 3.4.

Using the chain rule, the derivation in (37)–(41) can be expressed as follows:

$$\frac{{\partial s\left( t \right)\dot{s}\left( t \right)}}{{\partial \hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{w} }^{i} }} = \frac{{\partial s\left( t \right)\dot{s}\left( t \right)}}{{\partial \hat{u}_{\text{SOT2FNN}} }}\frac{{\partial \hat{u}_{\text{SOT2FNN}} }}{{\partial y_{l} }}\frac{{\partial y_{l} }}{{\partial \hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{w} }^{i} }} = - \frac{1}{2}g_{0} \left( x \right)s\left( t \right)\frac{{f_{l}^{i} }}{{\mathop \sum \nolimits_{i = 1}^{M} f_{l}^{i} }}$$
(42)
$$\frac{{\partial s\left( t \right)\dot{s}\left( t \right)}}{{\partial \hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{w} }^{i} }} = \frac{{\partial s\left( t \right)\dot{s}\left( t \right)}}{{\partial \hat{u}_{\text{SOT2FNN}} }}\frac{{\partial \hat{u}_{\text{SOT2FNN}} }}{{\partial y_{r} }}\frac{{\partial y_{r} }}{{\partial \hat{\bar{w}}^{i} }} = - \frac{1}{2}g_{0} \left( x \right)s\left( t \right)\frac{{f_{r}^{i} }}{{\mathop \sum \nolimits_{i = 1}^{M} f_{r}^{i} }}$$
(43)
$$\frac{{\partial s\left( t \right)\dot{s}\left( t \right)}}{{\partial \hat{m}_{j1}^{i} }} = \frac{1}{2}\frac{{\partial s\left( t \right)\dot{s}\left( t \right)}}{{\partial \hat{u}_{\text{SOT2FNN}} }}\left( {\frac{{\partial y_{l} }}{{\partial f_{l}^{i} }}\frac{{\partial f_{l}^{i} }}{{\partial \hat{m}_{j1}^{i} }} + \frac{{\partial y_{r} }}{{\partial f_{r}^{i} }}\frac{{\partial f_{r}^{i} }}{{\partial \hat{m}_{j1}^{i} }}} \right) = - \frac{1}{2}g_{0} \left( x \right)s\left( t \right)\left( {\frac{{\left( {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{w}^{i} - y_{l} } \right)}}{{\mathop \sum \nolimits_{i = 1}^{M} f_{l}^{i} }}\frac{{\partial f_{l}^{i} }}{{\partial \hat{m}_{j1}^{i} }} + \frac{{\left( {\bar{w}^{i} - y_{r} } \right)}}{{\mathop \sum \nolimits_{i = 1}^{M} f_{r}^{i} }}\frac{{\partial f_{r}^{i} }}{{\partial \hat{m}_{j1}^{i} }}} \right)$$
(44)
$$\frac{{\partial s\left( t \right)\dot{s}\left( t \right)}}{{\partial \hat{m}_{j2}^{i} }} = \frac{1}{2}\frac{{\partial s\left( t \right)\dot{s}\left( t \right)}}{{\partial \bar{u}_{\text{SOT2FNN}} }}\left( {\frac{{\partial y_{l} }}{{\partial f_{l}^{i} }}\frac{{\partial f_{l}^{i} }}{{\partial \hat{m}_{j2}^{i} }} + \frac{{\partial y_{r} }}{{\partial f_{r}^{i} }}\frac{{\partial f_{r}^{i} }}{{\partial \hat{m}_{j2}^{i} }}} \right) = - \frac{1}{2}g_{0} \left( x \right)s\left( t \right)\left( {\frac{{\left( {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{w}^{i} - y_{l} } \right)}}{{\mathop \sum \nolimits_{i = 1}^{M} f_{l}^{i} }}\frac{{\partial f_{l}^{i} }}{{\partial \hat{m}_{j2}^{i} }} + \frac{{\left( {\bar{w}^{i} - y_{r} } \right)}}{{\mathop \sum \nolimits_{i = 1}^{M} f_{r}^{i} }}\frac{{\partial f_{r}^{i} }}{{\partial \hat{m}_{j2}^{i} }}} \right)$$
(45)
$$\frac{{\partial s\left( t \right)\dot{s}\left( t \right)}}{{\partial \hat{\sigma }_{j}^{i} }} = \frac{1}{2}\frac{{\partial s\left( t \right)\dot{s}\left( t \right)}}{{\partial \hat{u}_{\text{SOT2FNN}} }}\left( {\frac{{\partial y_{l} }}{{\partial f_{l}^{i} }}\frac{{\partial f_{l}^{i} }}{{\partial \hat{\sigma }_{j}^{i} }} + \frac{{\partial y_{r} }}{{\partial f_{r}^{i} }}\frac{{\partial f_{r}^{i} }}{{\partial \hat{\sigma }_{j}^{i} }}} \right) = - \frac{1}{2}g_{0} \left( x \right)s\left( t \right)\left( {\frac{{\left( {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{w}^{i} - y_{l} } \right)}}{{\mathop \sum \nolimits_{i = 1}^{M} f_{l}^{i} }}\frac{{\partial f_{l}^{i} }}{{\partial \hat{\sigma }_{j}^{i} }} + \frac{{\left( {\bar{w}^{i} - y_{r} } \right)}}{{\mathop \sum \nolimits_{i = 1}^{M} f_{r}^{i} }}\frac{{\partial f_{r}^{i} }}{{\partial \hat{\sigma }_{j}^{i} }}} \right)$$
(46)

The elements \(f_{l}^{i}\) and \(f_{r}^{i}\) in (44, 45, 46) are \(\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{f}^{i}\) or \(\bar{f}^{i}\) depending on (24) and (25). Considering both cases, obtain

$$\frac{{\partial \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{f}^{i} }}{{\partial \hat{m}_{j1}^{i} }} = \frac{{\partial \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{f}^{i} }}{{\partial \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\mu }_{j}^{i} }}\frac{{\partial \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\mu }_{j}^{i} }}{{\partial \hat{m}_{j1}^{i} }} = \left\{ {\begin{array}{*{20}l} {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{f}^{i} \times \frac{{x_{j} - m_{j1}^{i} }}{{\left( {\sigma_{j}^{i} } \right)^{2} }},} \hfill & {x_{j} > \frac{{m_{j1}^{i} + m_{j2}^{i} }}{2} } \hfill \\ {0,} \hfill & { {\text{otherwise}}} \hfill \\ \end{array} } \right.$$
(47)
$$\frac{{\partial \bar{f}^{i} }}{{\partial \hat{m}_{j1}^{i} }} = \frac{{\partial \bar{f}^{i} }}{{\partial \bar{\mu }_{j}^{i} }}\frac{{\partial \bar{\mu }_{j}^{i} }}{{\partial \hat{m}_{j1}^{i} }} = \left\{ {\begin{array}{*{20}l} {\bar{f}^{i} \times \frac{{x_{j} - m_{j1}^{i} }}{{\left( {\sigma_{j}^{i} } \right)^{2} }},} \hfill & {x_{j} \le m_{j1}^{i} } \hfill \\ {0,} \hfill & {\text{otherwise}} \hfill \\ \end{array} } \right.$$
(48)
$$\frac{{\partial \bar{f}^{i} }}{{\partial \hat{m}_{j2}^{i} }} = \frac{{\partial \bar{f}^{i} }}{{\partial \hat{\mu }_{j}^{i} }}\frac{{\partial \hat{\mu }_{j}^{i} }}{{\partial \hat{m}_{j2}^{i} }} = \left\{ {\begin{array}{*{20}l} {\bar{f}^{i} \times \frac{{x_{j} - m_{j2}^{i} }}{{\left( {\sigma_{j}^{i} } \right)^{2} }},} \hfill & {x_{j} \le \frac{{m_{j1}^{i} + m_{j2}^{i} }}{2} } \hfill \\ {0,} \hfill & {\text{otherwise}} \hfill \\ \end{array} } \right.$$
(49)
$$\frac{{\partial \bar{f}^{i} }}{{\partial \hat{m}_{j2}^{i} }} = \frac{{\partial \bar{f}^{i} }}{{\partial \bar{\mu }_{j}^{i} }}\frac{{\partial \bar{\mu }_{j}^{i} }}{{\partial \hat{m}_{j2}^{i} }} = \left\{ {\begin{array}{*{20}l} {\bar{f}^{i} \times \frac{{x_{j} - m_{j2}^{i} }}{{\left( {\sigma_{j}^{i} } \right)^{2} }},} \hfill & {x_{j} > m_{j2 }^{i} } \hfill \\ {0,} \hfill & {\text{otherwise}} \hfill \\ \end{array} } \right.$$
(50)
$$\frac{{\partial \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{f}^{i} }}{{\partial \hat{\sigma }_{j}^{i} }} = \frac{{\partial \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{f}^{i} }}{{\partial \hat{\mu }_{j}^{i} }}\frac{{\partial \hat{\mu }_{j}^{i} }}{{\partial \hat{\sigma }_{j}^{i} }} = \left\{ {\begin{array}{*{20}l} {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{f}^{i} \times \frac{{\left( {x_{j} - m_{j2}^{i} } \right)^{2} }}{{\left( {\sigma_{j}^{i} } \right)^{3} }},} \hfill & {x_{j} \le \frac{{m_{j1}^{i} + m_{j2}^{i} }}{2} } \hfill \\ {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{f}^{i} \times \frac{{\left( {x_{j} - m_{j1}^{i} } \right)^{2} }}{{\left( {\sigma_{j}^{i} } \right)^{3} }},} \hfill & {x_{j} > \frac{{m_{j1}^{i} + m_{j2}^{i} }}{2} } \hfill \\ \end{array} } \right.$$
(51)
$$\frac{{\partial \bar{f}^{i} }}{{\partial \hat{\sigma }_{j}^{i} }} = \frac{{\partial \bar{f}^{i} }}{{\partial \bar{\mu }_{j}^{i} }}\frac{{\partial \bar{\mu }_{j}^{i} }}{{\partial \hat{\sigma }_{j}^{i} }} = \left\{ {\begin{array}{*{20}l} {\bar{f}^{i} \times \frac{{\left( {x_{j} - m_{j1}^{i} } \right)^{2} }}{{\left( {\sigma_{j}^{i} } \right)^{3} }},} \hfill & {x_{j} < m_{j1}^{i} } \hfill \\ {\bar{f}^{i} \times \frac{{\left( {x_{j} - m_{j2}^{i} } \right)^{2} }}{{\left( {\sigma_{j}^{i} } \right)^{3} }},} \hfill & {x_{j} < m_{j2}^{i} } \hfill \\ {0,} \hfill & {\text{otherwise}} \hfill \\ \end{array} } \right.$$
(52)

3.4 The Particle Swarm Optimization (PSO) Algorithm

The PSO algorithm is shown in Fig. 5. At the beginning of the off-line PSO algorithm, the swarm (n p set value of learning rates \(\hat{\eta }_{w} ,\hat{\eta }_{m} ,\hat{\eta }_{\sigma }\)) are randomly initialized. Then, apply each particle of swarm to SOT2FNN based on the fitness function to obtain the best set values of the particle (\(p_{{{\text{Best}}\,q}}^{l}\)). After trying all set values, calculate the best position of the swarm (\(g_{{{\text{Best}}\,q}}^{l}\)) and update the new value for each particle. Finally, the main loop will run again with the new swarm until it reaches the fixed number of iterations. The formula for the updating law is

$$p_{q}^{l} \left( {n + 1} \right) = p_{q}^{l} \left( n \right) + v_{q}^{l} \left( {n + 1} \right)$$
(53)

and

$$v_{q}^{l} \left( {n + 1} \right) = v_{q}^{l} \left( n \right) + c_{1} *{\text{rand}}\left( \cdot \right)*\left[ {p_{{{\text{Best}}\,q}}^{l} - p_{q}^{l} \left( n \right)} \right] + c_{2} *{\text{rand}}\left( \cdot \right)*\left[ {g_{{{\text{Best}}\,q}}^{l} - p_{q}^{l} \left( n \right)} \right]$$
(54)

where \(v_{q}^{l} \left( n \right)\) and \(p_{q}^{l} \left( n \right)\) are, respectively, the current velocity and current position of the particle, rand(·) is a random number in [0, 1]; \(c_{1}\) and \(c_{2}\) are the positive acceleration factors related to the local and global information, respectively, \(q = 1, 2, \ldots , n_{p}\) (n p is the population size) and \(l = 1, 2, \ldots , n_{d}\) (n d is the dimension of each particle). In this study, the fitness function is chosen based on the root mean square error (RMSE) of the slip tracking error.

Fig. 5
figure 5

Flowchart of PSO

Full size image

The online PSO operation is the same as the off-line PSO, with the only two small differences being the initial value of the swarm and the running time in each epoch. In the online PSO, the initial values of the swarm are setup based on the best optimal value gotten from off-line PSO, and the epoch time is short to response to the online real-time application.

3.5 Robust Compensation Control

The robust compensation controller is designed to deal with the effect of the approximation error in (33). Assume this approximation error can be bounded by an uncertainty bound \(E\) and \(0 \le \varepsilon \left( t \right) \le E\), where E is assumed to be a constant during the observation. However, it is difficult to know E precisely. Thus, an estimated value \(\hat{E}\left( t \right)\) is used. Define the estimation error of the uncertainty bound

$$\hat{E}\left( t \right) = E - \hat{E}\left( t \right)$$
(55)

The robust compensation controller \(u_{R} \left( t \right)\) is chosen as

$$u_{R} \left( t \right) = \hat{E}\left( t \right)\text{sgn} \left( {s\left( t \right)} \right)$$
(56)

Using some straightforward manipulation, the error equation can be obtained

$$\dot{s} = \dot{\lambda }_{\text{e}} \left( t \right) + k\lambda_{\text{e}} \left( t \right) = \varepsilon \left( t \right) - u_{R} \left( t \right)$$
(57)

Define a Lyapunov function as

$$V_{2} \left( {s\left( t \right), \tilde{E}\left( t \right)} \right) = \frac{1}{2}s^{2} \left( t \right) + \frac{{\tilde{E}^{2} \left( t \right)}}{{2\eta_{D} }}$$
(58)

where \(\eta_{D}\) is the learning rate of \(\hat{E}\).

Take the derivative of (58) and use (56), (57), then

$$\begin{aligned} \dot{V}_{2} \left( {s\left( t \right), \tilde{E}\left( t \right)} \right) & = s\left( t \right)\dot{s}\left( t \right) + \frac{{\tilde{E}\left( t \right)\dot{\tilde{E}}\left( t \right)}}{{\eta_{D} }} \\ & = s\left( t \right)\left( {\varepsilon \left( t \right) - u_{R} \left( t \right)} \right) + \frac{{\tilde{E}\left( t \right)\dot{\tilde{E}}\left( t \right)}}{{\eta_{D} }} \\ & = s\left( t \right)\varepsilon \left( t \right) - \hat{E}\left( t \right)\left| {s\left( t \right)} \right| + \frac{{\tilde{E}\left( t \right)\dot{\tilde{E}}\left( t \right)}}{{\eta_{D} }} \\ \end{aligned}$$
(59)

If the adaptive law for E is chosen as (56) and since E is a constant, so \(\dot{\tilde{E}}\left( t \right) = - \dot{\hat{E}}\left( t \right)\). Then (59) can be rewritten as

$$\begin{aligned} \dot{V}_{2} \left( {s\left( t \right),\tilde{E}\left( t \right)} \right) & = s\left( t \right)\varepsilon \left( t \right) - \hat{E}\left( t \right)\left| {s\left( t \right)} \right| - \left( {E - \hat{E}\left( t \right)} \right)\left| {s\left( t \right)} \right| \\ & = s\left( t \right)\varepsilon \left( t \right) - E\left| {s\left( t \right)} \right| \le \left| {s\left( t \right)} \right|\left| {\varepsilon \left( t \right)} \right| - E\left| {s\left( t \right)} \right| \\ & = - \left| {s\left( t \right)} \right| \left( {E - \left| {\varepsilon \left( t \right)} \right|} \right) \le 0 \\ \end{aligned}$$
(60)

Since \(\dot{V}_{2} \left( {s\left( t \right), \tilde{E}\left( t \right)} \right)\) is negative semidefinite, that is \(V_{2} \left( {s\left( t \right),\tilde{E}\left( t \right)} \right) \le V\left( {s\left( 0 \right), \tilde{E}\left( 0 \right)} \right)\), it implies s(t) and \(\tilde{E}\left( t \right)\) are bounded. Let the function \(\varOmega \equiv \left( {E - \varepsilon \left( t \right)} \right)s \le \left( {E - \left| {\varepsilon \left( t \right)} \right|} \right)\left| s \right| \le - \dot{V}_{2} \left( {s\left( t \right), \tilde{E}\left( t \right)} \right)\) and integrate \(\varOmega \left( t \right)\) with respect to time, then it is easy to obtain

$$\mathop \int \limits_{0}^{t}\Omega \left( \tau \right){\text{d}}\tau \le V_{2} \left( {s\left( 0 \right), \tilde{E}\left( 0 \right)} \right) - V_{2} \left( {s\left( t \right), \tilde{E}\left( t \right)} \right)$$
(61)

Since \(V_{2} \left( {s\left( 0 \right), \tilde{E}\left( 0 \right)} \right)\) is bounded, and \(V_{2} \left( {s\left( t \right), \tilde{E}\left( t \right)} \right)\) is non-increasing and bounded, so from (61) it is obtained

$$\mathop {\lim }\limits_{t \to \infty } \mathop \int \limits_{0}^{t} \varOmega \left( \tau \right)d\tau < \infty .$$
(62)

Also, \(\dot{\varOmega }\left( \tau \right)\) is bounded, so by Barbalat’s lemma [41], \(\mathop {\lim }\limits_{t \to \infty } \varOmega = 0\). That is, \(s\left( t \right) \to 0\) as \(t \to \infty\). As a result, the PSO-SOT2FNN control system can achieve robust tracking performance.

4 Simulation Results

This section describes the simulation results of ABS control under different road conditions. The parameters of ABS, the initial conditions and the slip command are chosen to be the same as in [3, 6], which is shown in Table 1. Figure 1 clearly shows for different road conditions that the maximal value of the tractive forces is near 20%, so the value \(\lambda_{\text{c}} \left( t \right)\) is chosen as 0.2. After the transition equation \(\dot{\lambda }_{\text{d}} \left( t \right) = - 10\lambda_{\text{d}} \left( t \right) + 10\lambda_{\text{c}} \left( t \right)\), the desired slip trajectory \(\lambda_{\text{d}} \left( t \right)\) can be obtained. The maximum braking torque is limited to 1200 N-m. The velocity of a vehicle and its wheel reaches almost zero at low speed, which means the magnitude of the slip tends to infinity as vehicle speed approaches zero. Therefore, effective control is applied until the vehicle slows to 5 m/s. To conduct the simulations, consider the braking action occurring when the vehicle is moving at a velocity of 25 and 12.5 m/s on an asphalt road and icy road, respectively.

Table 1 Model parameters of ABS
Full size table

To demonstrate the effectiveness of the PSO algorithm, the simulation results of SOT2FNN and PSO-SOT2FNN are conducted for three different road conditions. The parameters for PSO are n p = 20, n d = 3, c1 = c2 = 0.07. The initial Gaussian membership functions are shown in Fig. 6. The ABS simulations for the dry asphalt road and icy road are shown in Figs. 7, 8, 10 and 11, respectively. The simulation results for the transition from a wet asphalt road to an icy road are shown in Figs. 13 and 14. In all figures, part (a) shows the angular velocity of the wheel and the vehicle, part (b) is the control force, part (c) shows the reference model response and the ABS response and part (d) is the change of the rule number. Figures 9, 12 and 15 show the change of the learning rates. From these figures, it is obvious for all road conditions the PSO-SOT2FNN control system can rapidly achieve satisfactory control performance with small RMSE. Figures 7, 10 and 13 show without suitable learning rates that it will lead to many chattering in the control effort and the number of the rule used will be frequently changed. With the online PSO algorithm for updating learning rates, the simulation results in Figs. 8, 11 and 14 show the ability of PSO-SOT2FNN for achieving favorable control performance. Finally, in the same conditions, Table 2 shows the comparison results of RMSE of slip tracking error between the proposed control method and the methods in [5, 6, 8]. This also demonstrates the superiority of the proposed PSO-SOT2FNN over the other control methods (Figs. 8, 11 and 14).

Fig. 6
figure 6

Membership function for SOT2FNN

Full size image
Fig. 7
figure 7

Simulation result of SOT2FNN control ABS for a dry asphalt road: (a) The angular velocity of the wheel and the vehicle, (b) Control force, (c) Reference model response and ABS response, (d) Number of the rule

Full size image
Fig. 8
figure 8

Simulation result of PSO-SOT2FNN control ABS for a dry asphalt road: (a) The angular velocity of the wheel and the vehicle, (b) Control force, (c) Reference model response and ABS response, (d) Number of the rule

Full size image
Fig. 9
figure 9

Using online PSO update learning rates for a dry asphalt road: (a) Update learning rates for the weights, (b) Update learning rates for the variances, (c) Update learning rates for the means

Full size image
Fig. 10
figure 10

Simulation result of SOT2FNN control ABS for an icy road: (a) The angular velocity of the wheel and the vehicle, (b) Control force, (c) Reference model response and ABS response, (d) Number of the rule

Full size image
Fig. 11
figure 11

Simulation result of PSO-SOT2FNN control ABS for an icy road: (a) The angular velocity of the wheel and the vehicle, (b) Control force, (c) Reference model response and ABS response, (d) Number of the rule

Full size image
Table 2 Comparison of the RMSE of the slip tracking error
Full size table
Fig. 12
figure 12

Using online PSO update learning rates for an icy road: (a) Update learning rates for the weights, (b) Update learning rates for the variances, (c) Update learning rates for the means

Full size image
Fig. 13
figure 13

Simulation result of SOT2FNN control ABS for wet asphalt road to icy road: (a) The angular velocity of the wheel and the vehicle, (b) Control force, (c) Reference model response and ABS response, (d) Number of the rule

Full size image
Fig. 14
figure 14

Simulation result of PSO-SOT2FNN control ABS for wet asphalt road to icy road: (a) The angular velocity of the wheel and the vehicle, (b) Control force, (c) Reference model response and ABS response, (d) Number of the rule

Full size image
Fig. 15
figure 15

Using online PSO update learning rates for a wet asphalt road to icy road: (a) Update learning rates for the weights, (b) Update learning rates for the variances, (c) Update learning rates for the means

Full size image

In our research, the off-line PSO is trained as 500 epochs with 20 sets of learning rates. For case 1, the total elapsed time is 0.395 s and the total time for training is 1.097 h. For case 2, the total elapsed time is 0.682 s and the total time for training is 1.896 h. For case 3, the total elapsed time is 0.948 s and the total time for training is 2.635 h. After off-line training, for the real-time online control, the computing time is 0.000906 and 0.001236 s, respectively, for SOT2FNN and PSO-SOT2FNN at each control iteration. The simulations were done on Windows 7 64-bit and the processor is Core i5-4460 3.2 GHz, RAM 8 GB.

5 Conclusion

In this study, a PSO-SOT2FNN controller combined with a robust compensation controller is proposed to control an ABS, with the performance of the control system being illustrated under various road conditions. The major features of this study include the development of a PSO-SOT2FNN controller with parameter adaptive laws, the PSO algorithm for the relevant learning rates, the effective self-organizing algorithm for suitable construction of IT2FNN and the stability analysis of the control system. The simulation results of ABS control have shown the superiority of the proposed control method than the other control methods. The proposed control method can also be suitable for a large class of unknown nonlinear systems, since this design algorithm does not need to know the exact model of controlled systems. Applying the developed control algorithm to real systems will be our future work.