Abstract
The choice of a risk measure reflects a subjective preference of the decision maker in many managerial or real world economic problem formulations. To assess the impact of personal preferences it is thus of interest to have comparisons with other risk measures at hand. This paper develops a framework for comparing different risk measures. We establish a one-to-one relationship between norms and risk measures, that is, we associate a norm with a risk measure and conversely, we use norms to recover a genuine risk measure. The methods allow tight comparisons of risk measures and tight lower and upper bounds for risk measures are made available whenever possible. In this way we present a general framework for comparing risk measures with applications in numerous directions.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Risk measures are designed to quantify the risk which is associated with a random, uncertain outcome in a single real number. Risk measures have been considered in insurance first to price insurance contracts, but nowadays they constitute an essential basis for decision making and management in all areas of operations research, management science and (mathematical) finance whenever unobserved, random, future outcomes are involved.
This paper addresses comparisons of risk measures and continuity relations by establishing lower and upper bounds. We give tight relations wherever possible so that stochastic programs, e.g., can be compared easily when employing different risk measures. A sensitivity analysis thus can assess a subjective preference of a particular risk measure.
Our research is motivated by Iancu et al. (2015), but in addition to the methods outlined in this reference we involve convex functions (as norms or functionals derived from coherent risk measures, e.g.) to obtain explicit bounds. Some of these convex functionals perhaps violate usual axioms of coherent risk measures, but they are useful and eligible for comparisons or efficient in computations.
Risk measures are usually defined on vector spaces of real valued random variables and these vector spaces typically come with a norm. It has been observed that risk measures induce a norm themselves, which is occasionally equivalent to the genuine norm of the domain space. Here, we establish and employ the converse relations, that is, we develop a natural relationship between norms and risk measures so that both concepts can be exchanged against each other or employed alternatively to specify the other. This equivalence is a major tool of our analysis and in this way the risk measure naturally compares with the genuine norm and with the norm induced. To illustrate the methods we provide many examples of precise relations between risk measures and norms, and between different risk measures, thus supporting the analysis of personal preferential choices of risk measures.
Our results are related to Wozabal (2014), who robustifies risk measures with respect to changing the underlying probability space. López-Díaz et al. (2012) employ a specific norm (called an \(L_{p}\)-metric there), while Bellini and Caperdoni (2007), in contrast, relate and compare risk measures with stochastic dominance relations. The papers Wozabal (2010, 2014) contain typical applications in operations research and finance, as asset allocation.
Risk measures impose several difficulties in a multistage stochastic framework. Cheridito and Kupper (2011) investigate a natural composition of risk measures. This concept, or approach, is formalized by Lara and Leclère (2016). Asamov and Ruszczyński (2014), Ruszczyński (2010) and Miller and Ruszczyński (2011) elaborate on risk measures in relation to dynamic, multistage stochastic programming. Applications of these extended concepts of risk measures are finally provided, for example, by Philpott and Matos (2012) and Philpott et al. (2013), who involve compositions of risk measures to formulate and elaborate on multistage hydro-thermal scheduling problems in New Zealand and Brazil.
Outline of the paper. The following section (Sect. 2) repeats the axioms for risk measures and formulates corresponding axioms for norms. The Sects. 3 and 4 present explicit comparisons with norms and with other risk measures. We develop bounds on composite risk measures in Sect. 5, while Sect. 6 concludes with a comprehensive summary.
2 Preliminaries
We consider a linear vector space \(L\subseteq L^{1}(\Omega ,{\mathcal {F}},P)\) of \({\mathbb {R}}\)-valued random variables with pointwise ordering. The set L is used in this paper to represent random losses. The vector space \(L\subseteq L^{1}\) is the domain of a risk measure. We state the axioms of risk measure here in convex form, as we shall relate them to further axioms on (convex) norms on the domain space L later.
Definition 2.1
(Axioms for risk functionals) A version independent, coherent risk measure is a mapping \(\rho :\,L\rightarrow {\mathbb {R}}\cup \left\{ \infty \right\} \) satisfying the following axioms:
-
(RM)
Monotonicity: \(\rho \left( Y_{1}\right) \le \mathcal {\rho }\left( Y_{2}\right) \) whenever \(Y_{1}\le Y_{2}\) almost surely;
-
(RC)
Convexity \(\rho \bigl (\left( 1-\lambda \right) Y_{0}+\lambda Y_{1}\bigr )\le (1-\lambda )\rho \left( Y_{0}\right) +\lambda \rho \left( Y_{1}\right) \) for \(0\le \lambda \le 1\);
-
(RT)
Translation equivariance: \(\rho (Y+c\cdot {\mathbbm {1}})=\rho (Y)+c\) if \(c\in {\mathbb {R}}\) (\({\mathbbm {1}}(\cdot )=1\) is the constant random variable);
-
(RH)
Positive homogeneity: \(\rho (\lambda \,Y)=\lambda \,\rho (Y)\) whenever \(\lambda >0\);
-
(RD)
Version independence: \(\rho (Y_{1})=\rho (Y_{2})\), provided that \(Y_{1}\) and \(Y_{2}\) share the same law, i.e., \(P(Y_{1}\le y)=P(Y_{2}\le y)\) for all \(y\in {\mathbb {R}}\).Footnote 1
We shall call the set
the nonnegative orthant, or the nonnegative cone of L.
If only the properties (RM), (RC) and (RT) are fulfilled, then the functional \(\rho \) is often simply called risk functional as well, while positively homogeneous risk measures satisfying (RH) are also called coherent risk measures. In this paper we shall address the specific properties explicitly in the given context, if this is necessary.
The trivial risk measures satisfying the axioms (RM)–(RD) are the expectation \(\rho (Y)={\mathbb {E}}[Y]\) and the max-risk functional \(\rho (Y)={{\mathrm{ess\,sup}}}Y\). An example of a risk functional that is not necessarily version independent is \(\rho _{Z}(Y):={\mathbb {E}}[Z\cdot Y]\) (with \({\mathbb {E}}[Z]=1\) and \(Z\ge 0\) almost everywhere).
Norms. We equip the vector space \(L\subseteq L^{1}\) with a norm and relate risk functionals with the normed space \(\left( L,\left\| \cdot \right\| \right) \). In line with the axioms presented above on risk measures we make use of the following assumptions on the norm \(\left\| \cdot \right\| \) and the (Banach) space \(\left( L,\left\| \cdot \right\| \right) \).
-
(NM)
Monotonicity: \(\left\| Y_{1}\right\| \le \left\| Y_{2}\right\| \) whenever \(\left| Y_{1}\right| \le \left| Y_{2}\right| \) almost surely;
-
(N1)
Normalization (scaling): \(\left\| {\mathbbm {1}}\right\| =1\);
-
(ND)
Density: uniformly bounded random variables and \(L^{\infty }\) are dense in L with respect to the norm \(\left\| \cdot \right\| \);
-
(NP)
Representation on the nonnegative cone:Footnote 2
$$\begin{aligned} \sup _{\left\| Z\right\| ^{*}\le 1}{\mathbb {E}}[Y\cdot Z]=\sup _{Z\ge 0,\,\left\| Z\right\| ^{*}\le 1}{\mathbb {E}}[Y\cdot Z]\,\text { whenever }Y\ge 0\text { a.s.}, \end{aligned}$$(1)where
$$\begin{aligned} \left\| Z\right\| ^{*}:=\sup _{\left\| Y\right\| \le 1}{\mathbb {E}}[Y\cdot Z] \end{aligned}$$(2)is the norm on the dual, which is denoted \(\left( L^{*},\left\| \cdot \right\| ^{*}\right) \).
Remark 2.2
Note that (NP) is not more than the Hahn–Banach theorem for the bi-linear form \((Y,Z)\mapsto {\mathbb {E}}[YZ]\), just restricted to the nonnegative orthant \(L_{+}\).
From normalization (N1) and (2) it follows that
and particularly that \(\left\| {\mathbbm {1}}\right\| ^{*}\ge {\mathbb {E}}[{\mathbbm {1}}]=1\). Further it is evident from (1) that
Specifications of the norm. Obvious candidates for a norm satisfying all relations (NM)–(NP) are the norms \(\left\| \cdot \right\| _{p}\) on \(L^{p}\)-spaces. Further examples include the Luxembourg norm
on Orlicz spaces, where \(\Phi :[0,\infty )\rightarrow [0,\infty )\) is a convex function satisfying \(\Phi (0)=0\), \(\Phi (1)=1\) and \(\lim _{x\rightarrow \infty }\Phi (x)=\infty \) (cf. Bellini and Rosazza Gianin 2012, for example, for details). Further, we mention Orlicz hearts, the spaces \(\left( L_{\sigma }.\left\| \cdot \right\| _{\sigma }\right) \) and their dual \(\left( L_{\sigma }^{*}.\left\| \cdot \right\| _{\sigma }^{*}\right) \), as well as Lorentz spaces, they satisfy all specified relations as well (cf. Pichler 2013a).
3 Relations between norms and risk measures
Given a risk measure \(\rho \), then one may associate the function
with \(\rho \). The risk functional \(\rho \) is Lipschitz continuous with respect to the associated norm \(\left\| \cdot \right\| _{\rho }\) (cf. Pichler 2013a).
In this chapter we elaborate the converse construction by providing explicitly a risk measure, which is based on a norm. We demonstrate that the risk measure is completely specified by the nonnegative cone \(L_{+}\). We further demonstrate in this section that the risk measure obtained is again (Lipschitz-)continuous with respect to the initial norm.
Theorem 3.1
Let \(\left\| \cdot \right\| \) be a norm satisfying (NM)–(NP). Then, for \(c\ge 1\), the higher order risk measureFootnote 3
is a coherent risk measure. \(\rho _{c}^{ho}(\cdot )\) is version independent, iff the norm is version independent. Its dual representation is
Remark 3.2
We point out that (7) specifies the risk measure \(\rho _{c}^{ho}(\cdot )\) by considering the ball of radius c in the dual space. This emphasizes the strong relationship between a risk measure and a norm.
Remark 3.3
We mention Krokhmal (2007) for a construction leading to (6). The functional
corresponding to the Luxembourg norm is also called Haezendonck–Goovaerts risk measure (or Haezendonck–Goovaerts premium in insurance). Bellini and Rosazza Gianin (2008, 2012) involve (8) to define generalized \(\alpha \)-quantiles of the random variable Y. Dentcheva et al. (2010) establish the duality relation of (6)–(7) for the \(L_{p}\)-norm \(\left\| \cdot \right\| _{p}\) in this journal, which is called higher order risk measure (thus the name and superscript, \(\rho ^{ho}\)).
Remark 3.4
The constraint \(c\ge 1\) is a necessary condition, as otherwise the risk measure \(\rho _{c}^{ho}\) is degenerate and, e.g., \(\rho _{c}^{ho}({\mathbbm {1}})=-\infty \).
Proof of Theorem 3.1
Observe first that
by the Hahn–Banach theorem, and thus
as \(x+\left( Y-x\right) _{+}\ge Y\), establishing thus the first inequality relation.
As for the converse inequality we shall assume first that Y is bounded. It follows that
as one may drop the constraint \({\mathbb {E}}[Z]=1\): indeed,
unless \({\mathbb {E}}[Z]=1\), such that the \(\inf \) does not contribute to the outer \(\sup \) if \({\mathbb {E}}[Z]\not =1\).
Observe next that \(\inf _{x\in {\mathbb {R}}}\left\{ x+{\mathbb {E}}[(Y-x)Z]\right\} =x^{*}+{\mathbb {E}}[(Y-x^{*})_{+}\cdot Z]\) for \(x^{*}:={{\mathrm{ess\,inf}}}\,Y\) (recall that Y is bounded by assumption so that this quantity is well-defined). So it follows that
and by the Hahn–Banach theorem and (NP) again (as \(\left( Y-x^{*}\right) _{+}\ge 0\)) that
the remaining inequality.
If Y is not bounded, then for every \(\varepsilon >0\) there is a bounded random variable \(Y_{\varepsilon }\) so that \(\left\| Y-Y_{\varepsilon }\right\| <\varepsilon \) due to the assumption (ND). It follows by combining (9) and (11) that
The assertion is immediate, as \(\varepsilon >0\) is arbitrary. \(\square \)
The result (7) of the previous theorem is a dual characterization. The results allows a natural comparison of risk measures by employing the genuine norm. We shall elaborate corresponding bounds (lower and upper bounds) in the following statement. These results provide a tool to prove continuity in the sequel.
Theorem 3.5
(Bounds, and comparison with norms) Let the risk measure \(\rho _{c}^{ho}(\cdot )\) be induced by a norm as specified in (6). Then it holds that
The lower bound is sharp.
Proof
As for the first inequality recall the elementary inequality \(y\le x+\left( y-x\right) _{+}\le x+c\left( y-x\right) _{+}\) for \(c\ge 1\), and hence
It follows from monotonicity (NM) and the triangle inequality that
By passing to the infimum thus
Equality moreover is obtained for the constant random variable, \(Y={\mathbbm {1}}\) and \(x=1\) in (6).
We employ the dual representation (7) to verify the second inequality. It follows from the duality relation (NP) that
the remaining assertion. \(\square \)
Remark 3.6
(The special case \(c=1\): specification on the nonnegative cone \(L_{+}\)) The risk measure \(\rho _{1}^{ho}\) is completely specified by the norm \(\left\| \cdot \right\| \) on the nonnegative cone, as
by choosing \(c=1\) in the latter theorem. Together with (5) this equation establishes the one-to-one relationship between risk measures and norms.
It is thus enough to specify a risk measure \(\rho \) on the nonnegative cone \(L_{+}\), as it extends to the entire space by setting
This setting carries translation equivariance (RT) to the entire space L and it holds that \(\rho (Y)=\rho _{1}^{ho}(Y)\) for \(Y\in L_{+}\) [cf. also the inf convolution in e.g., Pflug and Römisch (2007, Section 2.4.3); a related construction is the homogenization outlined in Shapiro et al. (2009, Section 6.3.2) carrying homogeneity (RH) to the entire domain].
We finally remark that a local comparison on the nonnegative cone \(L_{+}\) extends to a global comparison on \(L\supseteq L_{+}\). Indeed, if \(\rho (Y)\le \rho ^{\prime }(Y)\) for all \(Y\in L_{+}\), then \(\rho (Y)\le \rho ^{\prime }(Y)\) for \(Y\in L\) by (12).
Corollary 3.7
(Continuity) The risk measure \(\rho _{c}^{ho}\) is Lipschitz continuous with respect to its norm,
for all \(Y_{1},\,Y_{2}\in L\).
Proof
Just observe that \(\rho _{c}^{ho}(Y_{2})=\rho _{c}^{ho}(Y_{2}-Y_{1} +Y_{1})\le \rho _{c}^{ho}(Y_{2}-Y_{1})+\rho _{c}^{ho}(Y_{1})\) by convexity, and thus
The assertion follows by interchanging the roles of \(Y_{1}\) and \(Y_{2}\). \(\square \)
Average Value-at-Risk The (upper) Average Value-at-Risk (\({\mathsf {AV@R}}\)) is the special case of the latter theorem for the norm \(\left\| \cdot \right\| _{1}\). The equivalent expressions
are well-known indeed (cf. Rockafellar and Uryasev 2000; Pflug 2000), but here they constitute a special case of Theorem 3.1 for the norm \(\left\| \cdot \right\| _{1}\) and its dual \(\left\| \cdot \right\| _{1}^{*}=\left\| \cdot \right\| _{\infty }\).
3.1 Higher order risk measures
Higher order risk measures constitute a special case of the risk measure (6) addressed in Theorem 3.1, as the \(L^{p}\)-norm \(\left\| \cdot \right\| _{p}\) takes the role of the general norm \(\left\| \cdot \right\| \). We denote them by
where \(c\ge 1\) and \(p\ge 1\).
For this particular choice we have the following extension of Theorem 3.1 with precise bounds.
Theorem 3.8
(Comparison with norms) Assume that \(1\le p\le p^{\prime }\). It holds that
-
(i)
$$\begin{aligned} \left\| Y\right\| _{p}\le \rho _{c,p^{\prime }}^{ho}\left( \left| Y\right| \right) , \end{aligned}$$(15)
-
(ii)
and
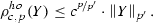 (16)
(16)
Both bounds are moreover sharp.
Proof
The first inequality is immediate from Theorem 3.5. For the second inequality recall the dual representation (7) (see also Dentcheva et al. 2010) that
where q is the Hölder conjugate exponent, \(\frac{1}{p}+\frac{1}{q}=1\).
Let \(q^{\prime }\) be the conjugate exponent to \(p^{\prime }\) (\(\frac{1}{p^{\prime }}+\frac{1}{q^{\prime }}=1\)). It follows that
Note now that \(\frac{1}{q^{\prime }}=\frac{1}{\frac{p^{\prime }}{p^{\prime } -1}}=\frac{1-\frac{p}{p^{\prime }}}{1}+\frac{\frac{p}{p^{\prime }}}{\frac{p}{p -1}}=\frac{1-\frac{p}{p^{\prime }}}{1}+\frac{\frac{p}{p^{\prime }}}{q}\), such that by Hölder’s interpolation inequality (\(\left\| Z\right\| _{q_{\theta }}\le \left\| Z\right\| _{q_{0}}^{1-\theta }\cdot \left\| Z\right\| _{q_{1}}^{\theta }\) whenever \(\frac{1}{q_{\theta }}=\frac{1-\theta }{q_{0}}+\frac{\theta }{q_{1}}\), cf. Wojtaszczyk 1991)

as \(Z\ge 0\) implies that \(\left\| Z\right\| _{1}={\mathbb {E}}[Z]=1\). It follows that

To see that this bound is sharp consider  , where \(P\left( A\right) =\frac{1}{c^{p}}\). Then
, where \(P\left( A\right) =\frac{1}{c^{p}}\). Then  , and
, and

for all  . As the mapping \(t\mapsto t+c\cdot \left\| \left( Y-t\right) _{+}\right\| _{p}\) is convex it follows that the infimum is
. As the mapping \(t\mapsto t+c\cdot \left\| \left( Y-t\right) _{+}\right\| _{p}\) is convex it follows that the infimum is  . This proves that the bound is sharp. \(\square \)
. This proves that the bound is sharp. \(\square \)
3.2 Higher order semideviation
The higher order semideviation is a risk measure addressed in Rockafellar et al. (2006) and discussed in Shapiro et al. (2009). In the chosen context of norms the dual representation is natural and straight forward again. We introduce and discuss the general case first before establishing the continuity relations. The results then are further specified to \(L^{p}\)-norms, as it is again possible to give explicit, precise bounds.
Theorem 3.9
For every \(0\le \lambda \le 1\),
is a risk functional. If the norm satisfies (NM)–(NP), then the representation
holds true.
Remark 3.10
Recall from (3) that \(\left\| Z\right\| ^{*}\ge {\mathbb {E}}[Z]=1\), such that (17) is a convex combination with nonnegative weights provided that \(0\le \lambda \le 1\). Further, the restriction to \(\lambda \le 1\) ensures monotonicity (RM).
Proof
Observe first that
as it is enough to restrict the supremum to \(Z\ge 0\) by (NP). Note that Z is in the nominator and the denominator, so by rescaling to \({\mathbb {E}}[Z]=1\) it follows that
which is the assertion. \(\square \)
Theorem 3.11
(Comparison of the higher order semideviation with the norm) It holds that
and
Proof
The first inequality in (19), \(\left\| Y\right\| _{1}={\mathbb {E}}\left[ \left| Y\right| \right] \le \rho _{\lambda }^{sd} \left( \left| Y\right| \right) \), is evident from the definition of \(\rho _{\lambda }^{sd}\).
Observe next that \(\lambda y\le t+\lambda \left( y-t\right) _{+}\) whenever \(t\ge 0\). Hence \(\lambda \left| Y\right| \le t+\lambda \left( \left| Y\right| -t\right) _{+}\) and thus
by the triangle inequality and the monotonicity assumption (NM) of the norm. By choosing \(t:={\mathbb {E}}\left[ \left| Y\right| \right] \) (note that \(t\ge 0\)) it follows that
As for the upper bound recall from Theorem 3.9 the representation
from which we deduce that
by (4), completing the proof. \(\square \)
As in the case for the higher order risk measure it is possible to give better and tight bounds by further specifying the norm. We state the results in what follows.
Definition
(Higher order semideviation) The higher order semideviation risk measure (for the parameters \(0\le \lambda <1\) and \(p\ge 1\)) is
The risk measure is also called mean upper semideviation of order p in the literature (cf. Shapiro et al. 2009; Pichler and Shapiro 2015). We present the following bounds for this risk measure, which is important in applications.
Theorem 3.12
(Comparison with \(L^{p}\)-norms) The following holds true:
-
(i)
if \(p=1\), then
$$\begin{aligned} \left\| Y\right\| _{1}\le \rho _{\lambda ,1}^{sd}\left( \left| Y\right| \right) \le (1+\lambda )\cdot \left\| Y\right\| _{1}; \end{aligned}$$(20) -
(ii)
if \(1<p<2\), then
$$\begin{aligned} \lambda \cdot \left\| Y\right\| _{p}\le \rho _{\lambda ,p}^{sd}\left( \left| Y\right| \right) \le k_{\lambda ,p}\cdot \left\| Y\right\| _{p}, \end{aligned}$$(21)where
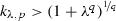 and q is the conjugate Hölder exponent, \(\frac{1}{p}+\frac{1}{q}=1\);
and q is the conjugate Hölder exponent, \(\frac{1}{p}+\frac{1}{q}=1\); -
(iii)
if \(p\ge 2\), then the inequalities
 (22)
(22)are tight.
All bounds are sharp, the upper bounds are sharp except that there is no closed, explicit expression for \(k_{\lambda ,p}\) whenever \(1<p<2\).
Remark 3.13
The inequalities in (i) are useful in practical situation. The lower bounds in (ii) and (iii) are tight, but particularly for small values of \(\lambda \) they are rather loose. We shall address this issue further in the section on compositions of risk measures (Sect. 5) below.
Proof of Theorem 3.12
(i) and the first inequality of (ii) and (iii) are immediate from Theorem 3.11.
To accept that the bounds are sharp consider \(Y:=\frac{1}{P\left( A\right) ^{1/p}}{\mathbbm {1}}_{A}\). Then \(\left\| Y\right\| _{p}=1\), but
provided that \(p>1\). It follows that the lower bound in (21) and (22) cannot be improved.
From Eq. (17) in Theorem 3.9 it follows that
by Hölder’s inequality. Equality in (23), however, is attained for
such that
Consider the function \(\sigma _{\beta }(\cdot ):=\frac{1}{\beta }{\mathbbm {1}}_{\left[ 1 -\beta ,\,1\right] }(\cdot )\) (for which \(\left\| \sigma _{\beta }\right\| _{q}=\frac{1}{\beta ^{\frac{q-1}{q}}}\)) and the random variable \(Z=\sigma _{\beta }(U)\) for some uniformly distributed random variable U.Footnote 4 Then
By letting \(\beta \rightarrow 0\) it follows that \(\lim _{\beta \rightarrow 0}(25)=1+\lambda ^{q}\), from which we conclude that
The upper bound can be rewritten as \(\sup \left\{ \rho _{\lambda ,p}^{sd}\left( \left| Y\right| \right) :\,\left\| Y\right\| _{p}\le 1\right\} \). As \(Y\mapsto \rho _{\lambda ,p}^{sd}\left( \left| Y\right| \right) \) is convex, it is enough to consider Y in the set of extreme points in the unit ball of \(L^{p}\), which are the random variables \(Y=\frac{{\mathbbm {1}}_{A_{1}}-{\mathbbm {1}}_{A_{2}}}{P\left( A_{1}\cup A_{2}\right) ^{1/p}}\) (cf. Sundaresan 1969), i.e.,
for \(A:=A_{1}\cup A_{2}\). Now if |Y| is as in (26), then, because of (24) and (25), the extremum is attained for \(\sigma _{\beta }=\frac{1}{\beta }{\mathbbm {1}}_{[1-\beta ,1]}\), \(\beta \in (0,1)\), which means that it is enough to maximize (25) with respect to \(\beta \in \left[ 0,1\right] \).
But (25) is a strictly decreasing in \(\beta \) for \(p\ge 2\) (i.e., \(q\le 2\)), such that the maximum as attained for \(\beta \rightarrow 0\).
For \(p>2\), the maximum in (25) is attained in the interior, at some \(\beta \in (0,1)\). However, a closed analytic expression is not available. \(\square \)
Example 3.14
(Dutch risk measure (cf. also Example 4.8 below)) The Dutch risk measure (or Dutch premium principle, cf. Heerwaarden and Kaas 1992) is the higher order semideviation risk measure
where \(0\le \lambda <1\). Shapiro (2013) provides the Kusuoka representation
It follows from (13) that \({\mathsf {AV@R}}_{1-\kappa }(Y)\le \frac{1}{\kappa }{\mathbb {E}}\left[ \left| Y \right| \right] \), such that
These estimates are sharp, and in line with the bounds (20) presented in Theorem 3.12.
4 Comparisons of risk measures, and nonlinear bounds
The previous section presents relations between a norm and a risk measure. This section compares risk measures by establishing direct relations. We start with the following remark to distinguish local and global comparisons. Finally we describe bounds which involve the random variable in a nonlinear and in a non-homogeneous way.
Global comparisons Suppose a comparison of the risk measures \(\rho _{1}\) and \(\rho _{2}\) is of the global form
By considering \(Y+c\cdot {\mathbbm {1}}\) instead of Y it follows from translation equivariance (RT) that \(\rho _{1}(Y)\le \rho _{2}(Y)+(K-1)c\) for all \(c\in {\mathbb {R}}\). This inequality is impossible unless \(K=1\). A comparison of risk functionals in the general, global form (29) thus can only read
(i.e., \(K=1\) in (29)).
Only a few risk measures allow a general, global comparison as in (30). The inequality for the Average Value-at-Risk,
for \(\alpha \le \alpha ^{\prime }\) is an example of a global comparison—a special case of \(\rho _{c}^{ho}(Y)\le \rho _{c^{\prime }}^{ho}(Y)\) for \(c\le c^{\prime }\). In what follows we state the global relations, if eligible.
Comparisons on the nonnegative cone To allow for more than global comparisons of risk measures we recall from the previous section that it is enough to know the risk measure—or the associated norm—on the nonnegative cone \(L_{+}\). Instead of the global form (30) we thus consider
as well, that is to involve only nonnegative random variables or the norms associated with the risk measure in order to obtain useful and non-trivial comparisons.
Many applications consider only nonnegative outcomes, and considering only nonnegative random variables is not as restrictive as it seems. Every payoff function of an insurance policy, for example, is always nonnegative (i.e., \(Y\ge 0\)). Some applications interested in financial risk occasionally ignore the profit by considering the loss \(\max \left\{ 0,Y\right\} \) instead of Y. Finally, instead of bounded random variables it is often enough to consider \(c+Y\) (for some appropriate \(c>0\)) instead of Y in order to have the comparison on the nonnegative cone (31) available. This approach is in line with the result reported in Theorem 3.5 and particularly with Remark 3.6.
4.1 Comparison of distortion risk functionals
Distortion risk functionals constitute a basic and elementary ingredient for risk functionals, as every general version independent risk functional is the supremum over a class of distortion risk functionals (cf. Kusuoka 2001; Shapiro 2013; Noyan and Rudolf 2014; they are related to extreme points in the dual set). The distortion risk functional (also spectral risk measure, cf. Acerbi 2002; Denneberg 1990) is defined by
where \(F_{Y}^{-1}(u):=\inf \left\{ y:\,P(Y\le y)\ge u\right\} \) is the generalized inverse of the cumulative distribution function (cdf) \(F_{Y}(y):=P(Y\le y)\). \(\sigma :\left[ 0,1\right) \rightarrow \left[ 0,\infty \right) \) is a nonnegative, nondecreasing function satisfying \(\int _{0}^{1}\sigma (u)\mathrm {d}u=1\). The function \(\sigma (\cdot )\) is called distortion functional. For convenience we shall associate the function \(\Sigma (p):=\int _{p}^{1}\sigma (u)\mathrm {d}u\) (i.e., its negative antiderivative) with \(\sigma (\cdot )\).
On the nonnegative cone we have the following additional formula for distortion risk functionals, which does not involve the quantile function \(F_{Y}^{-1}\), but Y’s cumulative distribution function (cdf) \(F_{Y}\) directly.
Proposition 4.1
For a random variable \(Y\in L_{+}\) in the nonnegative cone the distortion risk functional \(\rho _{\sigma }\) can be evaluated by the alternative expression
Proof
Cf. Denneberg (1990) or Pflug and Pichler (2014, Corollary 3.15).\(\square \)
Theorem 4.2
(Compararison of spectral risk measures) Suppose that
is finite (\(K<\infty \)), then
the bound is sharp. It holds moreover that  .
.
Proof
Pichler (2013a, Theorem 14) provides a proof. \(\square \)
We provide a few examples to illustrate the strength of the previous result.
Example 4.3
(Average Value-at-Risk) The distortion function of the Average Value-at-Risk is
For \(\alpha _{1}\le \alpha _{2}\) the non-trivial constant is \(K=\frac{1-\alpha _{1}}{1-\alpha _{2}}\) and as a particular consequence of (33) it follows that
Particularly, \({\mathsf {AV@R}}_{\alpha }\left( \left| Y\right| \right) \le \frac{1}{1 -\alpha }{\mathbb {E}}\left[ \left| Y\right| \right] \).
The risk measure \(\rho (Y):=\beta \cdot {\mathbb {E}}[Y]+(1-\beta )\cdot {\mathsf {AV@R}}_{\alpha }(Y)\) is popular in applications (referred to as risk measure for integrated risk management, cf. Pflug and Ruszczyński 2005), as it is a natural combination of elementary risk measures (compare also the Dutch risk measure (28)). Its \(\Sigma \)-function is \(\Sigma _{\alpha ,\beta }(u)=\min \left\{ 1-\beta u,\,\frac{1-\alpha \beta }{1-\alpha }(1-u)\right\} \). The global upper bound
follows by elementary computations and Remark 3.6, where the adapted risk level \(\alpha ^{\prime }:=\frac{\alpha -\alpha \beta }{1-\alpha \beta }\) is smaller than the initial risk level \(\alpha \), \(\alpha ^{\prime }\le \alpha \). The global bound (35) is sharp again, and the risk level \(\alpha ^{\prime }\) cannot be improved.
A lower, sharp bound expressed for a general risk level \(\tilde{\alpha }\) is
Recall that the comparisons (34) and (36) are not valid in case that \(Y\not \in L_{+}\). Finally, as a special case we note that \(\frac{1}{\Sigma _{\alpha ,\beta }\left( \alpha ^{\prime }\right) } =\frac{1-\alpha \beta }{1-\alpha \beta (2-\beta )}\) for the critical risk level \(\alpha ^{\prime }\) specified in (35).
Example 4.4
(Proportional hazards risk measure) The proportional hazards risk measure (adapted from insurance, cf. Young 2006), is
on the nonnegative cone, where \(0<c\le 1\) is a parameter accounting for risk aversion. The risk functional compares with the Average Value-at-Risk by
for every \(c>0\), again an immediate consequence of Proposition 4.1 and Theorem 4.2 with \(\Sigma (\alpha )=(1-\alpha )^{c}\).
Example 4.5
(Wang transform) Wang’s risk measure (cf. Wang 1995) employs the parametric family \(\Sigma _{\lambda }^{W}(u)=\Phi \left( \lambda +\Phi ^{-1}(1-u)\right) \) for \(\lambda \ge 0\), it is defined as
on the nonnegative cone (\(\Phi (\cdot )\) is the cdf of the normal distribution, cf. Proposition 4.1). It is a convex risk measure for \(\lambda \ge 0\). It is comparably easy to see that \(\sup _{u<1}\frac{\Sigma _{\alpha }(u)}{\Sigma _{\lambda }^{W}(u)}=\frac{1}{\Sigma _{\lambda }^{W}(\alpha )}\) and it follows that
The proportional hazards risk measure dominates the Wang transform for every combination of \(\lambda \) and c,
although an explicit expression for the constant \(K_{\lambda ,c}\) is not available. A converse inequality to (37) is not possible.
4.2 General version independent risk measures
This section provides bounds for risk functionals of different type. We start with comparing general version independent risk functionals and then give a general bound to compare higher order risk measures with higher order semideviations.
For a class S of distortion functions it is immediate that \(\rho _{S}(Y):=\sup _{\sigma \in S}\rho _{\sigma }(Y)\) is a risk functional satisfying all Axioms (RM)–(RD). To obtain a comparison of the form
on the nonnegative cone \(L_{+}\) one may choose
which is an immediate consequence of (33) in Theorem 4.2, although K is possibly not the best constant. It is evident from the max–min inequality that
and the latter are sometimes easier to evaluate in situations of practical relevance.
Example 4.6
(Entropic Value-at-Risk) The Entropic Value-at-Risk introduced in Ahmadi-Javid (2012) is
The \(\mathsf {EV@R}\) is the tightest upper bound that can be obtained from the Chernoff inequality for the Value-at-Risk. Delbaen (2015) elaborates the Kusuoka representation
using Kullback–Leiber divergence. We refer to the original reference Ahmadi-Javid (2012, Proposition 3.2) for the global comparison
whenever \(\alpha \in \left[ 0,1\right) \). Equality is attained, for example, for the random variable \(Y={\mathbbm {1}}_{[\alpha ,1]}(U)\), but strict inequality holds for \(Y={\mathbbm {1}}_{[\beta ,1]}(U)\), \(\beta \not =\alpha \).
Relations between higher order risk measures and the higher order semideviation We provide the following tight bounds to compare the risk measures discussed and introduced in the previous Sect. 3.
Theorem 4.7
(Comparison of different risk measures) The relation
is tight and holds globally (\(0\le \lambda \le 1\)).
For arbitrary chosen \(0\le \lambda \le 1\) and \(c\ge 1\) it holds that
and conversely
Proof
Assume first that \(Y\ge 0\). Recall from (18) the representation
of the higher order risk measure. Note that \({\mathbb {E}}[Y]\ge 0\) by assumption, so
Hence
by (7), which is the desired estimate on \(L_{+}\). The general assertion for \(L\supseteq L_{+}\) follows from Remark 3.6.
Recall finally from Theorems 3.5 and 3.11 that
and
to establish the remaining relations. \(\square \)
Example 4.8
(Dutch risk measure, cf. Example 3.14) As an application for the general constant (38) consider the Dutch risk measure (27). By applying the relations (27) and (40) from the previous theorem to the norm \(\left\| \cdot \right\| _{1}\) it follows that
The critical risk level \(\frac{\lambda }{1+\lambda }\) is the smallest possible risk level, for which (42) holds true. In contrast to the estimates already presented in Example 3.14 this is a global and tight upper bound for the Dutch risk measure.
To obtain a tight lower bound one may apply (38) and (36) to compute the constant K (cf. (28)), resulting in
This bound is tight, as can be seen by considering \(Y={\mathbbm {1}}_{A}\) with \(P(A^{\complement })=\alpha \).
For the crucial risk level \(\alpha =\frac{\lambda }{1+\lambda }\) the lower, tight bound is
This results further in the sandwich inequality
for \(\alpha \le \frac{1}{2}\), which demonstrates that the Dutch risk measure is basically—up to a multiplicative error of 25%—an Average Value-at-Risk with critical risk level \(\alpha \). This may give rise in some applications for replacing the more complicated \({\mathsf {AV@R}}\) in optimization problems by the simple semideviation risk measure, or vice versa.
4.3 The associated functional
Associated with the distortion risk measure and the distortion function \(\sigma (\cdot )\) is the functional
The associated functional naturally provides the upper bound
which holds for all \(\alpha <1\) (note that \(\rho _{\sigma }^{*}(Y)\) is not necessarily nonnegative).
The functional (43) satisfies the axioms of a risk measures (Definition 2.1), except translation equivariance (RT) and thus is not a risk measure.
As a corollary of Theorem 4.2 we have the following relations for the constant \(\rho _{\sigma }^{*}\).
Corollary 4.9
For \(Y\ge 0\) it holds that
where K is the constant (32) (Theorem 4.2).
Proof
\(\left\| Y\right\| _{\sigma }:=\rho _{\sigma }(|Y|)\) and \(\left\| Z\right\| _{\sigma }^{*}:=\rho _{\sigma }^{*}(|Z|)\) are norms, which are dual to each other (cf. Pichler 2013a) with respect to the bilinear form \((Y,Z)\mapsto {\mathbb {E}}[Y\,Z]\). From the Hahn–Banach theorem it follows that
which is the assertion. \(\square \)
4.4 Nonlinear upper bounds for the distortion risk functional
Approximations of the Average Value-at-Risk, which have been proposed in the literature, include
where \(y_{\tau ,+}=\frac{1}{2}\left( y+\sqrt{y^{2}+4\tau ^{2}}\right) \) (we refer to Luna et al. 2016 discussing also other variants of approximating \(y_{+}\) by some \(y_{\tau ,+}\)). In this setting it holds that \(x_{+}\le x_{\tau ,+}\le \tau +x_{+}\). This approximation apparently generalizes for the higher order risk measure
and consequently \(\rho _{p}^{ho}\left( Y\right) \le \rho _{p,\tau }^{ho}\left( Y\right) \le \rho _{p}^{ho}\left( Y\right) +\tau c\). The functional \(\rho _{p,\tau }^{ho}\left( Y\right) \) is translation equivariant, but not positively homogeneous. The particular advantage of the functional \(\rho _{p,\tau }^{ho}\left( \cdot \right) \) is given by the fact that the approximation \(y\mapsto y_{\tau ,+}\) is strictly convex and differentiable, while \(y\mapsto y_{+}\) is only subdifferentiable.
Distortions—upper bounds derived from Fenchel–Young inequality The upper bound
is valid for every (measurable) function \(h:{\mathbb {R}}\rightarrow {\mathbb {R}}\). (44) follows from the Fenchel–Young inequality \(\sigma (U)\cdot Y\le h(Y)+h^{*}(\sigma (U))\), where \(h^{*}(\sigma ):=\sup _{y\in {\mathbb {R}}}\sigma \cdot y-h(y)\) is the usual convex conjugate function of the function h. Pichler (2013b) demonstrates that the relation (44) is sharp, that is, for every random variable \(Y\in L\) there exists a function h such that equality holds in (44).
5 Composite and conditional risk measures
The risk measures considered in the previous sections are defined on a probability space with a sigma algebra. Extensions to filtered probability spaces are considered in several places, to the best of our knowledge the earliest occurrence is Artzner et al. (2007) in this journal. These risk measures are designed to capture the evolution of risk in a multistage environment, such that general results as Bellman’s principle can be used and adapted to multistage situations. Examples are given in Ruszczyński and Shapiro (2006), Ruszczyński and Yao (2015) and Densing (2014). Shapiro (2016) elaborates properties of these risk measures in the context of convex analysis, while Dentcheva et al. (2016) investigate statistical properties of composite risk measures.
Continuing the intention of the previous sections we develop bounds for composite risk measures by using the relations with norms developed in the previous sections. Having practical implementations in mind we restrict ourselves to higher order measures and the higher order semideviation. We employ conditional expectations to handle these conditional risk measures efficiently and to compare them with the respective norms.
Throughout this section we assume that \({\mathcal {F}}_{1}\) is a sub-sigma algebra, \({\mathcal {F}}_{1}\subseteq {\mathcal {F}}\). With \({\mathcal {F}}_{0}:=\left\{ \emptyset ,\,\Omega \right\} \) we denote the trivial sigma algebra, so that \({\mathcal {F}}_{0}\subseteq {\mathcal {F}}_{1}\subseteq {\mathcal {F}}\).
5.1 Higher order measures
For the definition of higher order risk measures we refer to Ruszczyński (2010, Example 3) and the references given therein.
Definition 5.1
The conditional higher order measure is
where \(c\lhd {\mathcal {F}}_{1}\). We write \(x\lhd {\mathcal {F}}_{1}\) (\(c\lhd {\mathcal {F}}_{1}\), resp.) for x (c, resp.) being measurable with respect to the sigma algebra \({\mathcal {F}}_{1}\). For convenience it is accepted in the literature to write also \(\rho _{c,p}^{ho}\left( Y|\,{\mathcal {F}}_{1}\right) := \rho _{c,p}^{ho}\left( Y,\,{\mathcal {F}}_{1}\right) \), which is in line with the notation of conditional expectation.
Remark 5.2
For the trivial sigma algebra \({\mathcal {F}}_{0}=\left\{ \emptyset ,\,\Omega \right\} \) it holds that \(\rho _{c,p}^{ho}\left( Y\right) =\rho _{c,p}^{ho}\left( Y,\, {\mathcal {F}}_{0}\right) \), this is the higher order measure introduced in (14). The composite risk measure \(Y\mapsto \rho _{c,p}^{ho}\left( \rho _{c,p}^{ho}\left( Y,{\mathcal {F}}_{1}\right) \right) \) is a functional satisfying (RM)–(RH), but it is not version independent (i.e., (RD) is not satisfied).
We have the following comparison with the norm.
Theorem 5.3
For the composite risk measure it holds that
where \(c_{0}\lhd {\mathcal {F}}_{0}\) is deterministic, \(c_{1}\lhd {\mathcal {F}}_{1}\) and q is the exponent conjugate to p, i.e., \(\frac{1}{p}+\frac{1}{q}=1\).
Proof
One may repeat the computations from the proof of Theorem 3.8 conditioned on \({\mathcal {F}}_{1}\) to see that

It follows that
by (46) and (15), and this is the first claim. As for the second observe that

by (16) and (46) again and Hölder’s inequality. This proves the second assertion. \(\square \)
Example 5.4
(Composition of \({\mathsf {AV@R}}\)) An example of a conditional higher order risk measure, which is been frequently addressed in the literature (cf., for example, Shapiro 2010 or Philpott and Matos 2012), is the conditional Average Value-at-Risk,
where \(c_{1}\) is the constant function \(c_{1}(\cdot )=\frac{1}{1-\alpha }\).
The Average Value-at-Risk is monotone, provided that the risk level is adapted to the stage. We have the following comparison (cf. Xin and Shapiro 2012).
Proposition 5.5
For \(\alpha ,\,\beta \in [0,1)\) it holds that
Proof
The statement is immediate from
(cf. (13)). Note that Z satisfying the constraints can be chosen \({\mathcal {F}}_{1}\) adapted (as the essential supremum is \({\mathcal {F}}_{1}\)-adapted), and it follows thus that \({\mathbb {E}}\left[ ZZ^{\prime }\right] ={\mathbb {E}}{\mathbb {E}}(ZZ^{\prime }|{\mathcal {F}}_{1})={\mathbb {E}}\left[ Z({\mathbb {E}}Z^{\prime }|{\mathcal {F}}_{1})\right] =1\). It obviously holds that \(0\le ZZ^{\prime }\le \frac{1}{1-\alpha }\frac{1}{1-\beta }\) and thus the assertion. \(\square \)
Comparions with the Average Value-at-Risk The nested Average Value-at-Risk allows a comparison with the Average Value-at-Risk on the positive cone. Indeed, for \(\alpha \), \(\beta \) and \(\gamma \in [0,1)\) it holds that
provided that \(Y\ge 0\) (the bounds in (49) are known for not being sharp.
To accept the inequality recall first that \({\mathbb {E}}Y\le {\mathsf {AV@R}}_{\alpha }(Y)\le \frac{1}{1-\alpha }{\mathbb {E}}Y\). Then the first inequality follows by monotonicity
while for the second inequality we find that
the latter inequality being due to Dentcheva and Ruszczyński (2003, Corollary 6.30). A simpler version of the right hand inequality in (49) can be found in Xin and Shapiro (2012).
5.2 Higher order semideviation
Higher order risk measures are defined by Ruszczyński (2010, Example 2) and Collado et al. (2012, (3)).
Definition 5.6
The conditional higher order semideviation measure is
Remark 5.7
The higher order semideviation risk measure introduced in Theorem 3.9 is \(\rho _{\lambda ,p}^{sd}\left( Y\right) =\rho _{\lambda ,p}^{sd}\left( Y,\, {\mathcal {F}}_{0}\right) \), where again \({\mathcal {F}}_{0}:=\left\{ \emptyset ,\,\Omega \right\} \) is the trivial sigma algebra.
Remark 5.8
\(\rho (Y):=\rho _{\lambda ,p}^{sd}\left( \rho _{\lambda ,p}^{sd}\left( Y,{\mathcal {F}}_{1}\right) \right) \) is a risk functional satisfying (RM)–(RH), but not version independent (i.e., (RD) is not valid).
We have the following multistage analog of Theorem 3.12.
Theorem 5.9
For \(\lambda _{0}\lhd {\mathcal {F}}_{0}\) deterministic and \(\lambda _{1}\lhd {\mathcal {F}}_{1}\) it holds that
and
where the constants \(k_{\lambda ,p}\) are as in Theorem 3.12.
Proof
The first claim is analogously to the second, so we prove only the second claim.
One may repeat the computations from the proof of Theorem 3.12 conditioned on \({\mathcal {F}}_{1}\) to see that
and

It follows that
by (50) and (21), and this is the first inequality. As for remaining inequality observe that

by (22) and (50), the second assertion. \(\square \)
Aggregation of risk—independent sigma algebras The inequalities in Theorems 5.3 and 5.9 are given for a general random variable Y and a sigma algebra \({\mathcal {F}}_{1}\). The constants in these inequalities improve significantly, if the random variable Y is independent from the sigma algebra \({\mathcal {F}}_{1}\) (i.e., \(P(A\cap B)=P(A)\cdot P(B)\) for every \(A\in {\mathcal {F}}_{1}\) and \(B\in \sigma (Y)\), the sigma algebra generated by Y) and \(\lambda \lhd {\mathcal {F}}_{0}\) constant. In this situation it holds that
and
(for \(c\lhd {\mathcal {F}}_{0}\) constant), i.e., the conditional risk measures are constant variables.
For \(Y_{2}\) independent from \({\mathcal {F}}_{1}\) and \(c_{2}\) constant it thus holds that
by (RT), and this identity gives rise to apply conditional risk functionals in a dynamic setting. If, in addition, \(Y_{1}\) is measurable with respect to \({\mathcal {F}}_{1}\) (\(Y_{1}\lhd {\mathcal {F}}_{1}\)) and \(c_{1},\,c_{2}\lhd {\mathcal {F}}_{0}\), then the equalities extend to
the risk can be aggregated in an additive way. Apparently, the same is true for the semi-deviation risk measure \(\rho _{\lambda ,p}^{sd}\).
5.3 The conditional Entropic Value-at-Risk
The Entropic Value-at-Risk is a further risk measure, which allows a conditional version based on conditional expectation by setting
(cf. (39)).
By altering the risk level \(\alpha \) we have the following inequality on the composition of Entropic Value-at-Risks, which is in line with Proposition 5.5.
Proposition 5.10
(Composition of entropic risk measures) For deterministic risk levels \(\alpha ,\,\beta <1\) we have that
Proof
Let t be optimal in (39) to compute the Entropic Value-at-Risk for the trivial sigma algebra \({\mathcal {F}}=\{\emptyset ,\Omega \}\). Then it follows from the tower property of the conditional expected value that
which concludes the proof. \(\square \)
5.4 The general conditional risk measure
The composite risk measures in the previous subsections are based on conditional expectation. This is enough to introduce a conditional version of the Average Value-at-Risk (cf. (47)). The methods addressed, however, do not constitute a general rule of defining a conditional risk measure based on a given risk measure. But to extend the theory of the previous sections it is necessary to have conditional risk functionals available. Cheridito and Kupper (2011) describe conditional risk functionals and Asamov and Ruszczyński (2014) give characterizations of coherent (and time-consistent) risk measures, but the definitions in Pflug and Pichler (2016), for example, differ, although the conditional Average Value-at-Risk is the same in all references given. For this reason we add a constructive definition of a general, conditional risk functional here, which is again useful in providing estimates.
The Average Value-at-Risk, as introduced in Example 5.4, is well-defined for \(\alpha \) a \({\mathcal {F}}_{1}\)-measurable random variable. By noting that the norm corresponding to the \({\mathsf {AV@R}}\) is \(\left\| \cdot \right\| _{1}\) with dual \(\left\| \cdot \right\| _{1}^{*}=\left\| \cdot \right\| _{\infty }\) one may repeat the arguments in Theorem 3.1 and obtain the alternative formulation
The dual representation of a general coherent risk measure,
can be employed to define the following variant of a conditional risk functional.
Definition 5.11
The conditional risk measure \(\rho _{S}(\cdot |\,{\mathcal {F}}_{1})\) corresponding to the risk measure \(\rho _{S}(Y):=\sup _{\sigma \in S}\int _{0}^{1}\sigma (u)F_{Y}^{-1}(u)\mathrm {d}u\) and the sigma algebra \({\mathcal {F}}_{1}\) is
We shall write \(\rho _{\sigma }(Y|\,{\mathcal {F}}_{1})\) if \(\mathcal {S}=\{\sigma \}\).
The idea in the preceding definition is to repeat the same risk profile on every atom of \({\mathcal {F}}_{1}\). This corresponds to the definition of the conditional Average Value-at-Risk, for example, where the risk level \(\alpha \) is repeated at every node. With this definition the results of Sect. 4 extend analogously and naturally, in line with the results already mentioned for the higher order measure (Sect. 5.1) and the higher order semideviation (Sect. 5.2).
We finally have the following estimates for compositions of risk measures. Note, that all these estimates are actually global comparisons of risk functionals.
Theorem 5.12
(Global comparison of conditional risk functionals) It holds that
-
(i)
\({\mathbb {E}}\left[ \rho _{\sigma }\left( Y|\,{\mathcal {F}}_{1}\right) \right] \le \rho _{\sigma }(Y),\)
-
(ii)
\(\rho _{S}\bigl ({\mathbb {E}}\left( Y|\,{\mathcal {F}}_{1} \right) \bigr )\le \rho _{S}(Y)\), and
-
(iii)
\({{\mathrm{ess\,sup}}}{\mathsf {AV@R}}_{\alpha }\left( Y|\,{\mathcal {F}}_{1}\right) \le \left\| Y\right\| _{\infty }.\)
Remark 5.13
The relation (i) holds for distortion functions \(\rho _{\sigma }\) and the Average Value-at-Risk, but it does not extend to general risk functionals \(\rho _{\mathcal {S}}\).
Proof
We prove the statement for the (conditional) Average Value-at-Risk first. For \(\alpha \lhd {\mathcal {F}}_{0}\) a fixed constant it follows with (45) that
and by taking expectations that
Now recall Kusuoka’s theorem and that \(\rho _{\sigma }(Y)=\int _{0}^{1}{\mathsf {AV@R}}_{\alpha }(Y)\mathrm {d}\mu (\alpha )\) for the measure \(\mu (A):=\sigma (0)\delta _{0}(A)+\int _{A}1-u\mathrm {d}\sigma (u)\) [cf. Pflug and Pichler (2014, Section 3.2)]. By integrating (54) with respect to the measure \(\mu \) and by interchanging the order of integration we obtain
the assertion.
The other assertions are obvious. \(\square \)
Remark 5.14
It is worth noticing that \({\mathsf {AV@R}}_{\alpha }(Y)\not \le \left\| {\mathsf {AV@R}}_{\alpha }\left( Y|\,{\mathcal {F}}_{1}\right) \right\| _{\infty }\). As a counterexample consider \(P(Y=0)=75\%\), \(P(Y=20)=5\%\) and \(P(Y=10)=20\%\), such that \({\mathsf {AV@R}}_{75\%}(Y)=12\). But with \({\mathcal {F}}_{1}=\sigma \left( \left\{ Y\not =10\right\} ,\left\{ Y=10\right\} \right) \) it holds that \({\mathsf {AV@R}}_{75\%}(Y|\,Y\not =10)=5\) and \({\mathsf {AV@R}}_{75\%}(Y|\,Y=10)=10\).
6 Conclusion and summary
This paper elaborates a natural relation between risk measures and norms of a corresponding Banach space. The relation established is one-to-one in the sense that every risk measure defines a norm, and conversely, every appropriate norm specifies a risk measure. We use these observations to establish continuity relations between risk functionals and norms.
A comprehensive collection of examples of important risk measures is included, for which precise upper and lower bounds are given, if available. In this way we obtain (tight) inequalities, relating all commonly used risk functionals. Applications involving risk functionals thus can be simplified by replacing the risk functional by another one, which is more convenient or simpler in implementations.
The second part of the paper addresses compositions of conditional risk functionals. Based on bounds of its components we elaborate multiplicative bounds for composite risk measures.
Notes
Also law invariant, or distribution based.
(NP) is mnemonic for positive.
\(x_{+}:=\max \left\{ 0,x\right\} . \)
U is uniformly distributed, iff \(P(U\le u)=u\).
References
Acerbi, C. (2002). Spectral measures of risk: A coherent representation of subjective risk aversion. Journal of Banking & Finance, 26, 1505–1518. doi:10.1016/S0378-4266(02)00281-9.
Ahmadi-Javid, A. (2012). Entropic Value-at-Risk: A new coherent risk measure. Journal of Optimization Theory and Applications, 155(3), 1105–1123. doi:10.1007/s10957-011-9968-2.
Artzner, P., Delbaen, F., Eber, J.-M., Heath, D., & Ku, H. (2007). Coherent multiperiod risk adjusted values and Bellman’s principle. Annals of Operations Research, 152, 5–22. doi:10.1007/s10479-006-0132-6.
Asamov, T., & Ruszczyński, A. (2014). Time-consistent approximations of risk-averse multistage stochastic optimization problems. Mathematical Programming, 153(2), 1–35. doi:10.1007/s10107-014-0813-x.
Bellini, F., & Caperdoni, C. (2007). Coherent distortion risk measures and higher-order stochastic dominances. North American Actuarial Journal, 11(2), 35–42. doi:10.1080/10920277.2007.10597446.
Bellini, F., & Rosazza Gianin, E. (2008). On Haezendonck risk measures. Journal of Banking & Finance, 32(6), 986–994. doi:10.1016/j.jbankfin.2007.07.007.
Bellini, F., & Rosazza Gianin, E. (2012). Haezendonck–Goovaerts risk measures and Orlicz quantiles. Insurance: Mathematics and Economics, 51(1), 107–114. doi:10.1016/j.insmatheco.2012.03.005.
Cheridito, P., & Kupper, M. (2011). Composition of time-consistent dynamic monetary risk measures in discrete time. International Journal of Theoretical and Applied Finance, 14(1), 137–162. doi:10.1142/S0219024911006292.
Collado, R. A., Papp, D., & Ruszczyński, A. (2012). Scenario decomposition of risk-averse multistage stochastic programming problems. Annals of Operations Research, 200(1), 147–170. doi:10.1007/s10479-011-0935-y.
De Lara, M., & Leclère, V. (2016). Building up time-consistency for risk measures and dynamic optimization. European Journal of Operational Research, 249, 177–187. doi:10.1016/j.ejor.2015.03.046.
Delbaen, F. (2015). Remark on the paper ”Entropic Value-at-Risk: A new coherent risk measure” by Amir Ahmadi-Javid. In P. Barrieu (Ed.), Risk and stochastics. World Scientific, ISBN 978-1-78634-194-5.
Denneberg, D. (1990). Distorted probabilities and insurance premiums. Methods of Operations Research, 63, 21–42.
Densing, M. (2014). Stochastic progamming of time-consistent extensions of AVaR. SIAM Journal on Optimization, 24(3), 993–1010. doi:10.1137/130905046.
Dentcheva, D., & Ruszczyński, A. (2003). Optimization with stochastic dominance constraints. SIAM Journal on Optimization, 14(2), 548–566. doi:10.1137/S1052623402420528.
Dentcheva, D., Penev, S., & Ruszczyński, A. (2010). Kusuoka representation of higher order dual risk measures. Annals of Operations Research, 181, 325–335. doi:10.1007/s10479-010-0747-5.
Dentcheva, D., Penev, S., & Ruszczyński, A. (2016). Statistical estimation of composite risk functionals and risk optimization problems. Annals of the Institute of Statistical Mathematics. doi:10.1007/s10463-016-0559-8.
Iancu, D. A., Petrik, M., & Subramanian, D. (2015). Tight approximations of dynamic risk measures. Mathematics of Operations Research, 40(3), 655–682. doi:10.1287/moor.2014.0689.
Krokhmal, P. A. (2007). Higher moment coherent risk measures. Quantitative Finance, 7(4), 373–387. doi:10.1080/14697680701458307.
Kusuoka, S. (2001). On law invariant coherent risk measures. In Advances in mathematical economics, Chapter 4 (Vol. 3, pp. 83–95). Springer. doi:10.1007/978-4-431-67891-5.
López-Díaz, M., Sordo, M. A., & Suárez-Llorens, A. (2012). On the \({L}_p\)-metric between a probability distribution and its distortion. Insurance: Mathematics and Economics, 51, 257–264. doi:10.1016/j.insmatheco.2012.04.004.
Luna, J. P., Sagastizábal, C., & Solodov, M. (2016). An approximatioin scheme for a class of risk-averse stochastic equilibrium problems. Mathematical Programming, 157(2), 451–481. doi:10.1007/s10107-016-0988-4.
Miller, N., & Ruszczyński, A. (2011). Risk-averse two-stage stochastic linear programming: Modeling and decomposition. Operations Research, 59, 125–132. doi:10.1287/opre.1100.0847.
Noyan, N., & Rudolf, G. (2014). Kusuoka representations of coherent risk measures in general probability spaces. Annals of Operations Research, 229, 591–605. doi:10.1007/s10479-014-1748-6. (ISSN 0254-5330).
Pflug, G. C. (2000). Some remarks on the Value-at-Risk and the Conditional Value-at-Risk, Chapter 15. In S. Uryasev (Ed.), Probabilistic constrained optimization (Vol. 49, pp. 272–281). New York: Springer.
Pflug, G. C., & Pichler, A. (2014). Multistage stochastic optimization. Springer Series in Operations Research and Financial Engineering: Springer. ISBN 978-3-319-08842-6. doi:10.1007/978-3-319-08843-3.
Pflug, G. C., & Pichler, A. (2016). Time-consistent decisions and temporal decomposition of coherent risk functionals. Mathematics of Operations Research, 41(2), 682–699. doi:10.1287/moor.2015.0747.
Pflug, G. C., & Römisch, W. (2007). Modeling, measuring and managing risk. River Edge, NJ: World Scientific. doi:10.1142/9789812708724.
Pflug, G. C., & Ruszczyński, A. (2005). Measuring risk for income streams. Computational Optimization and Applications, 32(1–2), 161–178, ISSN 0926-6003. doi:10.1007/s10589-005-2058-3.
Philpott, A. B., & de Matos, V. L. (2012). Dynamic sampling algorithms for multi-stage stochastic programs with risk aversion. European Journal of Operational Research, 218(2), 470–483. doi:10.1016/j.ejor.2011.10.056.
Philpott, A. B., de Matos, V. L., & Finardi, E. (2013). On solving multistage stochastic programs with coherent risk measures. Operations Research, 61(4), 957–970. doi:10.1287/opre.2013.1175.
Pichler, A. (2013). The natural Banach space for version independent risk measures. Insurance: Mathematics and Economics, 53(2), 405–415. doi:10.1016/j.insmatheco.2013.07.005.
Pichler, A. (2013). Premiums and reserves, adjusted by distortions. Scandinavian Actuarial Journal, 2015(4), 332–351. doi:10.1080/03461238.2013.830228.
Pichler, A., & Shapiro, A. (2015). Minimal representations of insurance prices. Insurance: Mathematics and Economics, 62, 184–193. doi:10.1016/j.insmatheco.2015.03.011.
Rockafellar, R. T., & Uryasev, S. (2000). Optimization of Conditional Value-at-Risk. Journal of Risk, 2(3), 21–41. doi:10.21314/JOR.2000.038.
Rockafellar, R.T., Uryasev, S., & Zabarankin, M. (2006). Generalized deviations in risk analysis. Finance and Stochastics, 10, 51–74, ISSN 0949-2984. doi:10.1007/s00780-005-0165-8.
Ruszczyński, A. (2010). Risk-averse dynamic programming for Markov decision processes. Mathematical Programming Series B, 125, 235–261.
Ruszczyński, A., & Shapiro, A. (2006). Conditional risk mappings. Mathematics of Operations Research, 31(3), 544–561. doi:10.1287/moor.1060.0204.
Ruszczyński, A., & Yao, J. (2015). A risk-averse analog of the Hamilton–Jacobi–Bellman equation. In Proceedings of the Conference on Control and its Applications, Chapter 62 (pp. 462–468). Society for Industrial & Applied Mathematics (SIAM). doi:10.1137/1.9781611974072.63.
Shapiro, A. (2010). Analysis of stochastic dual dynamic programming method. European Journal of Operational Research, 209, 63–72.
Shapiro, A. (2013). On Kusuoka representation of law invariant risk measures. Mathematics of Operations Research, 38(1), 142–152. doi:10.1287/moor.1120.0563.
Shapiro, A. (2016). Rectangular sets of probability measures. Operations Research, 64(2), 528–541. doi:10.1287/opre.2015.1466.
Shapiro, A., Dentcheva, D., & Ruszczyński, A. (2009). Lectures on stochastic programming. In MOS-SIAM series on optimization. SIAM. doi:10.1137/1.9780898718751.
Sundaresan, K. (1969). Extreme points of the unit cell in Lebesgue–Bochner function spaces. Proceedings of the American Mathematical Society, 23(1), 179–184. doi:10.2307/2037513.
van Heerwaarden, A. E., & Kaas, R. (1992). The Dutch premium principle. Insurance: Mathematics and Economics, 11, 223–230. doi:10.1016/0167-6687(92)90049-H.
Wang, S. S. (1995). Insurance pricing and increased limits ratemaking by proportional hazards transforms. Insurance: Mathematics and Economics, 17, 43–54. doi:10.1016/0167-6687(95)00010-P.
Wojtaszczyk, P. (1991). Banach spaces for analysts. Cambridge: Cambridge University Press.
Wozabal, D. (2010). A framework for optimization under ambiguity. Annals of Operations Research, 193(1), 21–47. doi:10.1007/s10479-010-0812-0.
Wozabal, D. (2014). Robustifying convex risk measures for linear portfolios: A nonparametric approach. Operations Research, 62(6), 1302–1315. doi:10.1287/opre.2014.1323.
Xin, L., & Shapiro, A. (2012). Bounds for nested law invariant coherent risk measures. Operations Research Letters, 40, 431–435. doi:10.1016/j.orl.2012.09.002.
Young, V. R. (2006). Premium Principles. Encyclopedia of Actuarial Science. Wiley Pennsylvania State University. ISBN 9780470012505. doi:10.1002/9780470012505.tap027.
Acknowledgements
We would like to thank the editor of the journal and the referees for their commitment to assess and improve the paper.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Pichler, A. A quantitative comparison of risk measures. Ann Oper Res 254, 251–275 (2017). https://doi.org/10.1007/s10479-017-2397-3
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10479-017-2397-3





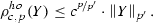
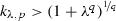 and q is the conjugate Hölder exponent,
and q is the conjugate Hölder exponent, 