Robust supply chain network design: an optimization model with real world application

Abstract

This paper presents a robust optimization model for the design of a supply chain facing uncertainty in demand, supply capacity and major cost data including transportation and shortage cost parameters. We first present a base model that aims to determine the strategic ‘location’ and tactical ‘allocation’ decisions for a deterministic four-tier supply chain. The model is then extended to incorporate uncertainty in key input parameters using a robust optimization approach that can overcome the limitations of scenario-based solution methods in a tractable way, i.e. without excessive changes in complexity of the underlying base deterministic model. The application of the approach is investigated in an actual case study where real data is utilized to design a bread supply chain network. Numerical results obtained from model implementation and sensitivity analysis experiments arrive at important managerial insights and practical implications.

1 Introduction and foundational literature background

Supply chain network design incorporates both strategic (long-term) and tactical (mid-term) decisions. Strategic decisions typically concern the supply chain structure/configuration (e.g. facility location decisions) with long-lasting impacts, generally over several years (Aryanezhad et al. 2010; Bashiri et al. 2012; Cordeau et al. 2006). Tactical decisions determine an outline of the regular operations, in particular the flow quantities for a given supply chain configuration (Fahimnia et al. 2013). Melo et al. (2009) review supply chain models with respect to incorporated strategic and tactical decisions. They find that both strategic and tactical decisions can be highly affected by various sources of uncertainty. Demand and supply interruptions, lead time variability, exchange rate volatility, and capacity variations are examples of such uncertainty sources (Esmaeilikia et al. 2014b).

A comprehensive review by Klibi et al. (2010) shows that ‘stochastic programming’ has been the predominant technique to tackle uncertainty issues in the past studies. Although a powerful approach for modeling non-deterministic problems form a theoretical perspective, stochastic programming, in the context of supply chain management, has serious limitation in real world applications. For instance, stochastic programming techniques usually require the availability of probability distributions of random variables (Klibi et al. 2010), such as the likelihood of an interruption occurrence and its magnitude of impact. Such historical data, especially for those rare events, is limited or non-existent making it difficult or impossible to estimate the actual distribution of uncertain parameters.

A popular type of stochastic programming for supply chain design problems under uncertainty is scenario-based stochastic programming which considers a set of discrete scenarios and their corresponding occurrence probabilities for random variables. Scenario-based stochastic programming typically optimizes the expected value of the objective functions without directly applying the decision makers’ preferences (Azaron et al. 2008). More recently, robust scenario-based supply chain design models have been proposed to overcome this drawback. Table 1 summarizes the characteristics of the published robust scenario-based supply chain models. Most of these models are based on the approach introduced by Mulvey et al. (1995), named robust stochastic optimization or scenario-based robust approach. Mulvey et al. (1995) extended scenario-based stochastic programming by defining the objective function as a mean-variance function incorporating risk measures and decision makers’ preferences in model formulation. Table 1 also shows the other scenario-based supply chain models that use regret criterion. Regret criterion is defined as the difference between the cost of a solution in a given scenario and the cost of the optimal solution for that scenario (Assavapokeea et al. 2008a).

Table 1 Summary of literature of scenario-based robust supply chain networks design

Solutions of a scenario-based robust model are highly dependent on the accuracy of the defined scenarios and their occurrence probabilities. For example, the discrete probabilities assigned to scenarios can have substantial impacts on the derived solutions. Solving such models becomes more difficult as the number of scenarios increases, and this is the primary reason why scenario relaxation methods (Assavapokeea et al. 2008b) or near optimal solution methods like heuristics and meta-heuristics (Bozorgi-Amiri et al. 2012;Jabbarzadeh et al. 2012) have become more popular. In this paper, we present a robust supply chain design model that enables determining the desirable robust decisions without the need to consider different scenarios and their occurrence probabilities. The proposed model is based on a robust optimization approach with interval data uncertainty (Bertsimas and Sim 2004).

The robust formulation with interval data uncertainty was first introduced in mathematical programming by Soyster (1973). Soyster considered the uncertain technological coefficients in the standard form of linear mathematical programming. In this methodology, the maximum level of conservatism is incorporated in the model by substituting the supremum values, or worst-case values, of the uncertain technological coefficients. The drawback of Soyster’s approach is that the robust solution can be highly over- conservative in practical cases because the probability at which uncertain parameters reach their worst values is as low as they reach their normal values. More recent developments in robust optimization have focused on the design of less conservative solution methods which are also computationally tractable. Ben-Tal and Nemirovski (2000) proposed a robust formulation for the linear problem under the box and ellipsoid uncertainty sets where uncertain parameters simultaneously take their worst values resulting in conservative solutions. To reduce the conservatism of robust formulation under the box uncertainty set, they defined ellipsoid uncertainty set which restricts uncertain parameters to obtain their worst values at the same time by applying a parameter to determine the magnitude of uncertainty. Under the ellipsoid uncertainty set, the model complexity increases, and a linear problem becomes a second order cone problem (SOCP).

Baron et al. (2011) applied the robust approach of Ben-Tal and Nemirovski (2000) to formulate uncertainties in demand parameter in a multi-period facility location problem. Their approach changed the MILP deterministic model to a mixed integer conic program model under the ellipsoidal uncertainty set. This robust formulation with interval data uncertainty was more recently applied to tackle the uncertainty of the number of emergency calls and the maximum number of concurrent calls in a bi-objective emergency medical service (EMS) design problem (Zhang and Jiang 2014). The deterministic model minimizes costs of locating EMS stations, assigning demands to EMS stations and the number of vehicles per EMS station. Using ellipsoidal uncertainty set, the deterministic MILP model is changed to a conic quadratic mixed-integer program. The study finds that the increase in the number of candidate EMS stations increases the computational efforts to a large extent.

Ben-Tal et al. (2004) introduced Adjustable Robust Counterpart (ARC) method which allows uncertain parameters to be adjusted as parameter values become realized. ARC is an infinite-dimensional problem and is computationally intractable. Dynamic programming was applied to enhance the tractability of ARC formulation. In other studies, Tang (2006) and Ben-Tal et al. (2011) demonstrated the application of Affinely Adjustable Robust Counterpart (AARC) in emergency logistics distribution and system optimum dynamic traffic assignment problems. Despite the successful application of AARC in these problems, its performance may be affected in situations where recourse variables contain high nonlinearity in terms of the primitive uncertainties (Chen and Zhang 2009).

To overcome the conservatism issue in the approach proposed by Soyster (1973) and computational intractability of methodologies proposed by Ben-Tal and Nemirovski (2000) and Ben-Tal et al. (2004), a robust formulation was presented by Bertsimas and Sim (2004) that has the flexibility of adjusting the conservativeness level of solutions while preserving the computational complexity of the nominal problem. The method can be effective in modeling complex optimization problems such as supply chain planning problem (Najafi et al. 2013; Alem and Morabito 2012). In a more recent study, Hatefi and Jolai (2014) presented a robust and reliable forward-reverse logistics model applying robust formulation of Bertsimas and Sim (2004) to address demand uncertainty.

This paper presents a robust supply chain network design model that incorporates different sources of uncertainty. The proposed model aims to simultaneously determine the strategic location decisions and tactical allocation decisions for a supply chain comprised of multiple suppliers, factories, warehouses and markets. Our model contributes to the existing literature of robust supply chain design in the followings ways. Unlike most of the published robust supply chain network design models that use scenario-based stochastic robust optimization approaches, we adopt the robust formulation with interval data uncertainty introduced by Bertsimas and Sim (2004) to overcome the aforementioned limitations of scenario-based models (e.g. dependency on the characteristics of scenarios defined as well as the computational overhead for managing a large number of scenarios). Using our approach, the model remains computationally tractable given the unchanged complexity of the underlying deterministic model. Addressing multiple uncertainty types including uncertainty in demand, supply and the key cost components is another feature of the model presented in this paper.

The remainder of the paper is organized as follows. Section 2 describes the background of robust optimization formulation. Problem statement and primary assumptions of the deterministic supply chain design modelunder investigation arepresented in Sect. 3. Section 4 presents the robust formulation of the proposed deterministic model. The application of the proposed robust model in a real world context is investigated in Sect. 5. Section 6 includes a summary of the study and results, model and study limitations, and guidance for future research.

2 Background of robust optimization

We first describe the framework of the robust formulation introduced by Bertsimas and Sim (2004). Let us consider a linear mathematical programming model as:

$$\begin{aligned}&Min \; \sum \limits _{i,j} {c_{ij} x_j } \nonumber \\&S.t: \; \sum \limits _j {\tilde{a}_{ij} x_j } \ge b_i \quad \forall i \nonumber \\&\quad \quad \quad x_j \ge \hbox {0 } \quad \forall j , \end{aligned}$$

(1)

where coefficients $\tilde{a}_{ij}$ are uncertain. Let $J_i$ be the set of uncertain coefficients in the $i$th constraint. Each uncertain parameter $\tilde{a}_{ij}$ for $j\in J_i$ is a symmetric and bounded random variable which takes values in interval $[a_{ij} -\hat{{a}}_{ij} ,a_{ij} +\hat{{a}}_{ij} ]$. Where $a_{ij}$ is the nominal value of the uncertain parameter and $\hat{{a}}_{ij}$ denotes the perturbation/variation in each uncertain parameter $\tilde{a}_{ij}$. For each $i$, a parameter $\varGamma _i$, not necessarily integer, is introduced. This parameter is called uncertainty budget and adjusts the uncertainty level in each row varying in interval of $\left[ {0,\left| {J_i } \right| } \right]$. The role of $\varGamma _i$ is thus to adjust the robustness of the proposed method against the level of solution conservatism. It seems unlikely that coefficient $a_{ij} ,j\in J_i$ will change from its nominal values. The robust formulation aims to protect against all cases that up to $\left| {\varGamma _i } \right|$ of these coefficients are allowed to change and coefficient $\tilde{a}_{ij}$ changes by $(\varGamma _i -\left\lfloor {\varGamma _i } \right\rfloor )\hat{{a}}_{ij}$. As a result, when $\varGamma _i$ is set equal to zero, the constraints are equivalent to that of the nominal problem. Similarly, when $\varGamma _i$ is set equal to $\left| {J_i } \right|$, the robust model acts as conservative as in the robust formulation of Soyster (1973). Varying $\varGamma$ helps adjusting the conservatism level of the robust formulation. Bertsimas and Sim (2004) proved that the nonlinear form of the uncertain model (1) can be written as:

$$\begin{aligned}&Min \; {\mathbf{c}}'{\mathbf{x}} \nonumber \\&S.t: \; \sum _j {a_{ij} x_j -\mathop {\max }\limits _\Omega } \left\{ \sum _{j\in S_i } {\hat{{a}}_{ij} x_j } +(\varGamma _i -\left\lfloor {\varGamma _i } \right\rfloor )\hat{{a}}_{it_i } x_j \right\} \ge b_i \quad \forall i \nonumber \\&\quad \qquad {\mathbf{x}}\ge \hbox {0} \end{aligned}$$

(2)

where $\Omega =\{S_i \cup \{t_i \}|S_i \subseteq J_i ,|S_i |=\left\lfloor {\varGamma _i } \right\rfloor ,t_i \in J_i \backslash S_i \}$ defines the uncertainty set. Recall that $S_i$ determines which coefficients can be changed by $\hat{{a}}_{ij}$, and $t_i$ shows the parameter which may change by $(\varGamma _i -\left\lfloor {\varGamma _i } \right\rfloor )\hat{{a}}_{ij}$. Suppose $\hbox {x}^{*}$ is the optimal solution of (2), Bertsimas and Sim (2004) demonstrate that the $i^{th}$ constraint is protected by $\beta _i (\hbox {x}^{{*}},\varGamma _i )=\max \nolimits _{\Omega } \{\sum \nolimits _{j\in S_i} {\hat{{a}}_{ij} x_j^*} +(\varGamma _i -\left\lfloor {\varGamma _i } \right\rfloor )\hat{{a}}_{it_i } x_j^*\}$ against uncertainty. The function $\beta _i (\hbox {x}^{{*}},\varGamma _i )$ is called protection function and can be written as a linear optimization problem as follows:

(3)

Since (3) is feasible and bounded for all $\varGamma _i \in \left[ {0,\left| {J_i } \right| } \right]$, its dual form is also feasible and bounded according to the strong duality property. Substituting the dual form of (3) in (2), the robust counterpart of the uncertain linear programming model is derived as:

$$\begin{aligned}&Min\sum _j {c_j x_j } \nonumber \\&S.t:\sum _j {a_{ij} x_j -\lambda _i \varGamma _i -\sum _{j\in J_i } {\mu _{ij} \ge b_i } } \hbox {, }\forall i \nonumber \\&\qquad \quad \lambda _i +\mu _{ij} \ge \hat{{a}}_{ij }\, x_j \quad \forall i,\, j\in J_i \nonumber \\&\qquad \quad \mu _{ij} \ge 0\hbox {, }\quad \forall i,\, j\in J_i \nonumber \\&\qquad \quad \lambda _i \ge 0\hbox {, }\quad \forall i \nonumber \\&\qquad \quad x_j \ge 0\hbox {, }\quad \forall \,\, j \end{aligned}$$

(4)

where $\lambda _i$ and $\mu _{ij}$ are dual auxiliary variables.

Note that this approach has the property that if up to $\varGamma _i$ number of uncertain coefficients perturb from their nominal values, the robust solution will remain feasible. If more than $\varGamma _i$ change in the $i$th constraint, the robust solution still remains feasible with the probability of:

$$\begin{aligned} P\left( \sum _j \tilde{a}_{ij} \,x_j^*>b_i \right) \le 1-\Phi \left( {{\varGamma _i -1}/{\sqrt{\left| {J_i } \right| }}} \right) . \end{aligned}$$

(5)

In inequality (5), $x_i^*$ is the optimal solution of the robust model, and $\Phi ( \theta )$ is the cumulative distribution function of a standard normal random variable. Identical steps can be followed to employ this robust formulation for uncertain coefficients of the objective function.

3 Formulation of the deterministic model

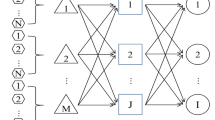
The objective is to design a supply chain network comprised of suppliers, factories, warehouses and markets. Suppliers provide the required raw materials to factories where a single product type is produced to satisfy the market demands through a set of warehouses. Figure 1 illustrates the structure of this supply chain network. The goal is to determine the optimal location of factories and warehouses (strategic decisions) and the quantity of material shipped from suppliers to factories, from factories to warehouses, and from warehouses to markets (tactical decisions).

Fig. 1

The schematic of the proposed supply chain network

Primary assumptions include the followings:

• (1) A shortage penalty is applied proportionate to unsatisfied market demand.

• (2) Candidate nodes for locating factories and warehouses are known.

• (3) Direct product flow from factories to markets is not allowed.

• (4) Suppliers and warehouses have limited and known capacities.

Parameters and decision variables are defined bellow.

Indices

$H$ :

Set of suppliers $(h=1,\ldots ,l)$

$I$ :

Set of potential factory locations $(i=1,\ldots ,n)$

$E$ :

Set of potential warehouse locations $(e=1,\ldots ,t)$

$J$ :

Set of markets $(j=1,\ldots ,m)$

Parameters

$d_j$ :

Demand of customer $j$

$k_i$ :

Production capacity of a factory located at $i$

$s_h$ :

Supply capacity of supplier $h$

$w_e$ :

Capacity of a warehouse located at $e$

$f_i^F$ :

Fixed cost of locating a factory at $i$

$f_e^W$ :

Fixed cost of locating a warehouse at $e$

$c_{hi}^{SF}$ :

Unit shipment cost from supplier $h$ to factory $i$

$c_{ie}^{FW}$ :

Unit shipment cost from factory $i$ to warehouse $e$

$c_{ej}^{WM}$ :

Unit shipment cost from warehouse$e$to market $j$

$p_j$ :

Unit penalty cost for unsatisfied demand at market $j$

$\omega _i$ :

Raw material consumption coefficient in a factory $i$

$\theta _e$ :

Product consumption coefficient in factory/warehouse $e$

Decision variables

$y_i$ :

A binary variable, equal to 1 if a factory is opened at site $i$; 0, otherwise.

$z_e$ :

A binary variable, equal to 1 if a warehouseis opened at site $e$; 0, otherwise.

$x_{hi}$ :

Quantity of raw material shipped from supplier $h$ to factory $i$

$u_{ie}$ :

Quantity of product shipped from factory $i$ to factory/warehouse $e$

$v_{ej}$ :

Quantity of product shipped from factory/warehouse $e$ to market $j$

$I_j$ :

Quantity of unsatisfied demand at market $j$

The deterministic supply chain network design model is formulated as follows:

$$\begin{aligned}&Min\hbox { F}=\sum _{i=1}^n {f_i^F } y_i +\sum _{e=1}^t {f_e^W } z_e +\sum _{h=1}^l \sum _{i=1}^n c_{hi}^{SF} x_{hi}\nonumber \\&\quad \quad \quad \quad \quad +\sum _{i=1}^n {\sum _{e=1}^t {c_{ie}^{FW} u_{ie} } } +\sum _{e=1}^t {\sum _{j=1}^m {c_{ej}^{WM} v_{ej} +\sum _{j=1}^m {p_j I_j } } } \end{aligned}$$

(6)

$$\begin{aligned}&S.t: \nonumber \\&\quad \quad \sum _{i=1}^n {x_{hi} } \le s_h \quad \forall \, h \end{aligned}$$

(7)

$$\begin{aligned}&\quad \quad d_j -\sum _{e=1}^t {v_{ej} } \le I_j \qquad \forall \, j \end{aligned}$$

(8)

$$\begin{aligned}&\quad \quad \sum _{e=1}^t {u_{ie} } \le k_i y_i \quad \forall \, i \end{aligned}$$

(9)

$$\begin{aligned}&\quad \quad \sum _{j=1}^m {v_{ej} } \le w_e z_e \quad \forall \, e \end{aligned}$$

(10)

$$\begin{aligned}&\quad \quad \sum _{h=1}^l {x_{hi} } =\omega _i \sum _{e=1}^t {u_{ie} } \quad \quad \forall \, i \end{aligned}$$

(11)

$$\begin{aligned}&\quad \quad \sum _{i=1}^n {u_{ie} } =\theta _e \,\sum _{j=1}^m {v_{ej} } \quad \forall e \end{aligned}$$

(12)

$$\begin{aligned}&\quad \quad x_{hi} \ge \hbox {0 } \,\forall \, h,i; u_{ie} \ge \hbox {0 }\,\forall \, i,e; v_{ej} \ge \hbox {0 }\quad \forall \, e,j; \nonumber \\&\quad \quad y_i \in \left\{ {0,1} \right\} \quad \forall \, i; z_e \in \left\{ {0,1} \right\} \quad \forall \, e; I_j \ge \hbox {0 }\quad \forall \, j \end{aligned}$$

(13)

The objective function (6) minimizes the total network cost including the costs of locating factories and warehouses, transportation costs for the shipment of raw materials and products (from suppliers to factories, from factories to warehouses, and from warehouses to markets) and shortage/penalty costs. Constraint (7) expresses limitations in supply capacities. Constraint (8) ensures that supply quantity does not exceed the market demands. Capacity restrictions of factories and warehouses are expressed in constraints (9) and (10). Constraint (11) ensures that the quantity of raw materials shipped to a factory is equal to the quantity of products shipped from the factory to warehouses. Constraint (12) guarantees that the quantity of products entered into a factory or warehouse is equal to the quantity of product leaving that warehouse to market locations. It should be noted that $\theta _e$ would be equal to 1 in situations when we have a warehouse in the third echelon of the supply chain.

4 The robust model formulation

This section aims to extend the deterministic model introduced in Sect. 3 to arobust optimization model in which demand, supply and all cost parameters are considered uncertain. The uncertain parameters$\tilde{f}_i^{ F} ,\tilde{f}_e^{ W} ,\tilde{d}_j ,\tilde{s}_h ,\tilde{c}_{hi}^{SF} ,\tilde{c}_{ie}^{FW} ,\tilde{c}_{ej}^{WM}$ and $\tilde{p}_j$ are bounded and distributed in their correspondent intervals with the nominal values of $f_i^{ F} ,f_e^{ W} ,d_j ,s_h ,c_{hi}^{SF} ,c_{ie}^{FW} ,c_{ej}^{WM}$ and $p_j$, and the maximum variations of $\hat{{f}}_i^{ F}, \, \hat{{f}}_{e}^{ W}, \, \hat{{d}}_j, \, \hat{{s}}_h, \, \hat{{c}}_{hi}^{SF}, \, \hat{{c}}_{ie}^{FW} , \, \hat{{c}}_{ej}^{WM}$ and $\tilde{p}_j$, respectively. For example, $\tilde{f}_i^{ F}$ belongs to the interval $[f_{i}^{F} -\hat{{f}}_{i}^{F} ,f_{i}^{F} +\hat{{f}}_{i}^{F} ]$. Given that the main concern in a robust formulation is the impact of parameters’ worst case under uncertainty and that only positive deviations in the uncertain parameters of the present logistics model, except supply parameter$(\tilde{s}_h )$, can lead to the worst cases, we assume that only positive deviations in $\tilde{f}_i^{ F}, \, \tilde{f}_e^{ W}, \, \tilde{d}_j, \, \tilde{c}_{hi}^{SF} , \, \tilde{c}_{ie}^{FW}, \, \tilde{c}_{ej}^{WM}$and $\tilde{p}_j$parameters are allowed. The uncertainty budgets ($\Gamma )$ are also assumed to take only integer values.

In the following subsections, we first apply uncertainties to the cost parameters, except the shortage cost. Next, demand and supply uncertainties are incorporated into the model. The model is then extended to include uncertainties in shortage costs. The resulting robust model is finally presented integrating uncertainty in all aforementioned parameters.

4.1 Uncertainty in cost parameters, except shortage cost

Assuming that parameters $\tilde{f}_i^{F} ,\,\tilde{f}_e^{ W} ,\, \tilde{c}_{hi}^{SF} ,\,\tilde{c}_{ie}^{FW}$, and $\tilde{c}_{ej}^{WM}$ are uncertain, by means of Equation (2), the nonlinear robust counterpart of the objective function can be written as:

$$ \begin{aligned} Min\,{\tilde{F}}&= \sum _{i=1}^n {f_i^F } y_i +\sum _{e=1}^t {f_e^W } z_e \nonumber \\&+\sum _{h=1}^l {\sum _{i=1}^n {c_{hi}^{SF} x_{hi} +\sum _{i=1}^n {\sum _{e=1}^t {c_{ie}^{FW} u_{ie} } } } } +\sum _{e=1}^t {\sum _{j=1}^m {c_{ej}^{WM} v_{ej} +\sum _{j=1}^m {p_j I_j } } } \nonumber \\&+\mathop {\max }\limits _{\Omega ^{f_1 }\Omega ^{f_2 }\Omega ^{C_1 }\Omega ^{C_2 }\Omega ^{C3}} \left\{ \sum _{j\in S^{f_1 }} {\hat{{f}}_i^{ F} } y_i+\sum _{j\in S^{f_2 }} {\hat{{f}}_e^{{ W}} } y_e +\sum _{(h,i)\in S^{C_1 }} {\hat{{c}}_{hi}^{SF} x_{hi}}\right. \nonumber \\&\left. + \sum _{(i,e)\in S^{C_2 }} {\hat{{c}}_{ie}^{FW} x_{ie} +} \sum _{(e,j)\in S^{C_3 }} {\hat{{c}}_{ej}^{WM} x_{ej} } \right\} \nonumber \\ \Omega ^{f_1 }&= \left\{ {S^{f_1 }|S^{f_1 }\subseteq J^{f_1 },|S^{f_1 }|\le \Gamma ^{f_1 }} \right\} ,\, J^{f_1 }=\left\{ {i|\hat{{f}}_i^{ F} >0} \right\} \, \& \,\Gamma ^{f_1 }\in [0,|J^{f_1 }|] \nonumber \\ \Omega ^{f_2 }&= \left\{ {S^{f_2 }|S^{f_2 }\subseteq J^{f_2 },|S^{f_2 }|\le \Gamma ^{f_2 }} \right\} ,\,J^{f_2 }=\left\{ {e|\hat{{f}}_e^{ W} >0} \right\} \, \& \,\Gamma ^{f_2 }\in [0,|J^{f_2 }|] \nonumber \\ \Omega ^{C_1 }&= \left\{ {S^{C_1 }|S^{C_1 }\subseteq J^{C_1 },|S^{C_1 }|\le \Gamma ^{C_1 }} \right\} ,\, J^{C_1 }=\left\{ {(h,i)|\hat{{c}}_{hi}^{SF} >0} \right\} \, \& \,\Gamma ^{C_1 }\in [0,|J^{C_1 }|] \nonumber \\ \Omega ^{C_2 }&= \left\{ {S^{C_2 }|S^{C_2 }\subseteq J^{C_2 },|S^{C_2 }|\le \Gamma ^{C_2 }} \right\} ,\, J^{C_2 }=\left\{ {(i,e)|\hat{{c}}_{ie}^{FW} >0} \right\} \, \& \,\Gamma ^{C_2 }\in [0,|J^{C_2 }|] \nonumber \\ \Omega ^{C_3 }&= \left\{ {S^{C_3 }|S^{C_3 }\subseteq J^{C_3 },|S^{C_3 }|\le \Gamma ^{C_3 }} \right\} ,\, J^{C_3 }=\left\{ {(e,j)|\hat{{c}}_{ej}^{WM} >0} \right\} \, \& \,\Gamma ^{C_3 }\in [0,|J^{C_3 }|]\nonumber \\ \end{aligned}$$

(14)

Using the approach discussed in Sect. 2, the nonlinear formulation (14) can be converted into the equivalent linear model. Linear protection functions are derived for the uncertain coefficients $\tilde{f}_i^{ F}, \, \tilde{f}_e^{ W}, \, \tilde{d}_j, \, \tilde{s}_h, \, \tilde{c}_{hi}^{SF}, \, \tilde{c}_{ie}^{FW}$and $\tilde{c}_{ej}^{WM}$, and to obtain the linear form of the robust counterpart. Considering (3), for instance, the protection function of the shipment cost from suppliers to factories ($\tilde{c}_{hi}^{SF} )$ for a given $x_{hi}^{*}$ is as follows:

$$\begin{aligned} \beta ^{C_1 }\left( x_{hi}^*,\Gamma ^{C_1 }\right) =\mathop {\max }\limits _{\Omega ^{C_1 }} \sum _{(h,i)\in J^{C_1 }} {\hat{{c}}_{hi}^{SF} x_{hi}^{*}} \end{aligned}$$

(15)

This can be written in form of an optimization problem as bellow:

$$\begin{aligned}&\max \sum _{(h,i)\in J^{C_1 }} {\hat{{c}}_{hi}^{SF} w_{hi}^{C_1 } x_{hi}^{*} } \nonumber \\&\quad S.t: \sum _{(h,i)\in J^{C_1 }} {w_{hi}^{C_1 } \le \Gamma ^{C_1 }} \nonumber \\&\quad 0\le w_{hi}^{C_1 } \le 1\qquad \forall \hbox {(}h,i)\in J^{C_1 } \end{aligned}$$

(16)

The dual form of (16) also can be obtained as:

$$\begin{aligned}&\min \qquad \lambda ^{C_1 }\Gamma ^{C_1 }+\sum _{(h,i)\in J^{C_1 }} {\mu _{hi}^{C_1 } }\end{aligned}$$

(17)

$$\begin{aligned}&S.t:\nonumber \\&\quad \quad \mu _{hi}^{C_1 } +\lambda ^{C_1 }\ge \hat{{c}}_{hi}^{SF} x_{hi} \qquad \forall (h,i)\in J^{C_1 } \nonumber \\&\quad \quad \mu _{hi}^{C_1 } \ge 0\qquad \qquad \qquad \qquad \forall (h,i)\in J^{C_1 } \nonumber \\&\quad \quad \lambda ^{C_1 }\ge 0 , \end{aligned}$$

(18)

where $\lambda ^{c_1 }$ and $\mu _{ij}^{c_1 }$ are dual variables. The linear dual forms of protection functions for the remaining uncertain parameters including $\tilde{f}_e^{W}, \, \tilde{c}_{ie}^{FW}$ and $\tilde{c}_{ej}^{WM}$ are also formulated. The protection function of $\tilde{f}_i^{F}$ is defined as:

$$\begin{aligned} \beta ^{f_1 }(y_i^*,\Gamma ^{f_1 })=\mathop {\max }\limits _{\Omega ^{f_1 }} \sum _{i\in J^{f_1 }} {\hat{{f}}_i^{F} y_i^*} \end{aligned}$$

(19)

The equivalent optimization problem of the protection function of $\tilde{f}_i^{F}$ is written as:

$$\begin{aligned}&\max \sum _{i\in J^{f_1 }} {\hat{{f}}_i^F w_i^{f_1 } y_i^*}\nonumber \\&S.t:\sum _{i\in J^{f_1 }} {w_i^{f_1 } \le \Gamma ^{f_1 }}\nonumber \\&0\le w_i^{f_1 } \le 1\quad \forall i\in J^{f_1 } \end{aligned}$$

(20)

Ultimately, the dual form of the abovementioned linear optimization problem can be expressed as bellows:

$$\begin{aligned}&\min \,\lambda ^{f_1 }\Gamma ^{f_1 }+\sum _{h\in J^{f_1 }} {\mu _h^{f_1 } }\end{aligned}$$

(21)

$$\begin{aligned}&S.t:\nonumber \\&\quad \quad \mu _i^{f_1 } +\lambda ^{f_1 }\ge \hat{{f}}_i^F y_i \quad \forall i\in J^{f_1 } \nonumber \\&\quad \quad \mu _i^{f_1 } \ge 0\quad \forall i\in J^{f_1 } \nonumber \\&\quad \quad \lambda ^{f_1 }\ge 0 \end{aligned}$$

(22)

$\lambda ^{f_1 }$ and $\mu _i^{f_1 }$ are dual variables corresponding to the constraints of the primal optimization model.

Furthermore, the protection function of $\tilde{f}_e^{ W}$ can be written as:

$$\begin{aligned} \beta ^{f_2 }(z_e^*,\Gamma ^{f_2 })=\mathop {\max }\limits _{\Omega ^{f_2 }} \sum _{e\in J^{f_2 }} {\hat{{f}}_e^{ F} z_e^*} \end{aligned}$$

(23)

And, the linear optimization problem of (23) can be defined as:

$$\begin{aligned}&\max \sum _{e\in J^{f_2 }} {\hat{{f}}_e^W w_e^{f_2 } z_e^*}\nonumber \\&S.t:\sum _{e\in J^{f_2 }} {w_e^{f_2 } \le \Gamma ^{f_2 }}\nonumber \\&0\le w_e^{f_2 } \le 1\quad \forall e\in J^{f_2 } \end{aligned}$$

(24)

The dual form of (24) can be expressed by applying $\lambda ^{f_2 }$ and $\mu _e^{f_2 }$ as dual variables:

$$\begin{aligned}&\min \,\lambda ^{f_2 }\Gamma ^{f_2 }+\sum _{e\in J^{f_2 }} {\mu _e^{f_2 } } \end{aligned}$$

(25)

$$\begin{aligned}&S.t: \nonumber \\&\mu _e^{f_2 } +\lambda ^{f_2 }\ge \hat{{f}}_e^W z_e \quad \forall e\in J^{f_2 } \nonumber \\&\mu _e^{f_2 } \ge 0\quad \forall e\in J^{f_2 } \nonumber \\&\lambda ^{f_2 }\ge 0 \end{aligned}$$

(26)

The protection function of $\tilde{c}_{ie}^{FW}$is defined as:

$$\begin{aligned} \beta ^{C_2 }(u_{ie}^*,\Gamma ^{C_2 })=\mathop {\max }\limits _{\Omega ^{C_2 }} \sum _{(i,e)\in J^{C_2 }} {\hat{{c}}_{ie}^{FW} u_{ie}^*} \end{aligned}$$

(27)

Also, the linear optimization problem of (27) can be written as:

$$\begin{aligned}&\max \sum _{(i,e)\in J^{C_2 }} {\hat{{c}}_{ie}^{FW} w_{ie}^{C_2 } u_{ie} ^{*}} \nonumber \\&S.t: \sum _{(i,e)\in J^{C_2 }} {w_{ie}^{C_2 } \le \Gamma ^{C_2 }}\nonumber \\&0\le w_{ie}^{C_2} \le 1\quad \forall \hbox {(}i,e)\in J^{C_2 } \end{aligned}$$

(28)

And, the dual form of the abovementioned formulation can be expressed as:

$$\begin{aligned}&\min \,\lambda ^{C_2 }\Gamma ^{C_2 }+\sum _{(i,e)\in J^{C_2 }} {\mu _{ie}^{C_2 } } \end{aligned}$$

(29)

$$\begin{aligned}&S.t:\nonumber \\&\mu _{ie}^{C_2 } +\lambda ^{C_2 }\ge \hat{{c}}_{ie}^{FW} u_{ie} \quad \forall (i,e)\in J^{C_2 } \nonumber \\&\mu _{ie}^{C_2 } \ge 0\quad \forall (i,e)\in J^{C_2 } \nonumber \\&\lambda ^{C_2 }\ge 0 \end{aligned}$$

(30)

$\lambda ^{ C_3 }$ and $\mu _{ej}^{c_3 }$ are dual variables corresponding to the constraints of the primal linear optimization model.

The protection function of $\tilde{c}_{ej}^{WM}$ is defined as:

$$\begin{aligned} \beta ^{C_3 }(v_{ej}^*,\Gamma ^{C_3 })=\mathop {\max }\limits _{\Omega ^{C_3 }} \sum _{(e,j)\in J^{C_3 }} {\hat{{c}}_{ej}^{WM} v_{ej}^*} \end{aligned}$$

(31)

Also, the linear form of (31) can be written as:

$$\begin{aligned}&\max \sum _{(e,j)\in J^{C_3 }} {\hat{{c}}_{ej}^{WM} w_{ej}^{C_3 } v^{*}_{ej} } \nonumber \\&S.t: \sum _{(e,j)\in J^{C_3 }} {w_{ej}^{C_3 } \le \Gamma ^{C_3 }} \nonumber \\&0\le w_{ej}^{C_3 } \le 1\quad \forall \hbox {(}e,j)\in J^{C_3 } \end{aligned}$$

(32)

The dual formulation of (32) is expressed as bellow, using $\lambda ^{ C_3 }$ and $\mu _{ej}^{c_3 }$ as dual variables:

$$\begin{aligned}&\min \,\lambda ^{C_3 }\Gamma ^{C_3 }+\sum _{(e,j)\in J^{C_3 }} {\mu _{ej}^{C_3 } } \end{aligned}$$

(33)

$$\begin{aligned}&S.t:\nonumber \\&\mu _{ej}^{C_3 } +\lambda ^{C_3 }\ge \hat{{c}}_{ej}^{WM} v_{\mathrm{ej}} \quad \forall (e,j)\in J^{C_3 } \nonumber \\&\mu _{ej}^{C_3 } \ge 0\quad \forall (e,j)\in J^{C_3 } \nonumber \\&\lambda ^{C_3 }\ge 0 \end{aligned}$$

(34)

Substituting the obtained linear dual forms of the protection functions for the uncertain parameters $\hat{{f}}_i^{F}, \, \hat{{f}}_e^W, \, \hat{{c}}_{hi}^{SF}, \, \hat{{c}}_{ie}^{FW}$ and $\hat{{c}}_{ej}^{WM}$in (14), the robust model can be written as follows:

$$\begin{aligned} Min\,\tilde{\hbox {F}}&= \sum _{i=1}^n {f_i^F } y_i +\sum _{e=1}^t {f_e^W } z_e +\sum _{h=1}^l {\sum _{i=1}^n {c_{hi}^{SF} x_{hi} +\sum _{i=1}^n {\sum _{e=1}^t {c_{ie}^{FW} u_{ie} } } } } +\sum _{e=1}^t {\sum _{j=1}^m {c_{ej}^{WM} v_{ej} } } \nonumber \\&+ \,\lambda ^{f_1 }\Gamma ^{f_1 }+\sum _{h\in J^{f}} {\mu _h^{f_1 } } +\lambda ^{f_2 }\Gamma ^{f_2 }+\sum _{e\in J^{f}} {\mu _e^{f_2 } } +\lambda ^{C_1 }\Gamma ^{C_1 }+\sum _{(h,i)\in J^{C_1 }} {\mu _{hi}^{C_1 } } \nonumber \\&+\, \lambda ^{C_2 }\Gamma ^{C_2 }+\sum _{(i,e)\in J^{C_2 }} {\mu _{ie}^{C_2 } +\lambda ^{C_3 }\Gamma ^{C_3 }+\sum _{(e,j)\in J^{C_3 }} {\mu _{ej}^{C_3 } } } +\sum _{j=1}^m {p_j I_j } \end{aligned}$$

(35)

S.t:

Constraints (7) to (13)

Constraints (18), (22), (26), (30) and (34).

4.2 Uncertainty in demand and supply capacity parameters

This section utilizes the robust approach proposed by Bertsimas and Thiele (2006) to formulate the uncertainty in demand and supply capacity parameters as right-hand side parameters in the model. According to this approach, the parameters $\tilde{d}_j$ and $\tilde{s}_h$ are independently distributed in the common ranges $[d-\hat{{d}},d+\hat{{d}}]$ and $[s-\hat{{s}},s+\hat{{s}}]$ corresponding to all markets and suppliers. Also, common uncertainty budgets are considered for demands ofall markets and supplies of all supply centers. Here,$\Gamma ^{m}$ denotes the common uncertainty budget for demands in all markets taking values between zero and the number of markets; that is, $\Gamma ^{m}\in [0,m]$. And, $\Gamma ^{l}$ is the common uncertainty budget for supply capacities in all supply centers, and takes the values between zero and the total number of suppliers ($\Gamma ^{l}\in [0,l])$.

Demand parameters can have influences on shortage costs. A unit shortage cost is denoted by $p_j$, and the total shortage cost at node $j$ is equal to $p_j I_j$.To formulate the influences of demand uncertainty on shortage costs, we define auxiliary variable $H_j$ and add constraint (36) to the model:

$$\begin{aligned} p_j I_j \le H_j \quad \forall j \end{aligned}$$

(36)

By this, the term $p_j I_j$ can be replaced by $H_j$ in the objective function. In other words,$H_j$ is related to the shortage cost of unsatisfied items that needs to be included in the objective function to be minimized ($p_j I_j )$. Considering (8), we can now rewrite (36) to include the uncertain demand $\tilde{d}_j$ as follows:

$$\begin{aligned} p_j \left( \tilde{d}_j -\sum _{e=1}^t {v_{ej} }\right) \le H_j \quad \forall j \end{aligned}$$

(37)

Using the adjusted upper bound of the interval $[d-\hat{{d}},d+\hat{{d}}]$ by the common budget of uncertainty in inequality (37), that is “$d+\frac{\Gamma ^{m}}{m}\hat{{d}}$”, its left hand side takes its maximum value that should be minimized. Hence, (37) and (8) can be modified to the following robust form:

$$\begin{aligned}&\tilde{p}_j \left( d+\frac{\Gamma ^{m}}{m}\hat{{d}}-\sum _{e=1}^t {v_{ej} }\right) \le H_j \quad \forall j \end{aligned}$$

(38)

$$\begin{aligned}&d+\frac{\Gamma ^{m}}{m}\hat{{d}}-\sum _{e=1}^t {v_{ej} } \le I_j \quad \forall j \end{aligned}$$

(39)

Following this logic, the adjusted lower bound of the interval $[s-\hat{{s}},s+\hat{{s}}]$ leads to the worst $S_h$ auxiliary variable value, what the model seeks to minimize. Therefore, (7) can be rewritten in robust forms as follows:

$$\begin{aligned} \sum _{i=1}^n {x_{hi} } -s+\frac{\Gamma ^{l}}{l}\hat{{s}}\le S_h \quad \forall h \end{aligned}$$

(40)

4.3 Uncertainty in the shortage cost

Shortage costs are next considered to be uncertain and, without loss of generality, only take the positive variations from their nominal values. Therefore, we can write $\tilde{p}_j =p_j+\hat{{p}}{ }_jw_j$ for $w_j \in \left[ {0,1} \right]$, where $w_j$ is derived by $w_j =\left( {\frac{\tilde{p}_j -p_j}{\hat{{p}}_j}} \right)$ as the scaled deviation. To determine $w_j$ in a way that the left hand side of constraint (38) is maximized, the following problem needs to be solved:

$$\begin{aligned}&\max \hat{{p}}_jw_j \left( d+\frac{\Gamma ^{m}}{m}\hat{{d}}-\sum _{e=1}^t {v_{ej} }\right) \nonumber \\&s.t: \nonumber \\&\quad \quad w_j \le \Gamma _j^p \quad \forall j \nonumber \\&\quad \quad 0\le w_j \le 1\quad \forall j \end{aligned}$$

(41)

Note that $\varGamma _j^p$ denotes the associate budget uncertainty belonging to the interval $\left[ {0,1} \right]$. The dual form of (41) is formulated as:

$$\begin{aligned}&\min \lambda _j^p \varGamma _j^p +\mu _j^p \quad \forall j \nonumber \\&s.t: \nonumber \\&\quad \quad \lambda _j^p +\mu _j^p \ge \hat{{p}}_j\left( d+\frac{\Gamma ^{m}}{m}\hat{{d}}-\sum _{e=1}^t {v_{ej} }\right) \quad \forall j \nonumber \\&\quad \quad \mu _j^p \ge \hbox {0 }\quad \forall j \nonumber \\&\quad \quad \lambda _j^p \ge \hbox {0 }\quad \forall j \end{aligned}$$

(42)

Thus, constraint (38) can be rewritten as bellow:

$$\begin{aligned}&\displaystyle p_j \left( d+\frac{\Gamma ^{m}}{m}\hat{{d}}-\sum _{e=1}^t {v_{ej} }\right) +\lambda _j^p \Gamma _j^p +\mu _j^p \le H_j \quad \forall j \nonumber \\&\lambda _j^p +\mu _j^p \ge \hat{{p}}_j\left( d+\frac{\Gamma ^{m}}{m}\hat{{d}}-\sum _{e=1}^t {v_{ej} }\right) \quad \forall j \nonumber \\&\mu _j^p \ge \hbox {0 }\quad \forall j \nonumber \\&\lambda _j^p \ge \hbox {0 }\quad \forall j \end{aligned}$$

(43)

According to Sects. 4.1 and 4.3, the resulting robust model that integrates uncertainties in demand, supply and cost parameters is expressed as follows:

$$\begin{aligned} Min\,\tilde{\hbox {F}}&= \sum _{i=1}^n {f_i^F } y_i +\sum _{e=1}^t {f_e^W } z_e +\sum _{h=1}^l {\sum _{i=1}^n {c_{hi}^{SF} x_{hi} +\sum _{i=1}^n {\sum _{e=1}^t {c_{ie}^{FW} u_{ie} } } } } +\sum _{e=1}^t {\sum _{j=1}^m {c_{ej}^{WM} v_{ej} } } \nonumber \\&+\, \lambda ^{f_1 }\Gamma ^{f_1 }+\sum _{h\in J^{f}} {\mu _h^{f_1 } } +\lambda ^{f_2 }\Gamma ^{f_2 }+\sum _{e\in J^{f}} {\mu _e^{f_2 } } +\lambda ^{C_1 }\Gamma ^{C_1 }+\sum _{(h,i)\in J^{C_1 }} {\mu _{hi}^{C_1 } } +\lambda ^{C_2 }\Gamma ^{C_2 } \nonumber \\&+\, \sum _{(i,e)\in J^{C_2 }} {\mu _{ie}^{C_2 } +\lambda ^{C_3 }\Gamma ^{C_3 }+\sum _{(e,j)\in J^{C_3 }} {\mu _{ej}^{C_3 } } } +\sum _{j=1}^m {H_j } \end{aligned}$$

(44)

S.t:

Constraints (9) to (13),

Constraints (18), (22), (26), (30), (34), (39), (40) and (43).

4.4 Applying stochastic programming on conservatism degrees

In the proposed robust supply chain model, there are various uncertain parameters ($\Gamma )$ the values of which have direct impact on the values of decision variables. One way to determine the values of these parameters is to run the model several times for each $\Gamma$ value and choose the most appropriate alternative that best suits a specific situation. This is typically a time-consuming process. To cope with this difficulty, we adopt the approach suggested by Alem and Morabito (2012) to aggregate different values of conservatism degrees using stochastic programming. A set of scenarios ($\Omega )$ is generated. An occurrence probability, denoted by $p_s ,$ is assigned to each scenario. Obviously, we will have:$\sum _{s=1}^S {p_s } =1,\, p_s \ge 0$. Each $\Gamma$ takes an index $s\in \Omega =\left\{ {1,\ldots ,S} \right\}$.

Auxiliary variables $S_{hs} ,\, I_{js}$ and $H_{js}$ are used to apply scenarios to constraints (39), (40) and (43) as follows:

$$\begin{aligned}&\displaystyle d+\frac{\Gamma _s^m }{m}\hat{{d}}-\sum _{e=1}^t {x_{ej} } \le I_{js} \quad \forall j,s \end{aligned}$$

(45)

$$\begin{aligned}&\sum _{i=1}^n {x_{hi} } -s+\frac{\Gamma _s^l }{l}\hat{{s}}\le S_{hs} \quad \forall h,s \end{aligned}$$

(46)

$$\begin{aligned}&p_j \left( d+\frac{\Gamma _s^m }{m}\hat{{d}}-\sum _{e=1}^t {x_{ej}} \right) +\lambda _j^p \Gamma _j^p +\mu _j^p \le H_{js} \quad \forall j,s \nonumber \\&\lambda _j^p +\mu _j^p \ge \hat{{p}}_{j}\left( d+\frac{\Gamma _s^m }{m}\hat{{d}}-\sum _{e=1}^t {x_{ej}} \right) \quad \forall j,s \nonumber \\&\mu _j^p \ge \hbox {0 }\quad \forall j \nonumber \\&\lambda _j^p \ge \hbox {0 }\quad \forall j \end{aligned}$$

(47)

The expected values for $S_{hs} ,\, I_{js}$ and $H_{js}$ are obtained from the following constraints:

$$\begin{aligned} \sum _{s=1}^S {p_s H_{js} \le H_j} \quad \forall j \end{aligned}$$

(48)

$$\begin{aligned} \sum _{s=1}^S {p_s I_{js} \le I_j } \quad \forall j \end{aligned}$$

(49)

$$\begin{aligned} \sum _{s=1}^S {p_s S_{hs} \le S_h } \quad \forall h \end{aligned}$$

(50)

Therefore, the objective function (44) can be rewritten as:

$$\begin{aligned}&Min\,{ \tilde{\hbox {F}}}=\sum _{i=1}^n {f_i^F } y_i +\sum _{e=1}^t {f_e^W } z_e +\sum _{h=1}^l {\sum _{i=1}^n {c_{hi}^{SF} x_{hi} +\sum _{i=1}^n {\sum _{e=1}^t {c_{ie}^{FW} u_{ie} } } } } +\sum _{e=1}^t {\sum _{j=1}^m {c_{ej}^{WM} v_{ej} } } \nonumber \\&\qquad \qquad \quad + \sum _{h\in J^{f}} {\mu _h^{f_1 } } \qquad +\sum _{e\in J^{f}} {\mu _e^{f_2 } } +\sum _{(h,i)\in J^{C_1 }} {\mu _{hi}^{C_1 } } +\sum _{(e,j)\in J^{C_3 }} {\mu _{ej}^{C_3 } +\sum _{(i,e)\in J^{C_2 }} {\mu _{ie}^{C_2 } } } \nonumber \\&\qquad \qquad \quad + \sum _{s=1}^S {p_s } (\lambda ^{f_1 }\Gamma _s^{f_1 } +\lambda ^{f_2 }\Gamma _s^{f_2 } +\lambda ^{C_1 }\Gamma _s^{C_1 } +\lambda ^{C_2 }\Gamma _s^{C_2 } +\lambda ^{C_3 }\Gamma _s^{C_3 } )+\sum _{j=1}^m {H_j } \end{aligned}$$

(51)

Applying stochastic programming to the conservatism degrees, the constraints of the ultimate model are constraints (9) to (13), constraints (18), (22), (26), (30), (34) and constraints (45) to (50).

5 Model implementation and numerical results

The application of the proposed model is investigated using real data collected from a bread supply chain in Iran. The model is coded in Lingo 11 and the numerical experiments are conducted on a PC with Pentium IV CPU and two gigabyte of RAM.

5.1 Case study description

According to a national report released by Iranian Ministry of Health and Hygiene, approximately one fifth of children under 6 years old, teenagers and pregnant women in Iran are diagnosed with anemia due to lack of minerals and vitamins in blood cells. Anemia is a blood disorder that may be cured by regular consumption of nutrients like iron and folic acid. Iranian health experts have found that an important action to prevent anemia is to produce and distribute enriched bread throughout the country because of the significant nutritional role of bread in Iranian meals. Enriched bread is produced by adding necessary minerals and vitamins includingiron, vitamin B, folic acid, riboflavin, niacin and thiamine to the white flour. The proposed robust optimization approach in this study was used to design an effective bread supply chain network consisting of wheat suppliers, flour factories, bread factories (second-stage factories) and markets. Demand was considered to be the bread consumption of Iran’s southern provinces where anemia is more common. These provinces were zoned according to their population and the supply capacity of wheat. For example, bread demand in Khouzestan province was zoned to three regions as Dezfoul, Khoramshahr and Ramhormoz cities. Table 2 outlines the locations of candidate wheat suppliers, flour and bread factories and markets. Figure 2 provides an illustration of the geographically dispersed location of these nodes on the country map.

Fig. 2

Schematic location of potential markets and candidate suppliers, wheat factories and bread factories

Table 2 Candidate suppliers and factories and potential markets in the proposed case problem

The values of the primary input parameters are shown in Table 3. The approximate demand was calculated by multiplying the estimated annual bread consumption per capita by the population of that zone. Tables 4, 5, 6 show the transportation costs between the supply chain participants obtained from the available third-party logistics providers. The consumption coefficient of wheat to produce enriched flour ($\omega _i )$ is 0.83 and the consumption coefficient of enriched flour to produce enriched bread ($\theta _e )$ is 1.3.

Table 3 Values of the primary input parameters

Table 4 Cost of transportation between candidate wheat suppliers and flour factories ($ per Ton)

Table 5 Cost of transportation between candidate flour factories and bread factories ($ per Ton)

Table 6 Cost of transportation between candidate bread factories and potential markets ($ per Ton)

5.2 Numerical results and practical implications

Computational experiments were conducted for 5, 10, 15 and 20 % of variability in uncertain parameters from their nominal values presented in Sect. 5.1. The variability percent of the uncertain parameters are tuned based on the expert advice received from professionals in food logistic domain. Let $\gamma$ denote the percent of variability in uncertain parameters. The variation in demand ($\hat{{d}}_m )$ can then be obtained from. Analogous approach is used to obtain the variations in the other uncertain parameters. The robust optimization model with interval data uncertainty has 669 variables, including 16 integer variables, and 412 constraints. Optimal solutions were found in 3,112 iterations completed in only 3 s with a optimality gap of $1.8 \times 10^{-12}$.

To determine the sensitivity of the objective function value to variations in uncertain parameters, sensitivity analysis experiments are performed using different degrees of conservatism. With nine suppliers, seven candidate flour factories, nine candidate bread factories and 19 markets, the corresponding conservatism degrees can take integer values in intervals of [0,9], [0,7], [0,9], [0,19], respectively. In addition, the conservatism degrees associated with transportation costs coefficients $c_{hi}^{SF}, \, c_{ie}^{FW}$ and $c_{ej}^{WM}$ belong to intervals [0,63], [0,63] and [0,171], respectively.

Figures 3, 4, 5, 6, 7, 8 and 9 show how the value of objective function is affected by different degrees of conservatism and variations in uncertain parameters. Normalized deviation of the optimal value of objective function is used in all experiments. For this, let $Z^{N}$ and $Z^{R}$ denote the optimal values for the deterministic model (6) and the robust formulation (32). The increase in the optimal value of objective function is obtained using $(Z^{R}-Z^{N})/Z^{N}$. In addition to the changes in the value of objective function, Figs. 3, 4, 5, 6, 7, 8 and 9 also show the probabilities of constraint violation (5) at different conservatism degrees $(\Gamma ^{m})$.

Fig. 3

Sensitivity of the proposed model to variations in demand data

Fig. 4

Sensitivity of the proposed model to variations in supply capacity data

Fig. 5

Sensitivity of the proposed model to variations in supplier-factory transportation cost data

Fig. 6

Sensitivity of the proposed model to variations in flour factory-bread factory transportation cost data

Fig. 7

Sensitivity of the proposed model to variations in factory-marker transportation cost data

Fig. 8

Sensitivity of the proposed model to variations in costs of locating flour factories

Fig. 9

Sensitivity of the proposed model to variations in costs of locating bread factories

Numerical results presented in Figs. 3, 4, 5, 6, 7, 8 and 9 can provide some interesting insights. Figures 3 and 4 show thatthe worst objective value is obtained at a point when the conservatism degree of uncertain demand and supply parameters have their highest values; that is when $\Gamma =\left| J \right|$.Conversely, Figures 5, 6, 7, 8 and 9 indicate thatthe worst objective value is reached at a point when conservatism degrees of uncertain cost parameters are smaller than their maximum (i.e.$\Gamma ^{C_1 }=15<\left| {J^{C_1 }} \right| =63,\Gamma ^{C_2 }=10<\left| {J^{C_2 }} \right| =63,\Gamma ^{C_3 }=25<\left| {J^{C_3 }} \right| =171,\Gamma ^{f_1 }=5<\left| {J^{f_1 }} \right| =7$ and $\Gamma ^{f_2 }=6<\left| {J^{f_2 }} \right| =9$, respectively). The initial implications are now evident. The greater the conservatism degree of uncertain demand and supply parameters are, the larger the impacts will be on the value of objective function. This is not the case for variations in cost parameters where increase in the degree of conservatism can only cause limited impacts on the objective value.

A second insight can be drawn by comparing the magnitude of impacts on the objective value caused by variations in uncertain parameters. When $\gamma$ is equal to 0.2 (i.e. a maximum 20 % variation in uncertain parameters), variation in demand data has a high deterioration impact of 22.7 % on the value of objective function. For the same situation of $\gamma =0.2$, the impacts on the value of objective function imposed by the other uncertain parameters include 2.05 % caused by supply uncertainty, 2.16 % caused by supplier-factory transportation cost uncertainty, 1.38 % caused by factory-factory transportation cost uncertainty, 1.52 % caused by factory-market transportation cost uncertainty, 1.09 % caused by uncertainty in cost of locating flour factories, and 2.62 % caused by uncertainty in cost of locating bread factories. A practical implication from this finding is that the primary focus should be placed on more accurate forecast of demand data as it can have the highest influence on overall system cost.

We next design additional experiments aiming to assist a decision maker in choosing the appropriate conservatism degrees. One method for selecting the appropriate conservatism degrees is the use of probability of constraint violation. In this method, a decision maker seeks the degrees of conservatism that ensure the probability of constraint violation will not exceed a specific value/percentage. Table 7 illustrates the choice of conservatism degrees so that violation probability (5) is less than a specific percentage $\alpha$, where $\alpha$ can be equal to 1, 5, 10, 30, 40 or 50 %. In other words, Table 7 provides the smallest values of conservatism ($\Gamma )$, that guarantee violation probability of less than $\alpha$%. It also includes the values of $\frac{\Gamma }{|J|}$, indicating the percentage of the number of uncertain data protected. For instance, to guarantee violation probability of less than 1 %, a $\Gamma$ equal to 11 is required, standing for 58 % of the number of uncertain demand data.

Table 7 Selection of the conservatism degrees based on $\alpha$% of violation probabilities (5)

Not surprisingly, the value of objective function is greater at larger variability levels in all probability sets. The objective value under the first probability set (the pessimistic behavior of Set1) is more sensitive to such variations when compared to the other two probability sets. What is interesting in these findings is that the optimal decisions of locating the flour and bread factories are analogous in pessimistic, neutral and optimistic decision-making behaviors. Flour factories F2, F3, F5 and F7 and bread factories B1, B3, B4, B5 and B9 are opened in three decision-making situations implying the decisions to locate flour and bread factories are robust. For the three probability sets, Tables 11, 12, 13 summarize the optimal allocation decisions for the wheat, flour and bread distribution at 20% variability level.

Comparing the values of $\frac{\Gamma }{|J|}$ for different uncertain parameters result in some additional insights. The highest value of $\frac{\Gamma }{|J|}$ in all instances belong to the uncertainty in cost of locating bread factories. For example, the results in Table 7 indicate that the complete protection against uncertainty in locating bread factories (i.e. $\frac{\Gamma ^{f_1 }}{\left| {J^{f_1 }} \right| } = 100 \% )$ ensures a violation probability of less than 1%, whereas other cost parameters require considerably smaller values of $\frac{\Gamma }{|J|}$to reach this goal (i.e.$\frac{\Gamma ^{c_1 }}{\left| {J^{c_1 }} \right| }=33\% ,\, \frac{\Gamma ^{c_2 }}{\left| {J^{c_2 }} \right| }=33\% \, \frac{\Gamma ^{c_3 }}{\left| {J^{c_3 }} \right| }=19.3\%$ and $\frac{\Gamma ^{f_2 }}{\left| {J^{f_2 }} \right| }=88\% )$. This implies that the cost of locating bread factories required more degrees of conservatism compared to the other cost parameters. Another observation from Table 7 is that for all $\alpha$ values, the percentage of $\frac{\Gamma ^{l}}{|J^{l}|}$ is greater than $\frac{\Gamma ^{m}}{|J^{m}|}$. An important practical implication from this observation is that supply uncertainty demands greater level of conservatism compared to demand uncertainty during supply chain design phase.

Another method of choosing the values of conservatism degrees is to run the model for different values of $\Gamma$and choose the most appropriate alternative that best fits a specific situation. Even though the flexibility of this method in adjusting the value of $\Gamma$ may be appealing at the beginning, the process of running the model for different $\Gamma$values can become extremely inefficient in terms of the time it demands (see Alem and Morabito 2012). To overcome this drawback, we design the following experiments based on the stochastic programming formulation presented in Sect. 4.4 in which different conservatism degrees are aggregated in one optimization model requiring a single model run. Ten scenarios of conservatism degrees are defined for use in the proposed scenario stochastic programming formulation. Table 8 shows the values of conservatism degrees for each scenario.

Table 8 Conservatism degrees at each scenario

To help examining the behavior of the proposed stochastic programming formulation, a sensitivity analysis is performed using different probability sets and variability levels. Three probability sets are defined for each scenario, denoted by Set 1, Set 2 and Set 3. The three sets stands for decision making under pessimistic, neutral and optimistic behaviors, respectively. For each scenario, Table 9 shows the occurrence probabilities at each probability set. Table 10 shows the values of objective function (50) corresponding to the defined probability sets and variability levels $(\gamma )$. The model has 1,162 variables, including 16 integer variables, and 1031 constraints. The model was solved in 15,678 iterations completed in 5 s with an optimality gap is $9.3 \times 10^{-9}$.

Table 9 Occurrence probabilities of scenarios for each set

Table 10 Objective values corresponding to different probability sets and variability degrees ${\$}$

Numerical results in Tables 11, 12, 13 show that the optimal assignment decisions for the three probability sets are very similar. The flour factories in most cases are assigned to the same suppliers under the three probability sets. Likewise, the optimal allocations of the flour factories to the bread factories and the optimal assignments of the bread factories to the markets are nearly analogous in all probability sets. However, the optimal quantities of flour and bread shipments from suppliers to flour factories, from flour factories to bread factories and from bread factories to markets differ at each probability set.Similarly, the shortage values at the bottom of Table 13 indicate that the shortage amounts (an indicator of service level) are larger at higher levels of conservatism. One managerial implication from these findings is that the shipment quantities (flow decisions) and shortage amounts (service level decisions) are more sensitive to probability degree and the decision maker behavior when compared to location and allocation decisions. Flow and service level decisions may hence require more careful attention in network design process due to the sensitivity of their optimal values to level of optimism.

Table 11 Wheat distribution from suppliers to opened flour factories at three probability sets

Table 12 Flour distribution from opened flour factories to opened bread factories at three probability sets

Table 13 Bread distribution from opened bread factories to markets at three probability sets

6 Conclusions

We presented in this paper a robust optimization model for the design of a supply chain operating in an uncertain environment. The proposed robust formulation minimizes the overall supply chain costs to determine optimal location and allocation strategieswhen uncertainty exist in product demand, supply capacity, and transportation and shortage cost data. A base deterministic location/allocation model was extended to incorporate uncertainty factors using a robust optimization approach with interval data uncertainty. The extended model remains a linear and traceable model, while overcoming the limitations of the equivalent scenario-based and heuristics methods.

Real data was utilized to investigate the application of the developed model in design of an actual supply chain involved in bread production and distribution. We have shown how the proposed model and solution method can be used to determine location/allocation decisions and complete sensitivity analysis experiments. Our discussions on the numerical results arrived at important managerial and practical insights. For example, we found that demand and supply uncertainties (associated with a decision maker’s conservatism degree) can have a more pronounceable direct influence on the supply chain costs and location/allocation decisions when compared to uncertainty in cost parameters. This observation could further allow us identify where across the supply chain the uncertainty mitigation efforts should be focused to minimize the impacts on the strategic supply chain costs.

While we have shown a real world application of our robust optimization model, our study is not without limitations. The proposed model can be extended for the incorporation of additional tactical and operational decisions such as production planning and routing decisions (Esmaeilikia et al. 2014a). The incorporation of such factors and measures can result in additional insights and managerial implications not fully grasped in other studies. The risks associated with supply chain disruptions, including both random and intended disruption risks, can also be incorporated in our model. Another direction for further research can be the incorporation of the decision-maker’s conservatism degree as a decision variable or fuzzy parameter to investigate system behavior in different scenarios. Our model can also set the stage for the inclusion and analysis of customer responsiveness and agility elements such as service time and delivery lead-time, the critical performance metrics of fast-paced business environments.