Robust design and planning for a multi-mode multi-product supply network: a dairy industry case study

Abstract

As a salient matter of decision, supply chain design and planning has been a point of attraction for both researchers and practitioners. In real-world problems, the data based on which the decision is made are subject to uncertainty. Robust optimization is a well-known approach developed for modeling the uncertainty in such cases. In this research, a robust supply chain network design (RSCND) problem considering multiple products, multiple transportation modes, monetary value of time and uncertainty in transportation costs, demand and supply is studied. To endorse applicability of the proposed model, a case study of dairy products packaging and distribution network is studied and comprehensive analyses are provided. In addition, through using the proposed linearization technique, the model can be solved within a reasonable amount of time by utilizing conventional exact methods for small- and medium-size problems.

1 Introduction

In today’s competitive business environment, customers demand products with higher qualities at lower prices. It is known that in most cases, the manufacturing lead time of a product is considerably shorter than that of its distribution time indicating the significance of supply chain design in the efficiency of companies (Choy et al. 2007). Supply chain management (SCM), introduced by Oliver and Webber (Oliver and Webber 1982), was a response to the competitive environment of the late 1970s caused by the quality revolution (Erenguc et al. 2006). A supply chain may be defined as a system comprised of facilities, infrastructures, processes and resources coordinating in processing raw materials (as inputs) to end products (as outputs). Many subsystems, including procurement, manufacturing, storage, transportation and retailing systems are involved in a supply chain (Noorul Haq and Kannan 2006). The competitive business environment urges the supply chain managers to consider several factors categorized into three levels of decisions: strategic, tactical and operational (Bender et al. 2002). Top level decisions are strategic with long-term effects. As one of the most important strategic decisions, supply chain network design (SCND) has its roots in facility location problem (Melo et al. 2009), and has attracted both researchers and practitioners (Simchi-Levi et al. 2003).

Uncertainty in decision parameters forces decision makers to take more reliable and robust measures. More specifically, the uncertainty in costs associated with transportation of raw material and products between supply network elements may be caused by traffic congestion, weather conditions, fuel price fluctuations, etc. (Jouzdani and Fathian 2012, 2016). In addition, the demand volumes and supply capacities are also subject to uncertainty due to economic instability and market fluctuations besides other endogenous and exogenous factors. Especially, in developing countries, the uncertainty in transportation costs, demand volumes and supply capacities are more significantly affected by economic climate. As an important instance, uncertainty in currency exchange rate drastically affects the transportation costs, products demand and production capacities. However, it is usually possible to define scenarios under which each key decision parameter is realized with a probability. The uncertainty in real-world production systems can be categorized into two groups: (1) environmental uncertainty and (2) systems uncertainty (Chrwan-Jyh 1989). In SCND context, the former translates to exogenous factors (e.g. demand, supply and transportation costs uncertainty) while the latter includes endogenous ones (e.g. the uncertainty in production and distribution processes of the supply chain). From a survey of the literature, it can be inferred that vast majority of researches are concentrated on exogenous uncertainty sources due to their relative importance and more significant effects on the supply chain performance. Especially, most of the published works have addressed demand uncertainties. In this paper, RSCND is investigated considering multiple products and multiple transportation modes with a focus on the uncertainty in transportation costs, products demands and production capacities. As mentioned before, it is usually possible to identify scenarios under which specific probabilities for critical decision parameters may be determined/estimated by experts. Therefore, in order to model the uncertainty, we follow the robust optimization approach proposed by Mulvey et al. (1995) and later further addressed by Feng and Rakesh (2010). In addition, monetary value of time and its effects on facility location and transportation decisions are studied. In order to linearize the proposed non-linear model, two linearization methods are introduced. The presented case study justifies the applicability of the proposed model and sheds light on the significant effects of the aforementioned factors in SCND decisions. To summarize, the current research is distinguished by combining the following features.

• Integrating location and transportation decisions in SCM context.

• Considering uncertainty in transportation costs, product demand volumes and supply capacities.

• Incorporating the monetary value of time into the RSCND model.

• Linearization of the non-linear RSCND model.

• The applicability of the proposed model; i.e. the proposed model may be utilized in a wide range of problems in the context of SCND under uncertainty.

• Providing a case study and the related comprehensive “what-if” analyses in order to investigate the effects of the various decision parameters on the optimal decisions.

The paper is structured as follows: in Sect. 2, the related literature is reviewed. Section 3, presents a brief discussion of the scenario-based robust optimization approach proposed by Mulvey et al. (1995). In Sect. 3, the mathematical formulation of the problem is presented. Section 4 provides a comprehensive case study and presents what-if analyses of important model parameters. The results from the case study and the related experiments can help determining the best decision variables including facility locations, shipment quantity and transportation modes (Le and Lee 2013). Finally, Sect. 5 concludes the paper and suggests guidelines for future researches.

2 Literature review

2.1 Uncertainty in supply chain network design

A major aspect of SCND, which has kept researchers’ attention for the past few years, is the uncertainty imposed by the complex nature of supply chains. Jouzdani et al. (2013) proposed a dynamic SCND considering demand uncertainty and traffic congestion. They justified the applicability of their model through a case study in dairy industry. Yang and Liu (2013) investigated a fuzzy supply chain network problem by mean-risk and presented a hybrid memetic solution algorithm. Pishvaee et al. (2014) presented an accelerated Benders decomposition algorithm for sustainable supply chain network design under uncertainty and presented a case study of medical needle and syringe supply chain. In a research by Ramezani et al. (2014), the application of fuzzy sets in designing a multi-product, multi-period, closed-loop supply chain network was investigated. Subulan et al. (2015) proposed a stochastic and possibilistic model for a lead/acid battery closed-loop supply chain network design case in Turkey considering financial and collection risks and uncertainty. A two-stage optimization method for multi-objective SCND under transportation costs and customer demands uncertainties is proposed by Yang et al. (2015). They presented an improved multi-objective biogeography-based optimization algorithm to solve their proposed model. Jouzdani and Fathian (2016) addressed the SCND problem under both demand and supply side uncertainties and proposed a fuzzy programming mixed integer programming model of the problem. They designed a hybrid electromagnetism-like algorithm to solve their model. It can be seen that, due to the nature of today’s business climate, uncertainty has become an inherent characteristic of supply chain networks and therefore, many researchers are incorporating uncertainties into their models in order to provide a more realistic representation of the real-world problems.

2.2 Robust optimization of supply chains

Obtaining robust solutions for optimization problems has been a point of attraction for both researchers and practitioners. Robust optimization approaches can be categorized into three classes of (1) deterministic, (2) possibilistic and (3) probabilistic (Beyer and Sendhoff 2007). In deterministic models of robust optimization, usually an extreme conservative position is taken considering the worst-case scenario (Kouvelis and Yu 1997). Possibilistic robust optimization is applicable to the cases where the uncertainty is present in form of vagueness or incompleteness of information. For such problems, interval scenario cases (Aissi et al. 2009) and fuzzy uncertainty sets (Beyer and Sendhoff 2007) can be applied. When the occurrence of scenarios is considered stochastic, the probabilistic robust optimization approach is utilized (Ben-Tal et al. 2009). For a more in-depth study of robust optimization approaches, the reader may refer to the book by Kouvelis and Yu (1997), the surveys by Aissi et al. (2009), Bertsimas et al. (2011) and the review paper by Beyer and Sendhoff (2007).

Robust optimization has been widely utilized in modeling uncertainty in supply chain problems. More specifically, De Rosa et al. (2013) presented a strategic capacitated SCND problem considering bi-directional product flows through a network of multiple supply stages following a scenario-based robust optimization approach. In a research by Baghalian and her colleagues, a stochastic mathematical formulation for SCND problem considering multi-product, several capacitated production facilities, distribution centers and retailers in markets under supply and demand uncertainties was proposed. They utilized a transformation based on the piecewise linearization method to solve their model and presented a case study of rice industry (Baghalian et al. 2013). Jabbarzadeh et al. (2014) proposed a robust model for blood supply in disasters and provided a real-world application of the model. A bi-objective mixed-integer linear programming model was proposed by Mousazadeh et al. (2015) for pharmaceutical SCND problem following possibilistic approach. They also presented a case study of pharmaceutical industry. Hasani and Khosrojerdi (2016) investigated the robust global SCND under disruption and demand and procurement uncertainties. They proposed a memetic algorithm and a case of medical devices manufacturer.

Bai and Liu (2016) presented a robust optimization method for SCND problem by using fuzzy concepts. They considered uncertainty in costs and demand and studied a case of food industry. Single allocation and multiple allocation hub location, as a special SCND problem, was investigated by Habibzadeh Boukani et al. (2016). They considered uncertainty in costs and capacities. Mohseni et al. (2016) proposed a two-stage sequential model microalgae-based biodiesel SCND problem considering uncertainty in supply, demand and costs and a case of Iran. A robust fuzzy optimization bi-objective model for a closed-loop green SCND problem was proposed by Talaei et al. (2016) who also presented a case of electronics industry. They considered costs and demand as uncertain parameters. Keyvanshokooh et al. (2016) proposed a hybrid robust and stochastic optimization model for closed-loop SCND and solved the model by Benders decomposition. A robust optimization model for SCND for biodiesel produced from waste cooking oil under price uncertainty was proposed by Zhang and Jiang (2017). Robust optimization of supply chains has recently attracted more researchers because of the significance of robustness in SCND problems in presence of uncertainty.

2.3 Dairy supply chains

Dairy industry can be differentiated from other sectors based on several factors. Ayağ et al. (2012) identified the crucial design requirements and supply chain management strategies by proposing a fuzzy quality function deployment methodology. They expressed the uncertainty in the decision elements though triangular fuzzy numbers. In their article, the most important peculiarities of the dairy industry are highly competitive environment in which companies gain an average margin of 1–2% of sales, highly perishable products and varying customer tastes. According to a research by Schelhaas (1999), perishability, daily-basis production, timely delivery requirements and high transportation and transaction costs of dairy products are the features that distinguish the dairy industry from others. Jouzdani et al. (2013) proposed a dynamic dairy SCND considering traffic congestion and demand uncertainty. They modeled the uncertainty in the demand of dairy products by expressing the demand as triangular fuzzy numbers. In another research, they investigated the robust location-routing problem in a case of dairy industry in Iran (Jouzdani and Fathian 2014).

The major drawback in most previous research on dairy industry is the assumption that the major parameters are deterministic (Bilgen and Çelebi 2013), while the uncertainty can be observed within the production process (e.g., operation time, machine availability, and late deliveries, etc.). Furthermore, long production periods, seasonality in production and variability of quality and quantity of supply are the characteristics of any food supply chain network which calls for responsiveness and flexibility in process and planning (van der Vorst et al. 2007). For a detailed list of food supply chain network characteristics, one may refer to books by van der Vorst et al. (2007) and Accorsi et al. (2016). The aforementioned distinguishing features result in the inherent uncertainty in the dairy supply chains. As important elements, in this paper our focus is on the uncertainty in transportation costs, supply and demand in the dairy supply chain. In our case, the experts and the decision makers were more comfortable with expressing the uncertainty through different parameter values under different scenarios and therefore, the robust optimization approach was considered as more appropriate.

From another point of view, dairy processing facilities usually produce a variety of products including processed milk, yoghurt, cream, butter and cheese. Even the producers that are concentrated on a single product type such as yoghurt may provide a variety of the same product by adding flavors with different fat contents (Doganis and Sarimveis 2007). In addition, each type of product requires a specific type of transportation. For example, in Iran, raw milk is usually transported by heavy or light tanker trucks while other dairy products are often transported by using mini trucks or pickups. Therefore, multiple vehicle types are required for transportation needs of a dairy supply chain with multiple product types.

Considering the aforementioned features of the dairy supply chains and inspired by our central Iran case, we utilized the data presented by the experts under different scenarios to propose a RSCND for the case. As mentioned earlier, the proposed model can be easily adopted for cases in other industries with characteristics similar to those of dairy industry.

2.4 Summary

In this section, the main areas of research which are closely related to the current paper were reviewed. In order to clearly determine the position of our work in the literature, a brief comparison of the related articles with this paper is provided in Table 1.

Table 1 A brief review of features of the related works in the literature (chronologically sorted)

According to this table and to the best of authors’ knowledge, demand uncertainty has been considered by most of the authors, only a few researchers have considered uncertainty in supply, demand and costs simultaneously. However, from these, even fewer have presented a real-world case study. Similar to demand uncertainty, multiple products is considered by many researchers in the context of SCND. However, few have contemplated multiple transportation vehicles and the time value of money.

Although many models in the literature may be utilized in dairy industry with some modifications, for our case, the availability of experts and their comfort in determining the probability of scenarios and the corresponding parameter values inspired us to utilize the robust optimization concepts. In addition, because “what if analyses” were more comprehendible for the decision makers of the dairy supply chain, the scenario-based robust optimization approach is utilized for capturing the uncertainties.

3 Problem formulation

In this section, some of the assumptions regarding the problem under investigation are explained and the nomenclature of the model is presented. Here, the nonlinear optimization formulation of the multi-product multi-mode SCND problem is introduced and a linearization technique is proposed to convert the original model to a linear mathematical programming model.

3.1 Assumptions

Considering all of the aspects of a real-world problem in a model is very difficult if not impossible. On the other hand, making wise assumptions results in a more practical model of the problem. In this research, the following assumptions are made:

• 1. The number of candidate facility locations is known and the fixed facility investment cost for each location is predetermined.

• 2. At most, one facility may be opened in each candidate location.

• 3. All model parameters are deterministic except the transportation costs, products demands and production capacities.

• 4. Due to the fact that the dairy products are highly perishable, backorders are not allowed and demand under-fulfillment results in lost sales.

• 5. Demand over-fulfillment occurs when the amount of products transported to a node exceeds its demand for that product. Since the dairy products are highly perishable, the supply chain incurs costs for demand over-fulfillment.

• 6. The transportation cost for each product and for each unit of each mode of transportation is known and subject to uncertainty described through probabilities in different scenarios.

• 7. The demand for each product in each demand node in the supply network is known under every scenario.

• 8. The maximum production capacity of facilities in each candidate location for each product is known under every scenario.

• 9. Each facility is capable of producing products more than its capacity by incurring the costs of over-allocating its production resources.

• 10. Producing less than the capacity leads to an unused capacity of facilities which translate to costs for the supply chain.

• 11. The capacity of each transportation mode is known.

• 12. Theoretically, the facilities are planned to operate permanently when opened in a candidate location. Practically, this may be translated to a long period of time.

• 13. The interest rate is known and constant. In addition, it is assumed that the interest rate has either no or negligible future fluctuations.

3.2 Nomenclature

In order to facilitate the understanding of the mathematical model, the sets, parameters and the decision variables are introduced in this section.

3.2.1 Sets

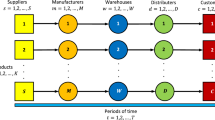
$N$	The set of network nodes (including candidate facility locations and demand points)
$S$	The set of scenarios
$P$	The set of products
$M$	The set of transportation modes

3.2.2 Subscripts

$i$	Subscript for candidate facility location ($i \in N$)
$j$	Subscript for demand point ($j \in N$)
$s$	Subscript for scenario ($s \in S$)
$p$	Subscript for product ($p \in P$)
$m$	Subscript for transportation mode ($m \in M$)

3.2.3 Parameters

$FC_{i}$	The fixed investment cost of opening a facility in candidate location $i \in N$
$PR_{s}$	The occurrence probability of scenario $s \in S$
$DM_{j,p}^{s}$	The demand for product $p \in P$ in demand node $j \in N$ under scenario $s \in S$
$SP_{i,p}^{s}$	The potential production capacity for product $p \in P$ in candidate location $i \in N$ under scenario $s \in S$
$CP_{m}$	The capacity of transportation mode $m \in M$
$IR$	The interest rate
$\varLambda$	Deviation cost coefficient used to penalize the deviation of the objective function from its expected values under different scenarios
$\varOmega_{d}^{ + }$	The penalty coefficient for positive violation of the demand constraints
$\varOmega_{d}^{ - }$	The penalty coefficient for negative violation of the demand constraints
$\varOmega_{s}^{ + }$	The penalty coefficient for positive violation of the supply constraints
$\varOmega_{s}^{ - }$	The penalty coefficient for negative violation of the supply constraints
$TC_{i,j,m}^{s,p}$	The transportation cost for one vehicle of mode $m \in M$ to transport product $p \in P$ from node $i \in N$ to node $j \in N$ if scenario $s \in S$ occurs

3.2.4 Decision Variables

$y_{i}$	A binary variable which is equal to 1 if a facility is opened in $i \in N$ and equals 0 otherwise
$x_{i,j}^{m,p}$	Total amount of product $p \in P$ transported from node $i \in N$ to node $j \in N$ by means of transportation mode $m \in M$

3.2.5 Control Variables

$v_{j,p}^{ + ,s}$	Positive violation from the demand for product $p$ in demand node $j$ under scenario $s$
$v_{j,p}^{ - ,s}$	Negative violation from the demand for product $p$ in demand node $j$ under scenario $s$
$w_{i,p}^{ + ,s}$	Positive violation from the supply capacity for product $p$ in node $i$ under scenario $s$
$w_{i,p}^{ - ,s}$	Negative violation from the supply capacity for product $p$ in node $i$ under scenario $s$

3.2.6 Auxiliary variable

$\theta_{s}$

The auxiliary variable used for Eq. (10) linearization (Yu and Li 2000)

3.3 Mathematical model

In what follows, the multi-product multi-mode SCND problem under transportation cost uncertainty is formulated according to the notations introduced above.

$$\hbox{min} \,\sum\limits_{i \in N} {y_{i} FC_{i} } + \,$$

(1-1)

$$\frac{1}{IR}\sum\limits_{s \in S} {PR_{s} \xi_{s} } +$$

(1-2)

$$\,\frac{\varLambda }{IR}\sum\limits_{s \in S} {PR_{s} \left[ {\left( {\xi_{s} - \sum\limits_{{s^{\prime} \in S}} {PR_{{s^{\prime}}} \xi_{{s^{\prime}}} } } \right) + 2\theta_{s} } \right]} +$$

(1-3)

$$\,\frac{1}{IR}\sum\limits_{s \in S} {PR_{s} \left( {\sum\limits_{p \in P} {\left( {\varOmega_{d}^{ + } \sum\limits_{j \in N} {v_{j,p}^{ + ,s} } + \varOmega_{d}^{ - } \sum\limits_{j \in N} {v_{j,p}^{ - ,s} } + \varOmega_{s}^{ + } \sum\limits_{i \in N} {w_{j,p}^{ + ,s} } + \varOmega_{s}^{ - } \sum\limits_{i \in N} {w_{j,p}^{ - ,s} } } \right)} } \right)}$$

(1-4)

Subject to

$$\xi_{s} - \sum\limits_{{s^{\prime} \in S}} {PR_{{s^{\prime}}} \xi_{{s^{\prime}}} } + \theta_{s} \ge 0\quad \forall s \in S$$

(2)

$$\sum\limits_{m \in M} {\sum\limits_{i \in N} {x_{i,j}^{m,p} } } = v_{j,p}^{ + ,s} - v_{j,p}^{ - ,s} + DM_{j,p}^{s} \quad \forall j \in N,\;\forall p \in P,\;\forall s \in S$$

(3)

$$\sum\limits_{m \in M} {\sum\limits_{j \in N} {x_{i,j}^{m,p} } } = y_{i} \left( {SP_{i,p}^{s} + w_{i,p}^{ + ,s} - w_{i,p}^{ - ,s} } \right)\quad \forall i \in N,\;\forall p \in P,\;\forall s \in S$$

(4)

$$y_{i} \in \left\{ {0,1} \right\}\quad \forall i \in N$$

(5)

$$x_{i,j}^{m,p} ,v_{j,p}^{ - ,s} ,v_{j,p}^{ + ,s} ,w_{j,p}^{ - ,s} ,w_{j,p}^{ + s} ,\theta_{s} \ge 0\quad \forall i,j \in N,\;\forall p \in P,\;\forall m \in M,\;\forall s \in S$$

(6)

In the above model, Eq. (1-1) calculates the total fixed investment cost and (1-2) is the expected total transportation cost where $\xi_{s}$ is obtained from the following equation.

$$\xi_{s} = \sum\limits_{m \in M} {\sum\limits_{p \in P} {\sum\limits_{i \in N} {\sum\limits_{j \in N} {TC_{i,j,m}^{s,p} \left( {\left\lfloor {\frac{{x_{i,j}^{m,p} }}{{CP_{m} }}} \right\rfloor + 1} \right)} } } } \quad \forall s \in S$$

(7)

In the above equation, $\left\lfloor x \right\rfloor$ is the largest integer number $z$ such that $z \le x$. Therefore, $\left( {\left\lfloor {{{x_{i,j}^{m,p} } \mathord{\left/ {\vphantom {{x_{i,j}^{m,p} } {CP_{m} }}} \right. \kern-0pt} {CP_{m} }}} \right\rfloor + 1} \right)$ represents the number of vehicles of mode $m$, utilized to transport $x_{i,j}^{m,p}$ units of product $p$ from node $i$ to node $j$ and Eq. (7) calculates the total transportation cost under scenario $s$. Contrary to the total fixed investment cost, the transportation costs are incurred during the operation life time of the supply chain. Therefore, time value of money should be considered in decision making in such cases. Considering the transportation costs as uniform series payments, by using the uniform series payments factor, the present worth of future transportation costs are calculated and the time value of money is incorporated into calculations. Equation (8) presents the uniform series payments factor in which $n$ is the number of planning periods (White et al. 1983).

$$\left( {{P \mathord{\left/ {\vphantom {P A}} \right. \kern-0pt} A};IR;n} \right) = \frac{{\left( {1 + IR} \right)^{n} - 1}}{{IR\left( {1 + IR} \right)^{n} }}$$

(8)

According to assumptions, the supply chain is designed to operate for practically a long time and theoretically for infinite number of planning periods. Therefore, we have $n \to \infty$ and from Eq. (8) we have

$$\left( {{P \mathord{\left/ {\vphantom {P A}} \right. \kern-0pt} A};IR;\infty } \right) = \frac{1}{IR}$$

(9)

${1 \mathord{\left/ {\vphantom {1 {IR}}} \right. \kern-0pt} {IR}}$ term in the above equation is used to convert the uniform series payments of transportation costs to their present worth. By means of this technique, the future transportation costs can be added to the present fixed investment costs considering the time value of money. Similar discussion justifies the use of the term ${1 \mathord{\left/ {\vphantom {1 {IR}}} \right. \kern-0pt} {IR}}$ in Eq. (1-3) and Eq. (1-3).

Equation (1-3) is the linearized form proposed by Yu and Li for the following nonlinear expression which calculates the expected total deviation of the objective function from its mean value (Yu and Li 2000).

$$\sum\limits_{s \in S} {PR_{s} \left( {\xi_{s} - \sum\limits_{{_{{s^{\prime} \in S}} }} {PR_{{s^{\prime}}} \xi_{{s^{\prime}}} } } \right)^{2} }$$

(10)

By using an auxiliary variable, $\theta_{s}$, and adding constraint (2), the above expression is linearized into Eq. (1-3).

The expected violations of demand and supply control constraints are penalized in Eq. (1-4). Constraint (3) confines the demands by utilizing the control variables, $v_{j,p}^{ + ,s}$ and $v_{j,p}^{ - ,s}$, defined as positive and negative violations of demand constraints, respectively. $v_{j,p}^{ + ,s}$ presents the demand over-fulfillment of product $p$ in node $j$ under scenario $s$. Similarly, $v_{j,p}^{ - ,s}$ is the demand under-fulfillment of product $p$ in node $j$ under scenario $s$. These violations are penalized in Eq. (1-4) by using $\varOmega_{d}^{ + }$ and $\varOmega_{d}^{ - }$ as penalty coefficients, respectively. In constraint (4), $w_{i,p}^{ + ,s}$ is the amount of product $p$ produced by over-allocation in facility $i$ under scenario $s$ and similarly, $w_{i,p}^{ - ,s}$ is the unused capacity of facility $i$ in terms of product $p$ under scenario $s$. These violations are penalized in Eq. (1-4) by using $\varOmega_{s}^{ + }$ and $\varOmega_{s}^{ - }$ as penalty coefficients, respectively.

Constraint (5) defines $y_{i}$ as a binary variable; however, it should be noted that by altering this constraint to $y_{i} \in Z^{ + }$, the values of $y_{i}$ may be chosen from the set of positive integers and several facilities may be opened in a single candidate location. From another point of view, this may be translated to selecting from identical production capacity levels for a single facility in a candidate location. Constraint (6) defines the rest of the variables as positive real numbers.

3.4 Linearization

Apparently, the proposed model is non-linear in Eq. (1-2) and (1-3) because of $\left\lfloor \cdot \right\rfloor$ function in Eq. (7). In addition, the terms $y_{i} \times w_{i,p}^{ + ,s}$ and $y_{i} \times w_{i,p}^{ - ,s}$ make constraint (4) also non-linear. In order to reduce the complexity, the model is linearized by means of the techniques introduced in what follows. From the definition of $\left\lfloor \cdot \right\rfloor$ we have

$$\frac{{x_{i,j}^{m,p} }}{{CP_{m} }} = \left\lfloor {\frac{{x_{i,j}^{m,p} }}{{CP_{m} }}} \right\rfloor + f_{i,j}^{m,p} \quad \forall i,j \in N,\;\forall p \in P,\;\forall m \in M$$

(11)

where

$$0 \le f_{i,j}^{m,p} < 1,\,\,\,f_{i,j}^{m,p} \in R\quad \forall i,j \in N,\;\forall p \in P,\;\forall m \in M$$

(12)

$$\frac{{x_{i,j}^{m,p} }}{{CP_{m} }} - f_{i,j}^{m,p} \in Z^{ + } \quad \forall i,j \in N,\;\forall p \in P,\;\forall m \in M$$

(13)

Hence, by replacing $\left\lfloor {{{x_{i,j}^{m,p} } \mathord{\left/ {\vphantom {{x_{i,j}^{m,p} } {CP_{m} }}} \right. \kern-0pt} {CP_{m} }}} \right\rfloor$ by ${{x_{i,j}^{m,p} } \mathord{\left/ {\vphantom {{x_{i,j}^{m,p} } {CP_{m} }}} \right. \kern-0pt} {CP_{m} }} - f_{i,j}^{m,p}$ in Eq. (7) and adding constraint (12) and constraint (13) to the original model, Eq. (1-2) and Eq. (1-3) are linearized.

In constraint (4), the non-linearity is caused by the multiplication of a binary variable, $y_{i}$, by a real positive variables, $w_{i,p}^{ - ,s}$ and $w_{i,p}^{ + ,s}$. In order to linearize these terms, we define corresponding auxiliary variables $z_{i,p}^{ - ,s}$ and $z_{i,p}^{ + ,s}$ as

$$z_{i,p}^{ - ,s} = y_{i} \times w_{i,p}^{ - ,s} \quad \forall i \in N,\;\forall p \in P,\;\forall s \in S$$

(14)

$$z_{i,p}^{ + ,s} = y_{i} \times w_{i,p}^{ + ,s} \quad \forall i \in N,\quad\forall p \in P,\;\forall s \in S$$

(15)

Constraint (4) is linearized by replacing the term $y_{i} \times w_{i,p}^{ - ,s}$ and $y_{i} \times w_{i,p}^{ + ,s}$ by the variables defined in Eq. (14) and Eq. (15), respectively, and adding the following constraints in which $A$ is a large positive number.

$$z_{i,p}^{ - ,s} \ge w_{i,p}^{ - ,s} - A\left( {1 - y_{i} } \right)\quad \forall i \in N,\quad\forall p \in P,\;\forall s \in S$$

(16)

$$z_{i,p}^{ - ,s} \le w_{i,p}^{ - ,s} + A\left( {1 - y_{i} } \right)\quad \forall i \in N,\quad\forall p \in P,\;\forall s \in S$$

(17)

$$z_{i,p}^{ - ,s} \le Ay_{i} \quad \forall i \in N,\quad\forall p \in P,\;\forall s \in S$$

(18)

$$z_{i,p}^{ + ,s} \ge w_{i,p}^{ + ,s} - A\left( {1 - y_{i} } \right)\quad \forall i \in N,\;\forall p \in P,\;\forall s \in S$$

(19)

$$z_{i,p}^{ + ,s} \le w_{i,p}^{ + ,s} + A\left( {1 - y_{i} } \right)\quad \forall i \in N,\;\forall p \in P,\;\forall s \in S$$

(20)

$$z_{i,p}^{s} \le Ay_{i} \quad \forall i \in N,\;\forall p \in P,\;\forall s \in S$$

(21)

By using the aforementioned linearization technique, constraint (4) is rewritten as

$$\sum\limits_{m \in M} {\sum\limits_{j \in N} {x_{i,j}^{m,p} } } = y_{i} SP_{i,p}^{s} + z_{i,p}^{ + ,s} - z_{i,p}^{ - ,s} \quad \forall i \in N,\;\forall p \in P,\;\forall s \in S$$

(21)

4 The dairy industry case study

Demand for animal-origin food products in developing countries is expected to increase significantly due to urbanization, increase in population and income growth (Delgado et al. 1999). For instance, new market opportunities, which connect rural producers to increasingly profitable markets in Addis Ababa and are mostly driven by the growth of dairy supply chains, have emerged in dairy sector in the past few years, in Ethiopia (Francesconi et al. 2010). In Iran, the production and consumption of dairy products are expected to rise in future. More specifically, according to OECD–FAO Agricultural Outlook 2012–2021 (OECD/FAO 2012), production and consumption of butter, cheese and milk are expected to grow in coming years in Iran (see Table 2).

Table 2 Production and consumption growth in 2012–2021 for butter, cheese and milk

The increase in demand creates supply chain investment opportunities which, in turn, call for optimal design and planning decisions. This research is inspired by a central Iran case of milk, cheese, butter and cream SCND in which experts were available to determine the values of the uncertain parameters under each scenario. Central Iran is of great interest due to relatively high rate of industrial growth and urbanization. Specifically, in Markazi province, located in central Iran, the total investment based on the total number of patents issued by the Industries and Mines Organization, soured from 21.68 million USD in 2001 to 622.04 million USD in 2011 showing more than 270% increase (Iran Statistics Center 2012a). In addition, the total and urban population in this area has had average growth rates of 5.6 and 2.8% from 2006 to 2011, respectively (Iran Statistics Center 2012b, c). The cities in our study, including Ashtiyan, Arak, Delijan, Qom, Golpayegan, Khomeyn, Tafresh and Mahallat, are shown on the map in Fig. 1. All these cities are both a candidate location and a demand point in our study.

Fig. 1

Map view of the studied geographical area (Gitashenasi 2009)

4.1 The parameters and the data

The data required for the case study are collected from different sources. The fixed facility investment costs and their corresponding production capacities are based on feasibility studies provided by the Ministry of Cooperatives (Bank Loans and Economic Affairs Office 2006). The uncertain demand data are estimated based on the population of each demand point and the consumption of each product per capita per year for which the data are provided by the Iran Statistical Center (2006, 2012d). In this study, 5 different types of transportation vehicles are considered (see Table 3) and several transportation companies are enquired to provide transportation costs for different vehicle types under each scenario.

Table 3 Transportation vehicles and their capacities

In our case, the robust optimization approach is well-suited due to the availability of experts for determining the probability of scenarios. Three different scenarios are defined: bad, fair and good. The fair scenario is a moderate situation in which parameters have their normal expected (most likely) values. In a bad scenario, the transportation costs are high (10% higher than expected) and the total supply barely satisfies the demand (demand is 10% higher and supply is 10% lower than expected). On the other hand, in a good scenario, the transportation costs are low (10% lower than expected) and the supply easily satisfies the demand (demand is 10% lower and supply is 10% higher than expected).

The results are obtained assuming $\varOmega_{s}^{ + } = 1.67$ USD and $\varOmega_{s}^{ - } = 1.00$ USD penalties per each unit of product for positive and supply constraint negative violations, respectively. In addition, we assume $\varOmega_{d}^{ + } = 1.67$ USD and $\varOmega_{d}^{ - } = 3.33$ USD penalties per each unit of product for positive and demand constraint negative violations, respectively. From a practical point of view, a positive deviation from the supply capacity usually results in overutilization of production resources; therefore, as in our case, $\varOmega_{s}^{ + }$ can be calculated by considering the overtime working cost of human resources and facilities. On the other hand, when there is a negative supply deviation, there is an unused supply capacity; therefore, in our case, $\varOmega_{s}^{ - }$ is approximated by considering the cost of the underutilization of capacity. In addition, a positive deviation from the demand translates to unsold products; hence, here, $\varOmega_{d}^{ + }$ is calculated as the benefit loss due to unsold products. On the other hand, the negative deviation from the demand results in loss of sales; therefore, in our case, $\varOmega_{d}^{ - }$ is calculated by considering the cost of lost sales.

$\varLambda$ and $IR$ are set to 1 and 10% in our calculations, respectively. In practice, the parameter $\varLambda$ is determined by the decision maker and represents the relative importance of the deviation from the expected value to the expected value of the objective function. In other words, this parameter defines the trade-off between the solution robustness and the model robustness (Samadi-Dana et al. 2017) and as it increases, the solution robustness improves while the model robustness degrades (Hassannayebi et al. 2017). Since the introduction of the robust optimization approach proposed by Mulvey et al. (1995), it has been a common practice to set this parameter to 1 (Paydar et al. 2017) therefore, in our case, we set this parameter to 1 and performed sensitivity analysis to study its effects. However, it is noticeable that assigning large values to this parameter, may make the variance term dominant and may produce results with zero deviations (Hassannayebi et al. 2017).

Several experts were asked to determine the probability of each scenario based on the current business environment, historical data and market predictions. Using a weighting method, the aggregate probabilities are 0.583, 0.305 and 0.112 for good, fair and bad scenarios, respectively showing that the experts are “optimistic” about the dairy industry.

4.2 The results

The collected data were fed into the model solved by LINGO 8.0 Software on a PC equipped with an Intel^® Core™ i3-3210 CPU @ 3.20 GHz and 4 GBs of RAM running Windows™ 7 Basic.¹ The model was solved in less than 1 s and the total system cost equals 423,564 USD (see Table 4) with facilities opened in Arak and Qom. The demand in Arak and Qom are satisfied by the facilities opened in those nodes. In order to transport the dairy products from suppliers to demand points, 2942 vehicles including 230 heavy trucks, 2612 light trucks are needed annually.

Table 4 Total system cost and its components

4.3 Sensitivity analysis

In order to investigate the effects of major model parameters on the optimal results, several “what-if analysis” experiments are carried out. $\varLambda$, $IR$, $DM_{j,p}^{s}$, $\varOmega_{d}^{ + }$, $\varOmega_{d}^{ - }$, $\varOmega_{s}^{ + }$, $\varOmega_{s}^{ - }$ and the scenarios and their probabilities are investigated assuming other parameters being fixed and the results are depicted in the following figures and described as follows.

4.3.1 The deviation cost

In our case, the deviation cost coefficient has no significant effect of the location cost (see Fig. 2a). However, the increase in this coefficient induces the rise in demand and supply violation costs. More specifically, the deviation cost coefficient determines the relative importance of the deviation of the amounts of products transported to the demand nodes from their corresponding means. Therefore, as this variance becomes more significant, the violation costs also gain importance and increase. In other words, the amounts of products transported to demand nodes become more precise; however, these amounts violate the demand and supply constraints to a higher degree. In addition, it is interesting to observe that the increase in the deviation cost coefficient decreases the transportation cost. This is can be explained through the fact that as the variance of the transported amounts of products is penalized, more specific and precise amounts are transported and logically, the transportation cost is lowered. Figure 2b presents the effect of the changes in the deviation cost coefficient on the positive and negative demand and supply violation costs. As can be seen in Fig. 2b, the increase in the demand and supply violation costs in Fig. 2a is mainly caused by the escalation in the negative violation costs; i.e., the changes in deviation cost coefficient only affect the negative violation costs. In other words, as the penalty for the variance of the amounts of transported products increases, the unused capacity of the facilities and demand under-fulfillment volume increases. Therefore, it can be concluded that in case of severe uncertainty, the unnecessary insist of decision makers on transporting precise amounts of products to demand nodes results in a decrease in demand fulfillment and facility utilization rate. Unfortunately, this is the case in many companies with traditional management systems in developing countries; especially in Iran.

Fig. 2

The effect of deviation cost coefficient on a optimal system cost components and b on optimal violation cost components

4.3.2 The interest rate

The interest rate has a direct impact on the operational costs including transportation cost, constraint violation cost and deviation cost while its impact on fixed facility investment costs is more indirect. From Fig. 3, it can be observed that as the interest rate increases, the total cost decreases due to the decline in total operational cost. As the interest rate increases, the relative importance of future operational costs to the fixed investment cost is decreased. Smaller number of facilities translates to smaller fixed present facility investment cost and larger future operational costs; especially, this is the case in Iran, due to high interest rate in unofficial capital market.

Fig. 3

The effect of interest rate on optimal system cost components

4.3.3 The demand

We call the percentage of the total demand satisfied by the supply chain being discussed, the market share. The effect of market share on cost components is illustrated in Fig. 4a. The market share may be also interpreted as demand changes. Obviously, it can be seen that the optimal fixed investment cost and constraint violation cost soar as the market share increases. Apparently, in order to satisfy a larger product demand volume, more facilities should be opened and therefore, the fixed facility investment cost escalates as the market share of the supply chain grows. In addition, as the market share increases, with the deviation cost coefficient being constant, the deviation cost grows due to the rise in the variance of the amounts of products transported to the demand nodes. Similarly, with the constraint violation penalty coefficients being constant, the demand and supply violation costs increase as more products are shipped to demand nodes. It can be observed that there is a tradeoff between supply constraint violation cost and the transportation cost. This can be more easily explained through Fig. 4b based on which one may conclude that when the market share is small (less than 5%), the optimal decision is to open few facilities neglecting the small demands in other nodes and accepting an unusually large demand violation cost for not satisfying the demands in those nodes. As the market share grows from 5 to 30%, the facilities can easily satisfy the demand of all nodes without being pushed to their capacity limits. The unused capacity of the facilities results in a negative supply violation cost. The increase in market share, urges the opening of new facilities. Since the facility opened in each node partially or wholly satisfies the demand of that node, the transportation cost is decreased as the number of facilities increases. Since the capacities of facilities are not arbitrary, opening a facility may create a surplus production capacity which may be partly unused. This phenomenon increases the supply constraint negative violation which in turn causes a rise in total supply violation cost. It can be concluded that market share greatly affects the demand and supply constraint violations. Therefore, market share strategic decisions should be made considering the preferences regarding these constraint violations.

Fig. 4

The effect of demand changes (market share) on a optimal system cost components and b on optimal violation cost components

4.3.4 The supply constraint violations

According to Fig. 5a, the change in supply constraint positive violation penalty coefficient does not significantly affect the location cost in our case. In addition, when the supply constraint positive violation is small (less than 7 USD per unit of product), the change in the penalty coefficient has no significant effect on optimal system components. However, for larger values of the penalty coefficient, there is a mild tradeoff between the supply constraint violation cost and each of the demand violation, deviation and transportation costs. As the supply constraint positive penalty grows, the surplus amounts of products produced by the facilities are reduced leading to a decrease in the supply constraint violation cost and an increase in that of demand constraint. As a result, more products are transported from the facilities to other demand nodes pushing up the transportation and deviation costs. Figure 5b sheds more light on the nature of the tradeoff. Specifically, as the supply constraint positive penalty coefficient increases, the positive demand violation cost is lowered due to the decrease in the surplus amounts of products produced by the facilities. Logically, a fall in the positive demand violation cost, translates to a rise in the negative counterpart which creates a balance and results in the neutral behavior of total demand constraint violation cost in Fig. 5a. As expected, the behavior of the supply constraint violation cost is mainly driven by the changes in the supply constraint positive violation cost. In general, it is crucial to note that imposing rigid and strictly limiting constraints on the surplus amount of products produced in facilities drives up the amount of products transported from the facilities to the demand nodes. On the other hand, due to the perishable nature of the dairy products, they are usually transported to the demand nodes frequently (e.g. on a daily basis). This in turn not only increases the transportation cost of the supply chain but also may increase the environmental and social costs.

Fig. 5

The effect of supply constraint positive violation penalty coefficient on a optimal system cost components and b on optimal violation cost components

Figure 6a shows that the supply constraint negative violation penalty has no effect on the deviation, location and transportation costs. This is sensible because the penalty put on the unused capacity of facilities does not change the location cost, the transportation cost and the deviation of the amounts of products transported to demand nodes from their corresponding means. However, there is an obvious tradeoff between supply violation cost and demand violation cost. Specifically, the increase in the supply constraint negative violation penalty decreases the unused capacity of the facilities; however, by forcing up the utilization rate of the facilities, the positive violation costs for both demand and supply increase; i.e. surplus amounts of products produced and transported to demand nodes. In addition, the rise in the facility utilization rate, logically results in the decrease in demand negative violation (see Fig. 6b). Generally, it can be concluded that pushing the facilities to their capacity limits result in a surplus amounts of products flowing to demand nodes. Therefore, a supply chain of expensive perishable products may incur high costs in such circumstances.

Fig. 6

The effect of supply constraint negative violation penalty coefficient on a optimal system cost components and b on optimal violation cost components

4.3.5 The demand constraint violations

As illustrated in Fig. 7a and similar to what shown in Fig. 6a, the demand constraint positive violation penalty has no impact on deviation, location and transportation costs. Considering the tradeoff between supply violation cost and demand violation cost, more similarities can be found between the behaviors of the optimal system cost components regarding the demand constraint, positive violation and supply constraint negative violation penalties. However, the sensitivity of the tradeoff is considerably higher for supply constraint negative violation penalty in comparison with that of demand constraint positive violation. In addition, the underlying components that bring about the behaviors are different as shown in Fig. 7b. The rise in penalty for the demand constraint positive violation reduces the amounts of products transported to demand nodes and in turn increases the negative violations of demand and supply constraints diving up the demand under-fulfillment and the unused capacity of facilities. In addition, as a side effect, the decrease in the surplus amounts lowers the supply positive violation cost.

Fig. 7

The effect of demand constraint positive violation penalty coefficient on a optimal system cost components and b optimal violation cost components

Figure 8a presents an illustration of the effects of demand constraint negative violation penalty changes on the optimal system cost components. It is noticeable that when the demand constraint negative violation penalty is small (1 USD per unit of product), the optimal decision is to incur a small facility investment cost accepting a large demand violation cost. As the penalty for the demand constraint negative violation rises, the number of facilities and in turn the fixed facility investment cost increases in order to lower the shortage in demand nodes. In addition, a tradeoff between the supply and demand violation costs can be observed. Furthermore, as the demand constraint negative violation penalty increases, the deviation and transportation costs grow due to the attempts to decrease the demand under-fulfillment. Figure 8b provides more details regarding the behavior of violation cost components in response to demand constraint negative violation penalty changes. As expected, it can be observed that the large demand violation cost for the small demand constraint negative violation penalty is mainly incurred due to high demand negative violation cost. There is an upward trend for both supply and demand positive violation costs as the penalty for the demand constraint negative violation grows. This is because the amounts of products produced in facilities and the amounts transported to demand nodes increase in order to lower the demand under-fulfillments. In addition, since the increase in demand constraint negative violation penalty generally translates to producing larger amounts of products, the supply negative violation cost tends to decrease as the demand constraint negative violation penalty increases. In general, similar to supply constraint negative violation penalty, a high demand constraint negative violation penalty may lead to production of surplus amounts of products and in case of perishable products of high value, may impose significant cost to the supply chain.

Fig. 8

The effect of demand constraint negative violation penalty coefficient on a optimal system cost components b on optimal violation cost components

4.3.6 The scenarios

Providing the Experts with the scenarios and their probabilities obtained for the “Optimistic” situation, they were asked to determine the probabilities of other situations for which the probabilities for each scenario are presented in Fig. 9. The probabilities of scenarios in each situation are given in Table 5.

Fig. 9

Probability of each scenario for different situations

Table 5 Probabilities of scenarios under different situations

The effect of these situations on the optimal system cost components are depicted in Fig. 10. In our case, the change in situation seems to have no significant effect on the optimal location costs. However, the violation and transportation costs generally increase as the situation worsens. Specifically, the demand violation and deviation costs reach their highest values when the situation is “Pessimistic”. It is interesting to observe that according to our analysis the total system cost for the “Pessimistic”, “Very Pessimistic” and “Worst Case” situations are 525,831 USD, 535,498 USD and 526,047 USD, respectively; indicating the significant effect of uncertainty on the total system cost. Specifically, the total system cost is lower in the “Worst Case” situation in comparison with “Very Pessimistic” as a more promising but more uncertain situation and it can be inferred that when a dismal economic climate is expected, the effect of uncertainty on driving up the total system cost is stronger. Therefore, in such cases, the government can reduce these costs by tapering off the uncertainty along with the attempts to improve the business environment.

Fig. 10

The effect of different situations on optimal system cost components

4.3.7 The total cost

In order to demonstrate the behavior of the optimal total system cost in response to the changes in important model parameters and providing an overall view of the analyses, Fig. 11 presents the results of analyses on these parameters.

Fig. 11

Optimal total system cost behavior in response to important model parameter changes

5 Conclusions and future works

In this paper, a RSCND problem considering demand, supply and transportation uncertainties was addressed and linearization techniques were introduced to linearize the proposed non-linear model. The central Iran case and its related “what if analysis” justified the applicability of the proposed model. The time value of money was considered RSCND by incorporating interest rate into calculations. The results from the case study and the analyses showed that due to high interest rates in developing countries, the importance of fixed investment cost was relatively higher than that of future operational costs. Especially, by the transportation costs being less important, social and environmental costs (e.g. the costs of traffic congestion and greenhouse gas emission) may significantly increase. Therefore, it is crucial for the governments of these devolving countries to facilitate the development of sustainable green supply chains; especially in industries with high frequency of transportations (e.g. supply chains with perishable goods such as dairy products). In addition, the analyses in our study showed that in a pessimistic situation, in which all scenarios are realized with almost equal probabilities, the total system cost may significantly increase. Therefore, an uncertain business environment with a pessimistic horizon may impose high costs to the supply chain.

In this research, the interest rate and other factors affecting future operational costs were assumed to be constant or to have ignorable fluctuations. In this regard, considering several planning periods in which decision factors change were left for future research. In addition, uncertainty in other model parameters such as the fixed facility investment costs may lead to a more realistic model. Furthermore, considering multiple layers in the supply chain including farms, wholesalers, retailers and other facilities in the dairy industry can be a subject for future researches.

Regarding solution process, the developed model was solved in a reasonable amount of time, by adopting a conventional exact method in conjunction with linearization. This indicates that the proposed model is applicable in many similar small- and medium-size problems without applying a heuristic and/or meta-heuristic method; however, developing a solution approach to tackle large-scale problems remains a subject of future research.