1 Introduction

People have paid more and more attention to the Olympic Games since the first modern games were held in Greece in 1896. The initial spirit of the Games was individual competition, but the Games soon became a competition among nations (Lins et al. 2003). Each participating nation strives for a better ranking in the Olympics. Naturally, the capacity of each nation varies greatly in achieving excellent performance. However, the International Olympic Committee (IOC) has never issued an official ranking for participating nations.

Recently, evaluating performance of participating nations in the Olympic Games is an important application of DEA (Charnes et al. 1978). DEA is an effective tool for efficiency measurement of decision making unit (DMU) with multiple inputs and outputs (Emrouznejad et al. 2010; Khodabakhshi and Aryavash 2014). It is popular in efficiency evaluation because it makes no assumptions on the production function and imposes no given weights on inputs and outputs (Bogetoft 1997). In the first three decades of DEA history, more than 4,000 research articles have been published in journals and book chapters (Emrouznejad et al. 2008). Moreover, DEA has been applied to areas that range from the public sector to the private sector (Emrouznejad 2014), such as hospitals (see, e.g. Du et al. 2014; Prior 2006), sports (see, e.g. Chen and Johnson 2010; Moreno and Lozano 2014), universities (see, e.g. De França et al. 2010; Bougnol and Dulá 2006), supply chains of enterprises (see, e.g. Chen et al. 2006; Zhou et al. 2013), and banks (see, e.g. Cook and Zhu 2010; Grigoroudis et al. 2013).

In the prior DEA literature on evaluating participants’ Olympics achievements, DMUs correspond to participating nations, and outputs are usually defined as the numbers of gold, silver and bronze medals, and inputs as population and GDP per capita or GNP. Lozano et al. (2002) used these three outputs, and the GNP and population as two inputs to measure performance of participating nations at five Summer Olympic Games (1984–2000). Lins et al. (2003) found that each sum of numbers of gold, silver and bronze medals was constant, and developed the so-called Zero-Sum Gains (ZSG) DEA model to rank participating nations in the Olympic Games. Churilov and Flitman (2006) used self-organizing maps to group participating countries into homogenous clusters, and then applied DEA models to evaluate the performance of each nation in clusters. To increase the validity of evaluation results, both Lozano et al. (2002) and Lins et al. (2003) applied the same set of assurance region (AR) constraints for all participating nations. Li et al. (2008) claimed that different countries should fit in with different ARs, and applied context-dependent assurance region DEA (CAR-DEA) to measuring sports levels of nations in the Summer Olympics.

Wu et al. (2009b) applied the cross efficiency method to assessing nations’ performance in six Summer Olympic Games. As compared to Hai (2007) which can effectively rank participating nations but cannot set targets for inefficient nations, Wu et al. (2009b) employed cluster analysis to select appropriate targets for inefficient nations. Considering competition among participating nations, Wu et al. (2009a) modified DEA game cross-efficiency model based on the assumption of variable return to scale to rank nations in the Olympic Games.

Zhang et al. (2009) discussed underlying preferences in DEA and proposed DEA models with lexicographic preference to analyze performance of participating nations. Soares de Mello et al. (2009) set a unitary constant input for all participating countries and built a general ranking for the Olympic Games. Wu et al. (2010) employed integer-valued DEA model to discuss the performance of each nation at 2008 Beijing Summer Olympics. Chiang et al. (2011) proposed a separation method to locate a common set of weights in DEA, and used the proposed method to measure efficiencies of participating nations in the Beijing Summer Olympics. Soares de Mello et al. (2012) used a non-radial DEA model to evaluate all participating nations in the 2008 Olympic Games in which the input “population of the participating nation” is defined as a non-discretionary variable. To overcome the drawback of the bounded DEA model in determining an efficiency interval for each DMU when there is a zero value for each output, Azizi and Wang (2013) proposed a pair of improved bounded DEA models and measured performance of participating nations in the 2004 Summer Olympics.

However, prior literature evaluates sports levels of participating nations only considering their performance in the Summer Olympic Games. It might be unfair to nations who have good performance in the Winter Olympic Games rather than in the Summer Olympic Games. For example, some countries located in cold zone like Canada, people there may be good at Ice Sports and Snow Sports, which belong to Winter Olympic Games. If we evaluate the sports level of these nations only considering the Summer Olympic Games, their good performance in the Winter Olympic Games would be neglected.

The Winter Olympic Games are also international multi-sports events organized by the IOC and are held every four years starting from 1924. It includes sports items, such as alpine skiing, figure skating, ice hockey, ski jumping, speed skating, and so on. All of these items are not included in the Summer Olympic Games. Similarly, sports items in the Summer Olympic Games, such as Swimming, Gymnastics, Shooting and Weightlifting, do not belong to the Winter Olympic Games. Therefore, sports items in the Summer Olympic Games and Winter Olympic Games are complementary in representing a nation’s comprehensive performance on sports, and it is better to take into account both Olympic Games when we measure the sporting performance of each nation.

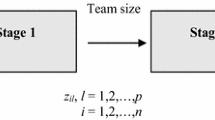
According to Kao (2012), DMUs can be treated in a parallel structure, if each DMU has the same number of different processes and each corresponding process performs the same function. In this sense, each participating nation in the Olympics described in this paper is a parallel system and the two Olympics are two parallel subsystems. Figure 1 shows the basic parallel system for each nation.

Fig. 1
figure 1

A parallel system comprised of two Olympics

Full size image

Similar to DEA-based prior literature on Olympics achievements evaluation, this paper defines inputs as GDP per capita (in US dollars) and population of the participating nation, and outputs as the numbers of gold, silver and bronze medals. Because we cannot get precise inputs for each Olympic subsystem, but can obtain overall inputs for the parallel system, we set that the two subsystems share all overall inputs. Here, \(X_j^1 \) and \(X_j^2 \) (\(Y_j^1 \) and \(Y_j^2 )\) are denoted as precise inputs (outputs) for the Winter Olympics and Summer Olympics, respectively. The total overall inputs for the system are denoted as \(X_j =X_j^1 +X_j^2 \).

Based on the definition of parallel systems (Kao 2012), the multi-activity and multi-component systems also belong to parallel systems. Approaches to measuring parallel systems can be divided into two categories. The first one is to measure the efficiency of a parallel system without shared flows (inputs or outputs), and it has been applied to areas such as grain farms (see, e.g. Färe et al. 1997) and macro-agricultural production systems (see, e.g. Yang et al. 2000). For details on such kind of approaches, one can refer to Kao (2012). The second category focuses on measuring the efficiency of a parallel system with shared flows among its subsystems. And it has been applied to many areas, such as universities (see, e.g. Beasley 1995; Kao 2012; Kao and Lin 2012; Molinero 1996), health service (see, e.g. Tsai and Mar Molinero 2002), banks (see, e.g. Amirteimoori and Nashtaei 2006; Cook et al. 2000; Jahanshahloo et al. 2004), bus companies (see, e.g. Yu 2008) and in the steel industry (see, e.g. Cook and Green 2004). For details on the second category models, one can refer to Castelli et al. (2010).

All of these researches either focused on evaluating the overall system’s efficiency or determined both the overall system’s and subsystems’ efficiencies. It is noteworthy that both the two kinds of efficiencies are calculated based on one of the optimal solutions to these parallel models. However, we may have alternative optimal solutions to parallel models in calculating the optimal efficiency of the overall system. In this case, the efficiency decomposition for subsystems may not be unique. That is, there may have many subsystems’ efficiency combinations when the overall system obtains its optimal efficiency. Then, it may be unreasonable to randomly select one of subsystems’ efficiency combinations to determine subsystems’ efficiencies. The same problem of non-uniqueness of subsystems’ efficiencies has also been pointed out in two-stage DEA models (see, e.g. Chen et al. 2009, 2010). However, none of prior studies in the parallel system tackled this problem. In this paper, the YMK DEA model of Yang et al. (2000) is extended to measure the efficiency of the overall parallel system. And, instead of randomly selecting one combination of subsystems’ efficiencies to represent their efficiencies, an efficiency decomposition procedure is developed to locate the efficiency range of each parallel subsystem.

There are two contributions of this paper. First, it considers both the Summer Olympics and Winter Olympics in one parallel system to reflect sports performance of participating nations in the Olympics for the first time. The sports performance evaluated based on this system can more roundly reflect participating nations’ level of sports competition. Namely, some participating nations may have good performance in the Summer Olympics while others in the Winter Olympics. In this sense, it is biased to use participating nations’ performance in one Olympics to represent their sports level. Second, it introduces an efficiency decomposition approach to calculate efficiencies of parallel subsystems. It employs the efficiency range to represent the efficiency decomposition for parallel subsystems, rather than randomly selecting one of subsystems’ efficiency combinations.

The rest of this paper is organized as follows: Sect. 2 represents the methodology to evaluate efficiencies of the overall Olympic system as well as each Olympic subsystem. Section 3 illustrates data sources and results for the Vancouver 2010 Winter Olympic Games and London 2012 Summer Olympic Games. Conclusions are given in Sect. 4.

2 Methodology

2.1 Overall system performance assessment model

In this section, we present the DEA model to evaluate performance of participating nations in the Olympic Games. In the DEA analysis, each DMU corresponds to a participating nation who has gained at least one medal from both 2010 Winter Olympic Games and 2012 Summer Olympic Games.

Output-orientation is assumed in this paper, since the Olympics achievement is measured with respect to medals won (Li et al. 2008). In addition, as all the DEA literature has stated, such as Lozano et al. (2002), Lins et al. (2003), Churilov and Flitman (2006), Wu et al. (2009a, b), the population of participating nations varies greatly, then the variable return to scale (VRS) is an another assumption in the model.

Denote each participating nation as \(DMU_j (j=1,\ldots ,n)\), in which its subsystem \(k\) (\(k=1,2\)), consumes inputs \((X_{ij}^k ,i=1,2)\) to generate outputs \((Y_{rj}^k ,r=1,2,3)\). In this paper, subsystem 1 and 2 correspond to the Winter Olympic Games and Summer Olympic Games, respectively. Let a parameter \(\alpha \left( {0< \alpha < 1} \right) \) denote the proportion of inputs to be dedicated to the Winter Olympic subsystem. Then, the overall inputs \(X_{ij} (i=1,2)\) are divided into two parts for the two subsystems as follows:

$$\begin{aligned} X_{ij}^1 =\alpha X_{ij} \quad \hbox {and} \quad X_{ij}^2 =(1-\alpha )X_{ij} ,\quad \forall \; i,j \end{aligned}$$
(1)

where \(\alpha \) is a parameter. If \(\alpha =0\), it means that all inputs are consumed by the Summer Olympic Games; On the contrary, \(\alpha =1\) means that all inputs \(X_{ij}\) are consumed by the Winter Olympic Games. Since participating nations considered in this paper are nations that have gained at least one medal from both 2010 Winter Olympic Games and 2012 Summer Olympic Games, inputs on each Olympics cannot be zero. That is, each participating nation has consumed some of the overall inputs to obtain the nonzero outputs in each Olympics. Thus, the parameter of \(\alpha \) is in a interval range of \(\alpha \in (0,1)\).

Based on the YMK DEA model (Yang et al. 2000), we obtain a following model to calculate the efficiency of the overall parallel Olympic system:

$$\begin{aligned} \begin{aligned} Min\,\,&\theta _0 =\frac{{\sum _{i=1}^{2}} {w_i X_{i0} +\,\, \mu _{0}^{1} +\mu _{0}^{2} }}{{\sum _{r=1}^{3}} {u_r \left( Y_{r0}^1 +Y_{r0}^2 \right) } }\\ s.t.\,\,&\theta _j^1 =\frac{{\sum _{i=1}^{2}} {w_i X_{ij}^1 +\mu _{0}^{1} } }{{\sum _{r=1}^{3}} {u_r Y_{rj}^1 } }\ge 1,\quad \forall \; j \\&\theta _j^2 =\frac{{\sum _{i=1}^{2}} {w_i X_{ij}^2 +\mu _{0}^{2} } }{{\sum _{r=1}^{3}} {u_r Y_{rj}^2 } }\ge 1,\quad \forall \; j \\&u_1 -\beta u_2 \ge 0\\&u_2 -\gamma u_3 \ge 0 \\&w_i ,u_r \ge 0,\quad \forall \; r,i,\mu _{0}^{\mathrm{k}} \ free. \end{aligned} \end{aligned}$$
(2)

where \((w_i, u_r)\) are multipliers attached to inputs and outputs, respectively. The first two sets of constraints ensure that efficiencies of the two subsystems for all DMUs are not more than one since \(\theta _j^1 \) and \(\theta _j^2 \) are the reciprocals of the two subsystems’ efficiencies. And the next two constraints \(u_{1} {-}\beta u_{2} \ge {0}\) and \(u_{2}{-}\gamma u_{3}\ge {0}\) indicate assurance regions (or the different importance) among gold, silver and bronze medals. For example, \(u_{1} {-}\beta u_{2} \ge {0}\) means that a gold medal is at least \(\beta \) times as important as a silver medal and \(u_{2} {-}\gamma u_{3} \ge {0}\) presents that a silver medal is at least \(\gamma \) times as important as a bronze medal (Lozano et al. 2002; Wu et al. 2009a, b). Since there is no access to know how much worthier is a gold (silver) medal than a silver (bronze) one, so sensitivity analysis will be performed with different ARs.

In model (2), the objective function is the aggregate performance measure for \(DMU_0 \), and the first two sets of constraints capture performance measures for the two Olympic subsystems. \(\theta _0^1 \) is the performance measure for the Winter Olympics and \(\theta _0^2 \) is for the Summer Olympics. It is noteworthy that the aggregate performance measure \(\theta _0 \) can be represented by a combination of \(\theta _0^1 \) and \(\theta _0^2 \), namely \(\theta _0 =\lambda _0^1 \theta _0^1 +\lambda _0^2 \theta _0^2 \). The variable of \(\lambda _0^k (k=1,2)\) represents the relative importance of subsystem \(k. \)And, it can be defined as the portion of all outputs that \(DMU_0 \) gains from subsystem \(k\) as follows:

$$\begin{aligned} \lambda _0^k =\frac{{\sum _{r=1}^{3}} {u_r Y_{r0}^k } }{{\sum _{r=1}^{3}} {u_r \left( Y_{r0}^1 +Y_{r0}^2 \right) }},\quad \forall \; k \end{aligned}$$
(3)

Formula (3) shows each nation can have different relative importance for its two subsystems. For example, Australians have good performance in some sports items such as diving and swimming which belong to the Summer Olympics. So some nations like Australia may believe that the Summer Olympic Games is more important than the Winter Olympics. While some nations like Canada with good performance in the Winter Olympic Games may believe that the Winter Olympic Games is more important than the Summer Olympic Games. Therefore, the relative importance of each subsystem can be reflected by the weighted medals it gains from that Olympic Games as above.

Therefore, the objective function of model (2) can be represented by performance measures for the two Olympic subsystems as follows:

$$\begin{aligned} \theta _{0}&= \lambda _{1} \times \theta _{0}^{1} +\lambda _2 \times \theta _{0}^{2} =\frac{{\sum _{r=1}^{3}} {u_r Y_{r0}^1 } }{{\sum _{r=1}^{3}} {u_r \left( Y_{r0}^1 +Y_{r0}^2 \right) } }\times \frac{{\sum _{i=1}^{2}} {w_i X_{i0}^1 +\mu _{0}^{1} } }{{\sum _{r=1}^{3}} {u_r Y_{r0}^1 } }\\&+\frac{{\sum _{r=1}^{3}} {u_r Y_{r0}^2 } }{{\sum _{r=1}^{3}} {u_r \left( Y_{r0}^1 +Y_{r0}^2 \right) } }\times \frac{{\sum _{i=1}^{2}} {w_i X_{i0}^2 +\mu _{0}^{2} } }{{\sum _{r=1}^{3}} {u_r Y_{r0}^2 } } =\frac{{\sum _{i=1}^{2}} {w_i X_{i0} +\mu _{0}^{1} +\mu _{0}^{2} } }{{\sum _{r=1}^{3}} {u_r \left( Y_{r0}^1 +Y_{r0}^2 \right) } } \\ \end{aligned}$$

Since \(\lambda _0^k \in [0,1](k=1,2)\), then the aggregate performance measure \(\theta _0 \) is a convex combination of the two subsystems measures for \(DMU_0 \).

Substituting (1) into model (2) and applying the Charnes–Cooper (C–C) transformation \(t=1/{\sum _{r=1}^3 {u_r (Y_{r0}^1 +Y_{r0}^2 )} },v_i =tw_i ,\mu _r =tu_r ,\omega _0^1 =t\mu _0^1 ,\omega _0^2 =t\mu _0^2\), model (2) is then equivalent to the following model:

$$\begin{aligned} \begin{aligned} Min\,\,&\theta _0 =\sum _{i=1}^2 {\nu _i X_{i0} } +\omega _{0}^1 +\omega _0^2\\ s.t.\,\,&\alpha \sum _{i=1}^2 {\nu _i X_{\hbox {ij}} } +\omega _{0}^1 -\sum _{r=1}^3 {\mu _r Y_{rj}^1 } \ge 0,\quad \forall \; j \\&({1}-\alpha )\sum _{i=1}^2 {\nu _i X_{\hbox {ij}} } +\omega _0^2 -\sum _{r=1}^3 {\mu _r Y_{rj}^2 } \ge 0,\quad \forall \; j \\&\sum _{r=1}^3 {\mu _r (Y_{r0}^1 +Y_{r0}^2 } )=1 \\&\mu _1 -\beta \mu _2 \ge 0 \\&\mu _2 -\gamma \mu _3 \ge 0 \\&\nu _i ,\mu _r \ge 0,\quad \forall \; r,i,\omega _{0}^1 ,\omega _0^2 \; free \end{aligned} \end{aligned}$$
(4)

Suppose an optimal solution and the objective function of model (4) are \((\alpha ^{{*}}, v^{*}=(v_1^*,v_2^*),\mu ^{*}\) \(=(\mu _1^*,\mu _2^*,\mu _3^*),\omega _0^{1*} ,\omega _0^{2*})\) and \(\theta _0^*\), respectively. Then, the optimal efficiency for \(DMU_0 \) is \(e_0^*=1/{\theta _0^*}\). We have a definition and a theorem as follows:

Definition 1

The overall Olympic Games system of \(DMU_{0}\) is efficient if \(e_{0}^*=1\).

Theorem 1

If the overall Olympic Games system of \(DMU_{0}\) is efficient, then its each subsystem is efficient, namely \(e_{0}^{1} =e_{0}^{2} =1\).

Proof

See the Appendix 1. \(\square \)

If the overall system is inefficient, then we should make an efficiency decomposition for each subsystem. According to prior literature, the two subsystems’ efficiencies can be indirectly calculated based on the optimal solution to model (4). Suppose one optimal solution is \((\alpha ^{{*}}, v^{*}=(v_1^*,v_2^*),\mu ^{*}=(\mu _1^*,\mu _2^*,\mu _3^*),\omega _0^{1*} ,\omega _0^{2*})\) as aforementioned. In this way, the efficiency of the Winter Olympic subsystem is \(e_0^1 =1/{\theta _0^1 }={\sum _{r=1}^3 {\mu _r^*Y_{r0}^1 } }/{(\sum _{i=1}^2 {\alpha ^{*}v_i^*X_{i0} } }+\omega _0^{1*} )\) and the efficiency of the Summer Olympic subsystem is \(e_0^2 =1/{\theta _0^2 }={\sum _{r=1}^3 {\mu _r^*Y_{r0}^2 } }/{(\sum _{i=1}^2 {(1-\alpha ^{*})v_i^*X_{i0} } }+\omega _0^{2*} )\). However, there may exist alternative optimal solutions to model (4). For instance, another optimal solution to model (4) is \((\alpha ^{*{\prime }},v^{*{\prime }}=(v_1^{*{\prime }} ,v_2^{*{\prime }} ),\mu ^{*{\prime }}=(\mu _1^{*{\prime }} ,\mu _2^{*{\prime }} ,\mu _3^{*{\prime }} ),\omega _0^{1*{\prime }} ,\omega _{0}^{2*{\prime }} )\). This may lead to another efficiency combination for the two Olympic subsystems (\(e_0^{1{\prime }} ,e_0^{2{\prime }} )\) such that \(e_0^{1{\prime }} ={\sum _{r=1}^3 {\mu _r^{*{\prime }} Y_{r0}^1 } }/{(\sum _{i=1}^2 {\alpha ^{*}v_i^{*{\prime }} X_{i0} } }+\omega _0^{1*{\prime }} )\) and \(e_0^{2'} ={\sum _{r=1}^3 {\mu _r^{*{\prime }} Y_{r0}^2 } }/{(\sum _{i=1}^2 {(1-\alpha ^{*})v_i^{*{\prime }} X_{i0} } }+\omega _0^{2*{\prime }} )\). Thus, the efficiency decomposition based on model (4) may not be unique, and there may be many efficiency combinations when the overall system obtains its optimal efficiency. In this sense, it is unreasonable to calculate subsystems’ efficiencies based on one optimal solution of model (4). In next Sect. 2.2, an efficiency decomposition procedure will be proposed to obtain the efficiency range of each parallel subsystem.

2.2 Subsystem performance assessment model: efficiency decomposition

To further identify the inefficiency sources of the overall Olympic system, and prevent the inefficiency of one subsystem to be compensated by the efficiency of the other, it is necessary to make efficiency decomposition for the two Olympic subsystems, especially when model (4) has alternative optimal solutions. The issue of efficiency decomposition has been proposed by several methods, such as additive efficiency decomposition (see, e.g. Chen et al. 2009, 2010; Yang et al. 2014), multiplicative efficiency decomposition (see, e.g. Kao and Hwang 2008; Yang et al. 2014), and game-theoretic approaches (see, e.g. Du et al. 2011; Liang et al. 2008; Li et al. 2012; Zha and Liang 2010). However, none of these efficiency decomposition methods has been applied to a parallel system. In this paper, we employ the additive efficiency decomposition to obtain the efficiency range for each subsystem. Suppose the maximum and minimum efficiencies of each Olympic Games subsystem of \(DMU_0\) can be denoted as \(\overline{E_0^k }\) and \(\underline{E_0^k}(k=1,2)\), respectively, then they can be calculated via the following models:

$$\begin{aligned} \begin{aligned}&Min/Max\,\, \theta _0^k =\frac{{\sum _{i=1}^{2}} {w_i X_{i0}^k +\mu _{0}^\mathrm{k} } }{{\sum _{r=1}^{3}} {u_r Y_{r0}^k } } \\&\quad s.t. \quad \frac{{\sum _{i=1}^{2}} {w_i X_{i0} +\mu _{0}^{1} +\mu _{0}^{2} } }{{\sum _{r=1}^{3}} {u_r (Y_{r0}^1 +Y_{r0}^2 )} }=\theta _0^{*} \\&\quad \frac{{\sum _{i=1}^{2}} {w_i X_{ij}^k +\mu _{0}^{\mathrm{k}} } }{{\sum _{r=1}^{3}} {u_r Y_{rj}^k } }\ge 1,\quad \forall \; j,k \\&\quad u_{1}-\beta u_{2} \ge {0} \\&\quad u_{2} {-}\gamma u_{3} \ge {0}\\&\quad w_i ,u_r \ge 0,\quad \forall \; r,i,\mu _{0}^{\mathrm{k}}\; free. \end{aligned} \end{aligned}$$
(5)

where \(\theta _{0}^{*}\) is the optimal objective function value of model (4). The first set of constraints ensures that the overall parallel Olympic system maintains its efficiency score as \(e_0^*={1}/{\theta _0^*}\). Other constraints are the same in model (2). Model (5) is a ratio program, and can be converted into model (6) by the C–C transformation \(t=1/{{\sum _{r=1}^3} {u_r Y_{r0}^k } },v_i =tw_i ,\mu _r =tu_r ,\omega _0^1 =t\mu _0^1 ,\omega _0^2 =t\mu _0^2 \) as follows:

$$\begin{aligned} \begin{aligned}&{Min}/Max\, \theta _0^k =\sum _{i=1}^{2} {\nu _i X_{i0}^k } +\omega _{0}^{\mathrm{k}} \\&\quad s.t. \quad \theta _0^{*} \times \sum _{r=1}^{3} {\mu _r (Y_{r0}^1 +Y_{r0}^2 )-\left( \sum _{i=1}^{2} {\nu _i X_{i0} +\omega _{0}^{1} +\omega _{0}^{2} } \right) =0}\\&\quad \sum _{i=1}^{2} {\nu _i X_{ij}^k } +\omega _{0}^{\mathrm{k}} -\sum _{r=1}^{3} {\mu _r Y_{rj}^k } \ge 0,\quad \forall \; j,k \\&\quad \sum _{r=1}^{3} {\mu _r Y_{r0}^k } =1 \\&\quad \mu _{1} {-}\beta \mu _{2} \ge {0} \\&\quad \mu _{2} {-}\gamma \mu _{3} \ge {0} \\&\quad \nu _i ,\mu _r \ge 0,\quad \forall \; r,i,\omega _{0}^{\mathrm{k}}\; free \end{aligned} \end{aligned}$$
(6)

Denote the maximum and minimum objective function values of model (6) as \(\overline{\theta _0^{k{*}} }\) and \(\underline{\theta _{0}^{k{*}} }\), respectively. Then maximum and minimum efficiencies of the two subsystems of \(DMU_0 \) are \(\overline{E_{0}^k } ={1}/{\underline{\theta _{0}^{k{*}} }}\) and \(\underline{E_0^k }={1}/{\overline{\theta _0^{k{*}} } } \quad (k=1,2)\). Therefore, the efficiency of each subsystem of \(DMU_0\) can be determined in an interval \([\underline{E_0^k },\overline{E_0^k } ]\), (\(k=1,2\)). If \(\overline{E_0^k } =\underline{E_{0}^k }, \exists k\) is satisfied, then the efficiency of the subsystem \(k\) is uniquely determined.

Theorem 2

If the overall Olympic Games system of \(DMU_{0}\) is efficient, then \(\underline{E_0^k }=\overline{E_0^k } =1,\forall k\)

Proof

See the Appendix 2 \(\square \)

3 An application

3.1 Data sources

The data set consists of 25 participating nations who have taken part in both the Vancouver 2010 Winter Olympic Games and London 2012 Summer Olympic Games. All of them gain at least one medal from each Olympic Games. As mentioned above, three outputs are the numbers of gold, silver and bronze medals, and two inputs are GDP per capita (in US dollars) and population of the participating nation. Similar to Lozano et al. (2002), this paper assumes that the GDP per capita captures the most important element affecting the economic and demographic power of the participating nation. Generally, the wealthy nation is more likely to obtain medals. However, it is insufficient to only take the wealth of participants into account. The numbers of good athletes from participating nations have to be considered as an input variable as well. In general, a nation with more good athletes is more likely to obtain more medals. Since the greater the population of a nation, the more possibility it obtains good athletes. Therefore, the population of the participating nation is considered as another input. In addition, the two kinds of inputs affect all sporting events of the two Olympic Games. The data set of outputs and inputs are collected from the official website of Olympics (http://www.olympic.org/en/content/All-Olympic-results-since-1896/) and the official website of World Bank (http://databank.worldbank.org/ddp/home.do), respectively.

It is noteworthy that the 2012 Summer Olympic Games is held after the 2010 Winter Olympic Games. Accordingly, the problem is which year should be selected as the input data year. The data year we select should capture the most influential factor to the two Olympic Games. If we select the year prior to the year that the Winter Olympic Games holds, then the earlier the year we select, the less influential inputs are reflected in the Summer Olympic Games. Likewise, if we select the year after the Winter Olympic Games holds, the inputs may have little impact on the Winter Olympic Games. Moreover, very few changes happen for GDP per capita and population of each nation in several years, thus we select the year that the Winter Olympic Games holds as the input data year. Therefore, the year 2010 is selected as the input data year in this application.

Summary statistics characterizing inputs and outputs of the 25 participating nations appear in Table 1, which contains the average level, standard variance, the minimum level and maximum level. Note in Table 1 that the large standard deviation of inputs indicates scales of participating nations vary greatly. This observation leads us to use the VRS DEA model.

Table 1 Descriptive statistics of input and output levels for 25 participating nations
Full size table

3.2 Results analysis

Similar to prior literature, we first measure the sports performance of 25 participating nations in 2010 Winter Olympic Games and 2012 Summer Olympic Games, respectively. We apply the BCC model in Lozano et al. (2002) to the dataset which descriptive statistics shown in Table 1. As mentioned above, we use the GDP per capital and population of the participating nation as inputs and the medals won in the Summer Olympics or Winter Olympics as outputs. The obtained results are reported in the second column of Table 2. It shows that fourteen nations, such as USA, Belarus, Canada, China, and so on, are efficient when only taking into account 2010 Winter Olympic Games, and eleven nations are efficient when just considering 2012 Summer Olympic Games.

Table 2 The efficiencies of 25 nations based upon BCC model and model (4)
Full size table

It can be seen that some nations may have completely different performance in the two Olympic Games. For example, Australia is efficient when only considering the Summer Olympic Games, while its performance is very poor (the efficiency is 0.1862) in the 2010 Winter Olympic Games. On the contrary, Canada is efficient when only considering the 2010 Winter Olympic Games, but has an efficiency score of 0.8540 in the 2012 Summer Olympic Games. Thus, Australia prefers to select the Summer Olympics to reflect the sports level, while Canada prefers to the Winter Olympics. Therefore, it is necessary to simultaneously consider the two Olympic Games to measure the sports levels of participating nations.

Considering the two Olympics as parallel subsystems, this paper uses model (4) to measure performance of participating nations. Model (4) is employed to obtain the efficiency of the overall Olympic system. It is a non-linear model, but can be solved as a linear one when treating \(\alpha \) as a parameter. We set \(\alpha =k\times \varepsilon \), where \(\varepsilon \) is a relative small positive number.Footnote 1 Then we increase \(\alpha \) via increasing \(k\) and set the initial value of \(k\) to be the minimum, namely \(k=1\). Corresponding to each \(\alpha \), model (4) can be solved as a linear program and the optimal efficiency value can be denoted as \(e_0 (\alpha )\). As a result, for any given nation, the relationship between \(\alpha \) and the efficiency score based on model (4) can be expressed by an efficiency function \(\hbox {e}_{0} =e_0 (\alpha )\).

To demonstrate the relationship between \(\alpha \) and the efficiency function \(\hbox {e}_{0} =e_0 (\alpha )\), we now take Canada as an example. The optimal objective function value of model (4) corresponding to each \(k\) is shown in Table 3. We set \(\alpha =k\times 0.01\), where \(k\) changes from 1 to 99 as shown in the first column of Table 3. It can be found that the maximum objective value of model (4) is \(\hbox {e}_{0} (0.01{-}0.21)=0.5750\), which implies that Canada can reach the best performance if the Winter Olympics shares 1 to 21 percentages of the whole inputs.

Table 3 The efficiency tendency for Canada based on model (4)
Full size table

Based on the similar calculation procedures, the achievable maximum efficiency and the corresponding optimal values of \(\alpha \) for each nation can be obtained as shown in the last column of Table 2. It shows that out of the 25 participating nations only 6 nations are efficient, namely USA, Belarus, China, Estonia, Latvia and Russia. Furthermore, USA, Belarus, China, Estonia and Latvia are always efficient regardless of the value of \(\alpha \in (0,1)\). Russia is efficient in part of the interval of \(\alpha \). That is, Russia would become inefficient if less than 6 percentages or more than 55 percentages of all inputs are dedicated to the Winter Olympics. A property of VRS model is that DMUs with the smallest input value or the biggest output value are always efficient (Ali 1994). In this paper, USA (biggest outputs) and Estonia (smallest inputs) are such the case. Besides, among the remaining 19 inefficient nations, 17 nations have a unique input allocation when they reach the maximum efficiency values, such as Australia, United Kingdom, Croatia and so on. However, Canada and Norway can achieve their maximum efficiencies in a interval range of \(\alpha \).

It is interesting to note that both Slovenia and Croatia are efficient when we only consider either the 2010 Winter Olympic Games or the 2012 Summer Olympic Games, but they are inefficient when we treat the two Olympics as parallel subsystems. It is not surprising for this result. The reason may be that constraints of model (4) are stricter than the ones in the BCC model of Lozano et al. (2002). So it may overestimate the efficiency of each nation when we only consider one kind of Olympic Games.

Figure 2 exhibits tendencies of efficiency values for four representative nations with the gradual changes of \(\alpha \). There are three typical types of efficiency tendency curve as depicted in Fig. 2: (i) the efficiency tendency curve keeps flat for all \(\alpha \in (0,1)\), USA is this case. (ii) the efficiency tendency curve is rising at first, then keeps flat and is declining at last. Nations such as Russia and Australia are this case, but they differ from the maximum efficiency scores and the interval ranges of \(\alpha \). (iii) the efficiency tendency curve is monotone rising at first, then is declining with the increase of \(\alpha \) after it obtains the maximum efficiency score. Canada is this case. Other nations are omitted here since their tendencies can be represented by the three types.

Fig. 2
figure 2

Tendency of efficiency values for four countries

Full size image

The sensitivity analysis should be performed for different ARs since we cannot accurately define the weight relations among three outputs. The above results are calculated by setting \(\beta =\gamma ={2}\), namely one golden medal is worth at least two silver medals and a sliver one at least two bronze medals. We should further perform sensitivity analysis for the overall system’s efficiency with the two parameters (\(\beta ,\gamma )\). Table 4 shows the efficiency of overall Olympic system for each nation by applying different ARs to \(\beta \) and \(\gamma \). It shows that few efficiency changes happen to each nation. Efficiencies of eight nations keep unchanged irrespective of different parameters values are applied. These nations are Belarus, United Kingdom, China, Estonia, Kazakhstan, Latvia, Russia and Switzerland. For other nations, their efficiency scores are generally decreasing with the increasing values of \(\beta \) and \(\gamma \). The reason is that the feasible region of output multipliers in model (4) gets smaller. Thus, the efficiency measure based on our proposed method seems not sensitive to the values of \(\beta \) and \(\gamma \).

Table 4 Sensitivity analysis of efficiencies to parameters \(\beta \) and \(\gamma \, \left( {\beta =\gamma =c} \right) \)
Full size table

Moreover, it is noteworthy that the six efficient nations (USA, Belarus, China, Estonia, Latvia and Russia) remain efficient with respect to different parameters values. Based on Theorem 1, efficiency scores of the Olympic subsystems for the six efficient nations are equal to 1. As for the inefficient nations, we should perform efficiency decomposition for the two Olympic subsystems.

To make an efficiency decomposition for each subsystem, we apply model (6) based on \(\beta =\gamma ={2}\). Results are given in Table 5. The last two columns of Table 5 show the maximum and minimum efficiency scores of two Olympics for all nations. It can be found that the efficiency of each subsystem for most nations can be uniquely determined except five nations, namely United Kingdom, Canada, Norway, South Korea and Switzerland. For instance, the minimum efficiency score of the Summer Olympic subsystem of United Kingdom is 0.9772 while the maximum value is 1, so the efficiency decomposition for the Summer Olympic subsystem of United Kingdom is not unique. The non-uniqueness of the subsystem’s efficiency verifies the necessity of the efficiency decomposition for parallel Olympic subsystems. For convenience of results’ comparison, the second column of Table 5 displays the efficiency of the overall parallel Olympic system for each nation, which is the same as shown in the last column of Table 2. It is noteworthy that the two Olympic subsystems of the six efficient nations are efficient, which accords with Theorem 1.

Table 5 Efficiency decomposition for two Olympics with \(\beta =\gamma =2\)
Full size table

Moreover, some inefficient nations have good performance in one of the Olympic subsystems. These nations include Australia, United Kingdom, Canada, Kazakhstan and Norway. Among of them, Canada and Norway have good performance in the Winter Olympic Games but poor performance in the Summer Olympic Games. Generally, nations located in the middle-high latitude areas may have good performance in the Winter Olympic Games. On the contrary, the other three nations have good performance in the Summer Olympic Games. This phenomenon accords with their geographical features.

These results show that our proposed approach is more general and reasonable. It may be due to the fact that we consider two Olympics simultaneously to evaluate the sports level of each nation. Besides, our approach also provides a guide for performance improvement. That is, nations who expect to be efficient in the overall Olympic system should pay more attention to improve the sports level of their inefficient subsystems. Nations are efficient in the overall Olympic system only when both the two Olympic subsystems are efficient.

4 Conclusions

The Olympic Games are the most important and most popular sporting event in the world, and people pay more and more attention to this event. Measuring the performance of participating nations in the Olympic Games is an important application of DEA. In this paper, an output-oriented VRS parallel DEA approach is presented to evaluate sports levels of participating nations. Prior DEA studies evaluate sports levels of nations only considering their performance in the Summer Olympic Games. It is unfair for some nations which are good at the Winter Olympics, but poor at the Summer Olympics. This paper treats the two kinds of Olympic Games as two parallel subsystems and defines a parameter to divide the shared inputs into two parts. Our proposed approach can measure the efficiency of overall Olympic system and an efficiency decomposition procedure is used to obtain the efficiency range of each Olympic subsystem. Such the efficiency decomposition for each subsystem can also provide a guide for performance improvement. Then, our proposed approach is applied to comprehensively measuring the performance of 25 nations participating both in the 2010 Winter Olympics and 2012 Summer Olympics. A more detailed and reasonable performance evaluation result has been obtained. The majority of nations display different performance in the two Olympics which is consistent with their geographical features. In addition, the majority of nations obtain their maximum efficiency scores when shared inputs for the Winter Olympics are uniquely determined.

Further developments in measuring efficiencies of participating nations in the Olympics should take the efficiency of selecting good athletes into account. It is no doubt that good athlete is an important factor for participating nations to obtain medals. Moreover, there are some nations that participated in both the Winter Olympic Games and Summer Olympic Games but did not obtain at least one medal from both Olympic Games. How to measure Olympics achievements of these nations is a possible direction of this study.