1 Introduction

Using graphs it is possible to model a large number of real world problems, and a significant portion of them is related to graph isomorphism. Particularly, the Maximum Common Induced Subgraph (MCIS) has several applications in areas like Computer Vision (Horaud and Skordas 1989; Pelillo et al. 1999), Video indexing (Shearer et al. 2001), Chemistry and Biology (Willet 1999; Gifford et al. 1996; Chen and Robien 1994). This problem can be defined as follows:

figure a

Here we should recall the concepts of isomorphism and of induced subgraph. Two graphs G=(V,E) and H=(W,F) with |V|=|W| are called isomorphic if there is a bijection π:V→W such that (i,j)∈E⇒(π(i),π(j))∈F and (i,j)∈F⇒(π −1(i),π −1(j))∈E. Besides, given a graph G=(V,E), a graph H=(W,F) is an induced subgraph of G if W⊆V and F={(i,j)∈E:i∈W and j∈W}, i.e., F is the set of edges with both extremities in W. In that case, we also say that H is the subgraph induced by W in G.

Another manner of defining the problem would be the following: given two graphs, find a mapping from a vertex subset in one graph to a vertex subset in the other graph such that these subsets have a maximum size (the subgraph is maximum) and the following restrictions are observed: each vertex in one graph can be mapped at most to one vertex in the other graph (the subgraphs are isomorphic) and a pair of adjacent vertices in one of the graphs cannot be mapped to a pair of non-adjacent vertices in the other graph (the subgraph is induced in both graphs).

The MCIS is an \({\mathcal {NP}}\)-hard problem and can be found in the classic list in Garey and Johnson (1979). Therefore, unless \(\mathcal{P}=\mathcal{NP}\), there are no polynomial algorithms to solve it. For this reason, several heuristics and approximation algorithms were proposed for the MCIS (Kann 1992; Messmer and Bunke 1999; Raymond and Willett 2002; Raymond et al. 2002a, 2002b; Suters et al. 2005; Wang and Maple 2005). However, despite its complexity, it is still important to know exact solutions for instances, even if small ones, of the problem. The most used methods in the literature to solve this problem exactly are based in backtracking algorithms as in Mcgregor (1982), Wong and Akinniyi (1983) and Krissinel and Henrick (2004), or in the reduction to another more studied \({\mathcal {NP}}\)-hard problem, such as the Clique problem, as done in Falkenhainer et al. (1989/1990) and in two of the algorithms presented in Conte et al. (2003).

In this work we try to address the problem directly through Integer Programming (IP) models and polyhedral combinatorics techniques. To do so, we perform a theoretical investigation of the MCIS using the tools provided by polyhedral theory. Doing that, we aim to find strong valid inequalities that allow us to build a better formulation of the problem as an IP. Later, we verify the impact of these theoretical results in the computational performance of Branch-and-Bound (B&B) and Branch-and-Cut (B&C) algorithms we developed to solve the problem and, also, compare these results with those achieved by an existing combinatorial algorithm.

The rest of the text is organized as follows. The next section introduces some basic definitions to help the understanding of the text. Section 3 presents the initial IP model for MCIS. Section 4 shows a polyhedral study of MCIS, including proofs that some of the valid inequalities we found are facet-defining. Section 5 discusses the relationship between MCIS and the Maximum Clique Problem. The computational results are discussed at Sect. 6. At last, in Sect. 7 some conclusions are presented.

2 Basic definitions

The purpose of this section is to briefly review some concepts from Graph Theory, Linear Algebra and Integer Programming necessary to the understanding of the text. A full treatment of these topics can be found in textbooks such as (West et al. 2001), for Graph Theory, and (Nemhauser and Wolsey 1988), for Integer Programming.

Graph theory

Let G be a graph. If there is an edge joining two vertices i and j of G they are adjacent. If i and j are non-adjacent, (i,j) is called a non-edge of G. The complement graph of G is the graph with the same vertices as G whose edges are precisely the non-edges of G. A clique in G is a complete subgraph of G (all vertices of the subgraph are adjacent to each other). An independent set (or IS for short) in G is a set of its vertices such that no two of them are adjacent. An isolated vertex (or singleton) in G is a vertex that is not adjacent to any other vertex in the graph. A vertex of G is said to be universal if it is adjacent to all the remaining vertices in G. Finally, for a positive integer t, if the vertex set of G can be partitioned into t subsets such that no edge of G joins two vertices in one subset, we say that G is t-partite.

Linear algebra

The vectors x 1,…,x q in \(\Bbb {R}^{n}\) are said to be affine independent if the only solution to the linear system \(\{\sum_{i=1}^{q}\lambda_{i}x^{i}=0, \sum_{i=1}^{q}\lambda_{i}=0\}\) is λ i =0 for all i=1,…,q. If S is a subset of \(\Bbb {R}^{n}\), the dimension of S corresponds to the size of the largest subset of points in S that are affine independent minus 1. Let U={u 1,…,u n } be a set and S be a subset of U. The n-dimensional binary vector x(S) with x(S) i set to one if and only if the element u i belongs to S, is called the characteristic vector of S.

Integer programming

We focus on the necessary background in Polyhedral Combinatorics. To this end, consider the set of feasible solutions of an integer programming formulation \(P=\{x\in \Bbb {R}^{n}_{+}~|~Ax=b\}\cap \Bbb {Z}^{n}\) for a problem Π. The convex hull of the points in P, denoted by conv(P), is named the Π polytope. This polytope is full-dimensional if its dimension is n (the dimension of \(\Bbb {R}^{n}\)). An inequality μx≤μ 0 is said to be valid for conv(P)—or for P, for that matter—if it is satisfied by all vectors in P. The face \(F_{(\mu,\mu_{0})}\) defined by the valid inequality μx≤μ 0 in conv(P) is the set \(F_{(\mu,\mu_{0})}=\{ x\in \mathrm{conv}(P)~|~\mu x=\mu_{0}\}\). If the dimension of \(F_{(\mu,\mu_{0})}\) is that of conv(P) minus one, then the face is called a facet. The relevance of finding facet-defining inequalities comes from the fact that they are necessary and sufficient to describe conv(P) in terms of a linear system. To prove that an inequality μx≤μ 0 defines a facet of conv(P) one can directly compute the dimension of the face by counting affine independent points. Alternatively, assuming that conv(P) is full-dimensional, one can show that any valid inequality πx≤π 0 whose face \(F_{(\pi,\pi_{0})}\) contains the face \(F_{(\mu,\mu_{0})}\) can be obtained by multiplying μx≤μ 0 by a positive value. A lifting of a valid inequality μx≤μ 0 for conv(P) is an operation in which one or more elements of μ are increased in such a way that the inequality remains valid while the new face it defines has higher dimension and contains the previous one.

3 Integer programming model for the MCIS

In this section we present a simple IP formulation for the MCIS problem. This model is based on the one given in Manić (2007) and reads:

(1)
(2)
(3)
(4)
(5)
(6)

In this formulation, for all i∈V(G) and j∈V(H), the binary variable y ij is set to 1 if, and only if, the vertex i is mapped to the vertex j. Constraints (2) and (3) guarantee, respectively, that every vertex in V(H) is mapped to at most one vertex in V(G) and that every vertex in V(G) is mapped to, at most, a single vertex in V(H). Constraints (4) and (5) though, guarantee, respectively, that no two adjacent vertices in V(G) are mapped simultaneously to two non-adjacent vertices of V(H) and that no two adjacent vertices in V(H) are mapped simultaneously to a pair of non-adjacent vertices in V(G). It is a simple task to show that this formulation is correct.

In the remainder of the text we denote by P the set of integer solutions of (2)–(5). The MCIS polytope is defined as the convex hull of P, denoted by conv(P). In the next section we investigate the facial structure of this polyhedron.

4 Theoretical study of the MCIS polytope

In this section, we introduce strong valid inequalities that we encountered in the theoretical study of the MCIS, establishing the conditions under which these inequalities are facet-defining and present the respective proofs. The section is organized in such a way that each specific group of inequalities is considered in a separate subsection. So, Sect. 4.1 is focused on the inequalities that guarantee that each vertex in one of the graphs is mapped to a single vertex in the other graph. As for Sect. 4.2, it is concentrated on the inequalities that determine that a pair of adjacent vertices in one of the graphs cannot be mapped to a pair of non-adjacent vertices in the other graph.

From now on, every inequality mentioned in this section should be considered as having an equivalent inequality in which the roles of the two input graphs of the MCIS are interchanged. For example, when the inequality

is discussed in the text, the reader must bear in mind that an analogous discussion applies to the inequality

in the sense that all properties found for the former also hold for the latter.

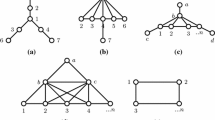
We present in Fig. 1 an example that is used throughout this section to illustrate the structure of the inequalities. In that figure, in graph B there are some marked subsets linked by dashed lines. These lines indicate that every vertex in one subset is adjacent to every vertex in the other subset.

Fig. 1
figure 1

Example of an input instance for the MCIS

Full size image

Prior to assess the strength of valid inequalities for the MCIS polytope we have to establish its dimension.

Proposition 1

The dimension of conv(P) is |V(G)|×|V(H)|, i.e., the MCIS polytope is full-dimensional.

Proof

Let e ij be the vector with 0 at all positions except at position ij whose value is 1. For every i∈V(G) and j∈V(H), the vector e ij satisfies the restrictions defining P and the same holds for the null vector. Hence, we have |V(G)|×|V(H)|+1 vectors in P that are affine independent and, therefore, we can say that the dimension of conv(P) is no smaller than |V(G)|×|V(H)|. However, since the dimension of the polytope cannot be higher than that of the space that contains it, we can deduce that conv(P) is full-dimensional, which completes the proof. □

4.1 Unique mapping

Now, consider the family of inequalities that enforces the unicity of vertex mappings and given by:

(7)

where:

  • C(j) is a maximal clique containing the vertex j;

  • I(j) is a maximal independent set containing the vertex j;

  • U G is the set of universal vertices in G; and

  • D G is the set of isolated vertices in G.

As an example, in Fig. 1, consider the graphs A 1⊂A induced by the vertex set V(A 1)={a 1,…,a 6} and B 1⊂B induced by the vertex set V(B 1)={b 1,…,b 4}. Setting G=A 1, H=B 1 and j=b 4, we have D G ={a 5,a 6} and C(j)={b 2,b 3,b 4}. In this case, the inequality is \(y_{a_{1}b_{4}} +\) \(y_{a_{2}b_{4}} +\) \(y_{a_{3}b_{4}} +\) \(y_{a_{4}b_{4}} +\) \(y_{a_{5}b_{4}} +\) \(y_{a_{6}b_{4}} +\) \(y_{a_{5}b_{2}} +\) \(y_{a_{5}b_{3}} +\) \(y_{a_{6}b_{2}} +\) \(y_{a_{6}b_{3}} \leq1\).

We first prove that these inequalities are valid for the MCIS polytope.

Proposition 2

The inequalities of the form of (7) are valid for the MCIS polytope.

Proof

First note that D G ≠∅ implies that U G =∅ and U G ≠∅ implies that D G =∅. It is still possible that D G =U G =∅.

Suppose that D G ≠∅, then, assume by contradiction that one inequality in (7) is not valid for the MCIS polytope. So, there must be some point in the polytope for which at least two variables in the LHS of the inequality have value 1 at the same time. There are three possible cases where that can happen:

  1. Case 1

    Two variables have value one in the first summation. This is not possible since, in this case, inequality (2) is not satisfied.

  2. Case 2

    Two variables have value one in the second summation. This implies that either one vertex in G is mapped to two vertices in H, or that a pair of isolated, and therefore, non-adjacent vertices in G is mapped to a pair of adjacent vertices in H (vertices in the clique C(j)). Thus, there is a violated inequality given by constraint (3) or by constraint (5).

  3. Case 3

    One variable in the first summation and another in the second summation have both value 1. This means that a vertex i in G is mapped to j and that, simultaneously, an isolated vertex k in G is mapped to a vertex l in H that is adjacent to j. However, in this situation, we have a non-edge in G that is mapped to an edge of H, contradicting constraint (5).

In the case where U G ≠∅ the reasoning is similar.

Therefore, there is no point in the MCIS polytope that violates the inequality, which contradicts the initial hypothesis. So, the inequalities of the form of (7) are valid for this polyhedron. □

Now, consider the following conditions:

(8)
(9)

where Adj(j) stands for the set of vertices adjacent to j whereas \(\overline{\mathrm{Adj}(j)}\) stands for the set of vertices not adjacent to j.

Notice that if we had G=A 1∖{a 6}, H=B 1∪{b 6} and j=b 4 with A 1 and B 1 defined as before, the inequality defined as in (7) could be lifted to have coefficient one for \(y_{a_{5}b_{6}}\). As a result, we can conclude that the original inequality is not facet-defining. Hence, we propose that an inequality of the form of (7) is facet-defining only if, condition (9) is satisfied as shall be proved below. The same reasoning can be used when there is a universal vertex.

Proposition 3

An inequality in (7) induces a facet \(F = \{x \in \mathrm{conv}(P):\sum_{i \in V(G)}y_{ij} + \sum_{l \in C(j)\setminus{\{j\}}}\sum_{k \in D_{G}} y_{kl} + \sum_{l \in I(j)\setminus{\{j\}}} \sum_{k\in U_{G}} y_{kl} = 1\}\) of conv(P) if, and only if, conditions (8) and (9) are satisfied.

Proof

(⇐) The face defined by an inequality in (7) is proper, because the null vector is not in the face and is in conv(P), and any vector with 0 at all the positions except at ij, for some i∈V(G) is in the face.

Let F′={x∈conv(P):πx=π 0} and F⊆F′. Now, if the inequality is facet-defining, then there must exist a positive constant \(\alpha\in \Bbb {R}\) satisfying: (π,π 0)=α(γ,1) where γ ij′=1 if j′=j ∀i∈V(G) or (i∈D G and j′∈C(j)) or (i∈U G and j′∈I(j)) and γ ij′=0 otherwise. i.e., we must show that π 0=α and π ij′=α=π 0 if j′=j or (i∈D G and j′∈C(j)) or (i∈U G and j′∈I(j)) and π ij′=0 otherwise.

If the inequality is facet-defining, we should be capable of getting to the same relations as above using the fact that F⊆F′. So, we have:

(1) In this first case of the proof we show that π ij′=π 0 for any i∈V(G), j′∈V(H) where the variable x ij′ have coefficient 1 in F. We do it by showing that every vector having value 1 for one of these variables and value 0 for every other variables is in F. So we have:

Obviously the vectors (…,0,1 ij′,0,…), where (i∈V(G) and j′=j) or (i∈D G and j′∈C(j)) or (i∈U G and j′∈I(j)) are in F. As F⊆F′ ⇒(…,0,1 ij′,0,…)∈F′⇒π ij′=π 0.

(2) This case proves that π kl =0 for any k∈V(G), k∉D G , k∉U G and l∈V(H)∖{j}. This is done by showing a vector in F representing a mapping from such a k to an l and from i∈V(G)∖{k} to j and no other mappings. From this vector we conclude that π ij +π kl =π 0 and from the previous case, that π kl =0. So the proof goes as follows:

Let (…,0,1 ij ,…,0,…,1 kl ,0,…)∈F, where k∈V(G), i∈V(G)∖k, l∈V(H)∖{j}, k∉D G and k∉U G . So we have two cases to consider, in the first one (l,j)∈E(H), then as k is not isolated we can always chose i so that (i,k)∈E(G). The second case occurs if (l,j)∉E(H), then as k is not universal we can always chose i so that (i,k)∉E(G). As F⊆F′ ⇒(…,0,1 ij ,…,0,…,1 kl ,0,…)∈F′⇒π ij +π kl =π 0. Therefore, from (1), we have π kl =0 ∀k∈V(G), \(k \not \in D_{G}\), k∉U G and l∈V(H)∖{j}.

(3) Here we show that π kl =0 for any k∈D G , l∉C(j). We do that by presenting a vector in F having value 1 for a variable mapping such a vertex k to an l and also having value 1 for a variable x ij′ where π ij′=π 0; every other variable have value 0. Thus we can conclude that π ij′+π kl =π 0 and so, π kl =0. The details of the proof are shown next:

Let (…,0,1 ij′,…,0,…,1 kl ,0,…)∈F, where k∈D G , i∈V(G)∖{k}, l∉C(j), j′∈C(j). We first consider the case where |D G |=1, so we choose j′=j and, from condition (9), we have (l,j′)∉E(H). In case |D G |>1, then i is chosen in D G and j′ is chosen in such a way that (l,j′)∉E(H), which is always possible because C(j) is maximal. Notice that for k∈D G , one of the two situations always happen because of condition (9). As F⊆F′ ⇒(…,0,1 ij′,…,0,…,1 kl ,0,…)∈F′⇒π ij′+π kl =π 0. Therefore, from (1), we have π kl =0 ∀k∈D G , l∉C(j).

(4) This is the equivalent to (3) when there is a universal vertex in G instead of an isolated. Thus, the proof is very similar.

Let (…,0,1 ij′,…,0,…,1 kl ,0,…)∈F, where k∈U G , i∈V(G)∖{k}, l∉I(j), j′∈I(j). We first consider the case where |U G |=1, so we choose j′=j and, from condition (8), we have (l,j′)∈E(H). In case |U G |>1, then i is chosen in U G and j′ is chosen in such a manner that (l,j′)∈E(H), which is always possible because I(j) is maximal. Notice that for k∈U G , one of the two situations always happen because of condition (8). As F⊆F′ ⇒(…,0,1 ij′,…,0,…,1 kl ,0,…)∈F′⇒π ij′+π kl =π 0. Therefore, from (1), we have π kl =0 ∀k∈U G , l∉I(j).

(⇒) If condition (8) is not satisfied, then for some k∈U G and l∉I(j) non-adjacent to j it would not be possible to choose i∈V(G) and j′=j, with i non-adjacent to k, because k is universal; i could not be universal because there is only one isolated vertex, which is k; and i, certainly could not be isolated, because k is universal. Therefore, there is no vector in F with value 1 at position kl, that is equivalent to say that in the polyhedron defined by F there is an equality y kl =0. Hence, its dimension is less than |V(G)|×|V(H)|−1, thus, it is not a facet of conv(P).

If condition (9) is not satisfied, then for some k∈D G and l∉C(j) adjacent to j it would not be possible to choose i∈V(G) and j′=j, with i adjacent to k, because k is isolated; i could not be isolated because there is only one isolated vertex which is k; and i, certainly could not be universal, because k is isolated. Therefore, there is no vector in F with value 1 at position kl, that is equivalent to say that in the polyhedron defined by F there is an equality y kl =0. Hence, its dimension is less than |V(G)|×|V(H)|−1, consequently, it is not a facet of conv(P).

Ergo, if (¬(8) or ¬(9)) the inequality in (7) is not facet-defining for conv(P). □

It is noteworthy that when there is neither an isolated nor a universal vertex in G (for example, in Fig. 1, suppose that G=A 2 induced by V(A 2)={a 1…a 4}, H=B 1 as defined as before and j=b 4), (7) is the same as (2). An analogous situation occurs if there are isolated vertices in G and j is isolated (for A 1 and B 1 defined earlier, in Fig. 1 suppose G=A 1, H=B 1∪{b 5} and j=b 5), because, then, C(j) is empty. Clearly a similar conclusion can be drawn if there are universal vertices in G and j is universal, because, in that case, I(j) is empty. It is not difficult to show that the previous conditions are necessary for (2) to be facet-defining. Such a proof can be found in Piva and de Souza (2011).

If there is exactly one isolated or one universal vertex in G, the inequalities

are facet defining, where k is the isolated vertex or p is the universal vertex in G. Of course, as mentioned earlier, only one such vertex can exist at a time in any graph. Therefore, at most one of the last two summations is present in the LHS of the inequalities. This result can be obtained starting from (7) and lifting the variables corresponding to the mapping of the isolated/universal vertex in G to the vertices in \(\mathrm{Adj}(j)\setminus C(j)/\overline{\mathrm{Adj}(j) \setminus I(j)}\) in H. Recall that this lifting was also explored right before the proof that the inequalities (7) define facets. Thus, not surprisingly, the proofs of validity and facet-definition of (10) are based on arguments that are similar to those in the analogous proofs for (7). They are also given in detail in Piva and de Souza (2011).

4.2 Edge mapping

So far we have considered vertex mappings. However, enforcing the correct edge mappings is also important. Since the IP model does not include variables representing edge mappings, the inequalities dealing with this situation involve the mappings of the endpoints of the edges or non edges being considered. In this way, as the input graphs are assumed to be undirected, the mapping of edge (i,j) in G to edge (k,l) in H may be understood as the mapping of i to k and j to l, or, i to l and j to k. Analogously, the mapping of a non-edge to another non-edge is the mapping of a pair of non-adjacent vertices of one graph to a pair of non-adjacent vertices in the other graph.

In this section, we are going to deal with inequalities whose goal is to guarantee that no edge is mapped to a non-edge or vice versa, which would violate the MCIS definition. As we show below, the inequalities presented in the model in Sect. 3 are too weak. In fact, through lifting, they can be strengthened to yield the following inequalities:

(10)

These are called the Clique-IS inequalities. They impose that, given a maximal clique C in G and a maximal independent set (IS) I in H, at most one mapping can be done between vertices in C and vertices in I. Clearly, they can be thought as being a generalization of the inequalities (4) of the original model presented in Sect. 3. Their validity can be established immediately from the problem definition.

Rather than investigating the CLIQUE-IS inequalities further, we focus on an even stronger family of inequalities which can be obtained from them by intensifying even more the lifting process. These new inequalities are called SeqClique-SeqIS and read:

(11)

where:

  • \(\mathcal{SC}(G) = (C(G_{0}), L(G_{0}), C(G_{1}), L(G_{1}), \ldots,C(G_{p}), L(G_{p}))\), with:

    1. (1)

      G 0=G;

    2. (2)

      C(G i ) is a maximal clique in G i , i=0,…,p;

    3. (3)

      L(G i )={v∈G i :v∉C(G i ) and ∃u∈C(G i ) with (u,v)∈E(G i )}, for all i∈{0,…,p}. In other words, L(G i ) is the subgraph composed by the vertices in V(G i ) that are adjacent to some vertex in C(G i ). Observe that |C(G i )|=1 implies that L(G i ) is empty. Besides, as C(G i ) is maximal, it is clear that for every v∈L(G i ) there exists a vertex u′ in C(G i ) that is not adjacent to v;

    4. (4)

      G i+1=G i −(C(G i )∪L(G i )), i=0,…,p. Hence, the graph G i+1 is obtained by removing from G i the vertices in C(G i ) and all their neighbors, i.e., the vertices in L(G i ). Notice that, there is no edge incident to one vertex in C(G a ) and another one in C(G b ), with a≠b, since, by construction, the cliques in the sequence are independent from each other.

  • \(\mathcal{SI}(H) = (I(H_{0}), L(H_{0}), I(H_{1}), L(H_{1}), \ldots,I(H_{q}), L(H_{q}))\), with:

    1. (1)

      H 0=H;

    2. (2)

      I(H j ) is a maximal independent set in H j , j=0,…,q;

    3. (3)

      L(H j )={v∈H j :v∉I(H j ) and ∃u∈I(H j ) with (u,v)∉E(H j )}, for all j∈{0,…,q}. In other words, L(H j ) is the subgraph composed by the vertices in V(H j ) that are non-adjacent to some vertex in I(H j ). Observe that |I(H j )|=1| implies that L(H j ) is empty. Besides, by construction, it is clear that for every vertex v in L(H j ) there is also a vertex u′ in I(H j ) which is adjacent to v since, otherwise, I(H j ) would not be maximal;

    4. (4)

      H j+1=H j −(I(H j )∪L(H j )), j=0,…,q. Hence, the graph H j+1 is obtained by removing from H j the vertices in I(H j ) and all their neighbors, i.e., the vertices in L(H j ). Notice that, there are edges linking every vertex in I(H a ) to every vertex in I(H b ), with a≠b, since, by construction, the independent sets in the sequence are completely connected to each other.

Before we continue, it is convenient to define the following sets:

  • \(R^{G} = G_{\mathrm{min}\{|\mathcal{SC}(G)|, |\mathcal{SI}(H)|\}}\);

  • \(R^{H} = H_{\mathrm{min}\{|\mathcal{SC}(G)|, |\mathcal{SI}(H)|\}}\).

Notice that these definitions imply that if R G is not empty then R H is empty, whereas if R H is not empty then R G is empty.

It is not hard to see that inequality (11) can be generated by lifting the Clique-IS inequality corresponding to C(G 0) in G and I(H 0) in H. Indeed, because no vertex in C(G 0) and C(G 1) are adjacent and any vertex in I(H 0) is adjacent to any vertex in I(H 1), we can add to the LHS of the original Clique-IS inequality all the variables associated to mappings of vertices in C(G 1) to vertices in I(H 1), making it stronger. Clearly, in any feasible solution, the sum of the new terms is at most one. Besides, this upper bound cannot be reached if the original LHS value for this solution is also one since, otherwise, there would be a non-edge in G mapped to an edge in H. Similar arguments, show that this lifting procedure can be repeated for C(G i ) and I(H i ), for all \(2 \geq i \geq \min\{|\mathcal{SC}(G)|,|\mathcal{SI}(H)|\}-1\), in which case, we end up with the SeqClique-SeqIS inequality.

As an example of a sequence of cliques in G and independent sets in H having the properties described above, consider again the graph depicted in Fig. 1. Define A 3⊂A as the subgraph induced by V(A 3)={a 1,…,a 4,a 6,…,a 12} and set G=A 3 and H=B. A possible clique sequence for G is \(\mathcal{SC}(G) = (C(G_{0}) = \{a_{1}, a_{3}\}, L(G_{0}) =\{a_{2}, a_{4}\}, C(G_{1}) = \{a_{6}, a_{7}, a_{8}\}, L(G_{1}) = \{a_{9},a_{10}\}, C(G_{2}) = \{a_{11}, a_{12}\}, L(G_{2}) = \{\})\). Now, in graph H, a possible IS sequence is \(\mathcal{SI}(H) = (I(H_{0}) =\{b_{1}, b_{4}, b_{5}\}, L(H_{0}) = \{b_{2}, b_{3}\}, I(H_{1}) = \{b_{6},b_{7}\}, L(H_{1}) = \{b_{8}, b_{9}\}, I(H_{2}) = \{b_{10}, b_{11}\}, L(H_{2}) =\{b_{12}\}, I(H_{3}) = \{b_{13}, b_{14}\}, L(H_{3}) = \{\}, I(H_{4}) =\{b_{15}, b_{16}\}, L(H_{4}) = \{b_{17}, b_{18}, b_{19}\}, I(H_{5}) =\{b_{20}, b_{21}, b_{22}\}, L(H_{5}) = \{b_{23}, b_{24}, b_{25}\})\). In this case, because \(\min\{|\mathcal{SC}(G)|, |\mathcal{SI}(H)|\} =|\mathcal{SC}(G)| = 3\), we have that R H=H 3=I(H 3)∪L(H 3)∪I(H 4)∪L(H 4)∪I(H 5)∪L(H 5).

Notice that, different sequences \(\mathcal{SC}(G)\), and \(\mathcal{SI}(H)\) give rise to different inequalities. Even the order at which each component is considered, has influence in the structure of the inequalities. So, it is easy to see that the number of inequalities in this family is huge, and in the worst case, grows exponentially with the number of vertices of the input graphs. Below we prove that, under certain conditions, some of the inequalities in this family are facet-defining for the MCIS polytope. But, prior to that, we show that they are valid.

Proposition 4

The inequalities of the form of (11) are valid for the MCIS polytope.

Proof

Assume that an inequality in (11) is not valid for the MCIS polytope. So, there must exist some point in that polyhedron that does not satisfy the inequality. There are two cases to consider.

Case 1 Two variables assume value one for the same index h of the summation in the LHS of the inequality. For this to occur, one of the following conditions must hold: (i) a single vertex in G is mapped to more than one vertex in H; (ii) more than one vertex in G is mapped to a single vertex in H, or (iii) a pair of adjacent vertices in C(G h ) is mapped to a pair of non-adjacent vertices in I(H h ), meaning that an edge of G is mapped to a non-edge of H. Clearly, none of these situations fulfill the definition of the MCIS, since the corresponding solution would violate constraints (2), (3) and (4), respectively.

Case 2 Two variables assume value one for different indexes of the summation in the LHS of the inequality. This means that, for two distinct values h and h′ in \(\{0,\ldots,\min\{|\mathcal{SC}(G)|, |\mathcal{SI}(H)|\}\}\), there exist four vertices i∈C(G h ), j∈I(H h ), k∈C(G h′) and l∈I(H h′), with i mapped to j and k mapped to l. However, by construction, vertices in different cliques of \(\mathcal{SC}\) are non-adjacent while vertices in different ISs of \(\mathcal{SI}\) are adjacent. Hence, this case implies the mapping of an non-edge in G to an edge in H, which does not satisfy constraint (5).

Therefore, any point in the MCIS polytope satisfies the inequality, contradicting the hypotheses. Thus, the inequality is valid. □

Now, consider the following conditions:

(12)
(13)

Proposition 5

If conditions (12) and (13) are satisfied, an inequality in (11) defines a facet \(F = \{x \in \mathrm{conv}(P)\ :\ \sum_{h=0}^{\min(|\mathcal{SC}(G)|,|\mathcal{SI}(H)|)-1}\,\sum_{i\in C(G_{h})} \sum_{j \in I(H_{h})} y_{ij} = 1\}\) of conv(P).

Proof

In this proof we consider that \(|\mathcal{SC}(G)| <|\mathcal{SI}(H)|\). For the other case, the proof is similar and, therefore, omitted. We first notice that F is a proper face because the null vector belongs to conv(P)∖F, and F is nonempty. The latter can be verified by noticing that, for any proper value h such that i is a vertex in C(G h ) and j is a vertex in I(H h ), the vector x representing only the mapping of i to j and no further mappings, belongs to F.

Now, let F′={x∈conv(P):πx=π 0} and F⊆F′. If the inequality (11) is facet-defining, then, there must exist a positive constant \(\alpha \in \Bbb {R}\) satisfying (π,π 0)=α(γ,1), where γ ij =1 if i∈C(G h ) and j∈I(H h ), \(h = 0 \ldots |\mathcal{SC}(G)|-1\) and γ ij =0, otherwise. In other words, we must show that: (i) π 0=α; (ii) π ij =α=π 0, if i∈C(G h ), j∈I(H h ) and \(h = 0 \ldots|\mathcal{SC}(G)|-1\), and (iii) π ij =0, in all other cases not covered in (ii).

To facilitate the understanding of the remainder of the proof, we present in Fig. 2 a diagram with the kinds of mappings covered in each case discussed below. In this diagram, a line connecting clique C(G h ) to IS I(H h ) represents a mapping of a vertex in C(G h ) to a vertex in I(H h ). The different kinds of lines used in the figure represent the different cases of the proof as described in the legend. To avoid overfilling the image, only the mappings for the sets C(G h ) and L(G h ) are shown, although, it is easily verifiable that the other mappings are encompassed by the cases treated in the proof.

Fig. 2
figure 2

Proposition 5: proof diagram

Full size image

Back to the proof itself, to show that the inequality is facet-defining, we must get to the same relations above by using the fact that F⊆F′. To this end, we considered the following cases:

(1) The first case proves that π ij =π 0 for any position ij having coefficient 1 in F. This is easily done by showing that a vector that represents a mapping from such an i to a j, and no other mappings, is in F and also in F′. Thus, we can conclude that relation as shown bellow:

Obviously the vectors (…,0,1 ij ,0,…), where i∈C(G h ) and j∈I(H h ), \(h = 0 \ldots|\mathcal{SC}(G)|-1\) are in F. As F⊆F′ ⇒(…,0,1 ij ,0,…)∈F′⇒π ij =π 0.

(2) The next case considered is the one that proves that π kl =0 for any k∈C(G h ) and l∈I(H r ), with different values for h and r. We can find a vector in F corresponding to a mapping of a vertex i to a vertex j where i and j satisfy the conditions from (1), also mapping such a k to an l and no other mapping. From this vector we conclude that π ij +π kl =π 0 and, from (1), that π kl =0. The details are present next:

Let us consider the vectors (…,0,1 ij ,…,0,…,1 kl ,0,…)∈F, where k∈C(G h ), l∈I(H r ), \(h, r= 0 \ldots|\mathcal{SC}(G)|-1\) and h≠r. We can choose i in C(G r ) and j in I(H r ) (which is always possible because of condition (13)), thus, (i,k)∉E(G) and \((j,l) \not \in E(H)\). As F⊆F′ ⇒(…,0,1 ij ,…,0,…,1 kl ,0,…)∈F′⇒π ij +π kl =π 0. Therefore, from (1), we have π kl =0 ∀k∈C(G h ), l∈I(H r ), \(h, r = 0 \ldots|\mathcal {SC}(G)|-1\), h≠r.

(3) Here we prove that π kl =0 for any k∈C(G h ) and l∈L(H r ). Once again it is simply a matter of finding a vector in F corresponding to a mapping of vertices satisfying the conditions from (1), a mapping of such a k and l and no other mapping. Then we can conclude that π ij +π kl =π 0 and, from (1), that π kl =0. The proof goes as follows:

Consider the vectors (…,0,1 ij ,…,0,…,1 kl ,0,…)∈F, where k∈C(G h ), l∈L(H r ), \(h, r = 0 \ldots \min(|\mathcal{SC}(G)|,|\mathcal{SI}(H)|)-1\). We have two cases to consider, the fist one occurs if r≥h. In this case we can choose j in I(H h ) so that (j,l)∈E(H) (which is always possible because I(H h ) is maximal) and we can choose i in C(G h ) (which is always possible because of condition (12)), thus, (i,k)∈E(G), because the two vertices are in the same clique. In the case r<h we can choose j in I(H r ) so that (j,l)∉E(H) (which is always possible by the definition of L(H r )) and we choose i in C(G r ), thus, (i,k)∉E(G). As F⊆F′ ⇒(…,0,1 ij ,…,0,…,1 kl ,0,…)∈F′ ⇒π ij +π kl =π 0. Therefore, from (1), we have π kl =0 ∀k∈C(G h ), l∈L(H r ), \(h, r = 0 \ldots|\mathcal{SC}(G)|-1\).

(4) This case is very similar to case (3), but instead of considering the mapping from a k∈C(G h ) to an l∈L(H r ), we consider the mapping of a k∈L(G r ) to an l∈I(H h ). Thus, the proof is very similar to the previous case.

Let (…,0,1 ij ,…,0,…,1 kl ,0,…)∈F, where k∈L(G r ), l∈I(H h ), h, \(r = 0 \ldots|\mathcal {SC}(G)|-1\). We have two cases to consider, the first one occurs when r≥h. In this case we can choose i in C(G h ) so that (i,k)∉E(G) (which is always possible because C(G h ) is maximal) and we can choose j in I(H h ) (which is always possible because of (13)), so, (j,l)∉E(H), because the two vertices are in the same IS. In the case r<h we can choose i in C(G r ) so that (i,k)∈E(G) (which is always possible by the definition of L(G r )) and we can choose j in I(H r ), so, (j,l)∈E(H). As F⊆F′ ⇒(…,0,1 ij ,…,0,…,1 kl ,0,…)∈F′ ⇒π ij +π kl =π 0. Therefore, from (1), we have π kl =0 ∀k∈L(G r ), l∈I(H h ), \(h, r = 0 \ldots \min(|\mathcal{SC}(G)|,|\mathcal{SI}(H)|)-1\).

(5) The fact proven here is that π kl =0 for any k∈L(G h ) and l∈L(H r ). The proof follows the same reasoning from the previous cases.

Let (…,0,1 ij ,…,0,…,1 kl ,0,…)∈F, where k∈L(G h ), l∈L(H r ), \(h, r = 0 \ldots|\mathcal {SC}(G)|-1\). We have two cases to consider, the first occurs when h≤r, in this case we can choose i in C(G h ) so that (i,k)∈E(G) (which is always possible, or else, k would be part of some clique in the sequence) and we can choose j in I(H h ) so that (j,l)∈E(H) (which is always possible because I(H h ) is maximal). In case h>r, we can choose j in I(H r ) so that (j,l)∉E(H) (which is always possible by the definition of L(G h )) and we can choose i in C(G r ) so that (i,k)∉E(G) (which is always possible because C(G r ) is maximal). As F⊆F′ ⇒(…,0,1 ij ,…,0,…,1 kl ,0,…)∈F′ ⇒π ij +π kl =π 0. Therefore, from (1), we have π kl =0 ∀k∈L(G h ), l∈L(H r ), \(h, r = 0 \ldots|\mathcal{SC}(G)|-1\).

(6) Here we prove that π kl =0 for any k∈C(G h ) and l∈R H. The ideas used in the proof are the same as before.

Let (…,0,1 ij ,…,0,…,1 kl ,0,…)∈F, where k∈C(G h ), \(h = 0 \ldots|\mathcal{SC}(G)|-1\), l∈R H. We can choose i in C(G h ), so, (i,k)∈E(G) and we can choose j in I(H h ), so, (j,l)∈E(H) (or else, l would be in I(H h ) or in L(H h )). As F⊆F′ ⇒(…,0,1 ij ,…,0,…,1 kl ,0,…)∈F′ ⇒π ij +π kl =π 0. Therefore, from (1), we have π kl =0 ∀k∈C(G h ), \(h = 0 \ldots|\mathcal {SC}(G)|-1\), l∈R H.

(7) This case proves that π kl =0 for any k∈L(G h ) and l∈R H. Once again the ideas used in the proof are very much alike the ones used in the previous cases.

Let (…,0,1 ij ,…,0,…,1 kl ,0,…)∈F, where k∈L(G h ), \(h = 0 \ldots|\mathcal{SC}(G)|-1\), l∈R H. We can choose i in C(G h ) so that (i,k)∈E(G) and we can choose j in I(H h ), so (j,l)∈E(H) (or else, l would be in I(H h ) or in L(H h )). As F⊆F′ ⇒(…,0,1 ij ,…,0,…,1 kl ,0,…)∈F′ ⇒π ij +π kl =π 0. Therefore, from (1), we have π kl =0 ∀k∈L(G h ), \(h = 0\ldots|\mathcal{SC}(G)|-1\), l∈R H. □

Now that we proved necessary conditions under which the SeqClique-SeqIS inequalities are valid and facet-defining, we comment on the strength of the Clique-IS inequalities. It is easily seen that whenever \(|\mathcal{SC}(G)| = 1\) or \(|\mathcal{SI}(H)| = 1\), (11) looks exactly the same as (10). This means that when there is only one clique or one IS with more than one vertex, the Clique-IS inequalities are also facet-defining. More accurately, it is possible to prove that Clique-IS inequalities are facet-defining if, and only if, for all k∈V(G)∖C, there exists in C a vertex adjacent to k; and, for all l∈V(H)∖I, there exists in I a vertex adjacent to l. Details of this proof can be found in Piva and de Souza (2011).

Conditions (12) and (13) are too stringent in the sense they force all cliques and independent sets in the sequences to have two or more vertices. A natural question arises when these sequences contain elements of size one. In this case, again, starting from the basic SeqClique-SeqIS inequality, one can perform lifting to get a stronger inequality that can be shown to be facet-defining. These new inequalities will be called LiftSeqClique-SeqIS and are displayed below:

(14)

where:

  • MC(G) is the set of vertices in the cliques of the sequence having size one in graph G.

  • MI(H) is the set of vertices in the ISs of the sequence having size one in graph H.

  • \(\mathit{mci}(G) = \{ k \in \Bbb {N}~:~k <min\{|\mathcal{SC}|,|\mathcal{SI}|\} \wedge|C(G_{k})| = 1\}\), i.e., the set of indexes in the sequence whose cliques have size one in graph G.

  • \(\mathit{mii}(H) = \{ k \in \Bbb {N}~:~k <min\{|\mathcal{SC}|,|\mathcal{SI}|\} \wedge|I(H_{k})| = 1\}\), i.e., the set of indexes in the sequence whose ISs have size one in graph H.

  • F(G r )⊆L(G r ), r∈mii(H). F(G r ) is maximal and satisfies the following properties:

    • ∀(u,v), u∈F(G r ), v∈C(G s ), (u,v)∉E(G), r∈H), \(s = r+1 \dots \min\{|\mathcal{SC}|,|\mathcal{SI}|\}-1\). In other words, the vertices in F(G r ) are not adjacent to any vertex in the cliques of the sequence in G with index greater than r;

    • ∀(u,v), u∈F(G r ), v∈F(G s ), r≠s, (u,v)∉E(G), r, s∈mii(H). In other words, the vertices in F(G r ) and F(G s ), for any distinct r and s, are non-adjacent (notice that nothing is imposed on the vertices in the same F(G r )); and

    • Is(R G) is a IS in R G such that ∀(u,v), u∈F(G r ), ∀r∈mii(H), v∈Is(R G), (u,v)∉E(G) and Is(R G) is maximal satisfying the previous properties. In other words, there is an IS in R G such that every vertex in F(G r ), for all r, is not adjacent to any vertex in this set. Besides, this set is maximal with respect to this last property.

  • F(H r )⊆L(H r ), r∈mci(G). F(H r ) is maximal and satisfies the following properties:

    • ∀(u,v), u∈F(H r ), v∈I(H s ), (u,v)∈E(H), r∈mci(G), \(s = r+1 \dots \min(|\mathcal{SC}|, |\mathcal{SI}|)-1\). In other words, the vertices in F(H r ) are adjacent to all vertices in the ISs of the sequence in H with index greater than r;

    • ∀(u,v), u∈F(H r ), v∈F(H s ), r≠s, (u,v)∈E(H), r, s∈mci(G). In other words, the vertices in F(H r ) and F(H s ), for any distinct r and s, are adjacent (notice that nothing is imposed on the vertices in the same F(H r )); and

    • Cl(R H) is a clique in R H such that ∀(u,v), u∈F(H r ), ∀r∈mci(G), v∈Cl(R H), (u,v)∈E(H) and Cl(R H) is maximal satisfying the previous properties. In other words, there is a clique in R H such that every vertex in F(H r ), for all r, is adjacent to all the vertices in this set. Besides, this set is maximal with respect to this last property.

The remaining sets and symbols are defined as before for (11).

Returning to Fig. 2, we now give an example of the inequality in (14). For G=A and H=B, one possible clique sequence for G is \(\mathcal{SC}(G) = (C(G_{0}) = \{a_{1}, a_{3}\}, L(G_{0}) = \{a_{2}, a_{4}\},C(G_{1}) = \{a_{5}\}, L(G_{1}) = \{\}, C(G_{2}) = \{a_{6}, a_{7}, a_{8}\},L(G_{2}) = \{a_{9}, a_{10}\},C(G_{3}) = \{a_{11}, a_{12}\},L(G_{3}) = \{\},C(G_{4}) = \{a_{13}\}, L(G_{4}) = \{\})\) and one possible IS sequence for H is the same as presented before. In that case, as \(\min\{|\mathcal{SC}(G)|, |\mathcal{SI}(H)|\} = |\mathcal{SC}(G)| = 5\), then, R H=H 5=I(H 5)∪L(H 5). It is not hard to see that with these sequences, the inequality of the form of (11) could be lifted to have coefficient one for the variables \(y_{a_{5}b_{20}}\), \(y_{a_{5}b_{23}}\), \(y_{a_{13}b_{17}}\), \(y_{a_{13}b_{20}}\) and \(y_{a_{13}b_{23}}\). This means that the original SeqClique-SeqIS inequality is not facet-defining and notice that, in this case, condition (12) does not hold. The proposed lifting is exactly the one appearing at (14) with MC(G)={a 5,a 13}, Cl(R H)={b 20,b 23}, F(H 4)={b 17} and the remaining sets empty. A formal proof that the inequalities (14) are valid and facet-defining is given in Piva and de Souza (2011).

When |MC(G)|=1, |MI(H)|=1, |MI(G)|=1 or |MC(H)|=1, the inequalities of the form of (14) are modified in such a way that the third and fourth terms of the sum are replaced, respectively, by:

(15)
(16)

The idea here is very much alike the one discussed for (7).

In addition to the inequalities presented in this section, it is possible to devise other valid inequalities for the MCIS polytope based on other graph structures such as odd-holes and odd-antiholes. However, the inequalities we found that are based on these structures are not facet-defining and, for this reason, are not discussed here. We just mention that, they can often be strengthened by lifting procedure which eventually leads to a facet. The interested reader is referred to Piva (2009) for more information.

5 The maximum clique problem

As said in Sect. 1, the MCIS is commonly solved through a reduction to the Maximum Clique problem, also referred here just as the Clique problem, or simply Clique when the meaning is clear from the context. In this section, we define the Clique problem and present a basic IP model for it. Then, this model is compared with the one given in Sect. 3 for the MCIS. We show that the two formulations are equivalent and that the inequalities presented in Sect. 4 correspond to some known inequalities for the Clique model.

The Clique problem can be defined as follows:

figure b

The rest of this section is organized as follows. In Sect. 5.1 an IP model is presented for the Clique problem. Next, in Sect. 5.2, we show how to reduce the MCIS to Clique. From this reduction, we establish the relationship between the inequalities we found for the MCIS model and those that are part of the Clique model, showing that the two formulations are in fact equivalent.

5.1 IP model

We start this section by recalling the well-known result that the set of vertices of clique in a graph forms an independent set in the complement graph. In the classical Maximum Independent Set problem, one is given a graph with weights assigned to the vertices and is asked to find an independent set for which the sum of the vertex weights is maximized. With these observations in mind, it is possible to formulate the Clique problem as an IP through simple modifications of an existing IP model for the Independent Set problem. This was the way we pursued here.

Integer programming formulations for the Maximum Independent set are discussed in Nemhauser and Sigismondi (1992). Here, we reproduce only the strongest of them, performing the necessary changes to it in order to model the Clique problem. Notice that, although the formulation presented in Nemhauser and Sigismondi (1992) treats the more general case in which the vertices are assigned to arbitrary weights, in our presentation all the vertex weights are assumed to be one since we are interested in cliques of maximum size. Finally, it is also worth noting that some other inequalities for the Maximum Independent Set problem and, as a consequence, for the Clique problem, can be found in Borndörfer (1997).

From Nemhauser and Sigismondi (1992), and according to the discussion above, a strong formulation for the Clique problem is given by:

(17)
(18)
(19)

In this model, for any i∈V(G), the binary variable y i has value one if and only if vertex i belongs to the maximum clique. With this definition, it is easy to see that the objective function seeks to maximize the clique size while the constraints avoid that two non-adjacent vertices of G to be present simultaneously in a feasible solution. Observe that an inequality of the form (18) is valid with respect to the set of characteristic vectors of cliques of G no matter the independent set I(G) is maximal or not. However, it is not hard to prove that it defines a facet for the convex hull of these vectors if and only if I(G) is maximal.

5.2 MCIS and the clique problem

It is well-known that any problem in \({\mathcal {NP}}\) can be reduced in polynomial time to a problem in \({\mathcal {NP}}\)-hard. Regarding the MCIS, this strategy is often used as an algorithmic strategy to solve it. In particular, the problem is reduced to Clique through the construction the association graph as described in the next paragraph.

Let G=(V(G),E(G)) and H=(V(H),E(H)) be the input graphs of an MCIS instance. From these two graphs, we define the association graph A=(V(A),E(A)) as follows. To each pair of vertices (i,j) in V(G)×V(H), we associate a vertex (ij) in A. Now, let i and k be two vertices in V(G) and, similarly, let j and l be two vertices in V(H). Then, and edge (ij,kl) is added to E(A) if one of the two conditions hold: (i) (i,k)∈E(G) and (j,l)∈E(H); or (ii) (i,k)∉E(G) and (j,l)∉E(H). Figure 3 shows two graphs and the corresponding association graph. Notice that each vertex in A refers to a possible mapping of a vertex in G to a vertex in H. Besides, an edge exists in A if the mappings corresponding to its extremities result either in the mapping of a non-edge of G to a non-edge in H or to the mapping of an edge of G to and edge of H. The proof that the solution of the Clique problem for the association graph immediately translates to a solution for the MCIS and, therefore, leads to a valid reduction between the two problems, is given in Edmonds (1975) apud (Garey and Johnson 1979).

Fig. 3
figure 3

Association graph constructed from two graphs. The dashed lines in the association graph represent edges associated to the mappings of pairs of non-adjacent vertices in the two graphs

Full size image

The IP model for the Clique problem defined over the association graph has |V(G)|×|V(H)| variables. Thus, we are working in a space of the same dimension as the one in the MCIS model. Moreover, from the construction of the association graph, the meaning of each variable in both cases is exactly the same, i.e., the binary variable y ij has value one if vertex i∈G is mapped to vertex j∈H. From this observation, it is easy to see that the two models are equivalent in the sense that they both have the same set of feasible solutions. A natural question then arises on how the known valid and facet defining inequalities for the Clique and the MCIS polytope relate to each other. The next two propositions provide a partial answer to this query.

Proposition 6

The set of inequalities obtained from (7) is a subset of the inequalities obtained from (18).

Proof

To prove that (7) defines a subset of (18), we need to show that any subgraph of the association graph obtained from the subgraphs defined by the variables with coefficient one in (7) is an IS.

Assume that the set of vertices in the association graph A corresponding to the variables with coefficient one in (7) is not an IS. Then, in this set there exist two vertices that are adjacent in A. Let us name these vertices (i,j) and (k,l) (remember that a vertex in the association graph is a pair of vertices that represents the mapping of the vertex in G to a vertex in H). So, by definition, the edge ((i,j),(k,l)) belongs to E(A). However, from the construction of the association graph, these vertices can only be adjacent if i and k are adjacent in G and j and l are adjacent in H or, if i and k are non-adjacent in G and j and l are non-adjacent in H. By the definition of the MCIS  in this situation, both variables y ij and y kl can take value one simultaneously. But then, this solution would not satisfy inequality (7) contradicting its validity. □

Notice that, as (7) is a lifting of (2), if the variables having coefficient one in (7) correspond to an IS in the association graph, the same holds for the analogous variables in (2). Hence, (2) is also an inequality of the form of (18).

Proposition 7

The set of inequalities obtained from (14) is a subset of the inequalities obtained from (18).

Proof

Using the same arguments used in the proof of Proposition  6, we can conclude that if the vertices of the association graph A corresponding to the variables having coefficient one in (14) do not form an IS, then (14) is not valid and we get a contradiction. □

As in the previous case, the inequalities in (14) are liftings of the inequalities in (11) and (10). So, the last two inequalities are also of the form of (18).

6 Computational results

In the previous sections we presented a theoretical study on an IP formulation for the MCIS and compare it to one that was proposed earlier for the Maximum Clique problem. In this section we show how these information were exploited to devise algorithms to solve the MCIS to optimality and report on computational experiments we carried out.

Algorithms tested

The inequalities found in the theoretical study were used to develop branch-and-bound (B&B) and branch-and-cut (B&C) algorithms for MCIS. In the B&B algorithms the inequalities were added a priori to the initial IP formulation whereas in the B&C algorithms they are generated by separation routines executed at each node of the enumeration tree. Also, we tried some other techniques such as multiway branching instead of the standard binary branching and changing the order in which the variables were chosen for branching.

None of the B&C algorithms we implemented were able to outperform the best B&B algorithm. In the former, the heuristic separation routines have been able to find violated inequalities. However, the improvement in the dual bounds obtained by adding the cuts did not compensate for the time spent by the separation routines. Also, the multiway branching strategy was ineffective relative to the binary branch.

Among the several algorithms we implemented with the various valid inequalities described in the previous section and the different branching techniques, the one that performed best was a B&B algorithm using a Clique-IS formulation and a branching strategy based on the mapping degree of the vertices. From now on, this algorithm is called the Clique-IS algorithm. The Clique-IS formulation given as input for this algorithm is obtained by substituting : (i) the inequalities in (4) by a small subset of inequalities in (10), and (ii) the inequalities in (5) by a small subset of inequalities of the form (10), but with the roles of the input graphs of the MCIS interchanged. For the correctness of the Clique-IS model, we first find a minimal set of maximal cliques (ISs) that form a covering of the edges (non-edges) of the respective graph of the MCIS instance. Then, we generate all the (10) inequalities (or their equivalents with the roles of the input graphs interchanged) corresponding to a pair of a maximal clique in one graph and a maximal IS in the other one.

To explain the branching strategy used in the Clique-IS algorithm we define the mapping degree of a vertex v belonging to an input graph of the MCIS instance as the sum of the degrees of the vertices of the association corresponding to mappings of v to the vertices of the other input graph. Once the mapping degrees had been computed, we start ordering the vertices by putting the vertex with smallest degree in the first free position of an order vector. This vertex is removed from its graph and the association graph is updated. These steps are repeated until every vertex has been ordered. After ordering the vertices of the two input graphs in this way, we order the variables according to the following procedure, in which it is assumed that |V(G)|≤|V(H)|. In the first position we put the variable corresponding to the mapping of the first vertex in G to the first vertex in H. Then, the variable corresponding to the mapping of the first vertex in G to the second vertex in H an so on, until the variables corresponding to all the mappings of the first vertex in G are ordered. Then, we take the mappings of the second vertex in G and the process is repeated until all the variables are ordered. This order gives a priority for branching, i.e., for a fractional solution, we inspect the variables in this order and branch on the first variable which is not integral.

We compared the results of the Clique-IS algorithm to those yielded by two other exact algorithms. To this end we implemented a B&B algorithm using the Clique formulation, named here the Clique algorithm, according to the material presented in Sect. 5.1. To generate the initial formulation passed to the algorithm, we built the association graph corresponding to the input graphs of the MCIS instance and found a minimal set of maximal ISs covering all its non-edges. As observed earlier, the inequalities in (18) associated to these minimal ISs constitute a correct formulation for Clique. The other exact algorithm used in our tests is the combinatorial algorithm implemented in the package Cliquer (Östergård 2002).

Benchmark

We now describe the instance set used in our tests. Initially, we randomly generated, according to Erdös-Rényi model, graphs with 10, 12, 15, 17 and 20 vertices in five density ranges: 10%, 30%, 50%, 70% and 90%. For each number of vertices and density range, two graphs were generated, in a total of 50 graphs. As the MCIS input has two graphs, every combination of pairs of graphs were used, resulting in a total of 1,225 test instances. The utilization of different density ranges aims to analyze which range is the hardest for the algorithms. For every test performed, a maximum of 1,800 seconds of computation was allowed.

Computational environment

The computational environment used in the experiments consisted in a computer with an Intel Core 2 Quad 2.40 GHz, 4096 KB cache, 4GB of RAM and Ubuntu 8.10 O.S. The programming language used in the implementation was C with a gcc (Ubuntu 4.3.2-1ubuntu12) 4.3.2 compiler and all the programs compiled with −O3 optimization flag. Besides, XPRESS-MP-Optimizer 64-bit v19.00.00 (xpressmp2008A.2) IP solver was used. The latter package contains special libraries to implement B&C, primal heuristics etc. The default XPRESS-MP cuts, heuristics and preprocessing were turned off.

Analysis of the results

In this work, we followed the recommendations in Johnson (2002) on how to perform computational experiments and to present the results. For this reason, in this text we chose not to include long tables containing experimental data individualized by instance. Instead, we condensed the results and displayed them as statistics and graphs. This was done mainly due to the huge amount of data collected during the experiments, hence, the presentation of all of them would be tedious and, in some aspects, of little or no significance. Concerning the execution times, it is worth noting that no draws occurred among the algorithms for any instance. Therefore, when we state, for example, that the execution times for Algorithm X were better than those for Algorithm Y in 23% of the cases, it is the same as saying that they were worse in 77% of the cases.

In the tests performed with Clique-IS algorithm 100% of the instances were solved to optimality in no more than 1,200 s and 91.51% of them were solved in 30 s or less. The time necessary to build the model and setup the solver was negligible when compared to the total time (less than 0.192 s for every instance). We observed that, for a fixed density of one of the input graphs, the hardest instances to solve were the ones where the other graph had density between 30% and 70%. Considering all the instances in the benchmark, the average distance between the dual bound at the root (DB root ) of the enumeration tree and the best dual bound (DB best ) throughout the execution of the algorithm—calculated by 100×(⌊DB root ⌋−⌊DB best ⌋)/⌊DB best ⌋—was 20.99%.

The Clique algorithm solved all instances in no more than 1,800 s, 99.92% in no more than 1,200 s and 82.20% were solved in 30 s or less. This does not seem much worse than the results obtained with the Clique-IS formulation. However, looking closer, we see that Clique-IS algorithm outperforms the Clique algorithm in 95.76% of the cases and the average time improvement (defined as 100×(tClique−tCliqueIS)/tClique, with tCliqueIS and tClique being, respectively, the times consumed by the Clique-IS and Clique algorithms) was of 60.98%. The inferior performance of the Clique algorithm can be explained by two facts. First, although the number of constraints in the Clique formulation is smaller than that of the Clique-IS formulation, the constraint matrix in the first model was denser in 86.94% of the cases. It is well-known that linear programs with denser constraint matrices tend to be harder to compute. The second fact concerns the inequalities used in the models. Notice that, by construction, all the inequalities in the Clique formulation are facet-defining since they correspond to maximal ISs. However, these ISs are built in an arbitrary way which did not exploit the fact that they are subgraphs of an association graph. On the other hand, the inequalities in the Clique-IS formulation are, in general, not facet-defining, since they can usually be lifted to obtain stronger valid inequalities of the form (14). Unexpectedly, we observed that, on average, the dual bound obtained at the root of the enumeration tree is 13% better in favor of the Clique-IS algorithm. The only reason we found to explain the superior performance of Clique-IS is that the ISs supporting the constraints in this model, although often not maximal, are among the most relevant ones for the MCIS problem. By relevance here, we mean that the inequalities supported by these ISs seem to be very effective in chopping off fractional solutions that are candidates to optimize the linear relaxations that are solved during the enumeration. This points to an advantage in the usage of a more focused view of MCIS in opposition to general treatments in which it is viewed as a Clique problem.

In Fig. 4 we show graphs comparing the execution times of the instances with the Clique-IS and Clique algorithms. The y axis corresponds to the time spent to solve the instances and the x axis represents the 1,225 instances of our benchmark represented by numerical indexes. The indexes were assigned to the instances by ordering them by number of vertices and by density of the first graph and by number of vertices and density of the second graph. So, the index 1 in the x axis corresponds to the instance where the first and second graphs have 10 vertices and 10% density; the index 2 corresponds to the instance in which the first graph has 10 vertices and 10% density and the second graph has 10 vertices and a 30% density, and so on. For better visualization, the graph was divided into six parts corresponding to segments of the x axis. The first part refers to the first 204 instances, the second to the next 204, and so on, until the sixth part which refers to the last 205 instances. It is noteworthy that although each graph is displayed as a continuous function, in reality, the x axis represents a discrete set. However, it was our understanding that showing in a discrete form would compromise the visualization. Note that the graph of the Clique-IS algorithm, which has a better performance, is shown with a continuous line whilst the one of the Clique algorithm is shown with a dashed line.

Fig. 4
figure 4

Comparison of the times of Clique-IS algorithm against Clique algorithm

Full size image

As we said before, we also compared our algorithm with a combinatorial algorithm named Cliquer. This combinatorial algorithm outperformed the Clique-IS algorithm in 99.67% of the instances, with an average improvement of 95.34%. To give an idea of the excellent performance reached by Cliquer in our benchmark, we mention here that the instance for which it spent more time was computed in 10.52 s. This is far quicker than the IP algorithms. As an example, in a test with an instance composed by two graphs randomly generated with 45 vertices each and approximately 50% density, Cliquer took 1,435.61 s to find the optimal solution, while Clique-IS algorithm could not solve it even after 12 hours of computation. Despite this, the study of IP algorithms for MCIS is still valuable since they are more adaptable than combinatorial algorithms. This is an important feature if, for example, one has to incorporate some side constraints to the original MCIS problem.

Additional experiments

As it is very common for algorithms to have very distinct behaviors with different kinds of instances, we executed further experiments to compare the Clique and Clique-IS formulations. For these tests we used a database of graphs for isomorphism benchmarking that is available in Foggia et al. (2001b). The database contains pairs of isomorphic graphs and pairs of graphs where one of them is a subgraph of the other with size corresponding to 20%, 40% and 60% of the size of the larger graph. The graphs are divided into five groups: random graphs, bounded (vertex) valence (or degree) graphs, 2D, 3D and 4D meshes. Each of these groups have subgroups, divided by valence number (in the case of bounded valence graphs), density (for the random graphs) and irregularity factors. For a full description of the database we refer to Foggia et al. (2001a).

As for the MCIS the input can be any two graphs, we arbitrarily chose to use the large graphs of the pairs where the other graph has 40% of the size of the larger one. Within each subgroup we chose graphs with sizes that are likely to result in MCIS instances solvable by the algorithms within in 1,800 seconds. In this way, for the bounded valence graphs we picked four graphs with 20 vertices and four with 40 vertices in each of the subgroups. For the 2D meshes we chose three graphs with 16 vertices, three with 32 and two with 64 vertices within each subgroup. From the 3D meshes subgroups we used four graphs with 27 vertices and two with 64 vertices. Within the 4D meshes subgroups we chose four graphs with 16 vertices and two with 81. We did not used any random graphs since they were already used in the experiments reported earlier in this section. After selecting the graphs we performed the experiments by using every pair of graphs within the same subgroup as input for the MCIS algorithms.

Some of these new instances are significantly bigger than the ones tested in our early experiments. For this reason, both algorithms were unable to solve all of them to optimality within the time limit. In this case we say that the instance is unsolved. For such an instance, we consider as being more effective the algorithm that produces the best dual bound.

Analyzing each of the subgroups of instances individually, we notice that the Clique-IS formulation outperforms the Clique formulation in all but four subgroups. For the instances obtained from regular bounded valence graphs with valence 6, the Clique formulation is better in 23 out of the 28 experiments with an average improvement of 8.47%. With respect to the unsolved instances in the modified bounded valence graphs with valences 6 and 9, the Clique-IS algorithm presented a better dual bounds in all 22 cases and in 21 out of the 22 cases, respectively. On the other hand, the Clique algorithm was faster in the 6 cases solved to optimality with an average time improvement of 2.98% for the valence 6 inputs. As for valence 9, it was also faster in all the cases solved to optimality and in one case where there was a gap with an average improvement of 5.88% in time. For the regular bounded valence graph instances with valence 9, this last situation is reversed. The Clique algorithm presents a better dual bound in all instances with some gap (17) and the Clique-IS algorithm presents a better time in all instances with no gap (11), having an average time improvement of 17.87%.

For all the other (14) instance subgroups the Clique-IS algorithm outperformed the Clique algorithm. For this reason, we decided not to analyze each subgroup separately. Instead, we present overall statistics and a graph of the computation times with the instances ordered by the graphs sizes as described before. Relative to computation times, the Clique-IS algorithm shows an average improvement of 23.45% in comparison to the Clique algorithm. Figure 5 exhibits graphs comparing the execution times of the Clique-IS and Clique algorithms for the instances from Foggia et al. (2001b). The y axis corresponds to the time spent to solve the instances and the x axis represents the 400 instances ordered in a similar fashion as in Fig. 4. Once again, for a better visualization, the graph was divided into six parts corresponding to segments of the x axis. The first part corresponds to the first 70 instances, the second to the next 70 and so on, up to sixth part which corresponds to the last 50 instances. The graph of the Clique-IS algorithm, which has a better performance, is shown with a continuous line whilst the one of the Clique algorithm is shown with a dashed line. The inspection of these graphs confirm the superior performance of the Clique-IS algorithm.

Fig. 5
figure 5

Comparison of the times of Clique-IS algorithm against Clique algorithm using the Graph Database instances (Foggia et al. 2001b)

Full size image

Now, we focus on the dual bounds generated at the root node of the enumeration tree by the two competing formulations. Once again, the Clique-IS formulation showed an average dual bound improvement of 5.15% when compared to the Clique formulation. Together with the considerations relative to computation times, these results reinforce our conclusion from the first group of experiments that it is advantageous to use a formulation directly based in the MCIS instead of a formulation constructed from a reduction to the Clique problem.

7 Conclusions

In the theoretical study about the MCIS polytope, we found several valid inequalities and identified necessary conditions for which they define facets. Moreover, we proved the equivalence of a formulation for MCIS and a formulation for the Maximum Clique problem. However, although the unique and edge mapping inequalities, and their generalization, from the MCIS formulation correspond to IS inequalities in the Clique formulation, they have a more natural interpretation in the MCIS model.

Besides, computational experiments comparing the Clique-IS algorithm with the Clique algorithm showed that, although the inequalities for both problems belong to the same class, choosing the inequalities to build the MCIS formulation produces better results than using arbitrary IS constraints. This was somehow unexpected since it is known that an IS inequality is facet-defining for the Clique polytope if and only if the IS is maximal, and we showed that, in general, the support graph of a Clique-IS inequality is not maximal. Our explanation for what occurred is that, not only the Clique-IS inequalities have a more natural interpretation in terms of the MCIS, but they also lead to inequalities which are more likely to be active in an optimal solution than other IS inequalities chosen arbitrarily.

On the other hand, comparisons of the best IP based algorithm with Cliquer, a combinatorial algorithm of public domain, showed that the latter is much more effective for the tested instances. Further polyhedral investigations on the MCIS polytope are required to improve the competitiveness of the IP algorithms. One possible approach in this direction is to encounter the complete convex hull corresponding to small instances of the MCIS, identifying the inequalities that are active in the optimal solution. The computation of convex hulls can be done with the help of computer programs like PORTA (Löebel 2010), for example. Another way of finding good inequalities for the MCIS is to take advantage of the equivalence shown in Sect. 5 between the MCIS and the Clique problem. For this purpose, we could specialize the polyhedral investigation of the Maximum Clique problem constrained to instances having the peculiar characteristics of the association graphs resulting from MCIS instances. In particular, we should focus on graphs having |V(G)|×|V(H)| vertices and that are, at the same time, |V(G)|-partite and |V(H)|-partite, where G and H are the MCIS input graphs.

It is important to remember that, despite the better performance of the combinatorial algorithm, the result of our investigation remain useful even when the MCIS appears as a part of a more complex problem. This situation occurs, for example, if one has to tackle a problem which is the MCIS with some side constraints. In this case, it may be very hard to adapt the Cliquer algorithm to solve the new problem. Besides, even if this can be done, this may affect badly its performance. This is a motivation to pursue the polyhedral investigation of the MCIS polytope to extend the results presented in this paper.