1 Introduction

Laminated composites have been increasingly used in the aeronautics and astronautics industry over the past few decades owing to their high performance-weight ratio and admirable design flexibility. However, poor through-thickness properties and low delamination resistance have limited their applications in the primary loading-bearing components. As a kind of new lightweight textile composites, 3D braided composites are believed to have broad applications as the primary loading-bearing structures in the aerospace industry because of their excellent integrated mechanical properties over laminated composites. Currently, because of the lack of comprehensive knowledge of mechanical behavior of 3D braided composites under complex stress states, composite structures are always over-safely designed, leading to the fact that their advantages of weight reduction and high load-bearing capacity have never been maximized. For the effective and improved safety-relevant design, a better understanding of their mechanical response under multi-axial loading cases is essential.

In physical experiments, multi-axial stress states of composite material are generally produced by off-axis specimens under tension/compression loading, cruciform specimens under biaxial loading and tube specimens under tension/compression-torsion loading [1]. Owing to the intrinsic anisotropy of composite material, an inherent multi-axial stress state can be obtained under uniaxial off-axis loading condition, which is termed as local multiaxiality. On the other hand, global multiaxiality happens when external loadings are imposed along different directions, as that in cruciform or tube specimens [2]. It should be noted that the loading ratio in off-axis specimen is pre-determined under uniaxial loading at a given off-axis angle while various biaxial loading ratios can be generated in cruciform specimen by changing the ratios of external loadings. Recently, off-axis and cruciform specimens are extensively used by researchers and designers to study multi-axial mechanical behavior of laminated composites and textile composites [3,4,5,6,7,8,9,10].

It is well-known that physical experiments are often expensive, time-consuming, and restrained to certain test conditions. Nowadays, with the development of FEA technique and commercial finite element (FE) software, considerable insights can be achieved by using numerical virtual experiments. Since the textile composites have good structural periodicity and are considered to be constructed by repeating unit-cells, the unit-cell based meso-scale FE model is commonly established to simulate the mechanical behavior of textile composites under multi-axial loading conditions. Zhou et al. [11] proposed a progressive damage analysis model to study the damage and failure behavior of 2D plain weave composites under various uniaxial and biaxial loadings. Lu et al. [12] evaluated the on-axis and off-axis tensile strength of 2.5D woven composites by a multi-scale damage analysis approach. Zhang et al. [13] studied the strength characteristics of 3D 5-directional braided composites subjected to uniaxial and biaxial loading through a combination of experiment investigation and meso-scale FE modeling. Wang et al. [14] implemented the damage models of braiding yarn and matrix in the meso-scale numerical simulation to reproduce the damage modes of 3D 4-directional braided composites observed in experiment. By this simulation, numerous failure points of the braided composites under biaxial loadings with different stress ratios were obtained.

3D braided composites own complicated microstructure and exhibit complex failure behavior under external loadings, which bring in great difficulties in the strength prediction and damage mechanism analysis. To date, the existing meso-scale FEA works are always focused on their mechanical behavior under uniaxial on-axial loadings [15,16,17,18,19,20,21] while those under other loading conditions are extremely limited. However, 3D braided composites are intended to design for primary loading-bearing structures in engineering applications and they are frequently subjected to multi-axial loading conditions during service. Therefore, it is of great value to propose a meso-scale damage analysis model to characterize failure behavior and predict strength properties of 3D braided composites under such loading cases.

The primary objective of this paper is to develop a unit-cell based FE model for assessment and investigation of mechanical behavior of 3D braided composites subjected to different biaxial tension loadings with distinct stress ratios. The damage initiation and evolution of braiding yarns and matrix in the unit-cell are numerically predicted by proposing an anisotropic damage model in terms of Murakami damage theory with Hashin failure criteria and maximum stress criteria. The present anisotropic damage model is subsequently implemented in the numerical simulation. In addition, the force loading mode of periodic boundary conditions which never been attempted before is first employed in the meso-scale FEA, which aims to attain exact stress ratio under biaxial tension loadings. We focus on numerical interpretation of biaxial mechanical properties of 3D braided composites under such aforementioned loading cases. The present study would provide a new reference for studying the multi-axial mechanical behavior of other textile composites by meso-scale FEA.

2 Unit-Cell Based Progressive Damage Model

In this section, a unit-cell based progressive damage model is described, which integrates stress analysis, failure analysis and material property degradation scheme. Stress analysis involves appropriate constitutive relations of constituents in the unit-cell model. Failure analysis requires proper damage initiation criteria able to identify main failure modes of composite material. Besides, a suitable damage evolution model is necessary to degrade the material property after damage initiation.

2.1 Damage Initiation Criteria

In this work, the unit-cell model of 3D braided composites consisting of braiding yarns and resin matrix is considered. 3D Hashin failure criteria and maximum stress criteria are selected to determine the damage initiation of braiding yarns and matrix. For ease of reference, the expressions of four distinct failure modes in Hashin criteria are repeated as follows [22]:

Yarn tensile failure in L direction (σL ≥ 0)

$$ {\varphi}_{Lt}={\left(\frac{\sigma_L}{F_L^t}\right)}^2+\alpha {\left(\frac{\sigma_{LT}}{S_{LT}}\right)}^2+\alpha {\left(\frac{\sigma_{LZ}}{S_{LZ}}\right)}^2\ge 1 $$
(1)

Yarn compressive failure in L direction (σL < 0)

$$ {\varphi}_{Lc}={\left(\frac{\sigma_L}{F_L^c}\right)}^2\ge 1 $$
(2)

Yarn tensile and shear failure in T and Z direction (σT + σZ ≥ 0)

$$ {\varphi}_{T\left(\mathrm{Z}\right)t}={\left(\frac{\sigma_T+{\sigma}_Z}{F_T^t}\right)}^2+\left(\frac{1}{S_{TZ}^2}\right)\left({\sigma}_{TZ}^2-{\sigma}_T{\sigma}_Z\right)+{\left(\frac{\sigma_{LT}}{S_{LT}}\right)}^2+{\left(\frac{\sigma_{LZ}}{S_{LZ}}\right)}^2\ge 1 $$
(3)

Yarn compressive and shear failure in T and Z direction (σT + σZ < 0)

$$ {\varphi}_{T\left(\mathrm{Z}\right)c}={\left(\frac{\sigma_T+{\sigma}_Z}{2{S}_{TZ}}\right)}^2+\left(\frac{\sigma_T+{\sigma}_Z}{F_T^c}\right)\left[{\left(\frac{F_T^c}{2{S}_{TZ}}\right)}^2-1\right]+\frac{1}{S_{TZ}^2}\left({\sigma}_{TZ}^2-{\sigma}_T{\sigma}_Z\right)+{\left(\frac{\sigma_{LT}}{S_{LT}}\right)}^2+{\left(\frac{\sigma_{LZ}}{S_{LZ}}\right)}^2\ge 1 $$
(4)

In the above equations, \( {F}_L^t \) and \( {F}_L^c \) are the longitudinal tensile and compressive strengths of braiding yarn; \( {F}_T^t \) and \( {F}_T^c \) are the transverse tensile and compressive strengths; SLT, SLZ and STZ are the LT, LZ and TZ shear strengths, respectively; α is the contribution coefficient of shear stresses on yarn L tensile failure, and α is set as 0.5 here. L-T-Z is the local coordinate definition of braiding yarn, and L, T and Z axis represent the longitudinal and two transverse directions.

2.2 Damage Evolution Model

Once the damage initiation criteria are reached, a damage evolution model is necessary to degrade the stiffness properties of the composite material. In this simulation, a gradual degradation scheme proposed by Lapczyk et al. [23] and Fang et al. [15] is introduced to characterize the damage evolution process of braiding yarns and matrix.

Considering the irreversibility of damage, the evolution of damage variables corresponding to distinct damage modes are defined by

$$ {d}_{\mathrm{I}}=\max \left\{{d}_{\mathrm{I}},\frac{\delta_{\mathrm{I}, eq}^f\left({\delta}_{\mathrm{I}, eq}-{\delta}_{\mathrm{I}, eq}^0\right)}{\delta_{\mathrm{I}, eq}\left({\delta}_{\mathrm{I}, eq}^f-{\delta}_{\mathrm{I}, eq}^0\right)}\right\}\kern1.3em \left(\mathrm{I}= Lt, Lc, Tt, Tc, Zt, Zc, Mt, Mc\right) $$
(5)

where \( {\delta}_{\mathrm{I}, eq}^0 \) and \( {\delta}_{\mathrm{I}, eq}^f \) are the initial and complete failure equivalent displacements for a certain failure mode, and they can be computed by

$$ {\delta}_{\mathrm{I}, eq}^0={\delta}_{\mathrm{I}, eq}/\sqrt{\varphi_{\mathrm{I}}} $$
(6)
$$ {\delta}_{\mathrm{I}, eq}^f=2{G}_{\mathrm{I}}/\left({\sigma}_{\mathrm{I}, eq}/\sqrt{\varphi_{\mathrm{I}}}\right) $$
(7)

In Eqs. (5–7), φΙ is the value of damage initiation criterion and GΙ is the fracture energy density; δΙ, eq and σΙ, eq are the equivalent displacement and equivalent stress related to a certain failure mode, and they are expressed by

$$ {\delta}_{\mathrm{I}, eq}=l\sqrt{\varepsilon_{ii}^2+{\alpha}_{\mathrm{I}}\sum \limits_{j=1,j\ne i}^3{\varepsilon}_{ij}^2}\kern0.5em \left(i=1,2,3\right) $$
(8)
$$ {\sigma}_{\mathrm{I}, eq}=l\left(\left\langle {\sigma}_{ii}\right\rangle \left\langle {\varepsilon}_{ii}\right\rangle +\sum \limits_{j=1,j\ne i}^3{\sigma}_{ij}{\varepsilon}_{ij}\right)/{\delta}_{\mathrm{I}, eq}\kern0.5em \left(i=1,2,3\right) $$
(9)

where l is the characteristic length of element.

2.3 Damage Constitutive Model

Murakami damage model [24] is adopted to describe the damage of constituents in the unit-cell. Three principal damage variables are used to represent the damage state, namely

$$ D=\sum \limits_i{D}_i{n}_i\otimes {n}_i\kern0.5em \left(i=L,T,Z\right) $$
(10)

where Di and ni are the principal value and principle unit vector of the damage tensor.

For the damaged composite material, the effective stress is defined as

$$ {\sigma}^{\ast }=\frac{1}{2}\left[{\left(I-D\right)}^{-1}\sigma +\sigma {\left(I-D\right)}^{-1}\right]=M(D)\sigma $$
(11)

Here σ∗ is symmetric and M(D) is a transformation matrix.

The energy identification is implemented in order to involve the damage variable into stiffness matrix as

$$ C(D)={M}^{-1}(D):{C}_0:{M}^{T,-1}(D) $$
(12)

where C(D) and C0 are the damaged and undamaged stiffness tensor.

The damaged stiffness matrix, which is the function of the undamaged stiffness constants and the principal values of damage tensor, can be expressed more explicitly as [25].

$$ C(D)=\left\{\begin{array}{cccccc}{b}_L^2{C}_{11}& 0& 0& 0& 0& 0\\ {}{b}_L{b}_T{C}_{12}& {b}_T^2{C}_{22}& 0& 0& 0& 0\\ {}{b}_L{b}_Z{C}_{13}& {b}_T{b}_Z{C}_{23}& {b}_Z^2{C}_{33}& 0& 0& 0\\ {}& & & {b}_{TZ}{C}_{44}& 0& 0\\ {}& \operatorname{sym}& & & {b}_{ZL}{C}_{55}& 0\\ {}& & & & & {b}_{LT}{C}_{66}\end{array}\right\} $$
(13)

In the above equation,

$$ {\displaystyle \begin{array}{l}{b}_L=1-{D}_L,\kern0.5em {b}_T=1-{D}_T,\kern0.5em {b}_Z=1-{D}_Z,\\ {}\begin{array}{lll}{b}_{TZ}={\left(\frac{2{b}_T{b}_Z}{b_T+{b}_Z}\right)}^2,& {b}_{ZL}={\left(\frac{2{b}_Z{b}_L}{b_Z+{b}_L}\right)}^2,& {b}_{LT}={\left(\frac{2{b}_L{b}_T}{b_L+{b}_T}\right)}^2\end{array}\end{array}} $$

Cij, is the component of undamaged stiffness tensor.

For braiding yarn, the principal damage variables in L, T, and Z direction are determined by

$$ {D}_L=\left\{\begin{array}{c}{d}_{Lt}\kern0.5em \left({\sigma}_{11}\ge 0\right)\\ {}\begin{array}{cc}{d}_{Lc}& \left({\sigma}_{11}<0\right)\end{array}\end{array}\right. $$
(14)
$$ {D}_T=\left\{\begin{array}{c}{d}_{Tt}\kern0.5em \left({\sigma}_{22}\ge 0\right)\\ {}\begin{array}{cc}{d}_{Tc}& \left({\sigma}_{22}<0\right)\end{array}\end{array}\right. $$
(15)
$$ {D}_Z=\left\{\begin{array}{c}{d}_{Zt}\kern0.5em \left({\sigma}_{33}\ge 0\right)\\ {}\begin{array}{cc}{d}_{Zc}& \left({\sigma}_{33}<0\right)\end{array}\end{array}\right. $$
(16)

For matrix, it is regarded as isotropic material and the damage variables are determined by

$$ {D}_M={D}_L={D}_T={D}_Z=\max \left({d}_{Mt},{d}_{Mc}\right) $$
(17)

3 Finite Element Modeling Strategies

3.1 Meso-Scale Finite Element Model and Periodic Boundary Conditions

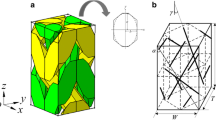
Based on the microscopic image analysis results [26], Xu and Xu [27] established an accurate unit-cell structural model of 3D braided composites, which is employed here to conduct the meso-scale FEA. As displayed in Fig. 1(a), an octagon containing an inscribed ellipse is assumed to approximate the cross-section shape of the braiding yarns. For the major radius a and minor radius b of the ellipse, one has

$$ a=\sqrt{3}b\cos \gamma $$
(18)

where γ is the interior braiding angle and it can be obtained by the braiding angle α on the surface of composite specimen, namely

$$ \tan \gamma =\sqrt{2}\tan \alpha $$
(19)
Fig. 1
figure 1

Meso-scale finite element model of 3D braided composites (a) Unit-cell structural model (b) Corresponding finite element mesh

Full size image

According to geometry relations, the width W, thickness T and height h of the unit-cell model can be determined by

$$ W=T=4\sqrt{2}b $$
(20)
$$ h=8b/\tan \gamma $$
(21)

In this simulation, two specimens with typical braiding angles are selected for FEA and their structural parameters of the unit-cell models are given in Table 1. Even the meso-scale FEA is based on a single unit-cell model, it does not mean that this single unit-cell is isolated from its neighboring unit-cells in the composite structure. The boundary effects from the neighboring unit-cells, that is, the displacement and traction continuity conditions, should be ensured at the opposite boundaries of the unit-cells. Thus, the periodic boundary conditions [28,29,30] should be employed and taken into account in the meso-scale FEA, and periodic mesh should be generated at the unit-cell opposite boundaries in the meshing process. Actually, because of the complicated microstructure of 3D braided composites, periodic mesh generation is one of the main difficulties to implement meso-scale FEA. In this paper, considering the excellent geometry adaptability, solid tetrahedral element (C3D4) is particularly used to mesh the unit-cell model, as depicted in Fig. 1(b).

Table 1 Structural parameters of unit-cell models of the specimens
Full size table

Force control is normally implemented to perform multi-axial loading physical experiments to attain exact stress ratios, while the displacement loading mode is always adopted in the current numerical simulations. In fact, either displacement or force can be used as the applied loading when employing periodic boundary conditions in the unit-cell based simulation subjected to any uniaxial or muti-axial loading cases. The feasibility and effectiveness of the force loading mode in the meso-scale FEA will be examined in the following section. The application of periodic boundary conditions to the unit-cell model is given in detail in our previous work [30].

3.2 Material Properties of Constituents and Unit-Cell Homogenization

The reinforcement architecture can be well reflected in the meso-scale unit-cell model. The braiding yarn regularly consisting of thousands of fibers is considered as a transversely isotropic material; the resin matrix is modeled as an isotropic material. The braiding yarns in different directions are intertwined such as to form the spatial reinforcement architecture and embedded into the resin matrix. The material properties of the constituents directly influence the homogenized macroscopic mechanical behavior of 3D braided composites, as given in Table 2. The stiffness and strength properties of braiding yarns used in the simulation are calculated using Chamis micromechanics formulae [31]. In addition, in order to facilitate the local material coordinate definition of braiding yarns in different directions, the yarns with the same direction are united into the same element set.

Table 2 Material properties of the constituents
Full size table

In the meso-scale FEA, the macroscopic mechanical properties of the composite material can be computed by a proper unit-cell homogenization technique. Based on the small deformation assumption, the constitutive relation of a unit-cell can be expressed as

$$ {\overline{\sigma}}_{ij}={E}_{ij kl}{\overline{\varepsilon}}_{kl} $$
(22)

where Eijkl is the effective stiffness matrix. The average stresses \( {\overline{\sigma}}_{ij} \) and average strains \( {\overline{\varepsilon}}_{kl} \) of the unit-cell can be obtained by homogenization, namely

$$ {\overline{\sigma}}_{ij}=\frac{1}{V}\underset{V}{\int }{\sigma}_{ij} dV,\kern0.5em {\overline{\varepsilon}}_{kl}=\frac{1}{V}\underset{V}{\int }{\varepsilon}_{kl} dV $$
(23)

where V is the volume of the unit-cell.

3.3 Numerical Analysis Process

In order to conduct the meso-scale FEA, the proposed progressive damage model is coded and implemented by a user-material subroutine UMAT based on ABAQUS/Standard platform. Figure 2 schematically describes the flow chart of the entire numerical analysis process, which contains stress analysis, failure analysis and material property degradation. During each loading increment, the stress analysis and failure analysis are performed at each Gauss integration point of the elements. Once a failure criterion is triggered, material stiffness properties degradation is carried out by updating the damage variables corresponding to the failure modes. The numerical analysis continues until the final loading increment is reached.

Fig. 2
figure 2

Flow chart of numerical analysis process

Full size image

4 Numerical Results and Discussions

4.1 Prediction of Elastic Properties

To predict the tensile modulus of 3D braided composites in x, y and z direction, three uniaxial loading cases are needed to be employed. It is well reported in the literature, e.g., see [32,33,34,35], that accurate elastic properties results can be predicted with the displacement loading mode. Therefore, first, the displacement loadings, \( {\overline{\varepsilon}}_x^0=0.1\% \), \( {\overline{\varepsilon}}_y^0=0.1\% \) and \( {\overline{\varepsilon}}_z^0=0.1\% \) are applied separately, and the elastic properties and reaction forces can be taken from the computation. Then, these obtained reaction forces are implemented as the concentrated forces to the unit-cell models again to attain the elastic properties with force loading mode. By comparison, it is found that the predicted elastic properties, including the stiffness constants, deformation states and stress distributions, of the unit-cell models with displacement and force loading modes are precisely identical in small deformation conditions. To get the exact stress ratios, force loading modes are thus selected for predicting the elastic properties of 3D braided composites under biaxial tension loadings.

The predicted tensile moduli of unit-cells under different loading cases are provided in Table 3. Under biaxial tension, the deformation in the two directions is mutually restricted, so that the deformation resistance ability of the material is improved to some extent and the tensile moduli are both increased. For x-y biaxial tension, with the decrease of stress ratio (σx: σy), the tensile modulus Ex increases significantly and Ey decreases. When the stress ratio was reduced to a certain level, the strain in x direction would become negative due to the Poisson effect. For x-z biaxial tension, the variation trend of tensile moduli is similar to that under x-y biaxial tension. Figure 3 illustrates the stress distributions on the deformed shape of unit-cell models under corresponding uniaxial and biaxial force loading cases (the deformation scale factor is 150). Attributable to the spatial rotation characteristics of 3D braided composites, the deformation and stress distribution of the unit-cell model under x and y tension are similar [34] thus only the numerical results under x tension are presented in this work. Obviously, the deformation states and stress fields correctly reflect the related loading features and continuity conditions of the applied periodic boundary conditions.

Table 3 Predicted tensile moduli of unit-cells under different loading cases
Full size table
Fig. 3
figure 3

Stress distributions on the deformed shape of unit-cell models under corresponding loading cases (a) 4DS1 (b) 4DS2

Full size image

4.2 Prediction of Stress-Strain Curves

4.2.1 Uniaxial Loading Cases

For the available works on strength properties prediction and damage mechanism analysis of 3D braided composites under uniaxial or biaxial loading, only the displacement loading is used in the meso-scale FEA [13,14,15,16,17,18,19,20,21]. However, it is generally impossible to achieve exact stress ratios with biaxial displacement loadings. Herein, first, the stress-strain curves of unit-cell models of the two specimens under uniaxial tension with displacement and force loading modes are predicted for the comparison study, as sketched in Fig. 4. It can be found that the predicted stress-strain curves consistent with each other with displacement and force loading mode in the loading stage. After the peak stress, the curves with displacement loading decrease suddenly or gradually according to the loading direction and specimen type. On the other hand, an obvious turning point appears on the curves with force loading and the curves become very gentle after the turning point. Actually, the carbon-fiber 3D braided composites always express brittle breaking characteristics under tension loadings thus the extended stage of stress-strain curve after the peak stress or turning point appears in numerical simulation will not take place in physical experiment. Accordingly, the numerical artifact stage can be ignored and the force loading mode is effective to predict the strength properties and damage mechanism of 3D braided composites.

Fig. 4
figure 4

Predicted stress-strain curves of unit-cell models under x and z uniaxial tension (a) 4DS1 (b) 4DS2

Full size image

4.2.2 Biaxial Loading Cases

The force loading mode is first adopted in the current biaxial tension loading cases and thus the stress ratios can remain constant throughout the entire simulation process. Figure 5 and Fig. 6 display the predicted stress-strain curves of the two specimens under biaxial tension loadings with different stress ratios. It can be found that the stress-strain curves show good linearity in the loading stage and present a little non-linearity when reaching the turning points. As shown in Fig. 5(a) and Fig. 6(a), when σx: σy = 1:1, the curves are completely coincident, indicating that the composite material has the same properties in these two directions. When σx: σy = 1:2, the failure strain in x direction is much smaller than that in y direction. The larger tensile loading in y direction causes an apparent increase of tensile modulus in x direction, as shown in Figs. 5(b) and 6(b). For specimen 4DS1 with a small braiding angle, the tensile modulus in z direction is much larger than that in x direction. The stress-strain curves in x and z direction have evident difference under x-z biaxial tension loading, as given in Fig. 5(c, d). The strain in z direction has a decreasing trend after the turning point, especially when σx: σy = 1:2. Since the force loading cannot be reduced in the simulation process and the strain in x direction after the turning point is relatively large, Poisson effect will cause the strain shrinkage trend in z direction. For specimen 4DS2 with a large braiding angle, the difference of tensile modulus in x and z direction is not such significant. As seen Fig. 6(c, d), the decreasing trend of strain in z direction after the turning point also exists when σx: σz = 1:1, however, it disappears when σx: σz = 1:2.

Fig. 5
figure 5

Predicted stress-strain curves of specimen 4DS1 under different biaxial tension loadings (a) σx: σy = 1:1 (b) σx: σy = 1:2 (c) σx: σz = 1:2 (d) σx: σz = 1:4

Full size image
Fig. 6
figure 6

Predicted stress-strain curves of specimen 4DS2 under different biaxial tension loadings (a) σx: σy = 1:1 (b) σx: σy = 1:2 (c) σx: σz = 1:1 (b) σx: σz = 1:2

Full size image

In this simulation, no peak stress appears on the predicted stress-strain curves with force loading mode. The strength is defined as the related stress of turning point on the stress-strain curves since it is considered as the maximum stress when the extended artificial stage is neglected. Table 4 summarizes the predicted tensile strengths of unit-cells under different force loading cases. Under x-y biaxial tension, the strengths are identical and lower than uniaxial strength when σx: σy = 1:1. The strength in x direction decreases while that in y direction increases when the stress ratio changes to 1:2, but both of the strengths are lower than uniaxial strength. Under x-z biaxial tension, with these determined stress ratios, the strength in one direction exceeds the corresponding uniaxial strength. Such phenomena were also reported in Ref. [13, 14] even biaxial displacement loadings were used in their simulation. It is clear that the uniaxial stiffness and strength in x and y direction are identical while those in z direction are much larger. The large difference of mechanical properties in these two directions may contribute to these phenomena. That is also the reason why the interaction coefficients between the two normal failure stresses should be considered strictly in this case to establish a reasonable strength criterion. In addition, from Table 4, it can also be found that under biaxial loadings, the predicted strength ratios are not equal to the corresponding applied stress ratios, which is in agreement with the experimental observation [4, 5]. However, for the failure point of composite material, it is determined by the stress of the turning point in one direction which is reached earlier in the simulation, and the stress in another direction can be computed with the stress ratio. For example, (44.00, 88.00) is regarded as a failure point of specimen 4DS2 under biaxial tension loading with σx: σy = 1:2.

Table 4 Predicted tensile strength of unit-cells under different loading cases
Full size table

4.3 Analysis of Damage Evolution and Failure Mechanisms

The damage evolution process and associated failure mechanisms, which are difficult to be observed and determined by physical experiment, can be simulated and analyzed conveniently by meso-scale FEA. Once the damage initiates, the stiffness reduction is governed by the damage evolution model. That is, the damage variables related to distinct failure modes keep evolving from 0 to 1 irreversibly, and the stiffness properties of the corresponding elements degrade accordingly until complete failure. Herein, the damage evolutions on the unit-cells of specimen 4DS1 under biaxial tension loadings with σx: σy = 1:1 and σx: σz = 1:4, and specimen 4DS2 under biaxial tension loadings with σx: σy = 1:2 and σx: σz = 1:1 are selected to analyze, as illustrated in Figs. 7, 8, 9, and 10. It is noticed that the stress concentration is always serious in the yarn/yarn contact zones, and thus damage initiation usually happens in these zones. In order to clearly demonstrate the damage distribution in the braiding yarns, only the braiding yarns in one-direction are given here.

Fig. 7
figure 7

Damage evolution of specimen 4DS1 under biaxial tension with σx: σy = 1:1 (a) Yarn T tensile shear failure (b) Yarn Z tensile shear failure

Full size image
Fig. 8
figure 8

Damage evolution of specimen 4DS1 under biaxial tension with σx: σz = 1:4 (a) Yarn T tensile shear failure (b) Yarn Z tensile shear failure (c) Matrix cracking

Full size image
Fig. 9
figure 9

Damage evolution of specimen 4DS2 under biaxial tension with σx: σy = 1:2 (a) Yarn T tensile shear failure (b) Matrix cracking

Full size image
Fig. 10
figure 10

Damage evolution of specimen 4DS2 under biaxial tension with σx: σz = 1:1 (a) Yarn T tensile shear failure (b) Yarn Z tensile shear failure (c) Matrix cracking

Full size image

For specimen 4DS1, under x-y biaxial tension with σx: σy = 1:1, the main failure modes are yarn T and Z tensile shear failure, which are similar to that under x uniaxial loading. Yarn L failure, T and Z compressive shear failure do not exist before the occurrence of turning point. When the stress-strain curve reaching near the turning point, matrix cracking appears in some matrix elements but the quantity is limited. As displayed in Fig. 7(a), yarn T tensile shear failure starts in the braiding yarns when σx = 46.08 Mpa, and propagates around the yarn/yarn contact zones discretely. The propagation speed accelerates after σx = 51.84 Mpa, and at the turning point, that is σx = 56.32 Mpa, the number of damaged elements is relatively large. After that, this failure mode spreads suddenly even with a little increasing of applied loading. Seen from Fig. 7(b), Z tensile shear failure occurs comparatively late. The propagation speed is slow and the number of damaged elements is relatively small in the simulation.

The main failure modes are yarn T tensile and compressive shear failure, yarn Z tensile shear failure and matrix cracking for specimen 4DS1 under x-z biaxial tension with σx: σz = 1:4, which are completely different to that under x or z uniaxial loading. Before the occurrence of turning point, yarn L failure does not emerge and the number of Z compressive shear failure is relatively small. As shown in Fig. 8(a), yarn T tensile shear failure occurs first in the yarn/yarn contact zones when σx = 93.60 Mpa and propagates mainly along the transverse direction of the braiding yarn. The propagation speed is steady at the beginning and increases gradually with the increasing of applied loading. From Fig. 8(b), the development trend of Z tensile shear failure is basically similar as that of T tensile shear failure except for the earlier appearance and more serious damage state. Matrix cracking appears comparatively late in the intersecting edges of the braiding yarns and matrix and propagates quickly along the fiber axial direction in these intersection regions, resulting in large numbers of damaged elements, as given in Fig. 8(c).

For specimen 4DS2, under x-y biaxial tension with σx: σy = 1:2, the main failure modes are yarn T and Z tensile shear failure and matrix cracking, which are also similar to that under x uniaxial loading. Yarn L failure and T compressive shear failure do not exist while Z compressive shear failure only emerges in some elements before reaching the turning point. When σx = 31.20 Mpa, yarn T tensile shear failure occurs first in the yarn/yarn contact zones and propagates quickly along the fiber axial and transverse directions simultaneously, as presented in Fig. 9(a). After σx = 44.00 Mpa, the damage state is rather serious with large number of damaged elements. Matrix cracking appears first in the intersecting edges of the braiding yarns and matrix when σx = 42.80 Mpa and propagates with a steady speed in these intersection regions, as shown in Fig. 9(b).

The main failure modes are yarn T and Z tensile shear failure and matrix cracking for specimen 4DS2 under x-z biaxial tension with σx: σz = 1:1, which are also different to that under x or z uniaxial loading. The development trend of yarn T and Z compressive shear failure is similar, and the failure elements are limited before reaching the turning point. Yarn L tensile failure exists in some elements, which can be attributed to the relatively larger shear stress components under x-z biaxial tension. As displayed in Fig. 10(a, b), with the increase of the applied biaxial loading, yarn T and Z tensile shear failure propagates progressively in the yarn/yarn contact zones and the propagation speed increases gradually. As can be observed in Fig. 10(c), matrix cracking initiates in the intersecting edges when σx = 123.00 Mpa. It appears quite late but propagates rapidly in the intersection regions. This is interesting and due to the fact that matrix cracking happens later than yarn damage modes (especially some yarn L tensile breaking) and in this condition, resin matrix will bear greater amount of further external loadings.

5 Conclusions

This paper has outlined the development of an accurate approach based on the meso-scale FEA for assessment of mechanical behavior of 3D braided composites. The fact is that in many engineering applications, 3D braided composites are frequently subjected to multi-axial loading conditions during service. However, their mechanical behavior, especially the strength and failure mechanisms under such loading cases have not yet been well understood. In this study, a unit-cell based progressive damage model is derived and implemented in the meso-scale FEA to evaluate the mechanical behavior of 3D braided composites under different biaxial tension loadings. The stress distribution, tensile modulus, ultimate strength, failure response and other aspects are computed and analyzed in detail. Some major conclusions drawn from the study are summarized as follows:

  • In meso-scale FEA, to attain exact stress ratios of external loadings, the force loading mode of periodic boundary conditions should be employed to the unit-cell model subjected to multi-axial loading cases.

  • Under biaxial tension, the deformation in the two loading directions is mutually restricted. Therefore, the deformation resistance ability of the material is improved and the tensile moduli are both increased. When the stress ratio σx: σy or σx: σz decreases, the larger tensile loading in y or z direction causes a significant increase of tensile modulus Ex while Ey or Ez decreases. However, the biaxial tensile modulus always larger than uniaxial tensile modulus.

  • For the biaxial strength properties, under x-y biaxial tension, the biaxial loading has a weakening effect on the tensile strength in both directions. Under x-z biaxial tension, the strength in one direction exceeds the corresponding uniaxial strength. It may be attributed to the large difference of material properties associated to these two directions. Therefore, the interaction coefficients between the two normal failure stresses should be considered strictly in this case to establish a reasonable strength criterion.

  • Under x-y biaxial tension, the main failure modes of 3D braided composites are yarn T and Z tensile shear failure and matrix cracking, which are similar to the observed under x uniaxial loading. However, under x-z biaxial tension, the main failure modes are yarn T and Z tensile shear failure and matrix cracking, which are quite different to that under x or z uniaxial loading. Yarn T and Z compressive shear failure also exist but the failure elements are relatively few before reaching the turning point. Largely, the mechanical properties and failure modes of the composite material subjected to the biaxial tensile loadings are determined by the components of the fiber yarns parallel to the loading directions.

  • The present meso-scale finite element model is able to predict the mechanical properties and analyze the damage mechanism of 3D braided composites under biaxial tension loadings and this numerical model is naturally general. It might be an appropriate new reference for future investigations on the mechanical behavior of other textile composites under multi-axial loadings by meso-scale FEA.