Stress field distribution of warp-reinforced 2.5D woven composites using an idealized meso-scale voxel-based model

Abstract

The evaluation of the stress field distribution of warp-reinforced 2.5D woven composites using meso-scale voxel-based model is described. The idealized geometry model is established by using measured parameters from the CT image. Comparison between voxel-based finite element method and experimental measurements is included. The results show that the proposed meso-scale voxel-based method is capable of accurately predicting the mechanical properties of warp-reinforced 2.5D woven composites, validated by the comparison of the initial modulus, max stress as well as the failure modes. Also, the numbers of representative volume element have an important effect on mechanical behaviors of warp-reinforced 2.5D woven composites.

Introduction

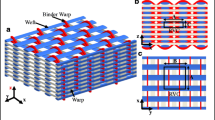
Angle-interlock (2.5D) woven fabric as reinforcement in polymeric composites continues to expand [1, 2]. The ability to manufacture such materials is highly influenced by the flexibility of the reinforcement (as shown in Fig. 1), and their mechanical properties depend largely on the details of the architectures. As such, the obtained representative volume cells (RVCs) are quite unique, and the resin zones between yarns are highly irregular and complex. Many finite element models exist which describe these RVCs using a large number of tetrahedral elements; however, it is difficult to guarantee the mesh quality [3]. Further, models which predict the stiffness and strength properties of textile composites are sensitive to the assumed mesh type. In these cases, it is necessary to develop a more simpler, universal and reasonable mesh generating method.

Figure 1

Structural evolution characteristics of angle-interlock (2.5D) preform

As reviewed in the previous references, meso-scale finite element analysis with an RVC is the main method for simulating the mechanical properties, such as stiffness, strength and damage initiation/evolution [4,5,6,7]. The early representative model seems to largely belong to Cox’s binary model [8]. Subsequently, based on the Cox’s binary model, the independent mesh method (IMM) [9] and the domain superposition methods (DST) [10] are proposed. Doubtlessly, it may provide a way to analyze the mechanical behavior of large-scale components. However, these early representations suffered from an inability to simplify the structural details, and thus, less accurate results are predicted. Also, these models are difficult to express the local mechanical behaviors and the full-field strain characteristics.

Recently, meso-scale finite element solid model has been gaining popularity with the rapid development of CAD and CAE software. For instance, Mahadik Y et al. [11] developed a finite element model in terms of the multi-element digital chain technique. Lu et al. [12] evaluated the stress–strain and progressive damage behaviors of 2.5D woven composites subjected to uniaxial tension loading. Song et al. [13] predicted the tensile and compressive progressive damage process of 2.5D woven composites. Unfortunately, current meso-scale finite element solid method is not robust enough to ensure the establishment of the geometrical model and the discrete mesh generation. As is the case for calculation, the required memory and run-time are also enormous.

In order to overcome the above difficulties, some regular mesh generating methods have been proposed for textile composites. One of these methods, widely used in the advanced numerical formulations, is voxel meshing [14, 15]. This method is quite straightforward to generate meshes of any complex architectures, including 2D braided [16], 3D braided [17], 2D woven [18] and 3D woven [19]. Also, several authors used voxel meshes to simulate the damage initiation and evolution of woven composites. For instance, Doitrand et al. [18] evaluated the mechanical behaviors of 2D plain woven composites using voxel and consistent meso-scale models. Fang et al. [3] proposed the stress averaging technique to smooth artificial stress concentrations of voxel-based textile composites. These studies, however, are limited to extend to the simulation of warp-reinforced 2.5D structure. Hence, the understanding of the structure–property relationships as well as the progressive damage behavior of warp-reinforced 2.5D composite is not presented adequately.

The present work is aimed at establishing an idealized meso-scale voxel-based model to calculate the stress field distribution of warp-reinforced 2.5D woven composites. The detailed outline of the work is as follows. First, the microstructure of warp-reinforced 2.5D woven composites is derived in “Microstructure” section. Next, meso-scale voxel-based finite element model is proposed in “Meso-scale voxel-based finite element model” section. Subsequently, the mechanical theory is described in “Mechanical theory” section. The experimental details, including the composite specimen preparation and the test process, are presented in “Experimental details” section. Then, the predicted results are shown and compared with the experimental ones in “Results and discussion” section. Finally, some valuable conclusions are summarized in “Conclusions” section.

Microstructure

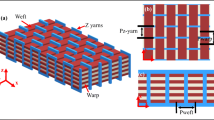
The weave style considered in this paper is a type of 2.5D woven reinforcement: warp-reinforced 2.5D structure (see Fig. 2). The warp and weft are oriented along the x-direction and y-direction, respectively. The binder warp interlocks with the weft layers through the thickness (z-direction). Also, the warp and binder warp arrange alternately with a certain ratio of 1:1 along the x-direction. In this structure, warp remains straight to the maximal degree so as to make the composite achieve higher in-plane mechanical properties. The architecture of the undeformed composite is periodic in warp, weft and thickness directions. The representative volume cell (RVC) is marked with black box in Fig. 2, as well as its basic dimensions: $A$, $B$ and $C$ The structural parameters as manufacturer-specified parameters of preform are the number of layers ($n$), the warp density ($P_{\text{warp}}$), the weft density ($P_{\text{weft}}$), the binder warp density ($P_{\text{blinder}}$), the warp fineness (${\text{Tex}}_{\text{warp}}$), the weft fineness (${\text{Tex}}_{\text{weft}}$) and the binder warp fineness (${\text{Tex}}_{\text{blinder}}$). These values are summarized in Table 1.

Figure 2

Schematic diagram of warp-reinforced 2.5D woven composite and definition of RVC

Table 1 The detailed manufacturing parameters of the considered preform

Then, the carbon/epoxy composite specimens are produced by using the process of resin transfer molding (RTM), as shown in Fig. 3. The mechanical properties of carbon fiber and epoxy resin are summarized in Table 2 [20, 21].

Figure 3

The process of the resin transfer molding

Table 2 Mechanical parameters of constituents

For all the textile composites, there exist several structural levels from yarns to preform and eventually to the composite. In each level, there are many uncertainly geometry variables which significantly influences the final composite behaviors. Therefore, basic assumptions regarding the shape of the yarn cross section and the yarn path are required. In this paper, on the basis of the microscopic CT image analysis (Fig. 4a), the following assumptions are provided.

Figure 4

Detailed structural information of warp-reinforced 2.5D woven composites: a real yarn cross sections, b ideal shapes of blinder warp, c ideal shape of warp and weft

• 1. The path of binder warp is divided into two parts: curve segment and line segment (see Fig. 4b). Note that the curve segment keeps intimate contact with weft.

• 2. The cross section of weft yarn is convex lens, whereas that of both warp and binder warp is rectangular, as shown in Fig. 4c.

• 3. The path of both warp and weft is straightened.

The dimension of a RVC is calculated as

$$ A = 2 \times \frac{10}{{P_{{{\text{wef}}t}} }},\,B = 2 \times \frac{10}{{P_{\text{warp}} }} = 2 \times \frac{10}{{P_{\text{binder}} }},\,C = T_{\text{warp}} + 2b $$

(1)

where $T_{\text{warp}} \,\left( {\text{mm}} \right)$ is the thickness of single warp. $b\,\left( {\text{mm}} \right)$ is the minor semi-axis length of weft.

According to Fig. 4b, the geometrical relationship is given by

$$ \begin{aligned} l_{c} = \left( {r + \frac{{T_{\text{warp}} }}{2}} \right) \times \theta_{1} ,\,a = r \times { \sin }\theta_{1} ,b = r - r \times { \cos }\theta_{1} ,S_{\text{weft}} = 4 \times r^{2} \times \theta_{1} - 2\left( {r - b} \right) \times a, \hfill \\ l_{d} \times { \cos }\theta_{2} = \frac{A}{2} - a - \left( {r + T_{\text{warp}} } \right) \times { \sin }\theta_{1} ,l_{d} \times { \sin }\theta_{2} = 4b + T_{\text{warp}} \hfill \\ \end{aligned} $$

(2)

where $a\,\left( {\text{mm}} \right)$ is the major semi-axis length of weft. The value of $\frac{a}{b}$ is measured in terms of the actual observation and here is equal to 4. $r$ is the drawing radius of the convex lens. $\theta_{1}$ is the angle of the curve segment of weft. $\theta_{2}$ is the dip angle of the linear segment of weft. $l_{c} \,\left( {\text{mm}} \right)$ and $l_{d} \,\left( {\text{mm}} \right)$ are the length of the curve and linear segments, respectively. $S_{\text{weft}} \,\left( {\text{mm}} \right)$ is the cross-sectional area of weft.

The geometrical parameters of yarns are then expressed by

$$ \begin{aligned} &S_{\text{warp}} = \frac{{Tex_{\text{warp}} }}{{\delta_{\text{warp}} \times \rho }},S_{\text{weft}} = \frac{{{\text{Tex}}_{\text{weft}} }}{{\delta_{\text{weft}} \times \rho }},S_{\text{binder}} = \frac{{{\text{Tex}}_{\text{binder}} }}{{\delta_{\text{binder}} \times \rho }}, \hfill \\ &T_{\text{warp}} = \frac{{S_{\text{warp}} }}{{W_{\text{warp}} }},T_{\text{binder}} = \frac{{S_{\text{binder}} }}{{W_{\text{binder}} }} \hfill \\ \end{aligned} $$

(3)

where $S_{\text{warp}} \,\left( {\text{mm}} \right)$ and $S_{\text{blinder}} \,\left( {\text{mm}} \right)$ are the cross-sectional areas of warp and binder warp, respectively. ${\text{Tex}}_{\text{warp}} \left( {\text{tex}} \right)$, ${\text{Tex}}_{\text{weft}} \left( {\text{tex}} \right)$ and ${\text{Tex}}_{\text{binder}} ({\text{tex}})$ are the warp, weft and binder warp finenesses, respectively. $\rho \,\left( {{\text{g}}/{\text{cm}}^{3} } \right)$ is the density of carbon fiber, $\rho = 1.78\;{\text{g}}/{\text{cm}}^{3}$. $\delta_{\text{warp}}$, $\delta_{\text{weft}}$ and $\delta_{\text{binder}}$ are the fiber volume fractions of warp, weft and binder warp, respectively. Here, it should be noted that the cross-sectional shapes of warp and binder warp are rectangular, $\delta_{\text{warp}} = \delta_{\text{binder}} = 0.785$. The cross-sectional shape of weft is nearly circular, $\delta_{\text{weft}} = 0.75$ [22]. $T_{\text{binder}} \,({\text{mm}})$ is the thickness of single binder warp, which is equal to $T_{\text{warp}}$. $W_{\text{warp}}$ and $W_{\text{binder}}$ are the width of warp and binder warp, respectively.

By calculation, the corresponding geometrical parameters are summarized in Table 3. Also, a careful statistical analysis based on the CT image (Fig. 5) is carried out for a comparison between experimental data and predicted result.

Table 3 Geometrical parameters of RVC of warp-reinforced 2.5D woven composites

Figure 5

Digital images of different cross sections obtained by CT

Meso-scale voxel-based finite element model

Warp-reinforced 2.5D woven composites RVC are divided into a lot of regular 3D grid of voxels to study the effective mechanical properties. In this study, RVC voxel meshes are generated using TexGen software. The advantages of this methodology are (1) generating quickly and automatically voxel meshes; (2) assigning automatically the material properties; and (3) providing the periodic mesh at the boundaries. A voxel mesh schematic view of yarns and matrix is shown in Fig. 6. However, a general problem of the voxel mesh is that the non-orthogonal interfaces appear stepped in nature. This phenomenon cannot be avoided, but its influence can be effectively reduced by refining the voxel mesh size. When the mesh sizes are enough small, the computational time and cost increase greatly. Hence, the mesh convergence study is crucial.

Figure 6

Meso-scale voxel-based RVC of warp-reinforced 2.5D woven composites: a yarns, b matrix

Undoubtedly, the fiber volume fraction has a first-order effect on the mechanical properties of the composites. Besides, Grail et al. [23] reported that the maximum edge length of the voxel mesh element is a key parameter which influences the final mechanical behaviors, whereas the shorter edge is used only where it is needed to precisely remodel the geometry shape. In order to eliminate this factor, the cubic voxel is used in most existing studies [24]. In this way, the mesh size depends only on the length of the voxel edge. Usually, the number of voxel mesh ($N_{\text{total}}$) made of the linear hexahedral element is given by

$$ N_{\text{total}} = n_{x} \times n_{y} \times n_{z} $$

(4)

The different edge lengths are then calculated as

$$ L_{x} = \frac{A}{{n_{x} }},L_{y} = \frac{B}{{n_{y} }},L_{z} = \frac{C}{{n_{z} }} $$

(5)

where $n_{x}$, $n_{y}$ and $n_{z}$ are the numbers of the meso-scale voxel mesh along the direction of warp, weft and thickness, respectively. $L_{x}$, $L_{y}$ and $L_{z}$ are the edge length of the meso-scale voxel mesh along the direction of warp, weft and thickness, respectively. In this paper, the three alternative edge values of $n_{x}$ and $n_{z}$ are selected, whereas the values of $n_{y}$ remain constant, as shown in Fig. 7. It should be seen that the increase in value of $n_{z}$ is chosen, independently, resulting in a flatter voxel mesh. The fiber volume fractions of the three models are summarized in Table 4. Note that a finer discretization shows an accurate value related to the yarn volume fraction. This study is presented in the part of results and discussion.

Figure 7

Meso-scale voxel-based model with different voxel sizes

Table 4 Fiber volume fraction of varying voxel mesh models

Moreover, the definition of the materials orientation of the element is crucial, especially for binder warp. Figure 8 illustrates the material orientation of binder warp. Clearly, the geometrical characteristics of RVC are sufficiently described. More importantly, RVC is not isolated from its adjacent RVC in the composites. Thus, in the present work, the applied periodic boundary conditions are carried out to ensure the continuity of displacements on the opposite faces of RVC. For the voxel meshes, applying the periodic boundary condition is more straightforward and easy. The detailed constraint equations of RVC are described in Refs [25, 26].

Figure 8

Illustration of local orientation of binder warp in voxel-based model

In the existing studies, the mechanical properties of woven composites are usually predicted by 1 RVC. In this study, the finite element models with different numbers of RVCs subjected to axial (warp) and transverse (weft) loadings are discussed, as shown in Fig. 9.

Figure 9

Longitudinal (warp) tensile (a) and transverse (weft) tensile (b) with different RVC numbers

Mechanical theory

Materials properties of matrix-impregnated fiber bundles

For the RVC of warp-reinforced 2.5D woven composites, all the yarns are thought to be the matrix-impregnated fiber bundles, which are assumed to be transversely isotropic. For the matrix-impregnated fiber bundles (see Fig. 10), the stress increments in the constituent fiber and matrix are correlated by the bridging matrix as follows [27]:

$$ \left\{ {{\text{d}}\sigma_{i}^{m} } \right\} = \left[ {A_{ij} } \right]\left\{ {{\text{d}}\sigma_{j}^{f} } \right\} $$

(6)

where

$$ \left\{ {{\text{d}}\sigma_{i}^{{}} } \right\} = \left\{ {{\text{d}}\sigma_{11} ,{\text{d}}\sigma_{22} ,{\text{d}}\sigma_{33} ,{\text{d}}\sigma_{23} ,{\text{d}}\sigma_{12} ,{\text{d}}\sigma_{13} } \right\}^{\text{T}} $$

(7)

$\left\{ {{\text{d}}\sigma_{i}^{m} } \right\}$ and $\left\{ {{\text{d}}\sigma_{i}^{f} } \right\}$ represent the matrix and fiber stress increments, respectively. $\left[ {A_{ij} } \right]$ is the bridging matrix, which is expressed by:

$$ \left[ {A_{ij} } \right] = \left[ {\begin{array}{*{20}c} {a_{11} } & {a_{12} } & {a_{13} } & 0 & 0 & 0 \\ {a_{21} } & {a_{22} } & {a_{23} } & 0 & 0 & 0 \\ {a_{31} } & {a_{32} } & {a_{33} } & 0 & 0 & 0 \\ 0 & 0 & 0 & {a_{44} } & 0 & 0 \\ 0 & 0 & 0 & 0 & {a_{55} } & 0 \\ 0 & 0 & 0 & 0 & 0 & {a_{66} } \\ \end{array} } \right] $$

(8)

where

$$ \left\{ \begin{aligned} &a_{11} = {{E^{\text{m}} } \mathord{\left/ {\vphantom {{E^{\text{m}} } {E_{11}^{\text{f}} }}} \right. \kern-0pt} {E_{11}^{\text{f}} }} \hfill \\ &a_{12} = a_{13} = {{\left( {S_{12}^{\text{f}} - S_{12}^{\text{m}} } \right)\left( {a_{11} - a_{22} } \right)} \mathord{\left/ {\vphantom {{\left( {S_{12}^{\text{f}} - S_{12}^{\text{m}} } \right)\left( {a_{11} - a_{22} } \right)} {\left( {S_{11}^{\text{f}} - S_{11}^{\text{m}} } \right)}}} \right. \kern-0pt} {\left( {S_{11}^{\text{f}} - S_{11}^{\text{m}} } \right)}} \hfill \\ &a_{21} = a_{31} = a_{23} = a_{32} = 0 \hfill \\ &a_{22} = a_{33} = {1 \mathord{\left/ {\vphantom {1 {2\left( {1 + {{E^{\text{m}} } \mathord{\left/ {\vphantom {{E^{\text{m}} } {E_{22}^{\text{f}} }}} \right. \kern-0pt} {E_{22}^{\text{f}} }}} \right)}}} \right. \kern-0pt} {2\left( {1 + {{E^{\text{m}} } \mathord{\left/ {\vphantom {{E^{\text{m}} } {E_{22}^{\text{f}} }}} \right. \kern-0pt} {E_{22}^{\text{f}} }}} \right)}} \hfill \\ &a_{44} = {1 \mathord{\left/ {\vphantom {1 {2\left( {1 + {{G^{\text{m}} } \mathord{\left/ {\vphantom {{G^{\text{m}} } {G_{23}^{\text{f}} }}} \right. \kern-0pt} {G_{23}^{\text{f}} }}} \right)}}} \right. \kern-0pt} {2\left( {1 + {{G^{\text{m}} } \mathord{\left/ {\vphantom {{G^{\text{m}} } {G_{23}^{\text{f}} }}} \right. \kern-0pt} {G_{23}^{\text{f}} }}} \right)}} \hfill \\ &a_{55} = a_{66} = {1 \mathord{\left/ {\vphantom {1 {2\left( {1 + {{G^{\text{m}} } \mathord{\left/ {\vphantom {{G^{\text{m}} } {G_{12}^{\text{f}} }}} \right. \kern-0pt} {G_{12}^{\text{f}} }}} \right)}}} \right. \kern-0pt} {2\left( {1 + {{G^{\text{m}} } \mathord{\left/ {\vphantom {{G^{\text{m}} } {G_{12}^{\text{f}} }}} \right. \kern-0pt} {G_{12}^{\text{f}} }}} \right)}} \hfill \\ \end{aligned}\right. $$

(9)

Figure 10

The schematic of a strand yarn

In the above formulas, $E^{\text{m}}$ and $G^{\text{m}}$ are the elastic and shear modulus of matrix, respectively. $E_{11}^{\text{f}}$ and $E_{22}^{\text{f}}$ are the longitudinal and transverse elastic modulus of fiber, respectively. $G_{12}^{\text{f}}$ and $G_{23}^{\text{f}}$ are the longitudinal and transverse shear modulus of fiber, respectively.

When the bridge matrix is given, the compliance matrix of the matrix-impregnated fiber bundles is defined as follows:

$$ \left[ {S_{ij} } \right]_{n} = \left( {\delta_{\text{f}} \left[ {S_{ij}^{\text{f}} } \right] + \delta_{\text{m}} \left[ {S_{ij}^{\text{f}} } \right]\left[ {A_{ij} } \right]} \right)\left( {\delta_{\text{f}} \left[ I \right] + \delta_{\text{m}} \left[ {A_{ij} } \right]} \right)^{ - 1} $$

(10)

where $\left[ {S_{ij}^{\text{f}} } \right]$ and $\left[ {S_{ij}^{\text{m}} } \right]$ represent the fiber and matrix compliance matrices, respectively. $\left[ I \right]$ is a unit matrix. $\delta_{f}$ and $\delta_{\text{m}}$ are the fiber and matrix volume fraction, respectively. And the relation is $\delta_{\text{f}} + \delta_{\text{m}} = 1$.

Furthermore, the relation between the compliance matrix and the engineering constants of the matrix-impregnated fiber bundles is given by

$$ \left[ S \right] = \left[ {\begin{array}{*{20}c} {\frac{1}{{E_{L} }}} & { - \frac{{\nu_{LT} }}{{E_{T} }}} & { - \frac{{\nu_{LZ} }}{{E_{Z} }}} & 0 & 0 & 0 \\ { - \frac{{\nu_{LT} }}{{E_{L} }}} & {\frac{1}{{E_{T} }}} & { - \frac{{\nu_{TZ} }}{{E_{Z} }}} & 0 & 0 & 0 \\ { - \frac{{\nu_{LZ} }}{{E_{L} }}} & { - \frac{{\nu_{TZ} }}{{E_{T} }}} & {\frac{1}{{E_{Z} }}} & 0 & 0 & 0 \\ 0 & 0 & 0 & {\frac{1}{{G_{TZ} }}} & 0 & 0 \\ 0 & 0 & 0 & 0 & {\frac{1}{{G_{LT} }}} & 0 \\ 0 & 0 & 0 & 0 & 0 & {\frac{1}{{G_{LZ} }}} \\ \end{array} } \right] $$

(11)

Also, the strength values of the matrix-impregnated fiber bundles are obtained by [28, 29]:

$$ F_{L}^{t} \approx X_{lt}^{f} V_{f} $$

(12)

$$ F_{L}^{c} \approx X_{lc}^{f} V_{f} $$

(13)

$$ F_{T}^{t} = \frac{{1 + V_{f} \left( {{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {\eta_{y} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\eta_{y} }$}} - 1} \right)}}{{K_{mt} }}X_{lt}^{m} $$

(14)

$$ F_{T}^{c} = \left( {3\sim7} \right)F_{T}^{t} $$

(15)

$$ S = \frac{{1 + V_{f} \left( {{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {\eta_{s} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\eta_{s} }$}} - 1} \right)}}{{K_{ms} }}S^{m} $$

(16)

In the above equations,

$F_{L}^{t}$ and $F_{T}^{t}$ are the longitudinal and transverse directional tensile strengths of the matrix-impregnated fiber bundles, respectively.

$F_{L}^{c}$ and $F_{T}^{c}$ are the longitudinal and transverse directional compression strengths of the matrix-impregnated fiber bundles, respectively.

$\eta_{y}$ and $\eta_{s}$ are empirical coefficients.

$K_{mt}$ and $K_{ms}$ are the tensile and shear stress concentration coefficients of matrix, respectively.

$S^{m}$ is the shear strength of matrix.

By calculation, the mechanical properties of the matrix-impregnated fiber bundles are listed in Table 5.

Table 5 Mechanical properties of matrix-impregnated fiber bundles

Progressive damage model

Usually, the failure mechanisms of 2.5D woven composites mainly include three different types, namely the yarn breaking, matrix cracking and interface debonding [30]. In this paper, the different damage modes including yarns’ longitudinal failure (L direction as shown in Fig. 10), yarns’ transverse failure (T, Z directions as shown in Fig. 10), yarns’ shear failure (LT, LZ and TZ directions) and matrix cracking are considered. The interface between yarns and matrix is assumed to be excellent, and the interface debonding is ignored. 3D Hashin failure criterion [31] and maximum stress criterion are employed to define the damage initiation of yarns and matrix, respectively. The corresponding initiation criteria relating to different damage modes are expressed as follows:

Yarn tensile failure in L direction ($\sigma_{L} \ge 0$):

$$ \delta_{fL}^{t} = \left( {\frac{{\sigma_{L} }}{{F_{L}^{t} }}} \right)^{2} +\, \beta \left( {\frac{{\sigma_{LT} }}{{S_{LT} }}} \right)^{2} + \,\beta \left( {\frac{{\sigma_{ZL} }}{{S_{ZL} }}} \right) \ge 1 $$

(17)

Yarn compression failure in L direction ($\sigma_{L} < 0$):

$$ \delta_{fL}^{c} = \left( {\frac{{\sigma_{L} }}{{F_{L}^{c} }}} \right)^{2} \ge 1 $$

(18)

Yarn tensile and shear failure in T and Z directions ($\sigma_{T} + \sigma_{Z} \ge 0$):

$$ \delta_{fT(Z)}^{t} = \left( {\frac{{\sigma_{L} + \sigma_{Z} }}{{F_{T}^{t} }}} \right)^{2} + \frac{{\left( {\sigma_{TZ}^{2} - \sigma_{L} \sigma_{Z} } \right)}}{{(S_{TZ} )^{2} }} + \left( {\frac{{\sigma_{LT} }}{{S_{LT} }}} \right)^{2} + \left( {\frac{{\sigma_{ZL} }}{{S_{LZ} }}} \right)^{2} \ge 1 $$

(19)

Yarn compression and shear failure in T and Z directions ($\sigma_{T} + \sigma_{Z} < 0$):

$$ \begin{aligned} \delta_{fT(Z)}^{t} & = \frac{1}{{F_{T}^{c} }}\left( {\left( {\frac{{F_{T}^{c} }}{{2S_{TZ} }}} \right)^{2} - 1} \right)(\sigma_{T} + \sigma_{Z} ) + \frac{{\left( {\sigma_{T} + \sigma_{Z} } \right)^{2} }}{{(2S_{TZ} )}} + \frac{{\left( {\sigma_{TZ}^{2} - \sigma_{T} \sigma_{Z} } \right)}}{{(S_{TZ} )^{2} }} \\ & \quad + \left( {\frac{{\sigma_{LT} }}{{S_{LT} }}} \right)^{2} + \left( {\frac{{\sigma_{ZL} }}{{S_{LZ} }}} \right)^{2} \ge 1 \\ \end{aligned} $$

(20)

In the above equations,

S _LT , S _LZ and $S_{TZ}$ are LT, LZ and TZ shear strengths of yarns, respectively.

β is the contribution factor in each failure mode.

Matrix tensile failure criterion ($\sigma_{\text{m}}^{\text{t}} \ge 0$):

$$ \delta_{\text{m}}^{\text{t}} = \left( {\frac{{\sigma_{\text{m}}^{\text{t}} }}{{F_{\text{m}}^{\text{t}} }}} \right)^{2} \ge 1 $$

(21)

Matrix compression failure criterion ($\sigma_{\text{m}}^{\text{c}} < 0$):

$$ \delta_{\text{m}}^{\text{c}} = \left( {\frac{{\sigma_{\text{m}}^{\text{c}} }}{{F_{\text{m}}^{\text{c}} }}} \right)^{2} \ge 1 $$

(22)

where $F_{\text{m}}^{\text{t}}$ and $F_{\text{m}}^{\text{c}}$ are the tensile and compression strength of matrix, respectively. $\sigma_{\text{m}}^{\text{t}}$ and $\sigma_{\text{m}}^{\text{c}}$ are the max tensile and compression stress of matrix, respectively.

When the damage initiation of yarns/matrix is reached, the damage development will follow the damage evolution law. Note that the damage variables d _I (L, T, Z) are introduced to define the damage modes of L, T and Z directions for yarns and matrix. When the constituents of woven composites fail, the element dissipated energy equals its elastic energy.

$$ \frac{1}{2}\varepsilon_{I,f} \sigma_{I,f} l^{3} = G_{l} l^{2} $$

(23)

where $l$ is the characteristic length of the element. $\sigma_{I,f}$, $\varepsilon_{I,f}$ and $G_{I}$ are the equivalent peak stress, failure equivalent strain and facture energy density of failure mode I, respectively. Moreover, each damage mode can be described by its corresponding equivalent displacement and stress, which are listed in Table 6. The damage evolution law is given by

$$ d_{I} = 1 - \frac{{X_{\text{eq}}^{li} \left( {X_{\text{eq}}^{If} - X_{\text{eq}}^{I} } \right)}}{{X_{\text{eq}}^{I} \left( {X_{\text{eq}}^{If} - X_{\text{eq}}^{li} } \right)}},\left( {I = Lt,Tt,Zt,Lc,Tc,Zc,Mt,Mc} \right) $$

(24)

where $X_{\text{eq}}^{li}$ and $X_{\text{eq}}^{if}$ are the initiation and full damage equivalent displacement of failure mode I, respectively. $X_{\text{eq}}^{li}$ and $X_{\text{eq}}^{if}$ are obtained by the following equations:

Table 6 Equivalence displacements and stresses corresponding to different failure modes

$$ X_{\text{eq}}^{li} = X_{\text{eq}}^{I} /\sqrt {\varphi_{I} } $$

(25)

$$ X_{\text{eq}}^{lf} = 2G_{I} /\sigma_{\text{eq}}^{li} $$

(26)

Here, $\varphi_{I}$ is the value of initiation damage criteria. $G_{I}$ and $\sigma_{\text{eq}}^{li}$, respectively, denote the fracture energy density and initiation damage equivalence stress of failure mode I. The initiation equivalence stress $\sigma_{\text{eq}}^{li}$ can be calculated from the following equation:

$$ \sigma_{\text{eq}}^{li} = \sigma_{\text{eq}}^{I} /\sqrt {\varphi_{I} } $$

(27)

where $\sigma_{\text{eq}}^{I}$ is the equivalence stress as expressed in Table 6. It is obvious that the damage evolvement equation is associated with the element strain, element characteristic length and material fracture density.

In the present paper, Murakami-Ohno damage model is used to characterize the damage process of yarns and matrix. Moreover, three principal damage variables are used to express the damage states. It is defined as:

$$ \varvec{D} = \sum {D_{i} \varvec{n}_{i} \otimes \varvec{n}_{i} \quad i = (L,T,Z)} $$

(28)

where D _i and n _i are the principal damage value and the principle unit vector of damage tensor, respectively. It should be noted that combining with d _I (L, T, Z), D _i is described as:

For yarns at L, T and Z directions:

$$ \begin{aligned} D_{L} = \hbox{max} \left( {d_{Lt} ,d_{Lc} } \right) \hfill \\ D_{T} = \hbox{max} \left( {d_{Tt} ,d_{Tc} } \right) \hfill \\ D_{Z} = \hbox{max} \left( {d_{Zt} ,d_{Zc} } \right) \hfill \\ \end{aligned} $$

(29)

For matrix:

$$ D_{L} = D_{T} = D_{Z} = \hbox{max} \left( {d_{Rt} ,d_{Rc} } \right) $$

(30)

By definition, the effective stress $\sigma^{*}$ is expressed as:

$$ \sigma^{*} = \frac{1}{2}\left[ {\left( {\varvec{I} - \varvec{D}} \right)^{ - 1} \cdot \sigma + \sigma \cdot \left( {\left( {\varvec{I} - \varvec{D}} \right)^{ - 1} } \right)} \right] = \varvec{M}(\varvec{D}):\sigma $$

(31)

where σ is the undamaged stress.

In order to introduce the damage variable into the undamaged stiffness matrix, Cordebois–Sidoroff energy assumptions [32] are used, and the detailed damage stiffness matrix C(D) can be expressed as follows:

$$ C(D) = \left[ {\begin{array}{*{20}l} {(1 - D_{L} )^{2} C_{11} } \hfill & {(1 - D_{L} )(1 - D_{T} )C_{12} } \hfill & {(1 - D_{L} )(1 - D_{Z} )C_{13} } \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ {} \hfill & {(1 - D_{T} )^{2} C_{22} } \hfill & {(1 - D_{T} )(1 - D_{Z} )C_{23} } \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ {} \hfill & {} \hfill & {(1 - D_{Z} )^{2} C_{33} } \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ {} \hfill & {} \hfill & {} \hfill & {\left( {\frac{{2(1 - D_{L} )(1 - D_{T} )}}{{2 - D_{L} - D_{T} }}} \right)^{2} } \hfill & 0 \hfill & 0 \hfill \\ {} \hfill & {} \hfill & {} \hfill & {} \hfill & {\left( {\frac{{2(1 - D_{L} )(1 - D_{Z} )}}{{2 - D_{L} - D_{Z} }}} \right)^{2} } \hfill & 0 \hfill \\ {} \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill & {\left( {\frac{{2(1 - D_{T} )(1 - D_{Z} )}}{{2 - D_{T} - D_{Z} }}} \right)^{2} } \hfill \\ \end{array} } \right] $$

(32)

where C _ij , (i,j = L, T, Z), is the undamaged stiffness matrix item.

After generating the meso-scale voxel-based finite element models, a commercial finite element software ABAQUS/Standard is employed to investigate the mechanical responses of warp-reinforced 2.5D woven composites. In order to implement the progressive damage model as mentioned above, a user-defined material subroutine (UMAT) is complied in ABAQUS. Three state damage variables (SDVs), including SDV1 (L directional damage), SDV2 (T directional damage) and SDV3 (Z directional damage), are set in UMAT. Here, note that the state damage variables are controlled by the damage equivalent strains and evolved from 0 to 1 irreversibly after the failure initiation. The detailed flowchart of the simulation process is shown in Fig. 11.

Figure 11

The flowchart of progressive damage analysis

Experimental details

Figure 12 shows the tensile specimens and the test equipment. For the tensile samples, each side is affixed to an aluminum strengthening plate with the epoxy glue film to protect the specimen from the damage that caused by the rigid test fixture during the test process. For the tensile tests, the standard test method ASTM D3039 is used. Here, it should be noted that the width of all the longitudinal (warp) specimens is 25 mm, whereas the width of the transverse (weft) specimens is specific values but according to the number of RVCs. Specimen widths include 6.7, 13.4 and 25 mm, which correspond to 1 RVC, 2 RVCs and 4 RVCs, respectively. Moreover, to validate the accuracy of the simulation, it is more worth mentioning that the digital image correlation technique (DIC) is employed to monitor the strain in the composite components under transverse (weft) tensile loading. This technique is becoming a popular tool in the field of the structural mechanics because of the low price and availability of the imaging equipment and the correlation software.

Figure 12

Tensile test setup (a), longitudinal samples (b) and transverse samples (c)

All the tests are conducted by SHIMADZU AG-250KNE universal material machine in the room temperature. Each test result in this paper is the mean of three repeats.

Results and discussion

Elastic properties

Three independent boundary conditions in the form of the uniform displacements are carried out to obtain the elastic modulus of voxel-based RVCs with different mesh numbers, as shown in Table 7. Apparently, the computed initial modulus of $n_{x} \times n_{y} \times n_{z} = 40 \times 40 \times 22$ and $n_{x} \times n_{y} \times n_{z} = 60 \times 40 \times 33$ is in good agreement with the experimental data. This is sufficient to ensure that the voxel mesh has a minor influence on the elastic modulus as long as the yarn volume fraction is correctly guaranteed. The detailed supporting results can also be found in [18].

Table 7 Predicted elastic constants of the three voxel models with different mesh numbers

Figure 13 illustrates the stress field distribution at strain level of 1.0% under the longitudinal (warp) loading. The local stress concentrations (white box in the binder warp and matrix) are clearly observed in all the voxel-based models, regardless of the voxel size. They are even more marked for the finer meshes. However, this phenomenon does not appear in the warp and weft zones. This is attributed to the step-like of the binder warp trajectory and the loading direction. Also, it is interesting to observe that for the two finest meshes, the stress fields are very similar. In other words, if the mesh size achieves a certain level, the local stress field does not vary obviously. Hence, in order to reduce the computing time, the mesh type with $n_{x} \times n_{y} \times n_{z} = 40 \times 40 \times 22$ will be used in the following comparisons.

Figure 13

Stress distribution in meso-scale voxel-based RVC at strain level of 1.0% under longitudinal (warp) loading

Tensile strength and failure behavior

Global stress–strain curves

Figure 14 illustrates the comparisons of the typical stress–strain curves between simulation and experiment under longitudinal (warp) loading. For both 1 RVC and 2 RVCs, the simulated initial modulus and max stress are essentially in accordance with the experimental ones. The margin of error is a range of 0.1%–3%. Also, the stress–strain curves show an obvious size dependency. The stress–strain curve of 2 RVCs exhibits significantly nonlinear characteristics, whereas that of 1 RVC is nearly linear. This difference indicates the length-scale effect, resulting in a varying progressive damage behavior. However, as compared to the predicted results, the stress–strain curve displays significantly nonlinear characteristic at nearly ε = 0.2%, indicating that the main failure mechanisms occur. Also, the predicted stress–strain curve tendency is distinct differences from the experimental one after the strain of 0.4%. This can be attributed to the reasonability of the stiffness reduction method when damage is activated [33]. Therefore, the development of this model still needs progress.

Figure 14

The comparisons of the typical stress–strain curves between simulation and experiment under longitudinal (warp) loading

In addition, Fig. 14 gives the stress nephogram at the point of the max stress. It is found that for 1 RVC and 2 RVCs, the yarn stress distribution at the edges is almost the same, while that of matrix at the edges displays significant difference. The analytical results obtained from the strain distribution are very close to that of the stress distribution, as shown in Fig. 15. This in fact demonstrates directly the effect of RVC numbers. Thus, its influence on the stress/strain distribution and the failure behaviors cannot be ignored. Figure 14 also illustrates the damage initiation points of yarns and matrix for 1 RVC and 2 RVCs. Here, it can be seen that the predicted stress–strain curves increase linearly until the initiation damage.

Figure 15

Strain distribution in meso-scale voxel-based RVC at the point of the max stress under longitudinal (warp) loading

Figure 16a, b presents measured and predicted strain contours of different width of the specimens under transverse tensile loading, respectively. The strain distribution contours are obtained near the strain level of 0.2% and 0.8% before fracture. Clearly, both DIC and voxel-based models successfully collect the strain fields. Furthermore, the predicted strain field is similar to DIC image. Compared with the result of voxel-based model, it can be concluded that the low strain areas are located in the weft, whereas the high strain regions occur mainly in the binder and resin zones.

Figure 16

Mechanical behaviors under transverse (weft) loading, a DIC strain image, b predicted strain contours and c the comparisons of the typical stress–strain curves between simulation and experiment

Figure 16c shows the experimental and numerical stress–strain curves of the transverse tension coupon specimens. Clearly, the numerically predicted moduli match well with the experimental results, indicating the capability of simulating the elastic response. Also, the transverse tensile strength exhibits an obvious size dependency, as increasing the specimen width results in a higher value.

Damage development

In order to make a better interpretation for the damage development, the damage nephograms at three key strain points under warp tension are chosen for the further study. For 1 RVC (see Fig. 17), the damage onset first occurs clearly in the region of binder warp and neighboring matrix at ε = 0.86%. With the external load reaching the peak value (ε = 1.20%), the matrix and binder warp damage zones become larger. Also, the discrete damage points occur initially in warp. Afterward, the crack extends gradually. Consequently, the final failure of 1 RVC under warp tensile direction is due to the warp and binder warp longitudinal breakage.

Figure 17

Progressive damage process of 1 RVC under uniaxial tension in warp direction

Figure 18 displays the detailed damage developments of 2 RVCs under warp tensile direction. The initial damage, damage evolution and final failure of 2 RVCs are similar to those of 1 RVC. However, as compared to 1 RVC, the initial damage of 2 RVCs occurs early at ε = 0.47%. The damage onset highly influences the local stress distribution. Thus, the nonlinear stress–strain responses of 2 RVCs are more apparent as mentioned earlier. Moreover, the damage of binder warp of 2 RVCs is more catastrophic at the max loading point (ε = 1.19%), and the fracture surface of 2 RVCs is different from that of 1 RVC.

Figure 18

Progressive damage process of 2 RVCs under uniaxial tension in warp direction

Local response and failure mechanism

To further characterize the local response and the failure mechanism, the typical damage elements, whose final state damage variable is maximum, are selected. Here, it should be noted that the stress ratio, namely the stress in yarns/matrix versus the predicted strength value (Table 5), is plotted as a function of the global axial strain. For 1 RVC, the axial stress/strength ($S_{11} /F_{\text{m}}^{t}$) histories of the typical matrix damage elements, including E33212 (next to binder warp), E68746 (next to warp) and E34655 (next to weft), are shown in Fig. 19a. Clearly, when the stress ratios are equal to 1 at the strain level of 0.68%, the matrix damage (Element 33212) is found to initiate. Then, the stresses increase because of the damage evolution law and eventually decrease when fracture energy is reached. The result is also indicated in Ref. [34]. Moreover, the matrix failure elements first occur next to binder warp. In the matrix failure elements next to weft and warp, the max value point of the stress ratio is closer to the peak loading. In brief, the matrix element failure occurs almost neighboring the yarns. For warp of 1 RVC, the axial stress/strength ($S_{11} /F_{w}^{t}$) and the shear stress/strength ($S_{12} /S_{w}^{{}}$) are considered, as shown in Fig. 19b. As observed, the max value of the axial stress/strength ratio of warp is close to 0.8, whereas the shear stress/strength ratio of warp only increases immediately after the max loading. The result indicates that for warp of 1 RVC, the effect of the axial stress is much more significant than the shear stress. For binder warp of 1 RVC, the axial stress/strength ratio ($S_{11} /F_{b}^{t}$) is considered as shown in Fig. 19b. It is found that the max value of the axial stress/strength ratio of binder warp is close to 0.6. Also, the stiffness descends slightly after the breakage initiation of binder warp. For yarns, there is no denying that the final fracture surface is the comprehensive effect of the warp axial stress, the warp shear stress and the binder warp axial stress.

Figure 19

Mechanical responses under longitudinal (warp) loading of 1 RVC, a elements in yarns, b elements in matrix

Also, for 2 RVCs, the typical yarn and matrix damage elements are selected, respectively, and the corresponding stress/strength versus global strain curves are described in Fig. 20. In comparison with 1 RVC, the local stress distribution of 2 RVCs has two obvious differences. Namely, (1) the stress/strength ratio of the matrix elements reaches the max value before ε = 0.8%, which is much smaller than the point of the max loading; (2) the warp breakage initiation occurs near ε = 0.8%, which is also before the point of the max loading. This phenomenon results in a nonlinear behavior of $S_{11} /F_{w}^{t}$ versus strain curve. The above stress/strength history analysis further confirms that the size effect plays an important role on the failure behaviors under warp tensile loading.

Figure 20

Mechanical responses of 2 RVCs under longitudinal (warp) loading, a elements in yarns, b elements in matrix

The final damage morphologies got from numerical simulation and experiment under warp tensile loading are compared in Fig. 21. According to the experiment result, the fracture plane is relatively smooth, and the final failure modes mainly occur in the inclined segments of binder warp, warp and matrix zones. This result is most consistent with the numerical one, regardless of the number of RVC. Meanwhile, the shear modes in warp of 2 RVCs are more significant as compared to that in warp of 1 RVC. Hence, further work will be conducted to predict the failure behaviors of different numbers of RVCs.

Figure 21

Comparison of failure morphology between finite element simulation and experiment under longitudinal (warp) loading

Figure 22 displays the experimental and numerical displacement contours under transverse (weft) loading. Clearly, the predicted results obtained from the voxel-based finite element model correlate the DIC image very excellently. Namely, the displacement isolines in these results are non-uniform, not surprisingly because the heterogeneity of the meso-structure is considered in the voxel-based model. This verifies the reliability of the voxel-based model to some extent. Also, under transverse loading, the numbers of RVC are insensitive to the displacement contours. Moreover, combined with the final damage morphologies (Figs. 22b, 23), it can be concluded that the strength of the transverse specimens is mainly decided by the tensile strength of weft and matrix.

Figure 22

Failure morphology under transverse (weft) loading, a numerically predicted in-plane displacement contours, b experimental failure morphology and in-plane displacement contours

Figure 23

Numerically predicted damage contours under transverse (weft) loading

Conclusions

The main objective of this study is to develop meso-scale voxel-based finite element model to predict the stress distribution of warp-reinforced 2.5D woven composites subjected to the axial tensile loading. For comparison, experimental tests are carried out. Based on the detailed analysis, the following conclusions are summarized:

• 1. From the comparisons of the stress distribution under longitudinal (warp) and transverse (weft) loadings, the predicted initial modulus, max stress and failure modes agree well with the experimental ones.

• 2. Under longitudinal tensile loading, the ultimate strength of warp-reinforced 2.5D woven composites is mainly influenced by the tensile strength of matrix, the tensile strength of binder warp and the tensile/shear strength of warp. However, under transverse tensile loading, the ultimate strength of warp-reinforced 2.5D woven composites is mainly decided by the tensile strength of weft and matrix.

• 3. The developed meso-scale voxel-based finite element model is capable of accurately predicting the mechanical properties of warp-reinforced 2.5D woven composites subjected to longitudinal (warp) and transverse (weft) tensile loading. Moreover, the geometrical model and the discrete mesh are simple and are easily implemented into the ABAQUS software through a user-defined element. Furthermore, meso-scale voxel-based finite element model possibly extends to other textile structural composites. As for the future studies, it is desirable to continue with an effort to address some of its limitations, including the damage theory and the length-scale effect. These insights can be extremely useful in dealing with the textile structural composites with arbitrarily shaped components subjected to complex loadings.