Trans-Theta Logistics: A New Family of Population Growth Sigmoid Functions

Abstract

Sigmoid functions have been applied in many areas to model self limited population growth. The most popular functions; General Logistic (GL), General von Bertalanffy (GV), and Gompertz (G), comprise a family of functions called Theta Logistic ($\Uptheta$ L). Previously, we introduced a simple model of tumor cell population dynamics which provided a unifying foundation for these functions. In the model the total population (N) is divided into reproducing (P) and non-reproducing/quiescent (Q) sub-populations. The modes of the rate of change of ratio P/N was shown to produce GL, GV or G growth. We now generalize the population dynamics model and extend the possible modes of the P/N rate of change. We produce a new family of sigmoid growth functions, Trans-General Logistic (TGL), Trans-General von Bertalanffy (TGV) and Trans-Gompertz (TG)), which as a group we have named Trans-Theta Logistic (T $\Uptheta$ L) since they exist when the $\Uptheta$ L are translated from a two parameter into a three parameter phase space. Additionally, the model produces a new trigonometric based sigmoid (TS). The $\Uptheta$ L sigmoids have an inflection point size fixed by a single parameter and an inflection age fixed by both of the defining parameters. T $\Uptheta$ L and TS sigmoids have an inflection point size defined by two parameters in bounding relationships and inflection point age defined by three parameters (two bounded). While the Theta Logistic sigmoids provided flexibility in defining the inflection point size, the Trans-Theta Logistic sigmoids provide flexibility in defining the inflection point size and age. By matching the slopes at the inflection points we compare the range of values of inflection point age for T $\Uptheta$ L versus $\Uptheta$ L for model growth curves.

1 Introduction

The sigmoid functions: Gompertz (G), General Logistic (GL) and General von Bertalanffy (GV) and their associate differential equations have been used over the years to model self limited population growth in such diverse fields as sociology, fish growth and tumor growth (Fokas 2007; Katsanevakis 2006; Bajzer et al. 2008). All three can be represented by the ODE designated the Theta Logistic equation:

$$ {\frac{{\dot{N}}}{N}} = {\frac{R}{\theta }}\left[ {1 - \left( {{\frac{N}{{N_{\infty } }}}} \right)^{\theta } } \right]\quad N(0) = N_{0} = 1. $$

(1)

N is the total population as function of time (t) non-dimensionalized and normalized to unity at t = 0. N can be viewed as the multiplication factor of the initial population size. $N_{\infty } = \mathop {\lim }\limits_{t \to \infty } N(t)$ is the population maximum, or carrying capacity, and R > 0 is the growth rate parameter. Equation 1 takes the form of the Gompertz ODE, Eq. 2, in the limit θ → 0⁺.

$$ {\frac{{\dot{N}}}{N}} = - R_{G} \ln \left( {{\frac{N}{{N_{\infty } }}}} \right) $$

(2)

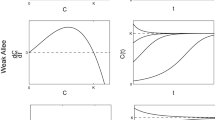
θ determines the sigmoid classification, see Fig. 1, and also determines the population total at the inflection point (N _I ) relevant to N _∞.

Fig. 1

Schematic for Theta-Logistic classification: $\theta > 0 \Rightarrow$ General Logistic, $\theta < 0 \Rightarrow$ General von Bertalanffy and $\theta \to 0^{ + } \Rightarrow$ Gompertz. θ > −1 is required for an inflection point. Note the x axis runs from left to right, ∞ → −1, to facilitate comparison with Fig. 3

$$ N_{I} = {\frac{{N_{\infty } }}{{\left( {1 + \theta } \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 \theta }}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$\theta $}}}} }}},\quad \theta > - 1 $$

(3)

As examples, for logistic growth: θ = 1, $N_{I} = {\frac{{N_{\infty } }}{2}}$ and for Gompertz: $N_{I} = {\frac{{N_{\infty } }}{e}}$.

Equation 1 has the solutions (implicit solutions provided for subsequent analysis):

$$ N(t) = N_{\infty } \left[ {{\frac{1}{{1 + \left( {\left\{ {N_{\infty } } \right\}^{\theta } - 1} \right)\exp \left\{ { - Rt} \right\}}}}} \right]^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 \theta }}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$\theta $}}}} ,\quad \theta \ne 0,\quad \theta > - 1 $$

$$ t = - \frac{1}{R}\ln \left| {\left\{ {{\frac{{1 - \left( {{\raise0.7ex\hbox{$N$} \!\mathord{\left/ {\vphantom {N {N_{\infty } }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${N_{\infty } }$}}} \right)^{\theta } }}{{1 - \left( {{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {N_{\infty } }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${N_{\infty } }$}}} \right)^{\theta } }}}} \right\}{\frac{{\left( {{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {N_{\infty } }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${N_{\infty } }$}}} \right)^{\theta } }}{{\left( {{\raise0.7ex\hbox{$N$} \!\mathord{\left/ {\vphantom {N {N_{\infty } }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${N_{\infty } }$}}} \right)^{\theta } }}}} \right| $$

(4)

Equation 2 has the solutions ($\mathop {\lim }\limits_{{\theta \to 0^{ + } }}$):

$$ N\left( t \right) = \exp \left\{ {\left( {\ln N_{\infty } } \right)\left( {1 - \exp \left\{ { - R_{G} t} \right\}} \right)} \right\}, $$

$$ t = - {\frac{1}{{R_{G} }}}\left\{ {\ln \left| {{\frac{{\left( {{\raise0.7ex\hbox{$N$} \!\mathord{\left/ {\vphantom {N {N_{\infty } }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${N_{\infty } }$}}} \right)\ln \left| {{\raise0.7ex\hbox{$N$} \!\mathord{\left/ {\vphantom {N {N_{\infty } }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${N_{\infty } }$}}} \right|}}{{\left( {{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {N_{\infty } }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${N_{\infty } }$}}} \right)\ln \left| {{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {N_{\infty } }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${N_{\infty } }$}}} \right|}}}} \right|} \right\} $$

(5)

While these ODEs and functions have been developed considering the total population (N) growth, insight can be gained by considering the sub-populations: P the reproducing population and Q the quiescent or non-reproducing population, where P and Q have been non-dimensionalized,

$$ N = P + Q,\quad P_{0} + Q_{0} = 1 $$

(6)

In Kozusko and Bourdeau (2007), we presented a PQ model applied to tumor growth that produces Eqs. 1 and 2 as a result of the equation for the decay rate, ${\frac{{d\left( {{\raise0.7ex\hbox{$P$} \!\mathord{\left/ {\vphantom {P N}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$N$}}} \right)}}{dt}}$, of the reproduction ratio: ${\raise0.7ex\hbox{$P$} \!\mathord{\left/ {\vphantom {P N}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$N$}}$. Here we will generalize the model to include populations where the new members are themselves reproducers (as in cancer modeling) or where new members are non-reproducers (at least initially) as in animal reproduction. We will extend the decay rate equation and produce a new family of sigmoids of which the Theta Logistic functions are a subclass, and also produce a unique new “trigonometric” sigmoid function.

2 The Model

Figure 2 presents a block diagram of a PQ subpopulation model where the new members are reproducers, such as in modeling cancer cell growth. P members can reproduce, while Q members cannot reproduce without first transitioning to P status. β > 0 is the reproduction rate parameter, μ _Q  > 0 and μ _Q  > 0 are the Q and P death rate parameters, respectively, and $N\Uppsi \left( {{\raise0.7ex\hbox{$P$} \!\mathord{\left/ {\vphantom {P N}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$N$}}} \right)$ represents the net transition rate between the two compartments. If the net transition rate is from Q to P, $N\Uppsi \left( {{\raise0.7ex\hbox{$P$} \!\mathord{\left/ {\vphantom {P N}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$N$}}} \right)$ is negative. The form of the transition rate function $\Uppsi \left( {{\raise0.7ex\hbox{$P$} \!\mathord{\left/ {\vphantom {P N}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$N$}}} \right)$ can be considered to define the sigmoid form of the population growth as discussed in Kozusko and Bourdeau (2007) and Kozusko, et al. (2007) but will remain in the background for the present development. See “Appendix A” for the model where the new members initially join the Q subpopulation.

Fig. 2

Block diagram for the subpopulation growth model. See text for descriptions

Rate balance analysis of Fig. 2 produces the population rate equations:

$$ \dot{P}\left( t \right) = \left( {\beta - \mu_{P} } \right)P - N\Uppsi \left( {{\raise0.7ex\hbox{$P$} \!\mathord{\left/ {\vphantom {P N}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$N$}}} \right) $$

(7)

$$ \dot{Q}\left( t \right) = N\Uppsi \left( {{\raise0.7ex\hbox{$P$} \!\mathord{\left/ {\vphantom {P N}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$N$}}} \right) - \mu_{Q} Q $$

(8)

$$ N = P + Q,\quad P(0) + Q(0) = P_{0} + Q_{0} = 1 $$

(9)

Where N(0) has been normalized to 1. Adding Eqs. 7 and 8 and substituting from Eq. 9 produces

$$ \dot{N} = mP - \mu_{Q} N \Rightarrow {\frac{{\dot{N}}}{N}} = m\left\{ {{\raise0.7ex\hbox{$P$} \!\mathord{\left/ {\vphantom {P N}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$N$}} - {\frac{{\mu_{Q} }}{m}}} \right\} $$

(10)

Where m = β − μ _P  + μ _Q  > 0 is required for $\dot{N}$ > 0. As t → ∞, $\dot{N}$ → 0 and we define ${\frac{{\mu_{Q} }}{m}} = \left( {{\raise0.7ex\hbox{$P$} \!\mathord{\left/ {\vphantom {P N}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$N$}}} \right)_{\infty }$ and rewrite Eq. 10 as

$$ {\frac{{\dot{N}}}{N}} = m\left\{ {\left( {{\raise0.7ex\hbox{$P$} \!\mathord{\left/ {\vphantom {P N}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$N$}}} \right) - \left( {{\raise0.7ex\hbox{$P$} \!\mathord{\left/ {\vphantom {P N}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$N$}}} \right)_{\infty } } \right\} $$

(11)

By differentiating and equating Eqs. 1 and 11 and using the substitutions provided by Eqs. 1 and 11, we produce a rate equation for ${\raise0.7ex\hbox{$P$} \!\mathord{\left/ {\vphantom {P N}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$N$}}$ (See “Appendix B” for details):

$$ \frac{d}{dt}\left\{ {\left( {{\raise0.7ex\hbox{$P$} \!\mathord{\left/ {\vphantom {P N}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$N$}} - \left( {{\raise0.7ex\hbox{$P$} \!\mathord{\left/ {\vphantom {P N}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$N$}}} \right)_{\infty } } \right)} \right\} = - R\left\{ {\left( {{\raise0.7ex\hbox{$P$} \!\mathord{\left/ {\vphantom {P N}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$N$}}} \right) - \left( {{\raise0.7ex\hbox{$P$} \!\mathord{\left/ {\vphantom {P N}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$N$}}} \right)_{\infty } } \right\} + m\theta \left\{ {\left( {{\raise0.7ex\hbox{$P$} \!\mathord{\left/ {\vphantom {P N}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$N$}}} \right) - \left( {{\raise0.7ex\hbox{$P$} \!\mathord{\left/ {\vphantom {P N}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$N$}}} \right)_{\infty } } \right\}^{2} $$

(12)

Equation 12 can be interpreted as approximating the rate of change of the net reproduction ratio $\left\{ {\left( {{\raise0.7ex\hbox{$P$} \!\mathord{\left/ {\vphantom {P N}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$N$}}} \right) - \left( {{\raise0.7ex\hbox{$P$} \!\mathord{\left/ {\vphantom {P N}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$N$}}} \right)_{\infty } } \right\}$ as a second order expansion in $\left\{ {\left( {{\raise0.7ex\hbox{$P$} \!\mathord{\left/ {\vphantom {P N}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$N$}}} \right) - \left( {{\raise0.7ex\hbox{$P$} \!\mathord{\left/ {\vphantom {P N}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$N$}}} \right)_{\infty } } \right\}$. Conversely, we can see that assuming a second order approximation for the rate equation

$$ \frac{d}{dt}\left\{ {\left( {{\raise0.7ex\hbox{$P$} \!\mathord{\left/ {\vphantom {P N}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$N$}}} \right) - \left( {{\raise0.7ex\hbox{$P$} \!\mathord{\left/ {\vphantom {P N}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$N$}}} \right)_{\infty } } \right\} = - \alpha_{1} \left\{ {\left( {{\raise0.7ex\hbox{$P$} \!\mathord{\left/ {\vphantom {P N}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$N$}}} \right) - \left( {{\raise0.7ex\hbox{$P$} \!\mathord{\left/ {\vphantom {P N}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$N$}}} \right)_{\infty } } \right\} - \alpha_{2} \left\{ {\left( {{\raise0.7ex\hbox{$P$} \!\mathord{\left/ {\vphantom {P N}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$N$}}} \right) - \left( {{\raise0.7ex\hbox{$P$} \!\mathord{\left/ {\vphantom {P N}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$N$}}} \right)_{\infty } } \right\}^{2} $$

(13)

combined with the model Eq. 11 yields Eq. 1 with α₁ = R and α₂ = −mθ. Phase diagram analysis of Eq. 13 reveals the requirement that α₁ > 0 for $\dot{N} > 0$ in Eq. 11 and that $\theta = {\frac{{\alpha_{2} }}{m}} > - 1$ is necessary to insure an inflection point for N. The solution to Eq. 13 is logistic decay with or without an inflection point (Lotka 1925).

3 The Expanded Model

It is interesting to see that Eq. 1 is derived through the model via Eq. 13 which uses a standard modeling approximation. Extending the model, we propose the following:

$$ \frac{d}{dt}\left\{ {\left( {{\raise0.7ex\hbox{$P$} \!\mathord{\left/ {\vphantom {P N}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$N$}}} \right) - \left( {{\raise0.7ex\hbox{$P$} \!\mathord{\left/ {\vphantom {P N}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$N$}}} \right)_{\infty } } \right\} = - \alpha_{1} \left\{ {\left( {{\raise0.7ex\hbox{$P$} \!\mathord{\left/ {\vphantom {P N}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$N$}}} \right) - \left( {{\raise0.7ex\hbox{$P$} \!\mathord{\left/ {\vphantom {P N}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$N$}}} \right)_{\infty } } \right\} - \alpha_{2} \left\{ {\left( {{\raise0.7ex\hbox{$P$} \!\mathord{\left/ {\vphantom {P N}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$N$}}} \right) - \left( {{\raise0.7ex\hbox{$P$} \!\mathord{\left/ {\vphantom {P N}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$N$}}} \right)_{\infty } } \right\}^{2} - \alpha_{3} \left\{ {\left( {{\raise0.7ex\hbox{$P$} \!\mathord{\left/ {\vphantom {P N}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$N$}}} \right) - \left( {{\raise0.7ex\hbox{$P$} \!\mathord{\left/ {\vphantom {P N}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$N$}}} \right)_{\infty } } \right\}^{3} $$

(14)

Again, phase diagram analysis of Eq. 14 requires α₁ > 0. Inflection point requirements will be discussed later. Differentiating Eq. 11, using Eqs. 11 and 14, and the chain rule for $\frac{d}{dt}\left( {{\raise0.7ex\hbox{${\dot{N}}$} \!\mathord{\left/ {\vphantom {{\dot{N}} N}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$N$}}} \right) = \dot{N}\frac{d}{dN}\left( {{\raise0.7ex\hbox{${\dot{N}}$} \!\mathord{\left/ {\vphantom {{\dot{N}} N}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$N$}}} \right)$ yields (See “Appendix B” for details):

$$ N\frac{d}{dN}\left( {{\raise0.7ex\hbox{${\dot{N}}$} \!\mathord{\left/ {\vphantom {{\dot{N}} N}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$N$}}} \right) = - {\frac{1}{{m^{2} }}}\left[ {\alpha_{1} m^{2} + \alpha_{2} m\left( {{\raise0.7ex\hbox{${\dot{N}}$} \!\mathord{\left/ {\vphantom {{\dot{N}} N}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$N$}}} \right) + \alpha_{3} \left( {{\raise0.7ex\hbox{${\dot{N}}$} \!\mathord{\left/ {\vphantom {{\dot{N}} N}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$N$}}} \right)^{2} } \right] $$

(15)

3.1 Trans-Theta Logistic ODEs

Solutions to Eq. 15, which depend on the values of the zeros of the polynomial in $\left( {{\raise0.7ex\hbox{${\dot{N}}$} \!\mathord{\left/ {\vphantom {{\dot{N}} N}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$N$}}} \right)$ and $\gamma^{2\,} \, = \,\alpha_{2}^{2} - 4\alpha_{1} \alpha_{3}$, are as follows:

3.1.1 Trans-General Logistic/Trans-General von Bertalanffy ODE (γ² > 0)

$$ {\frac{{\dot{N}}}{N}} = {\frac{{R_{TL} }}{{\theta_{T} }}}\left[ {{\frac{{1 - \left( {{\raise0.7ex\hbox{$N$} \!\mathord{\left/ {\vphantom {N {N_{\infty } }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${N_{\infty } }$}}} \right)^{{\theta_{T} }} }}{{1 - \kappa \left( {{\raise0.7ex\hbox{$N$} \!\mathord{\left/ {\vphantom {N {N_{\infty } }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${N_{\infty } }$}}} \right)^{{\theta_{T} }} }}}} \right], $$

$$ R{}_{TL} = \gamma \left| {{\frac{{\left| {\alpha_{2} } \right| - \gamma }}{{2\alpha_{3} }}}} \right| > 0,\,\kappa = {\frac{{\left| {\alpha_{2} } \right| - \gamma }}{{\left| {\alpha_{2} } \right| + \gamma }}},\quad - 1 \le \kappa < 1,\quad \theta_{T} = \pm {\frac{\gamma }{m}} $$

(16)

For $\theta_{T} < 0,\,\kappa < N_{\infty }^{{\theta_{T} }}$ is required to ensure $\dot{N} > 0$.

3.1.2 Trans-Gompertz ODE (γ² = 0, κ = 1, α₃ > 0)

$$ {\frac{{\dot{N}}}{N}} = - {\frac{{R_{TG} \ln (N/N_{\infty } )}}{{1 + \kappa_{TG} \ln (N/N_{\infty } )}}}, $$

$$ R_{TG} = \alpha_{1} ,\,\kappa_{TG} = {\frac{{\alpha_{2} }}{2m}} $$

(17)

$\kappa_{TG} < {\frac{1}{{\ln \left| {N_{\infty } } \right|}}}$ is required for $\dot{N} > 0$.

3.1.3 Trigonometric Sigmoid ODE (γ² < 0, α₃ > 0)

$$ {\frac{{\dot{N}}}{N}} = - R_{TS} \left\{ {{\frac{{{\text{Tan}}\left\{ {\kappa_{TS1} \ln \left| {{\raise0.7ex\hbox{$N$} \!\mathord{\left/ {\vphantom {N {N_{\infty } }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${N_{\infty } }$}}} \right|} \right\}}}{{1 + \kappa_{TS2} {\text{Tan}}\left\{ {\kappa_{TS1} \ln \left| {{\raise0.7ex\hbox{$N$} \!\mathord{\left/ {\vphantom {N {N_{\infty } }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${N_{\infty } }$}}} \right|} \right\}}}}} \right\}, $$

$$ R_{TS} = - {\frac{m\Updelta }{{2\alpha_{3} }}}\left[ {1 + \left( {{\frac{{\alpha_{2} }}{\Updelta }}} \right)^{2} } \right],\,\kappa_{TS1} = {\frac{\Updelta }{2m}},\,\kappa_{TS2} = {\frac{{\alpha_{2} }}{\Updelta }},\quad \Updelta \, = \,\sqrt {4\alpha_{1} \alpha_{3} - \alpha_{2}^{2} } $$

(18)

$\kappa_{TS2} < {\frac{1}{{{\text{Tan}}\left( {\kappa_{TS1} \ln \left| {N_{\infty } } \right|} \right)}}}$ is required to ensure $\dot{N} > 0$.

$\kappa_{TS1} < {\frac{\pi }{{2\ln \left| {N_{\infty } } \right|}}}$ keeps the argument $\kappa_{TS1} \ln \left| {{\raise0.7ex\hbox{$N$} \!\mathord{\left/ {\vphantom {N {N_{\infty } }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${N_{\infty } }$}}} \right|$ confined to the primary tangent branch.

3.2 Trans-Theta Logistic ODEs solution phase space

Figure 3 presents a schematic of the ${\raise0.7ex\hbox{${\alpha_{3} }$} \!\mathord{\left/ {\vphantom {{\alpha_{3} } m}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$m$}}\,{\text{versus}}\,{\raise0.7ex\hbox{${\alpha_{2} }$} \!\mathord{\left/ {\vphantom {{\alpha_{2} } m}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$m$}}$ solution space of Eq. 15 for an assumed value of α₁ > 0, but does not attempt to depict the complicated inflection point requirements which are presented later. When α₃ = 0, Fig. 3 collapses to a line diagram equivalent to Fig. 1, where $\theta = - {\raise0.7ex\hbox{${\alpha_{2} }$} \!\mathord{\left/ {\vphantom {{\alpha_{2} } m}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$m$}}$. The parabola $\alpha_{3} = {\frac{{\alpha_{2}^{2} }}{{4\alpha_{1} }}}$ corresponds to γ = 0 and represents the Trans-Gompertz solution separating the Trans-Theta Logistic and Trigonometric Solution subspaces. (See discussion around Eq. 13).

Fig. 3

Schematic of the ${\raise0.7ex\hbox{${\alpha_{3} }$} \!\mathord{\left/ {\vphantom {{\alpha_{3} } m}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$m$}}\,{\text{vs}}\,{\raise0.7ex\hbox{${\alpha_{2} }$} \!\mathord{\left/ {\vphantom {{\alpha_{2} } m}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$m$}}$ solution space for Eq. 15. The parabola $\alpha_{3} = {\frac{{\alpha_{2}^{2} }}{{4\alpha_{1} }}}$ corresponds to γ = 0

Equation 16 collapses to Eq. 1 as $\alpha_{3} \to 0 \Rightarrow \gamma \to \left| {\alpha_{2} } \right| \Rightarrow \kappa \to 0$ and Eq. 17 collapses to Eq. 2 as α₂ → 0 along curve $\alpha_{3} = {\frac{{\alpha_{2}^{2} }}{{4\alpha_{1} }}}$.

3.3 Trans-Theta Logistic implicit solutions

Equations 16, 17 and 18 have implicit solutions for $t = 0 \Rightarrow N = 1$. The solution for Eqs. 16 and 17 can be seen to collapse to Eqs. 4 and 5 when κ → 0 and κ _TG  → 0.

3.3.1 Trans-General Logistic/Trans-General von Bertalanffy implicit solution

$$ t = - {\frac{1}{{R_{TL} }}}\ln \left| {\left\{ {{\frac{{1 - \left( {{\raise0.7ex\hbox{$N$} \!\mathord{\left/ {\vphantom {N {N_{\infty } }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${N_{\infty } }$}}} \right)^{{\theta_{T} }} }}{{1 - \left( {{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {N_{\infty } }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${N_{\infty } }$}}} \right)^{{\theta_{T} }} }}}} \right\}^{1 - \kappa } {\frac{{\left( {{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {N_{\infty } }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${N_{\infty } }$}}} \right)^{{\theta_{T} }} }}{{\left( {{\raise0.7ex\hbox{$N$} \!\mathord{\left/ {\vphantom {N {N_{\infty } }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${N_{\infty } }$}}} \right)^{{\theta_{T} }} }}}} \right| $$

(19)

3.3.2 Trans-Gompertz implicit solution

$$ t = - {\frac{1}{{R_{TG} }}}\left\{ {\ln \left| {{\frac{{\left( {{\raise0.7ex\hbox{$N$} \!\mathord{\left/ {\vphantom {N {N_{\infty } }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${N_{\infty } }$}}} \right)^{{\kappa_{TG} }} \ln \left| {{\raise0.7ex\hbox{$N$} \!\mathord{\left/ {\vphantom {N {N_{\infty } }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${N_{\infty } }$}}} \right|}}{{\left( {{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {N_{\infty } }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${N_{\infty } }$}}} \right)^{{\kappa_{TG} }} \ln \left| {{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {N_{\infty } }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${N_{\infty } }$}}} \right|}}}} \right|} \right\} $$

(20)

3.3.3 Trigonometric Sigmoid implicit solution

$$ t = {\frac{1}{{\kappa_{TS1} R_{TS} }}}\left\{ {\ln \left| {{\frac{{\sin \left( {\kappa_{TS1} \ln \left| {{\raise0.7ex\hbox{$N$} \!\mathord{\left/ {\vphantom {N {N_{\infty } }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${N_{\infty } }$}}} \right|} \right)}}{{\sin \left( {\kappa_{TS1} \ln \left| {{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {N_{\infty } }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${N_{\infty } }$}}} \right|} \right)}}}} \right| + \kappa_{TS1} \kappa_{TS2} \ln \left| {{\frac{{{\raise0.7ex\hbox{$N$} \!\mathord{\left/ {\vphantom {N {N_{\infty } }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${N_{\infty } }$}}}}{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {N_{\infty } }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${N_{\infty } }$}}}}}} \right|} \right\} $$

(21)

3.4 Trans-Theta Logistic inflection points

Inflection point requirements ($\ddot{N} = 0$ at N = N _I ) for $X_{I} = {\frac{{N_{I} }}{{N_{\infty } }}}$, 0 < X _I  < 1 are as follows:

3.4.1 Trans-General Logistic/Trans-General von Bertalanffy

For a given value of X _I , κ and θ _T must satisfy

$$ \kappa = {\frac{{\left( {1 + \theta_{T} } \right)X_{I}^{{\theta_{T} }} - 1}}{{X_{I}^{{2\theta_{T} }} - \left( {1 - \theta_{T} } \right)}}},\quad - 1 \le \kappa < 1 $$

(22)

3.4.2 Trans-Gompertz

For a given value of X _I

$$ \kappa_{TG} = - {\frac{{1 + \ln \left| {X_{I} } \right|}}{{\left[ {\ln \left| {X_{I} } \right|} \right]^{2} }}} $$

(23)

3.4.3 Trigonometric Sigmoid

For given value of X _I , κ _TS1 and κ _TS2 must satisfy

$$ \left( {\kappa_{TS1} + \kappa_{TS2} } \right){\text{Tan}}^{2} \left[ {\kappa_{TS1} \ln \left| {X_{I} } \right|} \right] + {\text{Tan}}\left[ {\kappa_{TS1} \ln \left| {X_{I} } \right|} \right] + \kappa_{TS1} = 0 $$

(24)

4 Analysis

Trans-Logistic, Trans-Gompertz and Trigonometric sigmoids comprise a new family of sigmoid growth functions. In this section we will explore their significance versus the traditional Theta Logistic sigmoids.

Theta Logistic ($\Uptheta L$), Eq. 1, can be seen to be a special case of Trans-Theta Logistic $\left( {T\Uptheta L} \right)$ Eq. 16, with κ = 0 (α₃ = 0). $\Uptheta L$ has an inflection point ratio, $X_{I} = {\frac{N}{{N_{\infty } }}}$, fixed by the singular value θ (Eq. 3), and an inflection point age fixed by θ and R(Eq. 4). For $T\Uptheta L$, the inflection point ratio can vary with the values of κ and θ _T (Eq. 22) and the inflection point age varies with κ, θ _T and R _TL (Eq. 19). The Theta Logistic sigmoid has the advantage over the Gompertz sigmoid of being able to vary the inflection point ratio. The Trans-Theta Logistic sigmoids provide the additional advantage of being able to vary the growth age, hence the growth age at the inflection point (within bounded limits).

4.1 Comparing Logistics and Trans-logistic inflection point ratios and ages when R = R _TG and θ = θ _T

Examining Eqs. 3 and 22, we observe that $\Uptheta L$ and $T\Uptheta L$ can have the same inflection point ratio, X _I , only when they have different θ values for any non-zero value of κ. For a simple comparison, consider the case where Eqs. 1 and 16 have the same θ value and R = R _TG , they will then differ only by the term $1 - \kappa \left( {{\raise0.7ex\hbox{$N$} \!\mathord{\left/ {\vphantom {N {N_{\infty } }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${N_{\infty } }$}}} \right)^{{\theta_{T} }}$ in the denominator of Eq. 16. For κ < 0, the $T\Uptheta L$ growth rate is slower; the inflection is reached in a longer time period and is at smaller ratio as compared to $\Uptheta L$. For κ > 0, the $T\Uptheta L$ growth rate is faster; the inflection is reached in a shorter time period and is at greater ratio as compared to $\Uptheta L$. Figure 4 shows the comparisons for θ = 1 (X _I  = 0.5 for $\Uptheta L$). The difference in the inflection point ages is slight while those of the inflection point value and growth rate are more significant as κ varies from κ = 0. Figure 5 shows the comparison for R = R _TL and $\theta = \theta_{T} = {\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 4}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$4$}}$.

Fig. 4

Comparison of the growth characteristics of $T\Uptheta L$ and $\Uptheta L$, Eqs. 16 and 1, for the case R = R _TL and θ = θ _T  = 1; a the ratio of the inflection point ages, b ratio of the inflection point size and c ratio of growth rates, $\dot{N}_{T\Uptheta L} /\dot{N}_{\Uptheta L}$ at the respective inflection point

Fig. 5

Comparison of the growth characteristics of $T\Uptheta L$ and $\Uptheta L$, Eqs. 16 and 1, for the case R = R _TL and $\theta = \theta_{T} = {\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 4}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$4$}}$; a the ratio of the inflection point ages, b ratio of the inflection point size and c ratio of growth rates, $\dot{N}_{T\Uptheta L} /\dot{N}_{\Uptheta L}$ at the respective inflection point

4.2 Comparing Gompertz and Trans-Gompertz inflection point ratios and ages when R _G  = R _TG

The Gompertz (Eq. 2) with an inflection point ratio $X_{I} = {\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 e}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$e$}}$ is a special case of Trans-Gompertz (Eq. 17) with κ _TG  = 0 (α₂ = α₃ = 0). κ _TG  > 0 tends to increase the growth rate in Eq. 17 and produces $X_{I} < {\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 e}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$e$}}$ in Eq. 22, while a decreased rate and $X_{I} > {\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 e}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$e$}}$ occur for κ _TG  < 0. In Fig. 6 we compare ages, X _I ratios and growth rates $\left( {\frac{dN}{dt}} \right)$ of inflection points for the case where R _G  = R _TG . The variation in the inflection point age is significant. For example, with κ _TG  = 0.1165 the inflection point ratio is only 1.1 (0.368 for Gompertz and 0.405 for Trans-Gompertz), the ratio of growth rates at the respective inflection points is 0.900 while the inflection point age ratio is 1.73.

Fig. 6

Comparison of the growth characteristics of Trans-Gompertz and Gompertz, Eqs. 17 and 2, for the case R = R _TG: a the ratio of the inflection point ages, b ratio of the inflection point size and c ratio of growth rates, $\dot{N}_{TG} /\dot{N}_{G}$ at the respective inflection point

The Trigonometric Sigmoid has no daughters; as such the above analysis is not possible.

4.3 Comparing Theta Logistics and Trans-Theta Logistic inflection point ages when inflection point ratio and $\left( {\frac{dN}{dt}} \right)$ at the inflection point are matched

Another way to compare the sigmoids is to match them at their inflection points. That is, we require that the $T\Uptheta L/TS$ have the same inflection point ratio and the same $\left( {\frac{dN}{dt}} \right)$ at the inflection point as does a selected $\Uptheta L$ sigmoid. We can then compare the growth ages at the matched inflection points.

Equation (22) shows that the Trans-Theta Logistic inflection point ratio is determined by pair values of κ and θ _T . In Fig. 7, we make the comparison between $\Uptheta L$ with θ = 1, and $T\Uptheta L$ (Eq. 16). By taking the ratio of the inflection point ages, the respective R values are removed from the analysis. Figure 7 should be interpreted as follows: For any given $\Uptheta L$ sigmoid, we can meet the matching requirements with an infinite number of $T\Uptheta L$ sigmoids within the given age ratio span. As an example, if the $\Uptheta L$ sigmoid used has an inflection point age of 10 years, there is a matching $T\Uptheta L$ with θ _T  = 2 and κ = −0.99, with an inflection point age of 13 years.

Fig. 7

Comparison of the growth characteristics of Trans-Theta Logistic and Theta Logistic (θ = 1), Eqs. 16 and 1, for the case $\dot{N}_{T\Uptheta L} \, = \,\dot{N}_{\Uptheta L}$ and $X_{I} = {\frac{{N_{T\Uptheta L} }}{N\infty }} = {\frac{{N_{\Uptheta L} }}{{N_{\infty } }}}$ at the inflection point : a the ratio of the inflection point ages vs. κ, b ratio of the inflection point ages vs. θ _T . θ _T  > 0 represented by “+” and θ _T  < 0 values by “o” on both graphs

Figure 8 shows $T\Uptheta L$ matched to Gompertz. Figure 9 shows the comparison of the growth curves of the Gompertz function and its matching $T\Uptheta L$ (θ_T = −5, κ = −0.03). The Gompertz curves have been shifted horizontally to show the matching; the units of time are the Gompertz inflection point age. Notice that the $T\Uptheta L$ starts in negative time.

Fig. 8

Comparison of inflection point ages for Trans-Theta Logistic matched to Gompertz at the inflection point: a ratio of inflection point ages vs. κ and b ratio of inflection point ages vs. θ _T

Fig. 9

Comparison of Trans-Theta Logistic (θ _T  = −5) (solid line) and Gompertz (o) growths vs. time in units of Gompertz inflection point age where the curves have the same inflection point ratio and the same growth rate at the inflection points

4.4 Comparing Trans-Gompertz and Theta Logistic inflection point ages when inflection point ratio and $\left( {\frac{dN}{dt}} \right)$ at the inflection point are matched

The Trans-Gompertz sigmoid can only achieve an inflection point ratio $X_{I} = {\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 e}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$e$}}$ in the case it is identically the Gompertz function and the above matching would be an identity. We can match the Trans-Gompertz to the Theta-Logistic sigmoid, where the value of κ _TG is uniquely determined by Eq. 23 and only one Trans-Gompertz will match to any given Theta-Logistic. The growth curves for the match with $\theta = - {\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 4}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$4$}}$ are shown in Fig. 10. The Trans-Gompertz curve has been shifted to show the matching overlap. The horizontal axis is in units of Theta Logistic inflection point age for a universal comparison. The inflection point age of the Trans-Gompertz is 3.7 times that of any Theta-Logistic curve it matches.

Fig. 10

Comparison of Theta Logistic $\left( {\theta = - {\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 4}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$4$}}} \right)$ (solid line) and Trans-Gompertz (o) growth vs. time in units of Theta Logistic inflection point age where the curves have the same inflection point ratio and the same growth rate at the inflection point

4.5 Comparing Trigonometric sigmoid and Theta Logistic inflection point ages when inflection point ratio and $\left( {\frac{dN}{dt}} \right)$ at the inflection point are matched

Finally, we do the matching of the Trigonometric sigmoid with an inflection point determined by the paired values of κ _TS1 and κ _TS2. Figure 11 shows the matching to Theta-Logistic (θ = 1) and Fig. 12 shows the matching to Gompertz.

Fig. 11

Comparison of the inflection point ages of Trigonometric sigmoid and Gompertz sigmoid, Eqs. 18 and 1, for the case $\dot{N}_{\text{trig}} = \dot{N}_{\Uptheta L}$ and $X_{I} = {\frac{{N_{\text{trig}} }}{N\infty }} = {\frac{{N_{\Uptheta L} }}{{N_{\infty } }}}$ at the inflection point: a the ratio of the inflection point ages vs. κ _TS1, b the ratio of the inflection point ages vs. κ _TS2

Fig. 12

Comparison of the inflection point ages of Trigonometric sigmoid and Theta Logistic (θ = 1), Eqs. 18 and 1, for the case $\dot{N}_{trig} = \dot{N}_{G}$ and $X_{I} = {\frac{{N_{trig} }}{N\infty }} = {\frac{{N_{G} }}{{N_{\infty } }}}$ at the inflection point : a the ratio of the inflection point ages vs. κ _TS1, b the ratio of the inflection point ages vs. κ _TS2

5 Discussion

We have derived the Trans-Theta Logistic/Trigonometric sigmoid equations in terms of the primary parameters: α₁, α₂, α₃ and m, while we conducted our analysis in the secondary defined parameters R’s and κ’s. It is not necessary to consider the primary parameters unless analyzing the subpopulation (P and Q) profiles, which is beyond the present scope. While we have conducted our matching at the inflection point for universal analysis, the matching can be accomplished at any level of the growth curves.

From the above analysis, we have shown that Trans-Theta Logistic/Trigonometric provide for additional shaping of a sigmoid profile around an inflection point defined by its growth rate and relative size, as well as a varying growth age.

There are differences to be considered when fitting Trans-Theta Logistic/Trigonometric sigmoids to growth data versus fitting Theta Logistic sigmoids. T $\Uptheta$ L has one additional parameter, therefore would require at least one more data point and may require several additional data points to obtain an equivalent goodness of fit. Since T $\Uptheta$ L has only implicit solutions for N(t), the data fitting would use N data points as the independent variables. A true comparison of the T $\Uptheta$ L versus $\Uptheta$ L solutions of the data fit would necessitate fitting $\Uptheta$ L similarly using N as the independent variable.

6 Conclusion

The popular sigmoid modeling Theta-Logistic equations have been derived using our population growth model (Fig. 2) and a standard modeling approximation (Eq. 13). By extending the model (Eq. 14), we have produced a new family of sigmoid growth equations (Eqs. 16, 17 and 18) to which the Theta-Logistic equations belong. The Trans-Theta Logistic equation provides flexibility in the growth age of a sigmoid growth curve over the fixed points of the Theta-Logistic equations. However, once $\dot{N}$ is defined at the inflection point (or at any point) of the growth curve, the age at the inflection point (or any point) and the growth profile are completely defined and may be different from those of Theta-Logistic. The Trans-Logistic, Trans-Gompertz and Trigonometric sigmoids provide alternative growth profiles even when matched at the inflection point.

Appendix

1.1 Appendix A. Alternate PQ Model

Figure 13 presents the block diagram for the alternate PQ model where the new members produced by the P population initially join the Q non reproducing population. This model could be applied to any population where new members, such as human and animal populations, must mature before being capable of reproducing. Additionally, when the reproducers age, they again become members of the Q population.

Fig. 13

Block diagram for the subpopulation growth model where new members join the Quiescent subpopulation

Rate analysis of Fig. 13, produces the following rate equations:

$$ \dot{P}\left( t \right) = N\Uppsi \left( {{\raise0.7ex\hbox{$P$} \!\mathord{\left/ {\vphantom {P N}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$N$}}} \right) - \mu_{P} P $$

(25)

$$ \dot{Q}\left( t \right) = \beta P - N\Uppsi \left( {{\raise0.7ex\hbox{$P$} \!\mathord{\left/ {\vphantom {P N}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$N$}}} \right) - \mu_{Q} Q $$

(26)

Adding Eqs. 25 and 26 yields

$$ \dot{N} = mP - \mu_{Q} N \Rightarrow {\frac{{\dot{N}}}{N}} = m\left\{ {{\raise0.7ex\hbox{$P$} \!\mathord{\left/ {\vphantom {P N}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$N$}} - {\frac{{\mu_{Q} }}{m}}} \right\} $$

(27)

where m = β − μ _P  + μ _Q  > 0 and the analysis follows as from Eq. 10. We should note that the form of $\Uppsi \left( {{\raise0.7ex\hbox{$P$} \!\mathord{\left/ {\vphantom {P N}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$N$}}} \right)$ here will be different than that in Fig. 2.

1.2 Appendix B. Derivations of Equations 12 and 15

Differentiating Eq. 1 and using Eq. 1 for the value of $\left( {{\raise0.7ex\hbox{$N$} \!\mathord{\left/ {\vphantom {N {N_{\infty } }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${N_{\infty } }$}}} \right)^{\theta }$ yields

$$ \frac{d}{dt}\left( {{\raise0.7ex\hbox{${\dot{N}}$} \!\mathord{\left/ {\vphantom {{\dot{N}} N}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$N$}}} \right) = - R\left( {{\raise0.7ex\hbox{$N$} \!\mathord{\left/ {\vphantom {N {N_{\infty } }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${N_{\infty } }$}}} \right)^{\theta } \left( {{\raise0.7ex\hbox{${\dot{N}}$} \!\mathord{\left/ {\vphantom {{\dot{N}} N}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$N$}}} \right) = - R\left[ {1 - {\frac{\theta }{R}}\left( {{\raise0.7ex\hbox{${\dot{N}}$} \!\mathord{\left/ {\vphantom {{\dot{N}} N}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$N$}}} \right)} \right]\left( {{\raise0.7ex\hbox{${\dot{N}}$} \!\mathord{\left/ {\vphantom {{\dot{N}} N}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$N$}}} \right) $$

(28)

Using the value of $\left( {{\raise0.7ex\hbox{${\dot{N}}$} \!\mathord{\left/ {\vphantom {{\dot{N}} N}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$N$}}} \right)$ from Eq. 11 produces Eq. 12.

We derive Eq. 15, by first differentiating Eq. 11.

$$ \frac{d}{dt}\left( {{\raise0.7ex\hbox{${\dot{N}}$} \!\mathord{\left/ {\vphantom {{\dot{N}} N}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$N$}}} \right) = m\frac{d}{dt}\left\{ {\left( {{\raise0.7ex\hbox{$P$} \!\mathord{\left/ {\vphantom {P N}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$N$}}} \right) - \left( {{\raise0.7ex\hbox{$P$} \!\mathord{\left/ {\vphantom {P N}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$N$}}} \right)_{\infty } } \right\} $$

(29)

Using Eq. 14 for the right side of Eq. 29 and substituting for $\left\{ {\left( {{\raise0.7ex\hbox{$P$} \!\mathord{\left/ {\vphantom {P N}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$N$}}} \right) - \left( {{\raise0.7ex\hbox{$P$} \!\mathord{\left/ {\vphantom {P N}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$N$}}} \right)_{\infty } } \right\}$ from Eq. 11 produces

$$ \frac{d}{dt}\left( {{\raise0.7ex\hbox{${\dot{N}}$} \!\mathord{\left/ {\vphantom {{\dot{N}} N}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$N$}}} \right) = - {\frac{1}{{m^{2} }}}\left[ {\alpha_{1} m^{2} \left( {{\raise0.7ex\hbox{${\dot{N}}$} \!\mathord{\left/ {\vphantom {{\dot{N}} N}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$N$}}} \right) + \alpha_{2} m\left( {{\raise0.7ex\hbox{${\dot{N}}$} \!\mathord{\left/ {\vphantom {{\dot{N}} N}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$N$}}} \right)^{2} + \alpha_{3} \left( {{\raise0.7ex\hbox{${\dot{N}}$} \!\mathord{\left/ {\vphantom {{\dot{N}} N}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$N$}}} \right)^{3} } \right]\, $$

(30)

The chain rule provides the substitution $\frac{d}{dt}\left( {{\raise0.7ex\hbox{${\dot{N}}$} \!\mathord{\left/ {\vphantom {{\dot{N}} N}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$N$}}} \right) = N\left( {{\raise0.7ex\hbox{${\dot{N}}$} \!\mathord{\left/ {\vphantom {{\dot{N}} N}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$N$}}} \right)\frac{d}{dN}\left( {{\raise0.7ex\hbox{${\dot{N}}$} \!\mathord{\left/ {\vphantom {{\dot{N}} N}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$N$}}} \right)$ that transforms Eq. 30 to Eq. 15.