1 Introduction

Finding a simple curve or a justified equation that fit experimental data well is a standard problem in population dynamics, since the result allows improving predictions about future dynamics of the population. Exponential and logistic curves are classical examples for describing unrestrained and environmentally restrained population growth, respectively. The procedures for finding the best fitting curves within a certain class of formulas (equations) are well developed, and the problem is often considered to be solved when an appropriate curve is found. For instance, tumor growth can be described by logistic or Gompertz curves, and there exists a relatively extensive discussion about which curve is better, see for instance (Benzekry et al. 2014). Similarly, this question arises in describing microbial growth, which is crucial in food preservation and disease prevention (Peleg and Corradini 2011). In some cases, the predictive power of the obtained model can be evaluated experimentally, such as in cases of cancer cell or microbial growth. In other cases, due to large time scales or difficulties in experimental design, such validation is not possible, making predictions made by models is critical, such as in making policy decisions (see for instance Heesterbeek et al. 2015; Rönn et al. 2017; Verguet et al. 2015). Finding the right curve to describe the trends observed in global demography is another example, where finding a correct equation influences dramatically the predictions about future human population growth (von Forster et al. 1960; Kapitza 1996, 2006; Karev 2005).

Here, however, we are interested in investigating a different angle of the data-equation relationship: if a data set is best fit by a particular curve, what information about intrinsic population dynamics can be derived from this result? That is, we are interested not in making predictions about future population dynamics, but in inferring information about possible population structure and conditions, under which the population must have been growing, based on the data that have been collected.

Data that describe tumor growth dynamics, for instance, can be fit to various, often similarly shaped curves (e.g., logistic and Gompertz curves). We will use the demographic and tumor growth curves available in the literature as examples in the discussion of implications of our results.

2 Models of Polymorphic Populations

Natural selection and drift can operate only if the population is non-homogeneous. Models of heterogeneous populations are typically of very high or even infinite dimensionality. An effective method for reduction in a wide class of infinitely dimensional non-homogeneous models to low dimensionality was recently developed (see Karev 2005, 2010, 2014).

All models discussed here are of the following form. Consider an inhomogeneous population composed of individuals with different Malthusian parameters a. We refer to the set of all individuals that have a given value of the parameter a as an a-clone. Let \(l\left( {t,a} \right) \) be the size of a-clone at the moment t. The total size of the population is given by \(N(t)=\sum \nolimits _A l (t,a)\) if the parameter a takes on discrete values, and \(N(t)=\int _A l (t,a)\mathrm{d}a\) if a is continuous. A denotes the range of possible values of parameter a.

If the growth rate of the population depends on its total size \(N\left( t \right) \), then the dynamics of such a population can be described by the following model:

$$\begin{aligned} \frac{\mathrm{d}l\left( {t,a} \right) }{\mathrm{d}t}=al\left( {t,a} \right) g\left( N \right) , \quad N\left( t \right) =\mathop \int \limits _{A} l\left( {t,a} \right) \mathrm{d}a \end{aligned}$$
(1)

where \(g\left( N \right) \) is a function that accounts for intrapopulation competition between the individuals.

Denote \(P\left( {t,a} \right) =\frac{l\left( {t,a} \right) }{N\left( t \right) }\); the probability density function (pdf) \(P\left( {t,a} \right) \) describes the distribution of the parameter a within the population in t moment. We assume that the initial pdf \(P\left( {0,a} \right) \) is given; let \(M_0 \left( \lambda \right) =\int _A {\mathrm{e}^{\lambda a}} P\left( {0,a} \right) \mathrm{d}a\) be its moment generating function (mgf). Note: henceforth units are set as generic “time” and “population size” as necessary to balance them on both sides of the equations; specific units are used for relevant examples.

Here, we are interested in describing the dynamics of pdf \(P\left( {t,a} \right) \) and population size \(N\left( t \right) \) as they change over time. In order to solve this problem, let us define formally the “keystone” auxiliary variable \(q\left( t \right) \) as the solution to the Cauchy problem

$$\begin{aligned} \frac{\mathrm{d}q}{\mathrm{d}t}=g\left( N \right) ,q\left( 0 \right) =0. \end{aligned}$$
(2)

The clone densities and population size can be expressed with the help of \(q\left( t \right) \):

$$\begin{aligned} l\left( {t,a} \right)= & {} l\left( {0,a} \right) \mathrm{e}^{{aq}\left( t \right) }=N\left( 0 \right) P\left( {0,a} \right) \mathrm{e}^{{aq}\left( t \right) }, \end{aligned}$$
(3)
$$\begin{aligned} N\left( t \right)= & {} N\left( 0 \right) \mathop \int \limits _A \mathrm{e}^{{aq}\left( t \right) }P\left( {0,a} \right) \mathrm{d}a=N\left( 0 \right) M_0 \left( {q\left( t \right) } \right) . \end{aligned}$$
(4)

Now, Eq. (2) for the auxiliary variable \(q\left( t \right) \) can be written in a closed form

$$\begin{aligned} \frac{\mathrm{d}q}{\mathrm{d}t}=g\left( {N\left( 0 \right) M_0 \left( {q\left( t \right) } \right) } \right) , \quad q\left( 0 \right) =0. \end{aligned}$$
(5)

Now that we have the solution to Eq. (5), we can completely solve the initial problem (1).

The population size \(N\left( t \right) \) is given by Eq. (4) and solves the equation

$$\begin{aligned} \frac{\mathrm{d}N}{\mathrm{d}t}=E^{t}\left[ a \right] N(t)g\left( {N(t)} \right) \end{aligned}$$
(6)

where \(E^{t}\left[ a \right] =\int _A {aP(t,a)\mathrm{d}a} \) is the mean value of a at t moment. The current parameter distribution \(P\left( {t,a} \right) \) is determined by the formula

$$\begin{aligned} P\left( {t,a} \right) =P\left( {0,a} \right) \mathrm{e}^{q\left( t \right) a}/M_0 \left( {q\left( t \right) } \right) . \end{aligned}$$
(7)

The mgf of the current distribution \(P\left( {t,a} \right) \) is given by

$$\begin{aligned} M_t \left( \delta \right) =E^{t}\left[ {\mathrm{e}^{\delta a}} \right] =M_0 \left( {\delta +q\left( t \right) } \right) /M_0 \left( {q\left( t \right) } \right) . \end{aligned}$$

The mean value of distributed parameter a is given by the formula

$$\begin{aligned} E^{t}\left[ a \right]= & {} M_0^{\prime }\left( {q\left( t \right) } \right) /M_0 \left( {q\left( t \right) } \right) \end{aligned}$$
(8)

and solves the equation

$$\begin{aligned} \frac{\mathrm{d}E^{t}\left[ a \right] }{\mathrm{d}t}= & {} \mathrm{Var}^{t}\left[ a \right] g\left( {N(t)} \right) . \end{aligned}$$
(9)

The derivation of these formulas can be found in Karev (2010).

In what follows we show that some nonstandard curves of population growth that account for different stages in population development, as well as standard exponential and logistic curves, can be understood and explained within the frameworks of models of the type (1), which take into account the process of natural selection within the population.

3 Inhomogeneous F-Model for Exponential Curve

As an introductory example, let us consider the simplest inhomogeneous Malthusian model of a population growth. Capacity to grow exponentially under ideal environmental conditions is generally considered a common property of most populations.

Assume a population is composed of clones \(l\left( {t,a} \right) \) characterized by their relative growth rate (Malthusian parameter) a, such that

$$\begin{aligned} \frac{\mathrm{d}l\left( {t,a} \right) }{\mathrm{d}t}=al\left( {t,a} \right) . \end{aligned}$$
(10)

Then according to Eqs. (6) and (9)

$$\begin{aligned} \frac{\mathrm{d}N}{\mathrm{d}t}=E^{t}\left[ a \right] N \quad \mathrm{and}\quad \frac{\mathrm{d}E^{t}\left[ a \right] }{\mathrm{d}t}=\mathrm{Var}^{t}\left[ a \right] >0. \end{aligned}$$
(11)

This is the simplest version of the Fisher’s Fundamental theorem (Fisher 1958). It means that the per capita population growth rate, which is equal to \(E^{t}\left[ a \right] \), is not a constant, as is necessary for exponential growth, but increases with time with the rate \(\mathrm{Var}^{t}\left[ a \right] \) > 0, i.e., as long as the population remains inhomogeneous. Hence, an inhomogeneous population composed of different exponentially growing clones can never demonstrate exponential growth, but instead grows with “acceleration” of relative growth rate proportional to \(\mathrm{Var}^{t}\left[ a \right] \).

This may cause dramatic dynamical behavior, such as population size “blowing up,” i.e., tending to infinity in finite time (Karev 2005). Hence, one may conclude that in order for a population to grow exponentially, it must be homogeneous, such as when the process of natural selection has already been completed, resulting in a single type of the fittest survivor. This is likely to take a long time, so the population will probably face environmental restrictions, such resource limitations, which would prevent its free exponential growth and generate the struggle for existence, leading to natural selection.

This means that at both ends of the temporal scale, an inhomogeneous population composed of Malthusian clones cannot show exponential growth, either in the beginning of the population development when it grows over-exponentially, or at its end when it grows under-exponentially, possibly tending to an equilibrium, excluding a short transitional period between these two regimes.

Considering that all natural biological populations are inhomogeneous, we may ask the following question: do there exist models of inhomogeneous populations that demonstrate exponential/logistic growth of the total population size on the entire time scale? The answer is affirmative. Namely, both Malthusian and logistic equations describe the growth of total population size of specific inhomogeneous frequency-dependent models (F-models for brevity). By definition, F-models are models, where the growth rate of a clone is proportional to its frequency in the total population.

The simplest example of F-model is the model of Malthusian-type

$$\begin{aligned} \frac{\mathrm{d}l\left( {t,a} \right) }{\mathrm{d}t}=\frac{k}{N(t)}al(t,a)=kaP\left( {t,a} \right) . \end{aligned}$$
(12)

A possible rationalization of this as well as more general frequency-dependent models is as follows. Assume that the growth rate of individuals within the population is controlled by a limiting external factor or resource measured by parameter k, which is divided uniformly between all individuals, resulting in the term k / N. Then, the growth rate of a clone depends on its frequency. This resource can be dynamic and increase together with population size up to the saturation stage. Conversely, if a population grows in accordance with the F-model; then, we can assume that the population growth is controlled by an external dynamic resource, and individuals have equal probability of using this resource for reproduction.

Let us assume that the initial distribution \(P\left( {0,a} \right) \) of the parameter a in F-model (12) is exponential with the mean \(N\left( 0 \right) \),

$$\begin{aligned} P\left( {0,a} \right) =\frac{1}{N\left( 0 \right) }\mathrm{e}^{-\frac{a}{N\left( 0 \right) }}, \quad 0\le a<\infty . \end{aligned}$$
(13)

Then, the solution to the F-model (12), (13) is given by the formula (see Karev 2014 for details)

$$\begin{aligned} l\left( {t,a} \right) =\mathrm{e}^{-\frac{a}{N\left( 0 \right) }\mathrm{e}^{-kt}} \end{aligned}$$
(14)

and \(N\left( t \right) =\mathop \smallint \limits _0^\infty l\left( {t,a} \right) \mathrm{d}a=\mathop \smallint \limits _0^\infty \mathrm{e}^{-a/N(0)\mathrm{e}^{-kt}}\mathrm{d}a=N(0)\mathrm{e}^{kt}\) solves the Malthusian equation \(\frac{\mathrm{d}N}{\mathrm{d}t}=kN\).

An important corollary follows from these results. The inhomogeneous population described by the F-model (12), (13), which shows exponential growth of the total population size, consists of clones, each of which grows according the Gompertz curve (14) (see Online Appendix 1 for a brief survey of the Gompertz model).

The results of this section can be summarized as follows. A monomorphic population in ideal conditions may grow exponentially; however, if the exponentially growing population is polymorphic, then one can hypothesize that (a) the population is composed of Gompertzian clones; (b) the growth of the population is not free but depends on an external resource, which is distributed uniformly between the individuals and hence proportionally to the clone frequencies in the total population, thus limiting the growth rate of the population at each time moment.

4 F-Model for the Logistic Curve

Now let us construct a model of an inhomogeneous population that shows logistic growth of the total population size,

$$\begin{aligned} \frac{\mathrm{d}N}{\mathrm{d}t}=kN\left( {1-\frac{N}{C}} \right) . \end{aligned}$$
(15)

Its solution is given by the formula \(N\left( t \right) =\frac{C}{1+(C/N\left( 0 \right) -1)\mathrm{e}^{-kt}}\).

Firstly, let us consider an inhomogeneous population composed of different clones \(l\left( {t,a} \right) \), which now grow according to the logistic equation

$$\begin{aligned} \frac{\mathrm{d}l\left( {t,a} \right) }{\mathrm{d}t}=kal\left( {t,a} \right) \left( {1-\frac{N}{B}} \right) , \end{aligned}$$
(16)

where B is a common carrying capacity.

Then, according to (6), (9)

$$\begin{aligned}&\frac{\mathrm{d}N}{\mathrm{d}t}=kE^{t}\left[ a \right] N(t)\left( {1-\frac{N}{B}} \right) \quad \mathrm{and}\quad \frac{\mathrm{d}E^{t}\left[ a \right] }{\mathrm{d}t}=k\mathrm{Var}^{t}\left[ a \right] \left( {1-\frac{N}{B}} \right) ~>~0 \quad \mathrm{as}\quad N<B. \end{aligned}$$

Hence, an inhomogeneous population composed of different logistically growing clones grows not exactly logistically, but instead always grows faster during the initial phase of growth.

Now, instead of model (16) let us consider the following logistic-like F-model

$$\begin{aligned} \frac{\mathrm{d}l\left( {t,a} \right) }{\mathrm{d}t}= & {} kaP\left( {t,a} \right) \left( {1-\frac{N}{C}} \right) . \end{aligned}$$
(17)

Then, \(\frac{\mathrm{d}N}{\mathrm{d}t}=kE^{t}\left[ a \right] \left( {1-\frac{N}{C}} \right) \). In order to obtain logistic equation (15) we need to have \(E^{t}\left[ a \right] =N\left( t \right) \). To this end, introduce an auxiliary variable \(q\left( t \right) \), which solves the equation

$$\begin{aligned} \frac{\mathrm{d}q}{\mathrm{d}t}= & {} k\left( {1-\frac{N}{C}} \right) \Big /N,q\left( 0 \right) =0. \end{aligned}$$
(18)

According to (8), \(E^{t}\left[ a \right] =M_0^{\prime }\left( {q\left( t \right) } \right) /M_0 \left( {q\left( t \right) } \right) \). Taking into account Eq. (4), we arrive at the following equation for the unknown mgf \(M_0 \left( q \right) \):

$$\begin{aligned} \frac{\mathrm{d}M_0 \left( q \right) }{\mathrm{d}q}=N\left( 0 \right) M_0 \left( q \right) ^{2}, \quad M_0 \left( 0 \right) =1. \end{aligned}$$

Its solution is \(M_0 \left( q \right) =\left( {1-N\left( 0 \right) q} \right) ^{-1}\). This mgf corresponds to exponential distribution (13).

We can now write Eq. (18) in explicit form

$$\begin{aligned} \frac{\mathrm{d}q}{\mathrm{d}t}=k\left( {\frac{1}{N(t)}-\frac{1}{C}} \right) =k\left( {\frac{1}{N\left( 0 \right) M_0 \left( {q(t)} \right) }-\frac{1}{C}} \right) =k\left( {\frac{1}{N\left( 0 \right) }-\frac{1}{C}-q(t)} \right) . \end{aligned}$$

Its solution is given by \(q\left( t \right) =\left( {\frac{1}{N\left( 0 \right) }-\frac{1}{C}} \right) \left( {1-\mathrm{e}^{-kt}} \right) \), and hence

$$\begin{aligned} l\left( {t,a} \right) =N\left( 0 \right) P\left( {0,a} \right) \mathrm{e}^{aq\left( t \right) }=\exp \left( -a\left( {\frac{1}{C}+\left( {\frac{1}{N\left( 0 \right) }-\frac{1}{C}} \right) \hbox {e}^{-kt}} \right) \right) . \end{aligned}$$
(19)

One can easily check that \(N\left( t \right) =\mathop \smallint \limits _0^\infty l\left( {t,a} \right) \mathrm{d}a\) coincides with the solution to Eq. (15).

Let us now collect the obtained results in the following Theorem.

Theorem 1

Logistic equation (15) describes the dynamics of the total size of an inhomogeneous population growing according to F-model (17), where initial distribution of the parameter a is exponential (13) with the mean \(N\left( 0 \right) \). The solution to the F-model (17), (13) is given by Eq. (19). The distribution of the parameter a at moment t is exponential with the mean \(E^{t}\left[ a \right] =N\left( t \right) \).

We can see that each clone \(l\left( {t,a} \right) \) grows according to the Gompertz curve \(G\left( t \right) =r\exp (-be^{-kt})\) with \(r=\mathrm{e}^{-\frac{a}{C}}\) and \(b=\frac{a}{N\left( 0 \right) }-\frac{a}{C}\). This means that, similarly to the exponential population, a population that grows according to logistic equation (15) can be an inhomogeneous population composed of the Gompertzian clones.

Using the model given in Theorem 1 to describe dynamics of populations can be considered unrealistic, since the described population would contain clones with arbitrarily large values of parameter a. However, the contribution of clones with large values of the parameter a to the total population size is negligible. Indeed, let us denote \(N\left( {t,B} \right) =\mathop \smallint \limits _0^B l\left( {t,a} \right) \mathrm{d}a\). Then

$$\begin{aligned} \begin{array}{l} N\left( {t,B} \right) =\frac{C}{1+\mathrm{e}^{-kt}(C/N(0)-1)}\left( 1-\mathrm{e}^{-\frac{B\mathrm{e}^{-kt}(C+N(0)(\mathrm{e}^{kt}-1))}{CN(0)}}\right) \\ \end{array}. \end{aligned}$$

So, \(\frac{N\left( {t,B} \right) }{N\left( t \right) }\approx 1-\mathrm{e}^{-B/C}\) for large t.

Hence, \(N\left( {t,B} \right) \) gives a very good approximation of the exact solution to the logistic equation if \(\frac{B}{C}\sim 6-10\), in this case \(\mathrm{e}^{-B/C}\sim 0.0025-0.000045\).

Examples: Logistic versus Gompertz curves

Consider the following data set, which was extrapolated from Figure 3 in Biebricher et al. (1985).

As can be seen in Fig. 1 here, data set 1 (see Online Appendix 2 for details) is fit better by the logistic equation, from which we can imply that the studied population is more likely to be heterogeneous.

Fig. 1
figure 1

(Color figure online) Fitting of data set 1, obtained from Figure 3 in Biebricher et al. (1985), see Online Appendix 2 for data values. a Fitting with logistic curve, defined by \(\frac{\mathrm{d}N}{\mathrm{d}t}=kN\left( {1-\frac{N}{C}} \right) \), with C = 80.64, N(0) = 0.006 and k = 0.238. b Fitting with the Gompertz model, \(N\left( t \right) =N\left( 0\right) \exp (b\left( {1-\mathrm{e}^{-kt}} \right) ),\) with b = 4.732, k = 0.052, N(0) = 0.71. Parameter estimations were obtained using cftool in MATLAB

Full size image

The results obtained in this section can have important implications.

Assume there exist experimental data on population growth, but no a priori assumptions have been made about processes that govern its growth. Assume the logistic curve fits the data better than the Gompertz curve. Then, the population is more likely to be polymorphic than monomorphic, and in this case, it is composed from different Gompertzian clones.

Fig. 2
figure 2

(Color figure online) Examples of hyperbolic and two-phase growth curves obtained from published literature. a tumor growth curves reported Figure 1D in Naumov et al. (2006). b and c tumor growth curves reported in Figure 2b,i in Rogers et al. (2014). d World population since 10,000 BCE, reported at https://ourworldindata.org/world-population-growth/, plotted in logarithmic scale. Data sources include History Database of the Global Environment (HYDE) for before 1900, the UN publication “The World at Six Billion” for 1900–1940 and the UN’s World Population Prospects: the 2015 Revision for 1950–2015. e World population data plotted since year 0, to avoid potential issues with data extrapolation BC. f World population data plotted in logarithmic scale from year 1750

Full size image

Furthermore, assume one can determine that the population is indeed polymorphic. Then, one may assume that population growth is controlled by an external limiting factor (e.g., a dynamic resource) at all stages of population development, not only when the population size becomes large. Determination of this external factor may be of crucial interest, especially for such populations as tumor cells (Marusyk and Polyak 2010; Marusyk et al. 2012). This will be discussed in greater detail in following sections.

Remark

Different generalizations of the standard logistic equation are well described in the literature and have been applied to many specific problems, (see, e.g., Tsoularis and Wallace 2002; Peleg and Corradini 2011); most of them are special cases of the generalized logistic equation

$$\begin{aligned} \frac{\mathrm{d}N}{\mathrm{d}t}=kN^{\alpha }\left[ {1-\left( {\frac{N}{C}} \right) ^{\beta }} \right] ^{\gamma } \end{aligned}$$

where \(\alpha ,\beta ,\gamma \) are the model parameters. Similar to standard logistic equation and using the same method, we can show that the generalized logistic equation describes the dynamics of total size of an inhomogeneous population composed from clones \(l\left( {t,a} \right) =N\left( 0 \right) P\left( {0,a} \right) \mathrm{e}^{{aq}(t)}, \) where initial distribution of the parameter a is exponential (13). The difference with standard logistic equation is that now the key variable \(q\left( t \right) \) is not Gompertzian but is a solution to the equation

$$\begin{aligned} \frac{\mathrm{d}q}{\mathrm{d}t}= & {} N^{\alpha -1}\left[ 1-\left( \frac{N}{C}\right) ^{\beta }\right] ^{\gamma },\\ N\left( t \right)= & {} N\left( 0 \right) \left( {1-N\left( 0 \right) q} \right) ^{-1}, \quad q\left( 0 \right) =0. \end{aligned}$$

5 Hyperbolic and Hyperbolic–Exponential Growth

Curves that have hyperbolic shape have been observed in a variety of circumstances, ranging from tumor growth curves (Almog et al. 2006; Naumov et al. 2006; Rogers et al. 2014) to global demography (von Forster et al. 1960; Kapitza 2006). Some examples reported in the literature can be seen in Fig. 2.

Note: World population data since 10,000 B.C. were reported at https://ourworldindata.org/world-population-growth/. Certainly, there is no truly reliable information about actual world population size BC. The data set is plotted in Fig. 2d in the logarithmic scale; it clearly reveals that population size in the years BC was estimated under assumption that it grew exponentially. However, it seems that this assumption may have been incorrect, as suggested by the plot of world population data, in logarithmic scale since year 0 (see Fig. 2e). A closer look at these data clearly shows that before the middle of the twentieth century, population grows not exponentially, but faster, i.e., that Malthusian parameter was not a constant but increased in time. It was shown in von Forster et al. (1960), Kapitza (1996, 2006) that these data are fitted well by hyperbolic curve. There is no reason to assume that the growth law changed sharply after year 0 AD; therefore, a more reasonable assumption is that the hyperbolic growth law should be used to extrapolate the size of world population B.C. In contrast, after 1960 the hyperbolic growth indeed was followed by exponential growth, and then possibly by the saturation stage, see Fig. 2f. A model that shows all three hyperbolic–exponential–saturation stages was constructed in Karev (2005). Estimation of the time and level of saturation stage is a challenge; an interesting attempt was done by Kapitza (1996, 2006).

In this section, we will look at model types that can reproduce hyperbolic and hyperbolic–exponential growth curves. We will start with a simple parametrically heterogeneous Malthusian growth model, which was briefly discussed in an earlier section. Here, we will give the main results, since a more detailed discussion has previously been published in Karev (2005) in application to global demography, and in Kareva (2016) in application to tumor dormancy.

Consider a population of clones that grow with their own intrinsic growth rates, independently of other clones and of the population as a whole. Then, dynamics of these clones is given by the Malthusian equation (10), \(\frac{\mathrm{d}l\left( {t,a} \right) }{\mathrm{d}t}=al\left( {t,a} \right) \). If the initial distribution P(0, a) is the Gamma-distribution, then its mgf \(M_0 \left( t \right) =(1-st)^{-k}\), \(t<1/s\), \(k>0\). As a special case, \(k=1\) for exponential distribution.

In these cases, the total population size \(N\left( t \right) =N(0)M_0 (t)=N(0)(1-st)^{-k}\) shows hyperbolic growth, and \(N\left( t \right) \) increases very slowly at the initial stage of population growth, and then tends quickly to infinity at the moment of “population explosion” \(T=\frac{1}{s}\), see Fig. 2d.

This unrealistic scenario becomes actualized when the Malthusian parameter a can take arbitrarily large values, which can be avoided through truncating the initial distribution of parameter a to be restricted to a finite interval.

Let the initial distribution be truncated exponential in the interval [0, B], resulting in pdf

$$\begin{aligned} P\left( {0,a} \right) =Ce^{-sa} \quad \mathrm{for}\quad 0\le a\le B, \end{aligned}$$
(20)

where \(C=1/\mathop \smallint \limits _0^B \mathrm{e}^{-sa}sa=\frac{s}{1-\hbox {e}^{-Bs}}\) is the normalization constant. The mgf of the truncated exponential distribution is given by the formula

$$\begin{aligned} M_0 (t)=\int _0^B {\mathrm{e}^{at}} P(0,a)\mathrm{d}a=\frac{\left( {\hbox {e}^{Bs}-\hbox {e}^{Bt}} \right) s}{\left( {1-\hbox {e}^{Bs}} \right) \left( {t-s} \right) } \end{aligned}$$
(21)

and hence

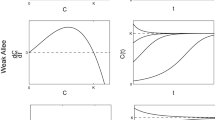
$$\begin{aligned} N\left( t \right) =N(0)M_0 (t)=N(0)\frac{\left( {\hbox {e}^{Bs}-\hbox {e}^{Bt}} \right) s}{\left( {1-\hbox {e}^{Bs}} \right) \left( {t-s} \right) }. \end{aligned}$$
(22)

Inhomogeneous Malthusian models (10) with any initial distribution concentrated in a bounded interval, \(a\in \left[ {0,B} \right] ,\) possess some common interesting properties. According to Equations (6), the population relative growth rate, which is equal to \(E^{t}\left[ a \right] \), increases with time as long as \(\mathrm{Var}^{t}\left[ a \right] \) > 0. Hence, if the initial distribution is not concentrated in a single point, then \(E^{t}\left[ a \right] \) tends to the maximal possible value of a, \(E^{t}\left[ a \right] \rightarrow B\). Then, the growth of the population will be asymptotically exponential with the growth rate equal to B. These phenomena are illustrated in Fig. 3b, where one can see that \(E^{t}\left[ a \right] \) increases very slowly for a long time and then suddenly undergoes rapid increase and tends to the maximal value of B.

Fig. 3
figure 3

(Color figure online) Fitting of inhomogeneous Malthusian model with initial truncated exponential distribution to world population data, reported at https://ourworldindata.org/world-population-growth/. Parameters are taken as B = 0.12, s = 2000. a Demographic data together with model predictions, tracking the dynamics over time of total population size \(N\left( t \right) \). b Change over time of the expected value of Malthusian parameter a, \(E^{t}[a]\), during the transition from hyperbolic to exponential phase of the model; c change over time of variance of the Malthusian parameter a, \({\mathrm{Var}}^{t}[a]\), during the transition from hyperbolic to exponential phase of the model. Deviation of model solution from real data around 1400 is partly explained by decline of the world population due to the Black Plague epidemic in Europe, in years 1346–1353

Full size image

The transition from hyperbolic to exponential phase of population growth is known as “demographic transition” (Kapitza 1996). Noticeably, the mean value \(E^{t}\left[ a \right] \), which in this case is equal to the relative growth rate of the total population, starts increasing sharply and tends to its maximal possible value; at this time, the population transitions to the stage of exponential growth. According to the mathematical model developed in Karev (2005), this transition is clearly connected with the behavior of the variance of Malthusian parameter a. During this short period one can observe a sharp bell-shaped growth and rapid decrease in variance (see Fig. 3c). This model prediction was endorsed by analysis of demographic data given in Tolstikhina et al. (2013).

5.1 Tumor Dormancy and Inhomogeneous Malthusian Growth

The simple inhomogeneous Malthusian-type model (10), (20) allows reproducing qualitatively a growth pattern of prolonged slow growth before a growth spurt through solely incorporating population heterogeneity in the model. One may conclude that the “dormancy” effect in tumor development (Folkman and Kalluri 2004; Almog et al. 2006; Naumov et al. 2006; Kareva 2016), i.e., the sudden exponential growth of a population of cancer cells after a long period of non-detected presence may be the evidence that the tumor is composed of clones, which grow freely and independently of both each other and of the population as a whole. In this case, each clone would have its own Malthusian growth rate, and the distribution of the Malthusian rates is skewed to very small values, similarly to truncated exponential distribution. Asymptotically, the growth rate of the tumor in the stage of exponential development is equal to the maximal value of the growth rate of the clones. This hypothesis, as well as application of other parametrically heterogeneous models to understanding tumor dormancy, is discussed in Kareva (2016).

Overall, if the hyperbolic–exponential growth of a population is observed, then one may hypothesize that the population is inhomogeneous and is composed of independent exponentially growing clones; the relative growth rates of the clones follow truncated exponential distribution. If it is the case, then the transition from hyperbolic to exponential phase should be accompanied by underlying sharp growth of the mean population growth rate and by a sharp bell-shaped curve of its variance, as demonstrated with demographic data in Fig. 3c.

6 Exponential–Linear Growth

Another type of a model that can qualitatively replicate the two-stage dynamics observed in Fig. 2c is the exponential–linear model, constructed within the frameworks of F-models.

Let us once again consider Malthusian-type F-model

$$\begin{aligned} \frac{\mathrm{d}l\left( {t,a} \right) }{\mathrm{d}t}=kal\left( {t,a} \right) /N(t)=kaP\left( {t,a} \right) \end{aligned}$$
(23)

and assume that the initial distribution of the Malthusian parameter is truncated exponential (20) concentrated in the interval \(\left[ {0,B} \right] \). According to Eqs. (6) and (9), \(\frac{\mathrm{d}N}{\mathrm{d}t}=kE^{t}\left[ a \right] \) and \(\frac{\mathrm{d}E^{t}\left[ a \right] }{\mathrm{d}t}=\frac{k}{N\left( t \right) }\mathrm{Var}^{t}\left[ a \right] .\) Therefore, \(E^{t}\left[ a \right] \) increases monotonically as long as \(\mathrm{Var}^{t}\left[ a \right] >0\), and \(E^{t}\left[ a \right] \rightarrow B\), implying asymptotical linear growth of N.

Next, let us define the auxiliary variable by the equation

$$\begin{aligned} \frac{\mathrm{d}q}{\mathrm{d}t}=\frac{k}{N},q\left( 0 \right) =0. \end{aligned}$$
(24)

The mgf of truncated exponential distribution (20) is given by formula (21). Therefore, according to Eq. (7), the total population size is given by

$$\begin{aligned} N\left( t \right) =N\left( 0 \right) M_0 \left( {q(t)} \right) =N\left( 0 \right) \frac{s\left( {1-\mathrm{e}^{B(q(t)-s)}} \right) }{\left( {1-\mathrm{e}^{-Bs}} \right) (s-q(t))}. \end{aligned}$$
(25)

Equations (24) and (25) make up our model.

With a solution to these equations, we can compute all statistical characteristics of interest:

$$\begin{aligned} P\left( {t,a} \right)= & {} \frac{\mathrm{e}^{aq\left( t \right) }}{M_0 \left( {q\left( t \right) } \right) }P\left( {0,a} \right) =\frac{\mathrm{e}^{a\left( {q\left( t \right) -s} \right) }(q\left( t \right) -s)}{\mathrm{e}^{B(q(t)-s)}-1}, \end{aligned}$$
(26)
$$\begin{aligned} E^{t}\left[ a \right]= & {} \mathop \smallint \limits _0^B aP\left( {t,a} \right) \mathrm{d}a=\frac{b}{1-\mathrm{e}^{b(s-q\left( t \right) )}}+\frac{1}{s-q\left( t \right) }. \end{aligned}$$
(27)

For the purposes of analysis and computation, we can write the model (24), (25) in equivalent form:

$$\begin{aligned} \begin{array}{l} \frac{\mathrm{d}q}{\mathrm{d}t}=\frac{k}{N\left( t \right) }, \\ \frac{\mathrm{d}N}{\mathrm{d}t}=kN\left( 0 \right) E^{t}\left[ a \right] =kN(0)\left( \frac{B}{1-\mathrm{e}^{B(s-q\left( t \right) }}+\frac{1}{s-q\left( t \right) }\right) . \\ \end{array} \end{aligned}$$
(28)

The initial growth stages of populations described by Eq. (23) with initial exponential and truncated exponential distributions are very similar if the value of boundary B is large and hence the initial dynamics of model \(N\left( t \right) \) defined by Eq. (25) or (28) is close to exponential.

For example, consider the initial truncated exponential distribution as defined in Eq. (20) with s = 1 and different values of the boundary B. As can be seen in Fig. 4, for large values of B, in the initial stages of growth the population increases exponentially (i.e., \(\log N(t)\) in Fig. 6a approximates well a linear function with respect to t). Then, after a transitional period, the shape of the curve changes and the population grows linearly (see Fig. 4b).

Fig. 4
figure 4

(Color figure online) Plots of N(t) as defined in Eq. (25) with different values of boundary B. a In the initial stages, the population grows exponentially, as is confirmed by logarithmic transformation of the growth curve. b At later time points, the population starts growing linearly

Full size image

Overall, we have arrived to the following statement.

Theorem 2

F-model (23) implies asymptotically linear growth of the total population size for any initial distribution of the distributed parameter a concentrated on a bounded interval. If the initial distribution is truncated exponential, then the model predicts exponential–linear population growth.

Fig. 5
figure 5

Schematic representation of three phases of replication process. Figure is adapted from Schuster (2011)

Full size image

The results obtained in this section can be summarized as follows. The nonstandard exponential–linear dynamics may be the evidence that the population (e.g., tumor cells) is inhomogeneous and is composed of clones such that distribution of their growth rates is close to truncated exponential distribution. Even more importantly, the population growth may be controlled by an external (possibly dynamic) factor or resource at all stages of population development, such that the resource is distributed uniformly between individuals within the population. These assumptions and the corresponding conceptual model compose a null-hypothesis that can explain the exponential–linear growth of a population. A more detailed model should contain a description of the controlling resource dynamics. For example, tumor growth depends on blood vessels and is controlled by the process of angiogenesis (Kareva et al. 2016); tumor cells also require nutrients, such as carbon and phosphorus, to support accelerated proliferation (Elser et al. 2007; Kareva 2013). Another example is presented in the following section.

7 Three-Stage Model and Virus-Specific RNA Replication

The models considered above that show indefinite growth of population size such as hyperbolic–exponential or exponential–linear models are clearly incomplete as populations cannot grow indefinitely. In most (but not all) cases, population growth is followed by a saturation stage. A model that shows hyperbolic–exponential–saturation growth in application to global demography was suggested and identified in Karev (2005).

In the works (Biebricher et al. 1983, 1985), the authors have proposed that in a closed system, where there exists no exchange of materials with the environment, the RNA replication process goes through three phases: exponential growth, linear growth and saturation. A schematic representation of the proposed kinetics of RNA replication, as adapted from Schuster (2011), is shown in Fig. 5.

In their original work, Biebricher et al. (1983, 1985) had the following hypothesis about the kinetics of RNA replication in closed systems. They proposed that “the time course of RNA replication by \(\hbox {Q}\beta \)-replicase shows three distinct growth phases: (i) an exponential phase, (ii) a linear phase and (iii) a phase characterized by saturation through product inhibition. The experiment was initiated by transfer of a very small sample of RNA suitable for replication into a medium containing \(\hbox {Q}\beta \)-replicase and the activated monomers, ATP, UTP, GTP and CTP in excess (consumed materials are not replenished in this experiment). In the phase of exponential growth, there was shortage of RNA templates, every free RNA molecule is instantaneously bound to an enzyme molecule and replicated, and the corresponding overall kinetics follows \(\frac{\mathrm{d}x}{\mathrm{d}t}=fx\) resulting in \(x\left( t \right) =x\left( 0 \right) \hbox {exp}(ft)\). In the linear phase, the concentration of template was exceeding that of enzyme, every enzyme molecule is engaged in replication, and overall kinetics is described by \(\frac{\mathrm{d}x}{\mathrm{d}t}=k_0 e_0 \left( E \right) =k,\) wherein \(e_0 \left( E \right) \) is the total enzyme concentration, and this yields after integration \(x\left( t \right) =x\left( 0 \right) +kt.\)”

The schematic given in Fig. 5 is somewhat exaggerated compared to the data that the authors cited, presumably to emphasize the transition from exponential to linear phase. In the reported data, the transition is smoother. Notably, the authors proposed describing the transition between three stages of growth using several separate models, which does not allow understanding how transition between the three stages can occur naturally, as a result of system dynamics.

Our numerical estimates of some of the reported data [such as curves reported in Biebricher et al. (1985)] are fitted well by a logistic model (see Fig. 1). However, there does exist a model that can realize all three regimes. Such a model can be constructed in the following way.

We have already shown that transition from exponential to linear growth can be described by an inhomogeneous F-model with a distributed Malthusian parameter, with initial truncated exponential distribution. The transition to a saturation stage can be realized through addition of a logistic-like term.

The resulting model is as follows. Consider an F-model

$$\begin{aligned} \frac{\mathrm{d}l\left( {t,a} \right) }{\mathrm{d}t}=kaP\left( {t,a} \right) \left( 1-\left( \frac{N(t)}{K}\right) ^{r}\right) \end{aligned}$$
(29)

where \(P\left( {0,a} \right) \) is the truncated exponential distribution (20).

Define the auxiliary variable q(t) by the equation

$$\begin{aligned} \frac{\mathrm{d}q}{\mathrm{d}t}=\frac{k\left( 1-\left( \frac{N(t)}{K}\right) ^{r}\right) }{N(t)}, \quad q\left( 0 \right) =0. \end{aligned}$$
(30)

The solution to the F-model can be written again as \(l\left( {t,a} \right) =l\left( {0,a} \right) \mathrm{e}^{aq\left( t \right) }\), so Eqs. (25)–(27) apply to this model as well. The difference is that the auxiliary variable q(t) is now defined not by Eq. (24), but by Eq. (30).

Similarly to the previous exponential–linear model, for the purposes of analysis and computations, we can write the obtained three-stage model in two different but equivalent forms:

$$\begin{aligned}&\mathbf{Version\, 1:}\quad \begin{array}{l} \frac{\mathrm{d}q}{\mathrm{d}t}=\frac{k(1-(\frac{N(t)}{K})^{r})}{N(t)},\quad q\left( 0 \right) =0; \\ N\left( t \right) =N\left( 0 \right) \frac{s\left( {1-\mathrm{e}^{B(q(t)-s)}} \right) }{\left( {1-\mathrm{e}^{-Bs}} \right) (s-q(t))}; \end{array} \end{aligned}$$
(31)
$$\begin{aligned}&\mathbf{Version\, 2}:\quad \begin{array}{l} \frac{\mathrm{d}q}{\mathrm{d}t}=\frac{k(1-(\frac{N(t)}{K})^{r})}{N(t)},\quad q\left( 0 \right) =0; \\ \frac{\mathrm{d}N}{\mathrm{d}t}=kN\left( 0 \right) E^{t}\left[ a \right] =kN(0)\left( \frac{B}{1-\hbox {e}^{B(s-q\left( {t)} \right) }}+\frac{1}{s-q\left( t \right) }\right) . \\ \end{array} \end{aligned}$$
(32)

The three distinct stages of System (32) are illustrated in Fig. 6. The initial exponential stage is shown in Fig. 6a and is confirmed by logarithmic transformation of the same curve in Fig. 6b. It is followed by the linear stage (Fig. 6c), which is followed by the saturation stage (Fig. 6d). The full curve is shown in Fig. 6e.

Fig. 6
figure 6

(Color figure online) Three-stage model, as described by System (32), with s = 1, B = 10, k = 1, K = 100, r = 4. The model realizes three distinct growth phases, beginning with a the exponential stage of the system growth, b confirmed by logarithmic transformation, followed by c the linear stage of population growth, followed by d the saturation stage of population growth. All three stages can be seen in subplot (e)

Full size image

Now let us compare the three-stage F-model (29) with r = 1 and the inhomogeneous logistic model (16). Both models can be reduced to identical systems of the form (5)–(8). The only difference is in the initial distribution of the Malthusian parameter a and hence in the functional form of the mgf \(M\left( q \right) \). For the logistic model, the initial distribution is exponential, while for three-stage model the initial distribution is truncated exponential. Hence, solution to the three-stage model tends to the solution of the logistic model as the boundary B of truncated exponential distribution increases.

The results obtained here and their implications are summarized in Table 1.

Table 1 Summary and implications of the proposed growth models
Full size table

As one can see, logistic function appears to provide a better fit, which is confirmed by low residual mean square error (see Online Appendix 2 for values), suggesting that the population grows in a frequency-dependent manner and depends on a uniformly distributed external resource during all stages of growth (Fig. 7).

Fig. 7
figure 7

(Color figure online) Data extracted from Naumov et al. (2006, Figure 1), breast cancer in vivo. Data fitted to a logistic, b Gompertzian, c exponential–linear and d three-stage model. The data and all the growth functions are plotted in e. Logistic function had the lowest mean square error (MSE)

Full size image

Data set 4. Rogers et al. (2014).

The following data set was obtained from Rogers etal. (2014, Figure 2b). Similarly to the previous case, the data are fitted to logistic (Fig. 8a), Gompertz (Fig. 8b), Linear–exponential (Fig. 8c) and three-stage (Fig. 8d) functions. Neither function in this case provides a good fit, with logistic and three-stage models providing better fit than others. One can certainly see that the Gompertz function (Fig. 8b) provides a particularly poor fit, confirmed but RMSE and relative least square deviation, at least suggesting that, according to Table 1, the population described here is highly unlikely to be monomorphic.

Fig. 8
figure 8

(Color figure online) Data extracted from Rogers et al. (2014, Figure 2B). Data fitted to a logistic, b Gompertzian, c exponential–linear and d three-stage model. The data and all the growth functions are plotted in e. Gompertzian curve provides the worst fit (highest RMSE), allowing elimination of monomorphic population

Full size image

Data set 5. Rogers et al. (2014).

The following data set was also obtained from Rogers et al. (2014), in this case from Fig. 2i. Here, both logistic (Fig. 9a) and Gompertz (Fig. 9b) functions provide a relatively good fit, with the Gompertz function having a slightly smaller MSE (see Online Appendix 2 for details). This suggests that in this case, the population is more likely to be monomorphic.

Fig. 9
figure 9

(Color figure online) Data extracted from Rogers et al. (2014, Figure 2i). Data fitted to a logistic, b Gompertzian, c exponential–linear and d three-stage model. The data and all the growth functions are plotted in e. Gompertzian curve provides the best fit (lowest MSE), suggesting monomorphic population

Full size image

Data set 6. Benzekry et al. (2014).

Finally, consider the following data set, which was extrapolated from Benzekry et al. (2014), Figure S1B, the lung cancer growth curve. Our calculations suggested that, while all the models provided a reasonable fit (Fig. 10), logistic model resulted in the lowest RMSE, suggesting that this population is inhomogeneous, grows in a frequency-dependent manner and depends on a uniformly distributed external resource during all stages of growth. Notably, in their analysis, the authors predicted a better fit with a Gompertzian growth function; this discrepancy may either be a result of variations in parameter estimation methods, or, which is more likely, in the fact that we had no access to original raw data and had to rely on the published figure to obtain the numbers for our analysis.

Fig. 10
figure 10

(Color figure online) Data extracted from Benzekry et al. (2014), Figure S1B, the lung cancer growth curve. Data fitted to a logistic, b Gompertzian, c exponential–linear and d three-stage model. The data and all the growth functions are plotted in e. Based on MSE values, logistic curve fits best, suggesting a polymorphic population that grows in a frequency-dependent manner and depends on a uniformly distributed external resource during all stages of growth

Full size image

8 Discussion

Finding an appropriate function that best fits the data may have not only predictive value. It may provide insights into the nature of the population that is growing according to one or another growth law, as well as the conditions under which this growth has occurred. Building a foundation for making these distinctions has been the focus of this work.

A homogeneous (monomorphic) population can grow exponentially in the absence of competition; it can grow logistically if there exists a limitation on external resources. If the population is polymorphic and consists of exponential or logistic clones, then the total population size grows faster than exponentially or logistically. Nevertheless, polymorphic population can show exponential or logistic growth if the population consists of clones that grow according to the Gompertz curve.

Inhomogeneous populations can demonstrate exponential and logistic growth of the total population size if the population is described by specific inhomogeneous frequency-dependent models (or F-models, where the growth rate of a clone is proportional to its frequency in the total population). If a population grows in accordance with the solution to an F-model, then we can assume that the population growth depends on an external (perhaps, dynamic) resource, which is divided uniformly between all individuals in the population at all stages of population development, not only when the population size becomes large. Determination of this external factor may be of crucial interest, especially for such populations as tumor cells.

In several mouse xenograft models (transplantation of human cancer cells into immune deficient mice, a standard albeit imperfect method for studying tumor growth dynamics in vivo), tumor growth curves were reported, which exhibit extended period of near-negligible growth, followed by a sharp exponential-like growth phase (see Fig. 4). Such behavior can be captured by the inhomogeneous Malthusian models (see Eqs. 10 and 20) that show hyperbolic–exponential growth (Eq. 22). Additionally, one may expect that the process of natural selection within the population will eventually result in elimination of relatively slowly growing clones; this process would be very slow, resulting in a long “lag time” phase preceding the rapid growth phase. The population becomes almost monomorphic during transition from hyperbolic to exponential growth.

Exponential–linear dynamics can imply that a tumor is inhomogeneous, and the distribution of the clones’ growth rates within the tumor is close to truncated exponential distribution. Even more importantly, this may mean that the population growth depends on an external resource at all stages of population development, such that the resource is distributed uniformly between individuals in the population. The population becomes almost monomorphic during transition from exponential to linear growth. One may expect that at this stage the system still has enough external resource for growth and has not yet reached the saturation stage.

Adding a saturation stage to the exponential–linear dynamics allows reproducing three-stage dynamics, including linear, exponential and saturation stages, which was observed in viral RNA replication models (Biebricher et al. 1985; Schuster 2011). A key difference of the proposed model from the models proposed by Schuster (2011) is that this model allows replicating all three dynamical regimes with just one model.

The constructed three-stage model is perhaps the simplest one, which allows us to explain the transition from one stage of development to another due solely to internal system dynamics. Hence, if one observes the three-stage exponential–linear–saturation growth curve, then one can assume that the system is inhomogeneous and the growth rates of different clones follow the truncated exponential distribution. Moreover, the population in this case is once again likely to depend on an external, possibly dynamic, resource at all stages of population development, not only during the saturation stage.

8.1 Applications and Implications

Here, we have extracted several data sets from published literature and compared the data to our models (see Figs. 8, 9, 10). We observed that depending on the data set, different functions fit it better, with logistic model providing better fits in the majority of cases, implying (according to our theory) that the population described is heterogeneous, grows in a frequency-dependent manner, and depends on a uniformly distributed external resource during all stages of growth. In one of the cases, where neither model provided good fit to the data (Fig. 8), we were nevertheless able to eliminate Gompertzian growth, suggesting at least that the population is not monomorphic.

Analysis and predictions made in this section are based on our theory, summarized in Table 1, but they of course require experimental verification. Nevertheless, should this theory prove correct, it can provide invaluable tools for inferring information about the nature of the population, i.e., whether it is monomorphic or polymorphic, and the conditions under which the population is evolving, whether it can grow freely up to a saturation stage or must depend on an external resource/limiting factor at all stages of growth.

An example of such a population would be hormone-dependent tumors, such as some breast and prostate cancers, among others (Wirapati et al. 2008; Jozwik and Carroll 2012; Brisken 2013; Spring et al. 2016). Other examples could be nutrient-related, such as phosphorus (Elser et al. 2007; Kareva 2013) or glucose and glutamine (Kareva and Hahnfeldt 2013; Chang et al. 2015; Gillies and Gatenby 2015; Kareva 2015). Identification of such resources for each tumor might provide crucial guidance into effective therapeutic avenues, such as with estrogen-dependent breast cancers (Wirapati et al. 2008; Spring et al. 2016).

Our theory, if confirmed, can also allow making better predictions about further population growth, since, even if the initial stages of growth look similar, over time the shape of the growth curves varies depending on the model. Such analytical insights can provide an additional biomarker and a predictive tool to complement experimental research.