Introduction

It is widely accepted that adverse hemodynamics can lead to the development and progression of common cardiovascular diseases.25,29 Adverse hemodynamics conditions are often characterized by disturbed or transiently turbulent flow, leading to abnormal flow patterns and bio-mechanical forces that can result in thrombosis, vessel wall degradation, or inefficient local or systemic transport. Due to the Reynolds numbers typically encountered in the cardiovascular system, such complex flow patterns mainly develop in larger vessels, at bifurcations, sharp bends or locations altered from acquired or congenital disease. Not surprisingly, since disturbed flow strongly influences vascular pathogenesis, and vice versa, flow information can be highly useful for diagnostic purposes. Indeed, the audible signatures of turbulence have long been used to detect common cardiovascular diseases, e.g., carotid artery disease and murmurs resulting from a host of pathological conditions in, or near to, the heart. Diagnostic decisions are shifting to more direct and detailed data regarding flow conditions as advances in imaging, computation and data processing enable greater capabilities to obtain patient-specific blood flow information. Additionally, proper characterization of flow in large vessels has strong potential to aide in treatment planning. Specifically, since most cardiovascular interventions intend to restore normal, or improved, flow in cases of acquired or congenital disease, detailed knowledge of pre-operative flow conditions, or the capability to predict post-operative flow conditions resulting from a particular intervention, can have dramatic clinical impact.34

The ability to obtain high-resolution, patient-specific blood flow data is becoming prevalent with recent technological advances. Using an image-based flow modeling paradigm, computational fluid dynamics (CFD) has become a powerful tool in evaluating patient-specific hemodynamics; see e.g.,35,37 for recent reviews. This framework utilizes in vivo image data, derived from magnetic resonance imaging (MRI) or computed tomography (CT), to construct 3D patient-specific geometric models of vascular anatomy. These models can subsequently be used as computational domains for CFD solvers to model blood flow through particular regions of the vasculature to nearly arbitrary level of detail. These techniques continue to evolve, becoming increasingly sophisticated in the handling of boundary conditions and vessel wall dynamics to incorporate increasing realism and patient-specific information.

Alternatively, imaging techniques to non-invasively measure flow conditions in vivo continue to gain traction in evaluating patient-specific hemodynamics. MRI currently offers the most versatile tool for blood flow quantification. Notably, multidimensional phase-contrast (PC) MRI7,39 is capable of providing three-directional (3D), time-resolved flow information at any location in the body with current spatial and temporal resolutions of about 1–3 mm and 30–70 ms, respectively.

As image-based blood flow modeling, or MRI-based velocity imaging, enters clinical decision making, it is critical to know how well the derived flow data matches reality, since both approaches contain respective modeling, measurement, and numerical errors. Determining the true error of these techniques is often not possible, thus comparison of experimental and computational results is regarded as the benchmark for validation. Relatively few results have been published comparing patient-specific hemodynamics computations with in vivo measurements. Validation studies have primarily used in vitro models. MRI and particle image velocimetry (PIV) in vitro validations of numerical blood flow studies were performed by Ford et al.,9 Hoi et al.,12 Marshall et al.,23 and Papathanasopoulou et al. 26; these studies used relatively idealized models and mostly laminar flow. Ku et al. 16 considered moderately higher Reynolds numbers in comparing numerical simulation and PCMRI measurements of a stenotic vessel with an in vitro bypass model. In an effort to incorporate more physiologic morphology and boundary conditions, Kung et al. 18 compared CFD simulations with in vitro PCMRI measurements from a patient-specific abdominal aortic aneurysm (AAA) phantom that incorporated a physical Windkessel module to model physiologic downstream conditions at the outlets. Kung et al. 17 also used similar boundary conditions to compare vessel wall motion and pulse propagation in a deformable tube with computational results. Regarding in vivo validation, Ford et al.,8 compared virtual angiography using image-based CFD with angiograms, Ku et al. 15 compared flow rates in arterial bypass grafts in porcine models and Rayz et al. 28 compared CFD simulations to in vivo measurements in cerebral aneurysms, including investigation of the influence of different inflow rates on the model. These studies primarily reported on integrated flow behavior. More detailed spatial field information was considered by Boussel et al.,1 who compared CFD data and in vivo MRI measurements in patient-specific intracranial aneurysms. They reported favorable agreement for flow patterns and velocities, but poor agreement for wall shear stress due to the incapability of MRI to capture near-wall velocity gradients.

None of the above studies dealt with direct quantification of turbulence, or more generally highly disturbed flow conditions. The objective of the present study is to provide a comparison between in vivo and numerical estimates of turbulence intensity in a patient-specific model. In “Methods” section we discuss how turbulence intensity was estimated in vivo and from CFD. Comparison of the results is presented in third section and discussed in fourth section. Our findings suggest generally good agreement between the in vivo MRI measurements and the CFD predictions of turbulence intensity. Due to the complex spatiotemporal variability of turbulent flow, point-wise comparison of in vivo and CFD data is not expected to provide a reasonable comparison, and this was confirmed in our findings. Arguably, characteristics that are eventually most useful in a clinical setting, e.g., maximum levels of fluctuation intensity and regions of elevated intensity, were relatively consistent between in vivo MRI measurement and CFD predictions.

Methods

This study used an aortic coarctation model. Aortic coarctation is a congenital disease where the aorta contains a local narrowing that hinders the passage of blood. This condition can lead to significant pressure loss across the coarctation, turbulent flow downstream, and hypertension in the proximal circulation. LaDisa et al. 20 reviewed recent developments in the treatment of this disease, and investigated the hemodynamic variations between untreated and treated patients using image-based flow modeling. The coarctation model was chosen because: it is clinically important, it enables validation of flow conditions that are close to the limit of complexity encountered in vivo, and the aorta is large enough to enable sufficient spatial resolution using clinical MRI scanners for comparison with CFD results.

PCMRI

In Vivo MRI Measurements

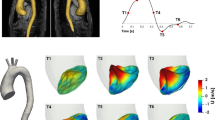
MR imaging was carried out on a 60-year-old female 46 years post-aortic coarctation repair with end-to-end anastomosis with a restenosis in the anastomitic area distal to the left subclavian artery (Fig. 1). In addition to the coarctation, the patient presented with an abnormal, minimally obstructive membrane in the left ventricular outflow tract. The study was approved by the regional ethics committee for human research at Linkoping University and informed consent was obtained prior to the MRI study. All MRI measurements were carried out on a clinical 1.5 Tesla scanner (Philips Achieva, Philips Medical Systems, Best, The Netherlands). The study consisted of a 3D contrast-enhanced MR angiography (MRA) to obtain high resolution data of the aortic geometry, a time-resolved 2D PCMRI velocity measurement acquired in the ascending aorta to provide inlet boundary conditions for the subsequent CFD modeling, and two time-resolved 3D PCMRI measurements to obtain velocity and turbulence intensity information, respectively, in the whole aorta.

Figure 1
figure 1

MRA data and derived geometric model used for CFD analysis: (a) maximum intensity projection and (b) 3D computer model

Full size image

The 3D MRA data was acquired with a resolution of 0.98 × 1.71 × 4.00 mm3 during a breathhold after gadolinium injection using a gradient-echo sequence with randomly segmented central k-space ordering (CENTRA). The three-dimensional MRA data were reconstructed to a resolution of 0.5 × 0.5 × 1.0 mm3. The two-dimensional through-plane PCMRI measurement was performed in the ascending aorta using a segmented gradient-echo pulse sequence. Imaging parameters included aliasing/velocity encoding (VENC) = 2 m/s, temporal resolution = 34 ms , pixel size = 2.78 × 2.84 mm2, reconstructed pixel size = 1.6 × 1.6 mm2, and slab thickness = 7 mm. Time-resolved three-directional PCMRI data were acquired during free breathing using a respiratory navigator-gated gradient-echo pulse sequence.4 To enable turbulence intensity estimation, the motion encoding scheme included a reference flow encoding segment with nulled motion sensitivity. Two scans with different motion encoding strengths were prescribed to acquire velocity (VENC = 3.5 m/s) and turbulence intensity (VENC = 1.4 m/s) data. Turbulence intensity data were acquired with isotropic spatial resolution of 3 × 3 × 3 mm3 and a temporal resolution of 81 ms, and velocity data with a spatial resolution of 3.4 × 3.4 × 3mm3 and a temporal resolution of 65 ms. On the scanner, all velocity data were reconstructed into 40 time frames per cardiac cycle with the same spatial resolution as acquired.

MRI estimation of turbulence intensity is achieved by exploiting the fact that the presence of multiple velocities within a voxel decreases the MRI signal amplitude under the influence of a bipolar magnetic field gradient.4–6,10 The MRI approach used in the present study is described in detail in Dyverfeldt and co-workers.3–5 While conventional experimental fluid dynamics methods measure turbulence intensity by sampling velocities at a small spatial area over time, the MRI signal is built up by ∼1 M water protons (spins) present within an image volume element (voxel). The voxel has a specific spatial extent and is sampled at several hundred points in time during the MRI acquisition. The spatial sampling of the turbulence scales is determined by the spatial extent of the voxel, which captures space scales smaller than the voxel size. The effect of the temporal sampling is more complex as the samples (k-space line) represent different spatial frequencies of the image. However, the key feature is that subsequent samples are separated by between 20 ms and one cardiac cycle, during which the larger turbulence scales have time to evolve. In this way, each sample corresponds to a new representation of the flow field. Thus the sampling of MRI data over time is expected to be beneficial in terms of resolving scales larger than the spatial extent of the voxel. The actual motion encoding is performed by bipolar magnetic field gradients that take about 0.0005 s to apply per lobe; eddies are considered stationary during this short period of time.

By assuming that intravoxel velocity distributions are normally distributed in transitional and turbulent flows, the data needed to estimate turbulence intensity can be obtained from a standard PCMRI experiment acquired with asymmetric flow encoding, in a way similar to how mean velocity is estimated. The complex-valued MRI signal of a voxel can be written as

$$ S(k_{v})=C \int\limits_{V} s({\mathbf{u}})e^{-{\rm i}{k_{v}} \cdot {\mathbf{u}}} d{\mathbf{u}}, $$
(1)

where C is a complex-valued constant affected by water proton density, relaxation effects, etc., \(s(\mathbf{u})\) is the velocity distribution within the voxel, \(\hbox{i}=\sqrt{-1}\) and k v describes the amount of applied motion sensitivity. The mean velocity component in each direction is estimated based on the phase difference between two MRI signals acquired with different motion sensitivity in the considered direction

$$ U=\frac{{\text{arg}}(S(k_{v2}))-{\text{arg}}(S(k_{v1}))}{\Updelta k_{v}},\quad |\Updelta k_{v}| < \frac{\pi}{U}. $$
(2)

Similarly, the standard deviation of the velocity distribution within a voxel (assumed here to be the turbulence intensity, σ) can be obtained using the relationship

$$ \sigma=\sqrt{\frac{2\ln\left(\frac{| S(k_{v2})|}{| S(k_{v1})|}\right) }{k_{v1}^{2}-k_{v2}^{2}}} , \quad |k_{v1}|\neq |k_{v2}|, $$
(3)

for each direction. A three-directional PCMRI experiment can be used to estimate σ i in three mutually perpendicular directions i = 1, 2, 3; and thus the MRI measured turbulent kinetic energy (TKE) is obtained by

$$ \sigma_{{\rm MRI}}({\mathbf{x}},t) = \frac{1}{2}\rho \sum\limits_{i=1}^{3}\sigma_{i}^{2}({\mathbf{x}}, t). $$
(4)

Image-Based CFD Modeling

A 3D patient-specific computer model of an aortic coarctation was constructed from the MRA data shown in Fig. 1. The model started near the aortic root and continued through the thoracic aorta, including the left subclavian, left common carotid, brachiocephalic, right subclavian, and right common carotid arteries, see Fig. 1. The model surface represents the lumenal surface of the arteries, which was obtained from the image data using a 2D levelset segmentation method.40 The segmentations were lofted to create a unified geometric model and the vessel bifurcations were blended for smooth transitions that matched the image data. The geometric model was subsequently used to create a volumetric computational mesh of tetrahedral elements.

The blood flow was modeled by the Navier–Stokes equations, which approximates blood as a homogeneous, Newtonian fluid with constant density ρ = 1.06 g/cm3 and viscosity μ = 0.04 P. The Newtonian fluid approximation is considered reasonable in large vessels.25 The vessels were assumed to be rigid with a no slip condition at the walls. While vessels are nominally compliant, the compliance was incorporated into the patient-specific boundary conditions since tissue properties and external tissue support were unknown. Boundary conditions are further discussed below.

Direct numerical simulation (DNS) was performed to solve the Navier–Stokes equations using a second-order accurate, stabilized finite element method13,36; this solver has been used extensively for image-based blood flow modeling. DNS was chosen because turbulence models are difficult to apply in cardiovascular flows since most models assume developed turbulence, however cardiovascular flows (at most) fluctuate between laminar and transitional states, and, moreover, the flow remains laminar in large portions of the domain. The mesh was anisotropic. The maximum edge size in the descending aorta, where disturbed conditions prevailed, was 250 μm. At this resolution the results appeared converged. The Kolmogorov microscale in this region based on peak Reynolds number was ≈100 and ≈200 μm based on average Reynolds number. The simulation time step size was 0.00083 s.

Boundary Conditions

In vivo volumetric flow rate data from the 2D PCMRI acquisition was used to prescribe inflow boundary conditions at the ascending aorta using a plug profile. The plug profile matches reasonably to in vivo experiments30 and is typical of simulations originating at the aortic root.24 To reproduce the physiologic influence of the arterial beds distal to the outlets, three-element Windkessel models were used and coupled to the computational domain using the method described in Vignon-Clementel et al. 38 While outlet volumetric flow rates were determined by the Windkessel models, the augmented Lagrangian method14 was used to constrain outlet profiles to be near parabolic for purposes of numerical stability. It has been shown that this method only affects the velocity field in close proximity to the constrained outlet.14

The three-element Windkessel model requires specification of a proximal resistance (R p), a terminal resistance (R t), and an arterial capacitance (C). The first step in the determination of these parameters involves knowledge of the mean flow rates at each outlet, which was estimated by the method of Zamir et al.,41 who proposed a power law relation between diameter and flow, and in particular that the relation for the first few branches of the arterial tree is governed by the square law

$$ d_{i} = D\left(\frac{q_{i}}{Q}\right)^{\frac{1}{2}}, $$
(5)

where D and Q are the diameter and volumetric flow rate at the aortic root, and d i and q i are the diameter and the flow rate at the location of interest, i.e., outlet i. To solve Eq. (5) for q i , diameters d i and D were obtained from the MRA and Q was obtained from the 2D PCMRI measurement. The terminal resistance R t at each outlet was obtained by dividing the mean blood pressure by the outlet’s flow rate.

Specification of the capacitances involved the knowledge of the total arterial compliance. The pulse pressure method32 was used to estimate total arterial compliance, as this method neither require zero flow in diastole nor information about the complete pressure waveform. This method was extended to the three-element Windkessel model, as in LaDisa et al. 19 An optimization algorithm that takes the pulse pressure and mean aortic flow rate as inputs was developed to find the total arterial compliance that best matched the desired pressure pulse. In this algorithm the value of the proximal resistance R p was set by assuming a characteristic total resistance ratio of 6%,21 i.e.,

$$ \frac{R_{\rm p}}{R_{\rm t}}=0.06. $$
(6)

The characteristic total resistance ratio was varied to verify that 6% was optimal. This total arterial compliance was then distributed among the outlets in proportion to their mean flow rates in accordance to Stergiopulos et al. 33 With the compliance known for each outlet, the proximal resistance R p was determined by repeating the same algorithm but this time varying the characteristic total resistance ratio to replicate the pressure pulse.

Turbulent Kinetic Energy

Recall that by Reynolds decomposition, the velocity field \(\mathbf{u}(\mathbf{x}, t)\) is decomposed into a mean \(\langle \mathbf{u} \rangle\) and a fluctuating \(\tilde{\mathbf{u}}\) component

$$ {\mathbf{u}}= \langle {\mathbf{u}} \rangle + \tilde{{\mathbf{u}}}, $$
(7)

where \(\tilde{\mathbf{u}}\) is assumed to arise due to turbulence. The TKE is defined as the kinetic energy of the fluctuating component, which on a per volume basis is given by

$$ \sigma({\mathbf{x}},t) = \frac{1}{2} \rho \, \tilde{{\mathbf{u}}}({\mathbf{x}},t) \cdot \tilde{{\mathbf{u}}}({\mathbf{x}},t), $$
(8)

and provides a direction-independent measurement of turbulence intensity. Traditionally, \(\tilde{\mathbf{u}}\) is defined by \(\tilde{\mathbf{u}} = \mathbf{u} - \langle \mathbf{u} \rangle\) after appropriately defining the mean velocity \(\langle \mathbf{u} \rangle.\) The traditional approach to defining \(\langle \mathbf{u} \rangle\) is to perform averaging over many realizations of an experiment. This is currently impractical for CFD simulations of the scale/complexity considered herein, and essentially impossible for in vivo MRI measurement. Alternatively since turbulence manifests in velocity fluctuations in space and time, it is common to the employ a spatial or, more commonly, temporal averaging to estimate \(\langle \mathbf{u} \rangle.\)

Due to the idiosyncrasies of MR measurement, derivation of TKE is not obtained from a direct velocity field decomposition per se, but rather from the MRI signal, which is influenced by both spatial and temporal variations in the velocity field. It is difficult to reproduce this methodology for CFD, however, to enable validation we considered a \(\langle \mathbf{u} \rangle\) derived from a spatiotemporal average that is heuristically similar to the averaging performed by the MRI method. We also performed temporal and spatial fluctuation intensity computations separately for comparison.

Spatiotemporal Fluctuation Intensity Definitions

A spatiotemporal mean velocity field was derived from the CFD data by performing spatial and temporal (cycle-based) averaging. Let T denote the period of the cardiac cycle and n denote the number of cardiac cycles of computed velocity data. For notational ease, assume this data starts from t = 0 so that \(t \in [0, nT). \) Footnote 1 Voxels of the same size (33 mm3) and (approximately same) location as the PCMRI voxels were superimposed on the computational domain and nodes of the computational grid located inside each voxel were used for computing spatial averages and fluctuations. That is, a spatiotemporal mean \(\langle \cdot \rangle_{{\rm st}}\) velocity field was computed as

$$ \langle {\mathbf{u}} \rangle_{{\rm st}}({\mathbf{x}}_v, \tau) = \frac{1}{N_v n} \sum_{k=0}^{n-1} \sum_{j \in {\mathbb{N}}_v} {\mathbf{u}}({\mathbf{x}}_j, \tau + k T), $$
(9)

where \({\mathbf{x}}_{v}\) is the center of voxel \(v,\tau \in [0, T),\) \({{\mathbb{N}}_{v}}\) is the set of indices of the CFD grid nodes located in voxel v, and N v is number of CFD grid nodes in voxel v. The inner sum considers spatial velocity variations, whereas the outer sum considers cycle-to-cycle velocity variations. It follows that the spatiotemporal mean squared velocity fluctuation components were defined as

$$ \langle \tilde{u}^2_i \rangle_{{\rm st}} ({\mathbf{x}}_v, \tau) = \frac{1}{N_v n} \sum_{k=0}^{n-1} \sum_{j \in {\mathbb{N}}_v} \left[ u_i({\mathbf{x}}_j, \tau + k T) - \langle u_i \rangle_{{\rm st}} ({\mathbf{x}}_v, \tau) \right]^2, $$
(10)

where i = 1, 2, 3 denotes vector components. Finally, the spatiotemporal velocity fluctuation kinetic energy per unit volume was defined as

$$ \sigma_{{\rm st}}({\mathbf{x}}_v, \tau) = \frac{1}{2} \rho \sum_{i=1}^3 \langle \tilde{u}^2_i\rangle_{{\rm st}} ({\mathbf{x}}_v, \tau), $$
(11)

which is also referred to herein as the spatiotemporal fluctuation intensity.

Temporal Fluctuation Intensity Definitions

Since the inflow is periodic, a cycle-to-cycle temporal mean \(\langle \cdot \rangle_{{\rm t}}\) of the velocity field was computed at each node of the computational grid \(\mathbf{x}_j\) as

$$ \langle {\mathbf{u}} \rangle_{{\rm t}} ({\mathbf{x}}_j,\tau) = \frac{1}{n}\sum_{k=0}^{n-1} {\mathbf{u}}({\mathbf{x}}_j,\tau+kT), $$
(12)

where \(\tau \in [0, T); \) this is essentially Eq. (9) without spatial averaging. Therefore, the temporal mean squared of the velocity fluctuation components were defined as

$$ \langle \tilde{u}^2_i \rangle_{{\rm t}} ({\mathbf{x}}_j, \tau) = \frac{1}{n}\sum_{k=0}^{n-1} \left[u_i({\mathbf{x}}_j, \tau+kT) - \langle u_i \rangle_{{\rm t}} ({\mathbf{x}}_j, \tau) \right]^2. $$
(13)

The cycle-to-cycle temporal velocity fluctuation kinetic energy per unit volume was defined by

$$ \sigma_{{\rm t}}({\mathbf{x}}_j, \tau) = \frac{1}{2} \rho \sum_{i=1}^3 \langle \tilde{u}^2_i \rangle_{{\rm t}} ({\mathbf{x}}_j, \tau), $$
(14)

which is also referred to herein as the temporal fluctuation intensity.

Spatial Fluctuation Intensity Definitions

An arbitrary cycle could be chosen to quantify spatial fluctuations in the flow field. However, to eliminate any bias resulting from this choice, we instead considered the temporal averaged flow field \(\langle u_i \rangle_{{\rm t}} (\mathbf{x}_j,\tau)\) defined by Eq. (12) to factor out cycle-to-cycle variations. To define the spatial mean, \(\langle u_i \rangle_{{\rm t}} (\mathbf{x}_j,\tau)\) was spatially averaged over each PCMRI voxel. This led to an identical mean velocity field as defined by Eq. (9), however, only spatial fluctuations were considered for defining the spatial fluctuation intensity. That is, defining

$$ \langle \tilde{u}^2_i \rangle_{{\rm s}} ({\mathbf{x}}_v, \tau) = \frac{1}{N_v}\sum\limits_{j \in {\mathbb{N}}_v} \left[ \langle u_i \rangle_{{\rm t}} ({\mathbf{x}}_j,\tau) - \langle u_i \rangle_{{\rm st}} ({\mathbf{x}}_v,\tau) \right]^2, $$
(15)

the spatial velocity fluctuation kinetic energy per unit volume was defined as

$$ \sigma_{{\rm s}}({\mathbf{x}}_v, \tau) = \frac{1}{2} \rho \sum_{i=1}^3 \langle \tilde{u}^2_i \rangle_{{\rm s}} ({\mathbf{x}}_v, \tau), $$
(16)

which is also referred to herein as the spatial fluctuation intensity.

Results

The fluctuation intensity fields were computed using the methods described above for the PCMRI and CFD data, and the fields were plotted as volume renders using Paraview (Kitware, Clifton Park, NY). All fields varied smoothly over time, with maximum turbulence appearing shortly after peak systole for each case, and decreasing to near zero during the diastolic phase. Figure 2 shows the fluctuation intensity volume renders shortly after peak systole, at a time instant most representative of when all fields where approximately maximized, which was 0.17 s from the start of the systole (the cardiac cycle length was 1.162 s). A consistent color map was used in Fig. 2 to facilitate comparison. It should be noted that the mesh type and resolution for the volume render of the temporal fluctuation intensity field were different than for the rest of the renders, which may have resulted in variations in the rendering. Notably, the temporal fluctuation intensity field was unstructured (vs. Cartesian for the others), and had a 12-fold greater spatial resolution in each direction (or 12 3 = 1728-fold overall).

Figure 2
figure 2

Fluctuation intensity fields for each method (0.17 s after the start of systole). Note that the mesh type and resolution for the volume render of the temporal fluctuation intensity field were different than for the rest of the renders: (a) PCMRI, (b) spatiotemporal, (c) temporal, and (d) spatial

Full size image

Table 1 summarizes the maximum level of fluctuation intensity over space and time observed for each method and the time this value occurred. Up to the temporal resolution of the PCMRI data, the time of maximum fluctuation intensity between the PCMRI and temporal fields was the same. However, quantitatively defining the time instant of maximum fluctuation intensity is subject to how maximum intensity is defined. For example, if defined as the maximum of the field over both space and time, the time of maximum intensity in each case is given by the parenthetical times shown in Table 1. Alternatively, if the maximum is defined as the maximum over time of the spatial integral of the fluctuation intensity field, then the time of maximum intensity for each case is given by the time each curve in Fig. 4 peaks. Visually, all fields appeared maximum around the time instant shown in Fig. 2.

Table 1 Maximum TKE comparison (time maximum TKE occurred)
Full size table

For quantitative comparison, Fig. 3 compares the percentage of the descending aorta that was exposed to fluctuation intensity over a certain threshold, as the threshold varied, between the PCMRI and CFD data. This comparison was done at the time instant shown in Fig. 2, which aligned most closely to the time of peak fluctuation intensity for the PCMRI and temporal fluctuation data. As an alternative, to compare the fluctuation intensity results over time, the fluctuation intensity fields were integrated over the descending aorta at several times in the cardiac cycle and are plotted in Fig. 4.

Figure 3
figure 3

Percentage of the descending aorta (boxed region) with fluctuation intensity above various thresholds values at time 0.17 s after the start of systole

Full size image
Figure 4
figure 4

Integral of the fluctuation intensity field over the descending aorta vs. time

Full size image

Convergence of the results was tested in several regards: the computational mesh size, the simulation time step size, the number of cardiac cycles used for temporal averaging, and the voxel size used for spatial averaging. Convergence of the velocity data was established using a nominal element size of 250 μm and time step of 0.00083 s. Results derived from the spatiotemporal and temporal fluctuation intensity fields showed little change once the number of cardiac cycles used for temporal averaging reached approximately 8. This was consistent with a previous aortic turbulence study involving abdominal aortic aneurysms.22 The size of the voxel used for spatial averaging was established by the PCMRI resolution for validation reasons. However, it was noticed that the spatiotemporal field did vary (<10% difference) when the voxel volume was decreased by a factor of 2 in each direction, or 8-fold overall.

Since velocity data was also obtained during the MRI sequencing, estimates for the total kinetic energy in the model were possible. Peak levels of estimated TKE for this flow were close to 23% of the peak estimated total KE. Specifically, for the CFD data the maximum KE occurring at peak systole was computed to be 5100 J/m3, from the peak observed velocity of 3.1 m/s in the model. For the PCMRI data, the maximum observed total KE was 4460 J/m3, corresponding to a peak observed velocity of around 2.9 m/s.

Discussion

Our general finding was that TKE predictions based on CFD modeling were relatively consistent with those obtained by PCMRI, with errors between the two estimates of around 10% in the quantitative comparisons made. The fields themselves also compared qualitatively well in both time and space, as shown Fig. 2. While the averaging methods used to obtain TKE estimates from the CFD data did not exactly replicate the PCMRI TKE derivation, the PCMRI and CFD velocity data compared similarly, suggesting that modeling and measurement errors inherent in both methods were as significant a factor in observed differences.

A traditional measure of turbulence intensity based on several realizations of the experiment was not possible, nor could modeling and measurement errors have been completely avoided. Hence it was not possible to quantify in a precise manner how close any estimate was to the true TKE for this flow. For fully developed turbulence, that is, isotropic and homogeneous, the ergodic assumption2 implies that velocity fluctuations are statistically stationary in space/time/ensemble. This assumption is questionable for the flow considered herein, nonetheless, it is reasonable to assume statistical properties do not change from cycle to cycle since the inflow to the model was periodic. That is, cycle-to-cycle fluctuations were assumed to be due to turbulence once the solution converged numerically. In this sense, the CFD temporal fluctuation intensity measure may be considered the baseline estimate for the true TKE (in the absence of modeling, measurement, and numerical errors). Using PCMRI, the TKE is not obtained from a direct velocity field decomposition per se, but rather from the MRI signal, which is influenced by both spatial and temporal variations in the velocity field. To enable validation, we computed a spatiotemporal fluctuation intensity, and temporal and spatial fluctuation intensity separately for comparison. It is interesting to note that in nearly all comparisons, the differences between the PCMRI and CFD temporal fluctuation intensity fields were smaller than the differences between the CFD spatiotemporal and temporal fluctuation intensity fields. Furthermore, in most cases the PCMRI results fell between the spatiotemporal and temporal CFD results. This may indicate that the spatiotemporal averaging did not perfectly model the PCMRI measurement and that the PCMRI estimate of TKE seems to be more dominated by temporal fluctuations than the spatiotemporal average used.

Comparison of the CFD results, e.g., Figs. 2c and 2d confirms that the spatial fluctuations are influenced by turbulence, but also are influenced by strong laminar gradients in the flow. High spatial fluctuation intensity was observed at the throat of the coarctation, even though no cycle-to-cycle variation in the velocity field was observed there. Therefore, the spatial fluctuation field is likely not a reliable estimate of TKE, which is why it was excluded from Figs. 3 and 4. The effect of the spatial fluctuations on the spatiotemporal fluctuation intensity measure seemed to be moderate, however, and the PCMRI method appeared more robust to this possible skewing.

Figure 3 demonstrates that near the time instant of peak TKE, the relative levels of fluctuation intensity in each case are consistent. Figure 4 shows that the integrated TKE for all methods coincide in the later part of systole, but showed greater difference in early and peak systole, with the integrated spatiotemporal and PCMRI fluctuation intensities being higher than the integrated temporal fluctuation intensity. This may suggest that in late systole, turbulence dominates the fluctuation intensity measures, whereas in early and peak systole (when turbulence has not yet fully developed) large laminar gradients may tend to elevate the spatiotemporal and PCMRI fluctuation intensity fields due to the spatial averaging inherent in both methods. Based on the above observations, it appears that the PCMRI estimate is closer to the true TKE for this flow than the spatiotemporal TKE estimate. Nonetheless, the maximum TKE estimates (cf. Table 1), which perhaps is of clinical significance, obtained from the PCMRI, temporal, and spatiotemporal methods were all within 5%.

Possible Error Sources

The PCMRI data demonstrated turbulence shed from the aortic valve, most likely caused by the subvalvular membrane. In the CFD modeling, a (laminar) plug profile was imposed at the aortic root. Nonetheless, PCMRI data indicated no appreciable elevated fluctuation intensities immediately proximal to the coarctation, suggesting that the flow relaminarizes upon reaching the coarctation. Furthermore, the throat of the coarctation itself should also filter disturbances introduced by the aortic valve that were not modeled by the inlet boundary condition.

There was a slight ambiguity on exactly where to superimpose the voxels on the computational model for spatial averaging. We were unable to obtain a common point of reference a posteriori between the PCMRI TKE data and the MRA data used to build the CFD model. Therefore, the voxels used for spatial averaging of the CFD data were likely offset from PCMRI voxels. While this makes point-wise comparison of the data difficult, on a more fundamental level it is typically unrealistic to perform point-wise comparison of turbulent flows due to the inherent chaoticness of the fields.

Discrepancies may be attributed to several other reasons. On the MRI side, helical flow patterns that are present in our model may lead to characteristic distortions of PCMRI measurements.31 In MRI, accelerating and fluctuating flows can cause spatial misregistration errors due to phase-shifts from higher order motion, flow related signal loss due to intravoxel phase-dispersion, and ghosting due to view-to-view variations.11,31 The effects of these artifacts on PCMRI velocity and TKE mapping were recently studied by Petersson et al. 27 for a jet flow similar to that present in the coarctation studied here. Their results indicate that artifacts caused by disturbed flows can increase the uncertainty of the measurements but that the accuracy is generally maintained. On the CFD side, several modeling assumptions went into the analysis, including rigid walls, Newtonian rheology, and boundary conditions as well as uncertainties in model parameters. Errors introduced by these assumptions have been previously explored (usually not by in vivo validation, but rather strictly computationally), see e.g.,37 and references therein, and errors due uncertainties in model construction, inflow waveform, and boundary conditions have been reported to result in (peak) flow field differences of 10–50%. In this light, the differences between measured and modeled peak and integrated TKE values observed in this study were favorable.

Conclusion

Proper identification and quantification of large and varying disturbances in flow resulting from turbulence, whether through PCMRI or image-based flow modeling, have important clinical significance, including implications to atherosclerosis, intimal hyperplasia, and platelet activation. To the best of our knowledge, this is one of the first studies to validate realistic patient-specific numerical computations of turbulence against in vivo experimental measurements. We observed overall good agreement between image-based CFD predictions of fluctuation intensities to those measured in vivo with PCMRI using an aortic coarctation model, including agreement in both range and distribution. Differences in results were well within those expected due to modeling and measurement errors, indicating a relative robustness of the TKE estimation.