Keywords

4.1 Introduction

Energy harvesting is commonly defined as a process where a certain amount of non electrical energy is transformed and stored into electrical energy for future use, mainly to power small electronic equipments such as wireless sensors in a remote network. Piezoelectric vibration energy harvesting fits in this context since it employs piezoelectric materials in the conversion of ambient structural vibration signals into usable electrical energy. Most of literature works have focused on the power harvested when the response behavior can be adequately characterized as a linear oscillator with harmonic excitation [1, 2]. The early studies about energy harvesting from piezoelectric material began in the 1990s with the work of Starner [2], and Umeda et al. [4, 5]. The piezoelectric cantilever is a key structure for energy harvesting applications. Erturk and Inman have recently published a series of papers on energy harvesting using the cantilever model and their work provide a broad coverage of several important modeling aspects that were validated with experimental data [6–9].

Recently, Erturk and Inman [7–10] proposed several mathematical models of beams to analyze the efficiency of cantilever beams used as piezoelectric energy harvesters. Anton and Sodano [11] presented a comprehensive review on relevant contributions on piezoelectric energy harvesting. Although there is a fairly large amount of publications on linear piezoelectric energy harvesting, in recent years nonlinear energy harvesting has received special attention from researchers. The main advantage of using nonlinear models over the common linear approach is the possibility of increasing the frequency range of operation of these harvesters. One of the most common mechanism to introduce nonlinear effects on a typical cantilever beam harvester is by magnetic materials to generate nonlinear magnetic forces that will in turn generate nonlinear elastic forces acting on the system magnetic [12–14]. The inherent material nonlinearities arising for example from piezoelectric constitutive equations also has influence on the energy harvester and it was first studied by Wagner and Hagedorn [15]. Later, Mann [16] highlight the importance of modeling inherent piezoelectric nonlinearities in energy harvesters.

The main goal of this article is to discuss the potential benefits of introducing nonlinearities in the dynamics of a typical piezoelectric vibration energy harvester. The device is essentially a cantilever beam partially covered by piezoelectric material with a magnet tip mass. We also consider the nonlinear constitutive piezoelectric equations to improve the harvester performance. Governing equations of motion are derived for the harvester considering the excitation applied at its fixed boundary. The nonlinear electromechanical nonlinear model is used in numerical simulations.

4.2 Harvester’s Electromechanical Model

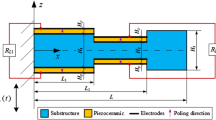
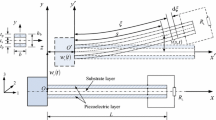
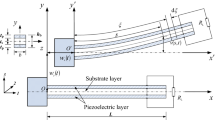
This section highlights some key features of the electromechanical model used to investigate the effects and potential benefits of nonlinearities on the output power generated by the energy harvesting system shown in Fig. 4.1. As seen the harvesting device consists of a cantilever metallic beam usually denoted as the substructure and partially covered by piezoelectric ceramic on both sides and carrying a lumped mass at its free end. The piezoceramic layers are connected in series to a load resistor R1 and the input to the system consists of a base input harmonic acceleration that is applied at the harvester’s grounded side. The tip mass consists of a neodymium magnet that is rigidly attached to the substructure’s free end and that oscillates in the vicinity of a second magnet. A repulsive or attractive nonlinear force can be then generated at the beam’s free end, depending on the magnetic polarity of these magnets. This contactless interaction between the magnetic fields of the tip magnets introduces a nonlinear force on the bimorph beam what in turn can generate nonlinear oscillations of the harvesting device.

Fig. 4.1
figure 1

Piezomagnetoelastic vibrational energy harvester model

Full size image

Motion and voltage equations of motion for the system shown in Fig. 4.1 can be obtained by employing Lagrange’s equations for electromechanical systems [17]

$$\begin{array}{lll} {}& \frac{d}{ dt}\left(\frac{\partial Lg}{\partial\dot{\eta}}\right)-\frac{\partial Lg}{\partial \eta}=-{c}_f\dot{\eta}\\ &{}\frac{d}{ dt}\left(\frac{\partial Lg}{\partial \dot{\lambda}}\right)-\frac{\partial Lg}{\partial\lambda }=-\frac{\dot{\lambda}}{R1}\end{array}$$
(4.1)

where L g is the so called Lagrangian operator that in the case of the system shown in Fig. 4.1 can be written as

$$ L={T}_v+{T}_p+{T}_m-{U}_v+{U}_p+{U}_m $$
(4.2)

where T and U are the harvester’s kinetic and potential energies. Subscripts v, p, and m in Eq. (4.2) refer to substrate, piezoelectric material and magnets, respectively. The beam’s dynamic w(x, t) deflection relative to the moving boundary is approximated by the single mode and can be written in terms of the mode shape W(x) and modal coordinate η(t)

$$ w\left(x,t\right)=W(x)\eta (t) $$
(4.3)

4.2.1 Kinetic Energy

Derivation of the system’s kinetic energy of the substrate and piezoelectric layers can be obtained from

$$ {T}_{v,p}=\frac{1}{2}{\rho}_{v,p}{A}_{v,p}{\displaystyle {\int}_0^L{\left(\dot{w}\left(x,t\right)+\dot{z}(t)\right)}^2 dx}$$
(4.4)

where the (⋅) indicates a time derivative, ρ v and ρ p are the density of the beam and the piezoelectric material, respectively. Constants A v and A p denote the cross sectional area of the beam and the piezoelectric material, respectively. The time dependent variable z(t) is the base motion and L p is the length of piezoelectric layer. A similar expression to Eq. (4.4) is used to account for the kinetic energy of the lumped magnetic mass m m attached to the beam’s end

$$ {T}_m=\frac{1}{2}{m}_m{\left[\dot{w}\left(L,t\right)+\dot{z}(t)\right]}^2 $$
(4.5)

Combination of Eqs. (4.4)–(4.6) leads to the following expression for the harvester’s total kinetic energy

$$\begin{array}{lll}T&=\left[\frac{1}{2}{\rho}_v{A}_v{W}_0^{2L}+{\rho}_p{A}_p{W}_0^{2Lp}+\frac{1}{2}{m}_mW{(L)}^2\right]\dot{\eta}{(t)}^2+\left[{\rho}_v{A}_v{W}_0^L+2{\rho}_p{A}_p{W}_0^{Lp}+{m}_mW(L)\right]\dot{\eta}(t)\dot{z}(t)+\nonumber\\& \quad+\frac{1}{2}\dot{z}{(t)}^2\left[{m}_m+{m}_v+2{m}_p\right]\end{array}$$
(4.6)

Constants m v , m p are the total mass of the beam and of the piezoelectric layers, respectively.

4.2.2 Potential Energy

The total potential energy of the system is found by adding the potential energy of the beam, the piezoelectric material and the tip mass. The potential energy distributed along the length of the beam is:

$$ {U}_v=\frac{1}{2}{Y}_v{I}_v{\displaystyle \underset{0}{\overset{L}{\int }}{\left[{w}^{{\prime\prime}}\left(x,t\right)\right]}^2 dx} $$
(4.7)

where Y v is the Young’s modulus of the beam material and I v is the area moment of inertia of the beam about its geometric center. Considering the nonlinearities from the piezoelectric material, the following constitutive equations are used to the compute of the potential energy of the piezoelectric material:

$$\begin{aligned}[b] {T}_1&={c}_{11}{S}_1+{c}_{111}{S}_1^2+{c}_{1111}{S}_1^3-{e}_{31}{E}_3-{e}_{311}{S}_1{E}_3-{e}_{3111}{S}_1^2{E}_3\\{}{D}_3&={e}_{31}{E}_3+{e}_{311}{S}_1{E}_3+{e}_{3111}{S}_1^2{E}_3+{\varepsilon}_{33}^s{E}_3\end{aligned}$$
(4.8)

where T 1 and S 1 are the stress and strain along the length of the beam while D 3 and E 3 indicate the electric displacement and electric field that develops through the thickness of the piezoelectric laminates. The material constants c 11, c 111 and c 1111 and e 31, e 311 and e 3111 are the second, third and fourth order elastic and electro-elastic tensor components, respectively.

The potential energy distributed along the length of the piezoelectric material is:

$$ {U}_p=\frac{1}{2}{\displaystyle \underset{ Vp}{\int}\left({T}_1{S}_1-{D}_3{E}_3\right)d{V}_p} $$
(4.9)

The potential energy associated to the magnetic force is given as [18, 19]

$$ {U}_m=-\frac{A}{2}W{(L)}^2\eta {(t)}^2+\frac{B}{4}W{(L)}^4\eta {(t)}^4 $$
(4.10)

Thus, the total potential energy of the system is given as

$$ U=\left(b+\frac{B}{4}W{(L)}^4\right)\eta {(t)}^4+\left(a-\frac{A}{2}W{(L)}^2+\frac{1}{2}{Y}_v{I}_v{D}^2{W}_0^{2L}\right)\eta {(t)}^2-c\frac{\dot{\lambda}(t)}{2}\eta (t)-d\frac{\dot{\lambda}(t)}{2}\eta {(t)}^3-e\dot{\lambda}{(t)}^2 $$
(4.11)

where

$$ a=\frac{1}{2}{c}_{11}{b}_w\left(\frac{1}{12}{h}_v^3+\frac{1}{2}{h}_v^2{h}_p+{h}_v{h}_p^2+\frac{2}{3}{h}_p^3\right){D}^2{W}_0^{2 lp} $$
(4.12)
$$ b=\frac{1}{2}{c}_{1111}{b}_w\left(\frac{1}{80}{h}_v^5+\frac{1}{8}\right.{h}_v^4{h}_p+\frac{1}{2}{h}_v^3{h}_p^2+{h}_v^2{h}_p^3+{h}_v{h}_p^4+\left.\frac{2}{5}{h}_p^5\right){D}^2{W}_0^{4 Lp} $$
(4.13)
$$ c=\frac{1}{2}{e}_{31}{b}_w\left({h}_v+{h}_p\right){D}^2{W}_0^{Lp} $$
(4.14)
$$ d=\frac{1}{2}{e}_{3111}{b}_w\left(\frac{1}{4}{h}_v^3+\frac{3}{4}{h}_v^2{h}_p+{h}_v{h}_p^2+\frac{1}{2}{h}_p^3\right){D}^2{W}_0^{3 Lp} $$
(4.15)
$$ e=\frac{1}{2}{\varepsilon}_{33}^s{b}_w\left(\frac{h_v}{4{h}_p^2}+\frac{1}{2{h}_p}\right){L}_p $$
(4.16)

4.2.3 Lagrangian

Once all energy quantities are determined, the Lagrangian can be found by substitution of all expressions into Eq. (4.2) with further algebraic manipulation. The following expression is then found

$$\begin{array}{lll}Lg&=\left(\frac{1}{2}{\rho}_v{A}_v{W}_0^{2L}+{\rho}_p{A}_p{W}_0^{2Lp}+\frac{1}{2}{m}_mW{(L)}^2\right)\dot{\eta}{(t)}^2+\left({\rho}_v{A}_v{W}_0^L+{\rho}_p{A}_p{W}_0^{Lp}+{m}_mW(L)\right)\dot{\eta}(t)\dot{z}(t)+\\&{} \ \quad \frac{1}{2}\left({m}_m+{m}_v+2{m}_p\right)\dot{z}{(t)}^2-\left(b+\frac{B}{4}W{(L)}^4\right)\eta{(t)}^4-\left(a-\frac{A}{2}W{(L)}^2+\frac{1}{2}{Y}_v{I}_v{D}^2{W}_0^{2L}\right)\eta{(t)}^2+\\ & \ \quad {}c\frac{\dot{\lambda}(t)}{2}\eta(t)+d\frac{\dot{\lambda}(t)}{2}\eta{(t)}^3+e\dot{\lambda}{(t)}^2 \end{array} $$
(4.17)

where c f is the damping coefficient of the mechanical spring and \( \dot{\lambda}=V \) is the voltage of the system. Performing the derivations in Eq. (4.1) and dividing the resulting equations for the modal mass of the system we achieve the following result for the dynamic equations of the energy harvester nonlinear.

$$\left\{\begin{aligned}{}&\ddot{\eta}+{\tilde{c}}_f\dot{\eta}+\tilde{k}\eta+\tilde{b}{\eta}^3-\tilde{c}V-\tilde{d}V{\eta}^2=-\frac{F}{m_t}cos\left(\omega t\right)\\&{}\dot{V}+\frac{V}{2R1e}=-\frac{c}{4e}\dot{\eta}-\frac{3d}{4e}{\eta}^2\dot{\eta}\end{aligned}\right.$$
(4.18)

The coefficients appearing in the system of Eq. (4.18) are given by:

$$ \tilde{m}={\rho}_v{A}_v{W}_0^{2L}+2{\rho}_p{A}_p{W}_0^{2 Lp}+{m}_mW{(L)}^2 $$
(4.19)
$$ \widehat{m}=\frac{\rho_v{A}_v{W}_0^L+2{\rho}_p{A}_p{W}_0^{Lp}+{m}_mW(L)}{\tilde{m}} $$
(4.20)
$$ \tilde{b}=\frac{4b+ BW{(L)}^4}{\tilde{m}} $$
(4.21)
$$ \tilde{c}=\frac{c}{2\tilde{m}} $$
(4.22)
$$ {\tilde{c}}_f=\frac{c_f}{\tilde{m}} $$
(4.23)
$$ \tilde{d}=\frac{3d}{2\tilde{m}} $$
(4.24)
$$ \tilde{k}=\frac{\left(2a- AW{(L)}^2+{Y}_v{I}_v{D}^2{W}_0^{2L}\right)}{\tilde{m}} $$
(4.25)

The sign of the stiffness constant k can be positive or negative. The positive sign corresponds to low intensity magnetic forces and in this situation occur the position of static equilibrium and the system is a nonlinear mono-stable oscillator. The natural frequency of the system is given by:

$$ {\omega}_n=\sqrt{\tilde{k}} $$
(4.26)

The electromechanical coupled equations given by system of Eq. (4.18) can be solved numerically, solving the initial value problems for ordinary differential equations. In this work it is used the explicit iterative method Runge–Kutta 4,5 in Matlab® for the simulation of Eq. (4.18) for the approximation of solutions of ordinary differential equations.

4.3 Numerical Simulations

In order to investigate potential benefits of introducing nonlinear effects on the performance of the energy harvesting system shown in Fig. 4.1 in terms of output voltage generation a series of numerical simulations were performed with Eq. 4.18 described in the previous section. Numerically simulated results employed the geometrical data and material properties shown in Table 4.1 below. A beam made of spring steel (130 × 0.0254 × 0.000635 mm) was used as the substructure. It was partially covered by two layers of piezoelectric material in a bimorph configuration. It should be emphasized that the numerical simulations considered the nonlinear effects from the piezoelectric material as defined in the constitutive equations from analytical model. Table 4.1 also shows the main characteristics of the magnetic tip mass used in the simulations. All numerically simulated results presented in this section were obtained with the harvester of Fig. 4.1 operating in the so called mono stable condition, that considers the magnetic gap between the tip masses larger than a given threshold, as previously pointed in [18, 20].

Table 4.1 Dimensions and properties of beam, PZT and tip mass
Full size table

Figure 4.2a shows the results of a numerical simulation where the effect of the nonlinearity coming from the piezoelectric material was considered. In this case all magnetic effects were absent and the only nonlinear effects from material properties were considered. Figure 4.2a shows the output power FRF, given as the ratio of the harvester’s electrical output to the input base acceleration for case where coefficients c 1111 and e 3111 are employed in the constitutive analytical model. When compared to the result from the linear model it is noticed that the presence of piezoelectric material nonlinearities introduce a softening behavior on the resulting output power FRF since the curve slightly bends to the left as the excitation frequency increases. It is also noticed that the nonlinear frequency response has higher amplitude in the vicinity of the harvester’s natural frequency than the corresponding linear result. Additionally, the base of the nonlinear power FRF is slightly wider than the linear one suggesting that the material nonlinearity can also contribute to increase the range of working frequencies for the harvester.

Fig. 4.2
figure 2

Influence of piezoelectric material nonlinearities: (a) linear model versus nonlinear model; (b) comparison between linear material and nonlinear associated to hardening effect; (c) Influence of load resistance on nonlinear material behavior

Full size image

The result shown in Fig. 4.2b shows numerical results for the case where a repulsive magnetic nonlinear effect was introduced in the numerical model in addition to the nonlinearity effect coming from the piezoceramics. The result is a hardening behavior as the power FRF bends to the right as the excitation frequency increases. It is noticed that the benefits of the material nonlinearities in this case are slightly more significant in comparison to the linear material assumption since the hardening effect from the magnetic field presents a dominant effect. Figure 4.2c shows the effects of the load resistance R1 on the power generation of the mono stable harvester. It is seen that as R 1 increases the amount of electrical power decreases thus suggesting an optimal value for the load resistance R 1 leads to the best performance of the device in terms of power generation.

Next, the effects of the gap between the tip magnets is considered in two situations, repulsive and attractive magnetic forces. Figure 4.3 shows the numerical results obtained in both cases. Figure 4.3a shows the results for the output power FRF when the distance between magnets is varied and a repulsive magnetic force is present. It is noticed that as the magnet gap is increased the value of the natural frequency significantly increases and the output power decreases. Thus the repulsive magnetic force tends to introduce a hardening behavior on the harvesting system associated to also causing a variation in the equivalent stiffness and power FRF amplitude. Figure 4.3b shows numerical results where a constant magnet distance was used and the amplitude of the repulsive magnetic force was varied. As expected as the magnetic force increases, higher values of the peak amplitude are obtained.

Fig. 4.3
figure 3

Influence of magnets on power FRF: (a) variation of magnet distance, repulsive; (b) variation of magnetic force, repulsive; (c) variation of magnetic force, attractive; (d) variation of magnet distance, attractive

Full size image

The results for the numerical simulations using attractive magnetic forces are shown in Fig. 4.3c, d. Figure 4.3c indicates that as the gap between the attractive magnets is increased the value of the natural frequency decreases and more power is generated. Similar behavior is found for the output power FRF for increasing values of the magnetic attractive force.

4.4 Experimental Results

In order to validate some of the results from the numerical simulations presented in the previous section, an experimental analysis were performed on an energy harvesting system. As depicted in Fig. 4.4 a special fixture was constructed in order to test the harvesting device in both linear and nonlinear testing configurations. Figure 4.4a shows an illustration of the testing apparatus and Fig. 4.4b shows the actual device used in the experimental work. A MIDÉ Volture V22BL energy harvester was used in the tests. The sensor is attached to the test fixture through a clamping device that is used to simulate the cantilever boundary condition. A neodymium magnet is attached to the harvester’s free end and a second magnet is mounted on a vertical tower that part of the fixture as shown in Fig. 4.4. The magnet gap between the tip and fixed magnet can be varied by moving the vertical tower along the longitudinal axis of the test fixture. The test fixture assembly is mounted on the top of linear tracks and attached to the armature of the vibration exciter that in turn will provide the excitation signals to the harvesting system. Table 4.2 shows the characteristic of the harvester used in the tests. All material properties available were obtained from the manufacturer data sheet.

Fig. 4.4
figure 4

Experimental setup used in tests: (a) illustration; (b) actual testing apparatus

Full size image

In relation to the instrumentation used in the tests, an B&K 4808 electromagnetic vibration exciter with B&K 2712 power amplifier was used to provide the excitation signals to the system. The tip velocity of the energy harvester was measured by a Polytec PDV 100 laser vibrometer and the input base acceleration on the harvester clamp fixture was measure by a tear drop PCB 352A24 (101.5 mV/g) piezoelectric accelerometer along with a PCB 482A16 power unit. All signals were acquired by an four channels SignalCalc ACE 104 PCMCIA spectrum analyzer from Data Physics Corporation. Two types of tests were performed on the system shown in Fig. 4.4, namely the Linear Test and the Nonlinear Test. In the linear tests no magnetic force of any nature was introduced since the main goal of conducting linear tests is to identify basic characteristics of the energy harvesting system such as the damped natural frequency. Therefore the linear tests were conducted in the absence of the magnet located on the vertical tower shown in Fig. 4.4. For the nonlinear tests, the second magnet was introduced and several testing conditions were experimentally examined, as it will be further discussed.

4.4.1 Linear Tests Results

Experimental results for linear tests were obtained by applying a random input excitation signal to the test system. A low amplitude excitation signal was used throughout the linear tests. Linear test results are shown in Fig. 4.5. Figure 4.5a, b show the voltage and electrical power FRF relating the harvester’s output voltage to the input base acceleration measured by the reference accelerometer located on the harvester’s base respectively. These results were obtained by employing several load resistors. It can be noticed that an increasing value for the load resistor leads to higher values of the harvester’s output voltage (Fig. 4.5a) and consequently for the output power (Fig. 4.5b). Figure 4.5c, d show the measured tip velocity obtained through the laser signal for all values of load resistors employed. Similar behavior to the results shown in Fig. 4.5 were previously observed [7–10].

Table 4.2 Properties of the energy harvester
Full size table
Fig. 4.5
figure 5

Experimental results from linear tests: (a) output voltage FRF; (b) output power FRF; (c) tip velocity; (d) tip velocity in zoom mode

Full size image
Fig. 4.6
figure 6

Test results for repulsive tests for several input acceleration levels

Full size image
Fig. 4.7
figure 7

Test results for repulsive tests for several input acceleration levels

Full size image

4.4.2 Nonlinear Tests Results

Nonlinear tests were performed by applying a sinusoidal excitation of variable frequency (sine sweep) to the test apparatus of Fig. 4.4. For both the repulsive and attractive configuration of the tip magnets two testing scenarios were analyzed. First the amplitude of the input excitation signal was varied and the output harvested voltage was measured. Second, the magnet distance between the magnets was varied and the corresponding output voltage was also measured. Figures 4.6 and 4.7 show the results for the repulsive and attractive configurations of the tip magnets when the input excitation voltage is varied. It can be noticed in both cases that increasing values of the input voltage leads to an increase in the harvester’s output voltage. However, for the repulsive case in Fig. 4.6 as the input voltage increases the FRF narrows what is clear indication of a reduction on the harvester working frequency range. For the case of attractive magnets it is seen from Fig. 4.7 that increasing values of the excitation signal leads to more electrical output power being generated and the working bandwidth of the harvester also tends to increase, what in principle points to an advantage over the repulsive configuration. Finally, Fig. 4.8 shows experimental results obtained when the distance between the tip magnet and the fixed magnet is varied, for both repulsive and attractive testing scenarios. It is observed that in the case of repulsive magnet force, Fig. 4.8a as the magnet distance increase the harvester natural frequency and power peak amplitude are affected. Similar results were obtained for the attractive case, as shown in Fig. 4.8b.

Fig. 4.8
figure 8

Test results for variable magnet spacing: (a) repulsive; (b) attractive

Full size image

4.5 Concluding Remarks

In this paper we presented the modeling and the analytical investigation of a nonlinear piezoelectric energy harvester. The device consisted of a cantilever beam partially covered by piezoelectric material with a magnetic tip mass. In this model was considered the nonlinearity inherent comes from the piezoelectric constitutive equations besides the nonlinearity comes from the magnetic tip mass. The electromechanically coupled equations were solved numerically, through the initial value problems for ordinary differential equations. The electrical power output was investigated varying the amplitude of the base acceleration, the distance between the magnets and the load resistor. We also concluded that the parameters investigated influence in the frequency range of operation of the device and the nonlinear effects present on the energy harvester extend the useful frequency range of studied device. Experimental data supported the results obtained from numerical simulations.