A criterion for high-cycle fatigue life and fatigue limit prediction in biaxial loading conditions

Abstract

This paper presents a criterion for high-cycle fatigue life and fatigue strength estimation under periodic proportional and non-proportional cyclic loading. The criterion is based on the mean and maximum values of the second invariant of the stress deviator. Important elements of the criterion are: function of the non-proportionality of fatigue loading and the materials parameter that expresses the materials sensitivity to non-proportional loading. The methods for the materials parameters determination uses three S–N curves: tension–compression, torsion, and any non-proportional loading proposed. The criterion has been verified using experimental data, and the results are included in the paper. These results should be considered as promising. The paper also includes a proposal for multiaxial fatigue models classification due to the approach for the non-proportionality of loading.

1 Introduction

To determine multiaxial fatigue life and strength in the case of service loadings, the influence of non-proportional loadings should often be considered. In cases of these kinds of loadings, the rotation of stress or strain principal axes takes place. For many materials non-proportional loading results in additional cyclic hardening and a significant decrease of fatigue life (even a 10-fold [1, 2]) and fatigue limit (even 25 % [3, 4]). Materials of low value for stacking fault energy are particularly sensitive to non-proportional loadings [5]. There are a lot of proposals for multiaxial fatigue criteria. The proper evaluation of the criteria is hampered by the lack of their classification due to the way of taking into account the non-proportionality of loading. Below, such a classification of multiaxial models is presented. Two features have been chosen for the classification of the criteria: introduction of loading non-proportionality function $f_\mathrm{np}$ and the material sensitivity for non-proportional loading $\lambda _\mathrm{np}.$ Four classes have been distinguished:

• NP1 class models which do not take into account the influence of non-proportionality on fatigue life or strength. An example of a criterion which lacks $f_\mathrm{np}$ and $\lambda _\mathrm{np}$ can be the Sines criterion [6]:

  $$\begin{aligned} \sqrt{J_{2\mathrm{a}}}+p\sigma _{\mathrm{H},\mathrm{mean}}=q, \end{aligned}$$

  (1)

  where $\sqrt{J_{2\mathrm{a}}}$ is the amplitude of the square root of the second invariant of the stress deviator, $\sigma _{\mathrm{H},\mathrm{mean}}$ is the mean hydrostatic stress, $p,\,q$ are materials parameters. Other solutions of this type include namely the Machas criteria [7, 8].

• NP2 class models which take into account the influence of non-proportionality, but do not calculate the degree of non-proportionality. Thus, the degree of non-proportionality is only passively included in these models. Among these models one can distinguish those in which the degree of non-proportionality is calculated by other, associated models, e.g., by cyclic plasticity models. The influence of non-proportionality in this case can be taken into consideration through the relationship between strains and stresses. Owing to the above, quantities $f_\mathrm{np}$ and $\lambda _\mathrm{np}$ do not occur in a fatigue model. An example of this model is, e.g., the solution proposed by Fatemi and Socie [9]:

  $$\begin{aligned} \frac{\Delta \gamma }{2}\left( {1+k\frac{\sigma _{\max }}{\sigma _\mathrm{y}}}\right) =f(N_{f}), \end{aligned}$$

  (2)

  where $\Delta \gamma$ is a range of the shear strain, $\sigma _{\max }$ is maximum normal stress, $\sigma _\mathrm{y}$ is yield stress and k is a material’s parameter. This group includes all strain–stress models, namely: Chen et al.’s [10], or Lagoda and Machas models [11].

• NP3 class models that allow the calculating of the degree of the non-proportionality of load, thus the degree of non-proportionality $\lambda _\mathrm{np}$ is actively integrated within the criterion. A simple example of this solution type is Lees criterion [11] for out-of-phase sinusoidal loading:

  $$\begin{aligned} \left( \frac{\tau _\mathrm{a}}{\tau _{-1}}\right) ^{2f_\mathrm{np}} +\left( \frac{\sigma _\mathrm{a}}{b_{-1}}\right) ^{2f_\mathrm{np}}=1, \end{aligned}$$

  (3)

  where $\tau _\mathrm{a}$ is the nominal amplitude of shear stress, $\sigma _\mathrm{a}$ is the nominal amplitude of normal stress, $\tau _{-1}$ is the fatigue limit in torsion, $b_{-1}$ is the fatigue limit in bending, $f_\mathrm{np}=1+q\sin {\delta },$ q is the materials parameter and $\delta$ is the phase shift angle. Other models that can be classified as being in this group are the criteria of Sonsino [12], Papadopoulos [13], and de Freitas and coworkers [14].

• NP4 class models which include a function defining the non-proportionality degree $\lambda _\mathrm{np}$ and sensitivity to the loadings non-proportionality parameter. Such a criterion is the criterion of Lee and Chiang [15]. This is the generalised Findleys experimental criterion for non-proportional loadings:

  $$\begin{aligned} \left( \frac{\tau _\mathrm{a}}{\tau _{-1}}\right) ^{2f_\mathrm{np}} +\left( \frac{\sigma _\mathrm{a}}{b_{-1}}\right) ^{\frac{1}{2}\lambda _\mathrm{np}f_\mathrm{np}}=1, \end{aligned}$$

  (4)

  where $\lambda _\mathrm{np}=1+q\sin (\delta )$ and $\lambda _\mathrm{np}=b_{-1}/\tau _{-1}.$ Remaining designations are identical to those as in Lees criterion (3). Another, well known example is a solution proposed by Itoh et al. [16, 17]:

  $$\begin{aligned} \Delta \varepsilon _\mathrm{NP}=\left( 1+\lambda _\mathrm{np}f_\mathrm{np}\right) \Delta \varepsilon _1, \end{aligned}$$

  (5)

  where $f_\mathrm{np}=\frac{\uppi }{2\varepsilon _{1\max }}\int \nolimits _{t}^{}\varepsilon _1(t)|\sin \beta |\mathrm{d}t,\,\varepsilon _1(t)$ is the maximum absolute value of principal strain at time t, $\varepsilon _{1\max }$ is the maximum value of $\varepsilon _1(t),\, \beta$ is the angle between vectors $\varvec{\varepsilon }_1(t)$ and $\varvec{\varepsilon }_{1\max },\,\lambda _\mathrm{np}=0.8\alpha +0.1$ for face centered cubic materials or $2(0.8\alpha +0.1)$ for body centered cubic and $\alpha$ is a materials parameter for evaluating the degree of additional hardening. This group also includes the models of Skibicki and Sempruch [18], Skibicki [19] and Lee et al.’s [20].

2 Criterion proposal

2.1 Assumptions

The proposed criterion is stress-based, hence, it is applicable to a high-cycle fatigue range, which is assumed to be the fatigue life range for which elastic strains dominate over plastic strains. The criterion is formulated for periodical loadings with no superimposed static mean value. Since it is considered that the presence of superimposed tensile static stress always reduces compressive static stress increases so the overall material fatigue strength and non-zero mean torsional stress can be neglected [21, 22], the influence of mean normal stress can be taken into account with equivalent normal stress given by the presented model using the Goodmans, Gerbers, Soderbergs, etc., relationships similarly as in other works [23–25]. The considered biaxial state of stress is given by:

$$\begin{aligned} \begin{aligned}&\sigma _{11}(t)=\sigma _{11,\mathrm{a}}\sin \left( \omega _1t\right) ,\\&\sigma _{12}(t)=\sigma _{12,\mathrm{a}}\sin \left( \omega _2t-\delta \right) , \end{aligned} \end{aligned}$$

(6)

where $\sigma _{11}$ and $\sigma _{12}$ are normal and shear components of a stress tensor. In such a state of stress, the following parameters decide on the non-proportionality of loading: amplitudes ratio $\lambda _\mathrm{a}=\sigma _{12,\mathrm{a}}/\sigma _{11,\mathrm{a}},$ frequency of components ratio $\omega _2/\omega _1$ and the phase shift angle $\delta .$ This is due to the formula for the position of principal stress axes:

$$\begin{aligned} \begin{aligned} \tan (2\varphi (t))&=2\frac{\sigma _{12}(t)}{\sigma _{11}(t)} =2\frac{\sigma _{12,\mathrm{a}} \sin (\omega _2t-\delta )}{\sigma _{11,\mathrm{a}}\sin (\omega _2t)}\\&=2\lambda _\mathrm{a}\frac{\sin (\omega _2t-\delta )}{\sin (\omega _2t)}, \end{aligned} \end{aligned}$$

(7)

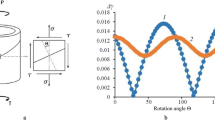
where $\varphi$ is an angle between the principal axes and the axes of the coordinates system. Proportional loading, that is $\tan (2\varphi (t))= \mathrm{const},$ takes place when $\omega _2/\omega _1=1$ and $\delta =0.$ For each of these cases of loading, correctly calculated proportional equivalent stress $\sigma _{\mathrm{eq},\mathrm{P}},$ for a particular fatigue life, should have the same value. For uniaxial loadings [ex. tension–compression (TC), torsion T,  Fig. 1a] and various complex loadings, equivalent stress produces approximately the same S–N curve (Fig. 1b).

Fig. 1

a S–N curves for uniaxial loadings in a nominal stresses coordinates system, and b S–N curves for uniaxial loadings in a proportional equivalent stress coordinates system. TC tension–compression, T torsion

The crucial role is played by the $\lambda _\mathrm{m}$ parameter, which includes the contribution of shear–normal stress ratio in the equivalent stress value. Because of the method of determining the value $\lambda _\mathrm{m}$ parameter, three groups of solutions can be specified:

• (1) group $\lambda _{\mathrm{m}1}$ class, where $\lambda _\mathrm{m}= \mathrm{const}.$ In these models, the same value of $\lambda _\mathrm{m}$ is assumed for different materials. The Garuds energetic criterion can be the example [6],

• (2) group $\lambda _{\mathrm{m}2}$ class, where $\lambda _\mathrm{m} \ne \mathrm{const}.\,\lambda _\mathrm{m}$ is dissimilar for different materials and constitutes a function of uniaxial properties (fatigue limits, Fig. 1a) of the material. Examples include Crossland [26], Zenner and Simburger [27] or Papadopoulos [13] criteria,

• (3) group $\lambda _{\mathrm{m}3},$ where $\lambda _\mathrm{m} \ne \mathrm{const}.= f(N_\mathrm{f}).$ For every material, $\lambda _\mathrm{m}$ is a different function of the number of cycles to failure. An example is the criterion of Kurek and Lagoda [28]. Thanks to such, it is possible to take into account the cases when S–N curves of component loadings are non-parallel.

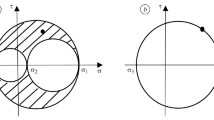
A non-proportional loading takes place when $\omega _2/\omega _1 \ne 1$ or/and $\delta \ne 0.$ In this case determining the S–N curves on the basis of a proportional criterion $\sigma _{\mathrm{eq},\mathrm{P}},$ results in errors in estimation of fatigue life (for example in underestimation Fig. 2a). Applying the non-proportional criterion $\sigma _{\mathrm{eq},\mathrm{NP}}$ produces approximately the same S–N curves for loadings of different non-proportionality levels (Fig. 2b). In the authors opinion it can be achieved by introducing the non-proportionality function $f_\mathrm{np}$ into the criterion and the materials parameter expressing its sensitivity to non-proportional loadings $\lambda _\mathrm{np}.$ To summarise, it can be stated that an effective calculation method of multiaxial fatigue should include at least two material parameters $\lambda _\mathrm{m},\,\lambda _\mathrm{np}$ and a function characterising non-proportional loading $f_\mathrm{np}.$

Fig. 2

a S–N curves for multiaxial loadings in a proportional equivalent stress coordinates system, and b S–N curves for multiaxial loadings in a non-proportional equivalent stress coordinates system. P proportional, NP1, NP2 non-proportional loadings cases with increasing non-proportionality degree

2.2 Generalization of the criterion for non-proportional loadings

For proportional loading the general form of the criterion can be written as follows:

$$\begin{aligned} \sqrt{\left( \lambda _\mathrm{m}\sigma _{11,\mathrm{a}}\right) ^2+{\sigma _{12,\mathrm{a}}}^2}\leqslant c, \end{aligned}$$

(8)

where the right side of the inequality c can be the limit quantity, depending on the application: S–N curve for $\sigma _\mathrm{TC}(N_\mathrm{f})$ or fatigue limit for fully reversed $\sigma _{-1}.$ Obviously, for $\lambda _\mathrm{m}=1/\sqrt{3}$ the right side of the Eq. (8) gives the Huber–von Mises criterion for biaxial state of stress. Let us introduce the following designation $f_\mathrm{p}=\sqrt{(\lambda _\mathrm{m}\sigma _{11,\mathrm{a}})^2+{\sigma _{12,\mathrm{a}}}^2}$ into the Eq. (8). Then we get:

$$\begin{aligned} \sigma _{\mathrm{eq},\mathrm{NP}}=\frac{1}{\lambda _\mathrm{m}}\sqrt{{f_\mathrm{p}}^2}\leqslant c. \end{aligned}$$

(9)

For non-proportional loading, a following development of (9) is proposed:

$$\begin{aligned} \sigma _{\mathrm{eq},\mathrm{NP}}=\frac{1}{\lambda _\mathrm{m}}\sqrt{{f_\mathrm{p}}^2+\lambda _\mathrm{np}{f_\mathrm{np}}^2}\leqslant c, \end{aligned}$$

(10)

where $f_\mathrm{p}=\max \sqrt{\sigma _{12}(t)^2+(\lambda _\mathrm{m}\sigma _{11}(t))^2},\,f_\mathrm{np}$ is a function of loadings non-proportionality, $\lambda _\mathrm{np}$ is a parameter expressing materials sensitivity to non-proportional loading. We require that for non-proportional loading $f_\mathrm{np}=0.$

2.3 A proposal of $\varvec{f_\mathrm{np}}$ function

The $f_\mathrm{p}$ function for Huber–von Mises criterion has a clear physical interpretation, which is the second invariant of the stress deviator:

$$\begin{aligned} f_\mathrm{p}=\sqrt{\left( \frac{1}{\sqrt{3}}\sigma _{11,\mathrm{a}}\right) ^2 +{\sigma _{12,\mathrm{a}}}^2}=\sqrt{J_{2}}_\mathrm{a}. \end{aligned}$$

(11)

In the proposed method (8), it has been assumed that $\lambda _\mathrm{m}$ doesn’t have to be equal to $1/\sqrt{3},$ so to distinguish them, the designation with prime has been introduced:

$$\begin{aligned} f_\mathrm{p}=\sqrt{\left( \lambda _\mathrm{m}\sigma _{11,\mathrm{a}}\right) ^2+{\sigma _{12,\mathrm{a}}}^2}={\sqrt{J^{\prime }_{2\mathrm{a}}}}, \end{aligned}$$

(12)

and for non-proportional loadings respectively:

$$\begin{aligned} f_\mathrm{p}=\max \sqrt{\left( \lambda _\mathrm{m}\sigma _{11}(t)\right) ^2+{\sigma _{12}(t)}^2}={\sqrt{J_{2\max }^{\prime }}}. \end{aligned}$$

(13)

The proposal of $f_{\max p}$ function present in Eq. (10) is based on the analysis of ${\sqrt{J_{2}^{\prime }}}\;$ evolution during the fatigue loading’s cycle. In the Fig. 3 values of ${\sqrt{J_{2\max }^{\prime }}}$, and ${\sqrt{J_{2\mathrm{mean}}^{\prime }}}$ and loading paths during different multiaxial fatigue loading cycles are shown. Quantities on the axes denoted as $s_{1}^{\prime }$ and $s_3$ are components of the stress deviator after the transformation described in Ref. [29]. As previously, the prime designation has been introduced to distinguish from the original stress deviators component $s_1=1/\sqrt{3}\sigma _{11}.$ Figures have been drawn for three cases of loading: proportional (Fig. 3a, b), non-proportional of some non-proportionality degree (Fig. 3c, d) and the most damaging, for which the loading path is a circle (Fig. 3e, f). Such a state is achieved for phase shift angle $\delta =90^{\circ }$, frequency ratio $\omega _2/\omega _1=1$ and amplitudes ratio $\lambda _\mathrm{a}=\sigma _{12,\mathrm{a}}/\sigma _{11,\mathrm{a}}=\lambda _\mathrm{m}$ [30]. It has been assumed that such a state is the state of the highest degree of non-proportionality or the most non-proportional loading state. Components of loadings have been selected in order to provide the same value of ${\sqrt{J_{2\max }^{\prime }}}$ in each case. Therefore, the ${\sqrt{J_{2}}^{\prime }}$ paths for proportional (Fig. 3b) and non-proportional (Fig. 3d) loading are inscribed into the path for the most non-proportional loading (Fig. 3f). From the time courses of ${\sqrt{J_{2}^{\prime }}},$ the maximum ${\sqrt{J_{2\max }^{\prime }}}$ and mean ${\sqrt{J_{2\mathrm{mean}}^{\prime }}}=\frac{1}{T}\int \nolimits _0^T\sqrt{J_{2}^{\prime }}(t)\mathrm{d}t$ values have been calculated. Let us note that for proportional loading of sine waveform shape, there is a relationship:

$$\begin{aligned} {\sqrt{J_{2\mathrm{mean}}^{\prime }}}=\frac{2}{\uppi }{\sqrt{J_{2\max }^{\prime }}}, \end{aligned}$$

(14)

and the loading path is a straight line (Fig. 3b). For any non-proportional loading (Fig. 3c), we have:

$$\begin{aligned} \frac{2}{\uppi }{\sqrt{J_{2\max }^{\prime }}} <{\sqrt{J_{2\mathrm{mean}}^{\prime }}}<{\sqrt{J_{2\max }^{\prime }}}. \end{aligned}$$

(15)

For the most non-proportional loading, the following relationship is satisfied (Fig. 3e, f):

$$\begin{aligned} {\sqrt{J_{2\mathrm{mean}}^{\prime }}}={\sqrt{J_{2\max }^{\prime }}}. \end{aligned}$$

(16)

With an increase of non-proportionality of load, the value of ${\sqrt{J_{2\mathrm{mean}}^{\prime }}}$ rises, that is, the ratio ${\sqrt{J_{2\mathrm{mean}}^{\prime }}}$ to ${\sqrt{J_{2\max }^{\prime }}}.$ On this basis the following form of non-proportionality function has been proposed:

$$\begin{aligned} f_\mathrm{np}={\sqrt{J_{2\mathrm{mean}}^{\prime }}} -\frac{2}{\uppi }{\sqrt{J_{2\max }^{\prime }}}. \end{aligned}$$

(17)

Fig. 3

a Evolution of stresses during the proportional loadings cycle. b ${\sqrt{J_{2}^{\prime }}}$ path for ${\omega _2/\omega _1=1},\,\delta =0^\circ ,\,\lambda _\mathrm{a}=0.4,\, \lambda _\mathrm{m}=0.6.$ c Evolution of stresses during the non-proportional loadings cycle. d ${\sqrt{J_{2}^{\prime }}}$ path for ${\omega _2/\omega _1=2},\,\delta =60^\circ ,\,\lambda _\mathrm{a}=0.4,\, \lambda _\mathrm{m}=0.6.$ e Evolution of stresses during the non-proportional loadings cycle. f ${\sqrt{J_{2}^{\prime }}}$ path for ${\omega _2/\omega _1=1},\,\delta =90^\circ ,\,\lambda _\mathrm{a}=0.6,\,\lambda _\mathrm{m}=0.6,$ on the background of previous paths

As it is apparent from Eq. (14), for sine-shaped proportional loading, the value ${\sqrt{J_{2\mathrm{mean}}^{\prime }}}$ is equal to ${\sqrt{J_{2\max }^{\prime }}}.$ Consequently, $f_\mathrm{np}$ equals zero when proportional case of loading is being analyzed. Whereas for most non-proportional loading, when ${\sqrt{J_{2\mathrm{mean}}^{\prime }}}={\sqrt{J_{2\max }^{\prime }}},\,f_\mathrm{np}$ reaches value of ${\sqrt{J_{2\max }^{\prime }}}\left( 1-\frac{2}{\uppi }\right) .$ By introducing these quantities to Eq. (10) we ultimately have:

$$\begin{aligned} \begin{aligned} \sigma _{\mathrm{eq},\mathrm{NP}}&\leqslant c\\&=\frac{1}{\lambda _\mathrm{m}}\sqrt{\left( {\sqrt{J_{2\max }^{\prime }}}\right) ^2 +\lambda _\mathrm{np}\left( {\sqrt{J_{2\mathrm{mean}}^{\prime }} -\frac{2}{\uppi }{\sqrt{J_{2\max }^{\prime }}}}\right) ^2}. \end{aligned} \end{aligned}$$

(18)

2.4 A proposal of $\varvec{\lambda _\mathrm{np}}$ parameter

For a given fatigue life the equivalent stress $\sigma _{\mathrm{eq},\mathrm{NP}}$ should take the same value for proportional and non-proportional loading:

$$\begin{aligned} {\sigma _{\mathrm{eq},\mathrm{NP}}}^{(\mathrm{P})}={\sigma _{\mathrm{eq},\mathrm{NP}}}^{(\mathrm{NP})}. \end{aligned}$$

(19)

After introducing the components of proportional loading to formula $\sigma _{\mathrm{eq},\mathrm{NP}}$ (10), the expression simplifies to $\frac{1}{\lambda _\mathrm{m}}{f_\mathrm{p}}^{(\mathrm{P})},$ because $f_\mathrm{np}=0.$ Then we have:

$$\begin{aligned} \frac{1}{\lambda _\mathrm{m}}{f_\mathrm{p}}^{(\mathrm{P})}=\frac{1}{\lambda _\mathrm{m}}\sqrt{{{f_\mathrm{p}}^{(\mathrm{NP})}}^2+\lambda _\mathrm{np}{{f_\mathrm{np}}^{(\mathrm NP)}}^2}. \end{aligned}$$

(20)

Through conversion, we achieve:

$$\begin{aligned} \lambda _\mathrm{np}=\frac{{{f_\mathrm{p}}^{(\mathrm{P})}}^2-{{f_\mathrm{p}}^{(\mathrm{NP})}}^2}{{{f_\mathrm{p}}^{(\mathrm{NP})}}^2}, \end{aligned}$$

(21)

or after taking into account of Eqs. (13) and (17) $f_\mathrm{np}={\sqrt{J_{2\mathrm{mean}}^{\prime }}} -\frac{2}{\uppi }{\sqrt{J_{2\max }^{\prime }}}{:}$

$$\begin{aligned} \lambda _\mathrm{np}=\frac{{{{\sqrt{J_{2\max }^{\prime }}}}^{(\mathrm{P})}}^2 -{{{\sqrt{J_{2\max }^{\prime }}}}^{(\mathrm{NP})}}^2}{{{\left( {\sqrt{J_{2\mathrm{mean}}^{\prime }}} -\frac{2}{\uppi }{\sqrt{J_{2\max }^{\prime }}}\right) }^{(\mathrm{NP})}}^2}. \end{aligned}$$

(22)

In most non-proportional loadings cases, there is the following relationship:

$$\begin{aligned} \sqrt{J_{2\mathrm{mean}}^{\prime }}=\frac{2}{\uppi }\sqrt{J_{2\max }^{\prime }}. \end{aligned}$$

(23)

Formula (22) can be written as:

$$\begin{aligned} \begin{aligned} \lambda _\mathrm{np}&=\frac{{{{\sqrt{J_{2\max }^{\prime }}}}^{(\mathrm{P})}}^2 -{{{\sqrt{J_{2\max }^{\prime }}}}^{(\mathrm{NP})}}^2}{{{\left( {\sqrt{J_{2\mathrm{mean}}^{\prime }}} -\frac{2}{\uppi }{\sqrt{J_{2\max }^{\prime }}}\right) }^{(\mathrm{NP})}}^2}\\&=\frac{{{{\sqrt{J_{2\max }^{\prime }}}}^{(\mathrm{P})}}^2 -{{{\sqrt{J_{2\max }^{\prime }}}}^{(\mathrm{NP})}}^2}{{{{\sqrt{J_{2\max }^{\prime }}}}^{(\mathrm{NP})}}^2}\cdot \frac{1}{{\left( 1-\frac{2}{\uppi }\right) }^2}\\&=\left[ {\left( \frac{{{\sqrt{J_{2\max }^{\prime }}}}^{(\mathrm{P})}}{{{\sqrt{J_{2\max }^{\prime }}}}^{(\mathrm{NP})}}\right) }^2-1\right] \cdot {\left( 1-\frac{2}{\uppi }\right) }^{-2}. \end{aligned} \end{aligned}$$

(24)

By multiplying the numerator and denominator of Eq. (18) by $1/\lambda _\mathrm{m}$ and taking into account of Eq. (23), the formula (26) can be also written in the following way:

$$\begin{aligned} \lambda _\mathrm{np}=\left[ {\left( \frac{{{\sigma _{\mathrm{eq},\mathrm{P}}}}^{(\mathrm{P})}}{{{\sigma _{\mathrm{eq},\mathrm{P}}}}^{(\mathrm{NP})}}\right) }^2-1\right] {\left( 1-\frac{2}{\uppi }\right) }^{-2}. \end{aligned}$$

(25)

3 Determination of materials parameters $\varvec{\lambda _\mathrm{m}}$ and $\varvec{\lambda _\mathrm{np}}$

3.1 A method of determining the value of $\varvec{\lambda _\mathrm{m}}$ parameter

The proposed procedure of determination of $\lambda _\mathrm{m}$ parameter can be presented in three steps:

• (1) Determination of S–N curves using the Basquins equation in the following form:

  $$\begin{aligned} \begin{aligned}&\sigma _\mathrm{a}=A_\mathrm{TC}{N_\mathrm{f}}^{b_\mathrm{TC}},\\&\tau _\mathrm{a}=A_\mathrm{T}{N_\mathrm{f}}^{b_\mathrm{T}}. \end{aligned} \end{aligned}$$

  (26)

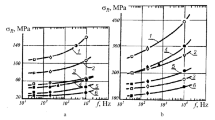
• (2) Determination of fatigue life range $\Delta N_{\mathrm{f}_\lambda }=[N_{\mathrm{f}_\lambda \min },\,N_{\mathrm{f}_\lambda \max }],$ which includes experimental data for both uniaxial tests (Fig. 4), where:

  $$\begin{aligned} N_{\mathrm{f}_\lambda \min }= & {} \max \left( N_{\mathrm{f}_{\mathrm{TC} \min }},\,N_{\mathrm{f}_{\mathrm{T} \min }}\right) , \end{aligned}$$

  (27)
  $$\begin{aligned} N_{\mathrm{f}_\lambda \max }= & {} \min \left( N_{\mathrm{f}_{\mathrm{TC} \max }},\,N_{\mathrm{f}_{\mathrm{T} \max }}\right) , \end{aligned}$$

  (28)

  where $N_{\mathrm{f}_{\mathrm{TC} \min }},\,N_{\mathrm{f}_{\mathrm{TC} \max }},\,N_{\mathrm{f}_{\mathrm{T} \min }}$, and $N_{\mathrm{f}_{\mathrm{T} \max }}$ denotes the beginning and the end of the fatigue life range in which S–N curves are designated appropriately for TC and torsion.

• (3) Determination of $\lambda _\mathrm{m}{:}$

  $$\begin{aligned} \lambda _\mathrm{m}=\frac{1}{2}\left( \frac{A_\mathrm{T}{N_{\mathrm{f}\lambda \min }}^{b_\mathrm{T}}}{A_\mathrm{TC}{N_{\mathrm{f}\lambda \min }}^{b_\mathrm{TC}}}+\frac{A_\mathrm{T}{N_{\mathrm{f}\lambda \max }}^{b_\mathrm{T}}}{A_\mathrm{TC}{N_{\mathrm{f}\lambda \max }}^{b_\mathrm{TC}}}\right) . \end{aligned}$$

  (29)

In the special case, when we assume parallelism of the S–N curves for TC and torsion $(b_\mathrm{T}=b_\mathrm{TC}),$ the Eq. (30) comes down to the $A_\mathrm{T}/A_\mathrm{TC}$ quotient. If we only know the values of fatigue limits for fully reversed TC $\sigma _{-1}$ and the fully reversed torsion $\tau _{-1},$ the $\lambda _\mathrm{m}$ parameter can be optionally determined as $\lambda _\mathrm{m}=\tau _{-1}/\sigma _{-1}$ (Fig. 1a).

Fig. 4

Illustration of $\Delta N_{\mathrm{f}\lambda }$ life range

3.2 A method of determining the value of $\varvec{\lambda _\mathrm{m}}$ parameter

Formally, according to the formula (27) to determine the $\lambda _\mathrm{np}$ parameter, there is a need to know the values of two equivalent stresses calculated using the formula for proportional stress $\sigma _{\mathrm{eq},\mathrm{P}}$ in Eq. (8). These stresses have to be calculated for the same fatigue life for two loading cases (Fig. 5):

• (1) TC (or optionally other proportional loading) ${\sigma _{\mathrm{eq},\mathrm{P}}}^{(\mathrm{P})},$

• (2) the most non-proportional loading ${\sigma _{\mathrm{eq},\mathrm{P}}}^{(\mathrm{NP})}.$

Fig. 5

Proportional equivalent stresses calculated for proportional ${\sigma _{\mathrm{eq},\mathrm{P}}}^{(\mathrm{P})}$ and non-proportional ${\sigma _{\mathrm{eq},\mathrm{P}}}^{(\mathrm{NP})}$ loadings, for the same fatigue life

It turns out however, that to determine the $\lambda _\mathrm{np}$ parameter, it is enough to know the S–N curve for non-proportional loading of any degree of non-proportionality. This is due to observed linear relationship between proportional $f_\mathrm{p}$ and the non-proportional $f_\mathrm{np}$ part of the proposed criterion. This relationship can be illustrated in the n–p diagram, on which ordinates are a function of the proportional part $p=f(f_\mathrm{p})$ and the abscissas are a function of the non-proportional part $n=f(f_\mathrm{np})$ (Fig. 6).

Fig. 6

Linear relationship between the proportional and non-proportional part of the criterion. p: proportional coordinate, n: non proportional coordinate

We assume that the non-proportional coordinate n is equal to: $\sqrt{J_{2\mathrm{mean}}^{\prime }}-\sqrt{J_{2\max }^{\prime }}.$ For the proportional its equal to 0, because $\sqrt{J_{2\mathrm{mean}}^{\prime }}=\sqrt{J_{2\max }^{\prime }}$ (Fig. 3a). We also require that for the most non-proportional loading the proportional coordinate p will be equal to 0. Therefore, for the most non-proportional loading, there is a relationship $\sqrt{J_{2\mathrm{mean}}^{\prime }}=\sqrt{J_{2\max }^{\prime }}$ (Fig. 3e), we assume that $p=\sqrt{J_{2\max }^{\prime }}-\sqrt{J_{2\mathrm{mean}}^{\prime }}.$ Points O (Fig. 6), that lay on the line, represent loading cases for which $N_{n(n,p)} = \mathrm{const}.$ The linear characteristic intersects the axes of coordinates system in two points: the first one representing a proportional state $P(0,\,p_\mathrm{g})$ and the second one representing the most non-proportional state $N(n_\mathrm{g},\,0).$ Values of $p_\mathrm{g}$ and $n_\mathrm{g}$ coordinates are:

$$\begin{aligned} p_\mathrm{g}= & {} {\sqrt{J_{2\max }^{\prime }}}^{(\mathrm{P})}\left( 1-\frac{2}{\uppi }\right) , \end{aligned}$$

(30)

$$\begin{aligned} n_\mathrm{g}= & {} {\sqrt{J_{2\max }^{\prime }}}^{(\mathrm{NP})}\left( 1-\frac{2}{\uppi }\right) . \end{aligned}$$

(31)

The assumption of linearity of n–p characteristic has been verified using the experimental data in Sect. 5.1. From the n–p diagram we have relation:

$$\begin{aligned}&\frac{p_\mathrm{g}}{n_\mathrm{g}}=\frac{p_\mathrm{g}-p_\mathrm{i}}{n_\mathrm{i}},\end{aligned}$$

(32)

$$\begin{aligned}&\frac{{\sqrt{J_{2\max }^{\prime }}}^{(\mathrm{P})}\left( 1-\frac{2}{\uppi }\right) }{{\sqrt{J_{2\max }^{\prime }}}^{(\mathrm{NP})}\left( 1-\frac{2}{\uppi }\right) }=\frac{p_\mathrm{g}-p_\mathrm{i}}{n_\mathrm{i}},\end{aligned}$$

(33)

$$\begin{aligned}&\frac{{\sqrt{J_{2\max }^{\prime }}}^{(\mathrm{P})}}{{\sqrt{J_{2\max }^{\prime }}}^{(\mathrm{NP})}}=\frac{p_\mathrm{g}-p_\mathrm{i}}{n_\mathrm{i}}. \end{aligned}$$

(34)

Knowing the $p_\mathrm{g}$ coordinate for TC (or any other proportional loading) and the coordinates for any non-proportional loading $(n_\mathrm{i},\,p_\mathrm{i})$ lets us determine the value of the quotient present in the formula (23) and thereby determine the value of $\lambda _\mathrm{np}.$

Fig. 7

n–p diagram for limited life in testing of a Cu-ETP copper [25], b X2CrNiMo17-12-2 steel [25], c 18G2A steel [27], d 30NCD16 steel [28] after Ref. [29], e 1045 steel [30], f 1045 steel [31], g 7075-T651 aluminum alloy [32], h C35 steel [33], i LY12CZ aluminum alloy [34], j SM45C steel [28] after Ref. [29] and for fatigue limits in testing of k XC18 steel [43, 44], l 34Cr4 steel [35] after Ref. [14], m 39NiCrMo3 steel [36], n 42CrMo4 steel [37] after Ref. [38], o C20 steel [39] after Refs. [26, 40], p EN-GJS800 cast iron [41, 42] after Refs. [26, 40], q FGS 800-2 cast iron [41, 43, 44], and r Nishiharas and Kawamotos hard steel [4] after Ref. [14]

Fig. 8

$N_\mathrm{fcal}$–$N_\mathrm{fexp}$ diagram for a Cu-ETP copper [25], b X2CrNiMo17-12-2 steel [25], c 30NCD16 steel [28] after Ref. [29], d 1045 steel [30], e 1045 steel [31], f 7075-T651 aluminum alloy [32], g C35 steel [33], h LY12CZ aluminum alloy [34], i SM45C steel [28] after Ref. [29], and j 18G2A steel [27]

4 Discussion

Considering the proposed methods of classification of the criteria, the presented criterion falls within the:

• (1) $\lambda _{\mathrm{m}2}$ group in view of $\lambda _\mathrm{m} \ne \mathrm{const},$

• (2) NP4 class in view of occurrence of $f_\mathrm{np}$ and $\lambda _\mathrm{np}$ in the criterions formula.

A similar form to the proposed criterion has been presented by Vu et al. [31]. As a function of non-proportionality of loading, $\sqrt{J_{2\mathrm{mean}}}$ has been introduced. In this criterion three materials parameters are present, which, as authors admit themselves, are difficult to determine due to the complicated form of the criterion. The authors suggest constant values of two of these parameters, and only for specific groups of materials, that is two classes of steels: low-strength steels and high-strength steels. This is a limitation of applicability of the criterion. It seems that the proposed criterion has the following advantages with respect to the Vu et al. criterion:

• (1) $\lambda _\mathrm{m}$ has a clear definition, which allows for easy determination of its value using two S–N curves for uniaxial loadings,

• (2) the form of the non-proportionality function $f_\mathrm{np}$ makes as it takes the value equal to zero for proportional loadings,

• (3) the $\lambda _\mathrm{np}$ parameter, which expresses the materials sensitivity to non-proportional loadings, has been introduced as well as the method of its determination using S–N curves for uniaxial and any non-proportional loading,

• (4) the proposed criterion allows for estimation of the fatigue life and not only the fatigue limit.

5 Verification

In order to verify the assumption of the linearity of the n–p characteristic and the quality of fatigue life and fatigue limit estimation using the proposed criterion, experimental data taken from the literature have been used. The data includes loading cases with different values of amplitude ratio $\lambda _\mathrm{a},$ different values of loading frequencies ratio $\omega _2/\omega _1$ and different phase shift angles $\delta .$ The data have been divided into two groups: (1) fatigue life results for high-cycle fatigue and (2) fatigue limit values. Group 1 includes tests conducted on Cu-ETP copper [30], X2CrNiMo17-12-2 steel [30], 18G2A steel [32], 30NCD16 [33] after Ref. [34], 1045 steel [35], 1045 steel [36], 7075-T651 aluminum alloy [37], C35 steel Ref. [38], LY12CZ aluminum alloy [39], SM45C steel [33] after Ref. [34]. Group 2 includes tests performed on 34Cr4 steel [40] after Ref. [14], 39NiCrMo3 steel [41], 42CrMo4 steel [42] after Ref. [43], C20 steel [44] after [31, 45], EN-GJS800 cast iron [46, 47] after Refs. [31, 45], FGS 800-2 cast iron [46, 48, 49], Nishiharas and Kawamotos hard steel [4] after Ref. [14], and XC18 steel [48, 49].

5.1 Verification of assumption of linearity of $\varvec{n}$–$\varvec{p}$ characteristic

In the Fig. 7a–j, the results of verification of the assumption that the n–p characteristic is linear are shown for data from group 1. Two or three limiting lines corresponding to different fatigue lives have been drawn. A number of lines depend on the fatigue lives range in which S–N curves for all types of loadings are available. In the Fig. 7k–r results for group 2, that is for fatigue limits, are presented. In these diagrams, one line, corresponding to the base number of $N_0$ has been drawn.

5.2 Verification of fatigue life and fatigue limit estimation

The verification of the proposed criterion for group 1 is based on the comparison of calculated fatigue lives $N_\mathrm{fcal}$ with experimental $N_\mathrm{fexp}$ ones. Calculated fatigue lives have been obtained by converting Basquins equation to:

$$\begin{aligned} N_\mathrm{fcal}={\left( \frac{\sigma _{\mathrm{eq},\mathrm{NP}}}{A_\mathrm{TC}}\right) }^{\frac{1}{b_\mathrm{TC}}}, \end{aligned}$$

(35)

where $A_\mathrm{TC}$ and $b_\mathrm{TC}$ stand for a coefficient and exponent of the Basquins equation determined in a $\sigma _\mathrm{TC}$–$n_\mathrm{f}$ coordinates system, for TC. In the event of lack of data for any of the uniaxial loading, available proportional loading is selected. The results of fatigue life comparisons are presented in $N_\mathrm{fcal}$–$N_\mathrm{fexp}$ diagrams (Fig. 8). In the diagrams, the solid line corresponds to the scatter band of factor 2 and the dashed line to the scatter band of factor 3. The diagram legend describes testing conditions specifying in order $\lambda _\mathrm{a}-\delta -\omega _2/\omega _1$ after the graphic symbol.

For data included in group 2, the verification consisted of the comparison of obtained equivalent stress with the fatigue limit value for TC. The comparison was made using the error index I applied previously for the same purpose in [29]:

$$\begin{aligned} I=\frac{\sigma _{\mathrm{eq},\mathrm{NP}}-\sigma _{-1}}{\sigma _{-1}}(\%). \end{aligned}$$

(36)

Distribution of error index frequency for the data in group 2 is presented in Fig. 9. In the Fig. 10 a summary of error index for all fatigue limits data is shown.

Fig. 9

Distribution of error index frequency for a 39NiCrMo3 steel [36], b 42CrMo4 steel [37] after Ref. [38], c C20 steel [39] after Refs. [26, 40], d EN-GJS800 cast iron [41, 42] after Refs. [26, 40], e FGS 800-2 cast iron [41, 43, 44], f Nishiharas and Kawamotos hard steel [4] after Ref. [14], g XC18 steel [43, 44], and h 34Cr4 steel [35] after Ref. [14]

5.3 Discussion of the verification results

The limit lines of n–p diagrams take the form of straight lines. In the majority of cases, limit lines for different lives are parallel to each other. Their non-parallelism stems mostly from the non-parallelism of uniaxial S–N characteristics. In this case the points of the axis p for a given life do not overlap (Fig. 8g, j). The results of fatigue life estimation generally lie in the scatter band of factor 2 (Fig. 8e) or 3 (Fig. 8a, g, j). Often, estimation errors stem from considerable non-parallelism of S–N characteristics for uniaxial loadings (e.g., Fig. 8f), see torsion Inf–0–Inf and Fig. 8i, see torsion Inf–0–Inf) or non-parallelism of non-proportional characteristics with regard to proportional ones (e.g., Fig. 8h, see 0.57–45–1). It is worth stressing, that the formula proposed for $\lambda _\mathrm{m}$ (30) averaging the values of strength ratio in the whole fatigue life range $\Delta N_{\mathrm{f}\lambda }$ and this reduces the influence of non-parallelism uniaxial S–N curves for the fatigue life estimation results. The achieved results of fatigue life estimation have been compared with results analyzes carried out by other authors. The works that uses the same experimental data have been taken into account:

• (1) work [34] in which CST criterion and the author model have been tested for 30NCD16 steel [33] after Ref. [34], 7075-T651 aluminum alloy [37] and SM45C steel [33] after Ref. [34],

• (2) work [50] in which SWT and modified SWT models have been tested for 7075-T651 aluminum alloy [37],

• (3) work [51] in which the author model has been tested for LY12CZ aluminum alloy [39],

• (4) work [52] in which the author model has been tested for SM45C steel [33] after Ref. [34].

In all cases the results are comparable, that is they lie in the same scatter bands. The experimental results, which are hard to describe using the proposed criterion, are characterized by significant scatter also in other works (e.g., Fig. 8h and Ref. [39]). Fatigue limit estimation errors rarely exceed 10 % (Fig. 10). Fatigue limits are more often underestimated than overestimated. The achieved results have been compared with verification carried out by Papadopoulos in Ref. [29] for six criteria. The comparisons have been carried out for materials which coincide in both analyzes, namely: 34Cr4 steel [40] after Ref. [14], 42CrMo4 steel [42] after Ref. [43] and Nishiharas and Kawamotos hard steel [4] after Ref. [14]. Asummary of error index for these materials is presented on Fig. 11a. It can be stated, that for five criteria analyzed by Papadopoulos (Crossland, Sines, Matake, McDiarmid, Dietmann and Papadopoulos criteria), the obtained results have lower scatter and are comparable with the Papadopoulos criterion. A similar comparison have been carried out for the Vu et al. [31] results. In this case, Crossland, Dang Van, Papadopoulos, Papuga and authors criterions have been analyzed. In the Fig. 11b results for materials are the subject of a common analysis, namely: 34Cr4 steel [40] after Ref. [14], 42CrMo4 steel [42] after Ref. [43], C20 steel [44] after Refs. [31, 45], EN-GJS800 cast iron [46, 47] after Refs. [31, 45], and Nishiharas and Kawamotos hard steel [4] after Ref. [14], have been presented. Based on a comparison, it can be stated that the proposed criterion gives a result of lower scatter than Crossland, Dang Van, and Papadopoulos criterions and are comparable to results obtained with the Papugas and Vu et al. criteria.

Fig. 10

Summary of error index for fatigue limit data

6 Verification

The n–p characteristics used to determine the materials sensitivity to non-proportional loadings $\lambda _\mathrm{np}$ are linear for the high-cycle fatigue life range and for the fatigue limit equally well. In the majority of cases, limit lines for different fatigue lives are parallel to each other. Their non-parallelism stems mostly from non-parallelism of uniaxial S–N curves, which causes the points on the p axis for a given life to not overlap (Fig. 7 g, j).

The results of fatigue life estimation generally fit the scatter band of factor 2 (Fig. 8e) or 3 (Fig. 8a, g, j). Often, estimation errors stem from considerable non-parallelism of S–N characteristics of uniaxial loading, which is difficult to describe using the formula proposed for $\lambda _\mathrm{m}$ (e.g., Fig. 8f, i) or non-parallelism of non-proportional characteristics in regard to proportional ones (e.g., Fig. 8h).

Fatigue limit estimation errors rarely exceed 10 % (Fig. 11). Fatigue limits are more often underestimated than overestimated.

Fig. 11

a Summary of the error index for fatigue limit data for 34Cr4 steel [35] after Ref. [14], 42CrMo4 steel [37] after Ref. [38] and Nishiharas and Kawamotos hard steel [4] after Ref. [14], and b summary of the error index for fatigue limit data for 34Cr4 steel [35] after Ref. [14], 42CrMo4 steel [37] after Ref. [38], C20 steel [39] after Refs. [26, 40], EN-GJS800 cast iron [41, 42] after Refs. [26, 40], Nishiharas and Kawamotos hard steel [4] after Ref. [14]

Based on the obtained results, it has been concluded that the main problem that needs to be solved in the next version of the criterion is taking into account the non-parallelism of S–N curves for uniaxial loadings and for non-proportional compared to proportional loadings.